Role of Foreign Phases, Synergistic Effects, and Morphology in the HER Performance of Trimetallic Pentlandites with Non-Equimolar Co:Fe:Ni Ratio
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Theoretical Characterization
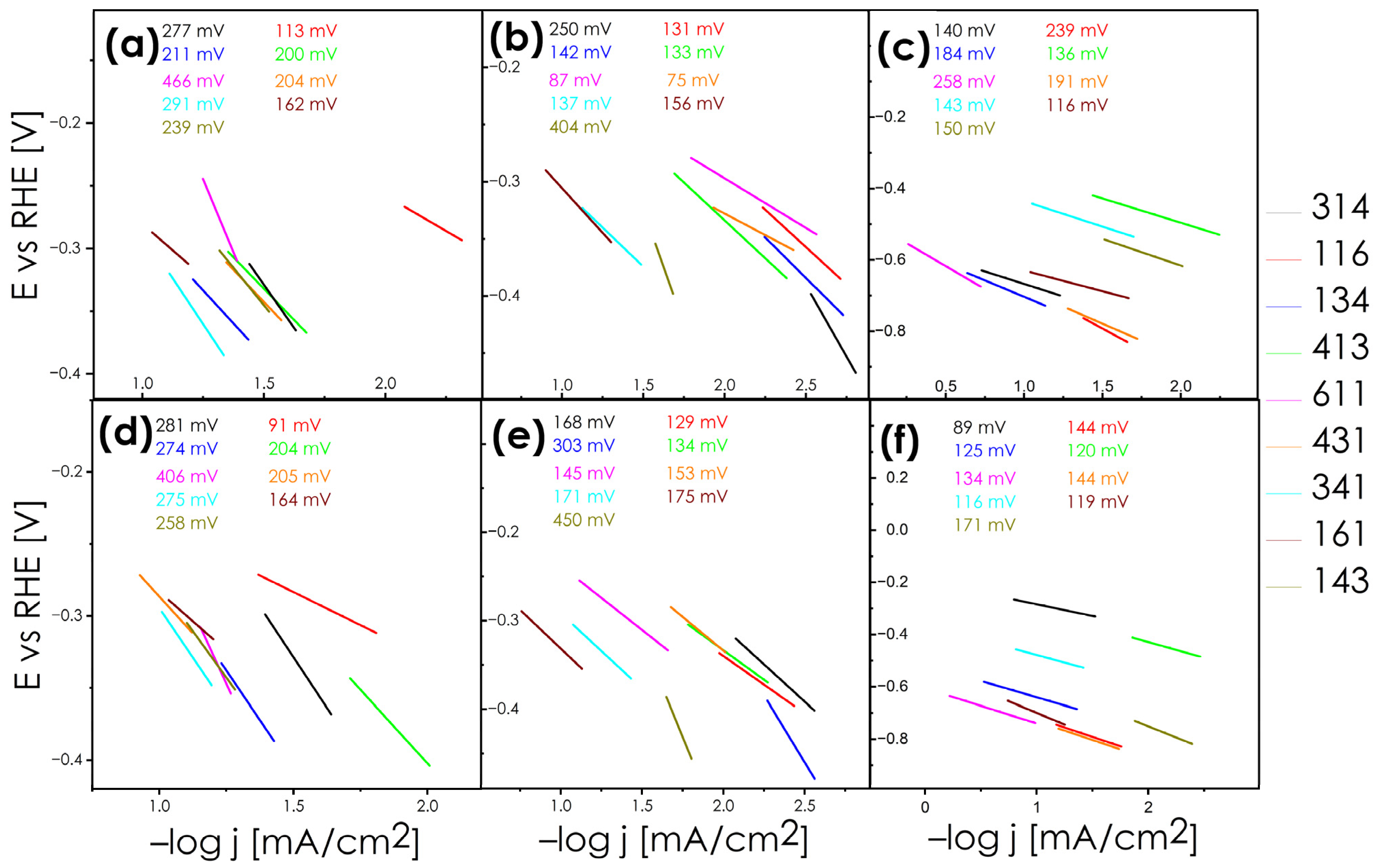
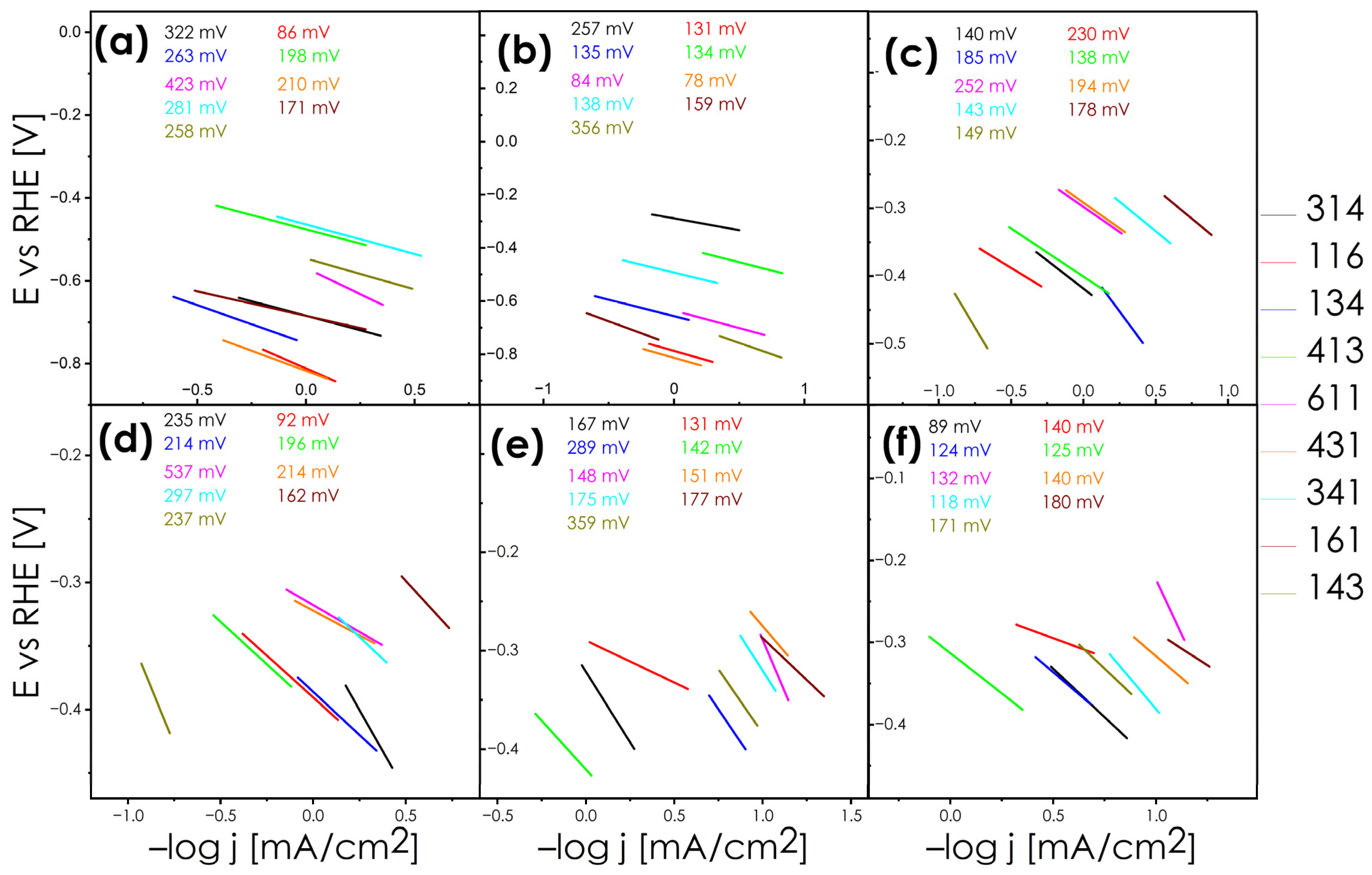
3.2. Catalytic Performance
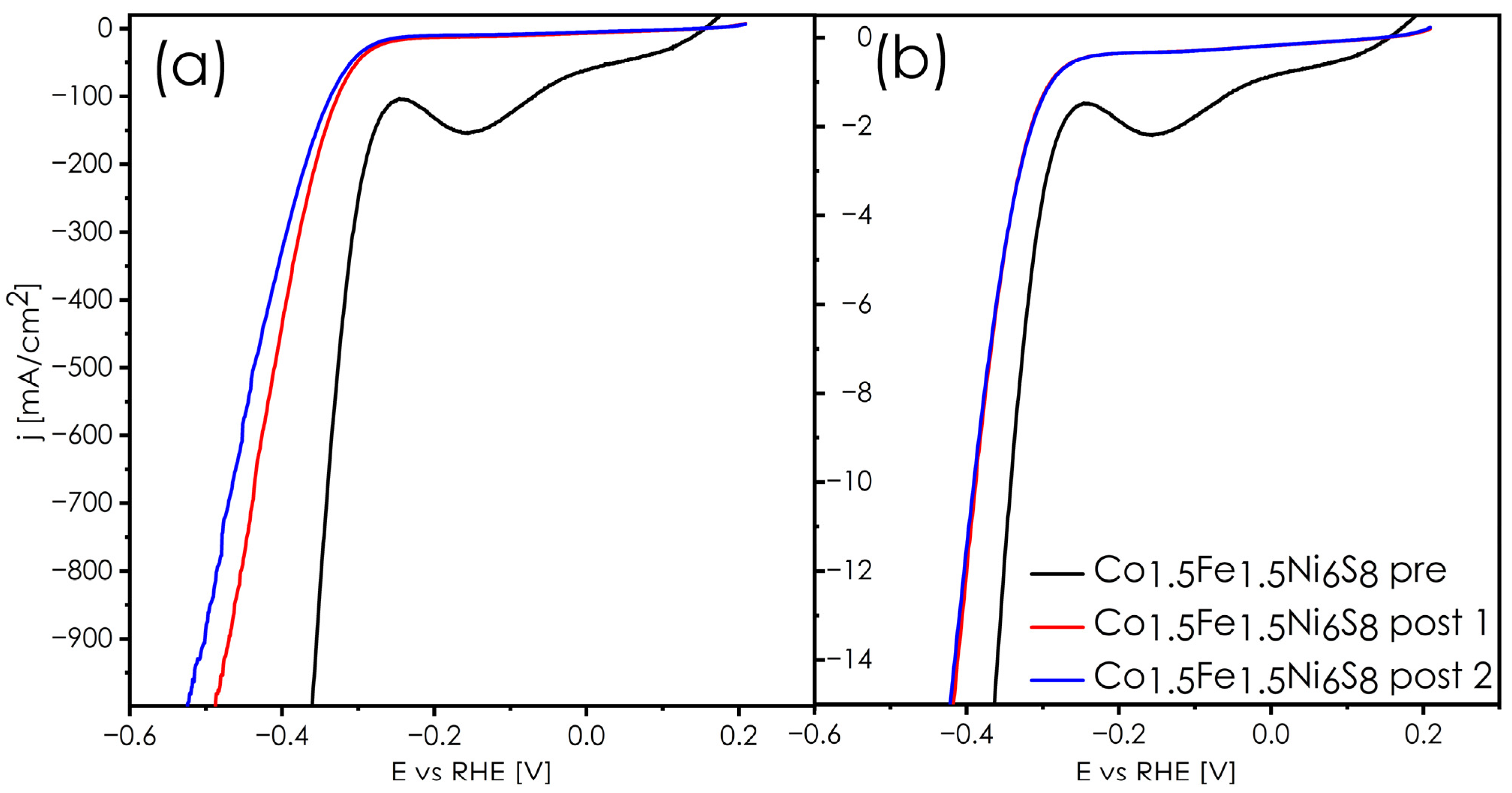
3.3. Co1.5Fe1.5Ni6S8 Phenomena
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Lu, A.; Zhong, C.J. Hydrogen production from water electrolysis: Role of catalysts. Nano Converg. 2021, 8, 4. [Google Scholar] [CrossRef]
- Carmo, M.; Fritz, D.L.; Mergel, J.; Stolten, D. A comprehensive review on PEM water electrolysis. Int. J. Hydrogen Energy 2013, 38, 4901–4934. [Google Scholar] [CrossRef]
- Molenda, J. Fundamentalne znaczenie badañ naukowych dla rozwoju gospodarki wodorowej. Polityka Energ. 2008, 11, 61–68. [Google Scholar]
- Smialkowski, M.; Siegmund, D.; Pellumbi, K.; Hensgen, L.; Antoni, H.; Muhler, M.; Apfel, U.-P. Seleno-analogues of pentlandites (Fe4.5Ni4.5S8-: YSey, y = 1-6): Tuning bulk Fe/Ni sulphoselenides for hydrogen evolution. Chem. Commun. 2019, 55, 8792–8795. [Google Scholar] [CrossRef]
- Zhao, G.; Rui, K.; Dou, S.X.; Sun, W. Heterostructures for Electrochemical Hydrogen Evolution Reaction: A Review. Adv. Funct. Mater. 2018, 28, 1803291. [Google Scholar] [CrossRef]
- Seunghwa, L.; Aliki, M.; You-Chiuan, C.; Chen, H.M.; Xile, H. Tracking high-valent surface iron species in the oxygen evolution reaction on cobalt iron (oxy)hydroxides. Energy Environ. Sci. 2022, 15, 206–214. [Google Scholar] [CrossRef]
- Pang, H.; Wei, C.; Li, X.; Li, G.; Ma, Y.; Li, S.; Chen, J.; Zhang, J. Microwave-assisted synthesis of NiS2 nanostructures for supercapacitors and cocatalytic enhancing photocatalytic H2 production. Sci. Rep. 2014, 4, 3577. [Google Scholar] [CrossRef]
- Akinaga, Y.; Kawawaki, T.; Kameko, H.; Yamazaki, Y.; Yamazaki, K.; Nakayasu, Y.; Kato, K.; Tanaka, Y.; Hanindriyo, A.T.; Takagi, M.; et al. Metal Single-Atom Cocatalyst on Carbon Nitride for the Photocatalytic Hydrogen Evolution Reaction: Effects of Metal Species. Adv. Funct. Mater. 2023, 33, 2303321. [Google Scholar] [CrossRef]
- Zhibo, C.; Wensheng, J.; Guanzhen, C.; Biao, Z.; Yunhu, H.; Wei, H. Design and Synthesis of Noble Metal-Based Alloy Electrocatalysts and Their Application in Hydrogen Evolution Reaction. Nano Mikro Small 2023, 19, e2301465. [Google Scholar] [CrossRef]
- Ďurovič, M.; Hnát, J.; Bouzek, K. Electrocatalysts for the hydrogen evolution reaction in alkaline and neutral media. A comparative review. J. Power Sources 2021, 493, 229708. [Google Scholar] [CrossRef]
- Dubouis, N.; Grimaud, A. The hydrogen evolution reaction: From material to interfacial descriptors. Chem. Sci. 2019, 10, 9165–9181. [Google Scholar] [CrossRef]
- Shinagawa, T.; Garcia-Esparza, A.T.; Takanabe, K. Insight on Tafel slopes from a microkinetic analysis of aqueous electrocatalysis for energy conversion. Sci. Rep. 2015, 5, 13801. [Google Scholar] [CrossRef]
- Konkena, B.; Puring, K.J.; Sinev, I.; Piontek, S.; Khavryuchenko, O.; Dürholt, J.P.; Schmid, R.; Tüysüz, H.; Muhler, M.; Schuhmann, W.; et al. Pentlandite rocks as sustainable and stable efficient electrocatalysts for hydrogen generation. Nat. Commun. 2016, 7, 12269. [Google Scholar] [CrossRef]
- Tsai, F.-T.; Deng, Y.-T.; Pao, C.-W.; Chen, J.-L.; Lee, J.-F.; Lai, K.-T.; Liaw, W.-F. The HER/OER mechanistic study of an FeCoNi-based electrocatalyst for alkaline water splitting. J. Mater. Chem. A 2020, 8, 9939–9950. [Google Scholar] [CrossRef]
- Zegkinoglou, I.; Zendegani, A.; Sinev, I.; Kunze, S.; Mistry, H.; Jeon, H.S.; Zhao, J.; Hu, M.Y.; Alp, E.E.; Piontek, S.; et al. Operando Phonon Studies of the Protonation Mechanism in Highly Active Hydrogen Evolution Reaction Pentlandite Catalysts. J. Am. Chem. Soc. 2017, 139, 14360–14363. [Google Scholar] [CrossRef]
- Mikuła, A.; Kubowicz, M.; Mazurków, J.; Mars, K.; Smialkowski, M.; Apfel, U.-P.; Radecka, M. Tailoring the electrocatalytic activity of multicomponent (Co,Fe,Ni)9S8–xSex pentlandite solid electrodes. J. Mater. Chem. A 2023, 11, 7526–7538. [Google Scholar] [CrossRef]
- Mikuła, A.; Dąbrowa, J.; Kusior, A.; Mars, K.; Lach, R.; Kubowicz, M. Search for mid- And high-entropy transition-metal chalcogenides—Investigating the pentlandite structure. Dalt. Trans. 2021, 50, 9560–9573. [Google Scholar] [CrossRef]
- Mikuła, A.; Dąbrowa, J.; Kubowicz, M.; Cieślak, J.; Lach, W.; Kożusznik, M.; Smialkowski, M.; Apfel, U.-P. Synthesis, properties and catalytic performance of the novel, pseudo-spinel, multicomponent transition-metal selenides. J. Mater. Chem. A 2023, 11, 5337–5349. [Google Scholar] [CrossRef]
- Smialkowski, M.; Siegmund, D.; Stier, K.; Hensgen, L.; Checinski, M.P.; Apfel, U.P. Trimetallic Pentlandites (Fe,Co,Ni)9S8for the Electrocatalytical HER in Acidic Media. ACS Mater. Au 2022, 2, 474–481. [Google Scholar] [CrossRef]
- Smialkowski, M.; Tetzlaff, D.; Hensgen, L.; Siegmund, D.; Apfel, U.P. Fe/Co and Ni/Co-pentlandite type electrocatalysts for the hydrogen evolution reaction. Chin. J. Catal. 2021, 42, 1360–1369. [Google Scholar] [CrossRef]
- Mikuła, A.; Kubowicz, M.; Smialkowski, M.; Sanden, S.; Apfel, U.-P. Tuning the Electrocatalytic Properties of Trimetallic Pentlandites: Stability and Catalytic Activity as a Function of Material Form and Selenium Concentration. ACS Mater. Lett. 2024, 6, 1581–1592. [Google Scholar] [CrossRef]
- Trotochaud, L.; Ranney, J.K.; Williams, K.N.; Boettcher, S.W. Solution-cast metal oxide thin film electrocatalysts for oxygen evolution. J. Am. Chem. Soc. 2012, 134, 17253–17261. [Google Scholar] [CrossRef]
- Bentley, C.L.; Andronescu, C.; Smialkowski, M.; Kang, M.; Tarnev, T.; Marler, B.; Unwin, P.R.; Apfel, U.; Schuhmann, W. Local Surface Structure and Composition Control the Hydrogen Evolution Reaction on Iron Nickel Sulfides. Angew. Chem.–Int. Ed. 2018, 57, 4093–4097. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Liu, H.; Gao, W.; Xue, W.; Liu, Z.; Huang, J.; Pan, X.; Huang, Y. Surface-Engineered PtNi-O Nanostructure with Record-High Performance for Electrocatalytic Hydrogen Evolution Reaction. J. Am. Chem. Soc. 2018, 140, 9046–9050. [Google Scholar] [CrossRef] [PubMed]
- Xiao, P.; Yan, Y.; Ge, X.; Liu, Z.; Wang, J.Y.; Wang, X. Investigation of molybdenum carbide nano-rod as an efficient and durable electrocatalyst for hydrogen evolution in acidic and alkaline media. Appl. Catal. B Environ. 2014, 154–155, 232–237. [Google Scholar] [CrossRef]
- Gao, W.; Shi, Y.; Zhang, Y.; Zuo, L.; Lu, H.; Huang, Y.; Fan, W.; Liu, T. Molybdenum Carbide Anchored on Graphene Nanoribbons as Highly Efficient All-pH Hydrogen Evolution Reaction Electrocatalyst. ACS Sustain. Chem. Eng. 2016, 4, 6313–6321. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, X.; Yu, S.; Wen, T.; Zhu, X.; Yang, F.; Sun, X.; Wang, X.; Hu, W. Ternary NiCo2Px Nanowires as pH-Universal Electrocatalysts for Highly Efficient Hydrogen Evolution Reaction. Adv. Mater. 2017, 29, 2–7. [Google Scholar] [CrossRef] [PubMed]
- Puring, K.J.; Piontek, S.; Smialkowski, M.; Burfeind, J.; Kaluza, S.; Doetsch, C.; Apfel, U.-P. Simple methods for the preparation of non-noble metal bulk-electrodes for electrocatalytic applications. J. Vis. Exp. 2017, 2017, 4–9. [Google Scholar] [CrossRef]
- Lu, L.; Yu, S.; Tian, H. Theoretical insight into surface structures of pentlandite toward hydrogen evolution. J. Colloid Interface Sci. 2022, 607, 645–654. [Google Scholar] [CrossRef]
- Knop, O.; Ibrahim, M.A. Chalkogenides of the transition elements: II. Existence of the π phase in the M9S8 section of the system Fe–Co–Ni–S. Can. J. Chem. 1961, 39, 297–317. [Google Scholar] [CrossRef]
- McCrory, C.C.L.; Jung, S.; Ferrer, I.M.; Chatman, S.M.; Peters, J.C.; Jaramillo, T.F. Benchmarking Hydrogen Evolving Reaction and Oxygen Evolving Reaction Electrocatalysts for Solar Water Splitting Devices. J. Am. Chem. Soc. 2015, 137, 4347–4357. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. J. Phys. Chem. A 2020, 124, 4053–4061. [Google Scholar] [CrossRef] [PubMed]
- Hong, W.T.; Welsch, R.E.; Shao-Horn, Y. Descriptors of Oxygen-Evolution Activity for Oxides: A Statistical Evaluation. J. Phys. Chem. C 2016, 120, 78–86. [Google Scholar] [CrossRef]
- Hong, W.T.; Stoerzinger, K.A.; Lee, Y.-L.; Giordano, L.; Grimaud, A.; Johnson, A.M.; Hwang, J.; Crumlin, E.J.; Yang, W.; Shao-Horn, Y. Charge-transfer-energy-dependent oxygen evolution reaction mechanisms for perovskite oxides. Energy Environ. Sci. 2017, 10, 2190–2200. [Google Scholar] [CrossRef]
- Giuffredi, G.; Asset, T.; Liu, Y.; Atanassov, P.; Di Fonzo, F. Transition Metal Chalcogenides as a Versatile and Tunable Platform for Catalytic CO2and N2Electroreduction. ACS Mater. Au 2021, 1, 6–36. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. ACS Appl. Mater. Interfaces 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Piontek, S.; Andronescu, C.; Zaichenko, A.; Konkena, B.; Puring, K.J.; Marler, B.; Antoni, H.; Sinev, I.; Muhler, M.; Mollenhauer, D.; et al. Influence of the Fe:Ni Ratio and Reaction Temperature on the Efficiency of (FexNi1-x)9S8 Electrocatalysts Applied in the Hydrogen Evolution Reaction. ACS Catal. 2018, 8, 987–996. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, H.; Sun, J.; Xia, M.; Guo, W.; Yu, L.; Yan, J.; Zheng, J.; Chang, L.; Gao, F. Phase-pure pentlandite Ni4.3Co4.7S8 binary sulfide as an efficient bifunctional electrocatalyst for oxygen evolution and hydrogen evolution. Nanoscale 2018, 10, 10459–10466. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Dou, Y.; He, T.; Zhou, A.; Kong, X.-J.; Wu, X.-Q.; Liu, T.; Li, J.-R. Revealing the effect of anion-tuning in bimetallic chalcogenides on electrocatalytic overall water splitting. Nano Res. 2021, 14, 4548–4555. [Google Scholar] [CrossRef]
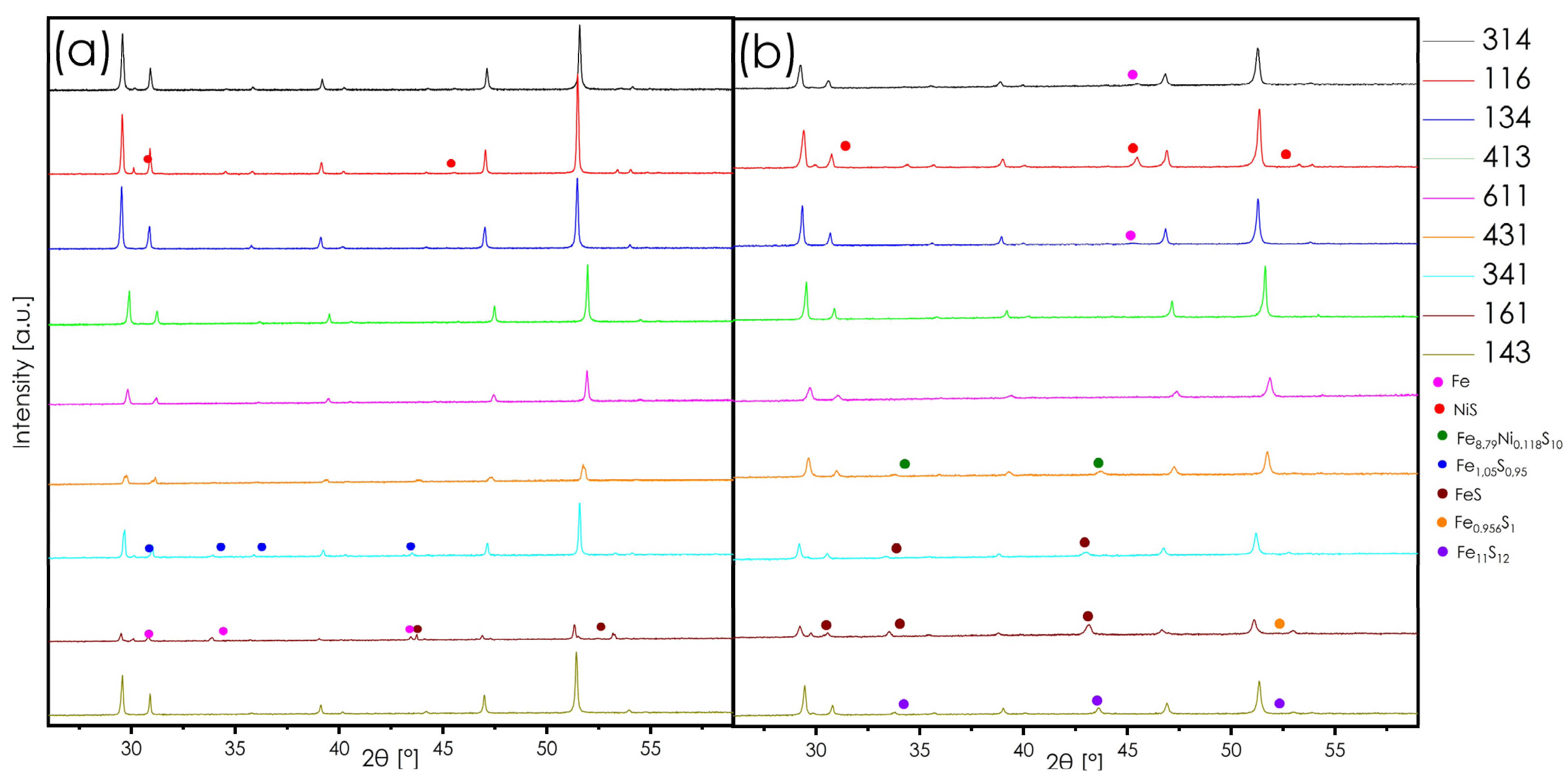
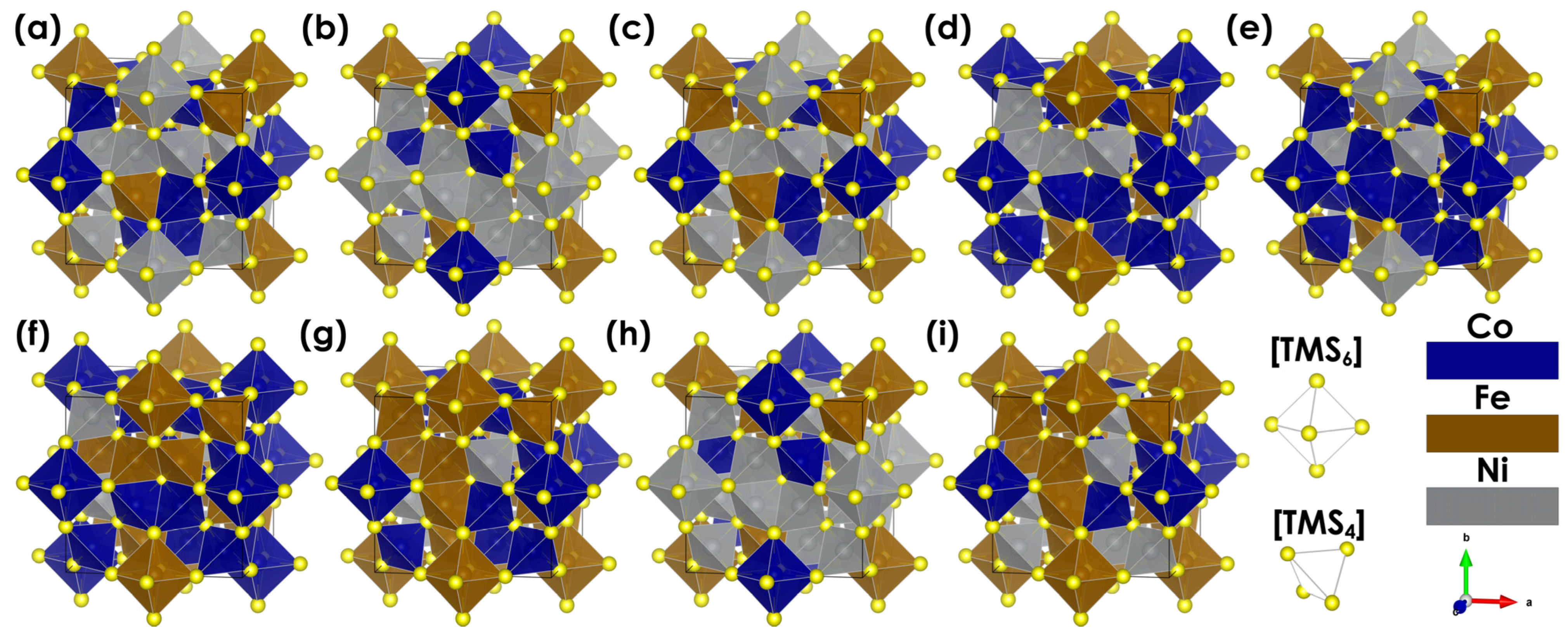
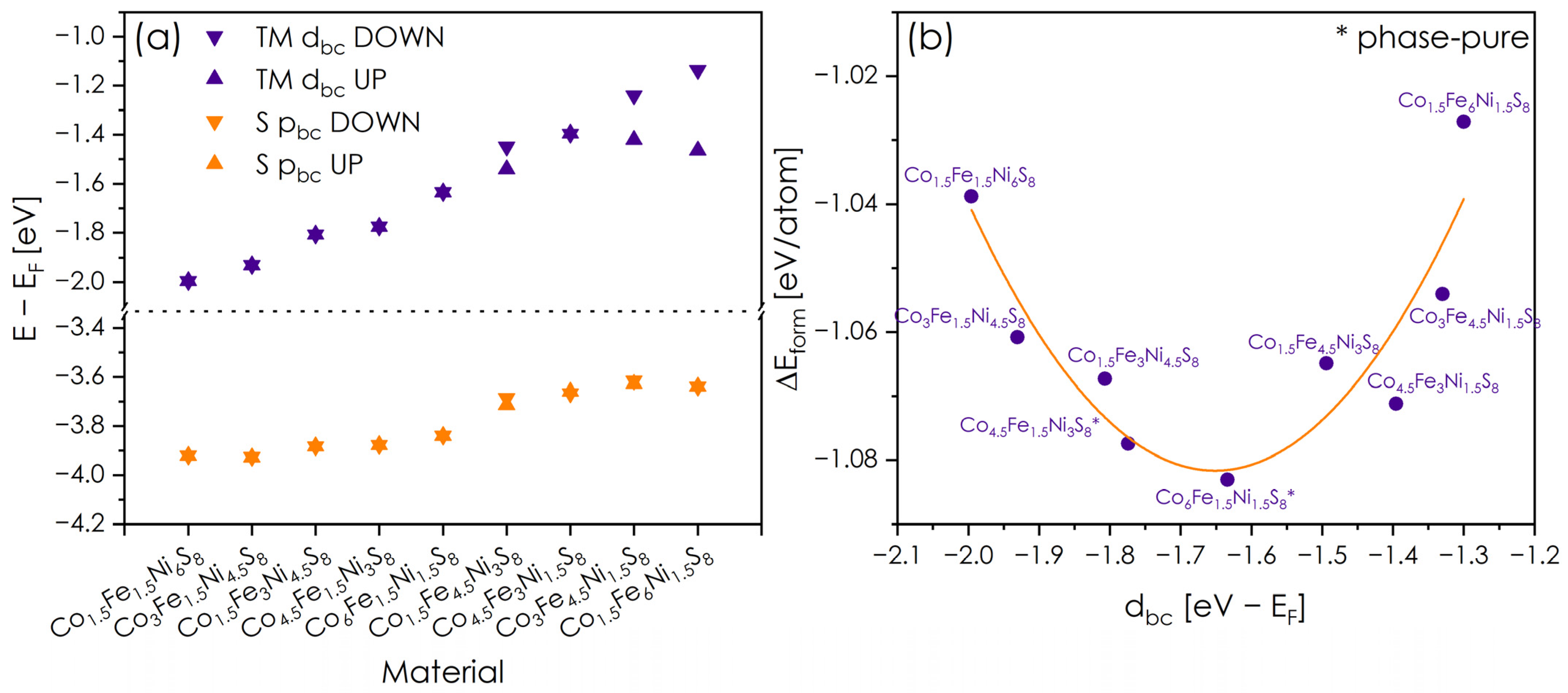

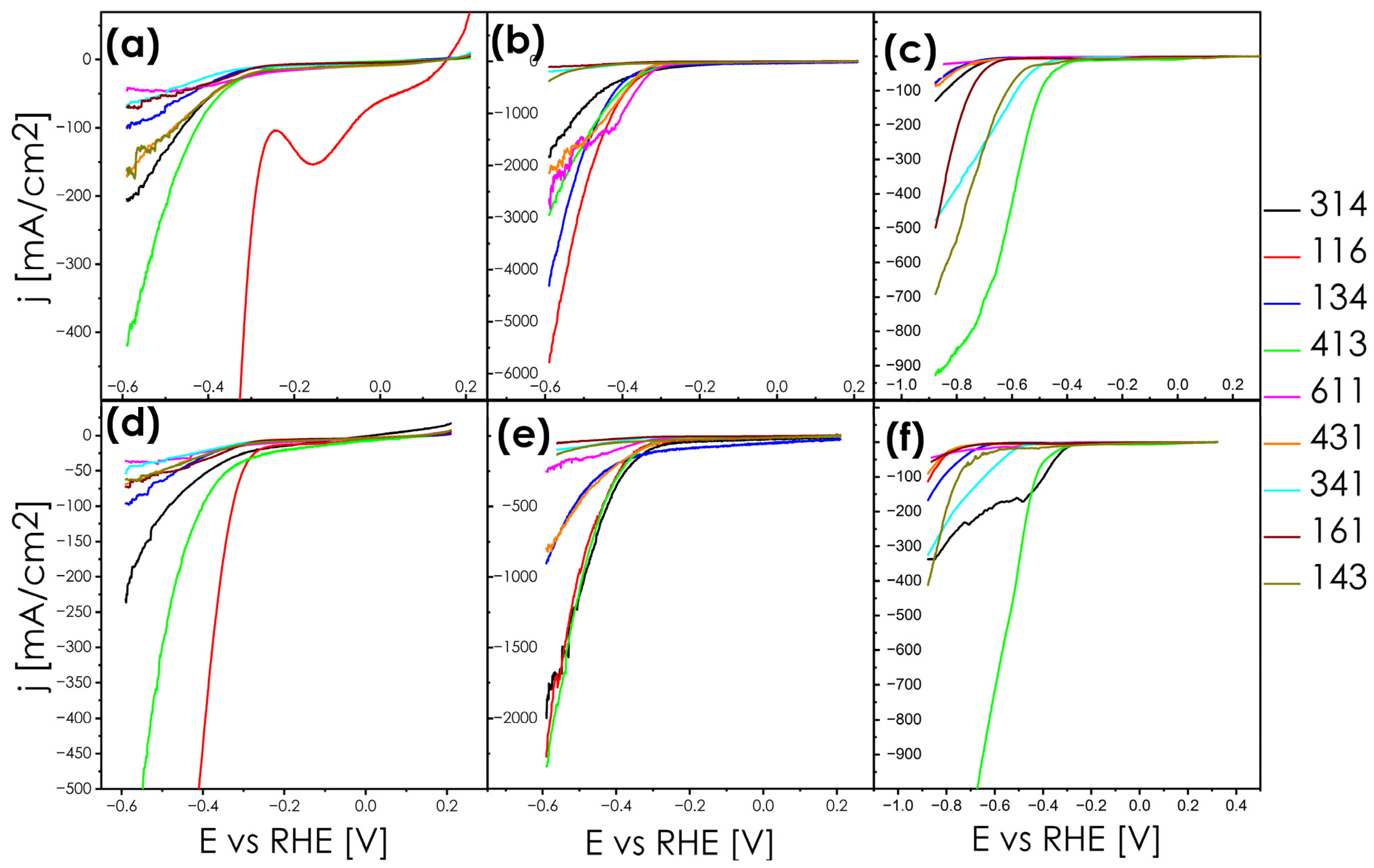



| Nominal Chemical Composition | Pellet | Ingot | Powder |
|---|---|---|---|
| Co3Fe1.5Ni4.5S8 | Pe314 | In314 | Po314 |
| Co1.5Fe1.5Ni6S8 | Pe116 | In116 | Po116 |
| Co1.5Fe3Ni4.5S8 | Pe134 | In134 | Po134 |
| Co4.5Fe1.5Ni3S8 | Pe413 | In413 | Po413 |
| Co6Fe1.5Ni1.5S8 | Pe611 | In611 | Po611 |
| Co4.5Fe3Ni1.5S8 | Pe431 | In431 | Po431 |
| Co3Fe4.5Ni1.5S8 | Pe341 | In341 | Po341 |
| Co1.5Fe6Ni1.5S8 | Pe161 | In161 | Po161 |
| Co1.5Fe4.5Ni3S8 | Pe143 | In143 | Po143 |
| ECSA [cm−2 ×103] | RF [- ×103] | |
|---|---|---|
| Pre | 1.72 | 14.23 |
| Post 1 | 3.32 | 27.46 |
| Post 2 | 4.24 | 35.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubowicz, M.; Kożusznik, M.; Kurek, T.; Mars, K.; Mikuła, A. Role of Foreign Phases, Synergistic Effects, and Morphology in the HER Performance of Trimetallic Pentlandites with Non-Equimolar Co:Fe:Ni Ratio. Energies 2024, 17, 2261. https://doi.org/10.3390/en17102261
Kubowicz M, Kożusznik M, Kurek T, Mars K, Mikuła A. Role of Foreign Phases, Synergistic Effects, and Morphology in the HER Performance of Trimetallic Pentlandites with Non-Equimolar Co:Fe:Ni Ratio. Energies. 2024; 17(10):2261. https://doi.org/10.3390/en17102261
Chicago/Turabian StyleKubowicz, Maciej, Miłosz Kożusznik, Tomasz Kurek, Krzysztof Mars, and Andrzej Mikuła. 2024. "Role of Foreign Phases, Synergistic Effects, and Morphology in the HER Performance of Trimetallic Pentlandites with Non-Equimolar Co:Fe:Ni Ratio" Energies 17, no. 10: 2261. https://doi.org/10.3390/en17102261
APA StyleKubowicz, M., Kożusznik, M., Kurek, T., Mars, K., & Mikuła, A. (2024). Role of Foreign Phases, Synergistic Effects, and Morphology in the HER Performance of Trimetallic Pentlandites with Non-Equimolar Co:Fe:Ni Ratio. Energies, 17(10), 2261. https://doi.org/10.3390/en17102261






