Supplementary Controller Design for SSR Damping in a Series-Compensated DFIG-Based Wind Farm

Abstract

The increasing presence of wind power in power systems will likely drive the integration of large wind farms with electrical networks that are series-compensated to sustain large power flows. This may potentially lead to subsynchronous resonance (SSR) issues. In this paper, a supplementary controller on the grid-side converter (GSC) control loop is designed to mitigate SSR for wind power systems based on doubly fed induction generators (DFIGs) with back-to-back converters. Different supplementary controller feedback signals and modulated-voltage injecting points are proposed and compared based on modal analysis and verified through root locus analysis to identify the optimal feedback signal and the most effective control location for SSR damping. The validity and effectiveness of the proposed supplemental control are demonstrated on the IEEE first benchmark model for computer simulations of SSR by means of time domain simulation analysis using Matlab/Simulink.

1. Introduction

Wind energy has proven to be a clean, abundant and completely renewable source of energy, and the large penetration of wind energy into the power grid indicates that wind energy is considered an effective means of power generation. Wind generation from large wind farms requires the transmission of power through transmission systems that can sustain large power flows [1]. It is well known that series compensation is an effective means of increasing the power transfer capability of an existing transmission network. However, the series capacitor compensation can produce a significant adverse effect called subsynchronous resonance (SSR) in electrical networks in which electrical energy is exchanged with the generator shaft system in a growing manner, which may result in damage of the turbine-generator shaft system [2].

Mitigating SSR using flexible AC transmission systems (FACTS) in a series-compensated wind farm has been demonstrated in the literature. These FACTS devices include a static var compensator (SVC), a thyristor-controlled series capacitor (TCSC) [1] and STATCOM [3]. A power system stabilizer (PSS) has also been employed in DFIG-based wind generation [4] to enhance the network damping. Moreover, a combined PSS and active damping controller has been proposed to provide a contribution of both network and shaft damping [5].

The use of the converters’ control capabilities has been recently proposed for damping power swings as well as inter-area oscillations [6,7,8,9] for wind energy systems based on doubly fed induction generators (DFIGs) with back-to-back power electronic converters. A preliminary study exploring the capability of the grid-side converter (GSC) of a DFIG in mitigating SSR is presented in [10,11]. It is indicated that SSR damping can be enhanced by introducing a supplementary control signal to the GSC control loop.

However, wind turbines are subjected to different mechanical vibration modes related to the mechanical system, such as vibration from the blades, the shaft, the drive train, the tower, and so on [12]. Meanwhile, the induction generator effect (IGE) is a unique feature of SSR phenomena in wind farms interfaced with a series-compensated network because the network resonant oscillatory mode is the major cause of SSR [13], therefore, further studies are still necessary. This paper extends the initial study presented in [10] and focuses on selecting the optimal feedback signal and the most effective modulated-voltage injecting point of supplementary controller for suppressing SSR. Different supplementary controller feedback signals and modulated-voltage injection points are proposed and compared based on the modal controllability, observability and residue, and then the best feedback signal and the effective controlling point are identified to achieve satisfactory performance for damping SSR in a serial-compensated DFIG-based wind farm.

The paper is organized as follows: Section 2 describes the system structure of a DFIG-based wind farm with a series-compensated line; Section 3 presents the modal analysis rules and their effects; Section 4 gives the modal-based analysis and root local diagram-based verification needed to choose the optimal supplementary controller feedback signal and most effective modulated-voltage injecting point for the SSR damping; Section 5 gives the time domain simulation results to demonstrate the effectiveness of the SSR damping controller. Section 6 concludes the analysis.

2. System Structure

The study system is shown in Figure 1, in which a DFIG-based wind farm (100 MW from an aggregation of 2 MW units) is connected to a series-compensated line whose parameters correspond to the IEEE first benchmark model for SSR studies [14]. The wind farms can be considered coherent generators and can be represented by one large DFIG. This approach has been used in system studies [15]. The parameters of a single 2 MW DFIG and the network are listed in

Table A1. Parameters of a single 2 MW DFIG and the network system.

2 MW DFIG		Network system
Rated power	2 MW	Transformer ratio	690 V/161 kV
Rated voltage	690 V	Base MVA	100 MVA
Xls	0.09231 pu	RL	0.02 pu (5.1842 Ω)
XM	3.95279 pu	XL	0.5 pu (129.605 Ω)
Xlr	0.09955 pu	XT	0.14 pu (36.2894 Ω)
Rs	0.00488 pu	XC at 50% compensation level	64.8 Ω
Rr’	0.00549 pu	Series compensation C	40 μF
H	3.5 s	Line length	154 miles
Xtg	0.3 pu

. The parameters of the shaft system are listed in

Table A2. Parameters of the shaft system.

Ht	4.29 s
Hg	0.9 s
Dt	0 pu
Dg	0 pu
Dtg	1.5 pu
Ktg	0.15 pu

.

Figure 1. The system structure.

Figure 1. The system structure.

The DFIG-based wind system includes the DFIG, the power electronic devices, and the drive train. A 7th-order induction generator model is used for the DFIG. The power electronic devices consist of the back-to-back rotor-side converter (RSC) and grid-side converter with the dc-link capacitor. The dynamics of the capacitor in the dc link between GSC and RSC is modeled as a first-order differential equation. A two-mass drive train model is used to express the torsional dynamics of the drive train. In a series-compensated transmission system, the transmission line usually consists of a transformer, a resistance, a reactance and a series-capacitor. The transmission line is connected to the grid, which can be represented by an infinite bus (a constant voltage source). The details of the models and the modeling procedure can be found in the previous research [13,16].

In this study, an auxiliary SSR damping controller will be designed and added to the GSC control loops, shown in Figure 2, in which the inner loops are current control loops and the outer loops are voltage control loops. In the GSC control loops, the q-axis loop is used to track the reference dc-link voltage, and the d-axis loop is used to track the terminal voltage of the DFIG. The control loop employs proportional integral (PI) controllers, where K_p1, K_i1, K_p2 and K_i2 are the parameters of the two PI controllers, and K_p1 = 1, K_i1 = 10, K_p2 = 0.1 and K_i2 = 0.05.

Figure 2. The GSC control scheme in the q-d reference frame.

Figure 2. The GSC control scheme in the q-d reference frame.

SSR damping is achieved by adding a supplementary signal at the GSC control loop, as shown in Figure 3. The supplemental SSR damping controller shown in Figure 3 may utilize different feedback signals as control input signals. Additionally, the modulated voltage, which is the SSR damping controller output, may have different injecting points. In this paper, the focus will be on using the modal analysis method to identify the optimal feedback signal and the most effective modulated-voltage injecting point for SSR damping.

Figure 3. The supplementary control scheme in the GSC control loop for mitigating SSR with different feedback signals and the modulated-voltage injecting points.

Figure 3. The supplementary control scheme in the GSC control loop for mitigating SSR with different feedback signals and the modulated-voltage injecting points.

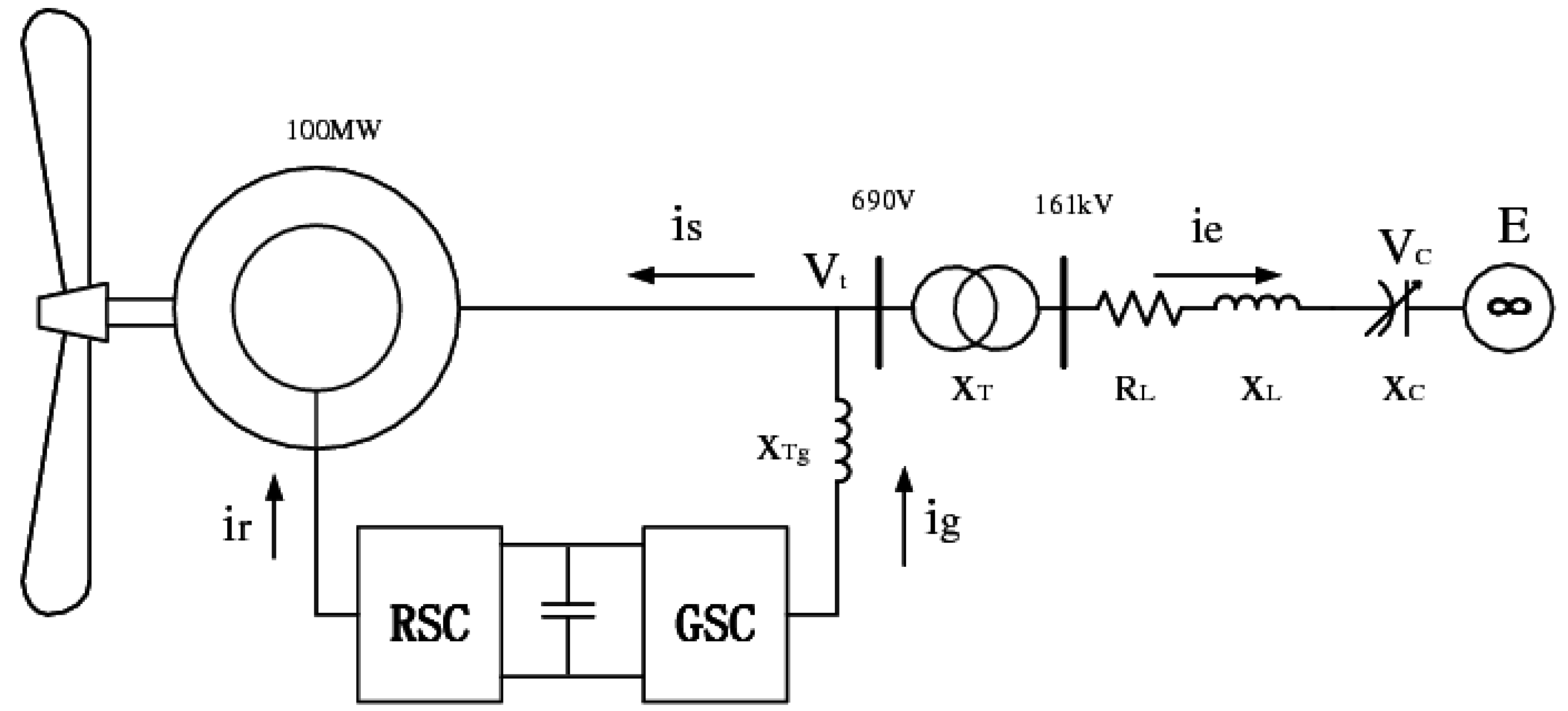
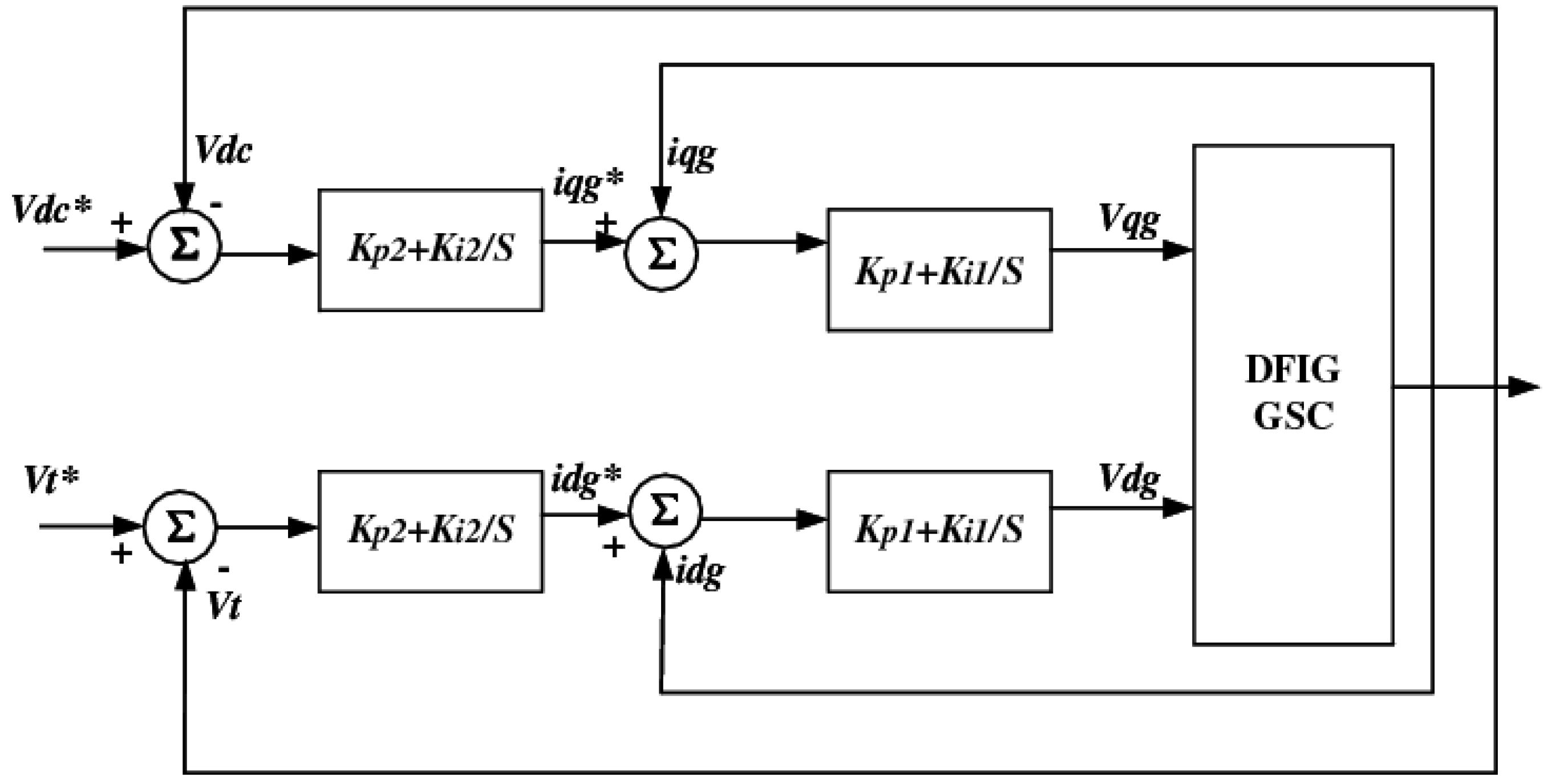
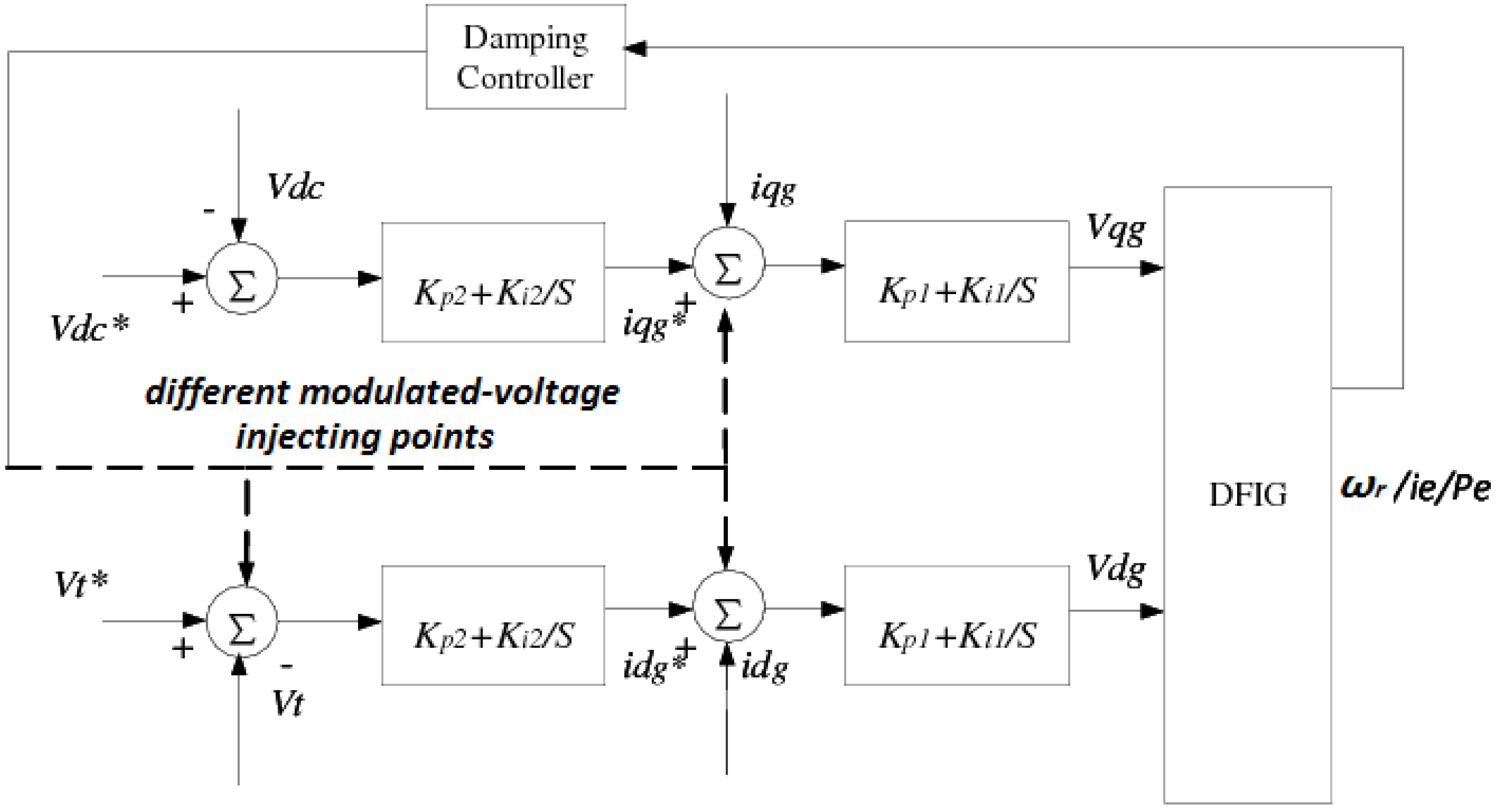
3. Modal Controllability, Observability, Residue and Their Effects

Modal analysis is a technique based on modal decomposition [17]. The mathematical model of the studied system can be written as a set of differential algebraic equations:

$$\{\begin{array}{l}X=AX+Bu\\ Y=CX+Du\end{array}$$

(1)

where A is the state matrix of size n × n, B is the input matrix of size n × r, C is the output matrix of size m × n and D (m × r) is the matrix that defines the proportion of input that appears directly in the output. To express the eigenproperties of A succinctly, it is convenient to introduce the following matrices:

$$\begin{array}{l}V=[V_1,V_2,...,V_n]\\ W=[{V_1}^T,{V_2}^T,...,{V_n}^T]\\ \mathrm{\Lambda }=\text{diagonal matrix, with the eigvalues} {\lambda }_1,{\lambda }_2,...,{\lambda }_{\mathrm{n}} \text{as diagonal elements}\end{array}$$

(2)

where V_i is the column eigenvector and W_i^T is the row eigenvector (i = 1, 2, ..., n). Each of the above matrices is n × n. In terms of these matrices, matrix A can be expressed as:

WAV = Λ

(3)

where AV = VΛ. To eliminate the cross-coupling between the state variables, consider a new state vector related to the original state vector X by the transformation:

$$\tilde{X}=WX$$

(4)

The new differential algebraic equations can be written as:

$$\{\begin{array}{l}\tilde{X}=\mathrm{\Lambda }\tilde{X}+WBu\\ Y=CV\tilde{X}+Du\end{array}$$

(5)

From Equation (5), the column eigenvector V_i gives the mode shape, which gives the relative activity of the state variables when a particular mode is excited. In addition, the product of V_ki and W_ik is the participation factor, which is a measure of the relative participation of the kth state variable in the ith mode.

With the analysis of mode shape and participation factor, the key participation factors of the system can be found. However, the participation factor only addresses the state variable and does not include the input and output signal [18]. Therefore, the participation factor matrix itself cannot effectively identify the controller site and the optimal feedback signal in the absence of information about the input and output, which is more important when the output feedback control loop is employed. However, the effectiveness of control can be indicated through modal controllability and observability indices.

The definitiona of the modal controllability and observability are described below. From Equation (5), it can be seen that the input is affected by the matrix product WB, which is called modal controllability. The modal controllability can be used to find the most effective control location. In a similar way, the product of the matrix C and V determines whether the variable contributes to the formation of the output, and this product, CV, is called the modal observability. The modal observability indices, in contrast, relate to feedback signals.

Equation (5) can also be written as:

$$G\left(s\right)=\frac{Y\left(s\right)}{u\left(s\right)}=CV{(SI-\mathrm{\Lambda })}^{-1}WB=\sum _{i=1}^n\frac{C{V}_i{W}_{i}B}{s-{\lambda }_i}=\sum _{i=1}^n\frac{R_i}{s-{\lambda }_i}$$

(6)

where R_i is known as the modal residue and is the product of the modal observability (CV_i) and the modal controllability (W_iB). Because the residue is a complex variable, both the magnitude and phase become important. The higher the magnitude of the residue, the less control effort (gain), whereas a higher phase lag requires more phase compensation in the damping control feedback path.

4. Comparison of Feedback Signals and Modulated-Voltage Injecting Points

As described in Section 3, the effectiveness of the control is decided by the modal controllability and observability. Therefore, in this section, different feedback signals and modulated-voltage injecting points are presented and compared based on the principles of the modal controllability, observability and residue. The optimal feedback signal and the modulated-voltage injecting point in the GSC control loop could be identified. Accordingly, the supplementary controller is designed to evaluate the SSR damping performance.

4.1. Base Case

In the system of a DFIG-based wind farm with a series-compensated line, the natural resonant frequency is represented as:

$$f_{SSR}=f_s\sqrt{\frac{X_C}{X_{total}}}$$

(7)

where fs is the nominal system frequency (60 Hz in this paper), and X_C and X_total are the total capacitive reactance and the total inductive reactance of the network system, respectively.

Figure 4 describes the network mode with various compensation levels and without any controller for wind speed from 7 to 10 m/s and the network mode is the mode corresponding to the phenomenon of SSR. It is shown that when the compensation level increase, the real part of the eigenvalue corresponding to the network mode will become more positive and the network mode of the system will be more unstable.

For the studied system, the base case is chosen as a wind speed of 7 m/s and a compensation level for X_C/X_L of 75%. An estimation finds that f_SSR is approximately 40 Hz for the 75% compensation level. Then, with the study system, the base-case eigenvalues and their labeling are shown in Table 1.

Figure 4. Network mode with various compensation levels for various wind speeds.

Figure 4. Network mode with various compensation levels for various wind speeds.

Table 1. System mode at 7 m/s wind speed with a 75% compensation level.

Mode	Λ = ρ ± jω	Frequency	Damping ratio	Nature of the Mode
λ1,2	4.9 ± j123.2	19.6079	−0.0397	SSR mode
λ3,4	−10.4 ± j629	100.1085	0.0165	Super synchronous resonance mode
λ5,6	−12.7 ± j99.1	15.7723	0.1271	Electromechanical mode
λ7,8	−1 ± j5.8	0.9231	0.1699	Shaft mode

Table 1. System mode at 7 m/s wind speed with a 75% compensation level.

Mode	Λ = ρ ± jω	Frequency	Damping ratio	Nature of the Mode
λ1,2	4.9 ± j123.2	19.6079	−0.0397	SSR mode
λ3,4	−10.4 ± j629	100.1085	0.0165	Super synchronous resonance mode
λ5,6	−12.7 ± j99.1	15.7723	0.1271	Electromechanical mode
λ7,8	−1 ± j5.8	0.9231	0.1699	Shaft mode

The base case has four modes, and the frequencies show the physical nature of the modes: λ_1,2 is an SSR mode associated with the compensation line, and its frequency equals f_s − f_SSR; λ_3,4 is a super synchronous resonance mode also associated with the compensation line, and its frequency equals f_s + f_SSR; λ_5,6 is an electromechanical mode associated with rotor circuit RL dynamics and the mechanical dynamics, and its frequency equals f_s − f_m (where f_m is the frequency of the shaft rotating speed, and it equals 45 Hz for a 7 m/s wind speed); and λ_7,8 is a shaft mode associated with the two-mass torsional dynamics. The SSR mode and shaft mode are the dominant modes in the study system because they will cause the phenomena of the induction generator effect (IGE) and torsional interaction (TI).

4.2. Modal Controllability, Observability and Residue for Different Feedback Signals and Different Modulated-Voltage Injecting Points

The state variables with a high participation factor are normally the candidate feedback signals for SSR damping [19]. However, the participation factor only deals with the state variable and does not consider the input and output parameters. It cannot effectively identify controller site and appropriate feedback signal in the absence of information on input and output. The effectiveness of control can, however, be indicated through modal controllability and observability indices. In this paper, the rotor speed, the magnitude of line current and the electrical power are selected as the candidate feedback signals for SSR damping. The d-axis of the GSC control outer loop and the d-axis and q-axis of GSC control inner loop, to which the modulated voltage are added, are different candidate modulated-voltage injecting points. The optimal feedback signal and the most effective control location for SSR damping will be identified through modal analysis and verified through root locus analysis.

The modal controllability, observability and residue for different feedback signals and different modulated-voltage injecting points with a 75% compensation level at a 7 m/s wind speed are computed and displayed in Table 2.

Table 2. Modal observability, controllability and residue for different feedback signals and modulated-voltage injecting points for the SSR mode.

Feedback signal	Modulated-voltage injecting point	Observability		Controllability		Residue
		Magnitude	Phase	Magnitude	Phase	Magnitude	Phase
Rotor speed	d-axis of GSC outer loop	0.0001	−21.0564	4.1891	−49.1602	0.004	−70.2166
	d-axis of GSC inner loop	0.0001	−21.0564	41.9	131.0720	0.04	110.0156
	q-axis of GSC inner loop	0.0001	−21.0564	31	94.6664	0.0296	73.6101
Line current	d-axis of GSC outer loop	0.2741	−112.4409	4.1891	−49.1602	1.1484	−161.6011
	d-axis of GSC inner loop	0.2741	−112.4409	41.9	131.0720	11.482	18.6311
	q-axis of GSC inner loop	0.2741	−112.4409	31	94.6664	8.5031	−17.7745
Electrical power	d-axis of GSC outer loop	0.1945	67.3696	4.1891	130.8398	0.8147	−161.7906
	d-axis of GSC inner loop	0.1945	67.3696	41.9	−48.9280	8.146	18.4416
	q-axis of GSC inner loop	0.1945	67.3696	31	−85.3335	6.0327	−17.964

Table 2. Modal observability, controllability and residue for different feedback signals and modulated-voltage injecting points for the SSR mode.

Feedback signal	Modulated-voltage injecting point	Observability		Controllability		Residue
		Magnitude	Phase	Magnitude	Phase	Magnitude	Phase
Rotor speed	d-axis of GSC outer loop	0.0001	−21.0564	4.1891	−49.1602	0.004	−70.2166
	d-axis of GSC inner loop	0.0001	−21.0564	41.9	131.0720	0.04	110.0156
	q-axis of GSC inner loop	0.0001	−21.0564	31	94.6664	0.0296	73.6101
Line current	d-axis of GSC outer loop	0.2741	−112.4409	4.1891	−49.1602	1.1484	−161.6011
	d-axis of GSC inner loop	0.2741	−112.4409	41.9	131.0720	11.482	18.6311
	q-axis of GSC inner loop	0.2741	−112.4409	31	94.6664	8.5031	−17.7745
Electrical power	d-axis of GSC outer loop	0.1945	67.3696	4.1891	130.8398	0.8147	−161.7906
	d-axis of GSC inner loop	0.1945	67.3696	41.9	−48.9280	8.146	18.4416
	q-axis of GSC inner loop	0.1945	67.3696	31	−85.3335	6.0327	−17.964

It can be seen that for the same feedback signal for the SSR mode, the computed modal observabilities are the same for different modulated-voltage injecting points, while the computed modal controllabilities are different, which provides valuable information about the potential control locations. Hence, the modal residues are different, which will result in different control designs. It can also be found that the magnitude of the modal controllability of the d-axis of the GSC inner loop is the largest, and it will require the least gain for the supplementary SSR damping control.

Traditionally, the selection of appropriate signals has been based on the magnitude of the residue as it combines the modal controllability and observability into a single index [20]. However, besides the magnitude, the phase angle of the residue is important in selecting appropriate signals [21]. Therefore, the following conclusions could be drawn from a comparison of the modal controllability, observability and residue for the three feedback signals with different modulated-voltage injecting points:

• The magnitude of modal observability for the line current as the feedback signal is high, and the electrical power has high modal observability too. Therefore, the line current and electrical power are both the candidate appropriate signals to damp SSR with less control effort.
• The magnitude of modal controllability for the d-axis of the GSC inner loop as the modulated-voltage injecting points is large, and the q-axis of GSC inner loop has large modal controllability too. Hence, less gain is required for these controlling points for the supplementary SSR damping control design.
• The magnitude of the modal residue for the rotor speed as the feedback signal is very small, which means a large control effort (gain). Meanwhile, the phase lag of the modal residue is high. Thus, the feedback control design requires both gain and phase compensation.
• The magnitude of the modal residue for the line current as the feedback signal is large, and the phase lag of the modal residue is low. Therefore, only gain compensation is required and phase compensation will not be used, which results in a simple feedback control design.
• The magnitude and phase of the modal residue for the electrical power as the feedback signal are similar to those for the line current as the feedback signal. Similarly, only gain compensation is required. Hence, the feedback control design will also be fairly simple.

The phase compensation required at each modal frequency is closely related to the phase angle of the residues. At the open loop pole location this relationship is given by [21]:

Ψ(i) = −Φ(i)

(8)

where, Ψ(i) is phase compensation angle required to move the open loop ith eigenvalue to the left, parallel to the real axis and Φ(i) is the phase angle of the residue for the ith mode

According to the principle of the lag-lead compensation design [22], the phase compensation of the modal residue for rotor speed as feedback with different modulated-voltage injection points is designed. For the modulated-voltage injection to the d-axis of the GSC outer or inner loop, the phase compensation is $C={\left(\frac{0.0163\times 4.0228\times s+1}{0.0163\times s+1}\right)}^3$. For the modulated-voltage injection to the q-axis of the GSC inner loop, the phase compensation is $C={\left(\frac{0.0163\times 4.0228\times s+1}{0.0163\times s+1}\right)}^2$.

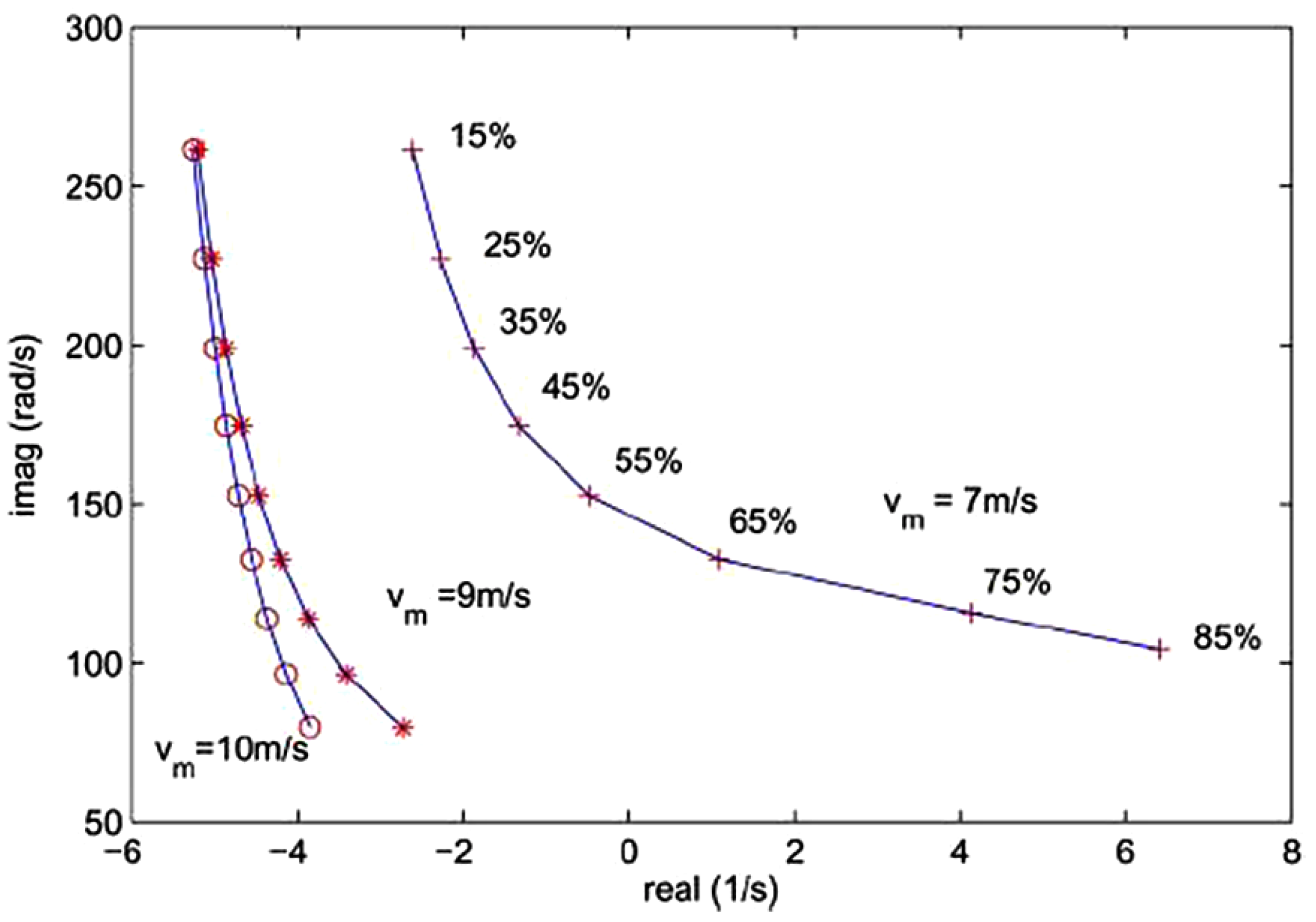
4.3. Root Locus Analysis Verification

To verify the modal analysis intuitively, the root locus diagrams of the open loop system with different feedback signals and different modulated-voltage injecting points are shown in Figure 5, Figure 6 and Figure 7. The root locus diagrams of the open loop system with the rotor speed as the feedback signal and different modulated-voltage injecting points are shown in Figure 5. From Figure 5a,b, the supplementary control for the modulated-voltage injection to the d-axis of the GSC inner or outer loop is realistic, and it can also be found that the supplementary control design for the modulated-voltage injection to the d-axis of the GSC outer loop requires a larger gain than to the d-axis of the GSC inner loop, which is coincident with the modal analysis. However, in Figure 5c, for the modulated-voltage injection to the q-axis of the GSC inner loop, there are a pair of zeros and a pair of poles on the right plane for the SSR mode. Therefore, it is not practical for this modulated-voltage injection.

Figure 5. The root locus diagrams of the open-loop system with the rotor speed as the feedback signal and different modulated-voltage injection (a) to the d-axis of the GSC outer loop, (b) to the d-axis of the GSC inner loop, and (c) to the q-axis of the GSC inner loop.

Figure 5. The root locus diagrams of the open-loop system with the rotor speed as the feedback signal and different modulated-voltage injection (a) to the d-axis of the GSC outer loop, (b) to the d-axis of the GSC inner loop, and (c) to the q-axis of the GSC inner loop.

The root locus diagrams of the open loop system with the line current as the feedback signal and different modulated-voltage injecting points are shown in Figure 6. From Figure 6a,b, it can be seen that the supplementary control for the modulated-voltage injection to the d-axis of the GSC outer loop requires a larger gain than to the d-axis of the GSC inner loop, which is consistent with the description of the modal residue in Table 2. However, in Figure 6a,b, there is a pair of zeros in the right plane corresponding to the SSR mode poles. That is, it will be useless to damp the SSR under these two control designs, although they require less gain. In Figure 6c, with the supplementary control for modulated-voltage injection to the q-axis of the GSC inner loop, the SSR mode can be damped. At the same time, it will require less gain compared with using the rotor speed as the feedback signal.

Figure 6. The root locus diagrams of the open-loop system with the line current as the feedback signal and different modulated-voltage injections (a) to the d-axis of the GSC outer loop, (b) to the d-axis of the GSC inner loop, and (c) to the q-axis of the GSC inner loop.

Figure 6. The root locus diagrams of the open-loop system with the line current as the feedback signal and different modulated-voltage injections (a) to the d-axis of the GSC outer loop, (b) to the d-axis of the GSC inner loop, and (c) to the q-axis of the GSC inner loop.

The root locus diagrams of the open loop system with the electrical power as the feedback signal and different modulated-voltage injecting points are shown in Figure 7. It can be seen that the root locus diagrams are also similar to those for the line current as the feedback signal, while some zeros are different in the complex plane. In Figure 7a,b, one zero point is in the right plane while the other zero point is in the left plane. The pair of zeros is not completely on the right plane. Therefore, with suitable control design, it is still possible to damp SSR. In Figure 7c, with the supplementary control for modulated-voltage injection to the q-axis of the GSC inner loop, the SSR mode can be damped.

Considering the magnitude of the modal residue in Table 2 and the root locus diagram in Figure 6 and Figure 7, the gain compensation for the electrical power as the feedback signal is a little larger than that for the line current as the feedback signal.

Figure 7. The root locus diagrams of the open loop system with the electrical power as the feedback signal and different modulated-voltage injections (a) to the d-axis of the GSC outer loop, (b) to the d-axis of the GSC inner loop, and (c) to the q-axis of the GSC inner loop.

Figure 7. The root locus diagrams of the open loop system with the electrical power as the feedback signal and different modulated-voltage injections (a) to the d-axis of the GSC outer loop, (b) to the d-axis of the GSC inner loop, and (c) to the q-axis of the GSC inner loop.

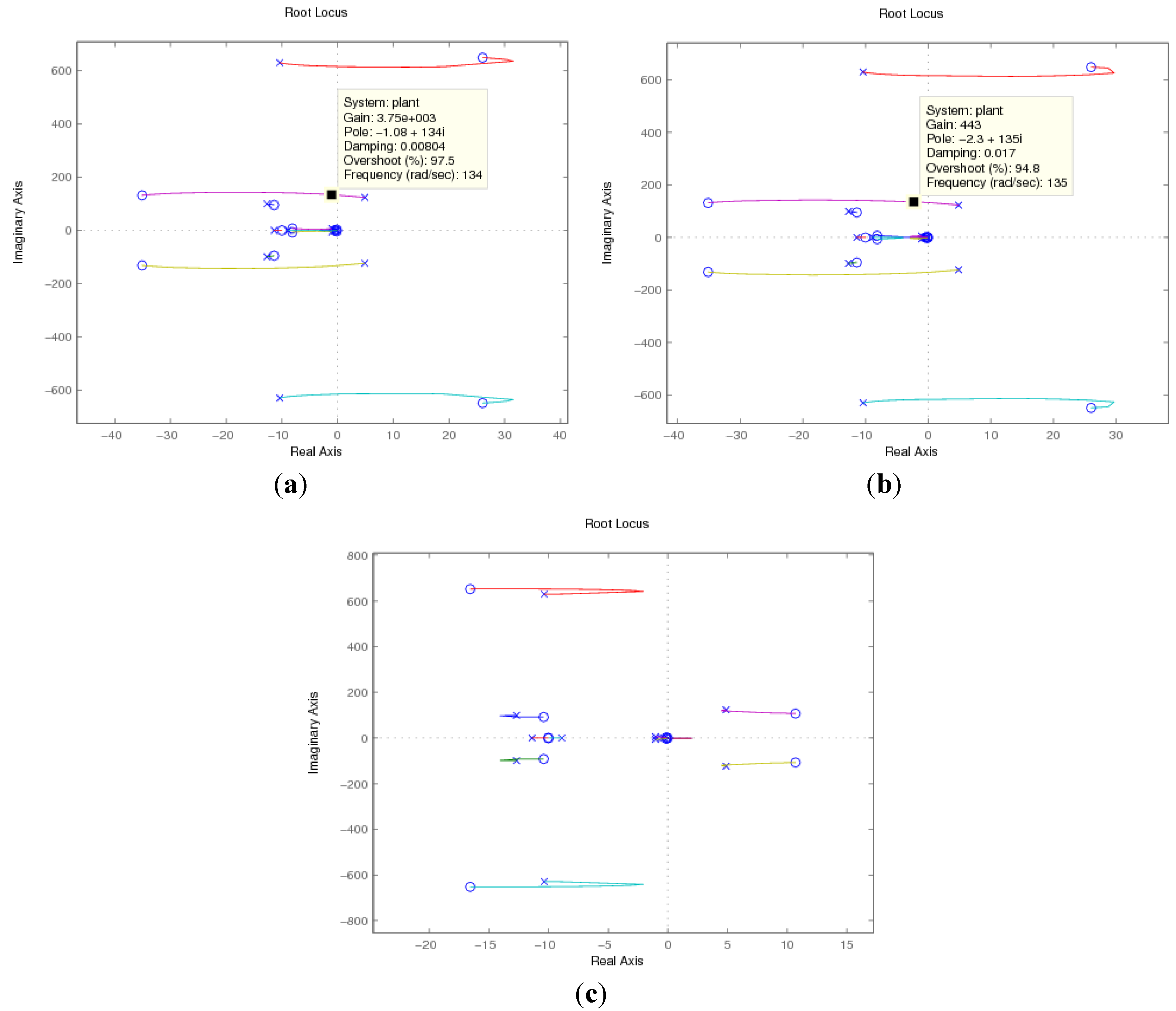
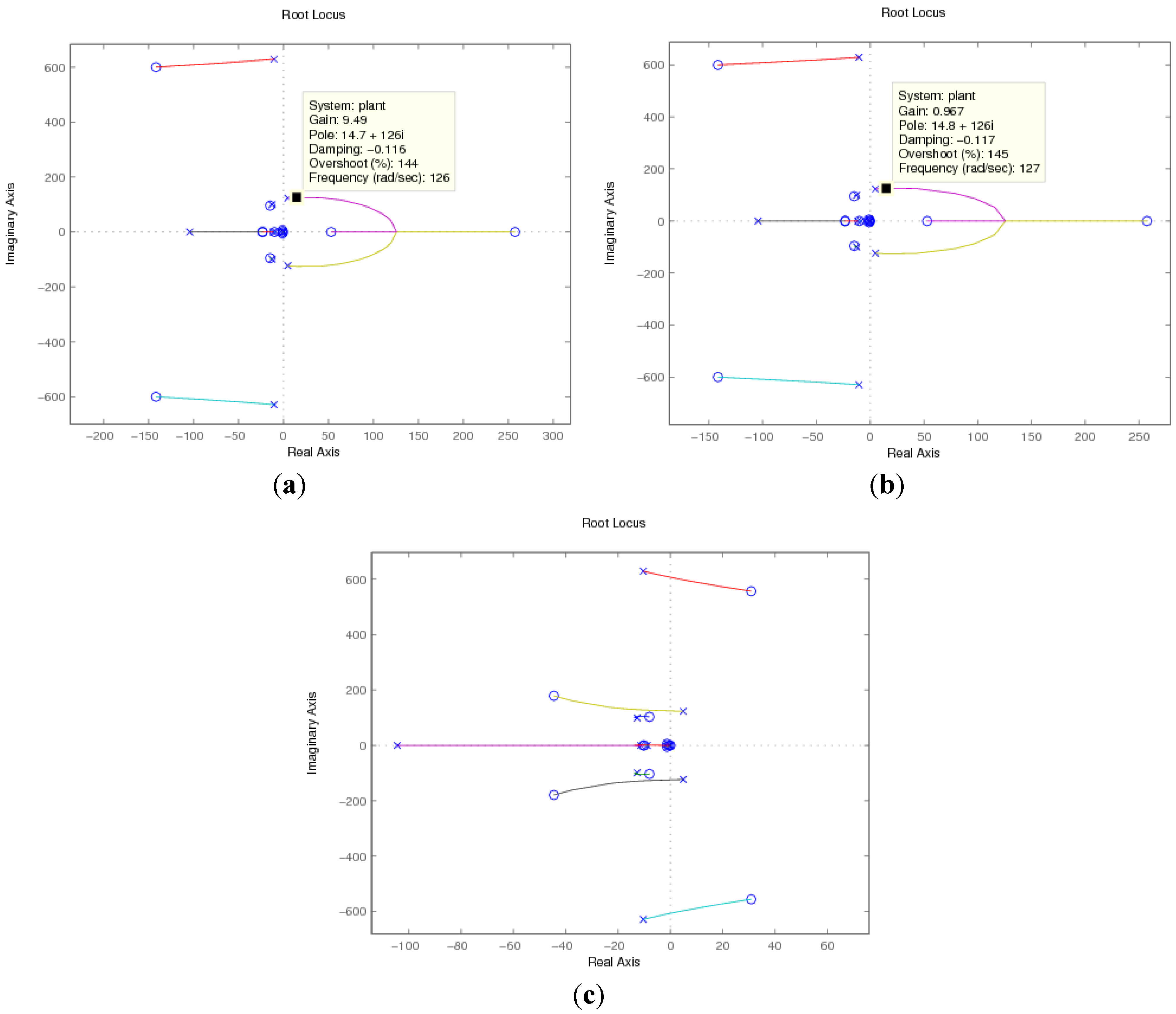
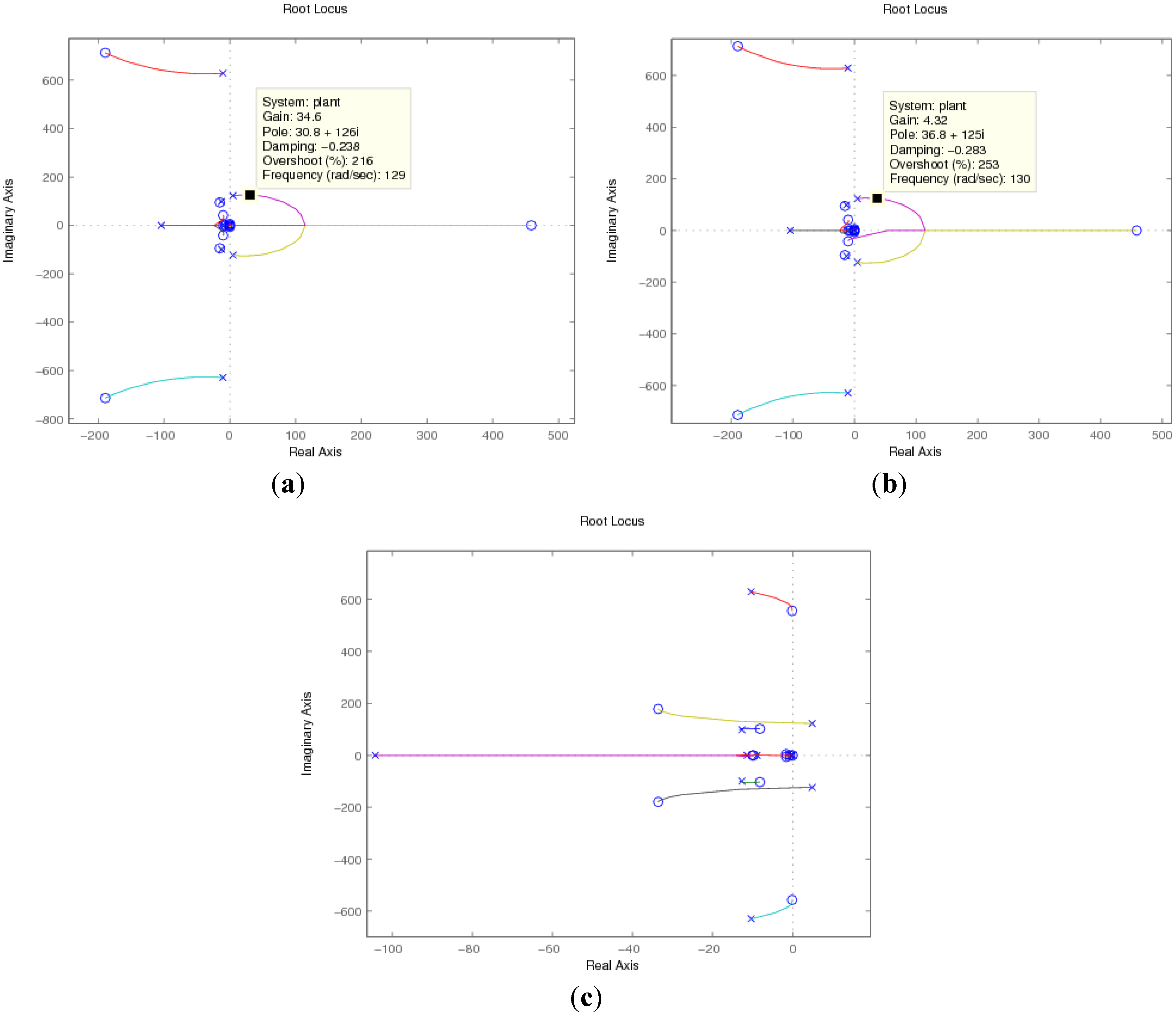
5. Time Domain Simulation Results Verification

A previous study [16] shows that when the wind speed is 7 m/s, the system can suffer SSR instability when the compensation level reaches 75% due to IGE. In the simulation study, initially, the compensation level is set at 25%. At t = 0.5 s, the compensation level changes to 75%. The dynamic responses of the system with and without the SSR damping controller are plotted.

5.1. Simulation Results for the Rotor Speed as a Feedback Signal of the Supplementary Control Loop

Figure 8 shows a comparison of the dynamic responses of the electromagnetic torque T_e for the rotor speed ω_r as the feedback signal with different modulated-voltage injecting points. It is found that a supplementary controller with the rotor speed as the feedback signal and modulated-voltage injection to the d-axis of the GSC outer loop and the d-axis of the GSC inner loop can damp the SSR mode effectively, while the modulated-voltage injection to the q-axis of the GSC inner loop cannot damp the SSR mode. These simulation results are consistent with the modal and root locus analysis.

Figure 8. Dynamic responses of T_e (a) without a supplementary damping controller, (b) supplementary control loop in the d-axis of the GSC outer loop (K_p = 60), (c) supplementary control loop in the d-axis of the GSC inner loop (K_p = −10), (d) supplementary control loop in the q-axis of the GSC inner loop (K_p = −10); ω_r is used as the damping controller input signal (K_p is the damping controller gain).

Figure 8. Dynamic responses of T_e (a) without a supplementary damping controller, (b) supplementary control loop in the d-axis of the GSC outer loop (K_p = 60), (c) supplementary control loop in the d-axis of the GSC inner loop (K_p = −10), (d) supplementary control loop in the q-axis of the GSC inner loop (K_p = −10); ω_r is used as the damping controller input signal (K_p is the damping controller gain).

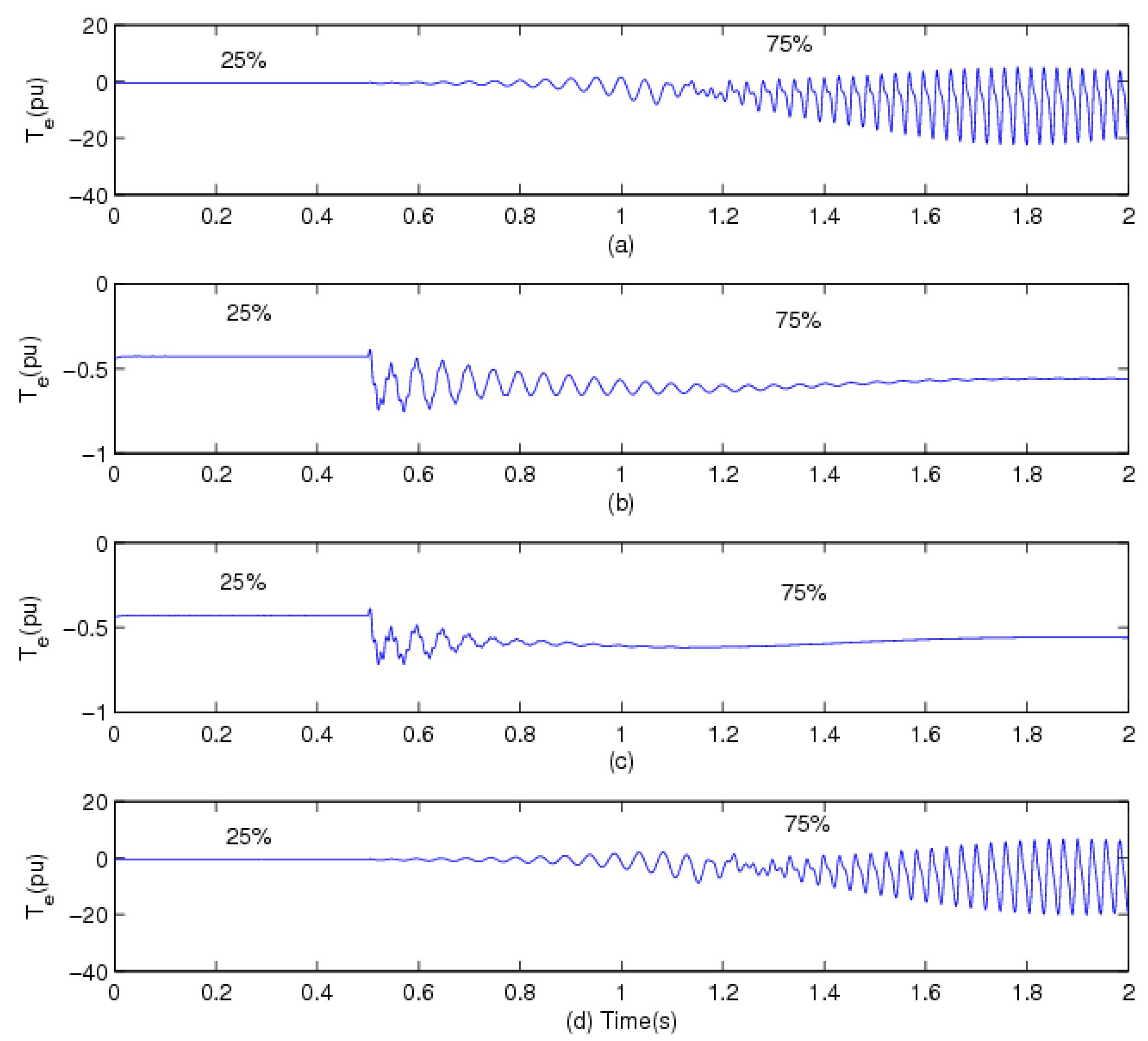
5.2. Simulation Results for the Line Current as the Feedback Signal of the Supplementary Control Loop

Figure 9 shows a comparison of the dynamic responses of the electromagnetic torque T_e for the line current I_e as the feedback signal with different modulated-voltage injecting points. From Figure 9a–d, a supplementary controller with the line current as the feedback signal and modulated-voltage injection to the d-axis of the GSC outer loop and the d-axis of the GSC inner loop cannot damp the SSR mode effectively, while the modulated-voltage injection to the q-axis of the GSC inner loop can damp the SSR mode well with reduced control effort (gain). These simulation results are consistent with the modal and root locus analysis.

5.3. Simulation Results for the Electrical Power as the Feedback Signal of the Supplementary Control Loop

Figure 10 shows a comparison of the dynamic responses of the electromagnetic torque T_e for the electrical power P_e as the feedback signal and different modulated-voltage injecting points. It is found that a supplementary controller with electrical power as the feedback signal and modulated-voltage injection to the q-axis of the GSC inner control loop can damp the SSR mode effectively. The simulation results are consistent with the modal and root locus analysis.

Figure 9. Dynamic responses of T_e (a) without a supplementary damping controller, (b) supplementary control loop in the d-axis of the GSC outer loop (K_p = −5), (c) supplementary control loop in the d-axis of the GSC inner loop (K_p = 0.5), (d) supplementary control loop in the q-axis of the GSC inner loop (K_p = 1). I_e is used as the damping controller input signal.

Figure 9. Dynamic responses of T_e (a) without a supplementary damping controller, (b) supplementary control loop in the d-axis of the GSC outer loop (K_p = −5), (c) supplementary control loop in the d-axis of the GSC inner loop (K_p = 0.5), (d) supplementary control loop in the q-axis of the GSC inner loop (K_p = 1). I_e is used as the damping controller input signal.

Figure 10. Dynamic responses of T_e (a) without a supplementary damping controller, (b) supplementary control loop in the d-axis of the GSC outer loop (K_p = −10), (c) supplementary control loop in the d-axis of the GSC inner loop (K_p = 1), (d) supplementary control loop in the q-axis of the GSC inner loop (K_p = 5). P_e is used as the damping controller input signal.

Figure 10. Dynamic responses of T_e (a) without a supplementary damping controller, (b) supplementary control loop in the d-axis of the GSC outer loop (K_p = −10), (c) supplementary control loop in the d-axis of the GSC inner loop (K_p = 1), (d) supplementary control loop in the q-axis of the GSC inner loop (K_p = 5). P_e is used as the damping controller input signal.

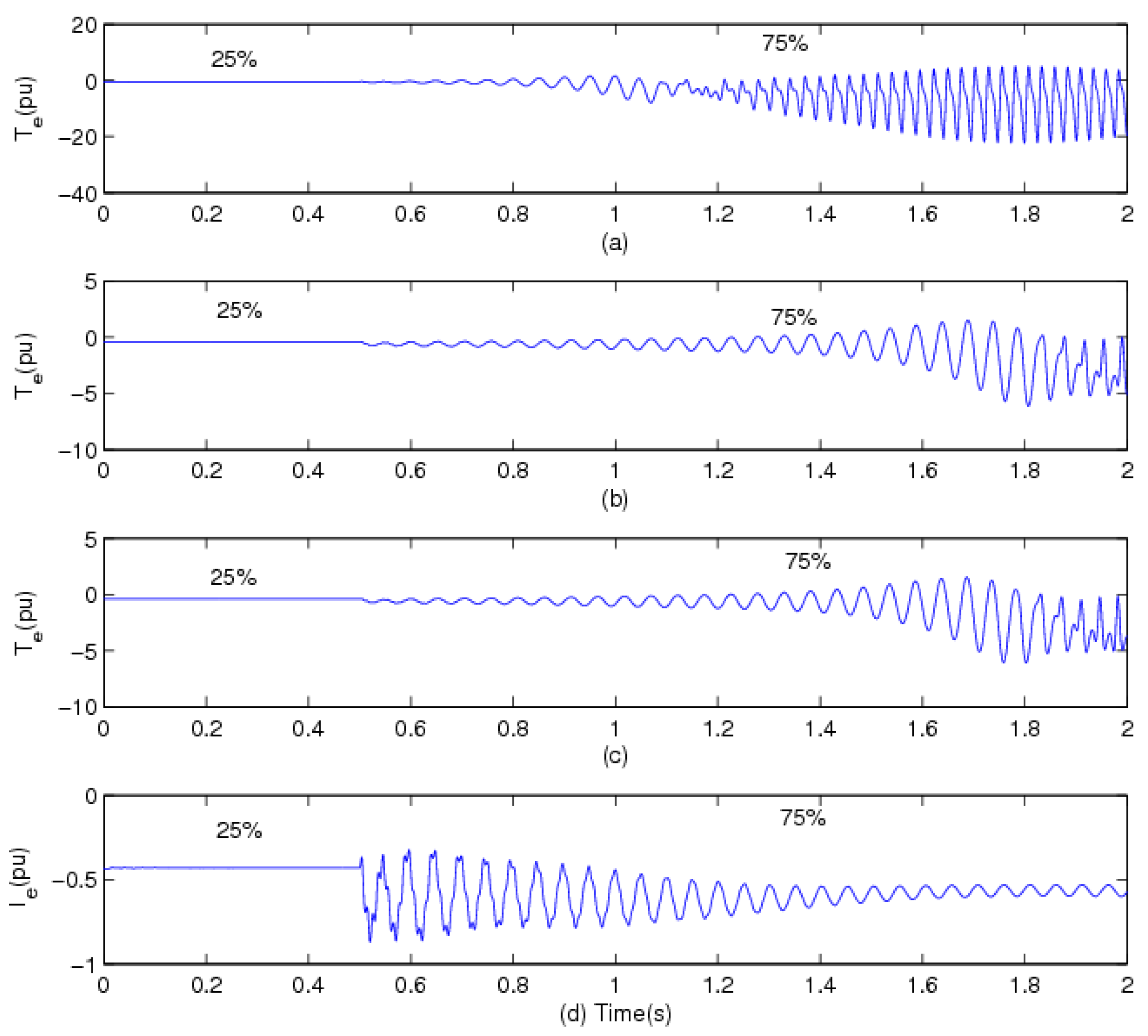
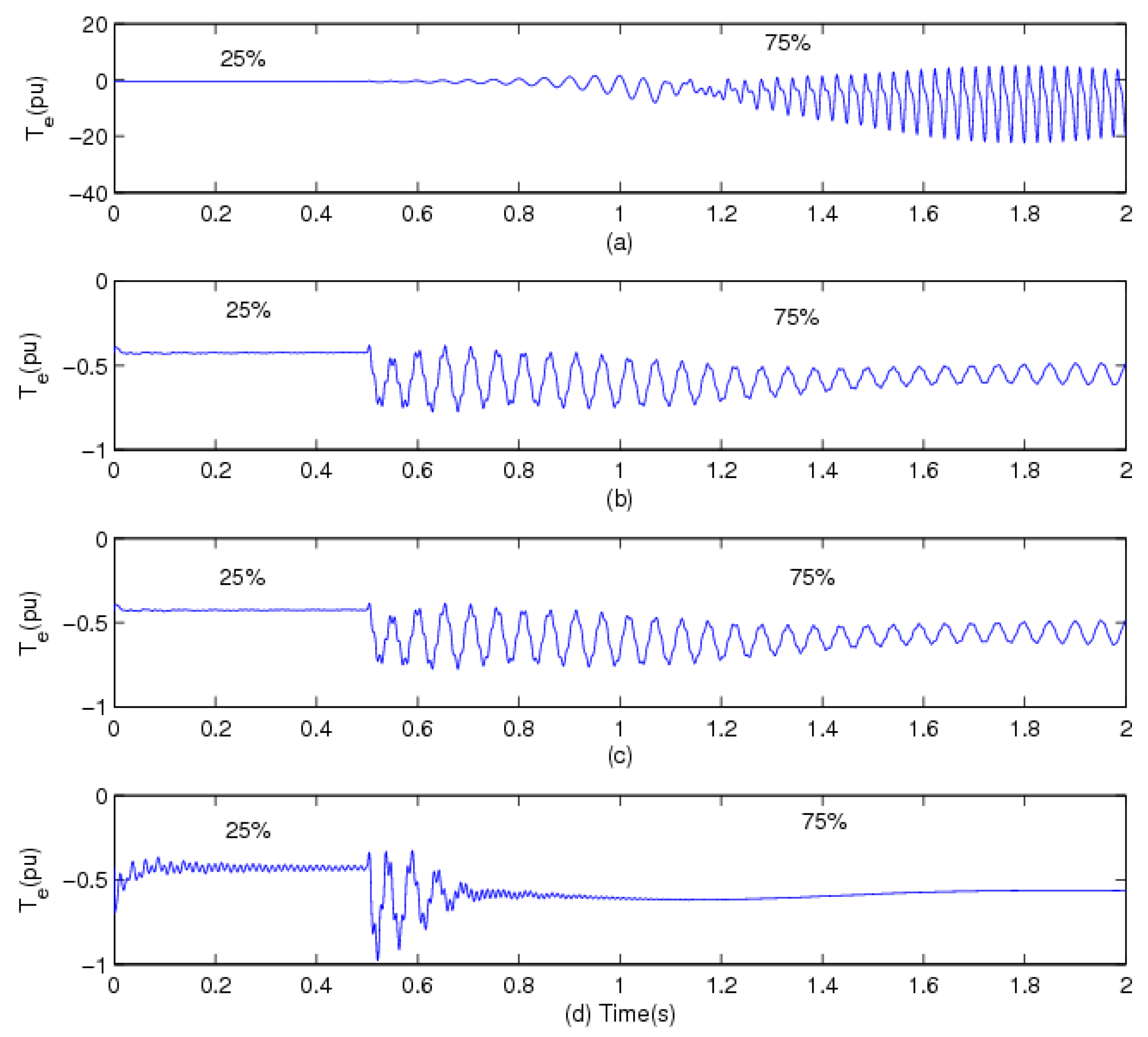
6. Conclusions

A series-compensated DFIG-based wind farm may suffer subsynchronous resonance issues. In this paper, a supplementary controller in GSC for SSR damping has been proposed, designed and investigated. To design a suitable and better performance supplementary controller to damp SSR, this paper tries to find the optimal feedback signal and the effective modulated-voltage injecting point. Different feedback signals and modulated-voltage injecting points are proposed and compared based on modal analysis computation. Further, they are verified and observed in the root locus plot in order to get the respective responding supplementary controller designs. The time-domain simulation results illustrate the validity of the SSR damping control scheme. Also it shows that for the studied system, electrical power is the best feedback signal and q-axis of the GSC inner loop is the most effective modulated-voltage injecting point, which results in fairly simple design of the supplementary control. A proportional feedback control is sufficient for the SSR mode.