Exergoeconomic Evaluation of a Modern Ultra-Supercritical Power Plant

Abstract

In this paper, the exergoeconomic analysis was conducted to an existing ultra-supercritical coal-fired power plant in China to understand the cost-formation process, to evaluate the economic performance of each component and to find possible solutions for more cost-effective designs. The total revenue requirement (TRR) and the specific exergy costing (SPECO) methods were applied for economic analysis and exergy costing, respectively. Quantitative balances of exergy and exergetic costs as well as necessary auxiliary equations for both individual component and the overall system were established. The results show that the exergoeconomic factors of the furnace and heat exchangers at low temperature levels, including air preheater and low-pressure feedwater preheaters, are rather small; while those of other components are relatively large. Moving more heat absorption into furnace to use the effective radiation heat transfer, increasing the air preheating temperature and adding more low pressure feedwater preheaters can be promising solutions for future design.

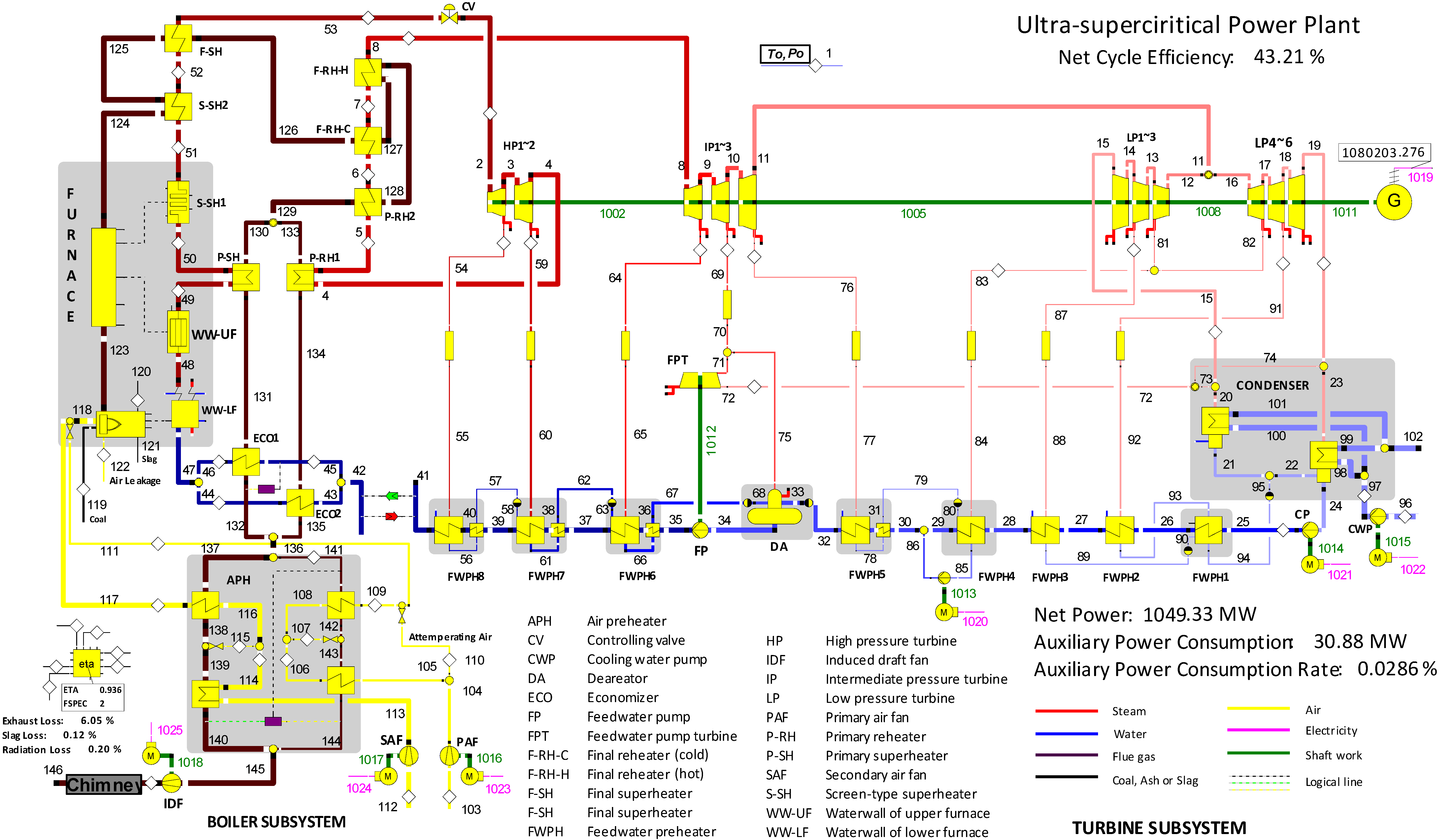
1. Introduction

In order to fulfill the objectives of a 20% reduction of national gross fuel consumption and a 10% reduction of total emission of mean pollutants during 2005 to 2010 [1], the efficiency improvement of coal-fired power plants, still contributing over 83% of China total power generation [2], became the first priority and called for a structure adjustment of the electricity generation industry in China.

In 2006, the coal-fired power plants less than 100 MW in China reached a total installed capacity as high as 125 GW with the annual coal consumption and SO₂ emission more than 400 and 5.4 million tons, respectively [3]. The pursues for higher efficiency, more economic benefits and lower pollutant emissions lead to the gradual phase-out of the small-scale backward power plants, which are replaced by advanced supercritical and ultra-supercritical ones with higher steam parameters [4].

In order to safely use higher temperature steam over 600 °C, more demanding requirements, especially in terms of advanced materials with higher allowed temperature and pressure, higher resistance to steam oxidation corrosion, better welding performance and larger heat conduction coefficient, largely increase the associated capital and maintenance costs of both boiler and turbine. It is apparent that the research on new material is the key factor for the development of supercritical and ultra-supercritical technologies. With lots of pioneer plant practices, the ferrite/martensite steels, mainly P91, P92, E991 and P122, have been the primary choices for high temperature materials for live steam pipelines; the austenitic steels such as HR3C and SUPER304H are commonly used for the high temperature heat surfaces [5]; Ni-based forging steel is currently selected as the material of rotary blades of high pressure turbine stages. In 2009, compared with the price of high temperature steel of subcritical power plants ranging from $15,000~18,000/ton, the specific cost of the four ferrite/martensite steels for supercritical and ultra-supercritical technologies is within the range of $20,000~30,000/ton [6]. The investment distribution of newly built modern power plants may be different from the subcritical ones and, therefore, has some influences on the cost formation process.

The exergoeconomic analysis is a powerful tool for evaluation and optimization of various energy systems by calculating the cost rates of each material and energy stream, and the component-related exergoeconomic variables. The term exergoeconomic was first introduced by Tsatsaronis [7] as an accurate and unambiguous characterization of a combination of economics and the exergy concept, and this methodology was greatly developed and applied with the contribution of many researchers including Valero and Lazano [8,9], Frangopoulos [9,10], von Spakovsky [11], Lazzaretto [12,13], Tsatsaronis [14,15,16,17,18,19,20] and some co-work [21,22,23] etc. Recently, there were also many applications of exergoeconomics for improving various power plants. Ahmadi et al., performed comprehensive exergy, exergoeconomic and exergoenvironmental impact analysis and multi-objective optimization to a cogeneration plant system [24], combined cycle power plants [25], a gas turbine power plant [26], with exact expressions of cost functions of each component and the cost expenditure due to pollutant and greenhouse gas emissions. Petrakopoulou [27] conducted the exergoeconomic and exergoenvironmental analysis on a newly-proposed chemical looping power plant and also combined an iterative optimization to reduce the cost and environmental impacts. Shamsi [28] optimized the steam pressure levels in a total site using thermoeconomic method and reached a total cost reduction of up to 8%.

Although the exergoeconomic analysis has been widely applied for analysis and optimization of power plants, seldom focuses on the modern ultra-supercritical large-scale coal-fired power plants, where the insights into the exergoeconomic performances of the subcomponents of the once-through boiler are needed. In this paper, an existing ultra-supercritical power plant designed in 2006, constructed in 2008 and operated in 2010, was modeled and analyzed from the exergoeconomic viewpoint by using the SPECO method [22]. In this regard, the specific objectives of this paper are as follows:

• To model the thermodynamic performance of the whole power plant and to obtain the basic information for cost estimation of the power plant.
• To perform detailed thermodynamic calculation for the design of boiler.
• To combine the standard design method of boiler with the corresponding economic analysis and to generate an equivalent approach to estimate boiler cost as the so-called cost function.
• To identify the cost-formation process, evaluate each component and provide some useful information for the future design improvement.

2. Exergoeconomic Analysis

The exergoeconomic analysis combines an exergetic analysis with an economic analysis to provide crucial information that is not obtainable through conventional thermodynamic analysis and simple exergy analysis or economic analysis [17]. With reasonable exergy costing method, the specific cost related with each exergy stream and the exergoeconomic variables are computed to provide some valuable information for a cost-effective enhancement by pinpointing the required changes in structure and parameter values [16,29]. A complete exergoeconomic analysis generally consists of an exergy analysis, an economic analysis and then an exergy costing method with the help of auxiliary equations.

2.1. Exergy Analysis

An exergy analysis identifies the location, the magnitude and the sources of thermodynamic inefficiencies in an energy system. By calculating chemical and physical exergy of each stream, the application of exergy analysis is quite straightforward with the calculation of exergy destruction within each component ${\dot{E}}_{D,k}$ and the corresponding exergetic efficiency ε_k and exergy destruction ratio y_D,k:

$${\epsilon }_k=\frac{{\dot{E}}_{P,k}}{{\dot{E}}_{F,k}}=1-\frac{{\dot{E}}_{D,k}}{{\dot{E}}_{F,k}}$$

(1)

$$y_{D,k}=\frac{{\dot{E}}_{D,k}}{{\dot{E}}_{F,tot}}$$

(2)

where the ${\dot{E}}_P$ and ${\dot{E}}_F$ are the product exergy and fuel exergy of k_th component (subscript k) and the whole system (subscript tot).

Combining the exergy balance equation of each component and the overall system, the detailed exergy destruction and loss rate, and overall exergetic efficiency can be obtained which can provide useful information for improvement from thermodynamic point of view:

$${\epsilon }_{tot}=\frac{{\dot{E}}_{P,tot}}{{\dot{E}}_{F,tot}}=1-\frac{{\dot{E}}_{L,tot}+{\sum }_{k=1}^{NC}{\dot{E}}_{D,k}}{{\dot{E}}_{F,tot}}$$

(3)

where ${\dot{E}}_{L,tot}$ means the exergy loss of the whole system while NC indicates the number of components.

Two points [16,22] should be emphasized in the exergy analysis are: (a) the dissipative components such as gas cleaning units and throttling valves as well as condensers without any thermodynamic benefits when considered in isolation cannot be assessed by the exergetic efficiency, and (b) the exergy loss are defined unambiguously as the transportation of exergy from the overall system to its surroundings which means that when no exergy loss term appears in the exergy balance equation at a component level.

It should be noted that the chemical exergy of mixtures such as flue gas is defined as follows [17]:

$$e_{mix}^{ch}=\left[{\displaystyle \sum }_{i=1}^n{X}_i{e}^{c{h}_i}+R{T}_0{\displaystyle \sum }_{i=1}^n{X}_{i}ln\left(X_i\right)\right]$$

(4)

where n, X, e^ch, R and T₀ represent the composition number of the mixture, the molar fraction of each composition, the specific chemical exergy of each composition, universal gas constant and the reference temperature, respectively.

The fuel exergy of fuel (e_f) is evaluated by the following exergy ratio ξ:

$$e_f=\xi ·HHV$$

(5)

where HHV means the higher heating value of coal and ξ for coal can be taken as 1.04 [17].

2.2. Economic Analysis

The annual values of capital-related charges (carrying charges), fuel cost and operating and maintenance expenses vary significantly within the plant economic life. Thus, levelized costs are need for the evaluation and cost optimization of an energy system. The TRR method [27] was applied based on the good estimation of the purchased equipment cost (PEC) and fixed capital cost FCI (FCI = PEC • F_BM and F_BM is the bare module factor), and cost escalation to the reference year in accordance with Chemical Engineering Plant Cost Index (CEPCI). At last, the levelized cost rates associated with the k_th component (${\dot{Z}}_k^{CI}$, ${\dot{Z}}_k^{OM}$ and ${\dot{Z}}_k$) and levelized fuel cost (c_F) can be obtained by Equations 6–9 as the input variables for exergoeconomic analysis:

$${\dot{Z}}_k^{CI}=\frac{C{C}_L}{\tau }\frac{PE{C}_k}{{\sum }_{n}PE{C}_n}$$

(6)

$${\dot{Z}}_k^{OM}=\frac{OM{C}_L}{\tau }\frac{PE{C}_k}{{\sum }_{n}PE{C}_n}$$

(7)

$$\dot{Z_k}=\dot{Z_k^{CI}}+{\dot{Z}}_k^{OM}$$

(8)

$$c_F=\frac{C{F}_L}{\tau }$$

(9)

where $\tau$ represents the equivalent working hours at full load.

2.3. Exergy Costing and Auxiliary Costing Equations

The specific cost (c_i) associated with each material and energy stream i is computed according to exergy costing and auxiliary costing equations, for which Lazzaretto and Tsatsaronis [22] proposed a systematic and general methodology (SPECO) with an explicit matrix form of these equations.

After clearly identifying each exergy stream, the exergy costing can be expressed by four exergy-based monetary costing Equations 10–12 and the cost balance (Equation 13) for each component:

$${\dot{C}}_i=c_i{\dot{E}}_i=c_i{\dot{m}}_i{e}_i$$

(10)

$${\dot{C}}_w={\dot{c}}_w\dot{W}$$

(11)

$${\dot{C}}_q=c_q{\dot{E}}_q$$

(12)

$${\displaystyle \sum }_e{\left(c_e{\dot{E}}_e\right)}_k+c_{w,k}{\dot{W}}_k=c_{q,k}{\dot{E}}_{q,k}+{\displaystyle \sum }_i{\left(c_i{\dot{E}}_i\right)}_k+{\dot{Z}}_k$$

(13)

where W, Q, ${\dot{C}}_w$ and ${\dot{C}}_q$ mean work, heat and cost rates of work and heat, respectively. The subscripts e and i indicate the exiting and inlet streams.

On the basis of F and P principles, totally (N_e − 1) auxiliary equations are required to determine the specific costs of products associated with the each component. The F principle states that the specific cost (cost per exergy unit) associated with this removal of exergy from a fuel stream must be equal to the average specific cost at which the removed exergy was supplied to the same stream in upstream components. While The P principle states that each exergy unit is supplied to any stream associated with the product at the same average cost. Combining the cost balance equations and the corresponding auxiliary equations, the explicit matrix can be straightforwardly solved by gaussian elimination and, therefore, the specific cost of each stream, the cost of thermodynamic inefficiency of each component and the related exergoeconomic variables can be obtained.

For the dissipative components, including the condenser and throttle valves in this case, the fictitious cost rates ${\dot{C}}_{diff,dc}$ must be calculated by Equation 14 based on their cost balance and the auxiliary equations in accordance with the F principle (c_e = c_i), and then apportioned to the cost of the final product of the overall system:

$${\dot{C}}_{diff,dc}={\displaystyle \sum }_i{c}_i\mathrm{∆}{\dot{E}}_i+{\dot{C}}_{aux}+{\dot{Z}}_{dc}$$

(14)

where ${\dot{C}}_{aux}$ indicates the cost rate of additional working fluid and ${\dot{Z}}_{dc}$ means the captital investment of dissipative components.

The costing of exergy loss exiting the k_th component is referred to the F principle of the k_th component. If no special treatments such as gas cleaning are conducted before the material stream is rejected to the environment, the cost rate of the exergy loss can be calculated by Equation 15:

$${\dot{C}}_L=c_{F,k}{\dot{E}}_L$$

(15)

2.4. Exergoeconomic Variables

The average unit cost of fuel c_F,k and product c_P,k, the cost rate of exergy destruction ${\dot{C}}_{D,k}$, the sum of ${\dot{C}}_{D,k}$ and Z_k, the relative cost difference r_k and exergoeconomic factor f_k are known as the thermoeconomic variables [29], among which r_k and f_k are the most important two exergoeconomic variables to rank the components based on their individual performance. The relative cost difference r_k is expressed as the difference between the specific cost of the product c_P,k and the fuel c_F,k:

$$r_k=\frac{{\dot{C}}_{P,k}-{\dot{C}}_{F,k}}{{\dot{C}}_{F,k}}=\frac{1-{\epsilon }_k}{{\epsilon }_k}+\frac{{\dot{Z}}_k}{{\dot{C}}_{D,k}}$$

(16)

The cost added to an exergy stream due to the thermodynamic inefficiency within one component can be evaluated by the component exergoeconomic factor, through which the monetary impact of exergy destruction and capital investment of each component can be revealed:

$$f_k=\frac{{\dot{Z}}_k}{{\dot{Z}}_k+{\dot{C}}_{D,k}}$$

(17)

3. Plant Description, Simulation and Cost Estimation

3.1. Plant Description

The single-reheat ultra-supercritical coal-fired power plant with total capacity 1000 MW comprises a Π-type once-through boiler, a condensing turbine, a generator as well as other auxiliary components and systems. The schematic and basic data of the reference plant are presented in Figure 1 and Table 1, respectively. The composition of the bituminous coal for the design is listed in Table 2.

Table 1. Basic data of the power plant.

Steam Cycle Data (100% Load)
Main steam	861.6 kg/s (274 bar, 605 °C)
Reheat steam	715.6 kg/s (56.8 bar, 603 °C)
Condenser pressure	0.052 bar
Gross power output	1100 MWe
Net power output	1070 MWe
Auxiliary power consumption	30 MWe
Net efficiency	44.15%

Table 1. Basic data of the power plant.

Steam Cycle Data (100% Load)
Main steam	861.6 kg/s (274 bar, 605 °C)
Reheat steam	715.6 kg/s (56.8 bar, 603 °C)
Condenser pressure	0.052 bar
Gross power output	1100 MWe
Net power output	1070 MWe
Auxiliary power consumption	30 MWe
Net efficiency	44.15%

Table 2. Coal composition.

Ultimate Analysis (wt %; as Received)
Carbon	57.37%
Hydrogen	4.19%
Oxygen	7.57%
Sulphur	0.87%
Nitrogen	1.4%
Moisture	21.3%
Ash	7.3%
LHV (kJ/kg)	22,000

Table 2. Coal composition.

Ultimate Analysis (wt %; as Received)
Carbon	57.37%
Hydrogen	4.19%
Oxygen	7.57%
Sulphur	0.87%
Nitrogen	1.4%
Moisture	21.3%
Ash	7.3%
LHV (kJ/kg)	22,000

Figure 1. Diagram of the reference ultra-supercritical power plant with detailed description of all components related to exergoeconomic analysis.

Figure 1. Diagram of the reference ultra-supercritical power plant with detailed description of all components related to exergoeconomic analysis.

Advanced combustion mode and devices, and reliable heat surface configuration with proper adjustment method for steam temperature are applied to guarantee high availability, good economic performance, reasonable dimension and heat flux of the furnace. After perheating, the feedwater first enters the two economizers (ECOs) placed in the front and back parts of rear flue gas duct, and then passes through the water wall (WW), one primary superheater (P-SH), two screen-type superheaters (S-SH1 and S-SH2) and one final superheater (F-SH) to generate live steam. The cold reheat steam coming from the exhaust of intermediate pressure turbine (IP) flows through the primary reheater (P-RH1 and P-RH2) and the final reheater (F-RH-H and F-RH-C). The temperature adjustment of reheat steam is based on the opening adjustment of the damper placed in the rear flue gas duct; while that of the live steam is mainly based on spray attemperators. Two Ljungström air pre-heaters (APHs) are configured to preheat the air by recovering low grade heat of flue gas.

The ultra-supercritical turbine is of a classical condensing configuration with four cylinders and four exhausts to enlarge the unit capacity. The feedwater regenerative system is composed of three high-pressure heaters, a deaerator and four low-pressure heaters to heat the feedwater to 300 °C. Large power consumption of feedwater pumps is supplied by the corresponding secondary condensing turbine. It is noted that the condenser is a dual-pressure one with two shells.

3.2. Plant Simulation

The power plant was modeled and simulated with the key features of each component or process, shown in Table 3 by Ebsilon Professional. The thermodynamic data for the selected streams are presented in Table 4. The heat transfer between auxiliary heat surfaces and the flue gas is neglected due to the small increase of steam temperature. The total outgoing flue gas of the furnace is assumed to pass the first screen-type superheater with the heat also absorbed by the auxiliary water wall, and then pass the second screen superheater. The air preheater is modeled in detail with the exact leakage air and attemperating air. The sealing steam leakage of turbine cylinders and the feedwater preheater using these leakage steams are omitted due to small mass flow rates of these steams and the small temperature increase of feedwater, respectively.

Table 3. Key features for different components or processes.

Name	Specification a	Name	Specification b
Combustion	α = 1.2; Δpfg = 100 Pa; ηc = 1; tslag = 600 °C	IP2	ηs = 0.915; ηm = 0.998
WW	Δpwf = 20.9 bar; Qt = 1104 MW	IP3	ηs = 0.929; ηm = 0.998
P-SH	Δpwf = 3.8 bar; Qt = 185 MW	LP1	ηs = 0.912; ηm = 0.998
S-SH1	Δpwf = 4.2 bar; Qt = 151 MW	LP2	ηs = 0.919; ηm = 0.998
S-SH2	Δpwf = 4.8 bar; Qt = 138 MW	LP3	ηs = 0.835; ηm = 0.998
F-SH	Δpwf = 5.0 bar; Qt = 133 MW	LP4	ηs = 0.912; ηm = 0.998
F-RH-C	Δpwf = 1.7 bar; Qt = 129 MW	LP5	ηs = 0.914; ηm = 0.998
F-RH-H	Δpwf = 2.0 bar; Qt = 44.8 MW	LP6	ηs = 0.788; ηm = 0.998
P-RH2	Δpwf = 2.5 bar; Qt = 45.1 MW	G	ηs = 0.99; ηm = 0.998
P-RH1	Δpwf = 2.5 bar; Qt = 177 MW	COND	Δtpinch = 5 K; Δpwf = 0.05 bar
ECO1	Δpwf = 1.0 bar; Qt = 86.9 MW	FPT	ηs = 0.81; ηm = 0.998
ECO2	Δpwf = 1.0 bar; Qt = 61.5 MW	FWPH1	Δtlow = 5.6 K; Δpfw = 0.54 bar
APH	Δppa = 420 pa; Δpsa = 2600 Pa;	FWPH2~4	Δtup = 2.8 K; Δpfw = 0.54 bar
	mL,pa→fg = 39.7 kg/s; mL,pa→fg = 9 kg/s	FWPH5	Δtup = 2.8 K; Δtlow = 5.6 K; Δpfw = 0.54 bar
	Qt,pa = 38 MW; Qt,sa = 236 MW	DA	P = 0.7 bar
IDF	ηs = 0.87; ηm = 0.99	FWPH6~7	Δtup = 0 K; Δtlow = 5.6 K; Δpfw = 1.12 bar
SAF	ηs = 0.88; ηm = 0.99	FWPH8	Δtup = −1.7 K; Δtlow = 5.6 K; Δpfw = 1.11 bar
PAF	ηs = 0.875; ηm = 0.99	FP	ηs = 0.84; ηm = 0.998
HP1	ηs =0.869; ηm = 0.998	CP	ηs = 0.87; ηm = 0.998
HP2	ηs = 0.925; ηm = 0.998	CWP	ηs = 0.8; ηm = 0.998
IP1	ηs = 0.894; ηm = 0.998	Motors	η = 0.97; ηm = 0.998

^a α–air ratio; Δp_fg—pressure drop of flue gas; η_c—combustion efficiency; t_slag—slag temperature; Δp_wf—pressure drop of working fluid; Q_t—heat transferred in this component; Δp_pa—pressure drop of primary air; Δp_sa—pressure drop of secondary air; m_L,pa→fg—air leakage from primary air to flue gas; m_L,sa→fg—air leakage from secondary air to flue gas; η_s—isentropic efficiency; η_m—mechanical efficiency; ^b Δt_pinch—pinch point; Δt_low—low terminal temperature difference; Δt_up—upper terminal temperature difference; Δp_fw—pressure drop of feedwater.

Table 3. Key features for different components or processes.

Name	Specification a	Name	Specification b
Combustion	α = 1.2; Δpfg = 100 Pa; ηc = 1; tslag = 600 °C	IP2	ηs = 0.915; ηm = 0.998
WW	Δpwf = 20.9 bar; Qt = 1104 MW	IP3	ηs = 0.929; ηm = 0.998
P-SH	Δpwf = 3.8 bar; Qt = 185 MW	LP1	ηs = 0.912; ηm = 0.998
S-SH1	Δpwf = 4.2 bar; Qt = 151 MW	LP2	ηs = 0.919; ηm = 0.998
S-SH2	Δpwf = 4.8 bar; Qt = 138 MW	LP3	ηs = 0.835; ηm = 0.998
F-SH	Δpwf = 5.0 bar; Qt = 133 MW	LP4	ηs = 0.912; ηm = 0.998
F-RH-C	Δpwf = 1.7 bar; Qt = 129 MW	LP5	ηs = 0.914; ηm = 0.998
F-RH-H	Δpwf = 2.0 bar; Qt = 44.8 MW	LP6	ηs = 0.788; ηm = 0.998
P-RH2	Δpwf = 2.5 bar; Qt = 45.1 MW	G	ηs = 0.99; ηm = 0.998
P-RH1	Δpwf = 2.5 bar; Qt = 177 MW	COND	Δtpinch = 5 K; Δpwf = 0.05 bar
ECO1	Δpwf = 1.0 bar; Qt = 86.9 MW	FPT	ηs = 0.81; ηm = 0.998
ECO2	Δpwf = 1.0 bar; Qt = 61.5 MW	FWPH1	Δtlow = 5.6 K; Δpfw = 0.54 bar
APH	Δppa = 420 pa; Δpsa = 2600 Pa;	FWPH2~4	Δtup = 2.8 K; Δpfw = 0.54 bar
	mL,pa→fg = 39.7 kg/s; mL,pa→fg = 9 kg/s	FWPH5	Δtup = 2.8 K; Δtlow = 5.6 K; Δpfw = 0.54 bar
	Qt,pa = 38 MW; Qt,sa = 236 MW	DA	P = 0.7 bar
IDF	ηs = 0.87; ηm = 0.99	FWPH6~7	Δtup = 0 K; Δtlow = 5.6 K; Δpfw = 1.12 bar
SAF	ηs = 0.88; ηm = 0.99	FWPH8	Δtup = −1.7 K; Δtlow = 5.6 K; Δpfw = 1.11 bar
PAF	ηs = 0.875; ηm = 0.99	FP	ηs = 0.84; ηm = 0.998
HP1	ηs =0.869; ηm = 0.998	CP	ηs = 0.87; ηm = 0.998
HP2	ηs = 0.925; ηm = 0.998	CWP	ηs = 0.8; ηm = 0.998
IP1	ηs = 0.894; ηm = 0.998	Motors	η = 0.97; ηm = 0.998

^a α–air ratio; Δp_fg—pressure drop of flue gas; η_c—combustion efficiency; t_slag—slag temperature; Δp_wf—pressure drop of working fluid; Q_t—heat transferred in this component; Δp_pa—pressure drop of primary air; Δp_sa—pressure drop of secondary air; m_L,pa→fg—air leakage from primary air to flue gas; m_L,sa→fg—air leakage from secondary air to flue gas; η_s—isentropic efficiency; η_m—mechanical efficiency; ^b Δt_pinch—pinch point; Δt_low—low terminal temperature difference; Δt_up—upper terminal temperature difference; Δp_fw—pressure drop of feedwater.

Table 4. Thermodynamic data for selected streams.

ID	m	t	p	Ech	E	ID	m	t	p	Ech	E
	kg/s	°C	bar	MW	MW		kg/s	°C	bar	MW	MW
2	861.6	601.4	262.5	2.15	1408.2	37	861.6	221.9	316.23	2.15	205.8
3	816.3	420.9	86.31	2.04	1072.6	39	861.6	279.4	315.11	2.15	306.1
4	715.6	380.3	65.56	1.79	888.1	41	861.6	299.9	314	2.15	347.7
5	715.6	476.0	63.06	1.79	987.2	47	861.6	332.0	313	2.15	421.8
6	715.6	501.0	60.56	1.79	1011.2	49	861.6	441.0	292.1	2.15	1038.7
7	715.6	577.0	58.86	1.79	1091.3	50	861.6	476.0	288.3	2.15	1148.2
8	715.6	603.0	56.86	1.79	1117.6	51	861.6	515.0	284.1	2.15	1240.5
9	679.9	472.0	24.79	1.70	871.2	52	861.6	558.0	279.3	2.15	1327.0
10	601.6	370.7	12.18	1.50	644.0	53	861.6	605.0	274.3	2.15	1412.7
11	564.8	289.7	6.490	1.41	511.3	72	49.9	36.8	0.062	0.12	6.4
13	282.4	289.7	6.490	0.65	185.3	104	231.5	32.1	1.144	0.46	2.9
14	262.0	192.9	2.677	0.59	110.7	111	191.8	200.0	1.14	0.39	10.0
15	236.9	90.1	0.704	0.59	23.7	113	746.0	24.4	1.058	1.50	4.4
17	236.9	33.6	0.052	0.71	255.7	117	737.0	336.0	1.031	1.48	79.8
18	282.4	289.7	6.490	0.65	185.3	124	1047.5	1139.8	0.998	55.95	888.6
19	262.0	192.9	2.677	0.59	74.8	125	1047.5	1037.8	0.998	55.95	780.1
24	573.9	33.6	0.052	1.43	2.1	126	1047.5	938.2	0.998	55.95	677.7
25	573.9	33.7	16.08	1.43	3.0	127	1047.5	839.9	0.998	55.95	580.8
26	573.9	37.1	15.54	1.43	3.4	128	1047.5	805.5	0.998	55.95	547.9
27	573.9	62.4	15.00	1.43	9.0	129	1047.5	770.8	0.998	55.95	515.2
28	573.9	85.9	14.46	1.43	17.7	131	575.1	503.6	0.998	30.72	158.1
30	651.5	125.5	13.92	1.63	44.7	134	472.4	456.7	0.998	25.23	114.2
32	651.5	158.3	13.38	1.63	71.5	136	1047.5	358.9	0.983	55.95	185.9
34	861.6	185.8	11.43	2.15	129.8	145	1096.2	119.2	0.972	54.40	69.8
35	861.6	192.4	317.32	2.15	162.6	146	1096.2	128.5	1.049	54.40	79.4

Table 4. Thermodynamic data for selected streams.

ID	m	t	p	Ech	E	ID	m	t	p	Ech	E
	kg/s	°C	bar	MW	MW		kg/s	°C	bar	MW	MW
2	861.6	601.4	262.5	2.15	1408.2	37	861.6	221.9	316.23	2.15	205.8
3	816.3	420.9	86.31	2.04	1072.6	39	861.6	279.4	315.11	2.15	306.1
4	715.6	380.3	65.56	1.79	888.1	41	861.6	299.9	314	2.15	347.7
5	715.6	476.0	63.06	1.79	987.2	47	861.6	332.0	313	2.15	421.8
6	715.6	501.0	60.56	1.79	1011.2	49	861.6	441.0	292.1	2.15	1038.7
7	715.6	577.0	58.86	1.79	1091.3	50	861.6	476.0	288.3	2.15	1148.2
8	715.6	603.0	56.86	1.79	1117.6	51	861.6	515.0	284.1	2.15	1240.5
9	679.9	472.0	24.79	1.70	871.2	52	861.6	558.0	279.3	2.15	1327.0
10	601.6	370.7	12.18	1.50	644.0	53	861.6	605.0	274.3	2.15	1412.7
11	564.8	289.7	6.490	1.41	511.3	72	49.9	36.8	0.062	0.12	6.4
13	282.4	289.7	6.490	0.65	185.3	104	231.5	32.1	1.144	0.46	2.9
14	262.0	192.9	2.677	0.59	110.7	111	191.8	200.0	1.14	0.39	10.0
15	236.9	90.1	0.704	0.59	23.7	113	746.0	24.4	1.058	1.50	4.4
17	236.9	33.6	0.052	0.71	255.7	117	737.0	336.0	1.031	1.48	79.8
18	282.4	289.7	6.490	0.65	185.3	124	1047.5	1139.8	0.998	55.95	888.6
19	262.0	192.9	2.677	0.59	74.8	125	1047.5	1037.8	0.998	55.95	780.1
24	573.9	33.6	0.052	1.43	2.1	126	1047.5	938.2	0.998	55.95	677.7
25	573.9	33.7	16.08	1.43	3.0	127	1047.5	839.9	0.998	55.95	580.8
26	573.9	37.1	15.54	1.43	3.4	128	1047.5	805.5	0.998	55.95	547.9
27	573.9	62.4	15.00	1.43	9.0	129	1047.5	770.8	0.998	55.95	515.2
28	573.9	85.9	14.46	1.43	17.7	131	575.1	503.6	0.998	30.72	158.1
30	651.5	125.5	13.92	1.63	44.7	134	472.4	456.7	0.998	25.23	114.2
32	651.5	158.3	13.38	1.63	71.5	136	1047.5	358.9	0.983	55.95	185.9
34	861.6	185.8	11.43	2.15	129.8	145	1096.2	119.2	0.972	54.40	69.8
35	861.6	192.4	317.32	2.15	162.6	146	1096.2	128.5	1.049	54.40	79.4

3.3. Cost Estimation

The power plant was designed for a 25-year economic life with an average interest rate 10%, average nominal escalation rates 3.5% for fuel (coal) and 3% for other costs and could operate for 6900 h/year at a load capacity 80%. The average price of the coal with the LHV of 29,270 MJ/kg was $84.3/ton (2.88 $/GJ-LHV) in 2009. It means the levelized FC reaches as high as $196.5 million.

The PEC of the entire sets of the once-through boiler, including the air preheaters, high pressure and low pressure regenerative heaters, the steam turbine and other separate components, could be obtained from [6]. The PEC of boiler and steam turbine needs to be apportioned to their sub-components shown in Figure 1. It is noted that the PEC of rotary air preheaters comprises approximately 2% of PEC of the boiler body [30], which means the boiler subsystem excluding SAF, PAF as well as IDF. The allocation of the remaining PEC of boiler is on the basis of Table 5, where the main material, average tube size, total tube surface area and weight are presented. Owing to the lack of information for the specific costs for different types of steel, weighting factors for each heat exchanger in boiler are assumed in accordance with properties of their material, while the allocation of turbine PEC is weighted based on both the power output and the pressure level of each sub-component with the weighting factors 1, 1.5 and 2 for HPs, IPs and LPs, respectively.

Table 5. Information of heat surfaces in the once-through boiler.

Name		Material	Tube Size δ × ro	Tube Surface Area (m2)	Weight *	Weighted Factor
			(mm × mm)		(ton)
FUR	WW-S	15CrMoG	38.1 × 7	8,880	406.77	1.0
	WW-V	12Cr1MoVG	31.8 × 7	4,603	207.24	1.0
	S-SH1	T91, S304H	41.3 × 7	3,308	143.66	3.0
S-SH2		S304H	47.7 × 10	2,880	180.44	3.0
F-SH		S304H, HR3C	44.5 × 10	4,105	252.27	3.0
F-RH-C		S304H, HR3C	57 × 6	5,916	233.11	3.0
F-RH-H		S304H, HR3C	57 × 6	2,843	112.02	3.0
P-RH2		T91	63.5 × 5	3,305	109.57	1.5
P-SH		12Cr1MoVG, T91	46.1 × 6	25,106	1038.82	1.0
ECON1		SA-210C	50.8 × 9	14,190	833.25	0.8
P-RH1		12Cr1MoVG, T91	63.5 × 5	25,137	833.38	1.0
ECON2		SA-210C	50.8 × 9	20,112	1180.99	0.8

* Equation for steel weight is [0.02491 ∙ δ ∙ (r_o − δ) ∙ L]/1000(ton), where units of δ, r, L should be m.

Table 5. Information of heat surfaces in the once-through boiler.

Name		Material	Tube Size δ × ro	Tube Surface Area (m2)	Weight *	Weighted Factor
			(mm × mm)		(ton)
FUR	WW-S	15CrMoG	38.1 × 7	8,880	406.77	1.0
	WW-V	12Cr1MoVG	31.8 × 7	4,603	207.24	1.0
	S-SH1	T91, S304H	41.3 × 7	3,308	143.66	3.0
S-SH2		S304H	47.7 × 10	2,880	180.44	3.0
F-SH		S304H, HR3C	44.5 × 10	4,105	252.27	3.0
F-RH-C		S304H, HR3C	57 × 6	5,916	233.11	3.0
F-RH-H		S304H, HR3C	57 × 6	2,843	112.02	3.0
P-RH2		T91	63.5 × 5	3,305	109.57	1.5
P-SH		12Cr1MoVG, T91	46.1 × 6	25,106	1038.82	1.0
ECON1		SA-210C	50.8 × 9	14,190	833.25	0.8
P-RH1		12Cr1MoVG, T91	63.5 × 5	25,137	833.38	1.0
ECON2		SA-210C	50.8 × 9	20,112	1180.99	0.8

* Equation for steel weight is [0.02491 ∙ δ ∙ (r_o − δ) ∙ L]/1000(ton), where units of δ, r, L should be m.

The module factors for different types of components to calculate the FCI from their PEC are referred to [31] and listed in Table 6. With the ratio of component PEC to the total PEC, the levelized CC and OMC can be readily apportioned to each component. The TCI estimation for the whole power plant is around $828 million, which means the specific cost of the power plant is nearly $774/kW.

The levelized CC, OMC and FC contribute 30%, 7% and 63% to the TRR $308 million/year, meaning that the price of the final product is 5.22 cent/kWh. It agrees quite well with the on-gird electricity price of 5.20 cent/kWh announced by the power plant [32].

Table 6. F_BM for different types of components [31].

Name	FBM	Name	FBM
Fired heaters and furnace	2.8	Other heaters	1.7
Main turbine	6	Drive turbine for pumps	3.7
Fans	2.8	Pumps	1.3
Generator	1.7

Table 6. F_BM for different types of components [31].

Name	FBM	Name	FBM
Fired heaters and furnace	2.8	Other heaters	1.7
Main turbine	6	Drive turbine for pumps	3.7
Fans	2.8	Pumps	1.3
Generator	1.7

4. Results and Discussion

Table 7 presents the results of the exergetic and exergoeconomic analysis for two conditions: with and without Z_k. Comparisons of the cost rates associated to each component enable us to understand how the cost structure or cost formation process changes after adding the capital, operation and maintenance investments.

The exergetic analysis reveals the location, magnitude and sources of exergy destruction. Chemical reaction and heat transfer process are always the largest sources of entropy generation in energy systems. It is shown that the exergy destruction in furnace has far larger exergy destruction than any other components, resulting in the lowest exergetic efficiency of 62.8%. The performance of other heat exchangers in boiler improves greatly with the decrease of average temperature difference for the heat transfer between the hot and cold fluids. The turbine stages except ones working within the range of wet steam have higher exergy efficiency (generally over 90%) than heat exchangers. The exergetic performances of regenerative feedwater preheaters improve with the increase of feedwater temperature level. The exergetic efficiency of the last preheater reaches as high as 96.4%. It should be noted that the exergetic efficiencies of air preheater, the first and second feedwater preheaters are far less than those of other heat exchangers, due to the low temperature level of their cold fluids. In addition, the auxiliary components, mainly pumps and fans here, are regarded to have relative high efficiency around 85%.

It is very clear from the exergoeconomic analysis with Z_k = 0 that the specific costs of the flue gases remain unchanged due to the F principles for boiler sub-components and the specific cost of the intermediate product accumulates gradually among the components towards the final product. Due to this accumulation, the distribution of hidden costs caused by the exergy destructions among different components tends to be quite different from that of their exergy destructions. The exergy destruction within boiler components excluding the furnace reaches as high as 150 MW which is almost two times more than that of turbine itself (82 MW); however, their hidden cost rates are proven to be almost the same with $2,180/h and $2,045/h for boiler and turbine, respectively. It indicates that the economic importance of exergy destruction within a component depends highly on its relative position of the component with respect to fuel and product streams of the overall system [27].

The sum ${\dot{C}}_{D,k}+{\dot{Z}}_k$ indicates the cost importance of different components and the improvement of design should be initially focused on the components with higher ${\dot{C}}_{D,k}+{\dot{Z}}_k$. From this point of view, the once-through boiler, among which almost all the sub-components, especially the furnace, have very large ${\dot{C}}_{D,k}+{\dot{Z}}_k$, and the components HP1, IP1 and LP6 of the turbine are the keys for improving initial design of the power plant.

Table 7. Results of the exergetic and exergoeconomic analysis for selected components of the reference power plant.

Name			Exergy Balance					$Z_k=\mathbf{0}$				$Z_k\ne \mathbf{0}$
			${\dot{E}}_D$	${\dot{E}}_F$	${\dot{E}}_P$	yD	εk	cf	cp	r	${\dot{C}}_D$	cf	cp	${\dot{C}}_D$	$\dot{Z}$	${\dot{C}}_D+\dot{Z}$	r	f
			MW	MW	MW	%	%	$/GJ	$/GJ	-	$/h	$/GJ	$/GJ	$/h	$/h	$/h	-	-
	Boiler Body	FUR	944.2	2542.0	1597	37.33	62.86	4.080	6.491	0.59	13,869	4.143	6.872	1,4082	1,615.3	15,697	0.66	0.10
Boiler Subsystem		S-SH2	22.0	108.5	86.5	0.87	79.70	4.018	5.041	0.26	318.7	4.018	7.728	318.7	836.7	1,155.4	0.92	0.72
		F-SH	16.7	102.4	85.7	0.66	83.72	4.018	4.800	0.19	241.1	4.018	8.592	241.1	1,169.8	1,410.9	1.14	0.83
		F-RH-C	16.9	97.0	80.1	0.67	82.60	4.018	4.865	0.21	244.1	4.018	8.614	244.1	1,081.0	1,325.0	1.14	0.82
		F-RH-H	6.5	32.9	26.3	0.26	80.18	4.018	5.012	0.25	94.2	4.018	10.490	94.2	519.5	613.7	1.61	0.85
		P-RH2	8.7	32.7	24.0	0.34	73.45	4.018	5.470	0.36	125.5	4.018	8.409	125.5	254.1	379.6	1.09	0.67
		P-SH	19.1	118.2	99.1	0.76	83.84	4.018	4.792	0.19	276.2	4.018	9.295	276.2	1,605.7	1,881.9	1.31	0.85
		ECON1	15.3	124.8	109.5	0.60	87.76	4.018	4.578	0.14	220.9	4.018	7.192	220.9	1,030.4	1,251.2	0.79	0.82
		P-RH1	4.5	37.5	33.1	0.18	88.10	4.018	4.561	0.14	64.6	4.018	15.379	64.6	1,288.2	1,352.8	2.83	0.95
		ECON2	7.6	48.6	41.0	0.30	84.28	4.018	4.767	0.19	110.6	4.018	14.662	110.6	1,460.4	1,571.0	2.65	0.93
		APH	33.5	116.1	82.5	1.33	71.11	4.018	5.651	0.41	485.1	4.018	6.397	485.1	221.7	706.7	0.59	0.31
	PAF		0.5	2.9	2.5	0.02	84.30	8.360	9.917	0.19	13.8	12.873	30.234	21.3	132.9	154.2	1.35	0.86
	SAF		0.5	3.4	2.9	0.02	84.50	8.360	9.894	0.18	16.1	12.873	26.340	24.7	116.3	141.1	1.05	0.83
	IDF		1.6	11.2	9.6	0.06	86.02	8.360	9.718	0.16	47.0	12.873	20.653	72.3	196.6	268.9	0.60	0.73
Turbine Subsystem	Turbine Body	HP1	17.2	276.1	258.8	0.68	93.76	8.185	8.729	0.07	507.7	10.875	12.182	674.6	542.9	1,217.4	0.12	0.45
		HP2	2.2	59.6	57.3	0.09	96.29	8.185	8.500	0.04	65.1	10.875	11.877	86.5	120.3	206.7	0.09	0.58
		IP1	9.4	200.6	191.2	0.37	95.31	7.513	7.882	0.05	254.4	10.511	11.902	355.9	601.5	957.4	0.13	0.63
		IP2	6.1	143.5	137.3	0.24	95.72	7.513	7.848	0.05	165.9	10.511	11.854	232.1	432.0	664.2	0.13	0.65
		IP3	4.0	99.4	95.4	0.16	95.96	7.513	7.829	0.04	108.6	10.511	11.827	151.9	300.1	452.0	0.13	0.66
		LP1	3.3	55.9	52.5	0.13	94.04	7.513	7.989	0.06	90.1	10.511	12.342	126.0	220.3	346.4	0.17	0.64
		LP2	4.3	62.9	58.6	0.17	93.17	7.513	8.063	0.07	116.2	10.511	12.446	162.6	246.0	408.6	0.18	0.60
		LP3	14.0	87.0	73.0	0.55	83.95	7.513	8.950	0.19	377.6	10.511	13.686	528.3	306.3	834.6	0.30	0.37
		LP4	3.3	55.9	52.5	0.13	94.04	7.513	7.989	0.06	90.1	10.511	12.342	126.0	220.3	346.4	0.17	0.64
		LP5	7.8	101.8	94.0	0.31	92.30	7.513	8.140	0.08	212.0	10.511	12.553	296.6	394.2	690.7	0.19	0.57
		LP6	10.6	51.3	40.8	0.42	79.39	7.513	9.464	0.26	286.2	10.511	14.405	400.4	170.9	571.3	0.37	0.30
	COND		39.3	-	-	1.55	-	9.900	-		1,399.1	13.851	-	1,957.4	1,370.9	3,328.3	-	0.41
	Regeneration System	FWPH1	0.586	0.962	0.377	0.023	39.13	7.513	19.200	1.56	15.8	10.511	27.668	22.2	1.1	23.3	1.63	0.05
		FWPH2	2.6	8.1	5.5	0.10	68.26	7.513	11.007	0.47	69.6	10.511	15.682	97.3	5.6	103.0	0.49	0.06
		FWPH3	2.0	10.7	8.8	0.08	81.70	7.513	9.195	0.22	53.1	10.511	13.014	74.4	4.7	79.1	0.24	0.06
		FWPH4	4.5	25.9	21.4	0.18	82.62	7.513	9.093	0.21	121.7	10.511	12.787	170.3	5.1	175.3	0.22	0.03
		FWPH5	3.6	30.5	26.9	0.14	88.06	7.513	8.532	0.14	98.5	10.511	11.992	137.8	5.3	143.2	0.14	0.04
		DA	3.1	29.7	26.6	0.12	89.56	7.583	8.467	0.12	84.7	10.549	12.645	117.8	83.1	200.9	0.20	0.41
		FWPH6	4.5	47.8	43.2	0.18	90.51	7.629	8.428	0.11	124.5	10.574	12.860	172.5	183.4	355.9	0.22	0.52
		FWPH7	7.1	107.4	100.3	0.28	93.35	8.185	8.768	0.07	210.5	10.875	12.315	279.7	240.1	519.8	0.13	0.46
		FWPH8	1.5	43.2	41.6	0.06	96.42	8.185	8.489	0.04	45.6	10.875	12.703	60.6	213.4	274.0	0.17	0.78
	FPT		8.6	46.7	38.2	0.34	81.68	7.513	9.198	0.22	231.5	10.511	15.838	323.9	407.8	731.6	0.51	0.56
	FP		5.4	38.2	32.8	0.21	85.88	9.198	10.711	0.16	178.4	15.838	22.285	307.2	453.3	760.5	0.41	0.60
	CP		0.2	1.1	0.9	0.01	84.61	8.360	9.880	0.18	5.1	12.873	30.092	7.8	49.9	57.7	1.34	0.86
	CWP		2.5	11.1	8.6	0.10	77.21	8.360	10.827	0.30	76.4	12.873	28.245	117.6	358.2	475.8	1.19	0.75
G			11.7	1111.5	1099.9	0.46	98.95	8.272	8.360	0.01	347.6	12.288	12.873	516.3	1,800.2	2,316.5	0.05	0.78
Total (EL = 175MW)			1283	2529	1070	50.75	42.31	3.911	9.244	1.36	18,069	3.911	14.512	18,069	20,293	38,362	2.71	0.53

Table 7. Results of the exergetic and exergoeconomic analysis for selected components of the reference power plant.

Name			Exergy Balance					$Z_k=\mathbf{0}$				$Z_k\ne \mathbf{0}$
			${\dot{E}}_D$	${\dot{E}}_F$	${\dot{E}}_P$	yD	εk	cf	cp	r	${\dot{C}}_D$	cf	cp	${\dot{C}}_D$	$\dot{Z}$	${\dot{C}}_D+\dot{Z}$	r	f
			MW	MW	MW	%	%	$/GJ	$/GJ	-	$/h	$/GJ	$/GJ	$/h	$/h	$/h	-	-
	Boiler Body	FUR	944.2	2542.0	1597	37.33	62.86	4.080	6.491	0.59	13,869	4.143	6.872	1,4082	1,615.3	15,697	0.66	0.10
Boiler Subsystem		S-SH2	22.0	108.5	86.5	0.87	79.70	4.018	5.041	0.26	318.7	4.018	7.728	318.7	836.7	1,155.4	0.92	0.72
		F-SH	16.7	102.4	85.7	0.66	83.72	4.018	4.800	0.19	241.1	4.018	8.592	241.1	1,169.8	1,410.9	1.14	0.83
		F-RH-C	16.9	97.0	80.1	0.67	82.60	4.018	4.865	0.21	244.1	4.018	8.614	244.1	1,081.0	1,325.0	1.14	0.82
		F-RH-H	6.5	32.9	26.3	0.26	80.18	4.018	5.012	0.25	94.2	4.018	10.490	94.2	519.5	613.7	1.61	0.85
		P-RH2	8.7	32.7	24.0	0.34	73.45	4.018	5.470	0.36	125.5	4.018	8.409	125.5	254.1	379.6	1.09	0.67
		P-SH	19.1	118.2	99.1	0.76	83.84	4.018	4.792	0.19	276.2	4.018	9.295	276.2	1,605.7	1,881.9	1.31	0.85
		ECON1	15.3	124.8	109.5	0.60	87.76	4.018	4.578	0.14	220.9	4.018	7.192	220.9	1,030.4	1,251.2	0.79	0.82
		P-RH1	4.5	37.5	33.1	0.18	88.10	4.018	4.561	0.14	64.6	4.018	15.379	64.6	1,288.2	1,352.8	2.83	0.95
		ECON2	7.6	48.6	41.0	0.30	84.28	4.018	4.767	0.19	110.6	4.018	14.662	110.6	1,460.4	1,571.0	2.65	0.93
		APH	33.5	116.1	82.5	1.33	71.11	4.018	5.651	0.41	485.1	4.018	6.397	485.1	221.7	706.7	0.59	0.31
	PAF		0.5	2.9	2.5	0.02	84.30	8.360	9.917	0.19	13.8	12.873	30.234	21.3	132.9	154.2	1.35	0.86
	SAF		0.5	3.4	2.9	0.02	84.50	8.360	9.894	0.18	16.1	12.873	26.340	24.7	116.3	141.1	1.05	0.83
	IDF		1.6	11.2	9.6	0.06	86.02	8.360	9.718	0.16	47.0	12.873	20.653	72.3	196.6	268.9	0.60	0.73
Turbine Subsystem	Turbine Body	HP1	17.2	276.1	258.8	0.68	93.76	8.185	8.729	0.07	507.7	10.875	12.182	674.6	542.9	1,217.4	0.12	0.45
		HP2	2.2	59.6	57.3	0.09	96.29	8.185	8.500	0.04	65.1	10.875	11.877	86.5	120.3	206.7	0.09	0.58
		IP1	9.4	200.6	191.2	0.37	95.31	7.513	7.882	0.05	254.4	10.511	11.902	355.9	601.5	957.4	0.13	0.63
		IP2	6.1	143.5	137.3	0.24	95.72	7.513	7.848	0.05	165.9	10.511	11.854	232.1	432.0	664.2	0.13	0.65
		IP3	4.0	99.4	95.4	0.16	95.96	7.513	7.829	0.04	108.6	10.511	11.827	151.9	300.1	452.0	0.13	0.66
		LP1	3.3	55.9	52.5	0.13	94.04	7.513	7.989	0.06	90.1	10.511	12.342	126.0	220.3	346.4	0.17	0.64
		LP2	4.3	62.9	58.6	0.17	93.17	7.513	8.063	0.07	116.2	10.511	12.446	162.6	246.0	408.6	0.18	0.60
		LP3	14.0	87.0	73.0	0.55	83.95	7.513	8.950	0.19	377.6	10.511	13.686	528.3	306.3	834.6	0.30	0.37
		LP4	3.3	55.9	52.5	0.13	94.04	7.513	7.989	0.06	90.1	10.511	12.342	126.0	220.3	346.4	0.17	0.64
		LP5	7.8	101.8	94.0	0.31	92.30	7.513	8.140	0.08	212.0	10.511	12.553	296.6	394.2	690.7	0.19	0.57
		LP6	10.6	51.3	40.8	0.42	79.39	7.513	9.464	0.26	286.2	10.511	14.405	400.4	170.9	571.3	0.37	0.30
	COND		39.3	-	-	1.55	-	9.900	-		1,399.1	13.851	-	1,957.4	1,370.9	3,328.3	-	0.41
	Regeneration System	FWPH1	0.586	0.962	0.377	0.023	39.13	7.513	19.200	1.56	15.8	10.511	27.668	22.2	1.1	23.3	1.63	0.05
		FWPH2	2.6	8.1	5.5	0.10	68.26	7.513	11.007	0.47	69.6	10.511	15.682	97.3	5.6	103.0	0.49	0.06
		FWPH3	2.0	10.7	8.8	0.08	81.70	7.513	9.195	0.22	53.1	10.511	13.014	74.4	4.7	79.1	0.24	0.06
		FWPH4	4.5	25.9	21.4	0.18	82.62	7.513	9.093	0.21	121.7	10.511	12.787	170.3	5.1	175.3	0.22	0.03
		FWPH5	3.6	30.5	26.9	0.14	88.06	7.513	8.532	0.14	98.5	10.511	11.992	137.8	5.3	143.2	0.14	0.04
		DA	3.1	29.7	26.6	0.12	89.56	7.583	8.467	0.12	84.7	10.549	12.645	117.8	83.1	200.9	0.20	0.41
		FWPH6	4.5	47.8	43.2	0.18	90.51	7.629	8.428	0.11	124.5	10.574	12.860	172.5	183.4	355.9	0.22	0.52
		FWPH7	7.1	107.4	100.3	0.28	93.35	8.185	8.768	0.07	210.5	10.875	12.315	279.7	240.1	519.8	0.13	0.46
		FWPH8	1.5	43.2	41.6	0.06	96.42	8.185	8.489	0.04	45.6	10.875	12.703	60.6	213.4	274.0	0.17	0.78
	FPT		8.6	46.7	38.2	0.34	81.68	7.513	9.198	0.22	231.5	10.511	15.838	323.9	407.8	731.6	0.51	0.56
	FP		5.4	38.2	32.8	0.21	85.88	9.198	10.711	0.16	178.4	15.838	22.285	307.2	453.3	760.5	0.41	0.60
	CP		0.2	1.1	0.9	0.01	84.61	8.360	9.880	0.18	5.1	12.873	30.092	7.8	49.9	57.7	1.34	0.86
	CWP		2.5	11.1	8.6	0.10	77.21	8.360	10.827	0.30	76.4	12.873	28.245	117.6	358.2	475.8	1.19	0.75
G			11.7	1111.5	1099.9	0.46	98.95	8.272	8.360	0.01	347.6	12.288	12.873	516.3	1,800.2	2,316.5	0.05	0.78
Total (EL = 175MW)			1283	2529	1070	50.75	42.31	3.911	9.244	1.36	18,069	3.911	14.512	18,069	20,293	38,362	2.71	0.53

In general, the components in boiler subsystem have much larger relative cost difference r_k than other components. The heat surfaces placed in the rear flue gas duct, such as P-RH1 and ECON2, achieve the greatest r as high as 2.8, while ones surrounded by higher-temperature flue gas, such as S-SH2, F-RH, F-SH and P-SH, have relative small r ranging from 0.9 to 1.5. Moreover, this parameter of the components in turbine and regeneration system is below 0.5, mostly around 0.1~0.3. What means by this is that the add costs of exergy streams through the heat surfaces after furnace due to their capital investment are much larger than that of turbine subsystem. By comparison, reducing the construction cost of these heat surfaces while keeping or lowering the level of exergy destruction must be achieved for future boiler design.

Exergoeconomic factors can identify the major cost sources (investment cost or cost of exergy destruction) of each component. It is clear that the air preheater and the furnace have far less exergoeconomic factors than any other components in the boiler. It indicates that the capital investments of these two components should be increased to improve their thermodynamic performance and the overall performance. The extremely high exergoeconomic factors of other heating surfaces indicate that more profits and cost effectiveness can be obtained if part of heat absorbed in these surfaces can be realized by the more effective radiation heat transfer in furnace with less heating surface areas. At the same time, the surface area of the air preheater can be increased to achieve a higher air preheating temperature, which can lead to a temperature increase of the flue gas and also a more even temperature field in furnace for more fierce radiation. Both the exergy destruction and the investment cost can be properly reduced and, therefore, better performance of the boiler can be achieved.

The turbine sections generally have large exergoeconomic factors within the range from 0.7 to 0.8 with the exception of the last two parallel sections LP3 and LP6, indicating that the performance of the final stages should be improved by increasing the capital investment. For the final turbine stages working in wet steam zone, more demanding blade metallurgy and coatings can be applied to against the blade erosion caused by condensed water droplets.

In addition, the factors of feedwater preheaters are rather small, less than 0.4, especially that of the low pressure feedwater preheaters, no more than 0.03. What is meant by this is that more feedwater preheaters can be configured to enhance the overall cycle performance by approaching the ideal feedwater preheating process.

5. Conclusions

In this paper, a modern ultra-supercritical power plant was analyzed by exergoeconomic methodology to evaluate the performances of each component and find possible solutions to improve overall plant performance from initial system design. The TRR method was used to determine CIL, OMCL and FCL while the SPECO method was applied for the exergy costing. The PECs of main components were referred to the quota design for coal-fired power plants, and were properly apportioned to related sub-components. With good agreement with the on-grid electricity, the levelized costs associated with each component were obtained and the exergoeconomic analysis was conducted with the following conclusions:

• A promising solution for the cost effective design for the once-through boiler may be moving more heat absorption to the furnace by using more effective radiation heat transfer and less area of heat surfaces.
• The area of air preheaters should be properly increased to achieve a higher air temperature and thus a more even radiation field in the furnace. However, this solution also confronts many problems such as the proper placement of the heat surfaces in the furnace and their influences on the aerodynamic of flue gas and so on.
• The design of turbine stages with exhaust steam to condenser should paid more attention to reduce their exergy destruction. Actually, in the near future, as the temperature of throttle and reheat steams reach 650 °C or even higher, the performance of these stages may achieve better performance if the wetness of exhaust steam has to be reduced to fulfill the largest potential for efficiency improvement from the elevation of temperature levels of throttle and reheat steams.