Comparative Study on Different Energy Management Strategies for Plug-In Hybrid Electric Vehicles
Abstract
:1. Introduction
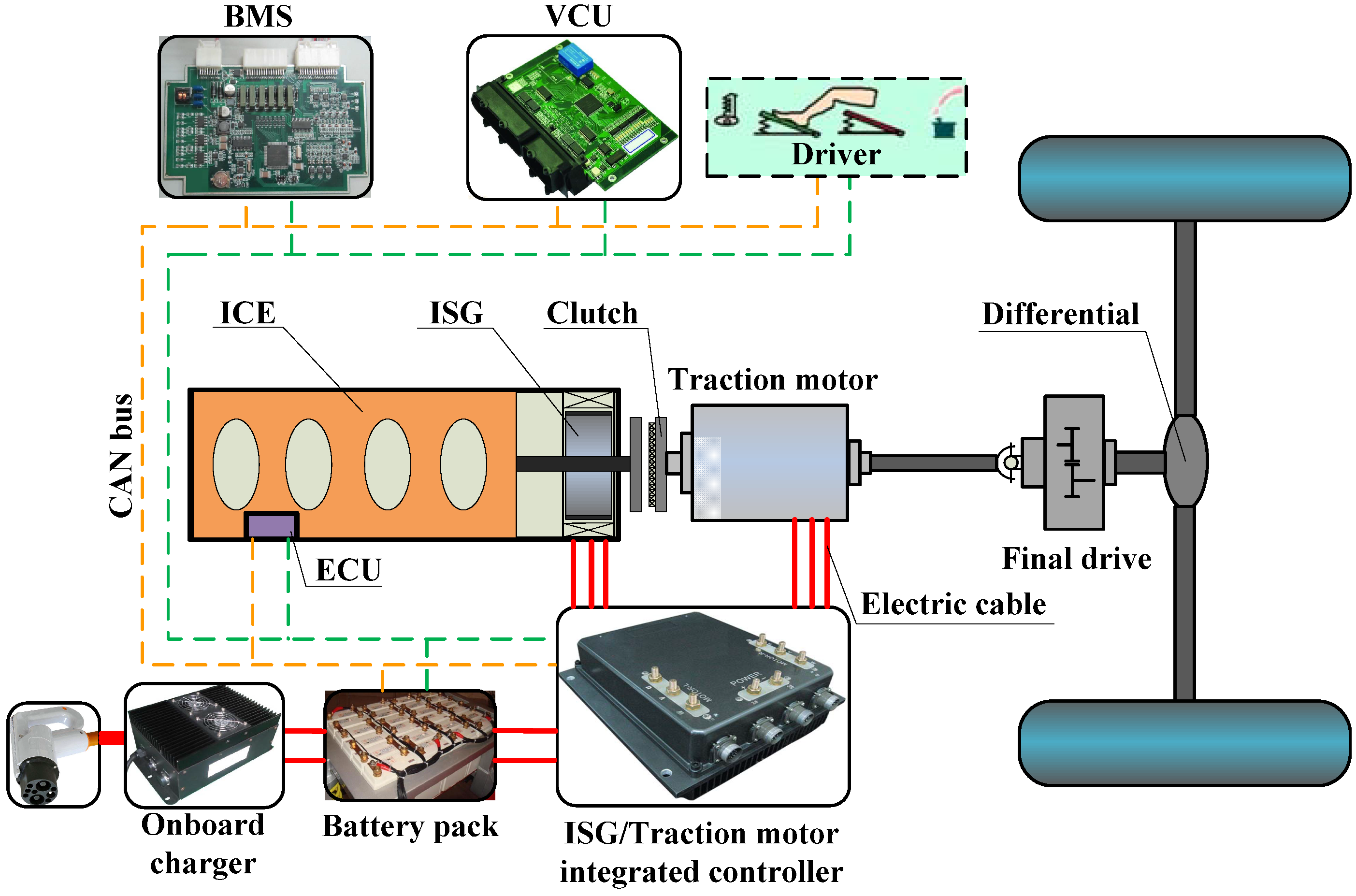
2. A Plug-In Hybrid Electric Bus Powertrain
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Curb weight/kg | 12,500 | Aerodynamic drag coefficient | 0.55 |
| Gross weight/kg | 18,000 | Rolling resistance coefficient | 0.0095 |
| Frontal area/m2 | 6.6 | transmission efficiency | 0.93 |
| Tire rolling radius/mm | 473 |
3. The Plug-In Hybrid Electric Bus Modeling
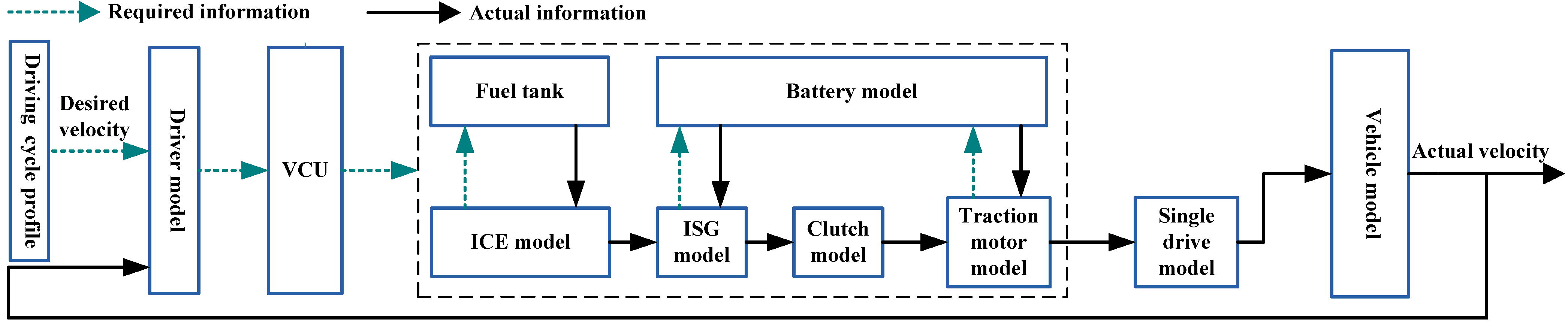
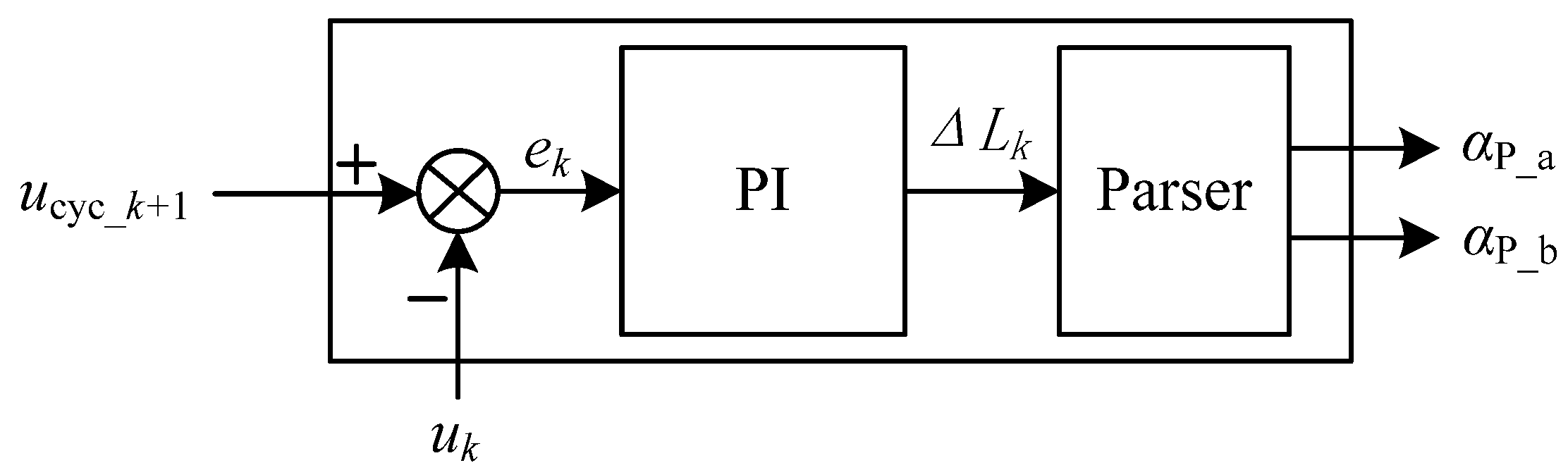
3.1. The Driver Model
3.2. The Vehicle Model
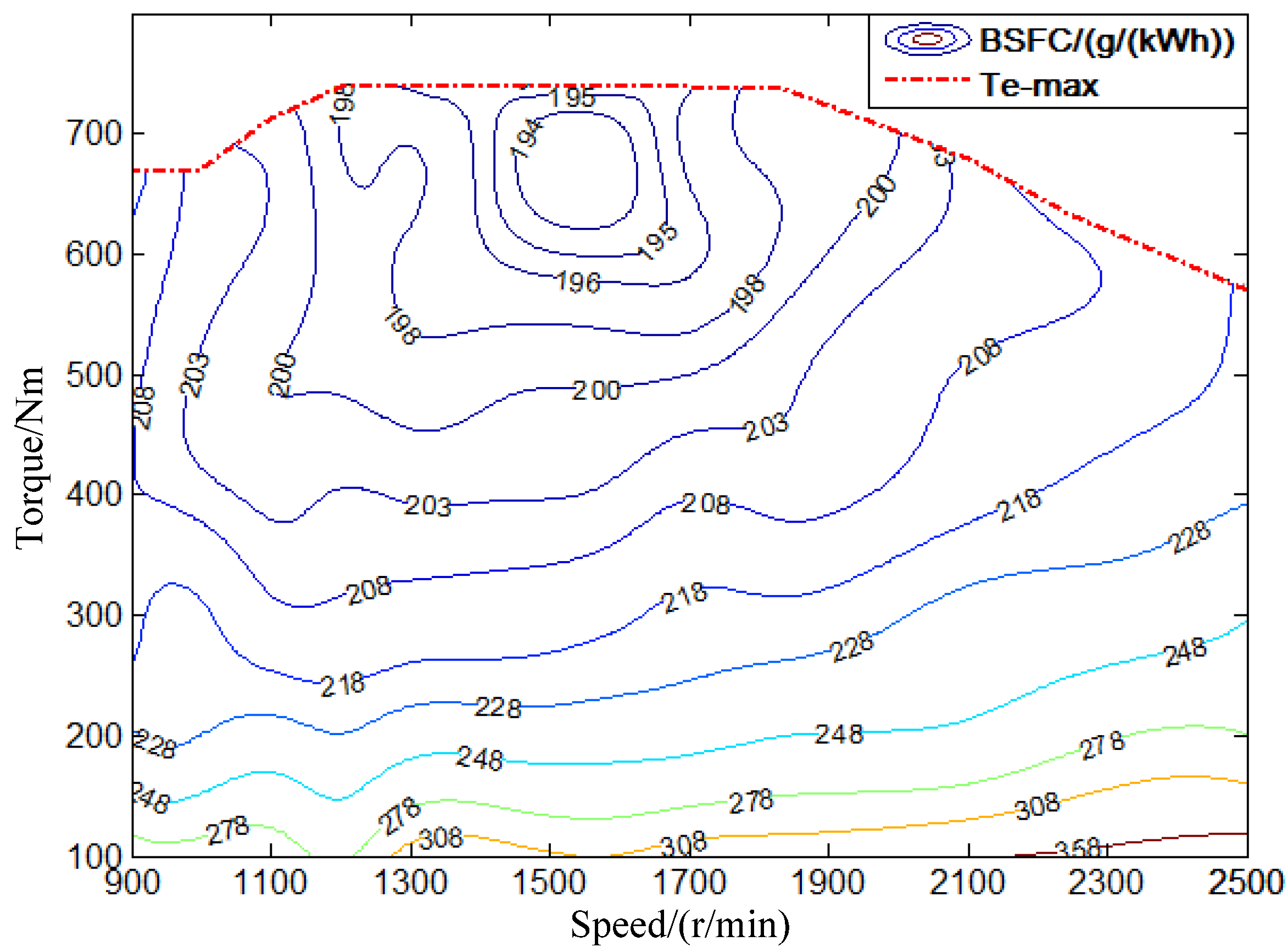
3.3. ICE Model
3.4. The ISG and TM Model
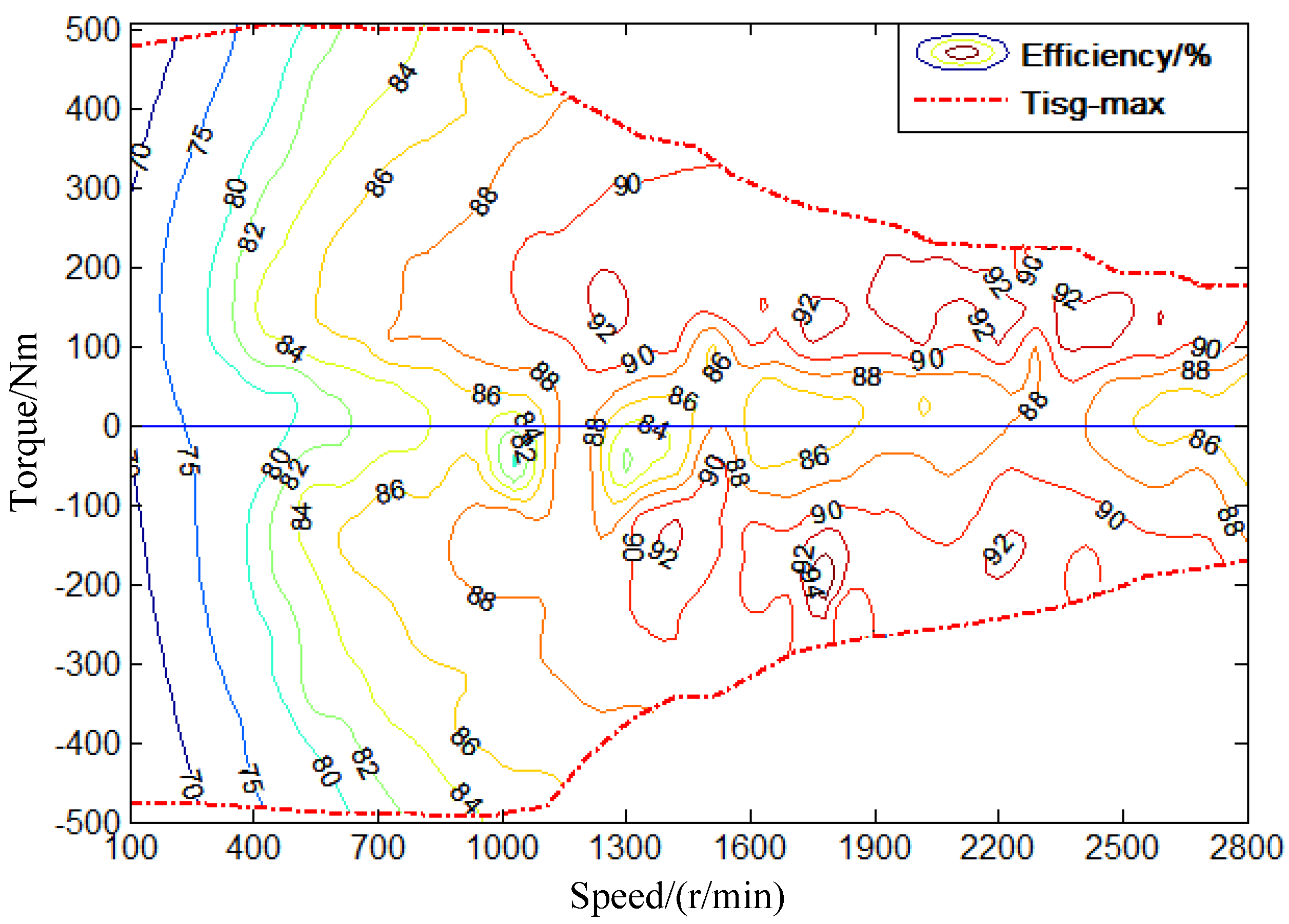
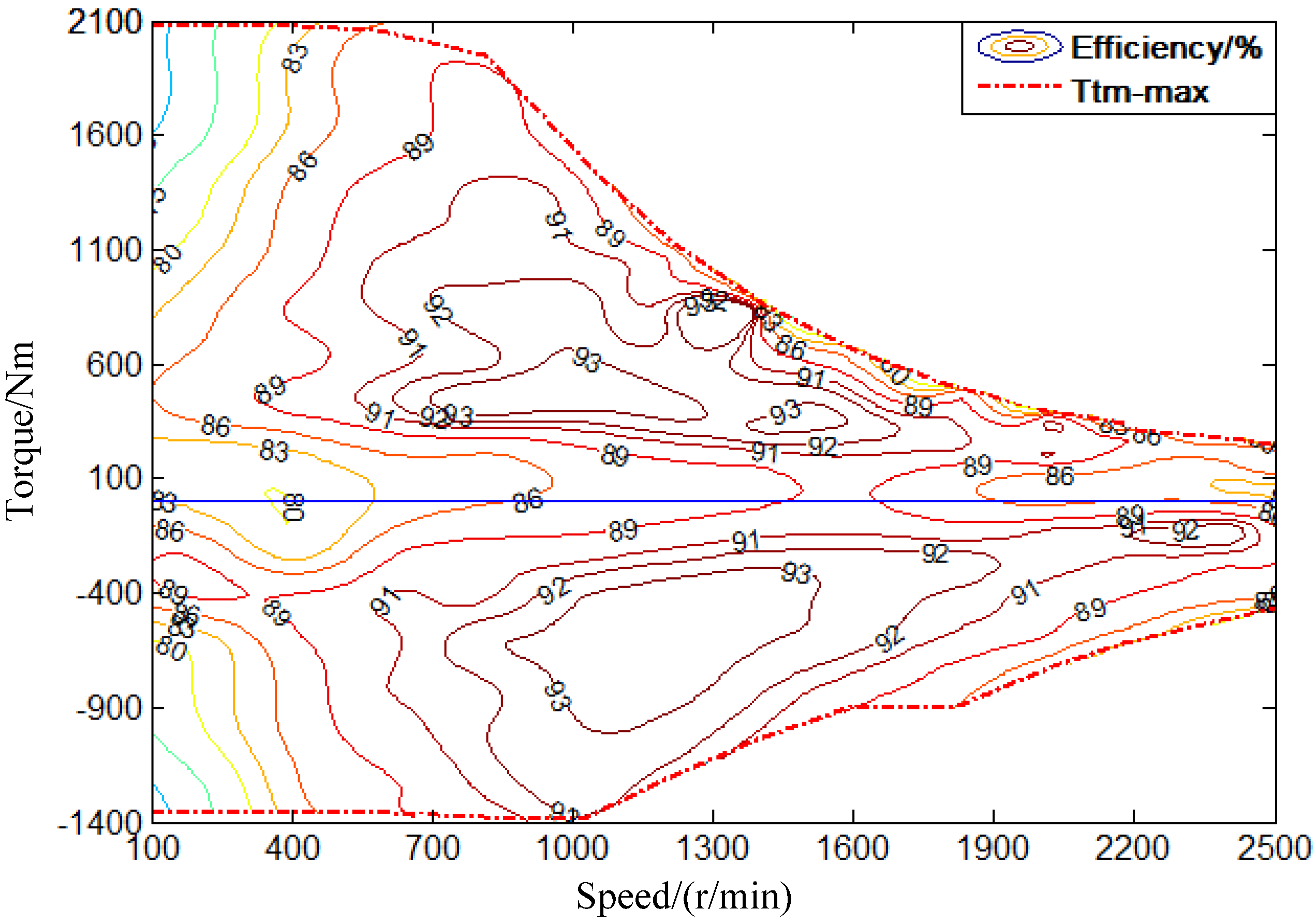
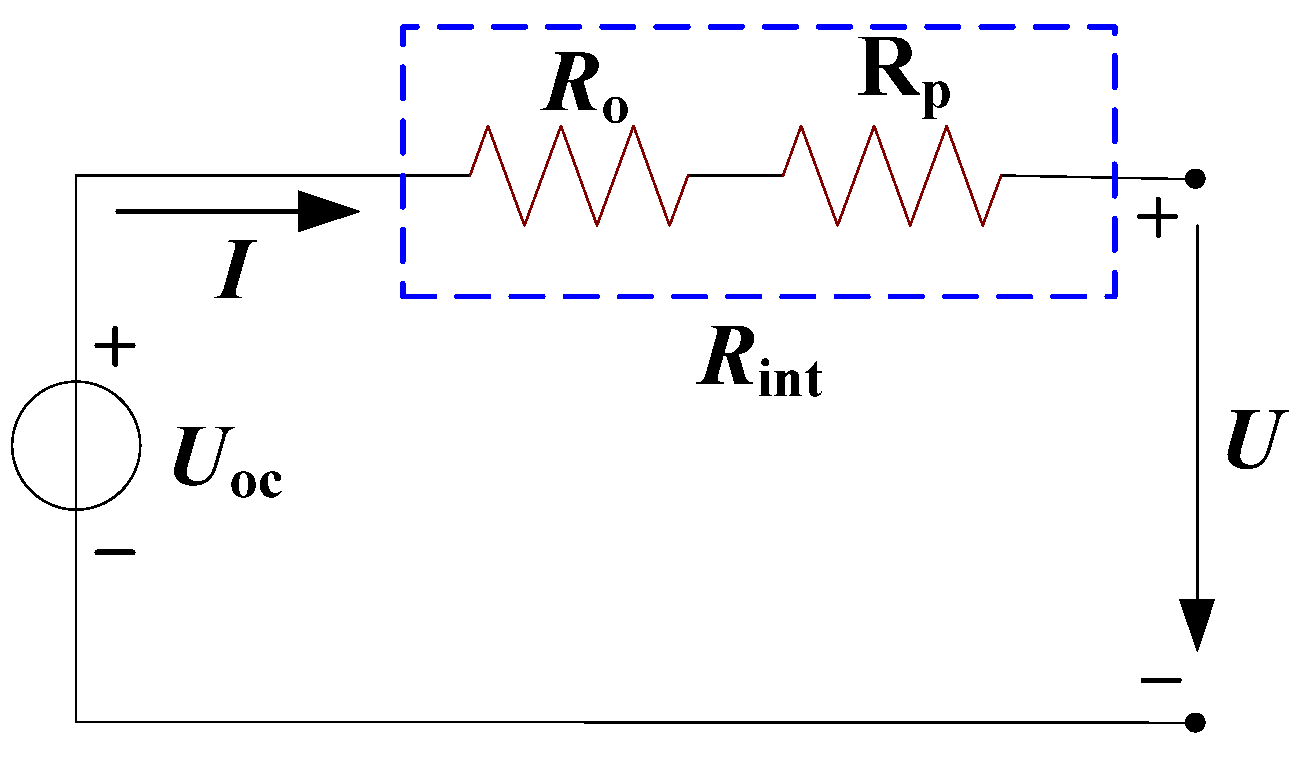
3.5. The Battery Model
4. The PHEB Energy Management Strategy
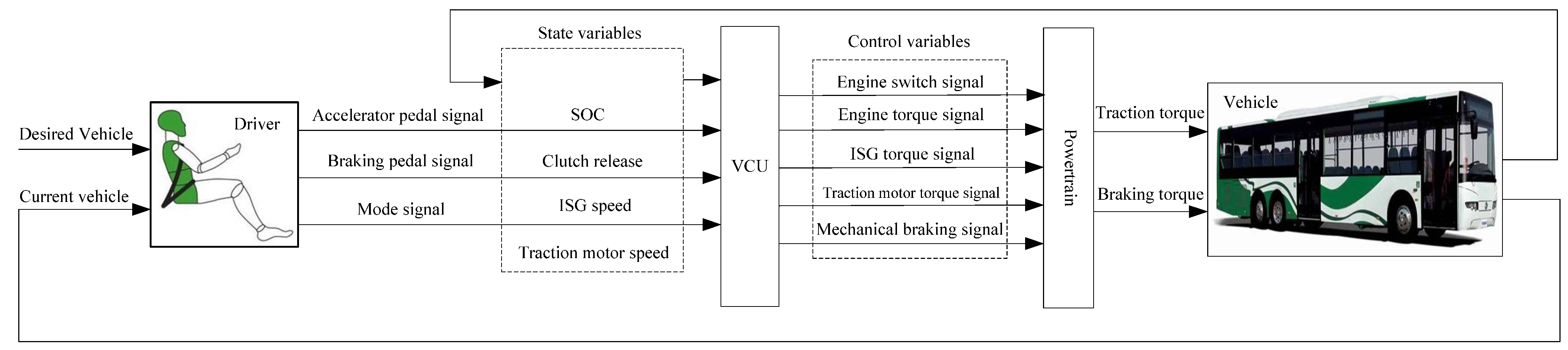
4.1. Power Flow Analysis
4.1.1. Pure Electric Driving Mode
4.1.2. Hybrid Driving Charge Depleting Mode

4.1.3. Hybrid Driving Charge Sustaining Mode

4.2. Energy Management Strategy
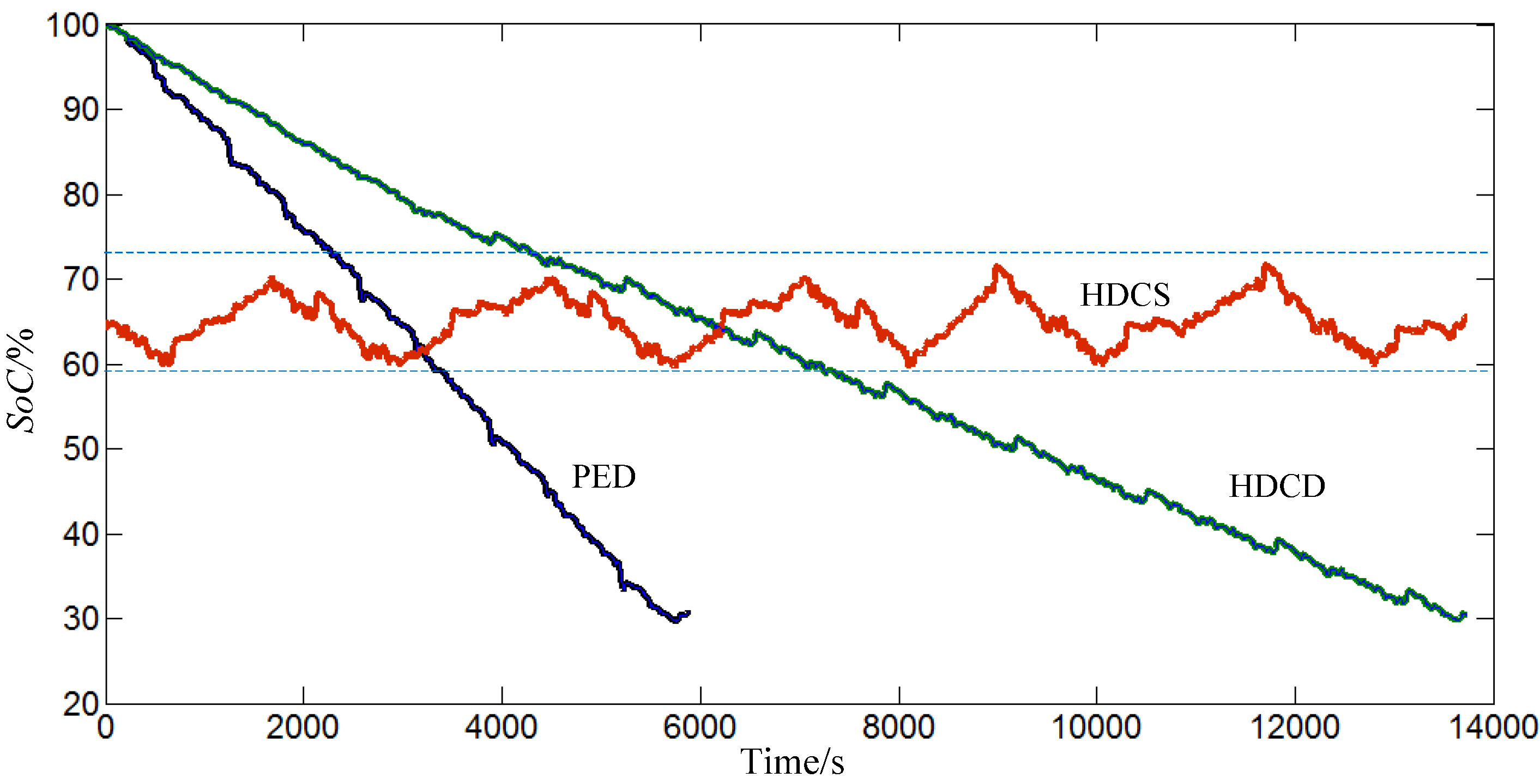
4.2.1. PED + HDCS Strategy
4.2.2. HDCD + HDCS Strategy
4.2.3. PED + HDCD + HDCS Strategy
5. Simulation Experiments and Discussions

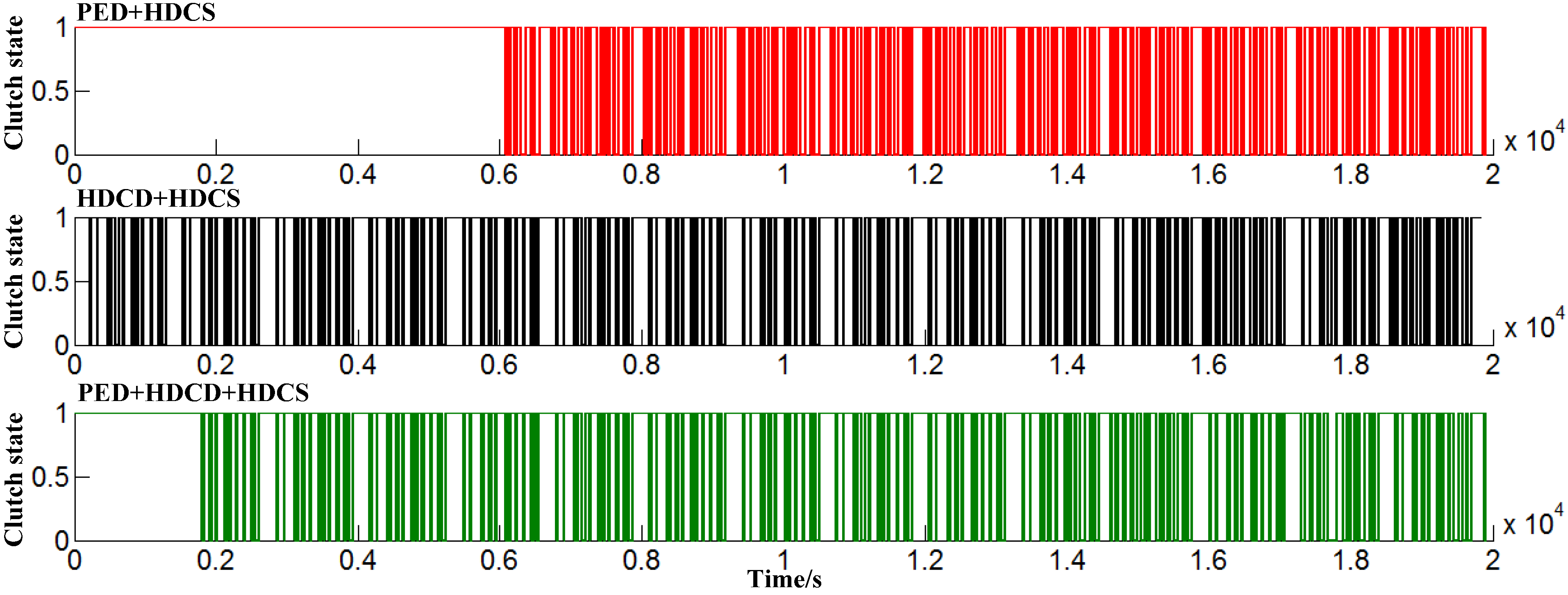
5.1. The Clutch State Profiles
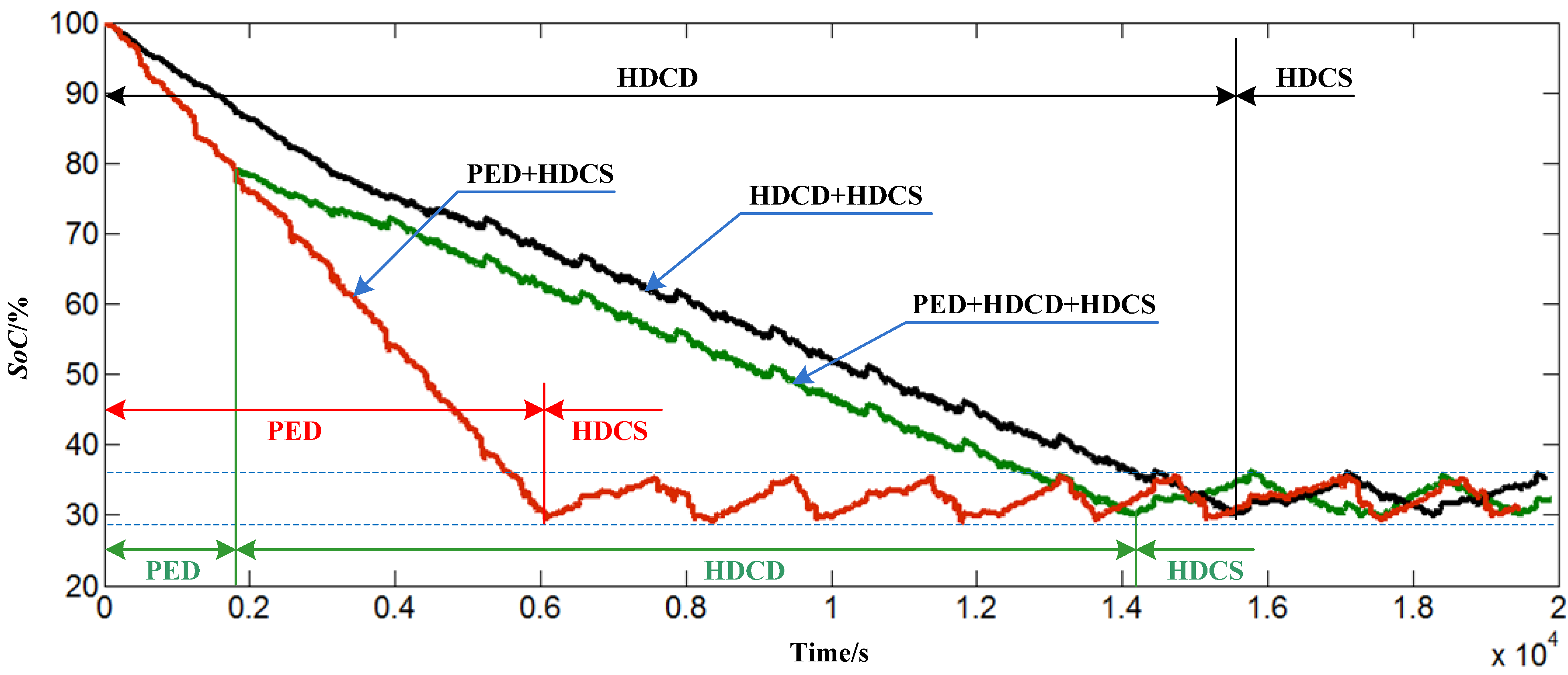
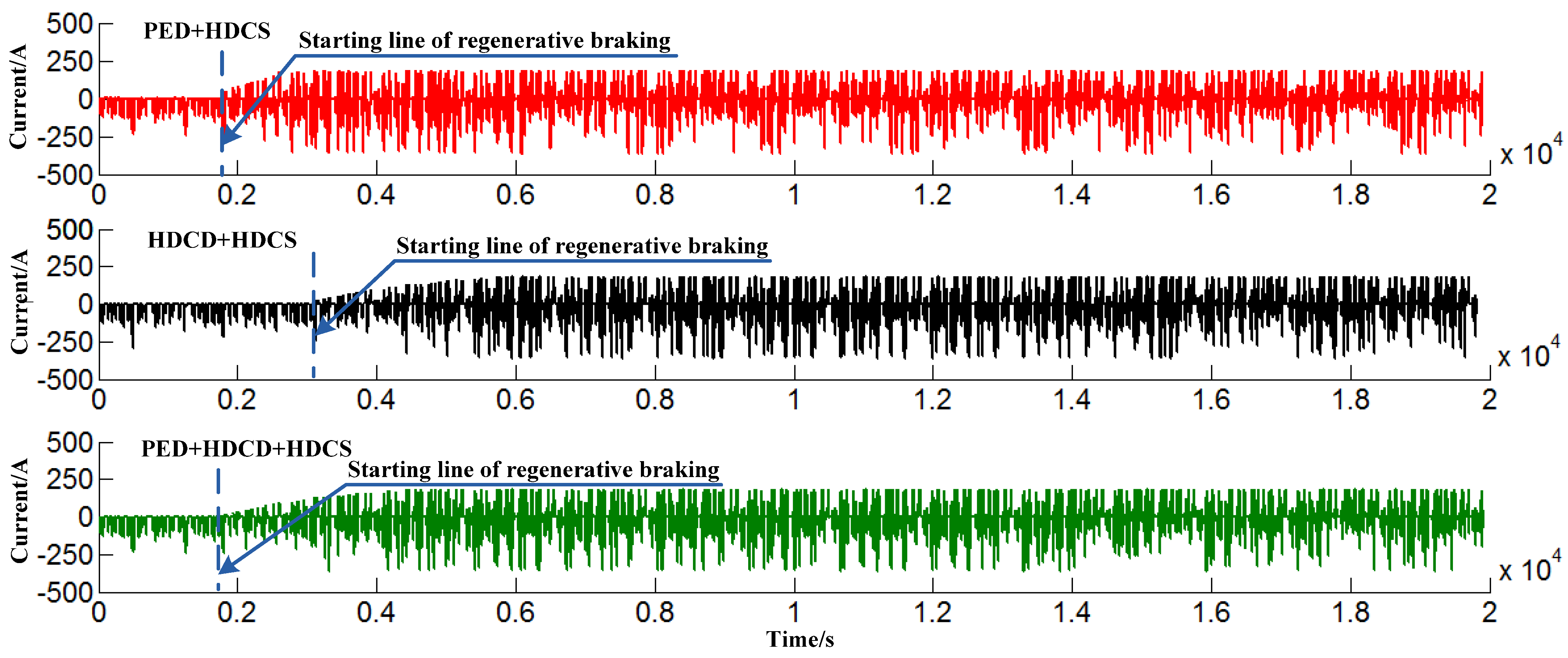
5.2. Fuel Economy Results and Discussion
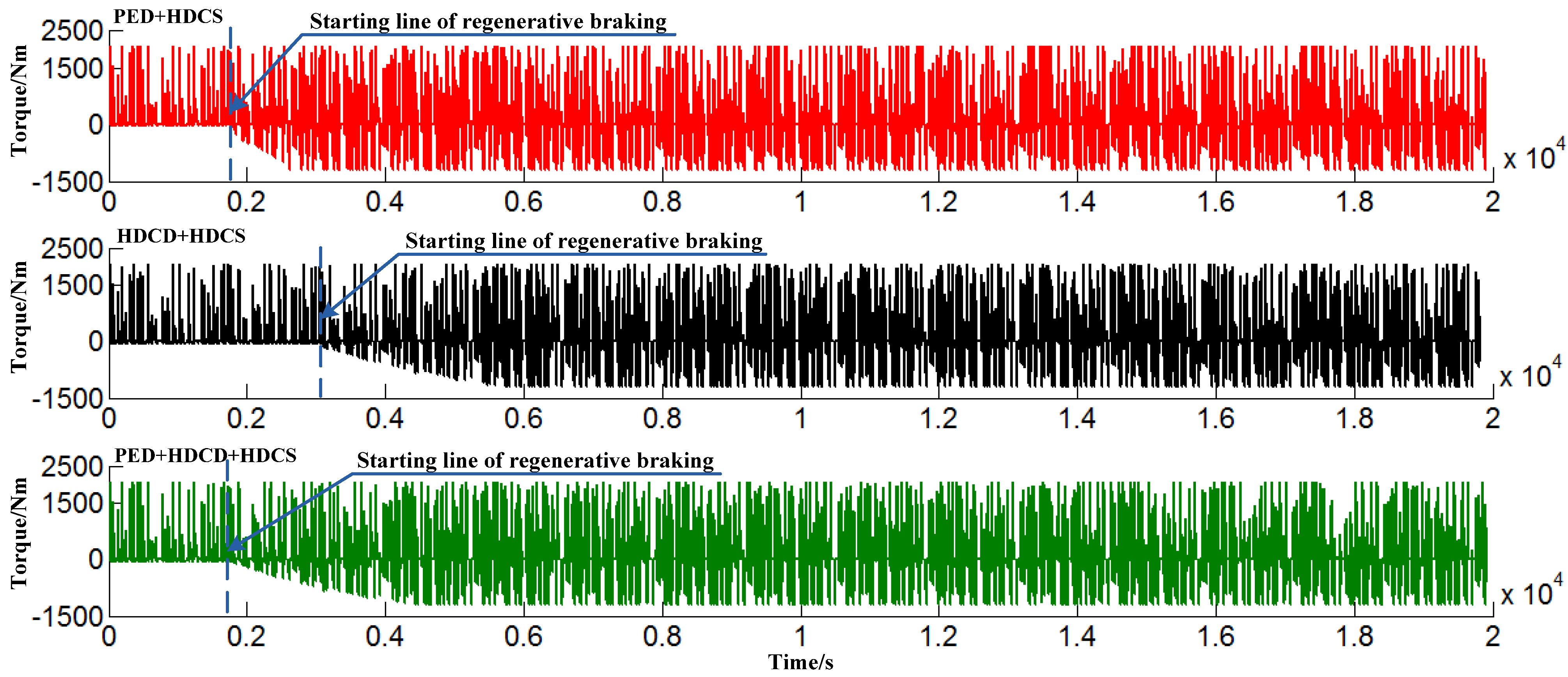
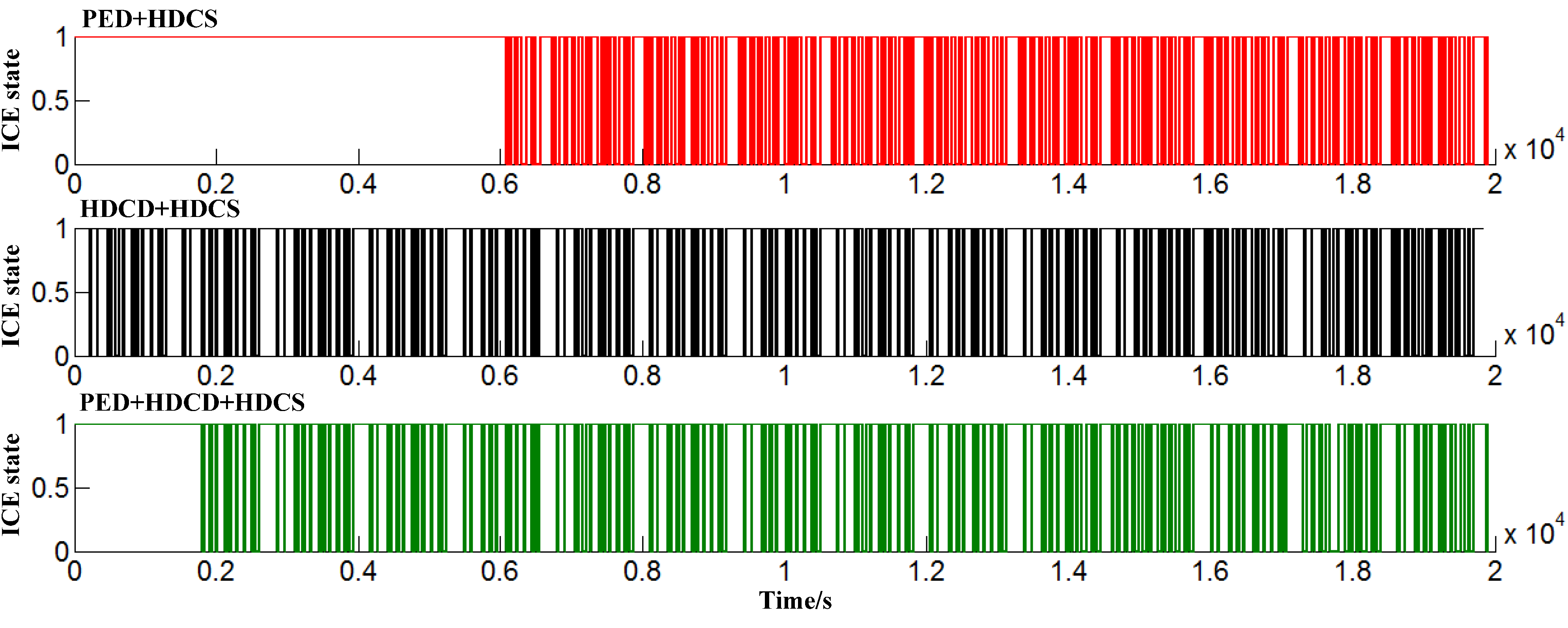
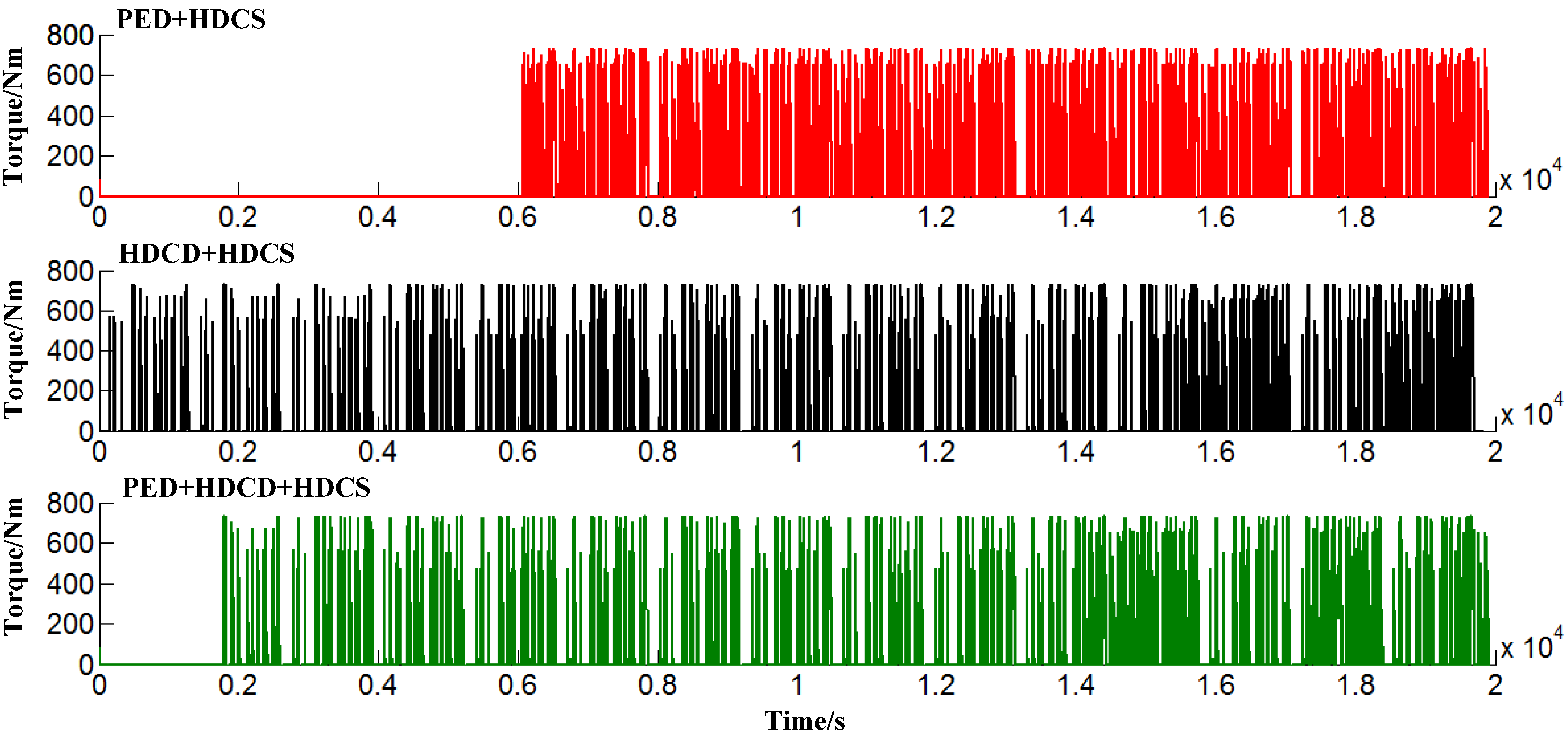
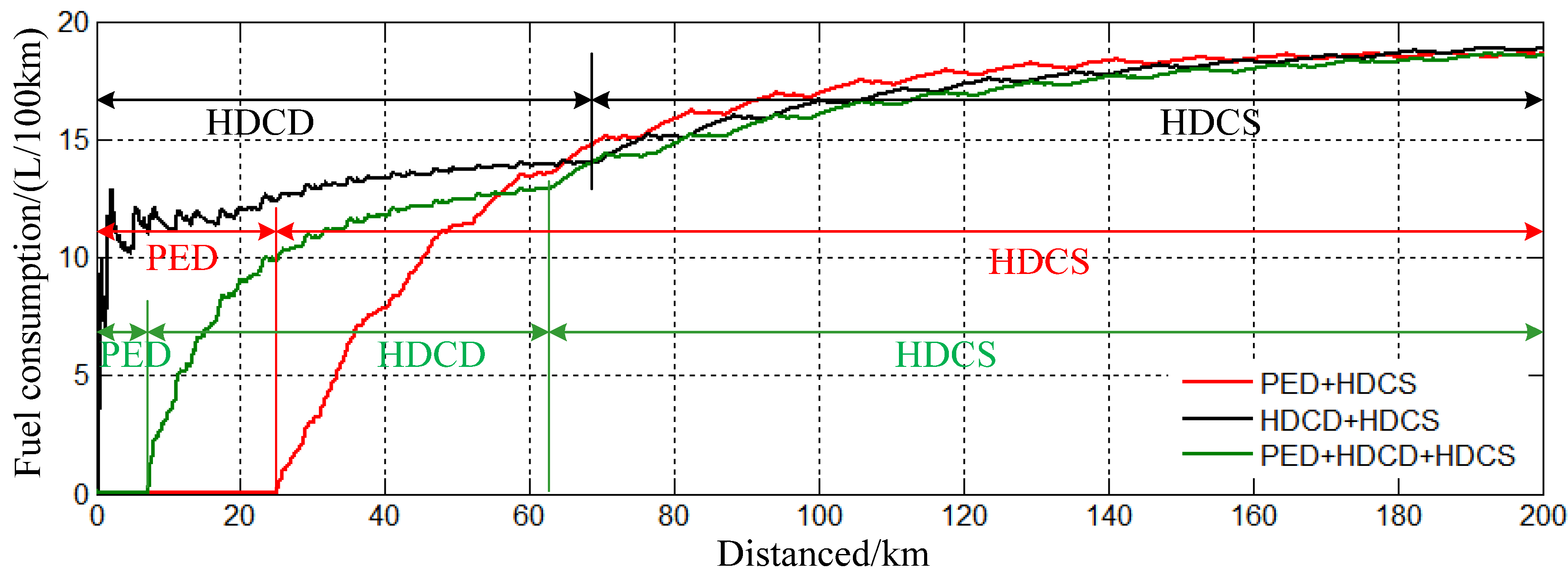


6. Conclusions
- (1)
- A single-axis series-parallel PHEB was modeled and its systematic model was built for energy flow analysis and fuel economy evaluations.
- (2)
- Three energy management strategies, which are the PED + HDCS strategy, the HDCD + HDCS strategy and the PED + HDCD + HDCS strategy, were put forward by combing the three basic PHEV operation modes. The corresponding models were built and the corresponding equations were listed.
- (3)
- A systematic simulation experiment was performed and the three energy management strategies were compared. It is shown that the more the proportion of the PED mode in the entire trip is, the better the fuel economy will be, while the HDCS mode does the reverse. The PHEB fuel consumption per 100 km differs as the driving distance increases with a general rising tendency. In general, the PED + HDCD + HDCS strategy, which is optimally composed of the PED mode, the HDCD mode and the HDCS mode, is the optimal one practicable for PHEVs.
Acknowledgments
References
- Lee, T.K.; Adornato, B.; Filipi, Z.S. Synthesis of real-world driving cycles and their use for estimating PHEV energy consumption and charging opportunities: Case study for Midwest/US. IEEE Trans. Veh. Technol. 2011, 60, 4153–4163. [Google Scholar] [CrossRef]
- Lunz, B.; Yan, Z.; Gerschler, J.B.; Gerschler, J.B.; Sauer, D.U. Influence of plug-in hybrid electric vehicle charging strategies on charging and battery degradation costs. Energy Policy 2012, 46, 511–519. [Google Scholar] [CrossRef]
- Ehsani, M.; Falahi, M.; Lotfifard, S. Vehicle to grid services: Potential and applications. Energies 2012, 5, 4076–4090. [Google Scholar] [CrossRef]
- Bradley, T.H.; Quinn, C.W. Analysis of plug-in hybrid electric vehicle utility factors. J. Power Sources 2010, 195, 5399–5408. [Google Scholar] [CrossRef]
- Gonder, J.; Markel, T. Energy management strategies for plug-in hybrid electric vehicles. SAE Tech. Paper 2007. [CrossRef]
- Falahi, M.; Chou, H.-M.; Ehsani, M.; Xie, L.; Butler-Purry, K.L. Potential power quality benefits of electric vehicles. IEEE Trans. Sustain. Energy 2013, 4, 1016–1023. [Google Scholar]
- Borhan, H.; Vahidi, A.; Phillips, A.M.; Kuang, M.L.; Kolmanovsky, I.V.; Di Cairano, S. MPC-based energy management of a power-split hybrid electric vehicle. IEEE Trans. Control Syst. Technol. 2012, 20, 593–603. [Google Scholar] [CrossRef]
- Zhang, B.; Mi, C.C.; Zhang, M. Charge-depleting control strategies and fuel optimization of blended-mode plug-in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2011, 60, 1516–1525. [Google Scholar] [CrossRef]
- Wirasingha, S.G.; Emadi, A. Classification and review of control strategies for plug-in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2011, 60, 111–122. [Google Scholar] [CrossRef]
- Tulpule, P.; Marano, V.; Rizzoni, G. Effects of Different PHEV Control Strategies on Vehicle Performance. In Proceedings of American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3950–3955.
- He, Y.; Chowdhury, M.; Pisu, P.; Ma, Y. An energy optimization strategy for power-split drivetrain plug-in hybrid electric vehicles. Transp. Res. Part C Emerg. Technol. 2012, 22, 29–41. [Google Scholar] [CrossRef]
- He, J.-H.; Yang, L.; Qiang, J.-X.; Chen, Z.-Q.; Zhu, J.-X. Novel flexible hybrid electric system and adaptive online-optimal energy management controller for plug-in hybrid electric vehicles. J. Cent. South Univ. 2012, 19, 962–973. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, N.W.; Jeong, J.R.; Park, Y.I.; Cha, S.W. Component sizing and engine optimal operation line analysis for a plug-in hybrid electric transit bus. Int. J. Auto. Technol. 2013, 14, 459–469. [Google Scholar] [CrossRef]
- Zhang, C.; Vahidi, A. Route preview in energy management of plug-in hybrid vehicles. IEEE Trans. Control Syst. Technol. 2012, 20, 546–553. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, Y.; Mi, C.C. Analytical approach for the power management of blended-mode plug-in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2012, 61, 1554–1566. [Google Scholar] [CrossRef]
- Tulpule, P.; Marano, V.; Rizzoni, G.; McGee, R.; Yu, H. A statistical approach to assess the impact of road events on PHEV performance using real world data. SAE Tech. Paper 2011. [CrossRef]
- Wei, X. Modeling and Control of a Hybrid Electric Drivetrain for Optimum Fuel Economy, Performance and Driveability. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 2004. [Google Scholar]
- Koprubasi, K. Modeling and Control of a Hybrid-Electric Vehicle for Drivability and Fuel Economy Improvements. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 2008. [Google Scholar]
- Huang, Y. A Study on Control Strategy and Implementation Technique for Pre and Pro Double Clutches Parallel Hybrid Electric Urban Buses. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2009. [Google Scholar]
- Albert, I.J.; Kahrimanovic, E.; Emadi, A. Diesel sport utility vehicles with hybrid electric drive trains. IEEE Trans. Veh. Technol. 2004, 53, 1247–1256. [Google Scholar] [CrossRef]
- Patil, R.M. Combined Design and Control Optimization: Application to Optimal PHEV Design and Control for Multiple Objectives. Ph.D. Thesis, The University of Michigan, Lansing, MI, USA, 2012. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, X.; He, H.; Sun, F.; Sun, X.; Tang, H. Comparative Study on Different Energy Management Strategies for Plug-In Hybrid Electric Vehicles. Energies 2013, 6, 5656-5675. https://doi.org/10.3390/en6115656
Wang X, He H, Sun F, Sun X, Tang H. Comparative Study on Different Energy Management Strategies for Plug-In Hybrid Electric Vehicles. Energies. 2013; 6(11):5656-5675. https://doi.org/10.3390/en6115656
Chicago/Turabian StyleWang, Ximing, Hongwen He, Fengchun Sun, Xiaokun Sun, and Henglu Tang. 2013. "Comparative Study on Different Energy Management Strategies for Plug-In Hybrid Electric Vehicles" Energies 6, no. 11: 5656-5675. https://doi.org/10.3390/en6115656
APA StyleWang, X., He, H., Sun, F., Sun, X., & Tang, H. (2013). Comparative Study on Different Energy Management Strategies for Plug-In Hybrid Electric Vehicles. Energies, 6(11), 5656-5675. https://doi.org/10.3390/en6115656





