A Photovoltaic Power System Using a High Step-up Converter for DC Load Applications

Abstract

This paper presents a power system using a high step-up converter for dc load applications. The high step-up converter adopts a boost converter with interleaved mode and a coupled inductor to raise its powering ability and increase its step-up voltage ratio, respectively. In order to increase conversion efficiency, an active clamp circuit is introduced into the proposed one to provide soft-switching features to reduce switching losses. Moreover, switches in the converter and active clamp circuit are integrated with a synchronous switching technique to reduce circuit complexity and component counts, resulting in a lower cost and smaller volume. A perturb and observe method is adopted to extract the maximum power from photovoltaic (PV) arrays. Furthermore, a microchip associated with PWM IC is used to implement maximum power point tracking operation, voltage regulation and power management. Finally, a prototype PV power system with 400 V/6 A has been implemented for verifying the feasibility of the proposed PV power system. It is shown to be suitable for PV energy conversion applications when the duty ratios of switches in the dc/dc converter are less than 0.5.

1. Introduction

Limited fossil energy and increased air pollution have spurred researchers to develop clean energy sources. One of these sources is the photovoltaic (PV) power generation system, which is a clean, quiet and an efficient method for generating electricity. In practical applications, PV arrays can be used in battery charging, water pumping, PV vehicles, satellite power systems, grid-connected power systems, standalone power systems, and so on. Due to the low conversion efficiency of PV arrays, on way to reduce the cost of the overall system is by using high efficiency power processors. The power processor usually adopts a dc/dc converter as its energy processing system.

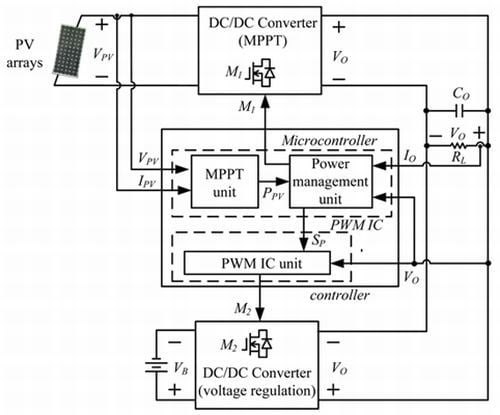
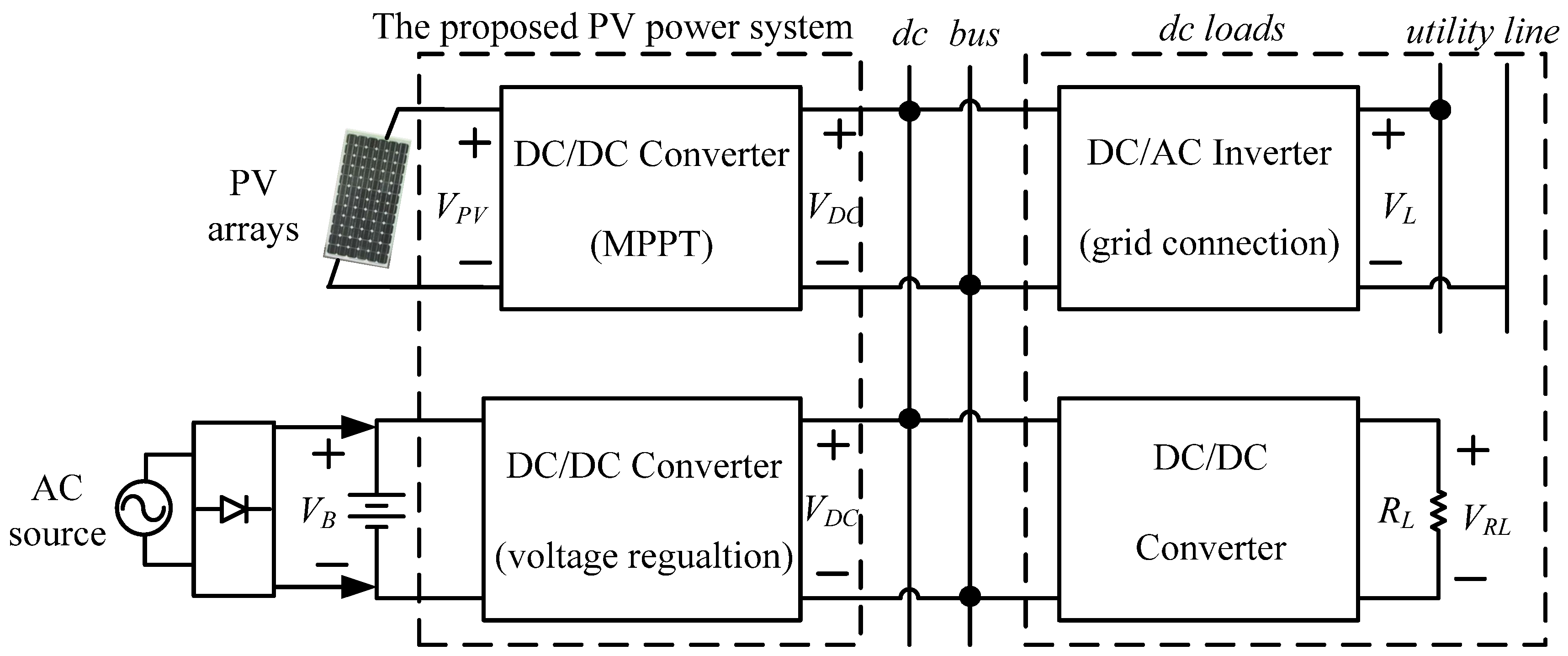
When a dc/dc converter is used in a PV array power system, it is operated at the maximum power point (MPP) of the PV arrays to extract the maximum possible power for increasing the utilization rate of the PV arrays. As a result, its output voltage does not remain at the desired constant dc voltage. Therefore, a dc/dc converter with voltage regulation is used to connect with PV power systems in parallel to keep the output voltage in the desired constant dc voltage range, as shown in Figure 1.

Figure 1. Block diagram of PV power generation system for DC load applications.

Figure 1. Block diagram of PV power generation system for DC load applications.

In Figure 1, the dc bus voltage can supply a dc/ac inverter for a grid-connected power system [1,2,3,4,5], a dc/dc converter for dc load [6,7,8,9,10], and so on. The dc/ac inverter and dc/dc converter are regarded as dc loads. In this paper, the proposed power supply includes a dc/dc converter as the maximum power point tracking (MPPT) point of the PV arrays and a dc/dc converter as the load voltage regulator.

To increase the utility rate of PV arrays, power systems using PV arrays must track MPP to extract as much power as possible from the arrays. Several MPPT algorithms have been proposed [11,12,13,14,15,16,17,18,19,20]. Some of the more popular MPPT algorithms are the constant voltage method [11,12], β method [13], system oscillation method [14,15], ripple correlation method [16], incremental conductance method [17] and perturb and observe method [18,19,20]. Due to its simplicity and ease of implementation, the perturb and observe method is often used. Therefore, the perturb and observe method was adopted to implement the MPPT of the proposed power system.

In order to increase the conversion efficiency of a PV power system, switching power converters are widely used as dc/dc converters. Since the proposed PV power system requires a high step-up dc/dc converter, a transformer or coupled inductor is usually introduced into switching power converters [21,22]. Compared with the converter using an isolation transformer, the one using a coupled inductor has a simpler winding structure and a higher coupling coefficient. It can reduce inductor currents to ensure lower conduction losses and decrease leakage inductance to attain a lower switching loss, respectively. As a result, the one can use a lower value of the input filter capacitor to obtain a good regulation of the output voltage. Therefore, a system using a coupled inductor is relatively attractive. However, since the energy is trapped in the leakage inductor of the coupled inductor, it will not only increase voltage stresses, but induce significant switching losses of the switches in the converter. In order to solve these problems, several methods have been proposed [23,24,25]. In [23], a resistor-capacitor-diode (R-C-D) snubber is used to alleviate switch voltage stresses, but the energy trapped in the leakage inductor is dissipated by the resistor, resulting in a lower conversion efficiency of the converter. Therefore, a passive losses circuit [24] is adopted to recover the energy and reduce voltage spikes across switches, but active switches are still operated in hard switching mode. Its conversion efficiency does not increase significantly. In [25], an active clamp circuit is introduced into the converter for recovering the energy of the leakage inductor and limit voltage spike across switches. Moreover, the one can also achieve zero-voltage switching (ZVS) in converter switches to increase their conversion efficiency. As mentioned above, a boost converter associated with a coupled inductor is adopted in this research as the dc/dc converter, as shown in Figure 2. In order to further increase the powering capability of the converter, boost converters with interleaved manner have been proposed by several authors [26,27,28,29], as shown in Figure 3.

Figure 2. Schematic diagram of a boost converter with coupled inductor.

Figure 2. Schematic diagram of a boost converter with coupled inductor.

Figure 3. Schematic diagram of interleaved active clamp boost converter with coupled inductor.

Figure 3. Schematic diagram of interleaved active clamp boost converter with coupled inductor.

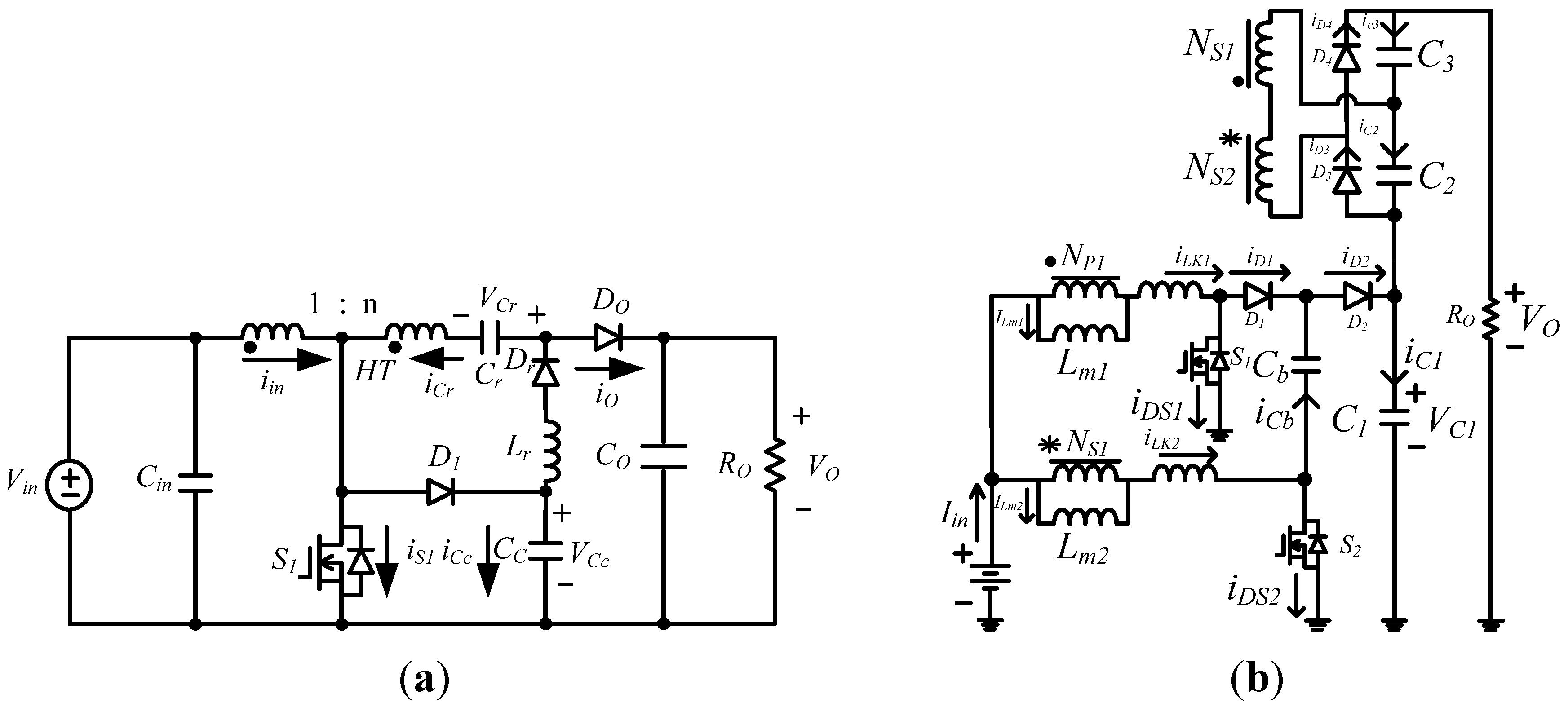
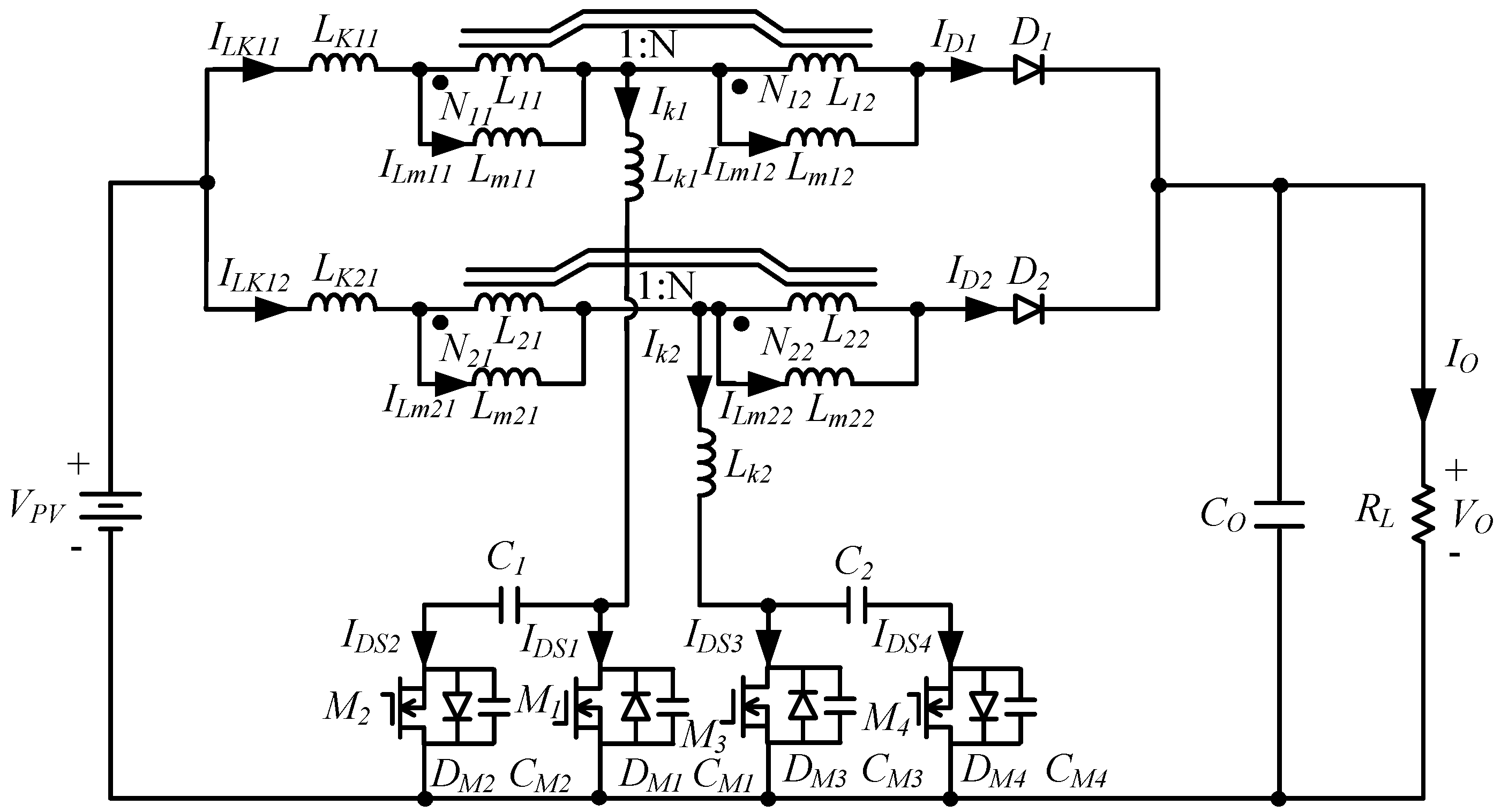
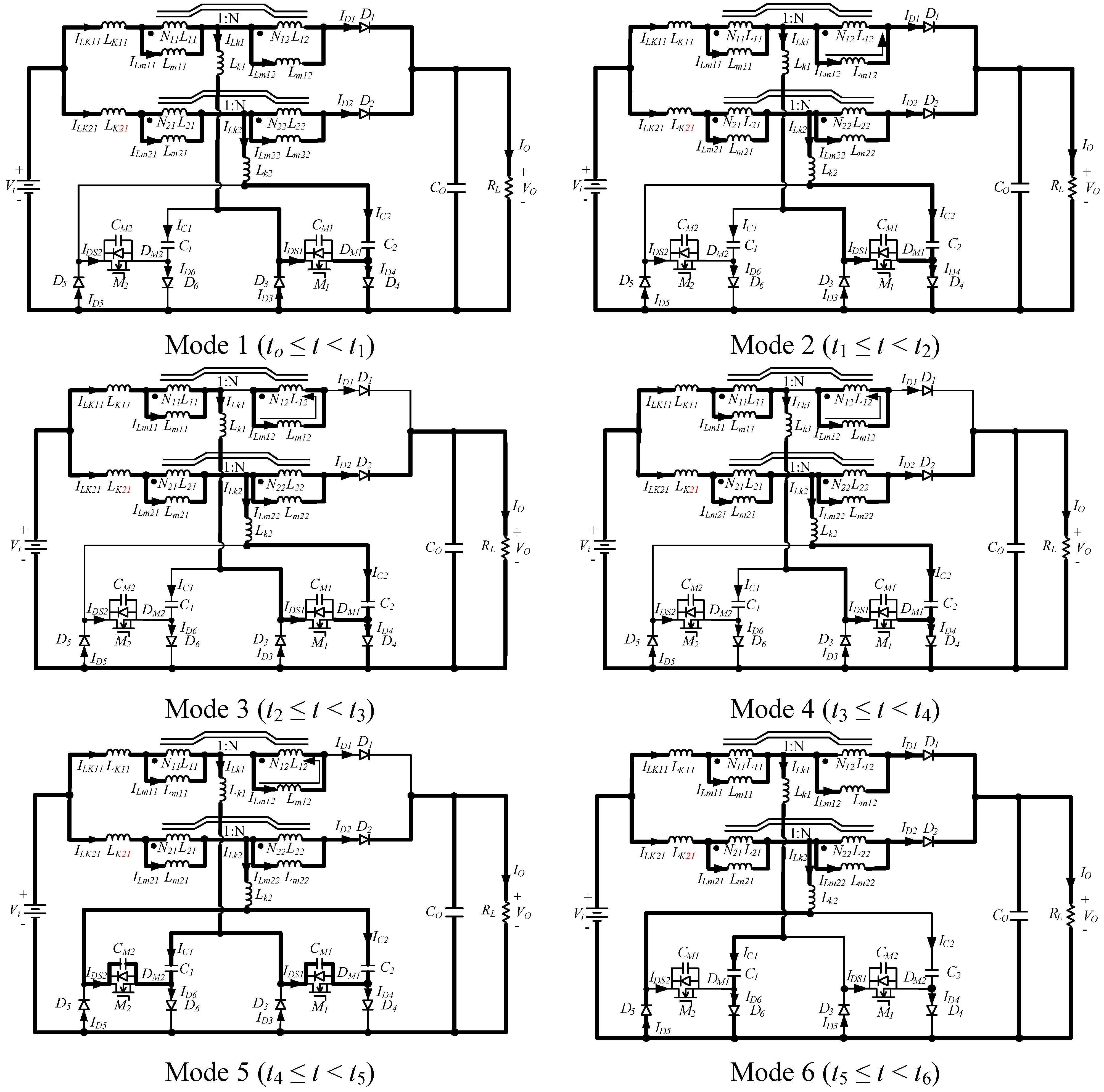
Due to the complexity of the circuit structure, the proposed dc/dc converter can be simplified however, as shown in Figure 4. From Figure 4, it can be seen that the proposed interleaved active clamp boost converter can use less component counts to achieve a high step-up voltage ratio and similar conversion efficiency for reducing the costs.

Figure 4. Schematic diagram of the proposed interleaved active clamp boost converter with coupled inductor.

Figure 4. Schematic diagram of the proposed interleaved active clamp boost converter with coupled inductor.

In particular, a general half-bridge converter, push-pull converter and full-bridge converter need pulse-width modulation (PWM) IC with two gate signals to drive their switches. Since the input sources of the converters adopt the voltage fed type, the duty ratios of their control PWM ICs are limited to within 0.5. If the dc/dc converter adopts a special PWM IC, which has a higher duty ratio (≥0.5), these are difficult to obtain and the cost will be increased.

In [28], as shown in Figure 5a, the duty ratios of switches in the proposed converters require that the duty ratios of the PWM ICs must be greater than 0.5, resulting in a higher cost. Moreover, its resonant capacitor has a higher current ripple rating (CRR), and it will need a special capacitor, which has a low ESR, high CRR and high operational bandwidth. Therefore, it is suitable for a low power level application. In [29] a voltage multiplier module to implement a high step-up voltage ratio was proposed, as shown in Figure 5b. Its voltage doubler capacitors also require a higher CRR. In particular, its controller adopts a DSP to implement its control method. Its cost is increased and its powering capability will be limited. In order to reduce the limitations of PWM ICs and capacitors for a voltage regulator, the proposed dc/dc converter can use a general PWM IC with two gate signals to achieve a high step-up voltage ratio and a high conversion efficiency with less component counts. As mentioned above, the proposed converter can reduce cost and further decrease its size, weight and volume. It is suitable for PV arrays applications when the PWM IC duty ratios are less than 0.5.

Figure 5. Schematic diagram of the conventional high step-up converters (a) proposed in [28]; and (b) proposed in [29].

Figure 5. Schematic diagram of the conventional high step-up converters (a) proposed in [28]; and (b) proposed in [29].

2. Control Algorithm of the Proposed PV Power System

In order to achieve a proper power management of the PV power system, the topology of the PV power system and power management are described in the following sections.

2.1. Circuit Topology of the Proposed PV Power System

The proposed PV power system consists of a dc/dc converter with MPPT, and a dc/dc converter with voltage regulation and controller, as shown in Figure 6.

Figure 6. Derivation of the proposed interleaved boost converter with coupled inductor.

Figure 6. Derivation of the proposed interleaved boost converter with coupled inductor.

Two dc/dc converters adopt an interleaved active clamp boost converter with coupled inductor, respectively, as shown in Figure 4. The one with MPPT control algorithm is used to extract the maximum power from the PV arrays. The other one, equipped with a voltage regulation control method, is required to regulate the power between the PV arrays and loads and to generate a constant output voltage for supplying power to the dc loads. Since the one with the MPPT control algorithm uses PV arrays as its power source, its controller, which is a microcontroller, is divided into two control units: MPPT unit and power management unit. The MPPT one can track the maximum power point (MPP) of the PV arrays. Its control method adopts the perturb and observe method, which is described in [18,19,20]. The power management one can separately regulate the output voltage of dc/dc converters with MPPT control algorithm and with the voltage regulation control method, according to the relationships between the maximum power P_PV(max) of the PV arrays and the load power P_L by signals M₁ and S_P. Moreover, the PWM IC unit is adopted to control the dc/dc converter by the voltage regulation control method to obtain a constant output voltage. Regulation of the output power by control signal S_p is also required. All of the protections are implemented by the microcontroller. The protections include over-current and -temperature protections of two dc/dc converters and battery undercharge. Therefore, the proposed PV power system can achieve the optimal utility rate of PV arrays.

2.2. Power Management

The proposed PV power system includes two dc/dc converters connected in parallel to supply power to the load. Its operational modes can be divided into eight modes. Note that P_PV is the output power of the PV arrays, P_VB is that of the battery and P_L is the load power. Moreover, “1” represents the power which is generated by PV arrays or is dissipated by load, while “0” is the power which is not generated or is not dissipated. According to the power management flow chart of the proposed PV power system shown in Figure 7, all operational modes are shut down, except for operational modes IV, VI and VIII. In the following, operational modes IV, VI and VIII are described.

2.2.1. Operational Mode IV

In the operational mode, the dc/dc converter with battery is adopted to supply power to the load. When the load power P_L > P_VB(max), the proposed PV power system is shut down. When the load power P_L < P_VB(max), the power curve of the PV arrays follows the load power, as shown in Figure 8, until energy stored in battery is completely discharged. The PV power system is then shut down.

2.2.2. Operational Mode VI

In operational mode VI, the dc/dc converter with PV arrays as its power source is used to supply power to the load, as shown in Figure 9. From Figure 9, it can be seen that when the maximum power P_PV(max) ≥ P_L, power curve of the PV arrays follows that of load power. If P_PV(max) < P_L, the proposed PV power system is shut down.

Figure 7. Flow chart of power management of the proposed PV power system.

Figure 7. Flow chart of power management of the proposed PV power system.

Figure 8. Plot of power curve of the proposed PV power system under operational mode IV.

Figure 8. Plot of power curve of the proposed PV power system under operational mode IV.

Figure 9. Plot of power curve of the proposed PV power system under operational mode VI.

Figure 9. Plot of power curve of the proposed PV power system under operational mode VI.

2.2.3. Operational Mode VIII

In operational mode VIII, two dc/dc converters using PV arrays and battery as their power sources are adopted to supply power to the load, respectively, as shown in Figure 10. When the total maximum output power of the two dc/dc converters is equal to or greater than P_L, the PV power system can be working. Under the other operational conditions within this operational mode, one is shut down. When the total maximum output power (P_PV(max) + P_VB(max)) > P_L, the dc/dc converter with PV arrays as its power source is operated at MPP of the PV arrays and the one with battery as its power source is operated under the output power of (P_L − P_PV(max)), as shown in Figure 10a. Moreover, when P_PV(max) > P_L, the one with battery as its power source is shut down and the output power P_PV of the PV arrays is equal to P_L, as shown in Figure 10b. According to the energy conservation of the PV power system, P_L is the sum of P_PV and P_VB and P_L extracts as much power as possible from the PV arrays to increase utilization rate of the PV array.

Figure 10. Plot of power curves P_PV, P_VB and P_L (a) under P_PV(max) + P_VB(max) ≥ P_L and (b) under P_PV(max) + P_VB(max) ≥ P_L and P_PV(max) ≥ P_L.

Figure 10. Plot of power curves P_PV, P_VB and P_L (a) under P_PV(max) + P_VB(max) ≥ P_L and (b) under P_PV(max) + P_VB(max) ≥ P_L and P_PV(max) ≥ P_L.

3. Operational Principle of the Proposed DC/DC Converter

When P_PV(max) < P_L, the dc/dc converter using PV arrays as its power source is operated at current regulation to extract the maximum power from the PV arrays. When P_PV(max) ≥ P_L, the one is operated at voltage regulation to supply power to the load. Its function is the same as the one using battery as its power source. Therefore, two dc/dc converters can adopt the same circuit structure. In the following, the operational principle of the proposed dc/dc converter is briefly described.

Operational Principle of the Proposed Converter

The dc/dc converter of the proposed PV power system using interleaved active clamp boost converter with coupled inductor is shown in Figure 4. According to the circuit operational principle of the proposed boost converter, its operational modes are divided into 12 modes, as show in Figure 11, and their key waveforms are illustrated in Figure 12. Since the operational modes between t₀ ~ t₆ are similar to those waveforms between t₆ ~ t₁₂, except that the operational switch changes from M₁ to M₂, each operational mode during half one switching cycle is briefly described in the following.

Figure 11. Equivalent circuit of each operational mode in the proposed interleaved active clamp boost converter with coupled inductor over half of one switching cycle.

Figure 11. Equivalent circuit of each operational mode in the proposed interleaved active clamp boost converter with coupled inductor over half of one switching cycle.

Figure 12. Key waveforms of the proposed converter operating over one switching cycle.

Figure 12. Key waveforms of the proposed converter operating over one switching cycle.

Mode 1 (Figure 11a: t_o ≤ t < t₁): before t₀, switches M₁ and M₂ are in the off state. Diodes D₃ and D₄ are forwardly biased, therefore, voltage V_DS1 across switch M₁ is equal to 0. When t = t₀, switch M₁ is turned on. Since diodes D₃ and D₄ are forwardly biased before switch M₁ is turned on, switch M₁ is operated with ZVS at turn-on transition. During this time interval, leakage inductor L_K21, external inductor L_K2 and capacitor C₂ form a resonant network and they start to resonate. Moreover, since current I_LK11 is a negative value, diode D₃ is set as freewheeling by inductors L_K1 and L_K11. Therefore, current I_DS1 of switch M₁ is equal to 0.

Mode 2 (Figure 11b: t₁ ≤ t < t₂): at t₁, current I_LK11 is equal to 0. Within this time interval, current I_LK11 ranges from 0 to a positive value, therefore, diode D₃ is reversely biased. Current I_DS1 ranges from 0 to a positive value and its value is equal to I_LK11. Diode D₄ is kept in the forwardly conduction state and its current I_D4 is the sum of I_LK11 and I_C2. The resonant network formed by L_K21, L_K2 and C₂ is still in the resonant state. Diodes D₁ and D₂ are set in freewheeling mode, respectively, by inductors L_m11, L_m12, L_m21 and L_m22.

Mode 3 (Figure 11c; t₂ ≤ t < t₃): when t = t₂, current I_LK11 reaches the initial value which is the initial current value of the coupled inductor when the proposed converter is operated in continuous conduction mode (CCM). At that moment, diode D₁ is in the reversely bias state. The voltage V_PV is approximately applied to inductor L_m11 because L_m11 is much greater than L_K11. Within this time interval, current I_LK11 is equal to I_DS1 and its value increases linearly. Moreover, current I_LK2 is equal to I_C2 and its value ranges from a positive value to 0 with the resonant manner. Current I_D4 is still sum of I_DS1 and I_C2. Diode D₂ is kept in freewheeling state by inductors L_m21 and L_m22.

Mode 4 (Figure 11d; t₃ ≤ t < t₄): at t₃, current I_LK21 (= I_C2) is equal to 0. Within this time interval, current I_LK21 ranges from 0 to a negative value with the resonant manner. Since current I_DS1 is greater than I_C2, diode D₄ is still kept in the forwardly biased state. Operational conditions of the other components are the same conditions of Mode 3. As a result, current I_LK11 (= I_DS1) increases linearly and current I_D2 decreases linearly.

Mode 5 (Figure 11e, t₄ ≤ t < t₅): at t₅, switch M₁ is turned off. At that moment, current I_DS1 is approximately equal to I_C2, therefore, diode D₄ is reversely biased. Within this time interval, energies stored in inductors L_K11, L_K1, L_K21 and L_K2 are released to the charge capacitor C_M1 and discharge capacitor C_M2. Voltage V_DS1 across capacitor C_M1 ranges from 0 to [V_C2 + (NV_PV + V_O)/(N + 1)], while V_DS2 across capacitor C_M2 ranges from [V_C1 + (NV_PV + V_O)/(N + 1)] to 0. Diodes D₁, D₃, D₅ and D₆ are still kept in the reversely bias state, while diode D₂ is kept in freewheeling mode by inductors L_m21 and L_m22.

Mode 6 (Figure 11f; t₅ ≤ t < t₆): when t = t₅, the voltage V_DS2 across switch M₂ is equal to 0. At the same time, diodes D₅ and D₆ are in the forwardly bias state, while diode D₁ is in freewheeling mode due to inductors L_m11 and L_m12. Inductor L_K11, L_K1 and capacitor C₁ form a resonant network and they start to resonate. Moreover, diode D₂ is still kept in freewheeling mode by inductors L_m21 and L_m22. When switch M₂ is turned on at the end of mode 6, the other half of one switching cycle will start.

4. Control and Design of the Proposed PV Power System

In design considerations, the proposed one must match the operation conditions of MPPT for PV arrays and regulate the power between PV arrays and load by battery. In the following, control and design of the proposed PV power system are described.

4.1. Control of the Proposed PV Power System

The proposed PV power system consists of two boost converters and controller. The controller adopts a microcontroller and PWM IC. A block diagram of the proposed PV power system is shown in Figure 13.

Figure 13. Block diagram of the proposed PV power system.

Figure 13. Block diagram of the proposed PV power system.

In Figure 13, microcontroller is divided into two units: MPPT and power management units. In the MPPT unit, the perturb and observe method is adopted to track MPP of the PV arrays. The maximum power P_p of PV arrays can be decided by the MPPT unit. In the power management unit, the maximum discharging current I_B(max) of the battery is set for obtaining the maximum battery charging power P_B(max), which is equal to V_BI_B(max). Output voltage V_O and current I_O are sent to the power management unit for attaining load power P_L. Power P_B(max) and P_L are calculated by the multiplexer inside microcontroller, respectively. Three powers P_p, P_VB(max) and P_L are sent to comparator #1 to judge the relationship of (P_p + P_VB(max)) and P_L. When (P_p + P_VB(max)) ≥ P_L, signal S_p1 is kept at a low level. PWM generators of PV arrays and battery are operated in a normal operational mode. In this operational condition, signals G_1A, G_2A, G_1B and G_2B are generated by two PWM generators to drive switches M_1A, M_2A, M_1B, and M_2B. As a result, the proposed boost converter depends on the MPPT control algorithm to extract the maximum power of the PV arrays to load, while the proposed one follows the voltage regulation control method to regulate the power between the PV arrays and load, and sustain a desired constant voltage across the load.

When (P_p + P_VB(max)) < P_L, signal S_p1 reaches a high level. Two PWM generators are shut down. That is, the proposed PV power system is also shut down. When (P_P + P_B(max)) ≥ P_L, comparator #2 is enabled by signal S_P1 when S_P1 is in a low level state. It is used to judge the power relationship of P_p and P_L. When P_p is equal to or greater than P_L, signal S₁ attains a high level. The output signal P_set of the power selector controlled by signal S₁ is set to be equal to P_L. When P_p < P_L, signal S₁ is in a low level state. The signal P_set is specified by P_P. The next step is to determine the current reference I_C. The P_set and V_ref are sent to the current reference unit. I_C can be obtained and it is equal to (P_set/V_ref). Note that V_ref is the reference voltage of the output voltage V_O. When current reference I_C is sent to the current error amplifier, it can be compared with I_OP, which is output current of the proposed boost converter with the MPPT control method to attain the current error value ΔI_C. When the PWM generator of the PV arrays receives ΔI_C, duty ratios of the PWM signals G_1A and G_2A can be determined by the value of ΔI_C. Signals G_1A and G_2A can drive switches M_1A and M_2A to generate power for supplying power to the load. Moreover, protection judgment receives signals of the practical values V_O, I_O and V_B, and those signals of the set values V_O(max), V_O(min), I_O(max) and V_B(min), which are determined by the operational conditions of the load and undercharge of the battery, respectively. When output voltage V_O ≥ V_O(max), the proposed PV power system is operated in over-voltage condition. Signal S_P2 becomes a high level signal to shut down two PWM generators. When V_O < V_O(min), the proposed one is operated in under-voltage condition. Therefore, signal S_p2 is in the high level state and two PWM generators are shut down. If output current I_O ≥ I_O(max), the proposed system enters over-current condition. Two PWM generators are shut down. Moreover, when battery voltage V_B ≤ V_B(min), the battery enters the undercharge condition. The proposed one is also shut down. As mentioned above, protections of the proposed PV power system include over-voltage, over-current, undervoltage and undercharge protections.

The proposed boost converter with voltage regulation uses a lead-acid battery as its power source. Its main objectives are to regulate the power between PV arrays and load, and to sustain a constant output voltage for supplying power to the load. In order to implement power balance among PV arrays, battery and load, and sustain a constant output voltage, a PWM IC is adopted to control the proposed boost converter. Its control unit includes a voltage error amplifier and battery PWM generator. The voltage error amplifier receives V_O and V_ref, which are determined by the voltage requirement of the load, to obtain the voltage error value ΔV_C, which is equal to (V_ref − V_O). The ΔVc is sent to the PWM generator of the battery to produce PWM signals G_1B and G_2B. Signals G_1B and G_2B can control switches M_1B and M_2B to regulate the power between the PV arrays and the load. Moreover, PWM IC can be shut down by signals S_P1 and S_P2 when signals S_P1 or S_P2 are in the high level state.

Figure 13 shows the block diagram of the proposed PV power system. The MPPT algorithm is implemented by a microcontroller. Since the power variation of PV arrays is slow, the compensator of the current error amplifier inside the microcontroller adopts proportional (P) control to implement MPPT control. In the proposed boost converter with voltage regulation, its compensator is set in the voltage error amplifier of PWM IC unit. According to the application note suggestions of the PWM IC datasheet supplied by the manufacturer, the compensator of the voltage error amplifier controller with two poles and one zero, as shown in Figure 14, is used to achieve a stable converter system.

Figure 14. Schematic diagram of voltage error amplifier in PWM IC unit.

Figure 14. Schematic diagram of voltage error amplifier in PWM IC unit.

In order to design a stable system for the proposed converter, a small signal model for the proposed one is derived. Since the proposed converter with active clamp circuit only helps switches achieve soft-switching features, it can be neglected in the derived converter. Moreover, the proposed one consists of two boost converters with interleaving manner to supply power to the load. In order to simplify the derivation of the small signal model, a single boost with coupled inductor is adopted to describe the control system design of the proposed one. In the proposed system, we assume that all the components are ideal and that the converter operates in a continuous conduction mode (CCM). Its equivalent circuit is shown in Figure 15. Figure 15a shows the corresponding equivalent circuit and Figure 15b illustrates the simple equivalent circuit. In Figure 15a, we can define the switching function as:

(1)

According to Equation (1), we can get:

(2)

When the parameter f is represented with duty ratio d, the average model is given by Figure 15c. The state space average equation of the equivalent circuit with state variables i_L1 and V_C is depicted by where:

(3)

By substituting , (I_L1, I_L2 and D are the steady components, while and are the small disturbance quantities ), and i_L2 = (1 − d)i_L1 in Equations (2) and (3), they can be rewritten by Laplace transformation and be expressed by:

(4)

where:

Its detailed analysis is proposed in [30]. The open-loop control of the proposed converter is shown in Figure 15c. Its block diagram of the closed-loop control system is illustrated in Figure 16. In Figure 16, H(s) (= 1/K_f) represents the sensor gain, G(s) (= (1 + sC₂R₂)/[sR₁(C₂ + C₃)][1 + sR₂(C₂//C₃)]) is the transfer ratio of the compensator, P(s) (= 1/V_M) depicts that of the pulse-width modulator and G(s) expresses that of the converter. Its closed-loop transfer function from V_ref to V_O is expressed by:

(5)

where T(s) (= [H(s)G_C(s)G(s)]/V_M) is the loop gain.

Figure 15. Equivalent circuit based on (a) ideal switch; (b) switching function; and (c) average equivalent circuit.

Figure 15. Equivalent circuit based on (a) ideal switch; (b) switching function; and (c) average equivalent circuit.

Figure 16. Block diagram of the closed-loop control system of the proposed converter.

Figure 16. Block diagram of the closed-loop control system of the proposed converter.

4.2. Design of the Proposed Interleaved Boost Converter

Since the dc/dc converter using PV arrays as its power source, as shown in Figure 14, can be operated under current and voltage regulation, respectively, according to the different operational conditions, the components of the two dc/dc converters have the same design values. Due to the fact the switches in the two boost converters use the synchronous switch technique to simplify them, the ratios are limited to 0.5. In the design of the interleaved active clamp boost converter, determination of duty ratio D, coupled inductances (L_m11 and L_m12) and (L_m21 and L_m22), active clamp capacitors C₁ and C₂, and output filter are important. In the following, their designs are analyzed briefly.

4.2.1. Duty Ratio D

To determine the duty ratio D, we must first establish the input to output voltage transfer ratio M. Since the active clamp circuit helps switches M₁ and M₂ to achieve soft-switching features, transfer ratio M of boost converter has a slightly different value compared with the one without active clamp circuit. As a result, transfer ratio M of the proposed one is regarded as that of the conventional one. According to the volt-second balance principle of a coupled inductor L_m11, the following equation can be obtained:

(6)

where N is turns ratio of couple inductor (L_m11 and L_m12) or (L_m21 and L_m22) and T_s is period switch M₁. From Equation (1), transfer ratio M can be expressed by:

(7)

Based on the operational condition of the proposed boost converter with switch integration, duty ratio D of switch M₁ or M₂ is limited to 0.5 and they are operated in complementary fashion. According to Equation (7), a large duty ratio D corresponds to a smaller turns ratio N of the coupled inductor, which results in a lower current stress being imposed on switches M₁ and M₂, as well as voltage stresses on diodes D₁ and D₂. However, in order to accommodate variations of load, line voltage, component values and duty loss, it is better to select an operating range D = 0.35~0.4.

4.2.2. Coupled Inductors (L_m11 and L_m12) or (L_m21 and L_m22)

Once the duty ratio D is selected, the turns ratio N of coupled inductors L_m11 and L_m12 can be determined using Equation (7), which yields

(8)

By applying Faraday’s law, N₁₁ of coupled inductor can be given by:

(9)

where A_c is the effective cross-section area of the coupled inductor core and ΔB is the working flux density. According to Equations (8) and (9), N₁₂ can therefore be determined.

To achieve a ZVS feature, the energy stored in the leakage inductor L_K11 (or L_k21) and external inductor L_k1 (or L_k2) must satisfy the following inequality:

(10)

where L_k1 is the external inductor to increase operational ranges of the soft-switching circuit, I_LK11(tv11) is the current of L_k11 at time t₁₁, I_Lk11(tv10) is that at time t₁₀, C_T is the total capacitor which is the sum of C_M1 and C_M2, and V_DS1(max) represents the maximum voltage across switch M₁ and its value is equal to [V_PV + (V_O − V_PV)/(N + 1)]. According to the circuit operational principle, the voltage V_C1 across capacitor C₁ can be approximately expressed by:

(11)

Once C_T, and I_LK11(tv10) and I_LK11(tv11) are specified, the inequality of inductor L_T (= L_K1 + L_K11) can determined as:

(12)

Since the proposed converter is operated in continuous conduction mode (CCM), inductances L_m11 and L_m12 must be greater than L_m11B and L_m12B, respectively, which are the inductances at the boundary of CCM and discontinuous conduction mode (DCM). Its boundary current waveforms are shown in Figure 17. From Figure 17, it can be seen that when switch M₁ is turned on, inductor current I_LK11 is the sum of I_Lm11 and I_N11, which is the equivalent reflected current from the secondary winding N₁₂ to the primary winding N₁₁. Therefore, current I_LK11 can be expressed by:

(13)

where I_N11 is equal to NI_N12 (= NI_Lm12). Therefore, I_LK11(1) can be determined as:

(14)

where L_m11 is the magnetizing inductor of primary winding of coupled inductor and L_m12 is its secondary winding inductor. According to Equation (14), I_LK11(1) can be rewritten by:

(15)

Moreover, I_LK11(2) can be given by:

(16)

Since current I_D1(1) is equal to I_LK11(2) and average current I_D1(av) equals half of output current I_O, the average current I_D1(av) can be expressed as follows :

(17)

According to Equation (17), the boundary inductance L_m11B can be determined as:

(18)

Based on the magnetic principle of coupled inductor, the relationship between inductances L_m11B and L_m12B can be expressed as follows:

(19)

Substituting Equations (18) in (19), inductor L_m12B can be determined as:

(20)

According to the operational requirements of the proposed boost convertor which is operated in CCM, inductors L_m11 and L_m12 must be greater than L_m11B and L_m12B, respectively. Since L_m21 = L_m11 and L_m22 = L_m12, inductors L_m21 and L_m22 are also separately greater than L_m11B and L_m12B.

Figure 17. Conceptual current waveforms of inductor currents and output current in the proposed converter operated at the boundary of CCM and DCM.

Figure 17. Conceptual current waveforms of inductor currents and output current in the proposed converter operated at the boundary of CCM and DCM.

4.2.3. Active Clamp Capacitor C₁ or C₂

The active clamp Capacitors C₁ and C₂ are used to achieve soft-switching features. In order to achieve ZVS features, one half of the resonant period formed by L_T and C₁ or L_T and C₂ should be equal to or greater than the maximum off time of switches M₁ or M₂. Therefore, capacitor C₁ (or C₂) must satisfy the following inequality:

(21)

From Equations (12) and (21), when L_T is specified, the capacitance ranges of C₁ (or C₂) can be determined as:

(22)

4.2.4. Output Capacitor C_o

The output capacitor C_o is primarily designed for reducing ripple voltage. The ripple voltage ΔV_rco across output capacitor C_o is determined by:

(23)

where I_O(max) is the maximum output current.

5. Experimental Results

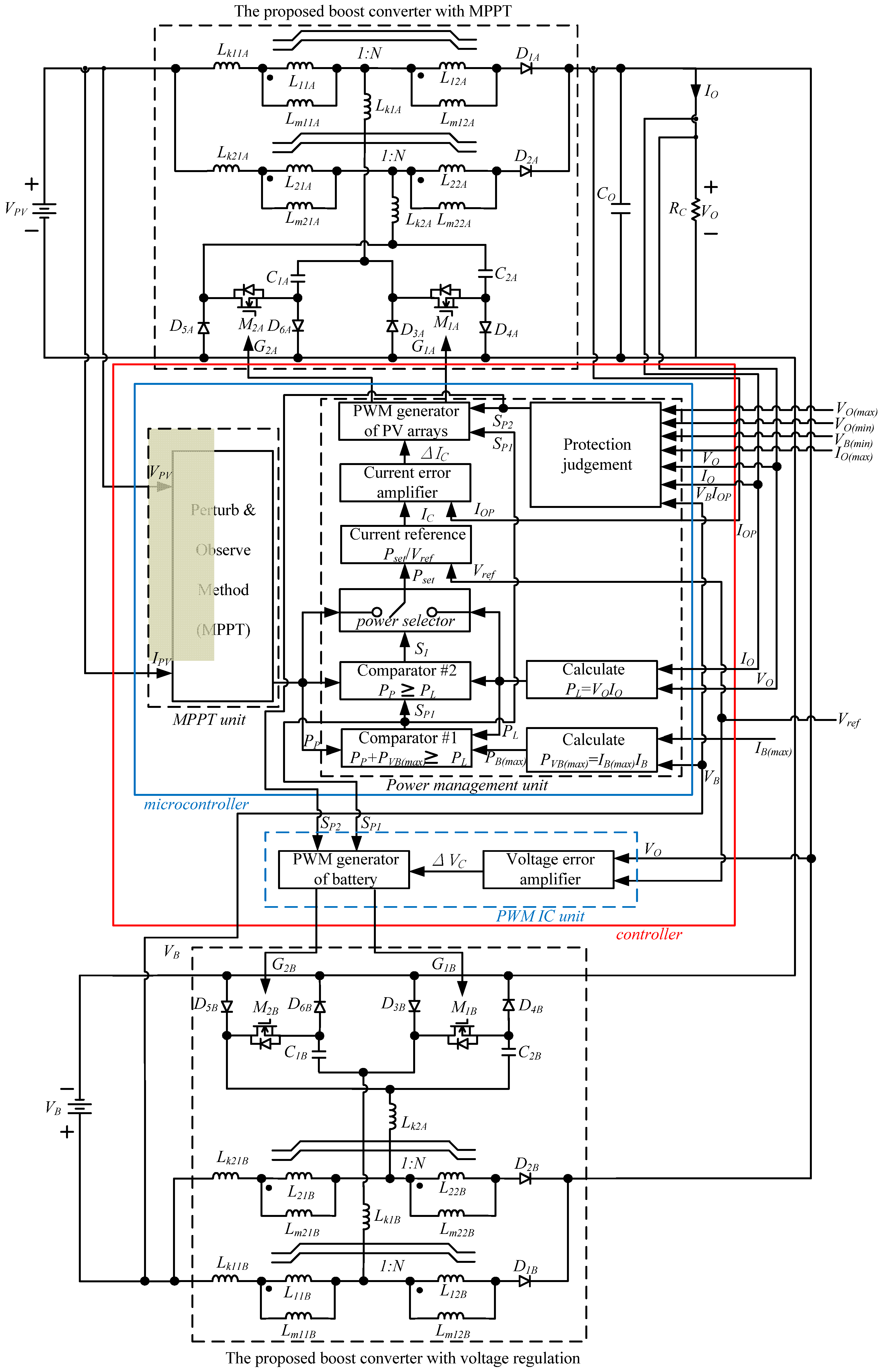
The proposed PV power system is shown in Figure 13. To verify the performance of the proposed PV power system, two dc/dc converters using an interleaved active clamp boost converter with coupled inductor to generate dc voltage of 400 V for dc load applications with the following specifications were implemented:

• The proposed boost converter with MPPT

  • Input voltage V_PV: 34~42 V_dc (PV arrays);
  • Output voltage V_O: 400 V_dc;
  • Output maximum current I_OP(max): 3 A; and
  • Output maximum power P_PV(max): 1.2 kW.
• The proposed boost converter with voltage regulation

  • Input voltage V_B: 40~54 V_dc (four sets of 12 V batteries connected in series);
  • Output voltage V_O: 400 V_dc;
  • Output maximum current I_OB(max): 3 A; and
  • Output maximum power P_B(max): 1.2 kW.

According to designs and specifications of the proposed boost converters, components of power stages in the proposed two boost converters are determined as follows:

• Switches M_1A, M_2A, M_1B, M_2B: IRFP260N×2 (connected in parallel);
• Diodes D_1A, D_2A, D_1B, D_2B: DSSK60-02A;
• Diodes D_3A, D_4A, D_5A, D_6A: DSSK60-02A;
• Diodes D_3B, D_4B, D_5B, D_6A: DSSK60-02A;
• Coupled inductors L_m11, L_m21: 28 μH;
• Leakage inductors of coupled inductor (L_m11, L_m12) and (L_m21, L_m22): 0.8 μH and 0.81 μH;
• Cores of coupled inductors (L_m11, L_m12) and (L_m21, L_m22): EE-55;
• Turns ratio N: 15; and
• Extera inductors L_k1, L_k2: 1.2 μH.

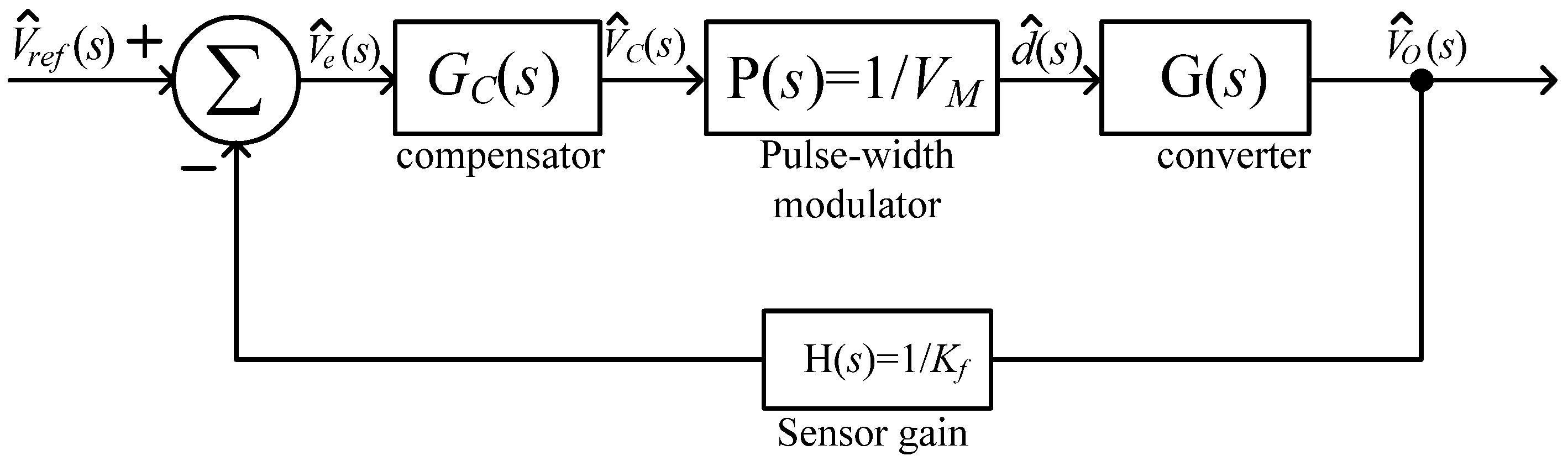
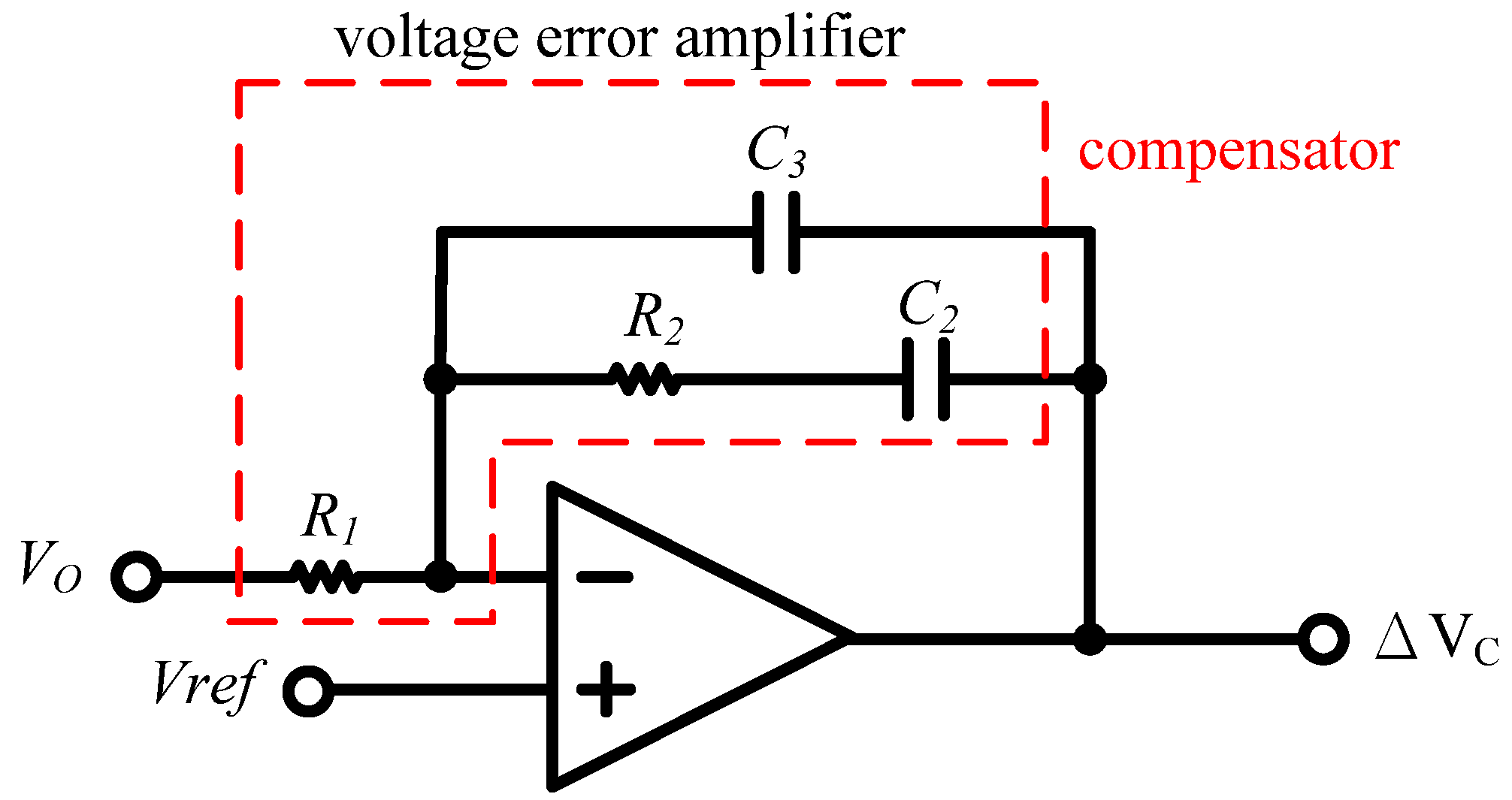
According to the previous specifications and the compensator of the proposed converter, parameter values of the small signal model in the proposed system (as shown in Figure 16) are listed in Table 1.

Table 1. Parameter values of small signal model of the proposed converter.

symbol	parameter value
VO	400
D	0.36
L1	28 μH
N	15
CO	780 μF
RL	266.66 Ω
R1	10 kΩ
R2	220 Ω
C2	2 μF
C3	6.8 nF
VM	2.5
Kf	160

Table 1. Parameter values of small signal model of the proposed converter.

symbol	parameter value
VO	400
D	0.36
L1	28 μH
N	15
CO	780 μF
RL	266.66 Ω
R1	10 kΩ
R2	220 Ω
C2	2 μF
C3	6.8 nF
VM	2.5
Kf	160

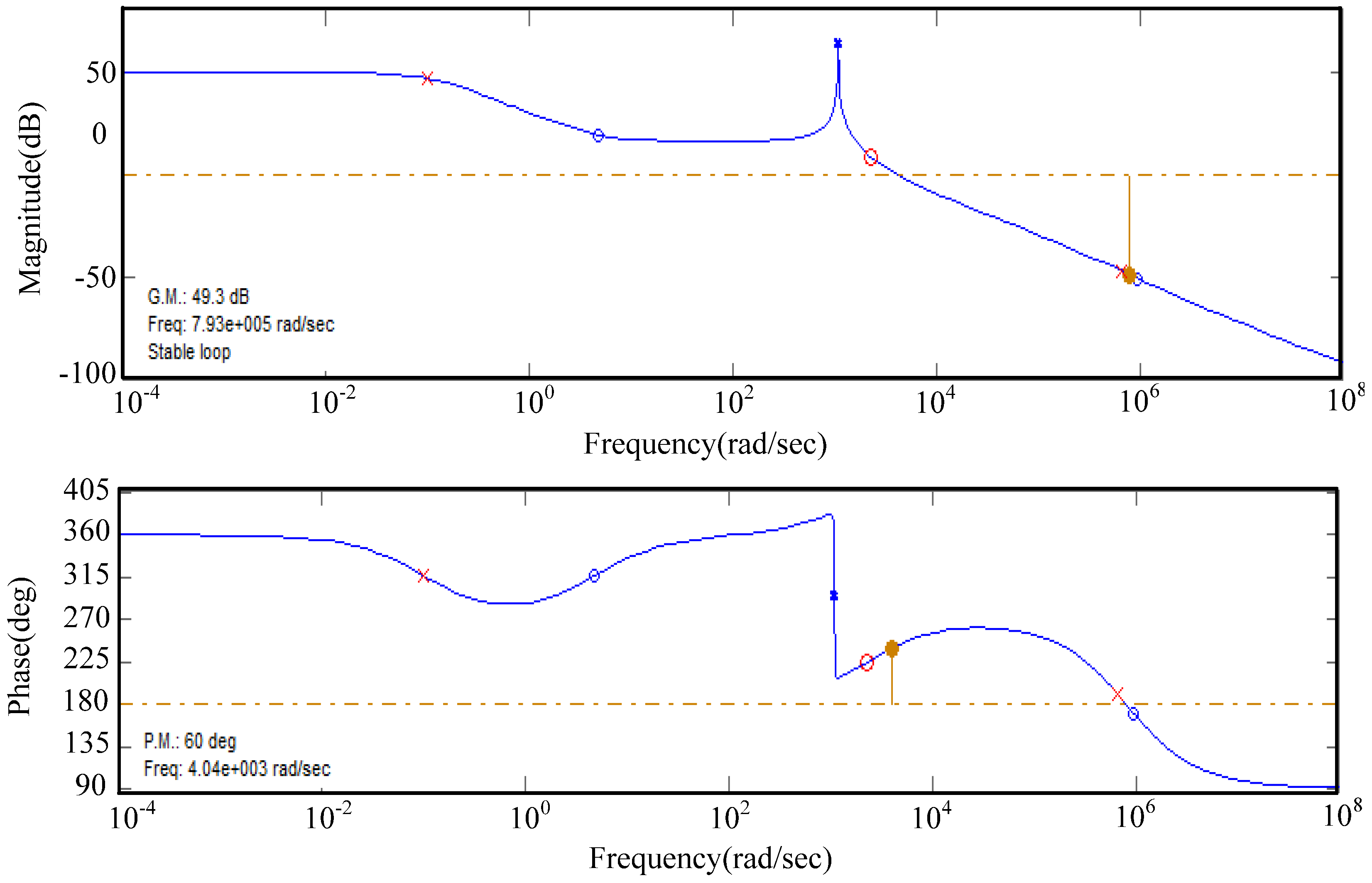
We can use the Matlab simulation tool to obtain Bode plots of the proposed converter under the closed loop condition. They are shown in Figure 18. From Figure 18, it can be seen that P.M. of the proposed one is 60°. Therefore, this can prove that the proposed converter is a stable system.

Figure 18. Bode plots of the proposed converter under the closed loop condition.

Figure 18. Bode plots of the proposed converter under the closed loop condition.

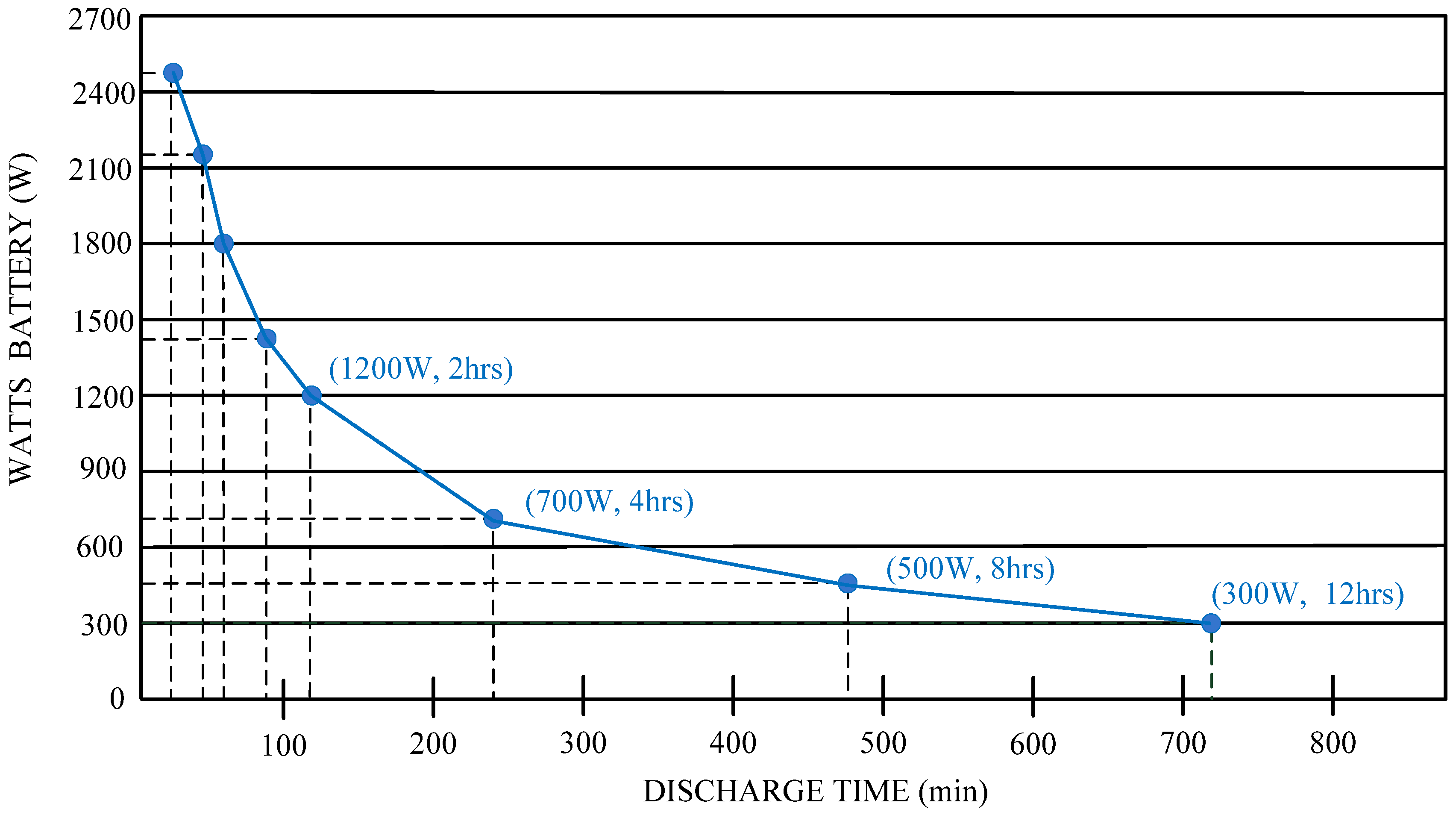
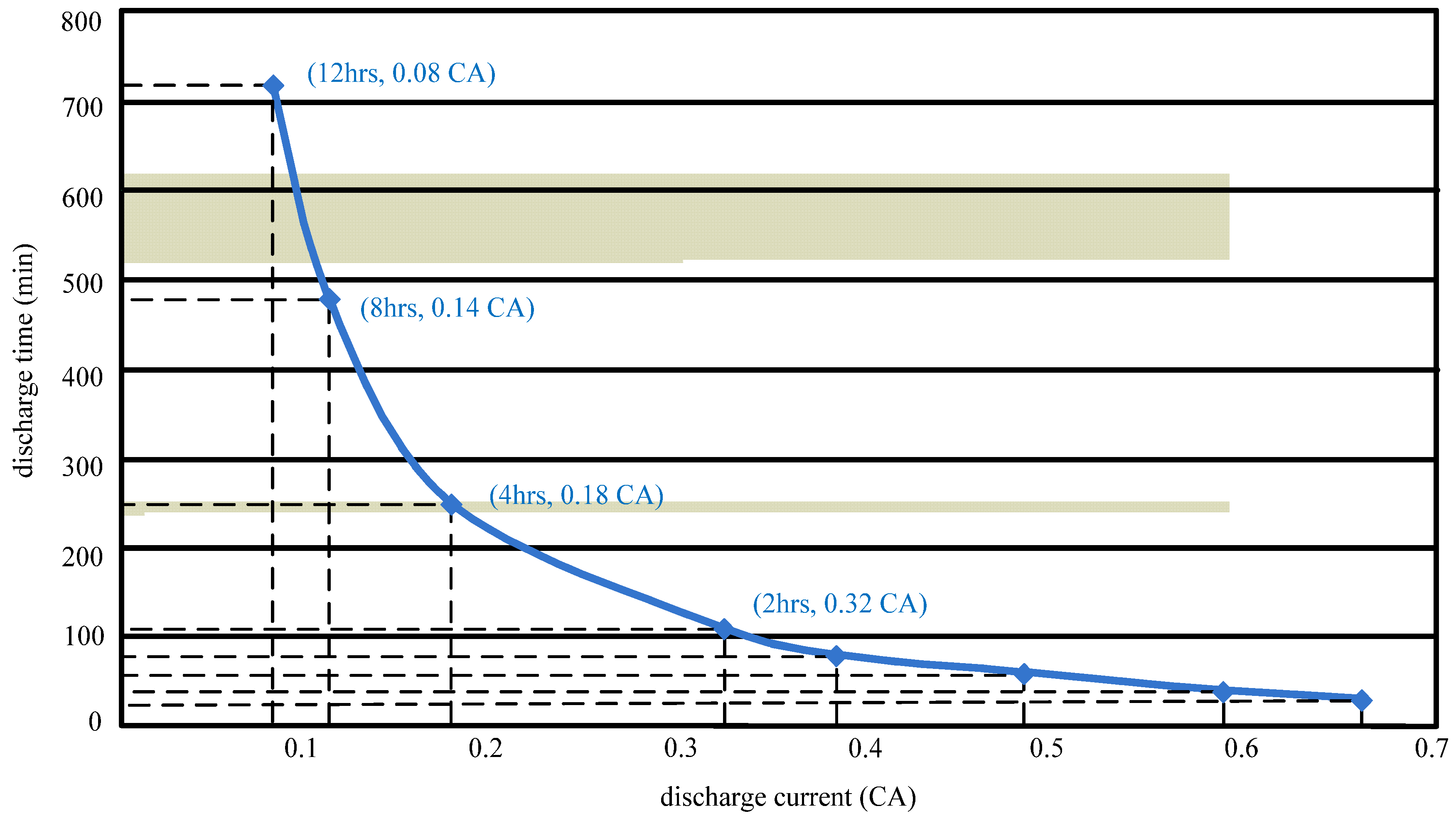
Since the proposed interleaved PV power system uses PV arrays and batteries as its input sources, the maximum output power of the proposed PV power system can supply 2.4 kW. In order to extend battery discharge time, the maximum output power of the battery module is suggested to be 1.2 kW. In our research, four sets of lead-acid batteries (12 V/75 Ah) connected in series are adopted in the proposed converter. According to discharge times supplied by the battery manufacturer, a sustained discharge time of 2 hours is possible when the output power of battery is 1.2 kW, while the discharge time can extend to 8 hours when it is 500 W. The curve of output power versus discharge time of batteries as supplied by the battery manufacturer is shown in Figure 19, while the curve of discharge time versus discharge current (CA) of the batteries is depicted in Figure 20.

Figure 19. Plot of output power versus discharge time of the batteries supplied by battery manufacturer.

Figure 19. Plot of output power versus discharge time of the batteries supplied by battery manufacturer.

Figure 20. Plot of discharge time versus discharge current (CA) of batteries supplied by the battery manufacturer.

Figure 20. Plot of discharge time versus discharge current (CA) of batteries supplied by the battery manufacturer.

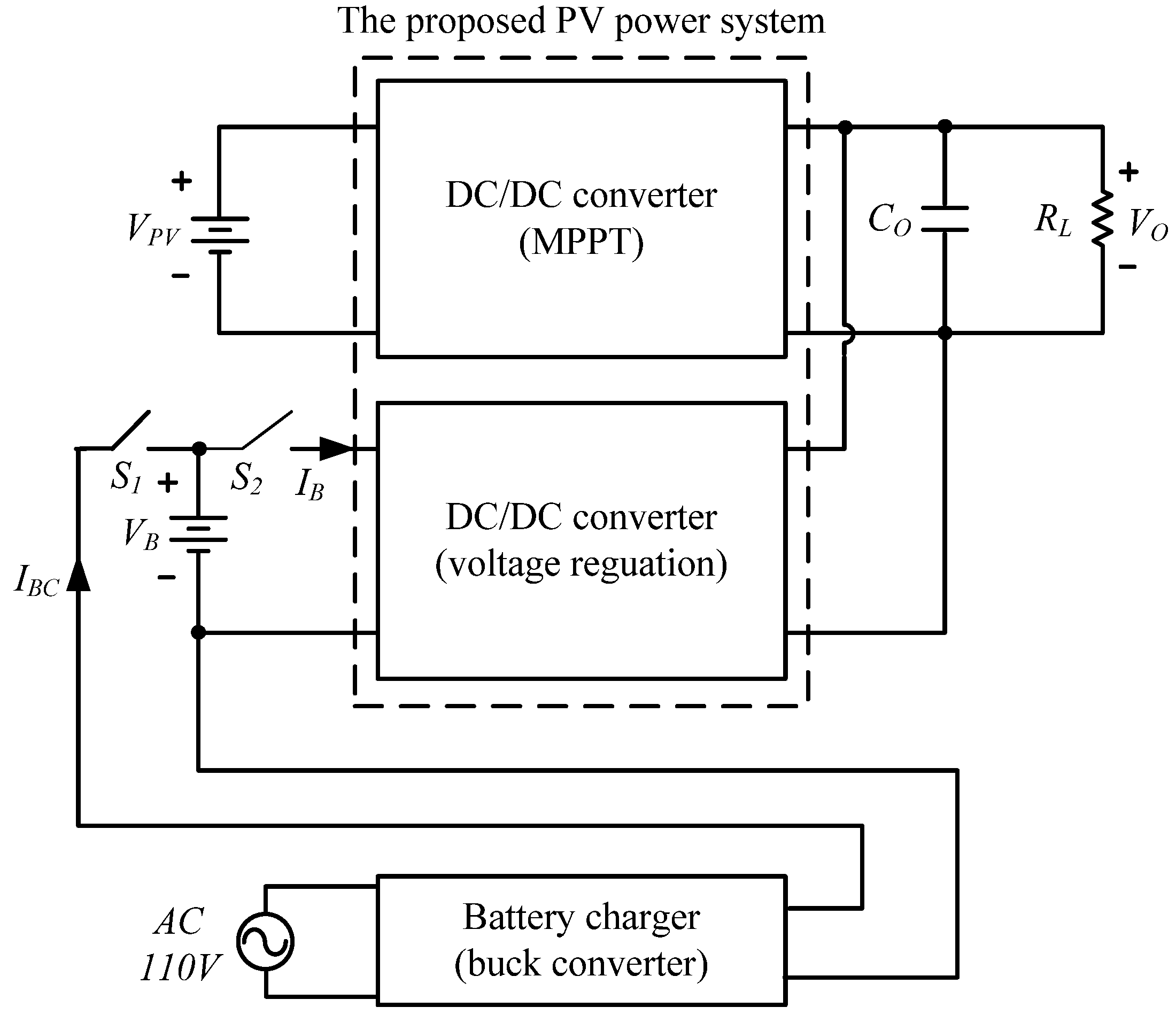
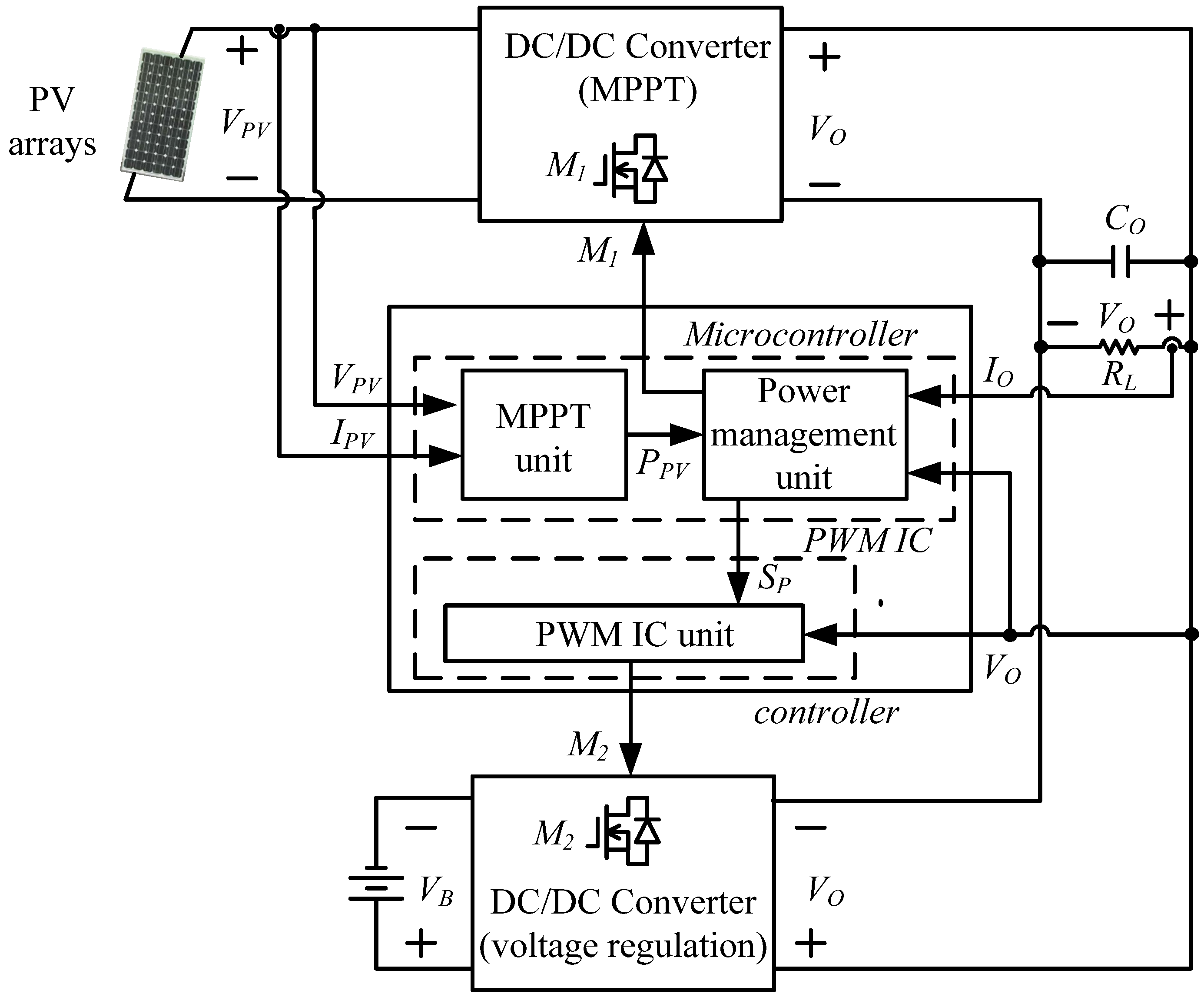
From Figure 20, it can be seen that when output power of battery is 1.2 kW, its discharge current is 0.32 CA. When the battery is completely discharged, a battery charger is adopted. The block diagram of the proposed PV power system and battery charger is shown in Figure 21. When the battery is in the charging state during the night, switch S₁ is turned on and a battery charger using a buck converter is adopted to charge the battery. On the other hand, when the battery in the discharging state during the day, switch S₂ is turned on and battery uses the proposed converter to supply power to the load. A photograph of the hardware is shown in Figure 22.

Figure 21. Block diagram of the proposed PV power system and battery charger.

Figure 21. Block diagram of the proposed PV power system and battery charger.

Figure 22. Photograph of the hardware for the proposed PV power system and battery charger.

Figure 22. Photograph of the hardware for the proposed PV power system and battery charger.

Figure 23 shows measured charging voltage V_B and current I_BC waveforms of the battery, illustrating that the charging current I_BC uses the pulse current charging method and its charging current I_BC is under the repeat period of 200 ms, duty ratio of 0.5 and peak charging current of 20 A. When the battery voltage V_B reaches its end of charge voltage V_FV (about 54 V), the battery charger is shut down. 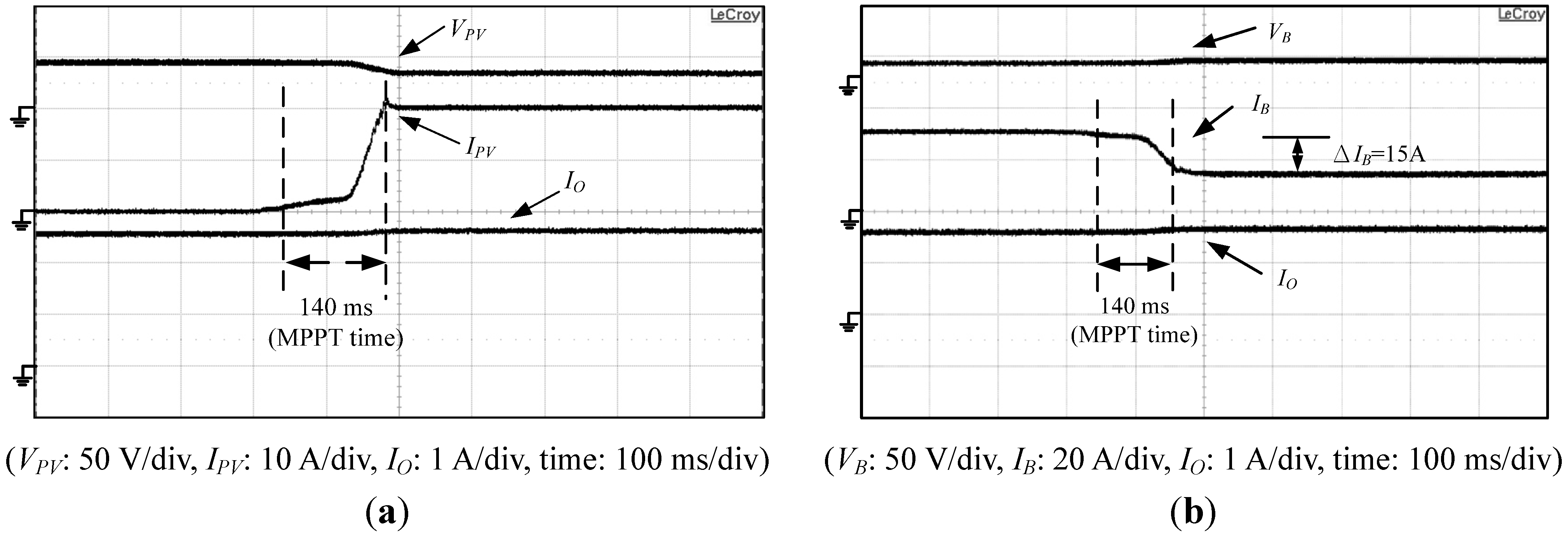Figure 24 shows measured voltages and currents waveforms of the proposed PV power system under output power P_O of 1 kW and PV arrays maximum output power P_PV(max) of 700W. Figure 24a shows measured PV arrays voltage V_PV, current I_PV and output current I_O waveforms, while Figure 24b depicts measured battery voltage V_B, current I_B and output current I_O waveforms.

Figure 23. Measured charge voltage V_B and charge current I_BC waveforms of battery under the repeat period of 200 ms, duty ratio of 0.5 and peak charging current of 20 A.

Figure 23. Measured charge voltage V_B and charge current I_BC waveforms of battery under the repeat period of 200 ms, duty ratio of 0.5 and peak charging current of 20 A.

(V_B: 20 V/div, I_BC: 20 A/div, time: 100 ms/div)

Figure 24. Measured voltage and currents waveforms of the proposed PV power system under output power P_O of 1 kW and PV arrays maximum power P_PV(max) of 700 W: (a) P_V arrays voltage V_PV, current I_PV and output current I_O waveforms; and (b) battery voltage V_B, current I_B and output current I_O waveforms.

Figure 24. Measured voltage and currents waveforms of the proposed PV power system under output power P_O of 1 kW and PV arrays maximum power P_PV(max) of 700 W: (a) P_V arrays voltage V_PV, current I_PV and output current I_O waveforms; and (b) battery voltage V_B, current I_B and output current I_O waveforms.

From Figure 24, it can be seen that MPPT time of PV arrays is about 140 ms from 0 to 700 W and battery discharging current I_B varies from 30 A to 15 A. This proves that the proposed PV power system can regulate the output powers of the battery and PV arrays to supply power to the load.

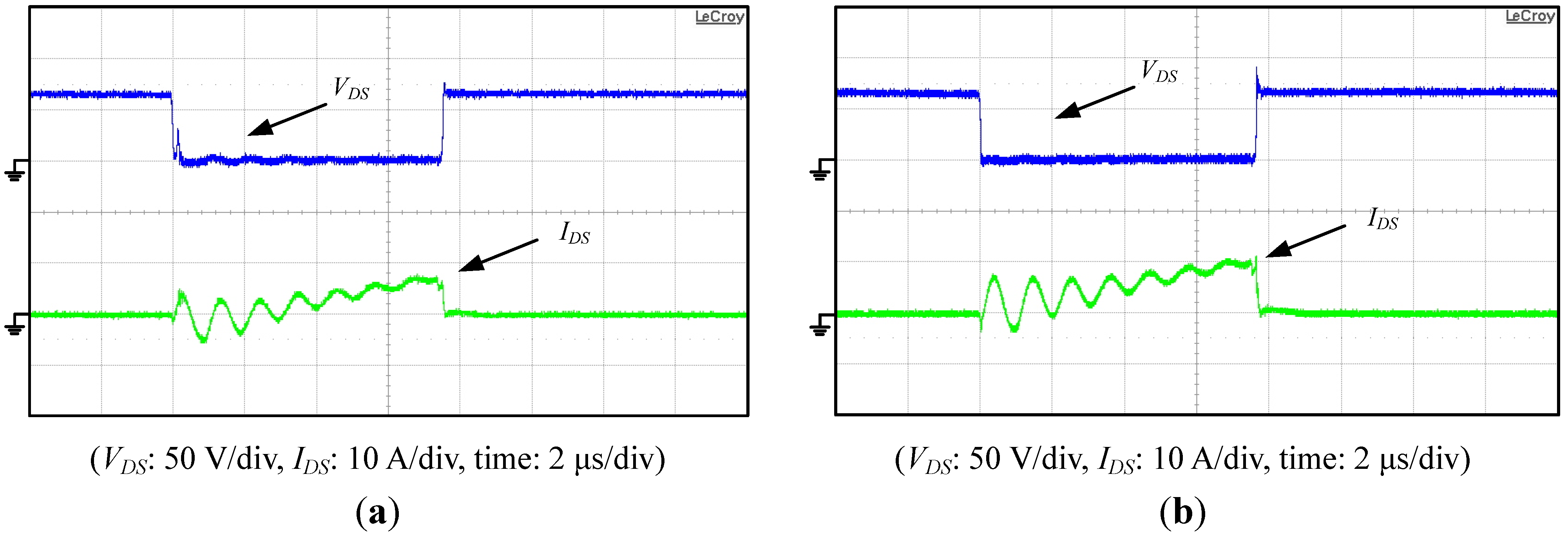
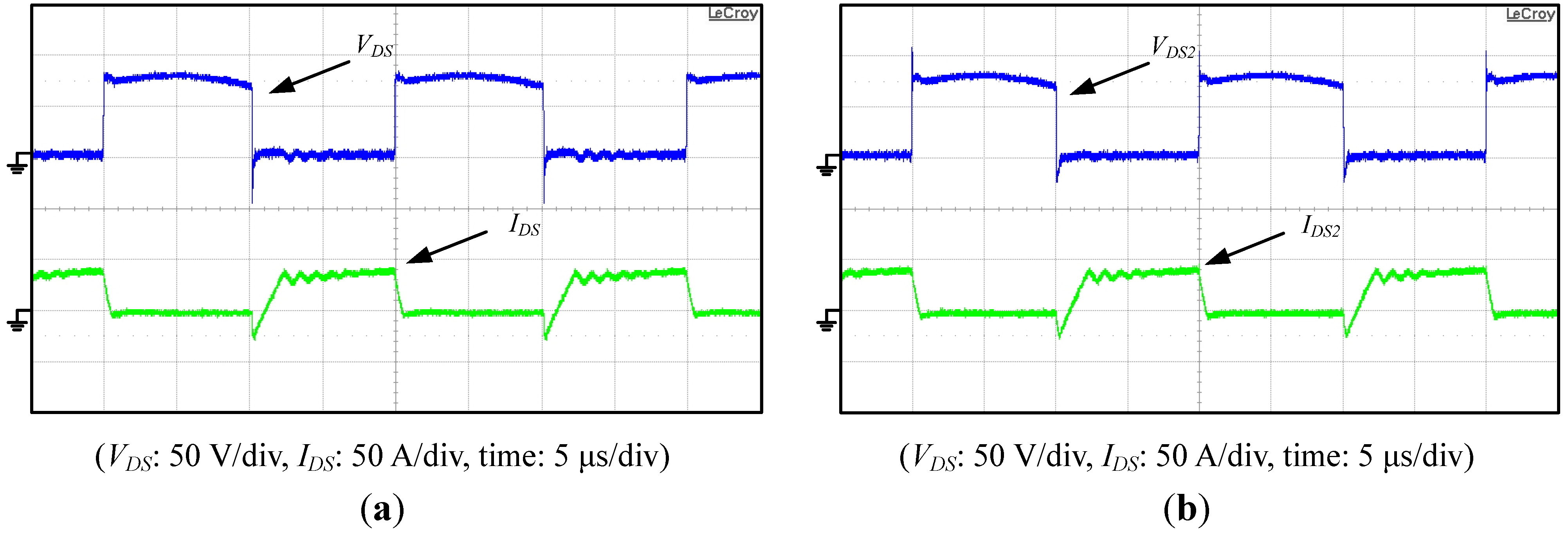
In order to verify the feasibility of the proposed interleaved active clamp boost converter with voltage regulation, measured voltage V_DS and I_DS waveforms of switches M_1B and M_2B are shown in Figure 25 and Figure 26, respectively. Figure 27 shows those waveforms under 10% of full load condition, while Figure 26 depicts those waveforms under full load condition. From Figure 25, it can be found that when load is at 10% of full load condition, switches M_1B and M_2B are in the hard switching and soft switching boundary, respectively.

Figure 25. Measured voltage V_DS and current I_DS waveforms of (a) switch M_1B and (b) switch M_2B of the proposed converter 10% of full load.

Figure 25. Measured voltage V_DS and current I_DS waveforms of (a) switch M_1B and (b) switch M_2B of the proposed converter 10% of full load.

Figure 26. Measured voltage V_DS and current I_DS waveforms of (a) switch M_1B and (b) switch M_2B of the proposed converter under full load.

Figure 26. Measured voltage V_DS and current I_DS waveforms of (a) switch M_1B and (b) switch M_2B of the proposed converter under full load.

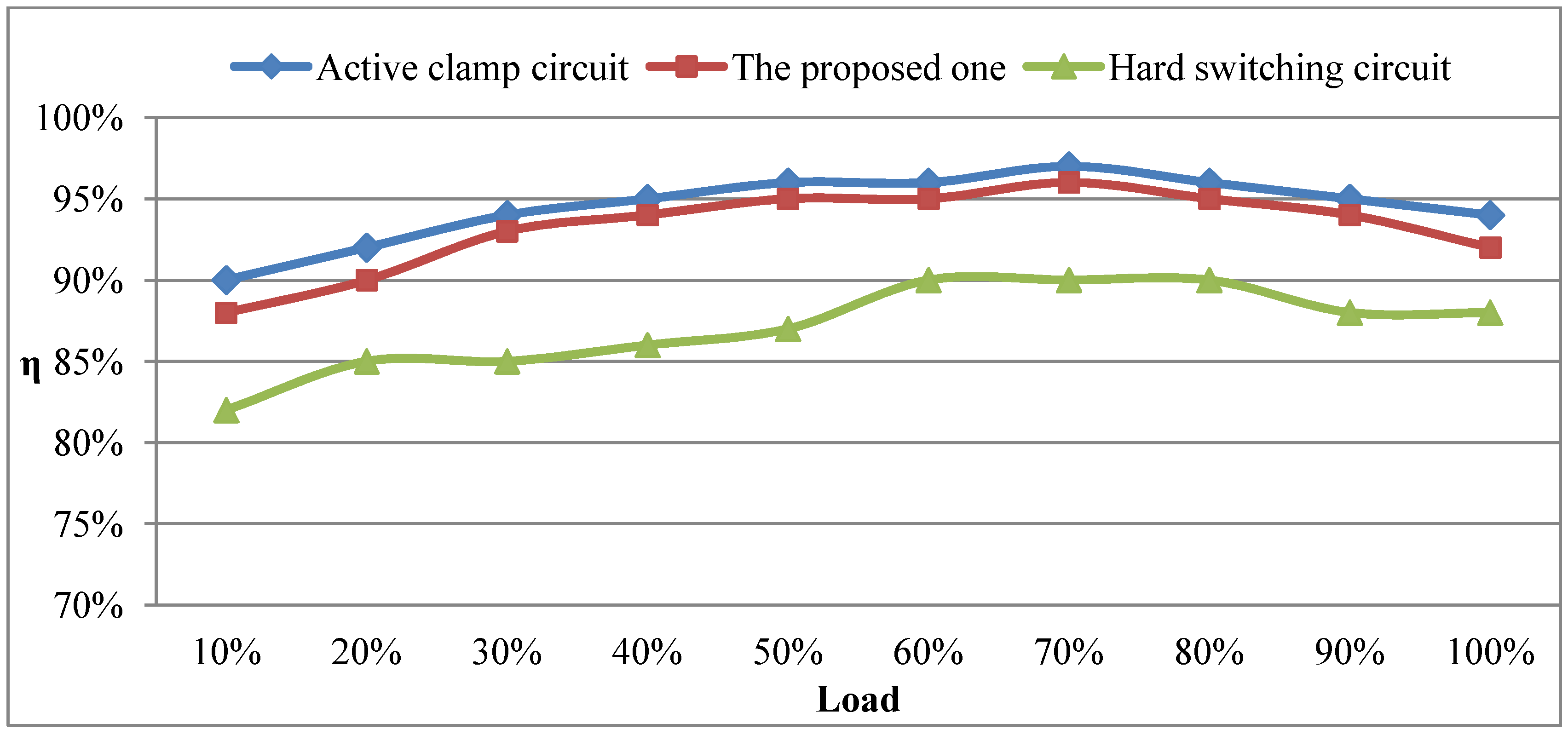
Figure 27. Comparison conversion efficiency among the interleaved active clamp boost converter with hard-switching circuit, active clamp circuit and the proposed one.

Figure 27. Comparison conversion efficiency among the interleaved active clamp boost converter with hard-switching circuit, active clamp circuit and the proposed one.

When the load is greater than 10% of full load, switches M_1B and M_2B can be operated with ZVS at turn on. Comparison of the conversion efficiency among the interleaved boost converter with hard-switching circuit, the active clamp circuit (as shown in Figure 3) and the proposed one is shown in Figure 27. It reveals that the efficiencies of the boost converter with the active clamp circuit and the proposed one are always higher than that with a hard-switching circuit from light load to heavy load. 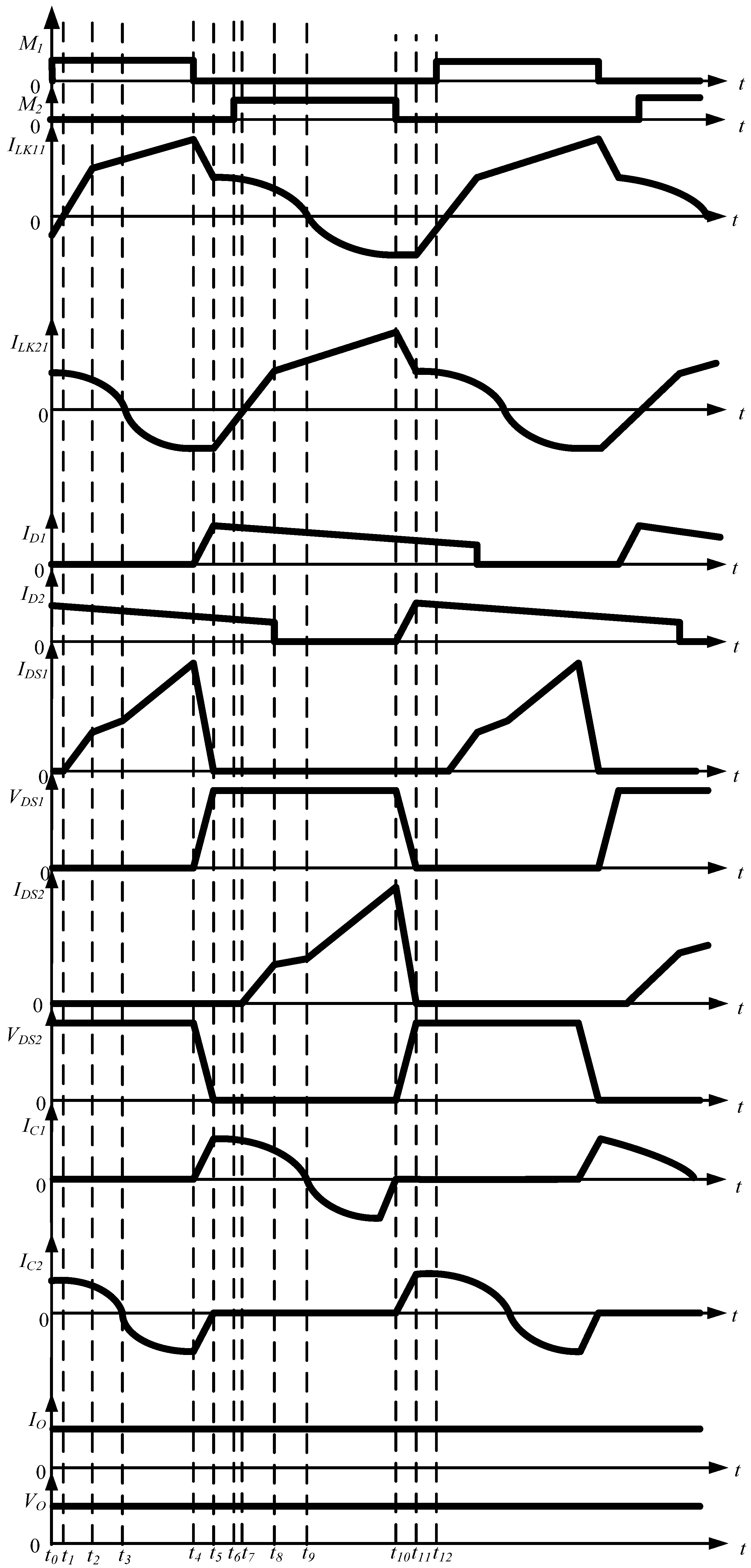Moreover, efficiency of the boost with the proposed circuit is approximately the same as that with the active clamp circuit (as shown in Figure 3) from light load to heavy load. The reason for this is that although currents flowing through diodes D_4B and D_6B have larger losses, compared with the boost converter with the active clamp circuit shown in Figure 3, the diode current I_D6B, which flows through diode D_6B shown in Figure 13, is the sum of current I_M2B and resonant current I_C1B. Since current I_C1B is a resonant current, the negative resonant current I_C1B, which is shown in Figure 12 during t₉~t₁₀ interval, does not flow through diode D_6B. Therefore, this can partially reduce the forward conduction losses of diode D_6B. Similarly, the forward conduction losses of diode D_4B can also be reduced. As mentioned above, the boost converter with the proposed circuit can also keep it at a high conversion efficiency from light load to heavy load. Its maximum efficiency is 96% under 70% of full load conditions and its full load efficiency is about 92%. According to the efficiency curve of the proposed interleaved boost converter shown Figure 27 and the circuit structure, its performance can compare with the results in [28] and [29]. The performance comparison results are listed in Table 2. Note that the special capacitor is required to possess a lower ESR and a higher CRR and the special PWM IC possesses a larger duty ratio, greater than 0.5.

Table 2. Performance comparison of interleaved high step-up converters.

High step-up interleaved converter	Converter in [28]	Converter in [29]	The proposed converter
Voltage gain	$\frac{N+2}{1-D}$	$\frac{2(N+1)}{1-D}$	$\frac{N+2}{1-D}$
Voltage stress on switch	$\frac{N+2}{1-D}$	$\frac{V_O}{N+2}$	$\frac{V_O+N{V}_{PV}}{N+1}$
Voltage stress on diodes	$\frac{N+2}{1-D}$	$\frac{N{V}_O}{N+1}$	VO + NVPV
Quantities of switches	2	2	2
Quantities of diodes	6	4	4
Quantities of cores	4	2	4 ( $\frac{2 \mathrm{main} \mathrm{cores}}{2 \mathrm{resonant} \mathrm{cores}}$)
Quantities of capacitors	4 (special capacitors)	(special capacitors)	3
Maximum duty ratio	>0.5	>0.5	<0.5
Controller	Complex (special PWM IC)	Complex (DSP)	Simple
Cost	High	Middle	Low
Efficiency	Higher	Higher	High
Power level	Small power	Small or middle power	Middle or high power

Table 2. Performance comparison of interleaved high step-up converters.

High step-up interleaved converter	Converter in [28]	Converter in [29]	The proposed converter
Voltage gain	$\frac{N+2}{1-D}$	$\frac{2(N+1)}{1-D}$	$\frac{N+2}{1-D}$
Voltage stress on switch	$\frac{N+2}{1-D}$	$\frac{V_O}{N+2}$	$\frac{V_O+N{V}_{PV}}{N+1}$
Voltage stress on diodes	$\frac{N+2}{1-D}$	$\frac{N{V}_O}{N+1}$	VO + NVPV
Quantities of switches	2	2	2
Quantities of diodes	6	4	4
Quantities of cores	4	2	4 ( $\frac{2 \mathrm{main} \mathrm{cores}}{2 \mathrm{resonant} \mathrm{cores}}$)
Quantities of capacitors	4 (special capacitors)	(special capacitors)	3
Maximum duty ratio	>0.5	>0.5	<0.5
Controller	Complex (special PWM IC)	Complex (DSP)	Simple
Cost	High	Middle	Low
Efficiency	Higher	Higher	High
Power level	Small power	Small or middle power	Middle or high power

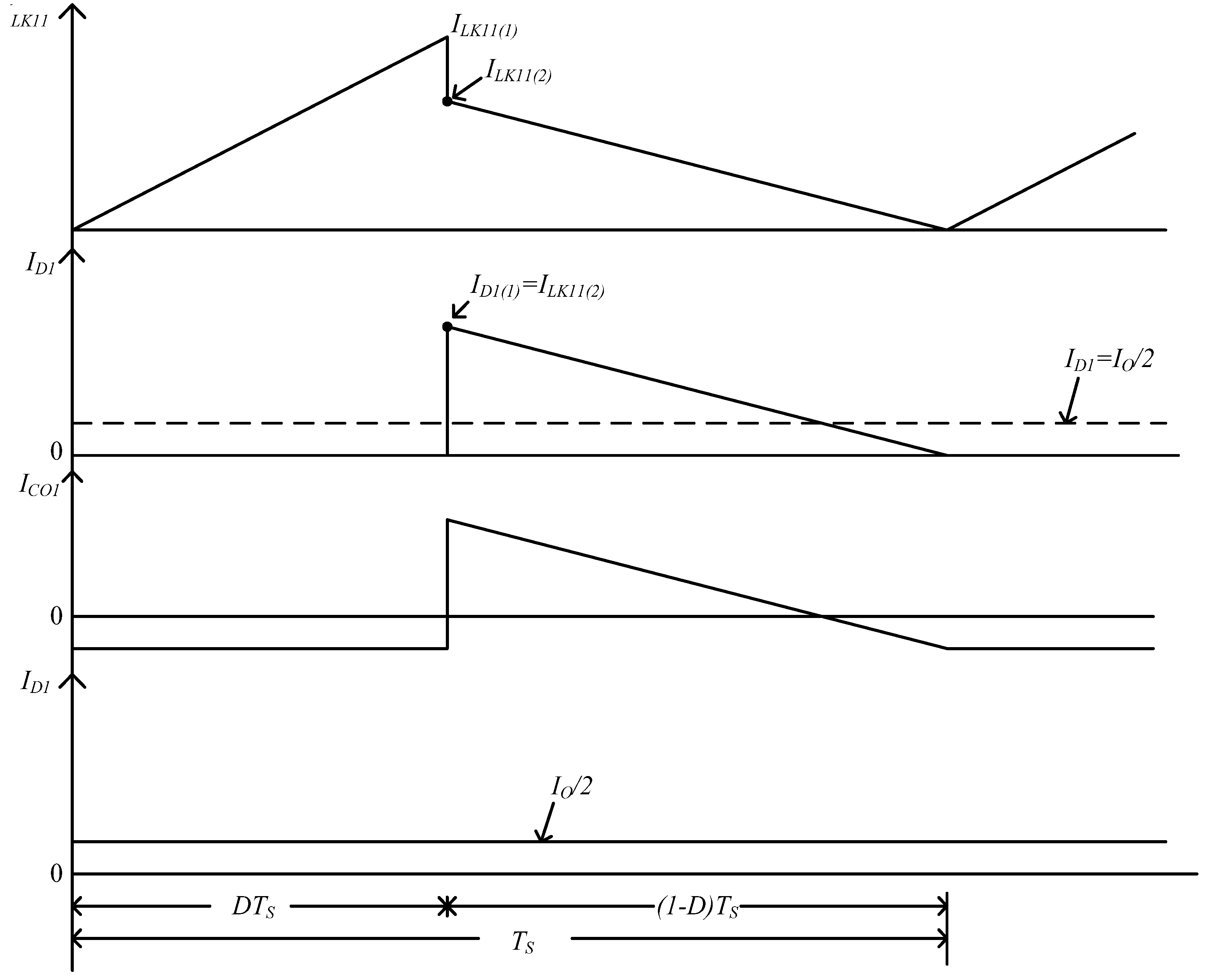
In order to simply analyze the CRR_S of the proposed one and the conventional one proposed in [29], we assume that values of output capacitors C_1, C₂ and C₃ of the conventional one are equal to that of output capacitor C_O, and their voltages V_C1, V_C2 and V_C3 are the same value. Each output capacitor of the proposed one and the conventional one adopt the same current I_D1 to charge them, as shown in Figure 28. According to the previously assumed conditions, the equivalent circuit of the output terminals is shown in Figure 29.

Figure 28. Conceptual current waveforms of inductor current, diode current, output capacitor current and output current in the proposed converter operated converter operated in the boundary of CCM and DCM.

Figure 28. Conceptual current waveforms of inductor current, diode current, output capacitor current and output current in the proposed converter operated converter operated in the boundary of CCM and DCM.

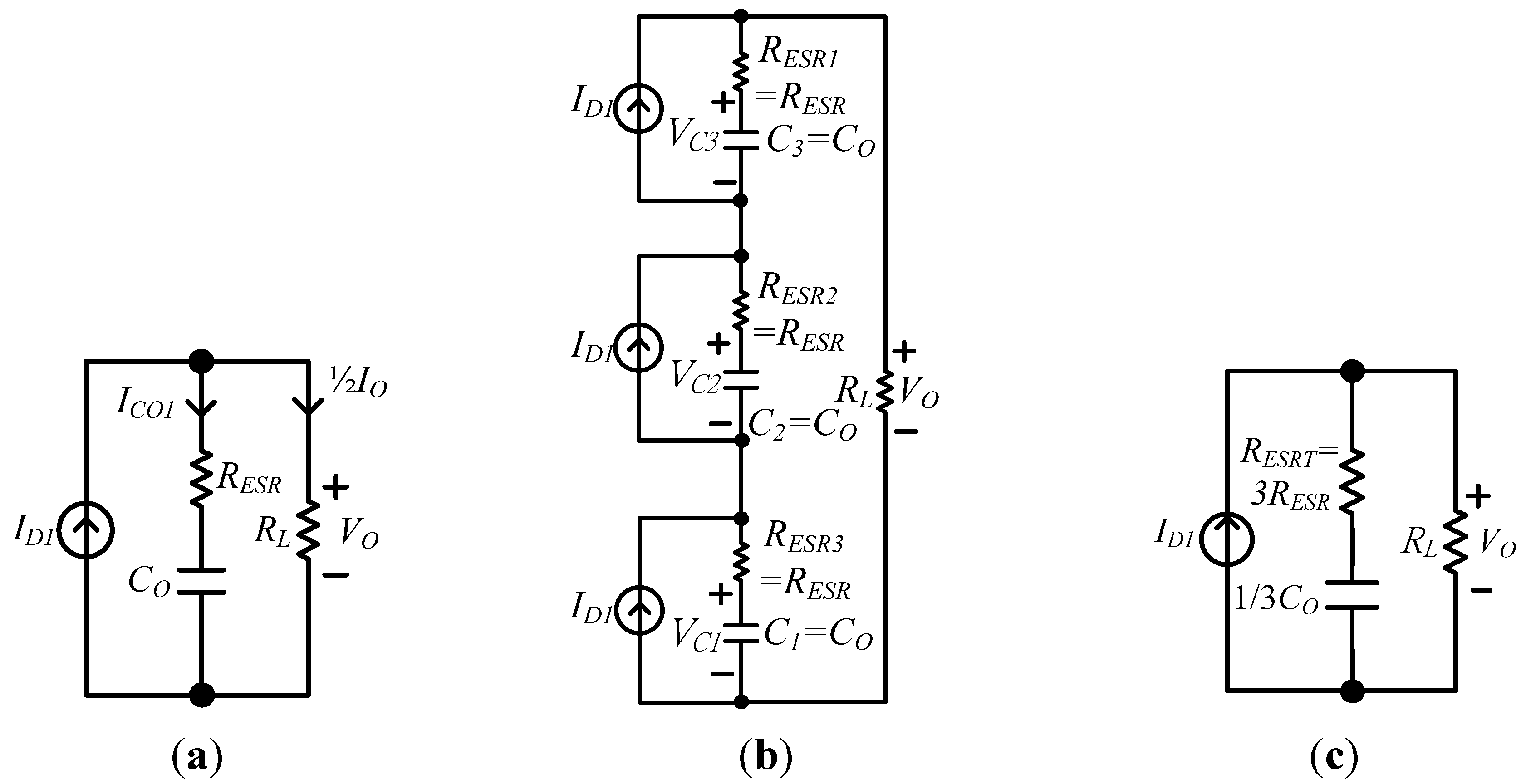
Figure 29. Equivalent circuit of output terminals: (a) the proposed converter; (b) the conventional converter proposed in [29]; and (c) the simplified conventional converter proposed in [29].

Figure 29. Equivalent circuit of output terminals: (a) the proposed converter; (b) the conventional converter proposed in [29]; and (c) the simplified conventional converter proposed in [29].

Figure 29a shows the one of the proposed converter, while Figure 29b illustrates the one of the conventional one. Its simplified equivalent circuit is shown in Figure 29c. From Figure 29, it can be found that the equivalent ESR R_ESRT (= 3R_ESR) of the conventional one is greater than that of the proposed one. That is, output capacitors of the conventional one must have a higher CRR, which is proportional to the ESR of the capacitor. Therefore, the system reported in [28] is suitable for low power level applications. The system in [29] is applied to low or middle power level applications. The proposed PV power system can be applied to a middle or high power level application. 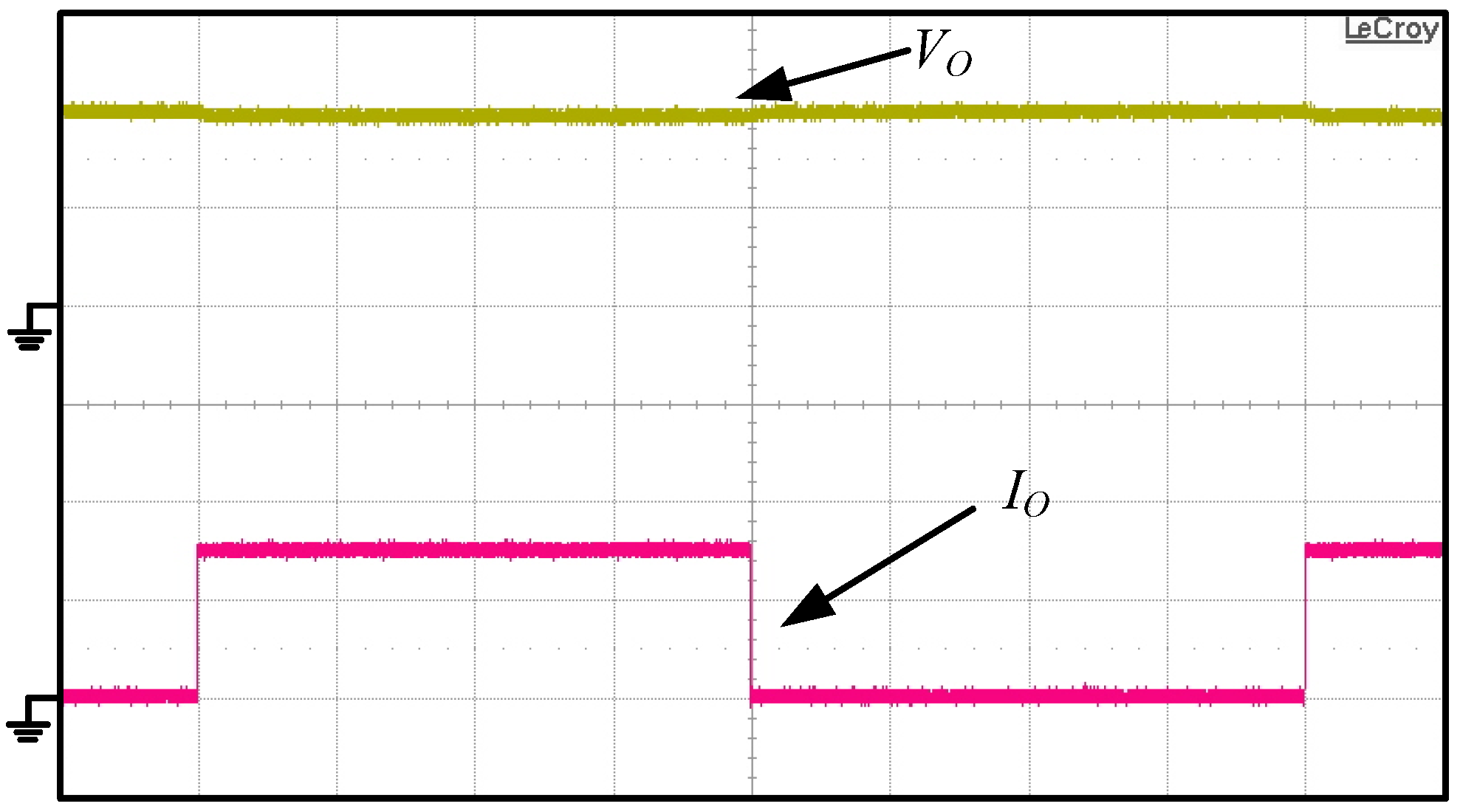Figure 30 illustrates the step-load change be between 0% and 100% of full load, from which it can be observed that voltage regulation of output voltage V_O has been limited with in ±1% to prove a good dynamic response.

Figure 30. Output voltage V_O and output current I_O under step-load changes between 0% and 100% of the full load condition of the active clamp interleaved boost converter.

Figure 30. Output voltage V_O and output current I_O under step-load changes between 0% and 100% of the full load condition of the active clamp interleaved boost converter.

(V_O: 200 V/div, I_O: 2 A/div, time: 50 ms/div)

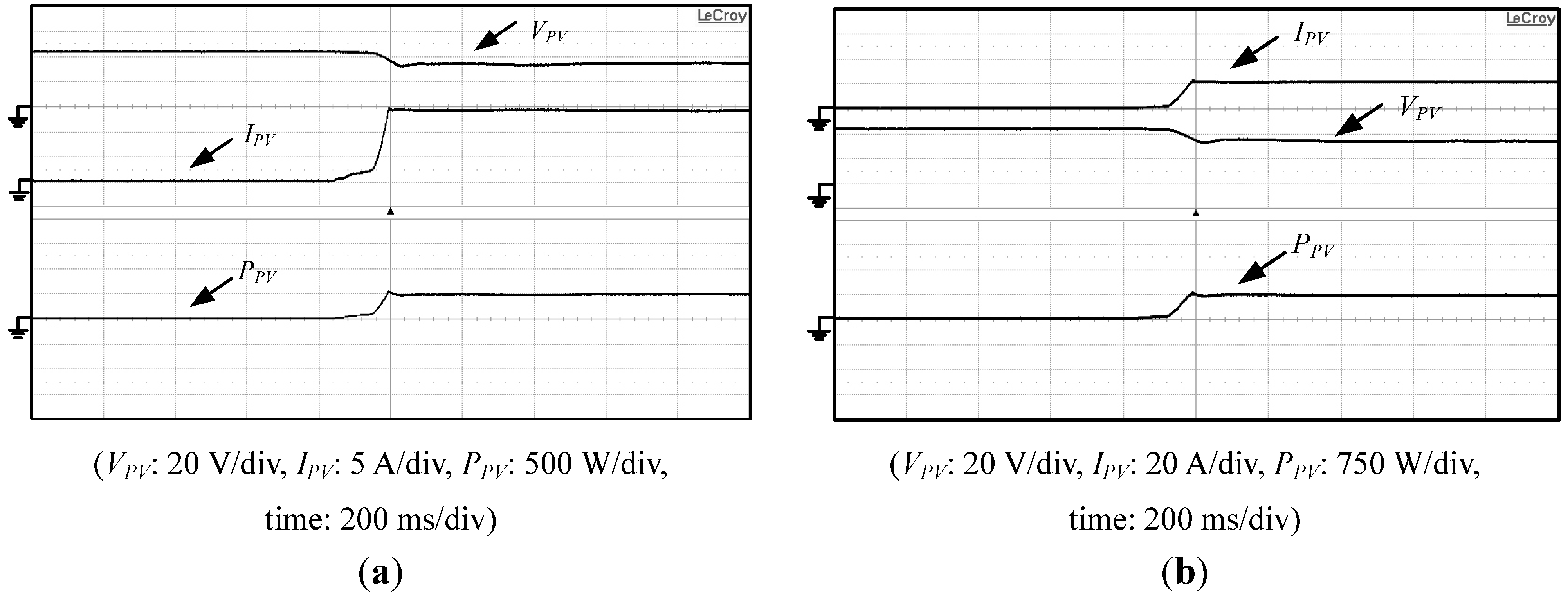
The MPPT waveforms of the proposed interleaved active clamp boost converter with MPPT are shown in Figure 31. Figure 31a shows those waveforms under the maximum PV arrays power of 500 W, while Figure 31b illustrates those waveforms under the maximum power of 750 W. From Figure 31, it can be found that the tracking time of MPPT is about 70 ms from 0 to the maximum power of PV arrays.

Figure 31. Measured voltage V_PV, current I_PV and power P_PV waveforms of PV arrays (a) under P_PV(max) = 500 W; and (b) under P_PV(max) = 750 W.

Figure 31. Measured voltage V_PV, current I_PV and power P_PV waveforms of PV arrays (a) under P_PV(max) = 500 W; and (b) under P_PV(max) = 750 W.

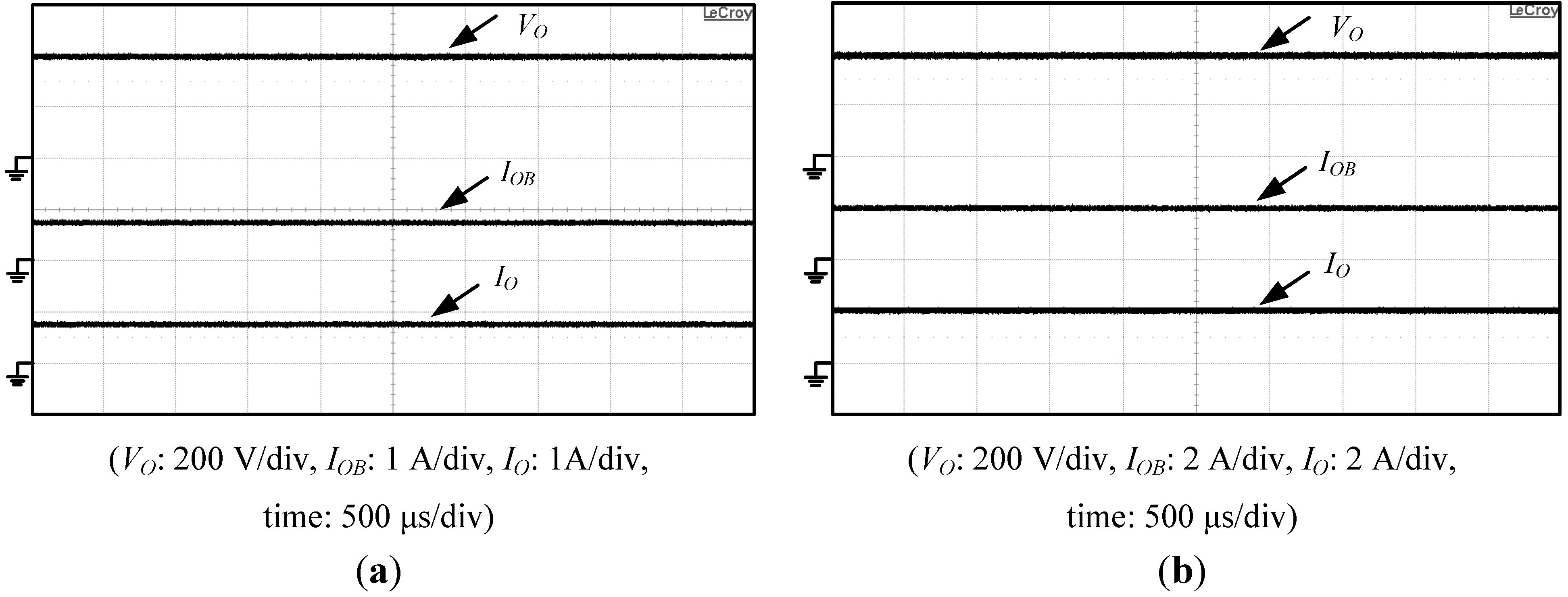
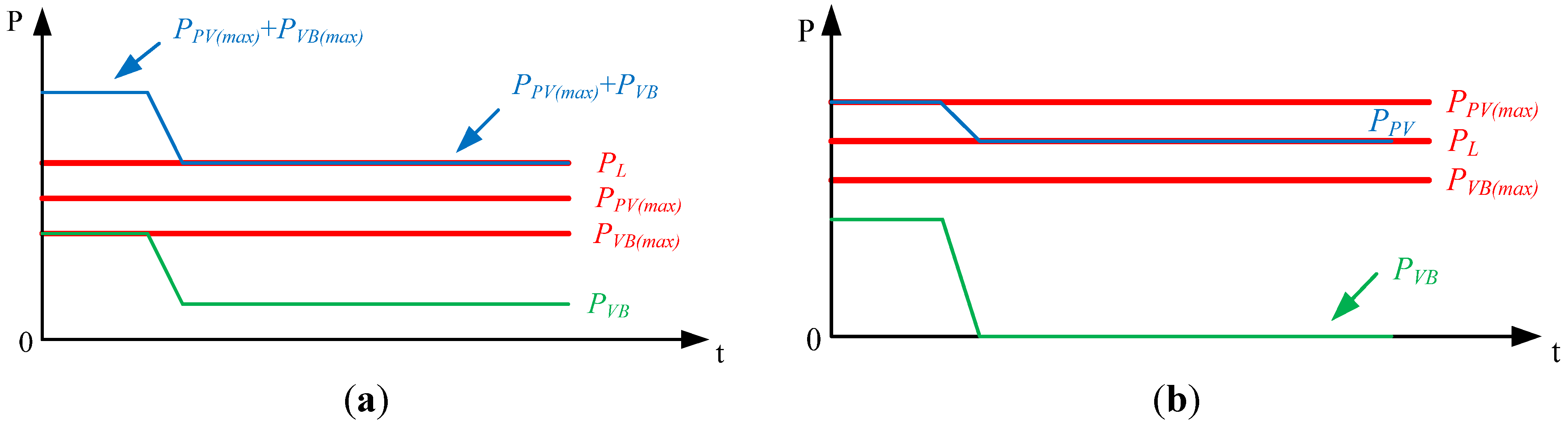
Measured output voltage V_O and current I_OB and I_O when the operational mode is within mode IV and P_VB(max) ≥ P_L in power management of the proposed PV system is shown in Figure 32. Figure 32a depicts those waveforms under P_L = 320 W, while Figure 32b shows those waveforms under P_L = 800 W. From Figure 32, it can be seen that output voltage V_O is sustained at 400 V and current I_OB is equal to I_L.

Figure 32. Measured voltage V_O, current I_OB and I_O waveforms of the proposed PV power system operated in mode IV (a) under P_L = 320 W; and (b) under P_L = 800 W.

Figure 32. Measured voltage V_O, current I_OB and I_O waveforms of the proposed PV power system operated in mode IV (a) under P_L = 320 W; and (b) under P_L = 800 W.

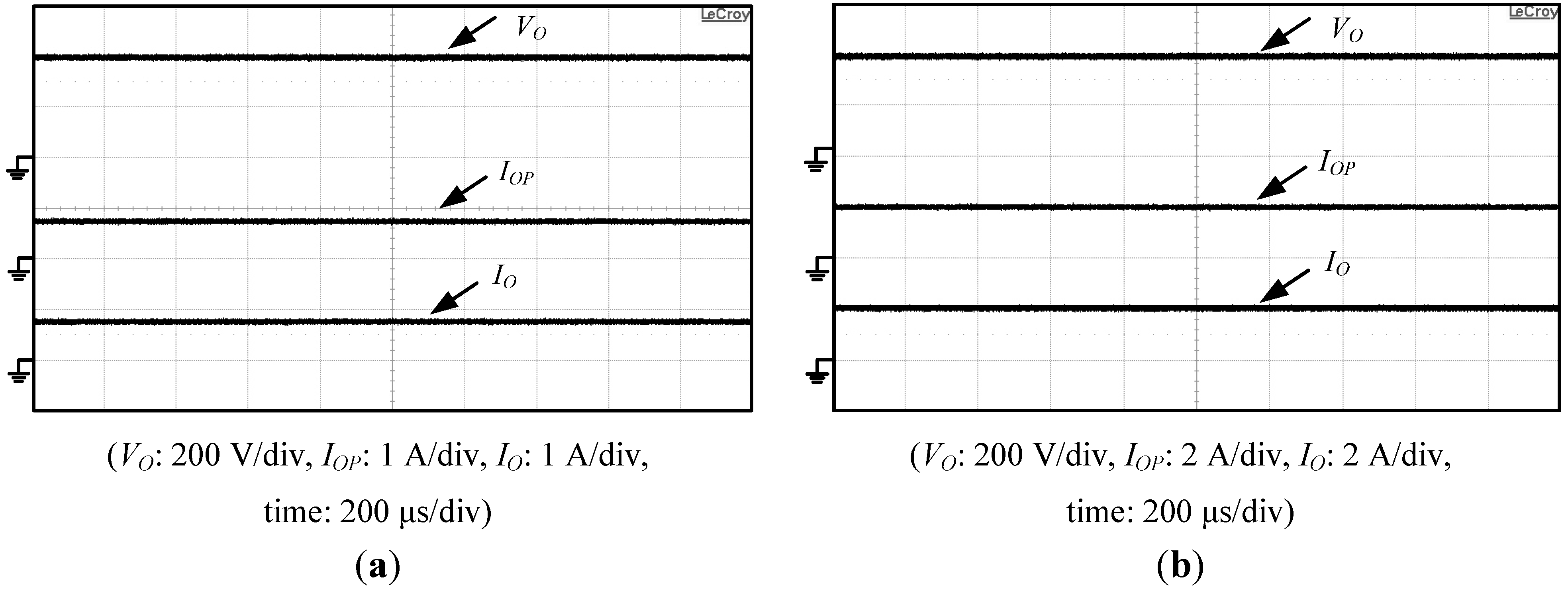
When the operational mode of the proposed PV power system is mode VI and P_PV(max) ≥ P_L, its measured output voltage V_O and current I_OP and I_L waveforms under P_PV(max) = 800 W and P_L = 320 W are shown in Figure 33a, illustrating that output voltage V_O is clamped at 400 V, current I_OP is equal to I_L and P_PV = 320 W. Figure 33b shows those waveforms under P_L = 800 W. When P_L = 800 W, output power P_PV is also equal to 800 W and it is operated at its MPP. As mentioned above, operational modes of the proposed PV power system are respectively in the mode IV and VI states, the proposed one can regulate power between PV arrays, battery and load.

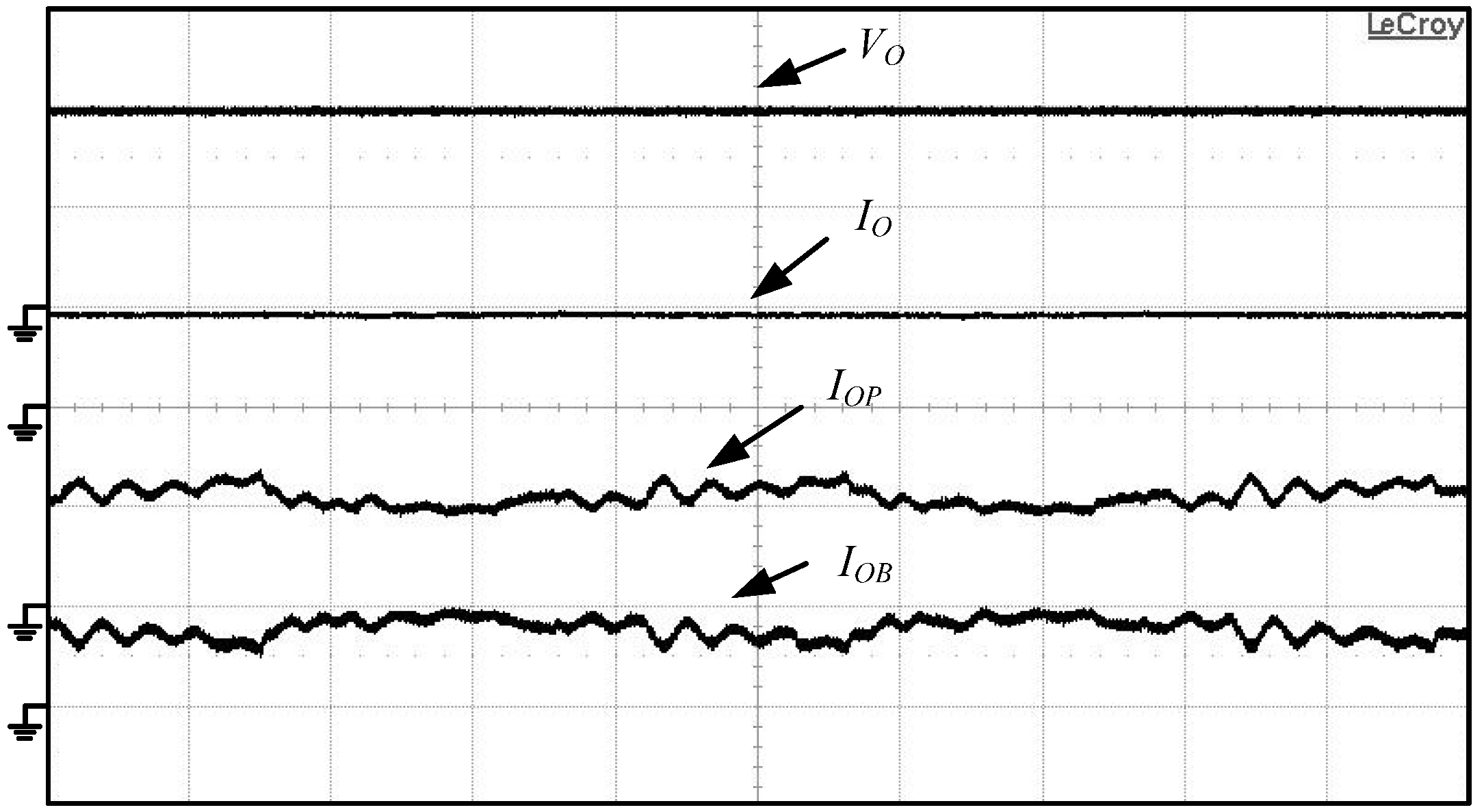
Figure 33. Measured voltage V_O, current I_OP and I_O waveforms of the proposed PV power system operated in mode VI (a) under P_L = 320 W; and (b) under P_L = 800 W.

Figure 33. Measured voltage V_O, current I_OP and I_O waveforms of the proposed PV power system operated in mode VI (a) under P_L = 320 W; and (b) under P_L = 800 W.

When the operational mode of the proposed one is mode VIII and (P_PV(max) + P_VB(max)) ≥ P_L, its operational conditions are divided into two conditions. One is P_PV(max) ≥ P_L and the other is P_PV(max) < P_L. When P_PV(max) ≥ P_L, its measured output voltage V_O, and currents I_OP, I_OB and I_L waveforms under P_PV(max) = 750 W and P_L = 375 W are shown in Figure 34. Under this operational condition, current I_OP is equal to I_O and I_OB is equal to 0. That is, the proposed boost converter with MPPT is used to supply power to the load and the PV arrays are not operated at MPP, while the proposed boost one with voltage regulation is shut down. When P_PV(max) < P_L, its measured output voltage V_O, and currents I_OP, I_OB and I_O under P_PV(max) = 375 W and P_L = 750 W is shown in Figure 35, illustrating that output voltage V_O is still lamped at 400 V and I_O = I_OP + I_OB. That is, the PV arrays can be operated at the maximum power point of 375 W and the battery can supply power to the load for balancing the power between the PV arrays and load. From experimental results, it can be seen that the proposed PV power system can use its power management circuit to achieve power balance between PV arrays, batteries and loads.

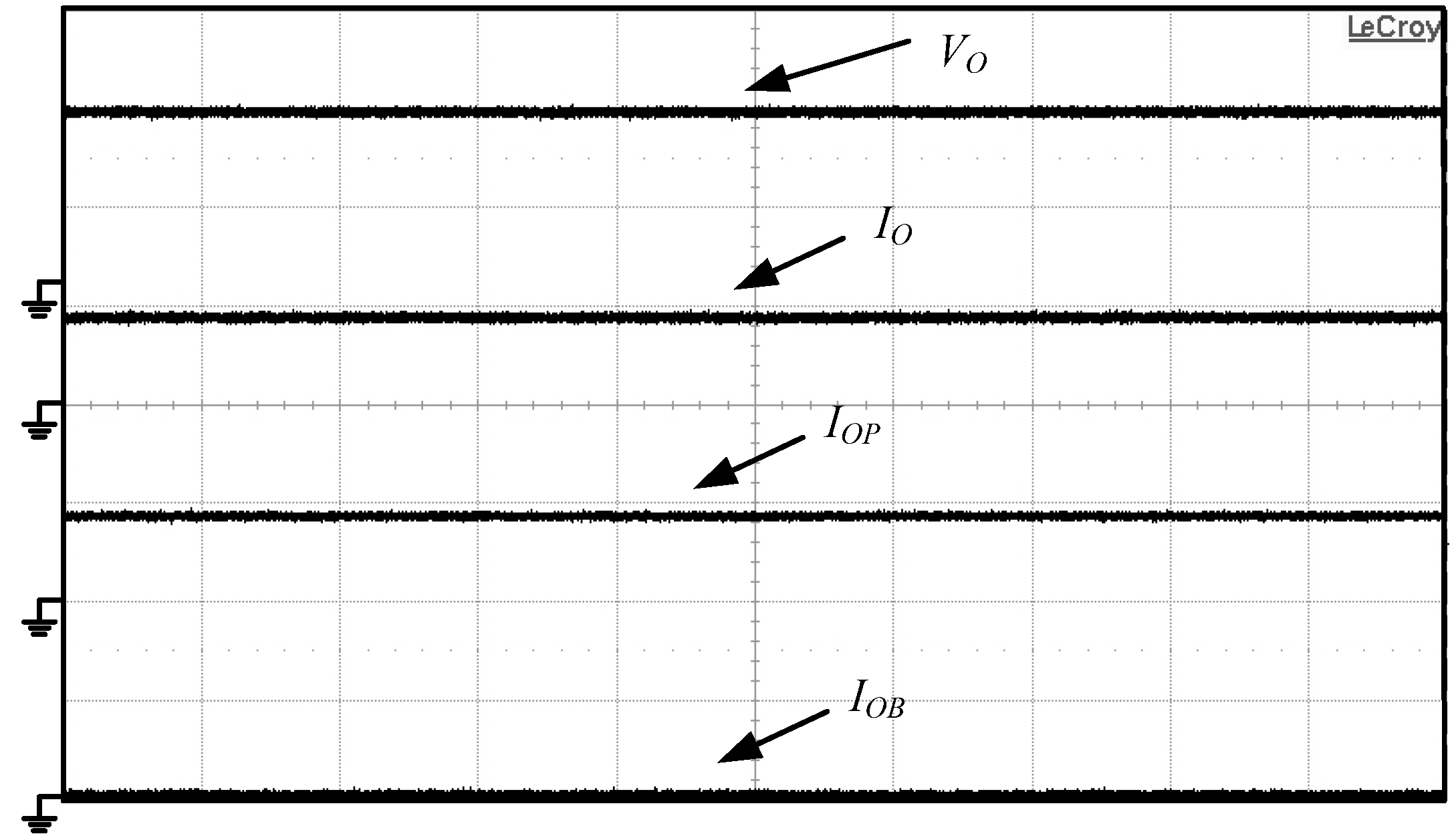
Figure 34. Measured voltage V_O, current I_OB, I_OP and I_O waveforms of the proposed PV power system operated in mode VIII under (P_P(max) + P_VB(max)) ≥ P_L and P_PV(max) ≥ P_L.

Figure 34. Measured voltage V_O, current I_OB, I_OP and I_O waveforms of the proposed PV power system operated in mode VIII under (P_P(max) + P_VB(max)) ≥ P_L and P_PV(max) ≥ P_L.

(V_O: 200 V/div, I_O: 1 A/div, I_OP: 1 A/div, I_OB: 1 A/div, time: 200 μs/div)

Figure 35. Measured voltage V_O, current I_OB, I_OP and I_O waveforms of the proposed PV power system operated in mode VIII under (P_P(max) + P_VB(max)) ≥ P_L and P_PV(max) < P_L.

Figure 35. Measured voltage V_O, current I_OB, I_OP and I_O waveforms of the proposed PV power system operated in mode VIII under (P_P(max) + P_VB(max)) ≥ P_L and P_PV(max) < P_L.

(V_O: 200 V/div, I_O: 1 A/div, I_OP: 1 A/div, I_OB: 2 A/div, time: 200 μs/div)

6. Conclusions

In this paper, two interleaved active clamp boost converters with coupled inductor are adopted to form a PV power system for dc load applications. The two proposed interleaved active boost converters using PV arrays and batteries as their power source, respectively, have been proposed to implement MPPT and power management. Moreover, their operational principle, derivation and design have been also described in detail. From experimental results, it can be seen that the proposed converter can yield higher efficiency than the one equipped with a hard-switching circuit. An experimental prototype for dc load applications [P_PV(max) = 1.2 kW, P_VB(max) = 1.2 kW] has been built and evaluated, achieving the efficiency of 91% under full load conditions and verifying the feasibility of the proposed active clamp circuit. Moreover, power management and MPPT with the perturb and observe method have also been implemented.