Research on an Axial Magnetic-Field-Modulated Brushless Double Rotor Machine
Abstract
:1. Introduction
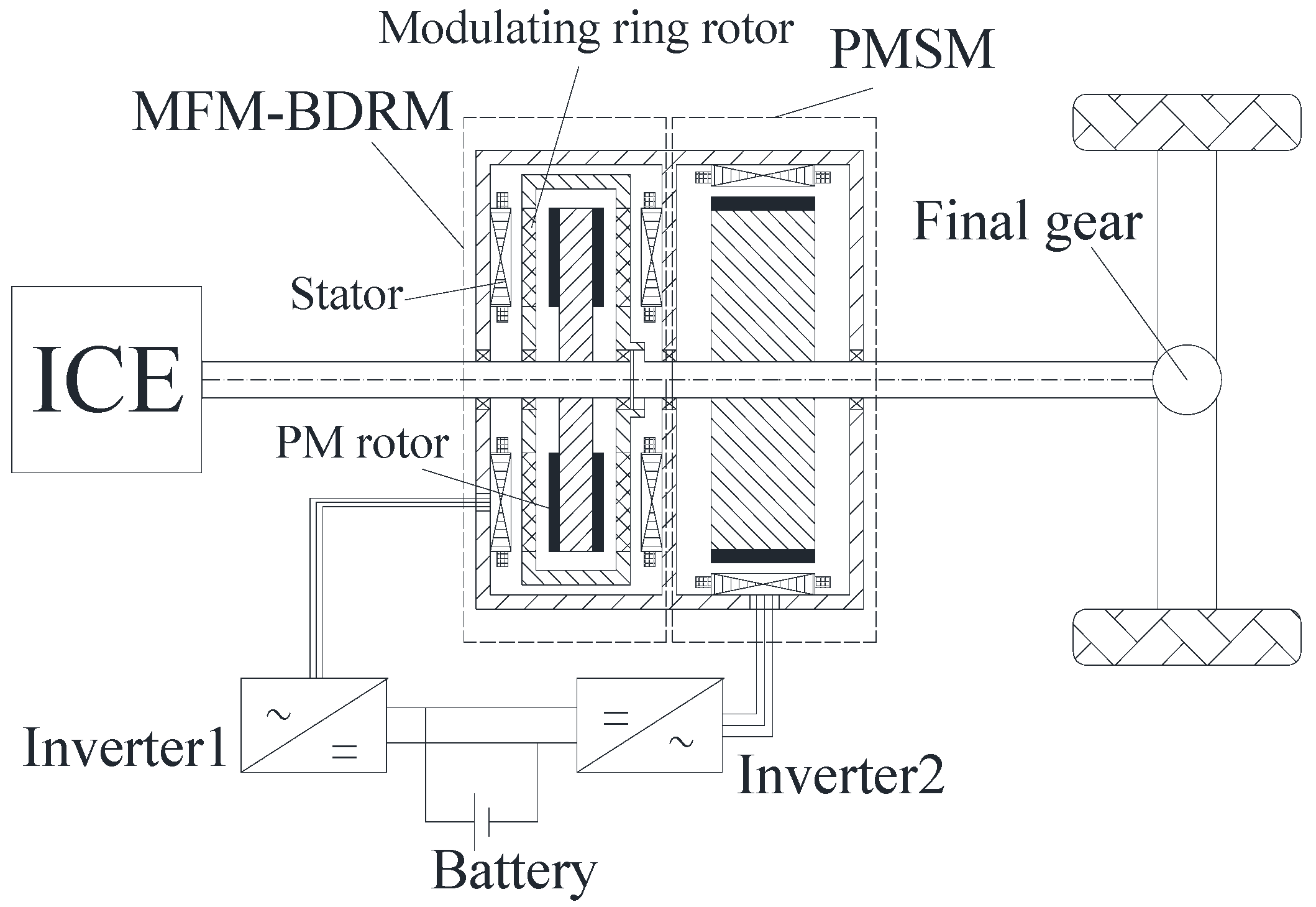
2. Theoretical Analysis
2.1. Principle of Operation
2.2. Torque Transmission
2.3. Torque Ripple
2.3.1. Cogging Torque
2.3.2. Electromagnetic Torque Ripple
3. FEM Simulation
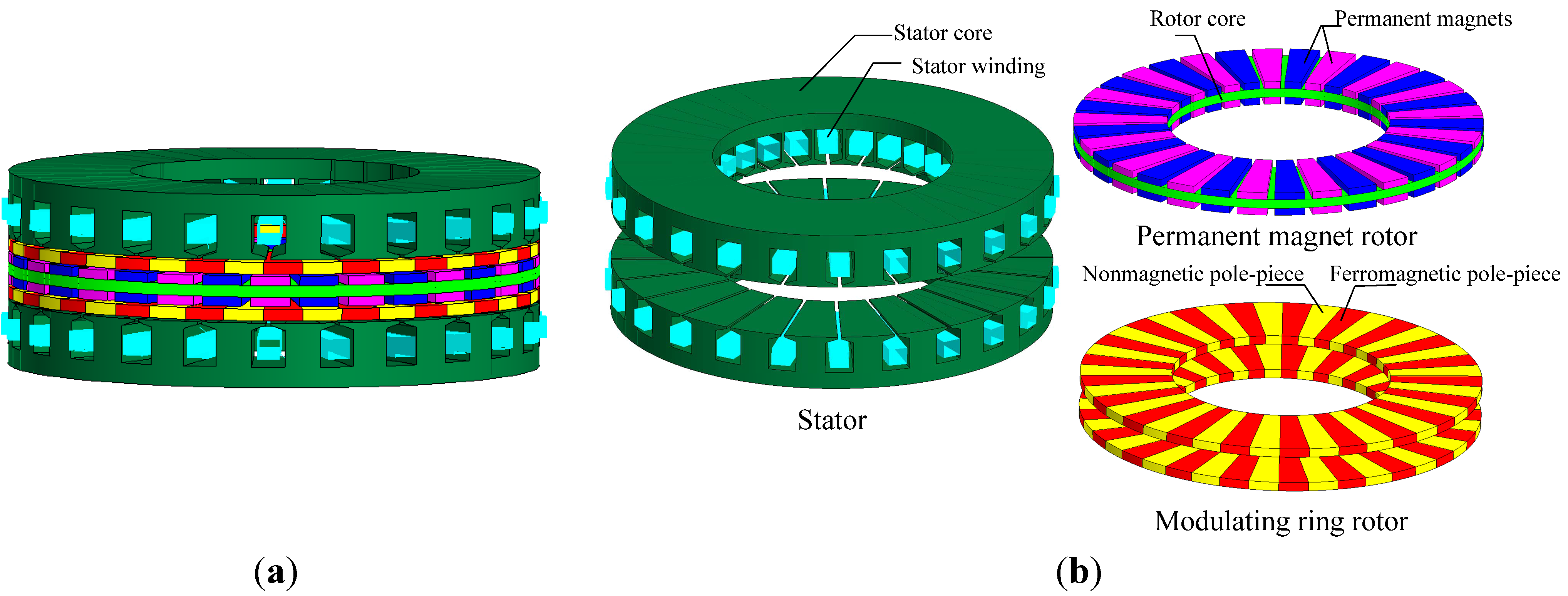
3.1. Flux Density Waveform and Harmonics Analysis
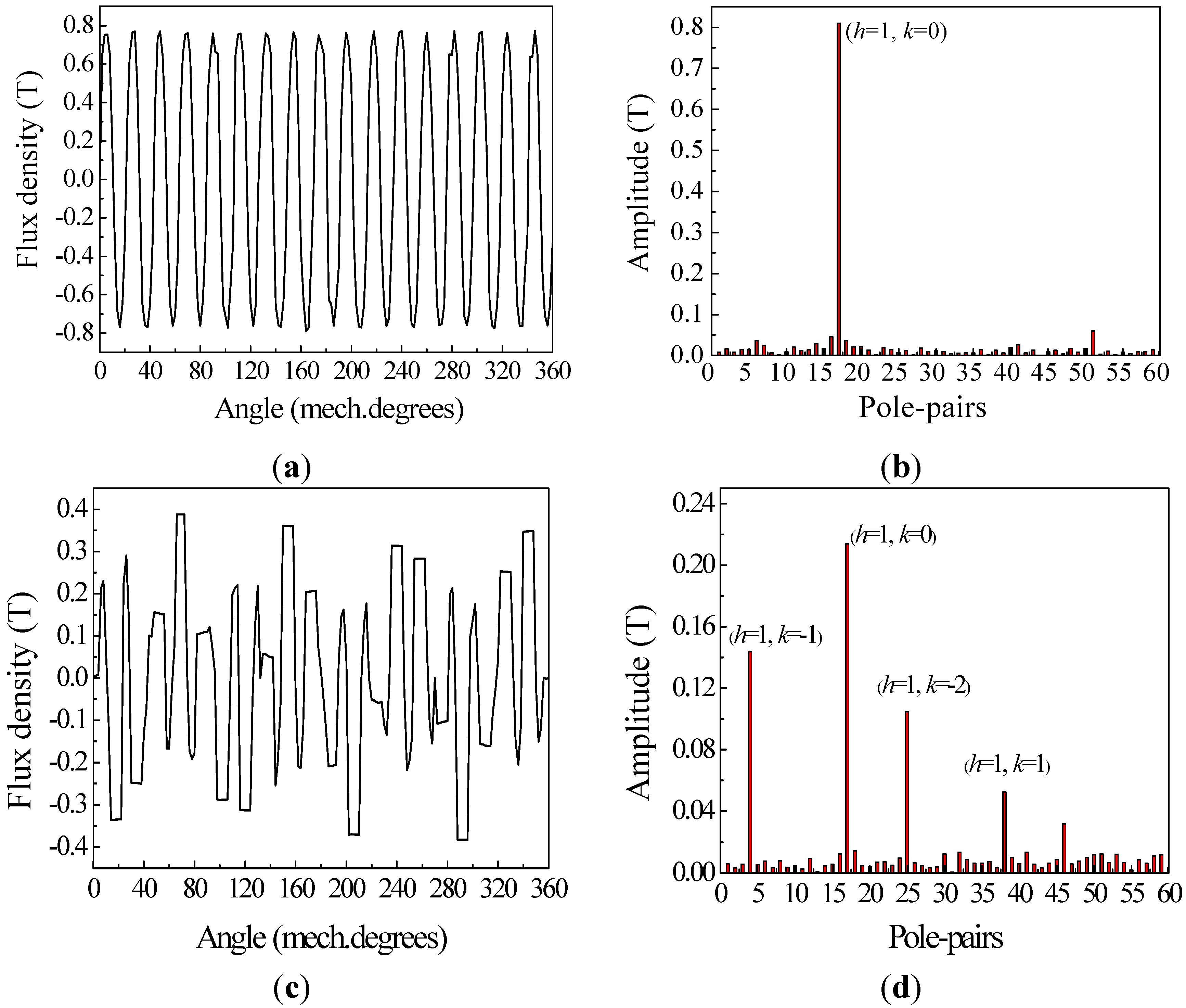
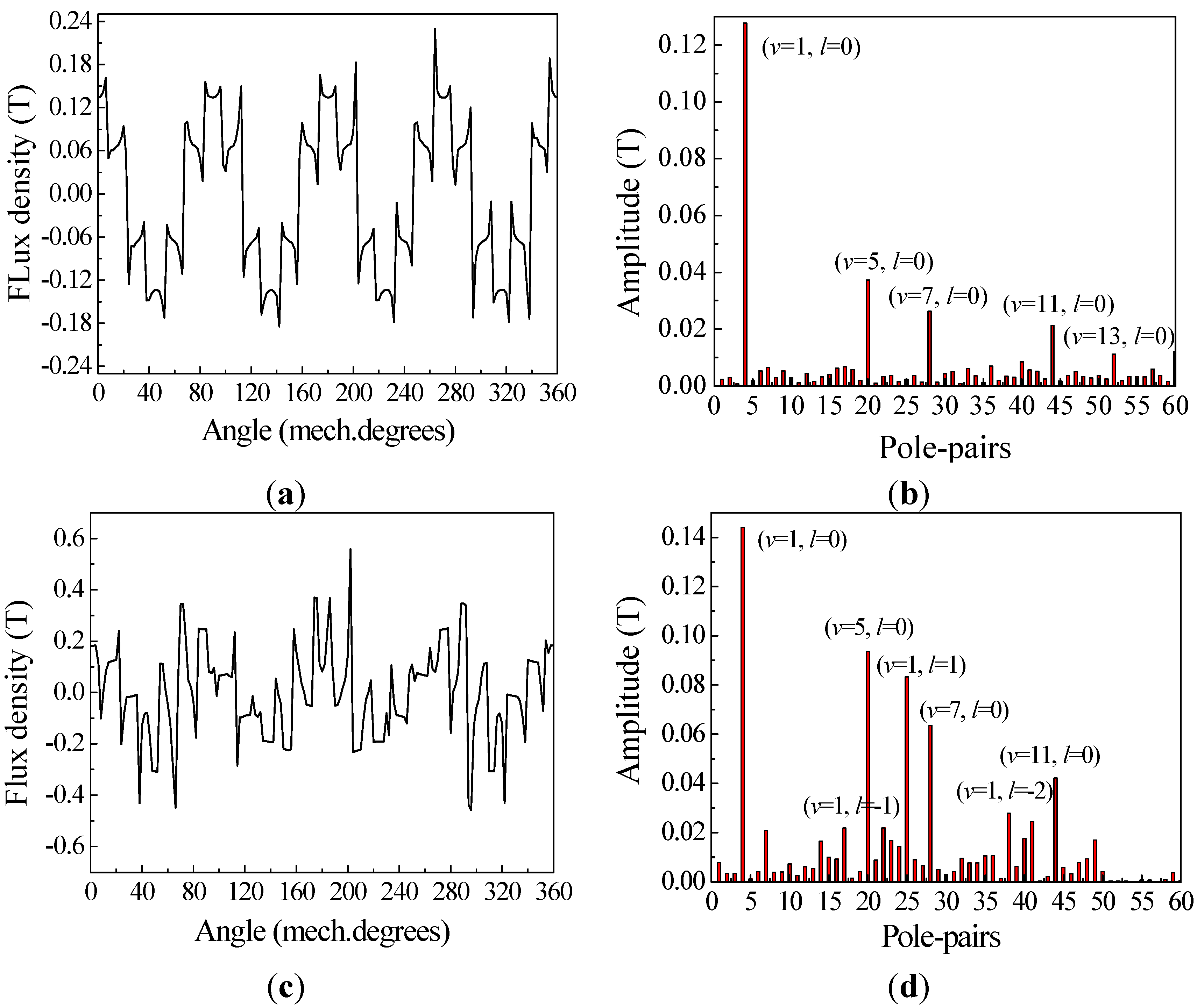
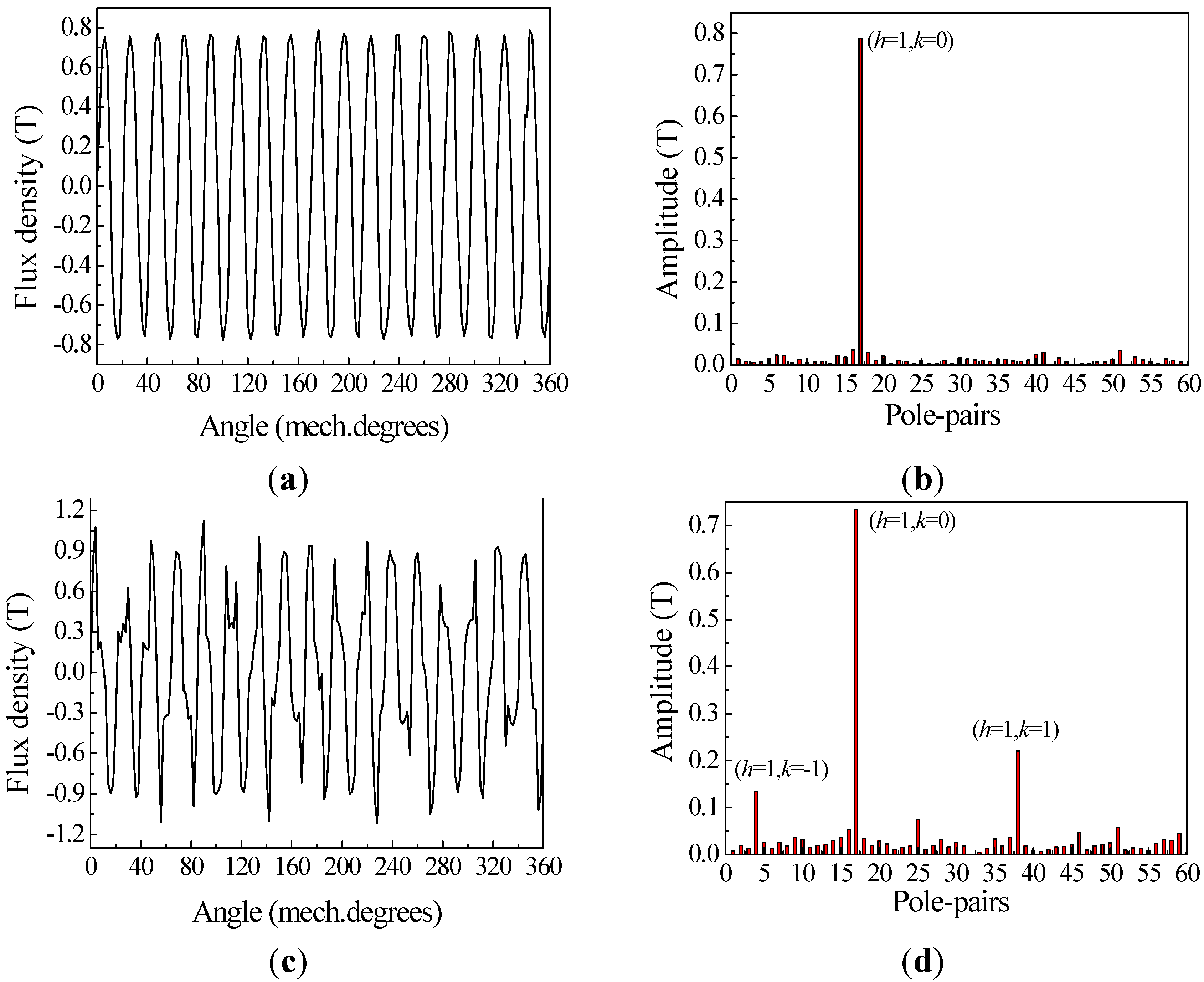

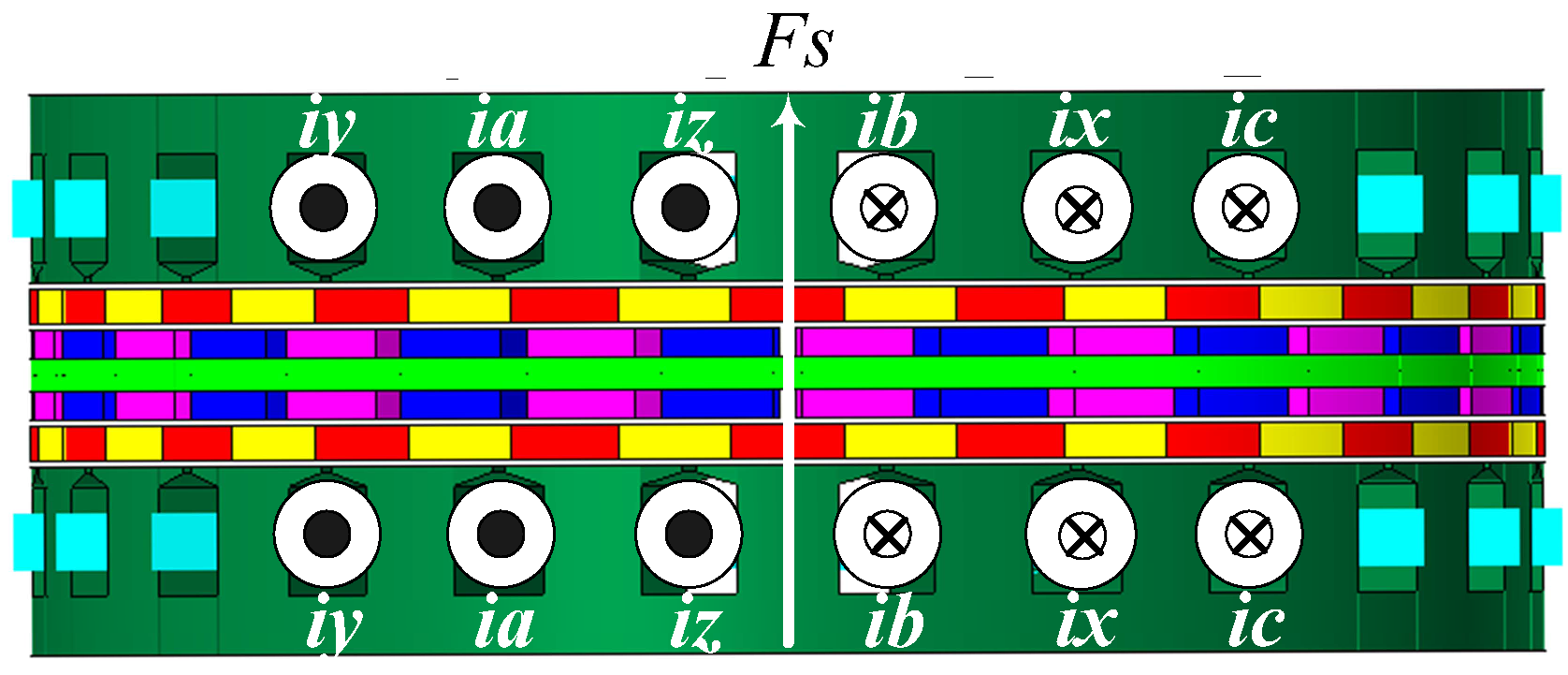
3.2. Operating Principle
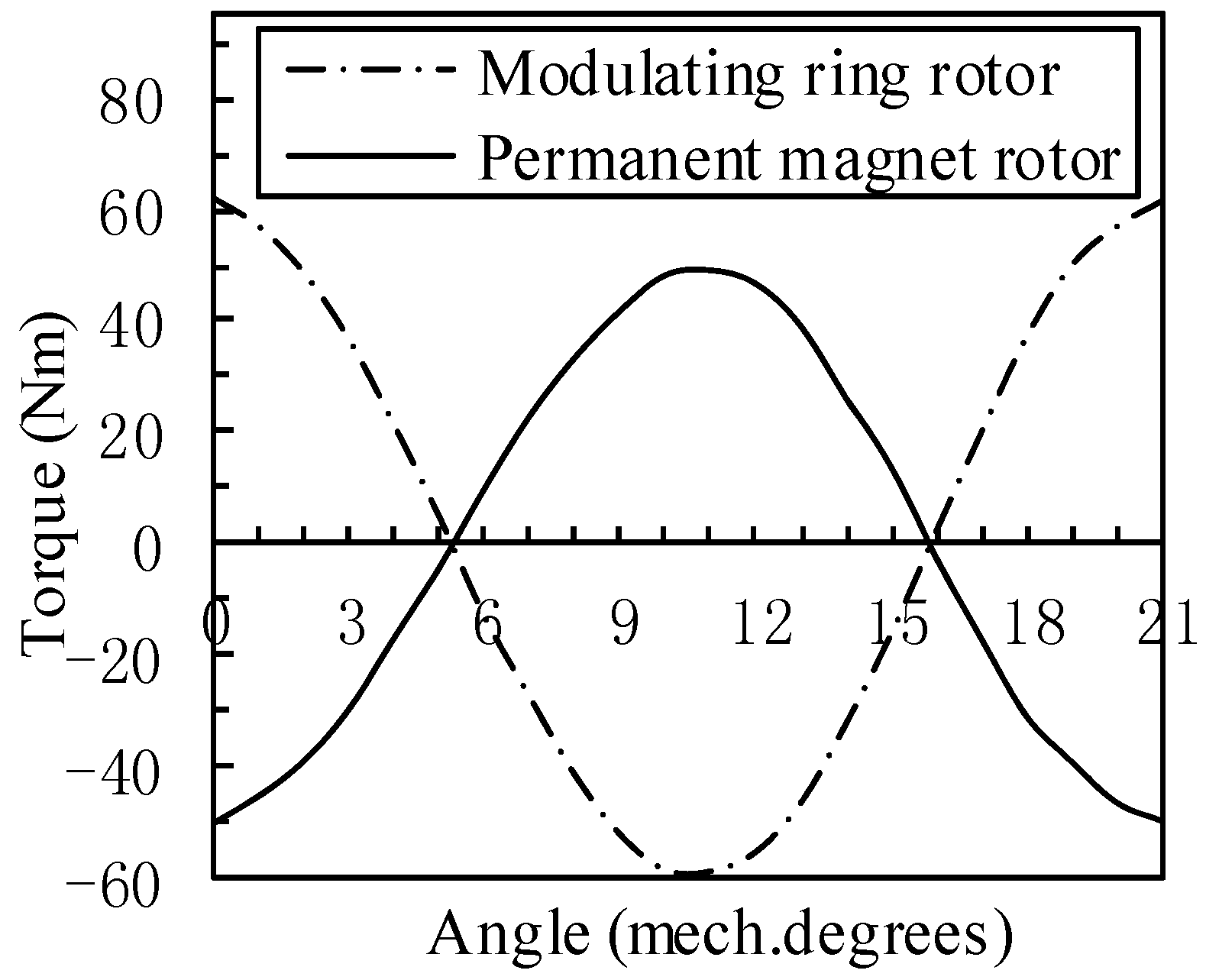
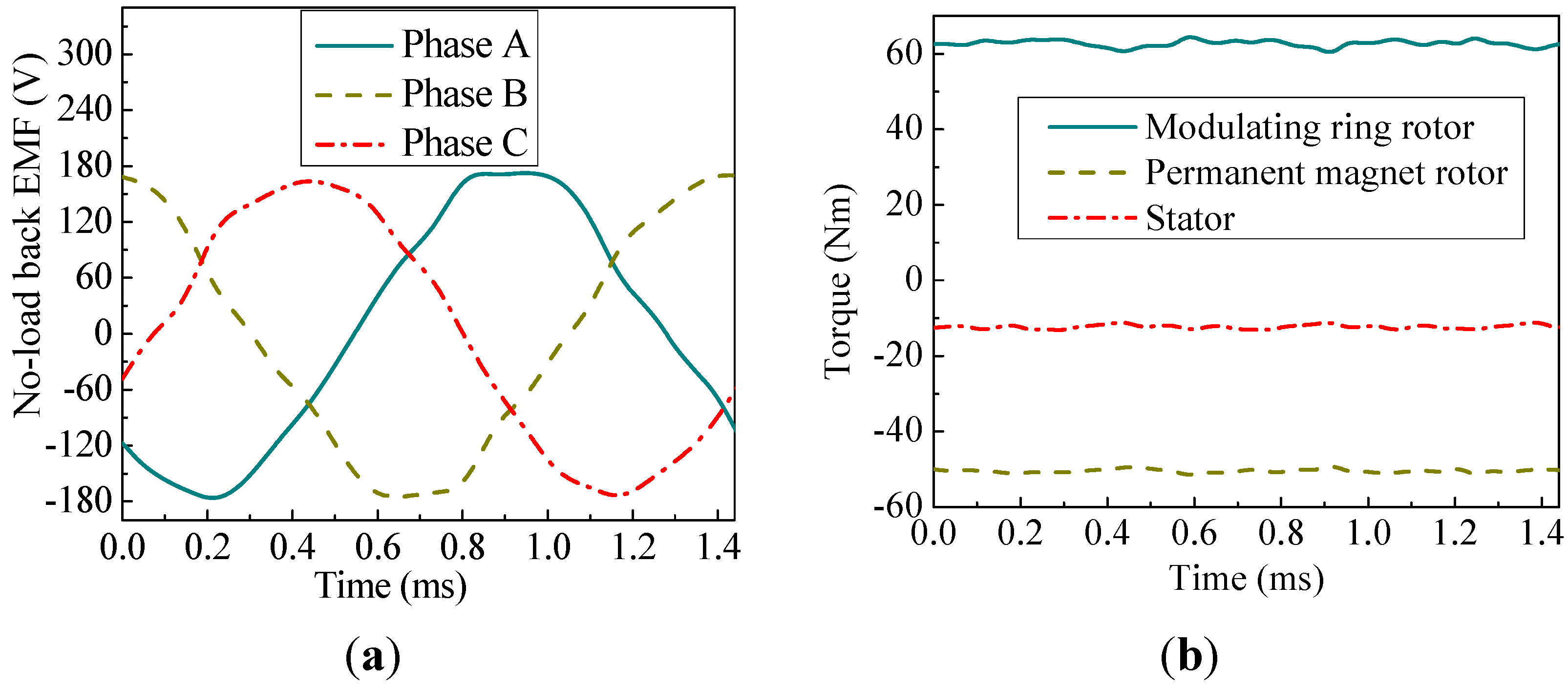
3.3. Torque Transmission
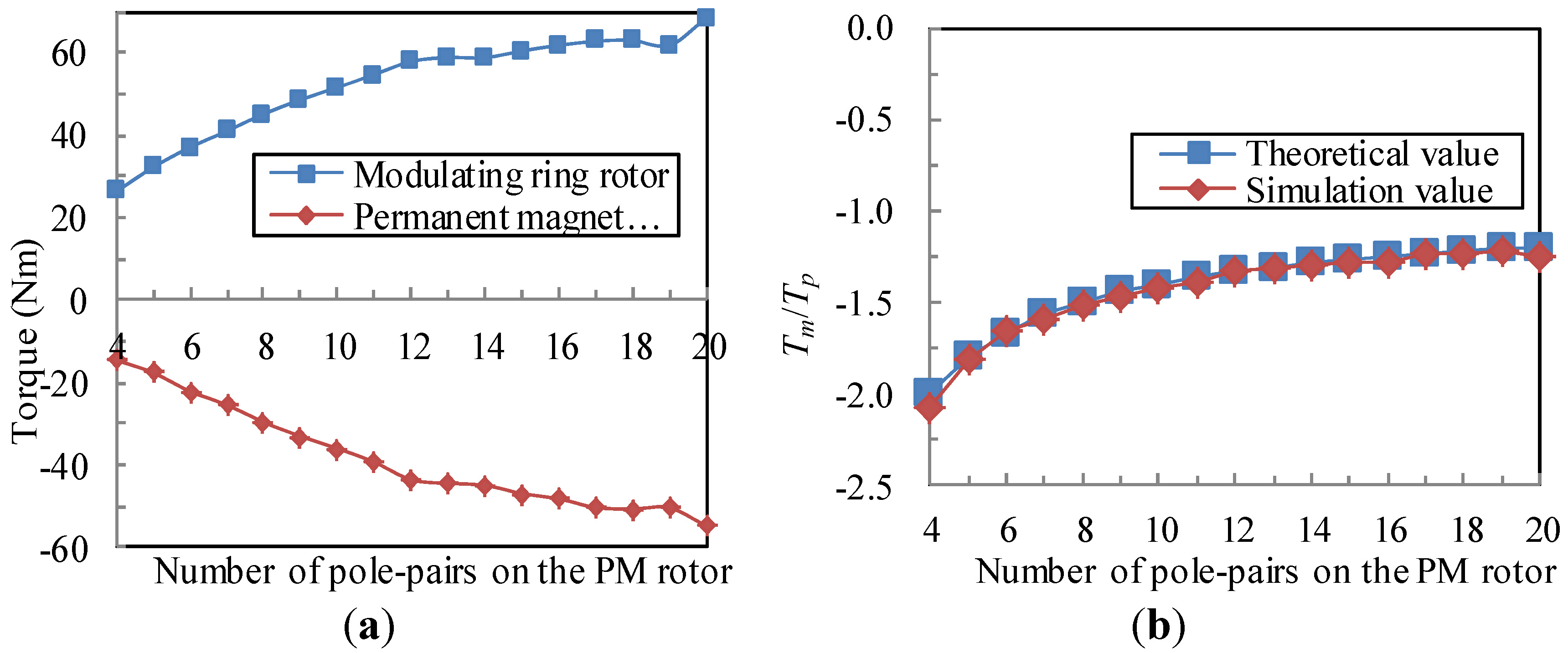
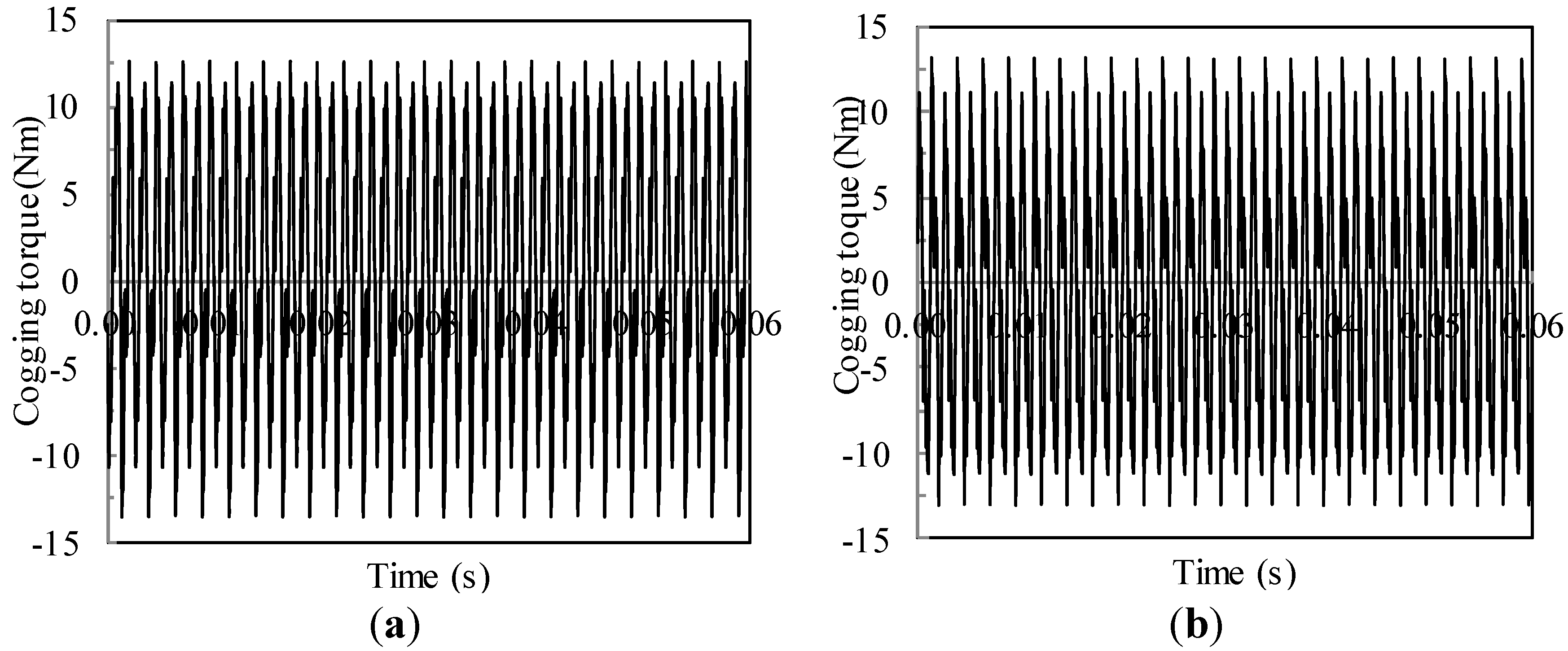
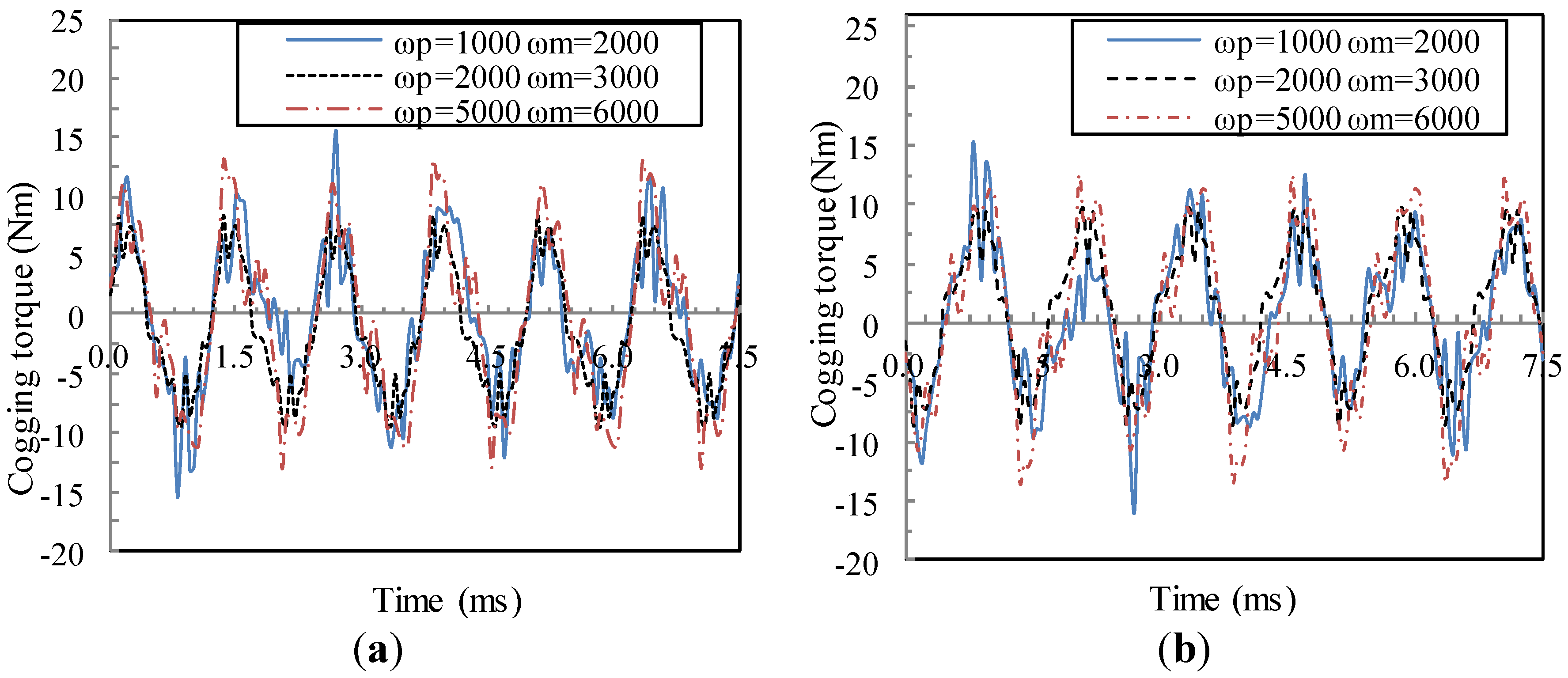
3.4. Torque Ripple Characteristics
- when ωp = 1000 rpm, ωm = 2000 rpm: ;
- when ωp = 2000 rpm, ωm = 3000 rpm: ;
- when ωp = 5000 rpm, ωm = 6000 rpm: .
| Circumstance | Constraint | Model with pp in study | |
|---|---|---|---|
| pp = 3g·ps, g = 1, 2, 3… | pp(1, 1) = ps(6g+1, 0) | 12 | |
| pp = (3g − 1)ps, g = 1, 3, 5… | pp(1, 1) = ps(6g−1, 0) | 8 | |
| pp = (3g − 1)ps, g = 2, 4, 6… | pp = ps(3g-1, 0) pp(1, 1) = ps(6g−1, 0) | 20 | |
| pp = (3g + 1)ps, g = 0, 2, 4… | pp = ps(3g+1) | 4 | |
3.5. Operation Performance
| Scheme | pp = 17 | pp = 18 | pp = 19 | pp = 20 |
|---|---|---|---|---|
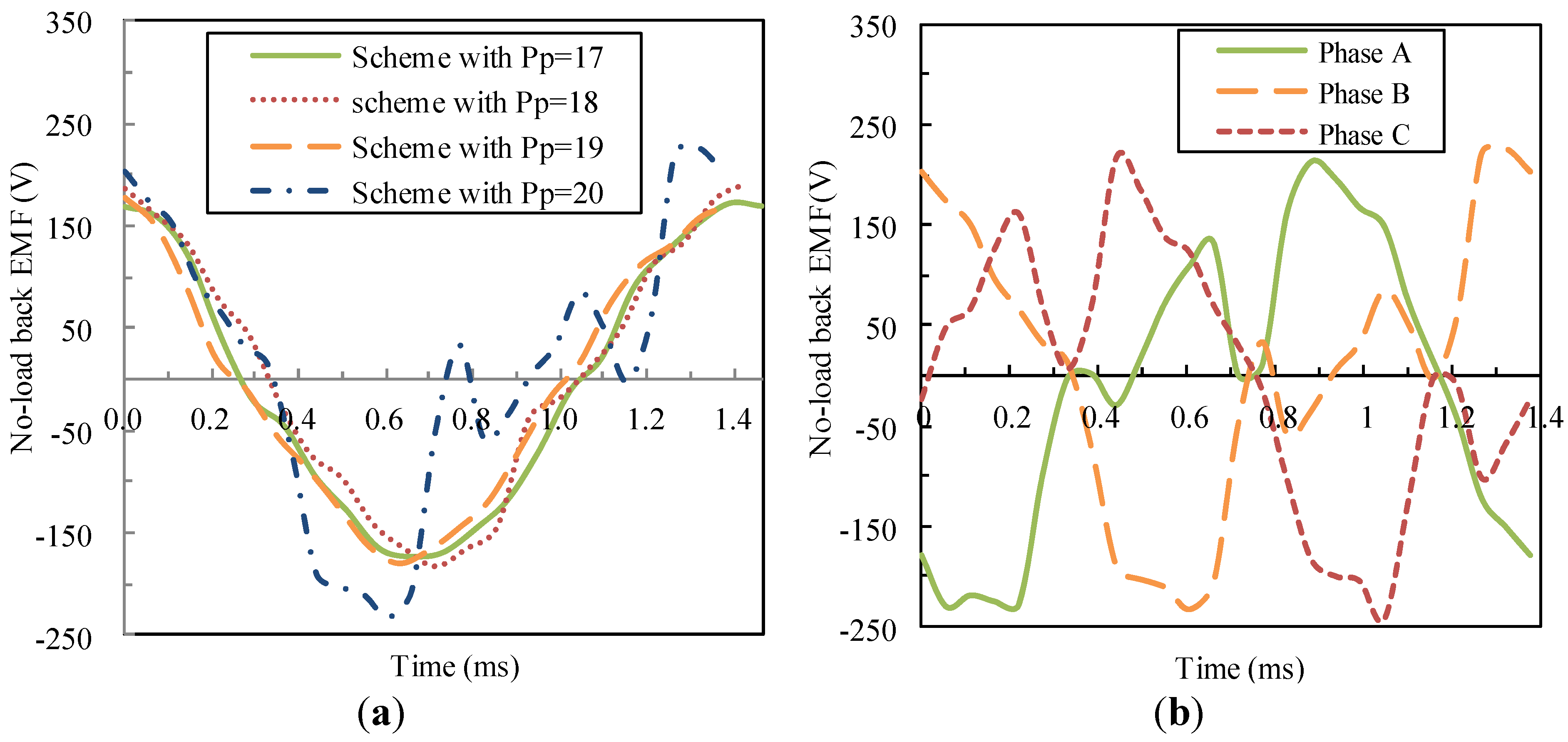
| RMS value of A-phase no-load back EMF (V) | 122.8 | 127.1 | 123.1 | 126.2 |
| THD of no-load back EMF (%) | 7.14 | 12.05 | 8.1 | 46.27 |
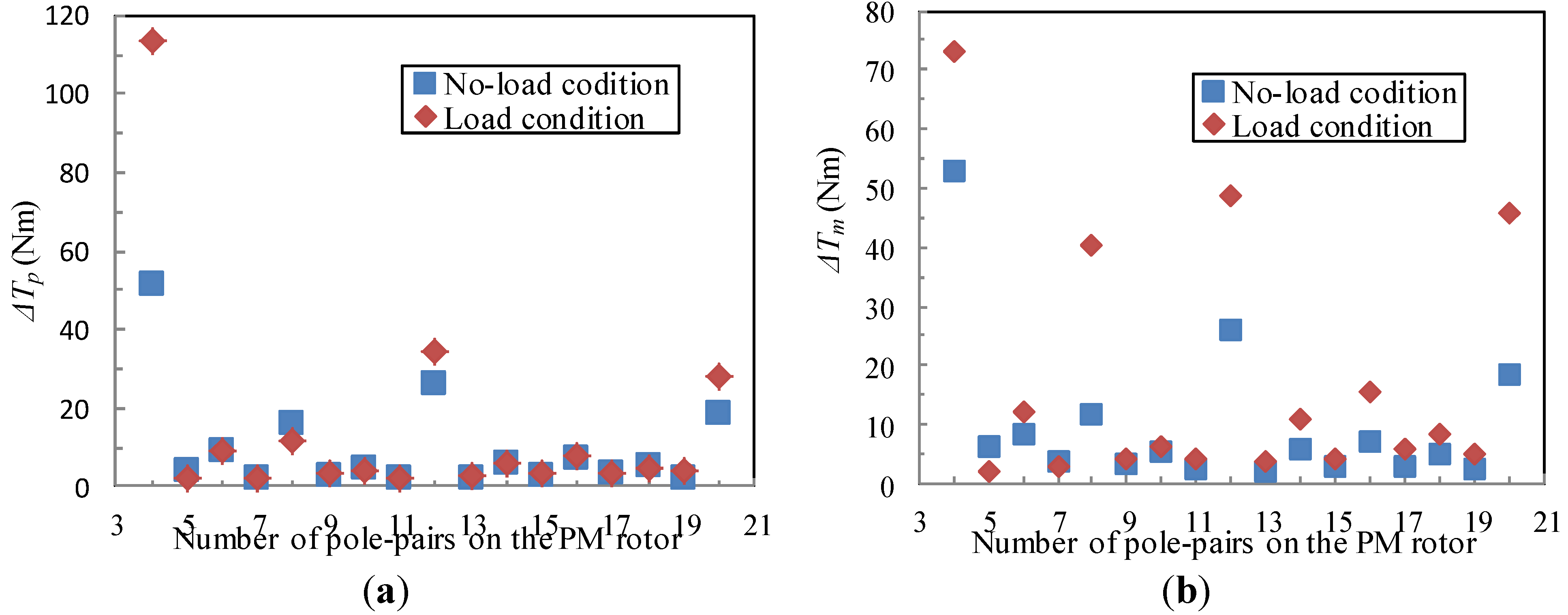
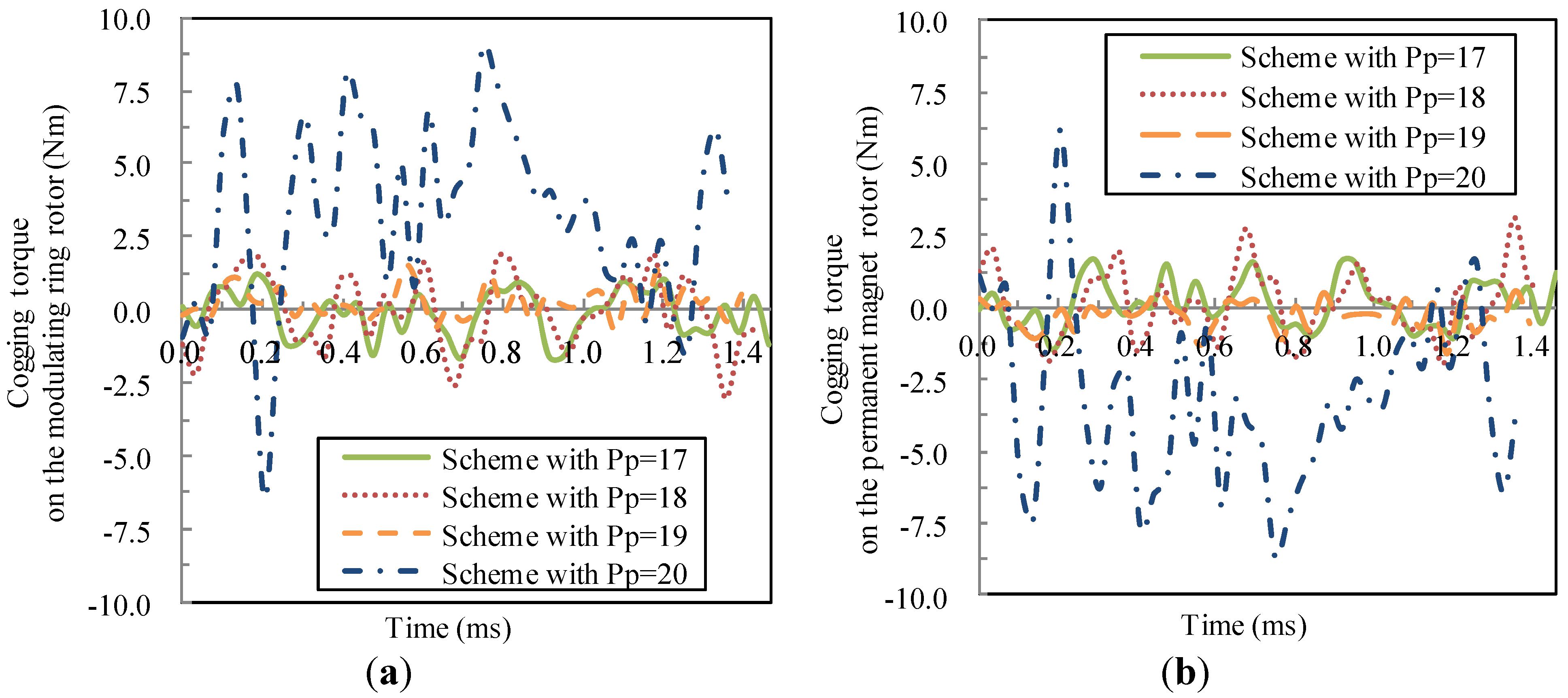
| ΔTp under no-load condition (Nm) | 3.13 | 5.1 | 2.19 | 14.85 |
| ΔTm under no-load condition (Nm) | 3.0 | 4.97 | 2.27 | 15.45 |
| LCM(pm, 2pp)/2pp | 21 | 11 | 23 | 3 |
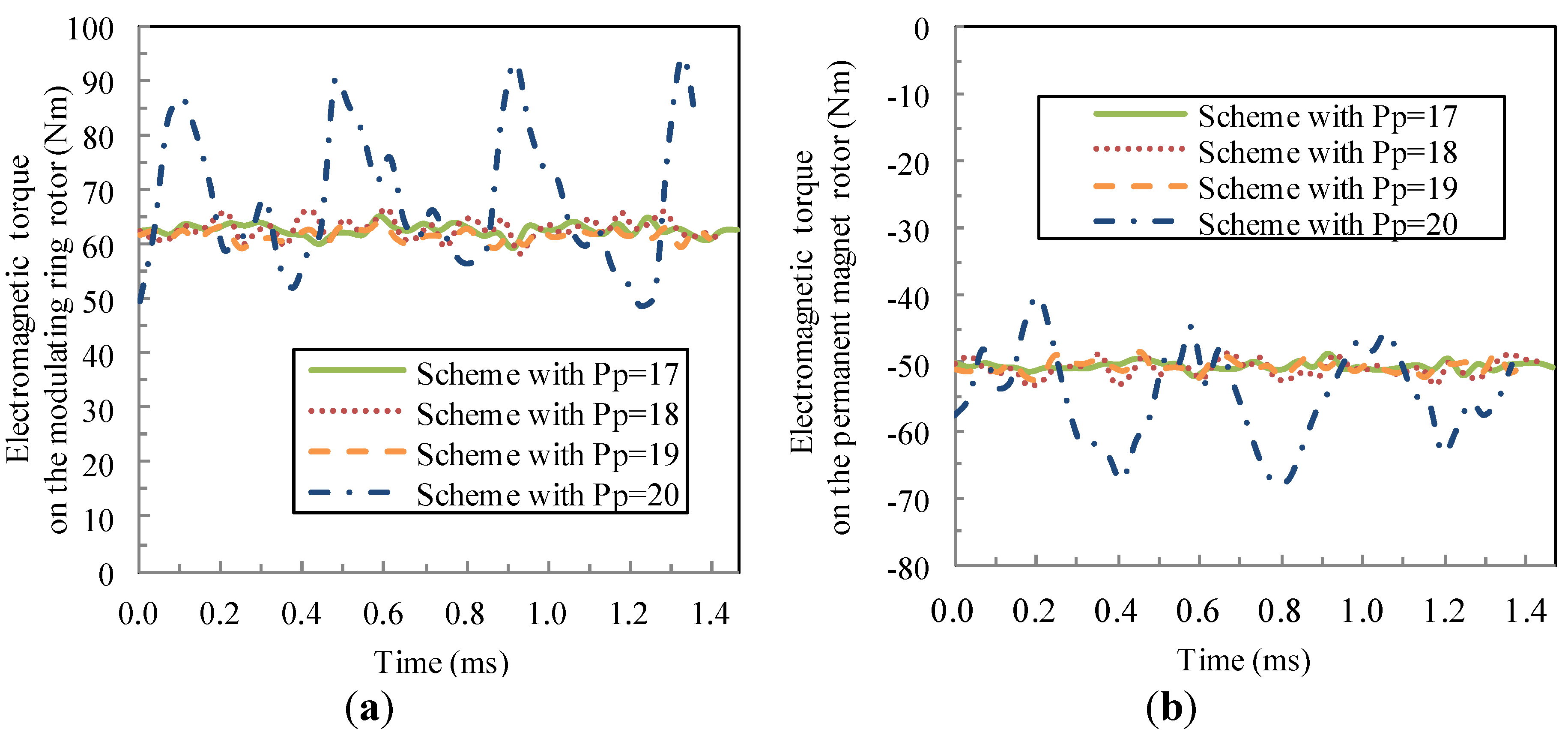
| Average torque on the modulating ring rotor (Nm) | 62.71 | 62.94 | 61.71 | 68.33 |
| Torque ripple on the modulating ring rotor (%) | 4.68 | 6.54 | 3.90 | 33.62 |
| Average torque on the permanent magnet rotor (Nm) | −50.44 | −50.76 | −50.51 | −54.91 |
| Torque ripple on the permanent magnet rotor (%) | 3.35 | 4.75 | 4.01 | 25.35 |
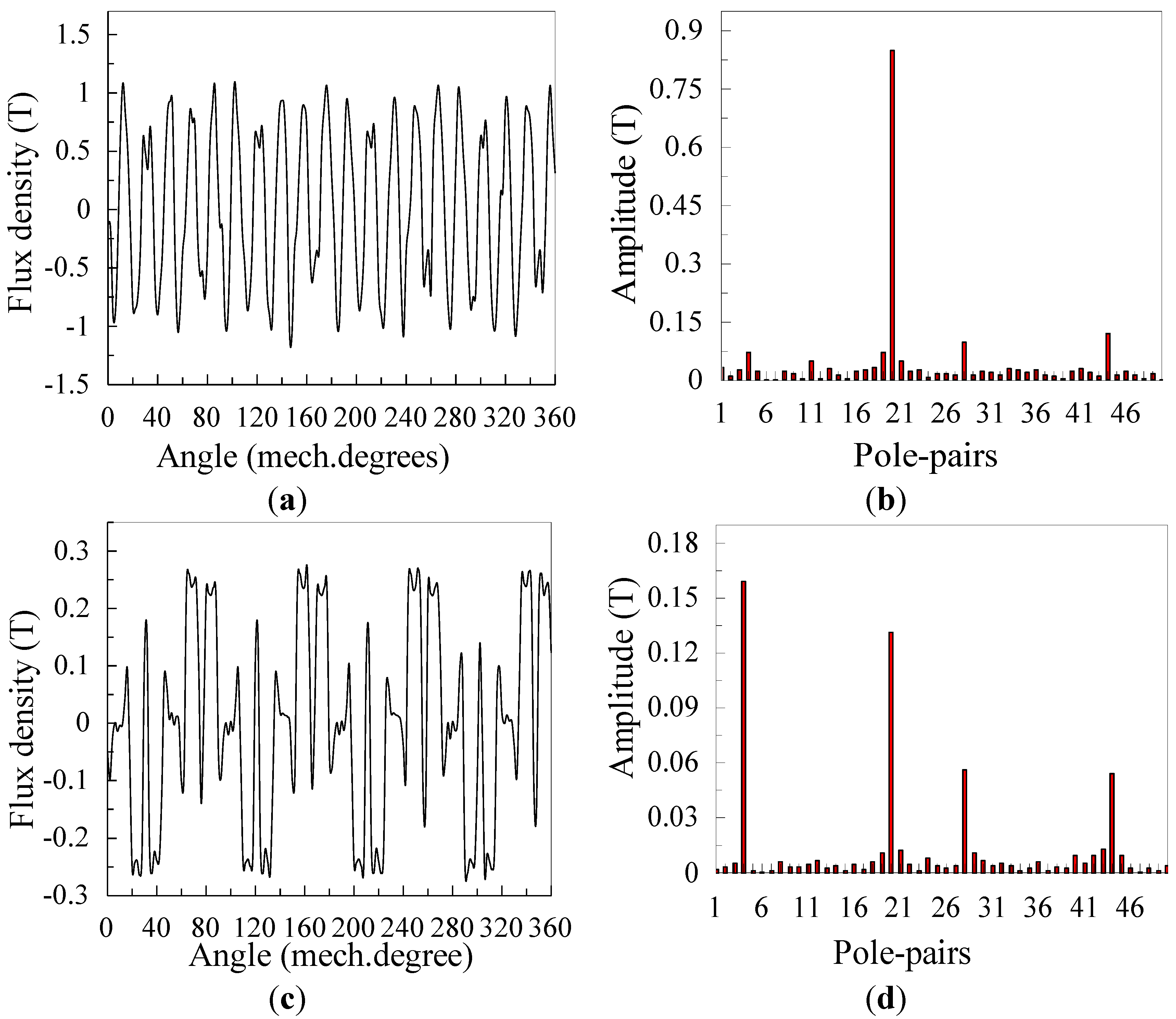
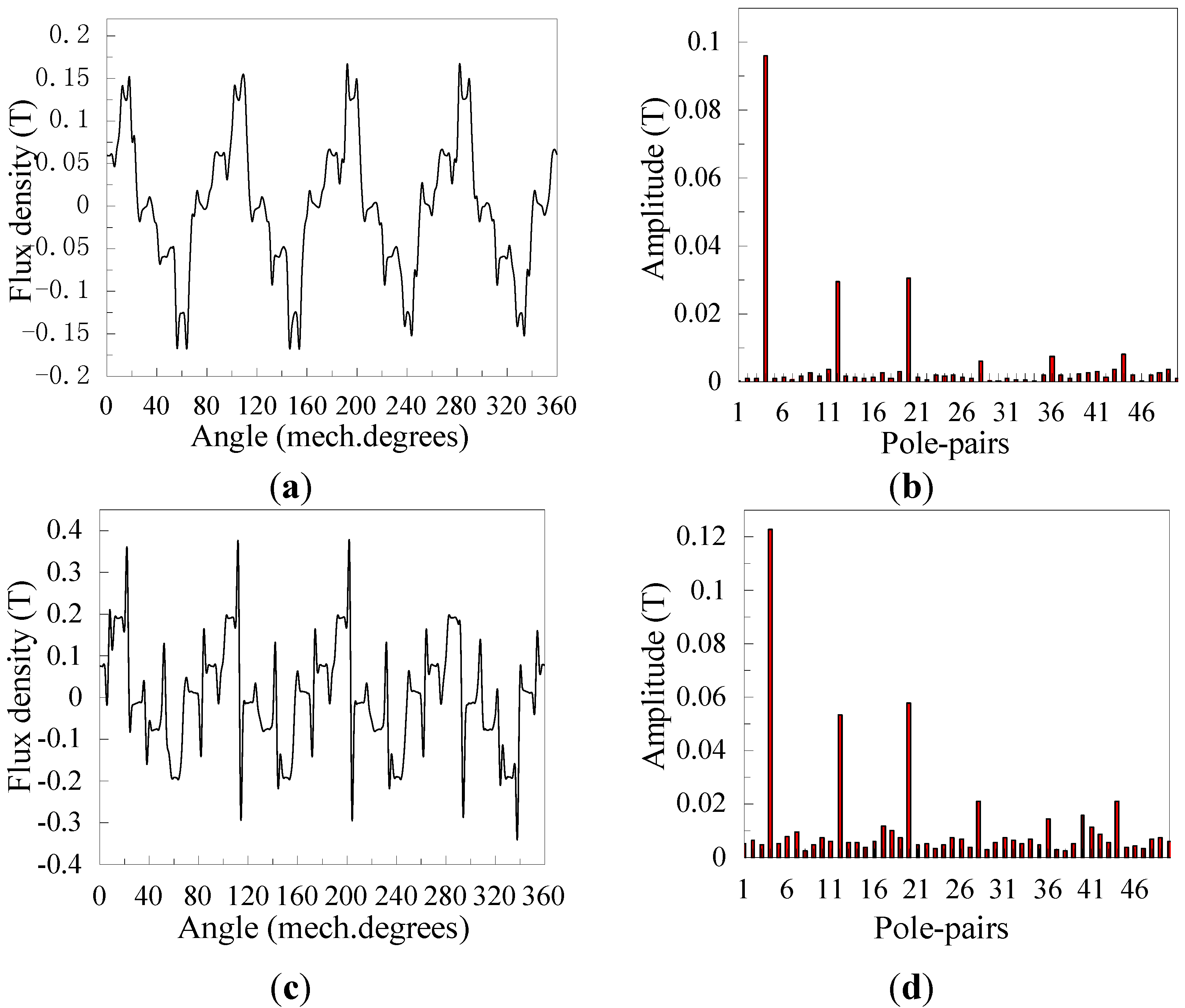
4. Conclusions
- (1)
- The matching relation of ps, pp and pm, and the relation of ωs, ωp and ωm have been deduced. It is found that the axial MFM-BDRM provides speed difference between the shaft of the modulating ring rotor and that of the permanent magnet rotor by adjusting the frequency of stator winding current.
- (2)
- The torque transmission relation has been deduced. The result shows that the axial MFM-BDRM transfers torque by a certain torque ratio.
- (3)
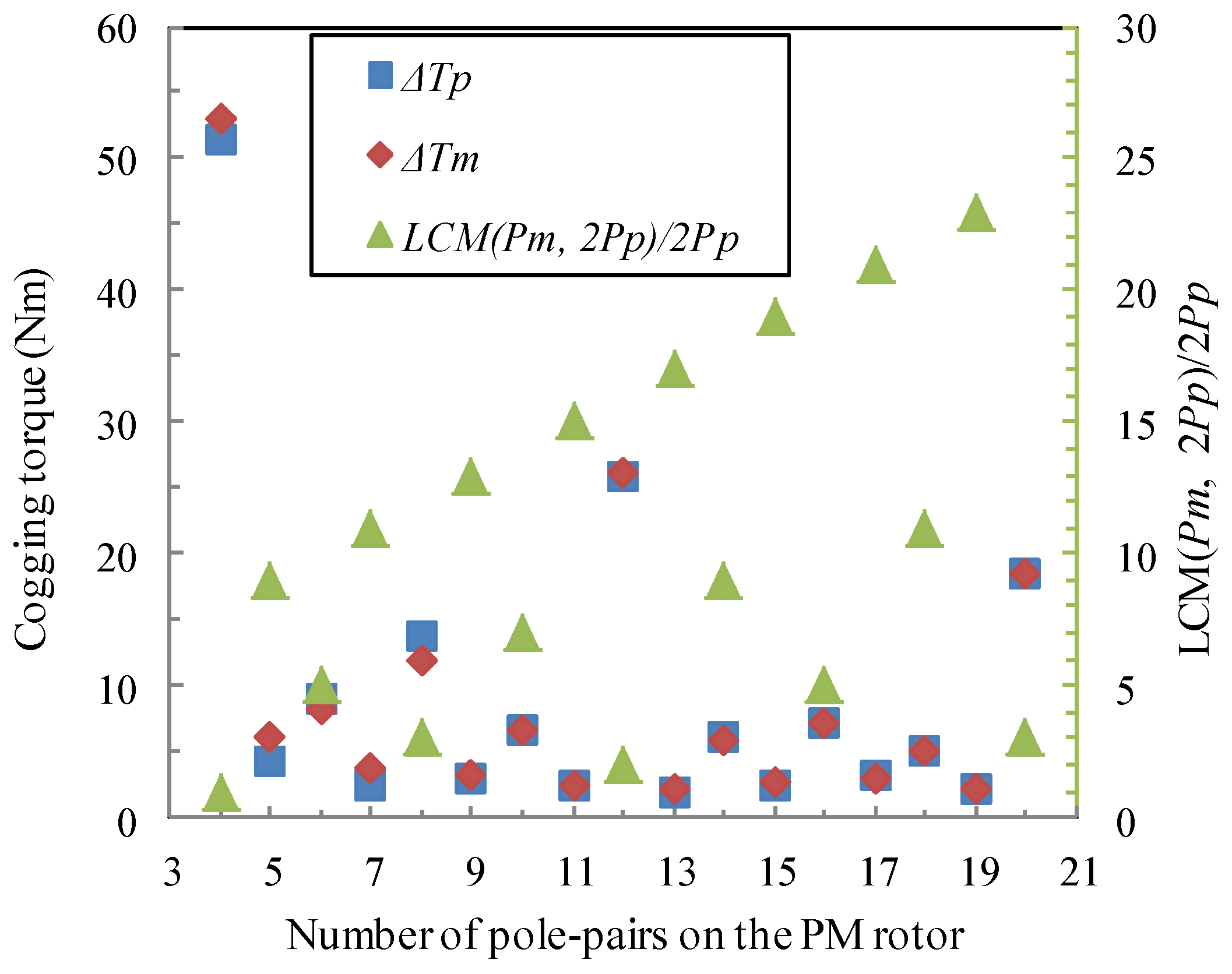
- The cogging torque characteristics have been mathematically formulated. The result demonstrates that the order of the cogging torque is LCM (pm, 2pp) and there is good correlation between the amplitude of cogging torque and . The smaller is, the larger the cogging toque will be.
- (4)
- The performance analysis verifies that the adoption of the scheme that the greatest common divisor between the pole-pair number of the permanent magnet rotor and that of the stator is 1 can prominently reduce torque ripple and make the no-load back EMF more sinusoid, resulting in good performance of the machine.
Nomenclature:
| pp | number of pole pairs of the permanent magnet rotor |
| ps | number of pole pairs of the stator |
| pm | number of ferromagnetic pole pieces |
| ωp | rotational speed of the permanent magnet rotor |
| ωs | rotational speed of the stator magnetic field |
| ωm | rotational speed of the modulating ring rotor |
| θop | initial phase angle of the permanent magnet rotor |
| θom | initial phase angle of the modulating ring rotor |
| θos | initial phase angle of the stator magnetic field |
| pp(h, k), ωp(h, k) | number of pole pairs in the space harmonic magnetic field distribution produced by the permanent magnet rotor and its rotational speed |
| ps(v, l), ωs(v, l) | number of pole pairs in the space harmonic magnetic field distribution produced by the stator winding and its rotational speed |
| Tp | electromagnetic torque on the permanent magnet rotor |
| Ts | electromagnetic torque on the stator |
| Tm | electromagnetic torque on the modulating ring rotor |
| Tcog | cogging torque of interaction between the permanent magnet rotor and ferromagnetic pole pieces of the modulating ring rotor |
| W | total magnetic energy |
| B | magnetic flux density in the air gap adjacent to the permanent magnet rotor |
| V | volume of the air gap adjacent to the permanent magnet rotor |
| Α | relative position angle between the permanent magnet rotor and modulating ring rotor |
| Ri | inner radius of the axial MFM-BDRM |
| Ro | outer radius of the axial MFM-BDRM |
| δ | length of the air gap adjacent to the permanent magnet rotor |
| Δθp | rotation angle of the permanent magnet rotor |
| Δθm | rotation angle of the modulating ring rotor |
| tcog | period of the cogging torque waveform |
| LCM(pm, 2pp) | the least common multiple between pm and 2pp |
| fph(z) | Fourier coefficient for the magnetomotive force produced by the permanent magnet rotor |
| FA(z, θ, t) | magnetomotive force produced by A-phase winding |
| FB(z, θ, t) | magnetomotive force produced by B-phase winding |
| FC(z, θ, t) | magnetomotive force produced by C-phase winding |
| fsv(z) | Fourier coefficient for the magnetomotive force produced by one-phase winding |
| bph(z) | Fourier coefficient for the axial component of the flux density distribution produced by the permanent magnet rotor without the modulating ring rotor |
| bsv(z) | Fourier coefficient for the axial component of the flux density distribution produced by the stator winding without the modulating ring rotor |
| λ0(z), λj(z) | Fourier coefficient for the modulating function |
| B0, Bh | Fourier coefficient for the square of flux density produced by the permanent magnet rotor along z axis without the modulating ring rotor |
| G0, Gj | Fourier coefficient for the square of the modulating function |
| ΔT | torque difference between the maximum and minimum value |
| ΔTp | ΔT of the permanent magnet rotor |
| ΔTm | ΔT of the modulating ring rotor |
Acknowledgments
Conflicts of Interest
References
- Ehsani, M.; Gao, Y.; Miller, J.M. Hybrid electric vehicles: Architecture and motor drives. IEEE Proc. 2007, 95, 719–720. [Google Scholar] [CrossRef]
- Chau, K.T.; Chan, C.C. Emerging energy-efficient technologies for hybrid electric vehicles. IEEE Proc. 2007, 95, 821–835. [Google Scholar] [CrossRef]
- Magnussen, F.; Sadarangani, C. Electromagnetic Transducer for Hybrid Electric Vehicles. In Proceedings of the Nordic Workshop on Power and Industrial Electronics, Stockholm, Sweden, 12–14 August 2002; pp. 5–6.
- Magnussen, F.; Thelin, P.; Sadarangani, C. Design of Compact Permanent Magnet Machines for a Novel HEV Propulsion System. In Proceedings of the 20th International Electric Vehicle Symposium and Exposition (EVS), Long Beach, CA, USA, 15–19 November 2003; pp. 1–12.
- Nordlund, E.; Eriksson, S. Test and Verification of a Four-Quadrant Transducer for HEV Applications. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 2–5 September 2005; pp. 37–41.
- Zheng, P.; Liu, R.R.; Thelin, P.; Nordlund, E.; Sadarangani, C. Research on the parameters and performances of a 4QT prototype machine used for HEV. IEEE Trans. Magn. 2007, 43, 443–446. [Google Scholar] [CrossRef]
- Sun, X.K.; Cheng, M. Thermal analysis and cooling system design of dual mechanical port machine for wind power application. IEEE Trans. Magn. 2013, 60, 1724–1733. [Google Scholar]
- Frank, N.W.; Toliyat, H.A. Gearing Ratios of a Magnetic Gear for Wind Turbines. In Proceedings of the Electric Machines and Drives Conference (IEMDC ’09), Miami, FL, USA, 3–6 May 2009; pp. 1224–1230.
- Frank, N.W.; Toliyat, H.A. Gearing Ratios of a Magnetic Gear for Marine Applications. In Proceedings of the Electric Ship Technologies Symposium (ESTS 2009), Baltimore, MD, USA, 20–22 April 2009; pp. 477–481.
- Zheng, P.; Liu, R.R.; Wu, Q.; Tong, C.D.; Tang, Z.J. Compound-Structure Permanent-Magnet Synchronous Machine Used for HEVs. In Proceedings of the International Conference on Electric Machines and Systems (ICEMS 2008), Wuhan, China, 17–20 October 2008; pp. 2916–2920.
- Eriksson, S.; Sadarangani, C. A Four-Quadrant HEV Drive System. In Proceedings of the IEEE 56th Vehicular Technology Conference (VTC 2002), Vancouver, BC, Canada, 24–28 September 2002; Volume 3, pp. 1510–1514.
- Hoeijmakers, M.J.; Ferreira, J.A. The electric variable transmission. IEEE Trans. Ind. Appl. 2006, 42, 1092–1010. [Google Scholar] [CrossRef]
- Cui, S.M.; Huang, W.X.; Cheng, Y.; Ning, K.W.; Chan, C.C. Design and Experimental Research on Induction Machine Based Electrical Variable Transmission. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC 2007), Arlington, TX, USA, 9–12 September 2007; pp. 231–235.
- Cui, S.M.; Yuan, Y.J.; Wu, Q.; Wang, T.C. Research on Switched Reluctance Double-Rotor Motor Used for Hybrid Electric Vehicle. In Proceedings of the International Conference on Electric Machines and Systems (ICEMS 2008), Wuhan, China, 17–20 October 2008; pp. 3393–3396.
- Xu, L.Y.; Zhang, Y. Design and Evaluation of a Dual Mechanical Port Machine and System. In Proceedings of the CES/IEEE 5th International on Power Electronics and Motion Control Conference (IPEMC 2006), Shanghai, China, 14–16 August 2006; Volume3, pp. 1–5.
- Liu, R.R.; Zhao, H.; Tong, C.D.; Chen, G.; Zheng, P.; Gu, G. Experimental evaluation of a radial-radial-flux compound-structure permanent-magnet synchronous machine used for HEVs. IEEE Trans. Magn. 2009, 45, 645–649. [Google Scholar] [CrossRef]
- Zheng, P.; Zhao, J.; Liu, R.R.; Tong, C.D.; Wu, Q.; Shi, W. Comparison and Evaluation of Different Compound-Structure Permanent-Magnet Synchronous Machine Used for HEVs. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 12–16 September 2010; pp. 1707–1714.
- Zheng, P.; Bai, J.G.; Tong, C.D.; Lin, J.; Wang, H.P. Research on Electromagnetic Performance of a Novel Radial Magnetic-Field-Modulated Brushless Double Rotor Machine. In Proceedings of the 2011 International Conference on Electrical Machines and Systems (ICEMS), Beijing, China, 20–23 August 2011; pp. 1–6.
- Zheng, P.; Bai, J.G.; Tong, C.D.; Sui, Y.; Song, Z.Y.; Zhao, Q.B. Investigation of a novel radial magnetic-field-modulated brushless double rotor machine used for HEVs. IEEE Trans. Magn. 2013, 49, 1231–1341. [Google Scholar] [CrossRef]
- Mezani, S.; Atallah, K.; Howe, D. A high-performance axial-field magnetic gear. J. Appl. Phys. 2006, 99, 08R303:1–08R303:3. [Google Scholar] [CrossRef]
- Niguchi, N.; Hirata, K.; Zaini, A.; Nagai, S. Proposal of an Axial-Type Magnetic-Geared Motor. In Proceedings of the 2012 International Conference on Electrical Machines (ICEM), Marseille, France, 2–5 September 2012; pp. 738–743.
- Atallah, K.; Howe, D. A novel high-performance magnetic gear. IEEE Trans. Magn. 2001, 37, 2844–2846. [Google Scholar] [CrossRef]
- Jian, L.N.; Chau, K.T.; Gong, Y.; Jiang, J.Z.; Yu, C.; Li, W.L. Comparison of coaxial magnetic gears with different topologies. IEEE Trans. Magn. 2009, 45, 4526–4529. [Google Scholar] [CrossRef]
- Rasmussen, P.O.; Andersen, T.O.; Jørgensen, F.; Nielson, O. Development of a high-performance magnetic gear. IEEE Trans. Ind. Appl. 2005, 41, 764–770. [Google Scholar] [CrossRef]
- Atallah, K.; Calverley, S.D.; Howe, D. Design, analysis and realization of a high performance magnetic gear. IEE Proc. Electr. Power Appl. 2004, 151, 135–143. [Google Scholar] [CrossRef]
- Atallah, K.; Rens, J.; Mezani, S.; Howe, D. A novel “Pseudo” direct-drive brushless permanent magnet machine. IEEE Trans. Magn. 2008, 44, 4349–4352. [Google Scholar] [CrossRef]
- Wang, L.L.; Shen, J.X.; Luk, P.C.K.; Fei, W.Z.; Wang, C.F.; Hao, H. Development of a magnetic-geared permanent magnet brushless motor. IEEE Trans. Magn. 2009, 45, 4578–4581. [Google Scholar] [CrossRef]
- Ho, S.L.; Niu, S.X.; Fu, W.N. Transient analysis of a magnetic gear integrated brushless permanent magnet machine using circuit-field-motion coupled time-stepping finite element method. IEEE Trans. Magn. 2010, 46, 2074–2077. [Google Scholar] [CrossRef]
- Lubin, T.; Mezani, S.; Rezzoug, A. Analytical computation of the magnetic field distribution in a magnetic gear. IEEE Trans. Magn. 2010, 46, 2611–2621. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Analytical prediction of the cogging torque in radial-field permanent magnet brushless motors. IEEE Trans. Magn. 1992, 28, 1371–1374. [Google Scholar] [CrossRef]
- Niguchi, N.; Hirata, K. Cogging torque analysis of magnetic gear. IEEE Trans. Ind. Electron. 2012, 59, 2189–2197. [Google Scholar] [CrossRef]
- Niguchi, N.; Hirata, K. Torque Ripple Analysis of a Magnetic-Geared Motor. In Proceedings of the 2012 International Conference on Electrical Machines (ICEM), Marseille, France, 2–5 September 2012; pp. 789–794.
- Jian, L.N.; Chau, K.T. A coaxial magnetic gear with halbach permanent-magnet arrays. IEEE Trans. Energy Convers. 2010, 25, 319–328. [Google Scholar] [CrossRef]
- Li, Y.; Xing, J.W.; Lu, Y.P.; Yin, Z.J. Torque analysis of a novel non-contact permanent variable transmission. IEEE Trans. Magn. 2011, 47, 4465–4468. [Google Scholar] [CrossRef]
- Niguchi, N.; Hirata, K. Torque-speed characteristics analysis of a magnetic-geared motor using finite element method coupled with vector control. IEEE Trans. Magn. 2013, 49, 2401–2404. [Google Scholar] [CrossRef]
- Van Wyk, J.D.; Skudelny, H.-Ch.; Müller-Hellmann, A. Power electronics control of the electromechanical energy conversion process and some application. IEE Proc. B Electr. Power Appl. 2008, 133, 369–399. [Google Scholar] [CrossRef]
- Liu, C.; Chau, K.T. Electromagnetic design and analysis of double-rotor flux-modulated permanent-magnet machines. Prog. Electromagn. Res. 2012, 131, 81–97. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zheng, P.; Song, Z.; Bai, J.; Tong, C.; Yu, B. Research on an Axial Magnetic-Field-Modulated Brushless Double Rotor Machine. Energies 2013, 6, 4799-4829. https://doi.org/10.3390/en6094799
Zheng P, Song Z, Bai J, Tong C, Yu B. Research on an Axial Magnetic-Field-Modulated Brushless Double Rotor Machine. Energies. 2013; 6(9):4799-4829. https://doi.org/10.3390/en6094799
Chicago/Turabian StyleZheng, Ping, Zhiyi Song, Jingang Bai, Chengde Tong, and Bin Yu. 2013. "Research on an Axial Magnetic-Field-Modulated Brushless Double Rotor Machine" Energies 6, no. 9: 4799-4829. https://doi.org/10.3390/en6094799
APA StyleZheng, P., Song, Z., Bai, J., Tong, C., & Yu, B. (2013). Research on an Axial Magnetic-Field-Modulated Brushless Double Rotor Machine. Energies, 6(9), 4799-4829. https://doi.org/10.3390/en6094799




