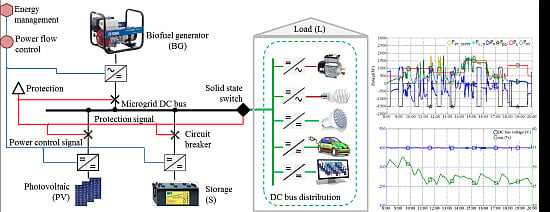
1. Introduction
Currently, some major preoccupations in urban area are the buildings energy performances and energy autonomy. Nowadays, in urban areas, there is a significant development of small plants of decentralized photovoltaic (PV) power production, therefore associated with or integrated in buildings [
1,
2]. Facing high PV sources penetration level in future, direct PV power injection may introduce additional regulations in grid power balancing, resulting in power quality or even stability issues. Therefore, microgrids are proposed as a key integration of renewable energy in the grid power energy mix [
3]. By grouping production, consumption and storage together, the microgrid operates in grid-connected and off-grid modes. In grid-connected operating mode, a microgrid can exchange power with the grid (to receive or to inject power). During off-grid operating mode, a microgrid should be able to continuously provide enough energy to an important part of its internal load. AC or DC microgrids combine power balancing control and energy management in order to control on-site generation and power demand [
4]. Despite existing researches on microgrid power balancing [
5,
6], local power optimization for building-integrated DC microgrid [
7,
8,
9,
10] has not been fully explored.
In this context, facing the emergence of the smart grid combined with AC or DC microgrids, on the one hand, and the increasing of the positive-energy buildings, on the other hand, one of the solutions is the local DC microgrid based on PV sources that are the most commonly used renewable sources in urban area. This paper presents an isolated DC microgrid with optimized power flow for improving PV penetration and positive-energy buildings. As concerns the building-integrated DC microgrid [
9,
10,
11], it is possible to design a DC power distribution in an energy efficient manner because most of its electric loads operate directly with DC power [
12]. Protection devices, such as solid-state circuit and hybrid breakers, are nowadays technically feasible, in accordance with the specification of breaking time and perturbation on the bus [
13].
The goal is to design an advanced local energy management and control, which optimizes power flow for improving PV efficiency for positive-energy buildings. Specifically, for buildings equipped with PV sources, this study presents an isolated DC microgrid which handles instantaneous power balancing following an optimal power flow scheduling while providing energy cost reduction. The optimization takes into account forecast of PV power production and load power demand, while satisfying constraints such as storage capability and sources operating modes [
14,
15]. Optimization, wherein efficiency is related to the prediction accuracy, may be carried out by several methods: linear and direct methods, meta-heuristic algorithms, rule-based methods,
etc. [
16,
17,
18]. In [
17] three optimization methods were chosen to solve an optimal power flow scheduling: mixed integer linear programming as a direct method that has guarantees of convergence, differential evolution as a meta-heuristic that is not limited to linear problems or constraints, and rule-based algorithm as a quick and fast method for a particular case. The goal was to optimize the use of the resources and to minimize the total energy cost. Following this comparison, the rule-based algorithm was arguably the fastest, but with increased complexity of the PV sources power forecasted curve, the efficiency of this rule-based algorithm has dropped considerably. The mixed integer linear programming had the best tradeoff between computational duration and accuracy, performing the optimization in less time than the differential evolution that depends on calculating many generations to reach the result.
This paper investigates power flow management for an isolated DC microgrid and focuses on efficiency and energy cost reduction by optimal scheduling. Based on PV sources, storage, and biofuel generator, the proposed DC microgrid is described in
Section 2. The power management and optimization are presented in
Section 3. Combined with robust power balance strategy, the optimization is able to minimize the total energy cost.
Section 4 gives experimental results and validates the feasibility of implementing optimization in real operation while respecting rigid constraints. The experimental results are analyzed in
Section 5. Conclusions are presented in
Section 6.
4. Experimental Tests of Isolated DC Microgrid Control
Table 1 gives the parameters used for optimization and power balancing control strategy.
Table 1.
Optimization and experimental parameters values.
Table 1.
Optimization and experimental parameters values.
| PBG_P | 1500 W | CREF | 130 Ah |
| dtBG | 1200 s | SOCMIN | 45% |
| PL_MAX | 1700 W | SOCMAX | 55% |
| v* | 400 V | cBG | 1.1 €/kWh |
| PS_MAX | 1200 W | cS | 0.01 €/kWh |
| PPV_MPPT at Standard Test Conditions | 2000 W | cPVS | 1 €/kWh |
| SOC0 = SOCF | 50% | cLS | 1 €/kWh |
These parameters are selected according to system configuration with an aim to involve as much system behavior as possible during the tests, such as storage events (full, empty), load shedding and PV sources power limiting. The energy tariffs values are chosen completely arbitrarily but in order to enhance the control strategy it is mandatory to respect the inequality
cBG >
cPVS(LS) >>
cS. Regarding DC bus voltage value which is the same as the DC bus distribution voltage value, in order to be economically profitable and to be able to use the already existing building cable infrastructure (400/230 V AC), research works show that an optimal value to adopt may be about 325 V DC [
12]. For technical reasons, and after verification of the AC
versus DC efficiency, in this study, the 400 V DC bus voltage is adopted.
The electrical scheme and images of experimental platform are presented in
Figure 4 and
Figure 5 respectively.
Figure 4.
Electrical scheme of experimental platform.
Figure 4.
Electrical scheme of experimental platform.
Figure 5.
Test bench image.
Figure 5.
Test bench image.
This experimental platform is installed in the laboratory of the research team EA 7284 AVENUES (Pierre Guillaumat Center of Universite de Technologie de Compiegne, France). The image of the DC load shows the PV panels on the roof of the Pierre Guillaumat Center. The biofuel generator and the DC load are emulated by a linear amplifier and a programmable DC electronic load respectively. In addition, a four-leg power converter (B1 to B4) and a set of inductors and capacitors, in order to ensure compatibility between the different elements, are added.
The control/optimization method was implemented in the experimental platform presented in
Figure 5. Regarding the overall control structure, firstly, the simulation was implemented on MATLAB Simulink. To make it work in real time, it is compiled by dSPACE, and then the system operates using the ControlDesk from dSPACE real-time as a human-machine interface. Optimized results are power flows of each element (PV sources, storage, biofuel generator, and DC load), which are translated into
to control the real operation. All controls are linear controls, operating with PI correctors, with PWM at 20 kHz. Finally, the PWM signals are routed to the driver cards which control independently the IGBT components. In order to simplify the control, in this study, all PI correctors are with disturbances compensation. Thus, note that the synthesis of PI correctors is not performed with high accuracy.
Regarding the actual load power and its prediction, for all experimental tests, they are considered arbitrary. Load power represents DC building consumption as shown in
Figure 6.
Figure 6.
Load power prediction PL_PRED and load power demand PL for experimental tests.
Figure 6.
Load power prediction PL_PRED and load power demand PL for experimental tests.
Three experimental tests are operated. Depending on meteorological day profile, the case studies retained are: high solar irradiance almost without fluctuations (Test 1), high solar irradiance with strong fluctuations (Test 2), and mixed high irradiance with strong fluctuations and low irradiance without fluctuations (Test 3).
4.1. Test 1
Test 1 is performed for operation on the 4 September 2013 in Compiegne, France [
30]. A few minutes ahead the test, based on solar irradiation hourly forecast data and PV source model [
29], the PV sources power prediction is calculated and also corrected to correspond to the PV panels tilt. The PV sources power uncertainty is shown in
Figure 7.
Figure 7.
PV sources power prediction for experiment and PV sources power measure for Test 1.
Figure 7.
PV sources power prediction for experiment and PV sources power measure for Test 1.
Based on these predictions, the microgrid optimizes the power flow by CPLEX as shown in
Figure 8a. Concerning the power flow curves, note that for storage, negative power means supplying the load, while positive means receiving power. For graphical clarity biofuel generator power is represented by negative values. The proposed optimization shows that the storage is used for power balancing and the biofuel generator is started by duty cycles in order to keep continuous supply for the load and ensure that at the end of the operation the storage capacity is above a preferred level
SOCF.
Figure 8.
(a) Predicted and optimized power flow for Test 1; (b) D and soc evolution given by optimization for Test 1.
Figure 8.
(a) Predicted and optimized power flow for Test 1; (b) D and soc evolution given by optimization for Test 1.
When the storage reaches
SOCMAX, the only way to keep power balancing is to limit PV sources power production; this is why there is PV sources power limiting in the period of 13:10–14:20. Optimum
time series sequence, calculated as the on-off signal for the biofuel generator, and the estimated
evolution given by the optimization are shown in
Figure 8b.
The operation is performed based on
and the power balancing control algorithm. The experimental real-time power flow is shown in
Figure 9a. The experimental
and DC bus voltage evolution are shown in
Figure 9b.
Figure 9.
(a) Experimental real-time power flow for Test 1; (b) Experimental DC bus voltage and soc evolution for Test 1.
Figure 9.
(a) Experimental real-time power flow for Test 1; (b) Experimental DC bus voltage and soc evolution for Test 1.
In this test, biofuel generator is started by duty cycle as commanded by for 8:00–8:20, 18:20–18:40, 19:20–20:00. No load shedding is performed. During 8:00–13:05, the power is balanced following . Despite uncertainties in both load and PV sources power prediction, the storage is fully charged around 13:05, as expected by optimization. During 13:05–14:20, there is no other possibility that can absorb PV sources production, and it is hard to calculate the PV sources power limiting reference to produce the accurate power needed by the load. As a solution, the control strategy slightly over limits the PV production, inducing storage discharging with low power. After the is reduced by certain amount, the PV sources are recovered to produce MPPT power again until the SOCMAX is reached again. That is why the PV sources power oscillation between MPPT mode and power limiting mode can be observed.
During 14:20–20:00 two differences relative to the optimization can be noted: firstly, the PV sources power limiting during 16:55–18:00 is not carried out in actual power flow since actual higher load power than PV production caused ; secondly, biofuel generator is started during 19:00–19:20, which is controlled by the power balancing control algorithm that starts biofuel generator when approaches SOCMIN.
As presented in
Figure 9b, due to uncertainties, the final
value is less than 50%. The power is well balanced during the operation, as shown in
Figure 9b by the steady DC bus voltage. The DC bus voltage fluctuates about 5% at the instants of limiting PV power and starting biofuel generator control, which is related to corresponding control dynamics and is acceptable. The DC bus voltage pulse is generally coming from two sides: on the one hand, the voltages and currents are filtered and the powers are calculated by the filtered signals; on the other hand, power references to stabilize the DC bus voltage are compensated by the filtered power, which is filtered as well and so it has a delay in time. This problem, whose development is not considered here, could be solved by using less filtered signal or improving the performance of correctors in order to cancel the compensation.
Table 2 shows the total energy cost
Ctotal based on energy tariff (€/kWh) given in
Table 1 (
cBG,
cS,
cPVS,
cLS) and taking onto account the operating time period of 12 h taken into account,
i.e., from 8:00 to 20:00.
Table 2.
Energy Cost Comparison.
Table 2.
Energy Cost Comparison.
| Case Operation | Energy Cost Ctotal (€) |
|---|
| Estimated optimum energy cost following power predictions | 3.629 |
| Actual energy cost (experiment) | 3.658 |
| Optimum energy cost for real conditions calculated after operation | 3.380 |
The total energy cost Ctotal is calculated for three cases: estimated optimum energy cost following power predictions, the experimental cost, which is the actual energy cost, and the optimum energy cost for real conditions calculated after operation. Thus, the actual energy cost is higher than the estimated cost by optimization before the operation; it is due to uncertainties. Aiming at a fair comparison, the total energy cost is calculated again at the end of the test based on real test conditions and using the optimization problem formulation. In this last case, the obtained cost is the total optimum energy cost that would have been possible to achieve following the real solar irradiation and the real load power. The difference between the actual total energy cost and the total optimum energy cost is about 8% for this experimental test. Given this small difference, the optimization problem formulation could be considered as demonstrated.
4.2. Test 2
Test 2 is performed for operation on 27 August 2013. PV sources power prediction uncertainty is shown in
Figure 10. It can be noted that the measure is less than the corrected prediction and for the periods of 8:00–10:00 and 15:30–20:00 the weather is heavily cloudy which is not predicted.
Figure 10.
PV sources power prediction and actual PV sources power measure for Test 2.
Figure 10.
PV sources power prediction and actual PV sources power measure for Test 2.
The optimized power flow by CPLEX is shown in
Figure 11a. As aforementioned, when the storage reaches
SOCMAX, the only way for keeping power balancing is to limit PV production; therefore, PV sources limited power control must be performed. In this case, the limited PV production is distributed randomly during 10:45–17:20. Based on optimum power flow evolution, optimum
D sequence is calculated for the experimental operation, which represents the on-off state for the biofuel generator, as shown in
Figure 11b.
Figure 11.
(a) Predicted and optimized power flow for Test 2; (b) D and soc evolution given by optimization for Test 2.
Figure 11.
(a) Predicted and optimized power flow for Test 2; (b) D and soc evolution given by optimization for Test 2.
Based on the power balancing algorithm, which implies the use of the control parameter
, the operation is performed and the obtained power flow is shown in
Figure 12a. Experimental
and DC bus voltage evolution are shown in
Figure 12b.
Figure 12.
(a) Experimental real-time power flow for Test 2; (b) Experimental DC bus voltage and soc evolution for Test 2.
Figure 12.
(a) Experimental real-time power flow for Test 2; (b) Experimental DC bus voltage and soc evolution for Test 2.
During this day operation, storage is used for regulating the power balance. The biofuel generator is started with interface value for 19:00–20:00 as commanded by optimization or when the approaches SOCMIN, i.e., 9:10–9:30, 9:45–10:05, 10:15–10:35, 11:30–11:50, 15:40–16:40, 17:40–18:00, 18:15–18:35, 18:37–18:57, which are controlled by power balancing strategy.
Storage power is limited to avoid high power charging by high PV sources plus biofuel generator that can shorten the storage lifetime. Therefore, in the case when redundant power exceeds storage power limit, the PV production is limited to protect storage, i.e., 10:20–10:35 and 11:30–11:50. When storage reaches SOCMAX, PV sources power limiting is performed during 13:20–13:50. To avoid oscillation, the PV sources limited power control is recovered with hysteresis as aforementioned in Test 1.
Load shedding is performed as another control degree of freedom in the case when storage is empty and biofuel generator plus PV sources power cannot supply the load demand,
i.e., 16:00–16:15. In this case, the prediction uncertainty is significant, so more biofuel generator production is performed. Nevertheless, the power balancing is able to be maintained as indicated by steady DC bus voltage in
Figure 12b. Due to prediction uncertainties, it can be seen that biofuel generator is started more than expected in order to keep continuous load supply.
Table 3 compares the energy cost among optimization, experiment, and optimum for real conditions. The experimental cost is much greater than the estimated cost by optimization.
Table 3.
Energy Cost Comparison for Test 2.
Table 3.
Energy Cost Comparison for Test 2.
| Case Operation | Energy Cost Ctotal (€) |
|---|
| Estimated optimum energy cost following power predictions | 3.259 |
| Actual energy cost (experiment) | 7.807 |
| Optimum energy cost for real conditions calculated after operation | 7.596 |
The difference is obvious, since more biofuel generator production is involved to ensure power balance, when in real conditions the PV production is much less than expected by prediction. However, the experimental cost is close to optimum energy cost for real conditions calculated after the experiment.
4.3. Test 3
Test 3 is performed on 6 September 2013. PV sources power prediction uncertainty is shown in
Figure 13. The prediction can correspond the two peak periods of production.
Figure 13.
PV sources power prediction and actual PV sources power measure for Test 3.
Figure 13.
PV sources power prediction and actual PV sources power measure for Test 3.
The optimized power flow by CPLEX is shown in
Figure 14a. As the solar irradiance is relatively low, no PV sources power limiting is performed. Based on optimum power flow evolution, optimum
sequence is given in
Figure 14b.
Figure 14.
(a) Predicted and optimized power flow for Test 3; (b) D and soc evolution given by optimization for Test 3.
Figure 14.
(a) Predicted and optimized power flow for Test 3; (b) D and soc evolution given by optimization for Test 3.
The obtained experimental power flow is shown in
Figure 15a. Experimental
and DC bus voltage evolution are shown in
Figure 15b.
Figure 15.
(a) Experimental real-time power flow for Test 3; (b) Experimental DC bus voltage and soc evolution for Test 3.
Figure 15.
(a) Experimental real-time power flow for Test 3; (b) Experimental DC bus voltage and soc evolution for Test 3.
Identical to Test 2, storage power is limited to avoid high power charging by high PV sources power plus biofuel generator production that can shorten the storage lifetime. Therefore, in case of storage injection power tending to exceed storage power limit PS_MAX, the PV production is limited to protect storage (around 9:10, 10:30, 11:30, 12:30, 15:40 and 17:20). It can be seen that the biofuel generator is started more than expected in order to maintain a continuous load supply.
The uncertainties make the actual instantaneous power evolution different as predicated. Nevertheless, the power balancing is able to be maintained and load can be supplied without load shedding. The power balancing is indicated by steady DC bus voltage in
Figure 15b.
The energy cost calculations are given in
Table 4 which validates again that in real conditions the experimental cost is close to optimum energy cost for real conditions calculated after operation.
Table 4.
Energy Cost Comparison for Test 2.
Table 4.
Energy Cost Comparison for Test 2.
| Case Operation | Energy Cost Ctotal (€) |
|---|
| Estimated optimum energy cost following power predictions | 4.366 |
| Actual energy cost (experiment) | 6.689 |
| Optimum energy cost for real conditions calculated after operation | 6.017 |
5. Analysis and Discussion
The optimization objective is to minimize biofuel consumption and keep certain storage capacity at the end of the operation. The experimental tests validate the proposed control strategy which can work under different weather conditions for providing robust power balancing while taking into account optimization results. As is defined as switch for biofuel generator operation, its values are given for each optimization case study. Regarding the experimental tests, the values can be seen following the evolution of biofuel generator power curve (pBG in black): when biofuel generator starts and outputs the rated power ; when biofuel generator has no specific order . It can be noted that for experimental test, the real sequence is not always identical to that the optimization gives. This shows that the proposed control algorithm is robust and able to maintain the power balancing with self-correcting ability and not only to follow the predicted optimization operation.
Table 5 summarizes the comparison of the cost of energies between the operated three tests.
Table 5.
Energy cost comparison between the operated three tests.
Table 5.
Energy cost comparison between the operated three tests.
| Test | Case Operation | Total Energy Cost (€) | Load Shedding Cost (€) | PV Power Limiting Cost (€) | Biofuel Generator Production Cost (€) |
|---|
| Optimization | 3.629 | 0 | 1.463 | 2.166 |
| 1. | Experimentation | 3.658 | 0 | 1.121 | 2.423 |
| Optimization for real conditions | 3.380 | 0 | 1.180 | 2.2 |
| Optimization | 3.259 | 0 | 1.575 | 1.684 |
| 2. | Experimentation | 7.807 | 0.211 | 0.835 | 6.761 |
| Optimization for real conditions | 7.596 | 0 | 1.030 | 6.566 |
| Optimization | 4.366 | 0 | 0 | 4.366 |
| 3. | Experimentation | 6.689 | 0 | 0.175 | 6.514 |
| Optimization for real conditions | 6.017 | 0 | 0.001 | 6.016 |
Experimental results show that the proposed microgrid structure is able to implement optimization in real power control and ensures self-correcting capability. The power flow can be controlled to approach optimum cost when the prediction error is within certain limits. Even if the prediction is quite imprecise, the power balancing can be maintained with respect of rigid constraints.
It is obvious that the optimization effectiveness depends on prediction precision. In the first test, despite of the biofuel generator duty cycles assigned by optimization, biofuel generator is started for one more duty cycle by operation control algorithm. More biofuel generator duty cycle is started for the second test, but the final is close to 50%. In the third test, the final is far from 50%. Load shedding occurs only in Test 2, though it was not expected in the optimization. This is due to a relatively large gap between the solar irradiance prediction and reality, on the one hand, and the imposed limits to storage, on the other hand. Regarding the PV sources shedding, there are differences between optimization and experimentation in all three tests; however, these facts do not affect the total energy costs.
Generally, besides the prediction precision, other factors that affect the effectiveness exist such as converter efficiency and control security margin. As the general prediction data is provided for a large area about 20 km2, for a single location, the prediction precision may not be satisfactory, especially for cloudy weather conditions. Improvement can be done by adding local forecasting techniques such as sky camera and local weather measurement and forecasting station. On the other hand, for these tests, the storage is used for only 10% of its capacity that corresponds to the energy of 1.25 kWh; however, this condition is imposed just to show more control event during a day test. Certainly, a larger storage capacity could be more resistant to the prediction errors.
The experimental costs, which are the actual energy costs, are different from the estimated cost by anterior optimization; this is due to forecast uncertainties. In posterior optimization for real conditions case, the obtained costs are the ideal optimum energy costs that could be reached following the real solar irradiation and the real load power. Indeed, this calculation is performed by completely eliminating uncertainties. Therefore, the total energy cost, as result of this operation, can be considered the indicator of optimum operating. This indicator would be helpful to analyze the system behavior, but its calculation is not possible until the end of the operation. The results presented in
Table 5 highlight the role of uncertainties in microgrid control to obtain the minimum energy cost. The gap between the indicator and the actual outcome depends heavily on gap between the meteorological forecast data and actual measurements.
Even with uncertainties, the experimental cost can be controlled close to optimization for real conditions cost, which is the ideal experimental cost. Thus, it can be considered that these results validated the effectiveness of the proposed optimization and power management control. The power balancing can be maintained and rigid constraints such as storage power limit, storage capacity limit are fully respected.
6. Conclusions
The microgrids systems will become more and more complex and selective according to needed applications. For tertiary buildings equipped with renewable energies, which form an isolated DC microgrid, the overall performance of a building-integrated microgrid is improved by the use of DC electric distribution bus instead of AC distribution bus. This paper shows the interest in the improvement of the overall system efficiency for the local production, local consumption, and usages.
Regarding the islanded DC microgrid operation, optimal scheduling and real-time power management are presented in this paper. Aiming to minimize the total energy cost and based on forecasting data, a cost function is formulated and solved. Thus, based on this prediction-based optimization, for real-time power balancing, the experimental results validate the feasibility of the proposed control of islanded DC microgrid. The minimization of the total energy cost is possible and its implementation could be interesting and does not require high cost. However, the optimization efficiency is based on the power predictions precision. Prediction uncertainties do not influence power balancing but the optimal energy cost is affected. Future work may focus on the impact reducing of uncertainties. One approach could be to re-perform the optimization calculation during the operation with latest forecasting data and real-time system status without interrupting power balancing. In further work real-time optimization will be re-performed with hourly updated weather forecast.