Design and Experimental Study of a VCM-Based Stewart Parallel Mechanism Used for Active Vibration Isolation
Abstract
:1. Introduction

2. Kinematics and Dynamics Analysis of the Stewart Platform
2.1. Coordinate Transformation

2.2. Kinematics and Dynamics of a Leg
2.3. Dynamical Equations of the Payload

3. Control Strategy of the Vibration Isolation System
3.1. The State Space Model and the H∞ Control Law
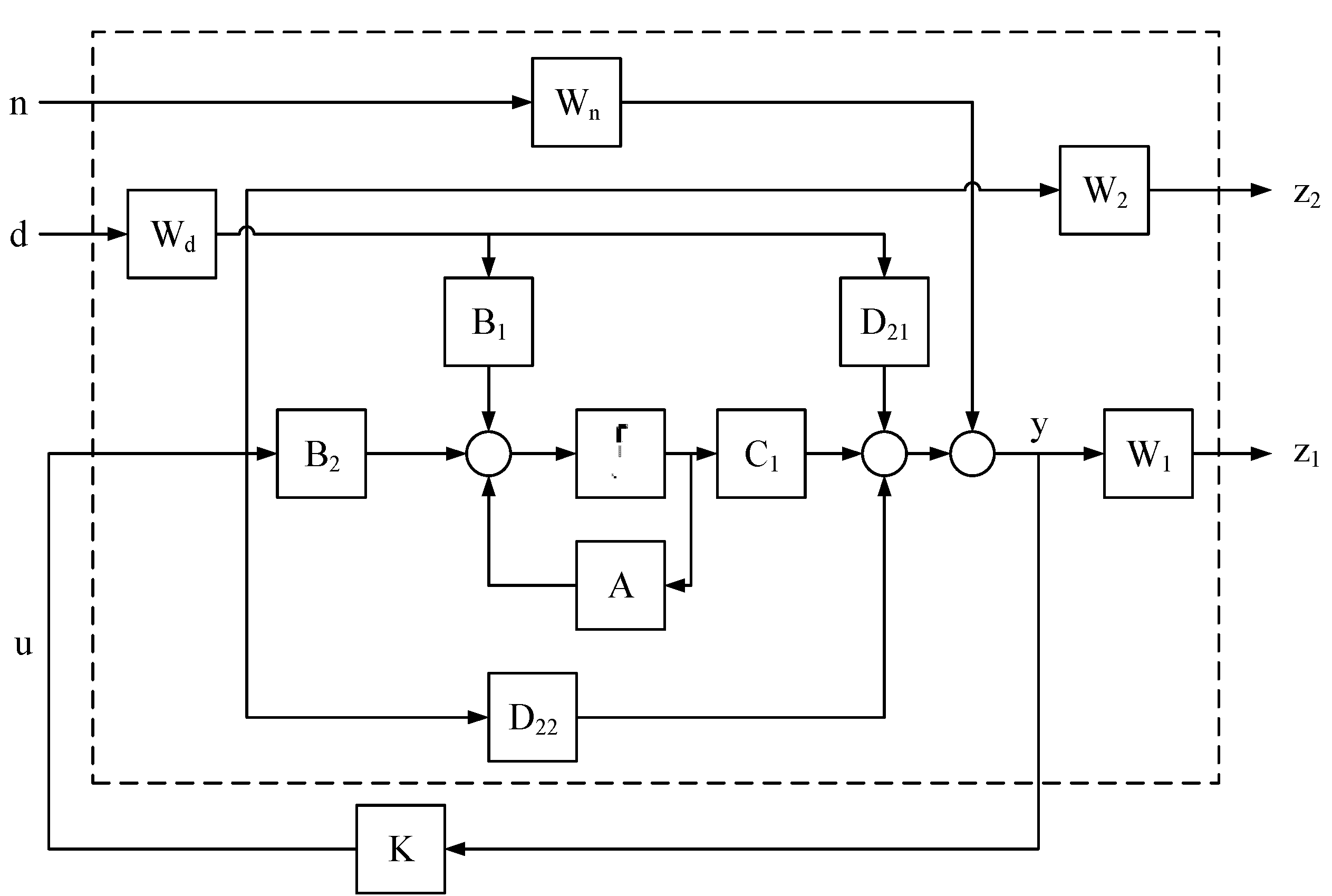
3.2. Selection of Weighting Functions

3.3. Simulation Results
| Parameters | Values |
|---|---|
| Top Platform Radius | 0.165 m |
| Height | 0.079 m |
| Length of legs | 0.162 m |
| Mass of top platform | 3.29 kg |
| Moment of Inertia of top platform | |
| Moment of Inertia of upper leg | |
| Moment of Inertia of lower leg | |
| Mass of each upper leg | 0.0793 kg |
| Mass of each lower leg | 1.16 kg |
| Stiffness of diaphragm spring | |
| Natural Frequency | 14.5 Hz |
| Mass of payload | 4.85 kg |
| Leg extension range | ±5 mm |

4. System Implementation and Experimental Results
4.1. Experimental Setup




4.2. Experimental Results
4.2.1. Sinusoidal Sweeping-Frequency Vibration Tests

| Damping | Resonance Frequency (Hz) | Vibration Amplitude (m/s2) | Magnification (dB) |
|---|---|---|---|
| Without damping | 14.524 | 2.000 | 12.041 |
| Passive damping | 14.117 | 0.916 | 5.259 |
| H∞ control | 15.375 | 0.253 | −5.917 |
| Damping | Resonance Frequency (Hz) | Vibration Amplitude (m/s2) | Magnification (dB) |
|---|---|---|---|
| Without damping | 14.524 | 2.539 | 14.114 |
| Passive damping | 14.905 | 0.815 | 4.244 |
| H∞ control | 11.650 | 0.442 | −1.071 |
| Damping | Resonance Frequency (Hz) | Vibration Amplitude (m/s2) | Magnification (dB) |
|---|---|---|---|
| Without damping | 14.562 | 10.878 | 26.752 |
| Passive damping | 14.905 | 3.854 | 17.739 |
| H∞ control | 15.576 | 2.502 | 13.986 |
4.2.2. Fixed-Frequency Vibration Tests
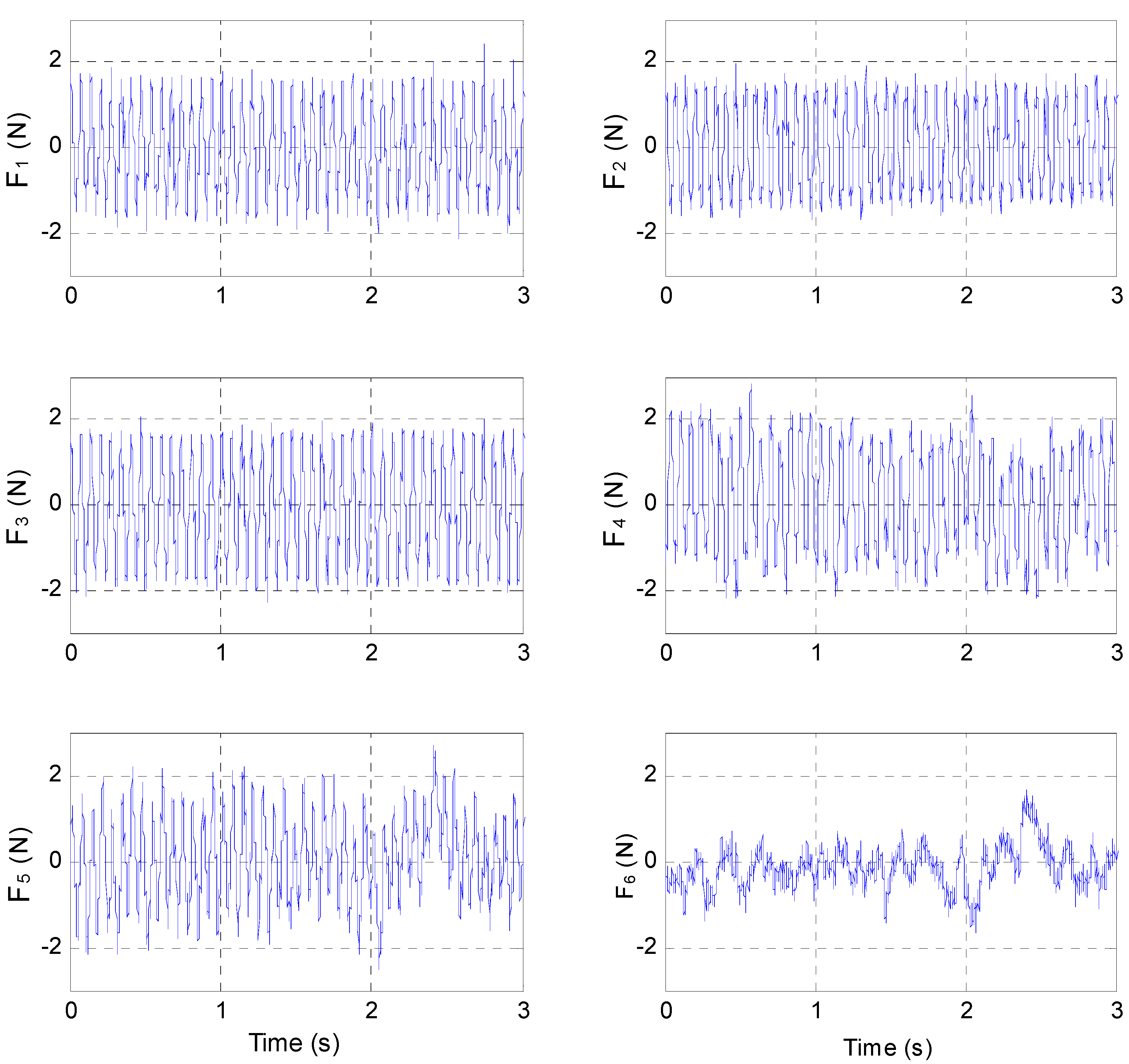
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
position of platform | |
position of upper end of ith leg | |
position of lower end of ith leg | |
position of center of mass of payload | |
vector of the ith leg | |
transformation matrix | |
rotation matrix | |
moment of inertia | |
rotation angle | |
acceleration | |
angular velocity | |
force vector between the upper and the lower legs | |
active control force | |
external force on the top platform | |
external torque on the top platform | |
the mass of the top platform | |
stiffness matrix of the legs | |
damping matrix of the legs |
References
- Kurt, M.; Slavkin, I.; Eriten, M.; McFarland, D.M.; Gendelman, O.V.; Bergman, L.A.; Vakakis, A.F. Effect of 1:3 resonance on the steady-state dynamics of a forced strongly nonlinear oscillator with a linear light attachment. Arch. Appl. Mech. 2014, 84, 1189–1203. [Google Scholar] [CrossRef]
- Kurt, M.; Eriten, M.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Frequency-energy plots of steady-state solutions for forced and damped systems, and vibration isolation by nonlinear mode localization. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2905–2917. [Google Scholar] [CrossRef]
- Fuller, C.C.; Elliott, S.; Nelson, P.A. Active Control of Vibration; Academic Press: Salt Lake City, UT, USA, 1996. [Google Scholar]
- Preumont, A.; François, A.; Bossens, F.; Abu-Hanieh, A. Force feedback versus acceleration feedback in active vibration isolation. J. Sound Vib. 2002, 257, 605–613. [Google Scholar] [CrossRef]
- Chen, Y.-D.; Fuh, C.-C.; Tung, P.-C. Application of voice coil motors in active dynamic vibration absorbers. IEEE Trans. Magn. 2005, 41, 1149–1154. [Google Scholar] [CrossRef]
- Fujii, Y.; Hashimoto, S. Evaluation of the dynamic properties of a Voice Coil Motor (VCM). In Proceedings of the 14th International Conference on Mechatronics and Machine Vision in Practice, 2007. M2VIP 2007, Xiamen, China, 4–6 December 2007; pp. 57–61.
- Park, K.; Choi, D.; Ozer, A.; Kim, S.; Lee, Y.; Joo, D. A voice coil actuator driven active vibration isolation system with the consideration of flexible modes. Rev. Sci. Instrum. 2008, 79. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Kim, S.; Park, K. Magnetic force driven six degree-of-freedom active vibration isolation system using a phase compensated velocity sensor. Rev. Sci. Instrum. 2009, 80. [Google Scholar] [CrossRef] [PubMed]
- Kerber, F.; Hurlebaus, S.; Beadle, B.; Stöbener, U. Control concepts for an active vibration isolation system. Mech. Syst. Signal Process. 2007, 21, 3042–3059. [Google Scholar] [CrossRef]
- Chi, W.; Cao, D.; Huang, W. Design of active whole-spacecraft vibration isolation based on voice-coil motor. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 9–13 March 2014. [CrossRef]
- Stewart, D. A platform with six degrees of freedom. Proc. Inst. Mech. Eng. 1965, 180, 371–386. [Google Scholar] [CrossRef]
- Fichter, E.F. A Stewart platform-based manipulator: General theory and practical construction. Int. J. Robot. Res. 1986, 5, 157–182. [Google Scholar] [CrossRef]
- Bonev, I.A.; Ryu, J. A new method for solving the direct kinematics of general 6-6 Stewart Platforms using three linear extra sensors. Mech. Mach. Theory 2000, 35, 423–436. [Google Scholar] [CrossRef]
- Lebret, G.; Liu, K.; Lewis, F.L. Dynamic analysis and control of a Stewart platform manipulator. J. Robot. Syst. 1993, 10, 629–655. [Google Scholar] [CrossRef]
- Dasgupta, B.; Mruthyunjaya, T. A Newton-Euler formulation for the inverse dynamics of the Stewart platform manipulator. Mech. Mach. Theory 1998, 33, 1135–1152. [Google Scholar] [CrossRef]
- Dasgupta, B.; Mruthyunjaya, T. Closed-form dynamic equations of the general Stewart platform through the Newton-Euler approach. Mech. Mach. Theory 1998, 33, 993–1012. [Google Scholar] [CrossRef]
- McInroy, J.E. Dynamic modeling of flexure jointed hexapods for control purposes. In Proceedings of the 1999 IEEE International Conference on Control Applications, Kohala Coast, HI, USA, 22–27 August 1999; pp. 508–513.
- Mukherjee, P.; Dasgupta, B.; Mallik, A. Dynamic stability index and vibration analysis of a flexible Stewart platform. J. Sound Vib. 2007, 307, 495–512. [Google Scholar] [CrossRef]
- Preumont, A.; Horodinca, M.; Romanescu, I.; de Marneffe, B.; Avraam, M.; Deraemaeker, A.; Bossens, F.; Hanieh, A.A. A six-axis single-stage active vibration isolator based on Stewart platform. J. Sound Vib. 2007, 300, 644–661. [Google Scholar] [CrossRef]
- Xu, P.; Wang, D.H. Vibration damping modeling of Stewart platform through Newton-Euler approach. In Proceedings of the Smart Structures and Materials, San Diego, CA, USA, 17 May 2005. [CrossRef]
- Chi, W.C.; Cao, D.Q.; Huang, W.H. An Observer-Based Active Vibration Isolation System Using the Voice-Coil Actuator. Adv. Mater. Res. 2014, 846, 161–166. [Google Scholar] [CrossRef]
- Chow, T.L. Introduction to Electromagnetic Theory: A Modern Perspective; Jones & Bartlett Learning: Burlington, MA, USA, 2006. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, W.; Cao, D.; Wang, D.; Tang, J.; Nie, Y.; Huang, W. Design and Experimental Study of a VCM-Based Stewart Parallel Mechanism Used for Active Vibration Isolation. Energies 2015, 8, 8001-8019. https://doi.org/10.3390/en8088001
Chi W, Cao D, Wang D, Tang J, Nie Y, Huang W. Design and Experimental Study of a VCM-Based Stewart Parallel Mechanism Used for Active Vibration Isolation. Energies. 2015; 8(8):8001-8019. https://doi.org/10.3390/en8088001
Chicago/Turabian StyleChi, Weichao, Dengqing Cao, Dongwei Wang, Jie Tang, Yifan Nie, and Wenhu Huang. 2015. "Design and Experimental Study of a VCM-Based Stewart Parallel Mechanism Used for Active Vibration Isolation" Energies 8, no. 8: 8001-8019. https://doi.org/10.3390/en8088001






