Droop Control Design of Multi-VSC Systems for Offshore Networks to Integrate Wind Energy
Abstract
:1. Introduction
2. System Configuration
3. Mathematical Modeling
3.1. Active Power Sharing Using Frequency Droop
3.2. Reactive Power Sharing Using Voltage Droop
3.3. Method of Selecting Voltage and Frequency Droop Gain
4. System Analysis and Dynamic Simulation
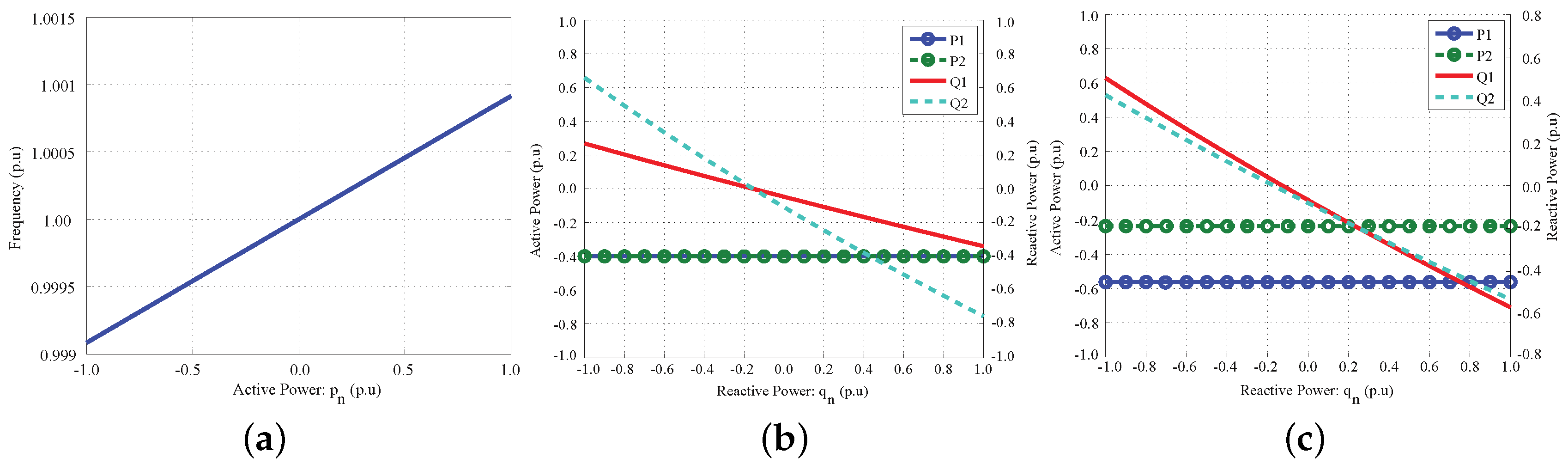
4.1. Steady-State Analysis
4.2. Time Domain Simulation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| DC | Direct Current |
| EU | European Union |
| EWEA | European Wind Energy Association |
| HVDC | High Voltage Direct Current |
| LCC | Line Commutated Converter |
| MMC | Modular Multi-level Converters |
| PCC | Point of Common Coupling |
| VSC | Voltage Source Converter |
| WPP | Wind Power Plant |
| WT | Wind Turbine |
| WTag | Wind Turbine Aggregated Model |
References
- Pineda, I.; Ruby, K.; Ho, A.; Mbistrova, A.; Corbetta, G. The European Offshore Wind Inductry: Key Trends and Statistics 2015; Technical Report; European Wind Energy Association: Brussels, Belgium, 2016. [Google Scholar]
- Fichaux, N.; Wilkes, J. Oceans of Opportunity. Harnessing Europe’s Largest Domestic Energy Resource; Technical Report; European Wind Energy Association: Brussels, Belgium, 2009. [Google Scholar]
- Sellick, R.; Åkerberg, M. Comparison of HVDC light (VSC) and HVDC classic (LCC) site aspects, for a 500 MW 400 kV HVDC transmission scheme. In Proceedings of the 10th IET International Conference on AC and DC Power Transmission (ACDC 2012), Birmingham, UK, 4–5 December 2012; Institution of Engineering and Technology: Stevenage, UK, 2012. [Google Scholar]
- Glasdam, J.; Hjerrild, J.; Kocewiak, L.H.; Bak, C.L. Review on multi-level voltage source converter based HVDC technologies for grid connection of large offshore wind farms. In Proceedings of the 2012 IEEE International Conference on Power System Technology (POWERCON), Auckland, New Zealand, 30 October–2 November 2012.
- De Decker, J.; Kreutzkamp, P.; Woyte, A.; Dierckxsens, C. The impact of large scale offshore electricity transmission: The European project offshore grid. In Proceedings of the 2012 9th International Conference on the European Energy Market, Florence, Italy, 10–12 May 2012.
- Rokrok, E.; Golshan, M. Adaptive voltage droop scheme for voltage source converters in an islanded multibus microgrid. IET Gener. Transm. Distrib. 2010, 4, 562–578. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.P. Modeling and control of VSC HVDC links connected to island systems. IEEE Trans. Power Syst. 2011, 26, 783–793. [Google Scholar] [CrossRef]
- Karlsson, P.; Bjornstedt, J.; Strom, M. Stability of voltage and frequency control in distributed generation based on parallel-connected converters feeding constant power loads. In Proceedings of the IEEE 2005 European Conference on Power Electronics and Applications, Dresden, Germany, 11–14 September 2005.
- Raza, M.; Gomis-Bellmunt, O. Multi infeed control of VSC HVDC transmission system for offshore wind power plant integration. In Proceedings of the 13th International Workshop on Large-Scale Integration of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Plants, Berlin, Germany, 11–13 November 2014.
- Hu, X.; Liang, J.; Rogers, D.J.; Li, Y. Power flow and power reduction control using variable frequency of offshore AC grids. IEEE Trans. Power Syst. 2013, 28, 3897–3905. [Google Scholar] [CrossRef]
- Hassanzahraee, M.; Bakhshai, A. Transient droop control strategy for parallel operation of voltage source converters in an islanded mode microgrid. In Proceedings of the 2011 IEEE 33rd International Telecommunications Energy Conference (INTELEC), Amsterdam, The Netherlands, 9–13 October 2011.
- Liu, H.; Chen, Z. Contribution of VSC-HVDC to Frequency Regulation of Power Systems with Offshore Wind Generation. IEEE Trans. Energy Convers. 2015, 30, 918–926. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W.H.; Kling, W.L.; Ferreira, J.A. Wind turbines emulating inertia and supporting primary frequency control. IEEE Trans. Power Syst. 2006, 21, 433–434. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, J.; Wu, Q.H.; Zhou, X. Frequency Control of DFIG based Wind Power Penetrated Power Systems Using Switching Angle Controller and AGC. IEEE Trans. Power Syst. 2016. [Google Scholar] [CrossRef]
- Conroy, J.; Watson, R. Aggregate modelling of wind farms containing full-converter wind turbine generators with permanent magnet synchronous machines: Transient stability studies. IET Renew. Power Gener. 2009, 3, 39–52. [Google Scholar] [CrossRef]
- Raza, M.; Gomis-Bellmunt, O. Control design strategy to enhance fault right through capability of vsc hvdc transmission system interconnecting offshore wind power plant. In Proceedings of the European Wind Energy Association Annual Conference (EWEA), Paris, France, 17–20 November 2015.
- Raza, M.; Gomis-Bellmunt, O. Dynamic modelling and implementation of vsc hvdc system: The grid connected large offshore wind power plant application. In Proceedings of the 3rd International Conference on Smart Grids and Green IT Systems, Barcelona, Spain, 3–4 April 2014.













| Network Parameters | Value | Unit |
|---|---|---|
| Converter rated power | 500 | MVA |
| Offshore ac hub rated voltage | 150 | kV |
| Onshore grid rated voltage | 400 | kV |
| Converter station rated voltage | 220 | kV |
| DC rated voltage level | kV | |
| DC filter capacitance | 33 | F |
| DC cable resistance | 19 | mΩ/km |
| DC cable length | 250 | km |
| Series inductance | 55 | mH |
| Series resistance | mΩ | |
| Shunt capacitance | F | |
| Transformer impedance | 12 | % |
| Transformer copper losses | 1100 | kW |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, M.; Schönleber, K.; Gomis-Bellmunt, O. Droop Control Design of Multi-VSC Systems for Offshore Networks to Integrate Wind Energy. Energies 2016, 9, 826. https://doi.org/10.3390/en9100826
Raza M, Schönleber K, Gomis-Bellmunt O. Droop Control Design of Multi-VSC Systems for Offshore Networks to Integrate Wind Energy. Energies. 2016; 9(10):826. https://doi.org/10.3390/en9100826
Chicago/Turabian StyleRaza, Muhammad, Kevin Schönleber, and Oriol Gomis-Bellmunt. 2016. "Droop Control Design of Multi-VSC Systems for Offshore Networks to Integrate Wind Energy" Energies 9, no. 10: 826. https://doi.org/10.3390/en9100826
APA StyleRaza, M., Schönleber, K., & Gomis-Bellmunt, O. (2016). Droop Control Design of Multi-VSC Systems for Offshore Networks to Integrate Wind Energy. Energies, 9(10), 826. https://doi.org/10.3390/en9100826






