Numerical Study on the Formation of Shear Fracture Network
Abstract
:1. Introduction
2. The Model
2.1. Numerical Method
2.2. Model Validation
2.3. Dimensionless Numbers
3. Fracture Sliding During Pressure Dissipates
4. Shear Fracture Network
4.1. Numerical Setting
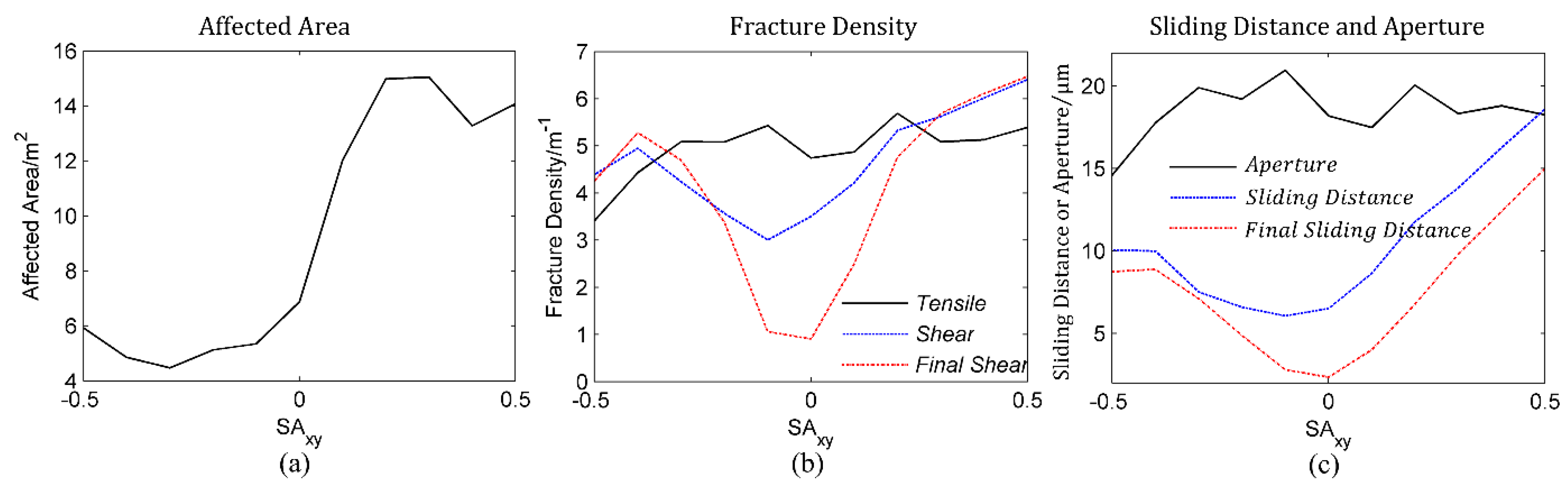
4.2. Effects of Stress Anisotropy
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Riahi, A.; Damjanac, B. Numerical Study of Interaction between Hydraulic Fracture and Discrete Fracture Network; International Society for Rock Mechanics: Salzburg, Austria, 2013. [Google Scholar]
- Fu, P.C.; Johnson, S.M.; Carrigan, C.R. An explicitly coupled hydro-geomechanical model for simulating hydraulic fracturing in arbitrary discrete fracture networks. Int. J. Numer. Anal Methods Geomech. 2013, 37, 2278–2300. [Google Scholar] [CrossRef]
- Perkins, T.; Kern, L. Widths of hydraulic fractures. J. Pet. Technol. 1961, 13, 937–949. [Google Scholar] [CrossRef]
- Nordgren, R. Propagation of a vertical hydraulic fracture. Soc. Pet. Eng. J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Geertsma, J.; De Klerk, F. A rapid method of predicting width and extent of hydraulically induced fractures. J. Pet. Technol. 1969, 21. [Google Scholar] [CrossRef]
- Lee, J. Three-dimensional modeling of hydraulic fractures in layered media: Part I—Finite element formulations. J. Energy Res. Technol. 1990, 112, 1–9. [Google Scholar] [CrossRef]
- Rahman, M.M.; Rahman, S.S. Studies of hydraulic fracture-propagation behavior in presence of natural fractures: Fully coupled fractured-reservoir modeling in poroelastic environments. Int. J. Geomech. 2013, 13, 809–826. [Google Scholar] [CrossRef]
- Mohammadnejad, T.; Khoei, A.R. An extended finite element method for fluid flow in partially saturated porous media with weak discontinuities; the convergence analysis of local enrichment strategies. Comput. Mech. 2013, 51, 327–345. [Google Scholar] [CrossRef]
- Rabczuk, T.; Gracie, R.; Song, J.H.; Belytschko, T. Immersed particle method for fluid-structure interaction. Int. J. Numer. Methods Eng. 2010, 81, 48–71. [Google Scholar] [CrossRef]
- Zhuang, X.; Augarde, C.; Mathisen, K. Fracture modeling using meshless methods and level sets in 3D: Framework and modeling. Int. J. Numer. Methods Eng. 2012, 92, 969–998. [Google Scholar] [CrossRef]
- Zhuang, X.; Cai, Y.; Augarde, C. A meshless sub-region radial point interpolation method for accurate calculation of crack tip fields. Theor. Appl. Fract. Mech. 2014, 69, 118–125. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T. A three-dimensional large deformation meshfree method for arbitrary evolving cracks. Comput. Methods Appl. Mech. Eng. 2007, 196, 2777–2799. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T. Cracking particles: A simplified meshfree method for arbitrary evolving cracks. Int. J. Numer. Methods Eng. 2004, 61, 2316–2343. [Google Scholar] [CrossRef]
- Zhuang, X.; Huang, R.; Liang, C.; Rabczuk, T. A coupled thermo-hydro-mechanical model of jointed hard rock for compressed air energy storage. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Crouch, S.L.; Starfield, A.M. Boundary Element Methods in Solid Mechanics; George Allen & Unwin: London, UK, 1983. [Google Scholar]
- Zhang, Z.; Li, X.; Yuan, W.; He, J.; Li, G.; Wu, Y. Numerical analysis on the optimization of hydraulic fracture networks. Energies 2015, 8, 12061–12079. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; He, J.; Wu, Y.; Zhang, B. Numerical analysis on the stability of hydraulic fracture propagation. Energies 2015, 8, 9860–9877. [Google Scholar] [CrossRef]
- Kresse, O.; Weng, X.W.; Gu, H.R.; Wu, R.T. Numerical modeling of hydraulic fractures interaction in complex naturally fractured formations. Rock Mech. Rock Eng. 2013, 46, 555–568. [Google Scholar] [CrossRef]
- Weng, X. Modeling of complex hydraulic fractures in naturally fractured formation. J. Unconv. Oil Gas Res. 2015, 9, 114–135. [Google Scholar] [CrossRef]
- McClure, M.; Horne, R. Characterizing Hydraulic Fracturing with a Tendency-for-Shear-Stimulation Test; Society of Petroleum Engineers: Richardson, TX, USA, 2014. [Google Scholar]
- Sesetty, V.; Ghassemi, A. Numerical Simulation of Sequential and Simultaneous Hydraulic Fracturing. In Proceedings of the ISRM International Conference for Effective and Sustainable Hydraulic Fracturing, Brisbane, Australia, 20–22 May 2013.
- Safari, R.; Ghassemi, A. 3D thermo-poroelastic analysis of fracture network deformation and induced micro-seismicity in enhanced geothermal systems. Geothermics 2015, 58, 1–14. [Google Scholar] [CrossRef]
- Verde, A.; Ghassemi, A. Modeling injection/extraction in a fracture network with mechanically interacting fractures using an efficient displacement discontinuity method. Int. J. Rock Mech. Min. Sci. 2015, 77, 278–286. [Google Scholar] [CrossRef]
- Verde, A.; Ghassemi, A. Fast multipole displacement discontinuity method (FM-DDM) for geomechanics reservoir simulations. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 1953–1974. [Google Scholar] [CrossRef]
- Pine, R.J.; Batchelor, A.S. Downward migration of shearing in jointed rock during hydraulic injections. Int. J. Rock Mech. Min. Sci. 1984, 21, 249–263. [Google Scholar] [CrossRef]
- Willis-Richards, J.; Watanabe, K.; Takahashi, H. Progress toward a stochastic rock mechanics model of engineered geothermal systems. J. Geophys. Res. Solid Earth 1996, 101, 17481–17496. [Google Scholar] [CrossRef]
- Zhang, X.; Jeffrey, R.; Llanos, E.M. A Study of Shear Hydraulic Fracture Propagation; American Rock Mechanics Association: Houston, TX, USA, 2004. [Google Scholar]
- De Bremaecker, J.C.; Ferris, M.C. Numerical models of shear fracture propagation. Eng. Fract. Mech. 2004, 71, 2161–2178. [Google Scholar] [CrossRef]
- Majer, E.L.; Baria, R.; Stark, M.; Oates, S.; Bommer, J.; Smith, B.; Asanuma, H. Induced seismicity associated with enhanced geothermal systems. Geothermics 2007, 36, 185–222. [Google Scholar] [CrossRef]
- Chipperfield, S.T.; Wong, J.R.; Warner, D.S.; Cipolla, C.L.; Mayerhofer, M.J.; Lolon, E.P.; Warpinski, N.R. Shear Dilation Diagnostics: A New Approach for Evaluating Tight Gas Stimulation Treatments; Society of Petroleum Engineers: College Station, TX, USA, 2007. [Google Scholar]
- Nagel, N.B.; Sanchez-Nagel, M. Stress Shadowing and Microseismic Events: A Numerical Evaluation; Society of Petroleum Engineers: Denver, CO, USA, 2011. [Google Scholar]
- Nagel, N.B.; Gil, I.; Sanchez-nagel, M.; Damjanac, B. Simulating Hydraulic Fracturing in Real Fractured Rocks—Overcoming the Limits of Pseudo3D Models; Society of Petroleum Engineers: The Woodlands, TX, USA, 2011. [Google Scholar]
- Zoback, M.D.; Kohli, A.; Das, I.; McClure, M.W. The Importance of Slow Slip on Faults during Hydraulic Fracturing Stimulation of Shale Gas Reservoirs; Society of Petroleum Engineers: Pittsburgh, PA, USA, 2012. [Google Scholar]
- Jung, R. Egs—Goodbye or Back to the Future 95. In Proceedings of the ISRM International Conference for Effective and Sustainable Hydraulic Fracturing, Brisbane, Australia, 20–22 May 2013.
- Zangeneh, N.; Eberhardt, E.; Marc, R.; Busti, A. A Numerical Investigation of Fault Slip Triggered by Hydraulic Fracturing. In Proceedings of the ISRM International Conference for Effective and Sustainable Hydraulic Fracturing, Brisbane, Australia, 20–22 May 2013.
- McClure, M.W.; Horne, R.N. Conditions required for shear stimulation in EGS. In Proceedings of the 2013 European Geothermal Congress, Pisa, Italy, 3–7 June 2013.
- Palmer, I.D.; Moschovidis, Z.A.; Cameron, J.R. Modeling shear failure and stimulation of the barnett shale after hydraulic fracturing. Society of Petroleum Engineers: College Station, TX, USA, 2007. [Google Scholar]
- Weng, X.; Kresse, O.; Cohen, C.; Wu, R.; Gu, H. Modeling of hydraulic-fracture-network propagation in a naturally fractured formation. Spe Prod. Oper. 2011, 26, 368–380. [Google Scholar] [CrossRef]
- Zhang, X.; Jeffrey, R. Development of Fracture Networks Through Hydraulic Fracture Growth in Naturally Fractured Reservoirs. In Proceedings of the ISRM International Conference for Effective and Sustainable Hydraulic Fracturing, Brisbane, Australia, 20–22 May 2013.
- Wu, K.; Olson, J.E. Investigation of the impact of fracture spacing and fluid properties for interfering simultaneously or sequentially generated hydraulic fractures. Spe Prod. Oper. 2013, 28, 427–436. [Google Scholar] [CrossRef]
- Olson, J.E. Predicting fracture swarms—The influence of subcritical crackgrowth and the crack-tip process zone on joint spacing in rock. In The Initiation, Propagation, and Arrest of Joints and Other Fractures; Geological Society of London Special Publication: London, UK, 2004; Volume 231, pp. 73–87. [Google Scholar]
- Erdogan, F.; Sih, G.C. On the crack extension in plates under plane loading and transverse shear. J. Fluids Eng. 1963, 85, 519–525. [Google Scholar] [CrossRef]
- De, X.; Qin, Q.; Changan, L. Numerical Method and Engineering Application of Fracture Mechanics (Chinese Version); Science Press: Beijing, China, 2009. [Google Scholar]
- Wu, K.; Olson, J.E. Simultaneous Multifracture Treatments: Fully Coupled Fluid Flow and Fracture Mechanics for Horizontal Wells. SPE J. 2014, 20, 337–346. [Google Scholar] [CrossRef]
- Kresse, O.; Cohen, C.; Weng, X.; Wu, R.; Gu, H. Numerical Modeling of Hydraulic Fracturing in Naturally Fractured Formations. In Proceedings of the 45th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011.












| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Fracture length | 1 m | Layer thickness | Infinite |
| 1 | Far-field stress | ||
| Poisson’s ratio | 0.1 |
| Grid Number | Numerical (m) | Analytical (m) | Analytical/Numerical |
|---|---|---|---|
| 5 | 0.498 | 0.392 | 0.787 |
| 10 | 0.354 | 0.281 | 0.793 |
| 15 | 0.290 | 0.230 | 0.794 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Injection Rate | 8.8 × 10−4 m3/s/m | Layer Thickness | 120 m |
| Fluid Viscosity | 1.0 cP | Fracture Toughness | 1.0 × 106 Pa·m0.5 |
| Young’s modulus | 3.0 × 1010 Pa | Far-field stress | |
| Poisson’s ratio | 0.35 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Injection Rate | 1.0 × 10−3 m3/s/m | Stress Angle | |
| Fluid Viscosity | 1.0 cP | Fracture Toughness | Infinite |
| Young’s Modulus | 1.8 × 1010 Pa | Stress Difference | 0.5 × 106 Pa |
| Poisson’s ratio | 0.2 | The coefficient of friction | 0.9 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Li, X. Numerical Study on the Formation of Shear Fracture Network. Energies 2016, 9, 299. https://doi.org/10.3390/en9040299
Zhang Z, Li X. Numerical Study on the Formation of Shear Fracture Network. Energies. 2016; 9(4):299. https://doi.org/10.3390/en9040299
Chicago/Turabian StyleZhang, Zhaobin, and Xiao Li. 2016. "Numerical Study on the Formation of Shear Fracture Network" Energies 9, no. 4: 299. https://doi.org/10.3390/en9040299
APA StyleZhang, Z., & Li, X. (2016). Numerical Study on the Formation of Shear Fracture Network. Energies, 9(4), 299. https://doi.org/10.3390/en9040299






