Anti-Windup Load Frequency Controller Design for Multi-Area Power System with Generation Rate Constraint
Abstract
:1. Introduction
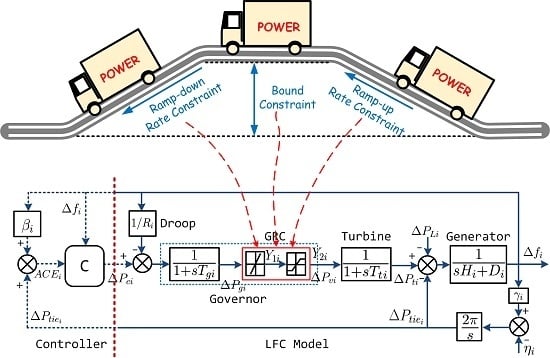
2. Load Frequency Control Model
3. Anti-Windup Load Frequency Controller Design
3.1. Original Controller Design
3.2. Anti-Windup Compensator Design
- The origin of the anti-windup closed-loop system is asymptotically stable.
4. Case Study
4.1. Scenario 1: Simulations on Single-Area System
4.2. Scenario 2: Simulations on a Two-Area System
4.3. Scenario 3: Simulations on Three-Area Systems
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rerkpreedapong, D.; Hasanovic, A.; Feliachi, A. Robust load frequency control using genetic algorithms and linear matrix inequalities. IEEE Trans. Power Syst. 2003, 18, 855–861. [Google Scholar] [CrossRef]
- Shayeghi, H.; Shayanfar, H.A.; Jalili, A. Load frequency control strategies: A state-of-the-art survey for the researcher. Energy Convers. Manag. 2009, 50, 344–353. [Google Scholar] [CrossRef]
- Khodabakhshian, A.; Edrisi, M. A new robust PID load frequency controller. Control Eng. Pract. 2008, 16, 1069–1080. [Google Scholar] [CrossRef]
- Tan, W. Unified tuning of PID load frequency controller for power systems via IMC. IEEE Trans. Power Syst. 2010, 25, 341–350. [Google Scholar] [CrossRef]
- Ghoshal, S.P. Application of GA/GA-SA based fuzzy automatic generation control of a multi-area thermal generating system. Electr. Power Syst. Res. 2004, 70, 115–127. [Google Scholar] [CrossRef]
- Cam, E.; Kocaarslan, I. Load frequency control in two area power systems using fuzzy logic controller. Energy Convers. Manag. 2005, 46, 233–243. [Google Scholar] [CrossRef]
- Sabahi, K.; Teshnehlab, M.; Shoorhedeli, M.A. Recurrent fuzzy neural network by using feedback error learning approaches for LFC in interconnected power system. Energy Convers. Manag. 2009, 50, 938–946. [Google Scholar] [CrossRef]
- Bevrani, H.; Daneshmand, P.R.; Babahajyani, P.; Mitani, Y.; Hiyama, T. Intelligent LFC concerning high penetration of wind power: Synthesis and real-time application. IEEE Trans.Sustain.Energy 2014, 5, 655–662. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Pradhan, P.C. Design and analysis of hybrid firefly algorithm-pattern search based fuzzy PID controller for LFC of multi area power systems. Int. J. Electr. Power Energy Syst. 2015, 69, 200–212. [Google Scholar] [CrossRef]
- Al-Hamouz, Z.M.; Al-Duwaish, H.N. A new load frequency variable structure controller using genetic algorithms. Electr. Power Syst. Res. 2000, 55, 1–6. [Google Scholar] [CrossRef]
- Vrdoljak, K.; Perić, N.; Petrović, I. Sliding mode based load-frequency control in power systems. Electr. Power Syst. Res. 2010, 80, 514–527. [Google Scholar] [CrossRef]
- Al-Hamouz, Z.; Al-Duwaish, H.; Al-Musabi, N. Optimal design of a sliding mode AGC controller: Application to a nonlinear interconnected model. Electr. Power Syst. Res. 2011, 81, 1403–1409. [Google Scholar] [CrossRef]
- Aldeen, M.; Trinh, H. Load-frequency control of interconnected power systems via constrained feedback control schemes. Comput. Electr. Eng. 1994, 20, 71–88. [Google Scholar] [CrossRef]
- Alrifai, M.T.; Hassan, M.F.; Zribi, M. Decentralized load frequency controller for a multi-area interconnected power system. Int. J. Electr. Power Energy Syst. 2011, 33, 198–209. [Google Scholar] [CrossRef]
- Trinh, H.; Fernando, T.; Iu, H.H.C.; Wong, K.P. Quasi-decentralized functional observers for the LFC of interconnected power systems. IEEE Trans. Power Syst. 2013, 28, 3513–3514. [Google Scholar] [CrossRef]
- Pham, T.N.; Trinh, H.; Hien, L.V. Load frequency control of power systems with electric vehicles and diverse transmission links using distributed functional observers. IEEE Trans. Smart Grid 2016, 7, 238–252. [Google Scholar] [CrossRef]
- Rahmani, M.; Sadati, N. Hierarchical optimal robust load-frequency control for power systems. IET Gener. Transm. Distrib. 2012, 6, 303–312. [Google Scholar] [CrossRef]
- Vachirasricirikul, S.; Ngamroo, I. Robust LFC in a smart grid with wind power penetration by coordinated V2G control and frequency controller. IEEE Trans. Smart Grid 2014, 5, 371–380. [Google Scholar] [CrossRef]
- Dong, L.L.; Zhang, Y.; Gao, Z.Q. A robust decentralized load frequency controller for interconnected power systems. ISA Trans. 2012, 51, 410–419. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Yao, W.; Wu, Q.H.; Wen, J.Y.; Cheng, S.J. Delay-dependent stability for load frequency control with constant and time-varying delays. IEEE Trans. Power Syst. 2012, 27, 932–941. [Google Scholar] [CrossRef]
- Dey, R.; Ghosh, S.; Ray, G.; Rakshit, A. H∞ load frequency control of interconnected power systems with communication delays. Int. J. Electr. Power Energy Syst. 2012, 42, 672–684. [Google Scholar] [CrossRef]
- Zhang, C.K.; Jiang, L.; Wu, Q.H.; He, Y.; Wu, M. Delay-dependent robust load frequency control for time delay power systems. IEEE Trans. Power Syst. 2013, 28, 2192–2201. [Google Scholar] [CrossRef]
- Atić, N.; Rerkpreedapong, D.; Hasanović, A.; Feliachi, A. NERC compliant decentralized load frequency control design using model predictive control. In Proceedings of the IEEE on Power Engineering Society General Meeting, Toronto, ON, Canada, 13–17 July 2003.
- Franze, G.; Tedesco, F. Constrained load/frequency control problems in networked multi-area power systems. J. Frankl. Inst. 2011, 348, 832–852. [Google Scholar] [CrossRef]
- Tedesco, F.; Casavola, A. Fault-tolerant distributed load/frequency supervisory strategies for networked multi-area microgrids. Int. J. Robust Nonlinear Control 2014, 24, 1380–1402. [Google Scholar] [CrossRef]
- Moon, Y.H.; Ryu, H.S.; Lee, J.G.; Song, K.B.; Shin, M.C. Extended integral control for load frequency control with the consideration of generation-rate constraints. Int. J. Electr. Power Energy Syst. 2002, 24, 263–269. [Google Scholar] [CrossRef]
- Velusami, S.; Chidambaram, I.A. Decentralized biased dual mode controllers for load frequency control of interconnected power systems considering GDB and GRC non-linearities. Energy Convers. Manag. 2007, 48, 1691–1702. [Google Scholar] [CrossRef]
- Sudha, K.R.; Santhi, R.V. Robust decentralized load frequency control of interconnected power system with generation rate constraint using Type-2 fuzzy approach. Int. J. Electr. Power Energy Syst. 2011, 33, 699–707. [Google Scholar] [CrossRef]
- Tan, W. Tuning of PID load frequency controller for power systems. Energy Convers. Manag. 2009, 50, 1465–1472. [Google Scholar] [CrossRef]
- Anwar, M.N.; Pan, S. A new PID load frequency controller design method in frequency domain through direct synthesis approach. Int. J. Electr. Power Energy Syst. 2015, 67, 560–569. [Google Scholar] [CrossRef]
- Forni, F.; Galeani, S.; Zaccarian, L. Model recovery anti-windup for plants with rate and magnitude saturation. In Proceedings of the European Control Conference, Budapest, Hungary, 23–26 August 2009; pp. 324–329.
- Forni, F.; Galeani, S.; Zaccarian, L. An almost anti-windup scheme for plants with magnitude, rate and curvature saturation. In Proceedings of the American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 6769–6774.
- Chilali, M.; Gahinet, P. H∞ design with pole placement constraints: An LMI approach. IEEE Trans. Autom. Control 1996, 41, 358–367. [Google Scholar] [CrossRef]
- Scherer, C.; Gahinet, P.; Chilali, M. Multiobjective output-feedback control via LMI optimization. IEEE Trans. Autom. Control 1997, 42, 896–911. [Google Scholar] [CrossRef]
- Gahinet, P.M.; Nemirovskii, A.; Laub, A.J.; Chilali, M. The LMI control toolbox. In Proceedings of the 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; pp. 2038–2038.
- Forni, F.; Galeani, S.; Zaccarian, L. Model recovery anti-windup for continuous-time rate and magnitude saturated linear plants. Automatica 2012, 48, 1502–1513. [Google Scholar] [CrossRef]


















© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Yue, D.; Xie, X.; Xie, J. Anti-Windup Load Frequency Controller Design for Multi-Area Power System with Generation Rate Constraint. Energies 2016, 9, 330. https://doi.org/10.3390/en9050330
Huang C, Yue D, Xie X, Xie J. Anti-Windup Load Frequency Controller Design for Multi-Area Power System with Generation Rate Constraint. Energies. 2016; 9(5):330. https://doi.org/10.3390/en9050330
Chicago/Turabian StyleHuang, Chongxin, Dong Yue, Xiangpeng Xie, and Jun Xie. 2016. "Anti-Windup Load Frequency Controller Design for Multi-Area Power System with Generation Rate Constraint" Energies 9, no. 5: 330. https://doi.org/10.3390/en9050330