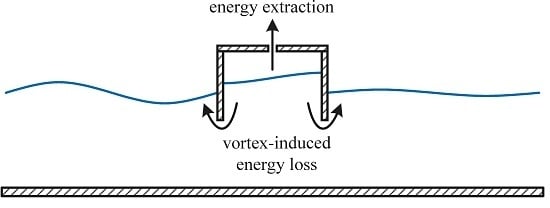
An Experimental Study of Pile-Supported OWC-Type Breakwaters: Energy Extraction and Vortex-Induced Energy Loss
Abstract
:1. Introduction
2. Experiments
2.1. Experimental Setup and Test Procedures
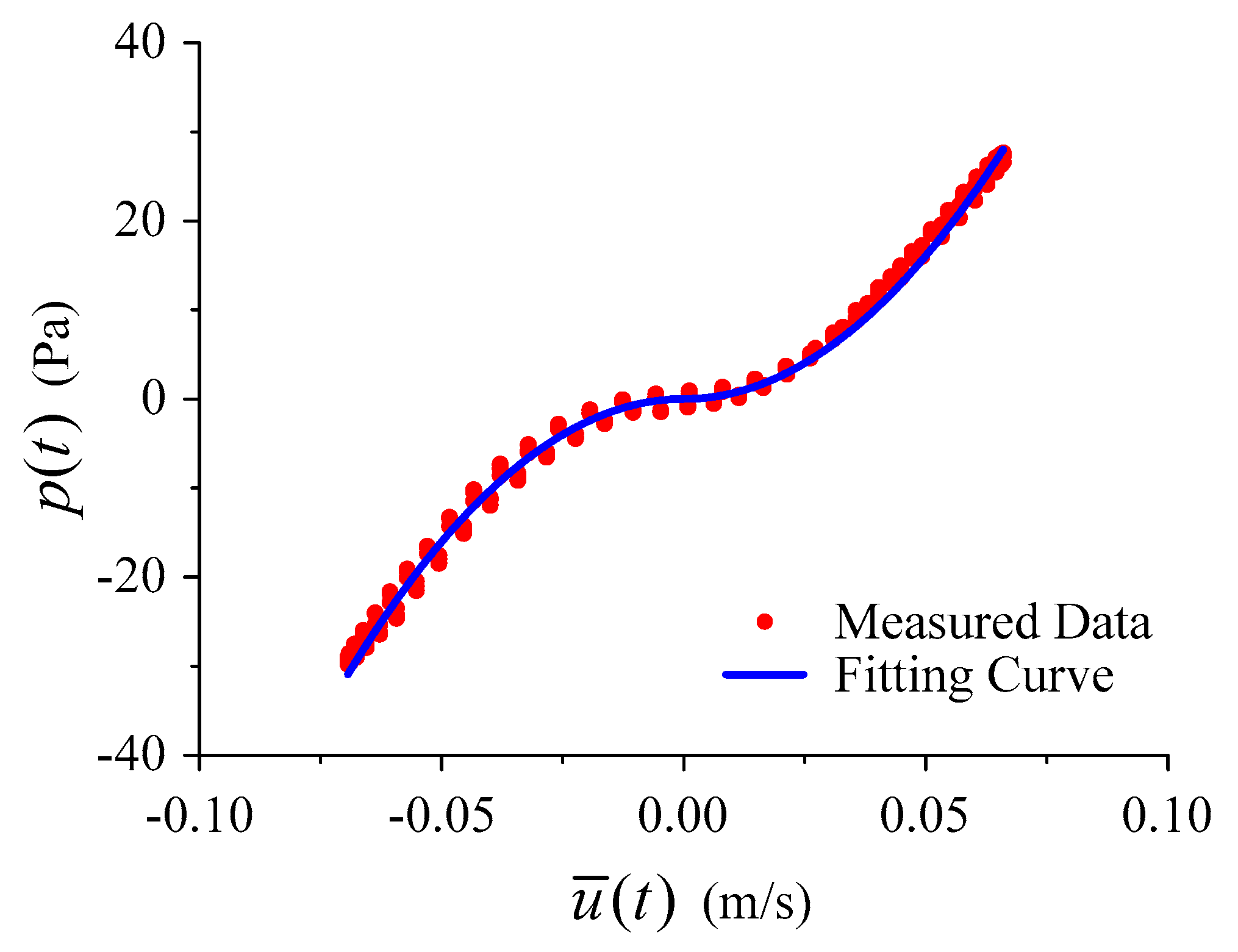
2.2. Data Analysis
3. Results and Discussion
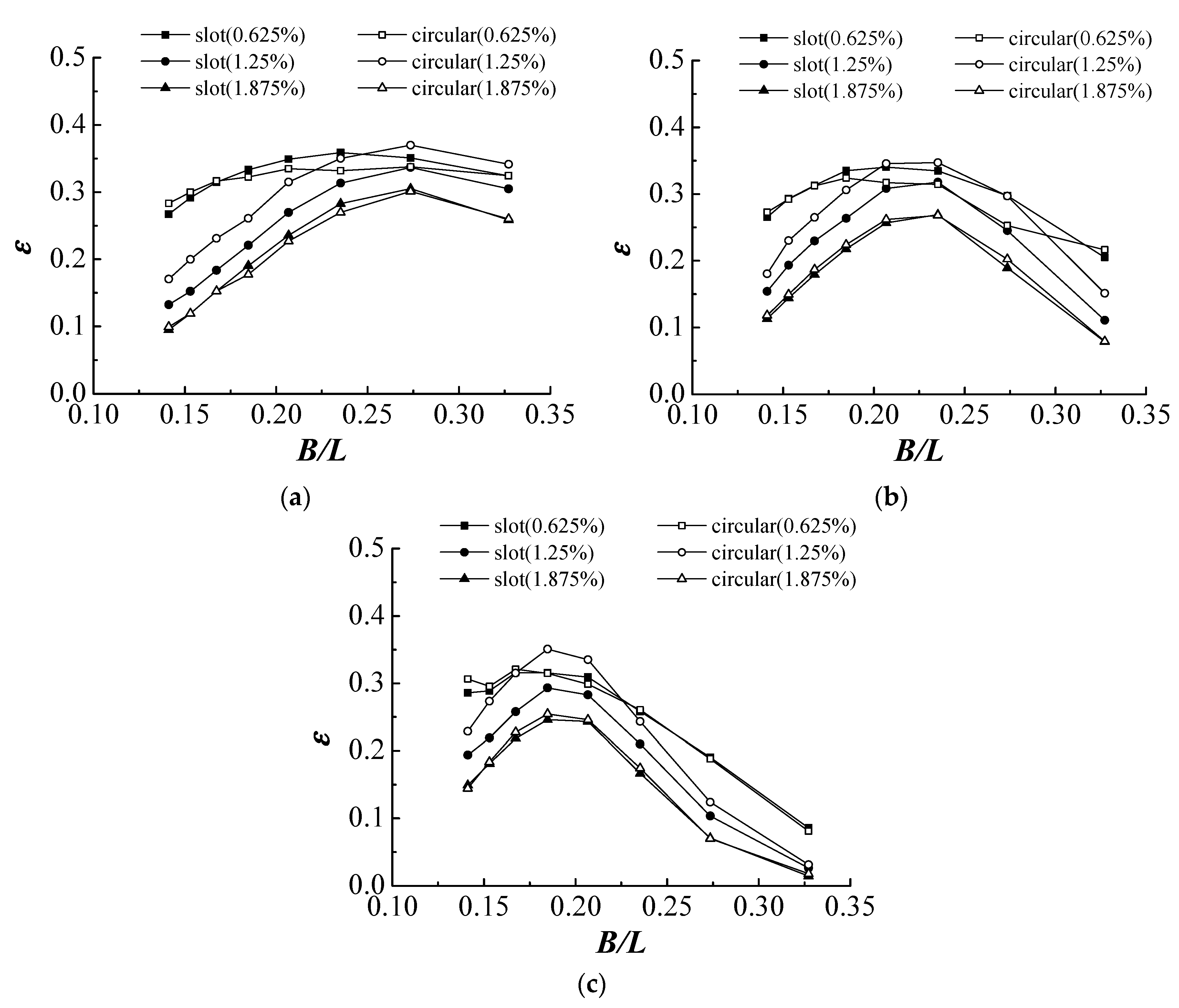
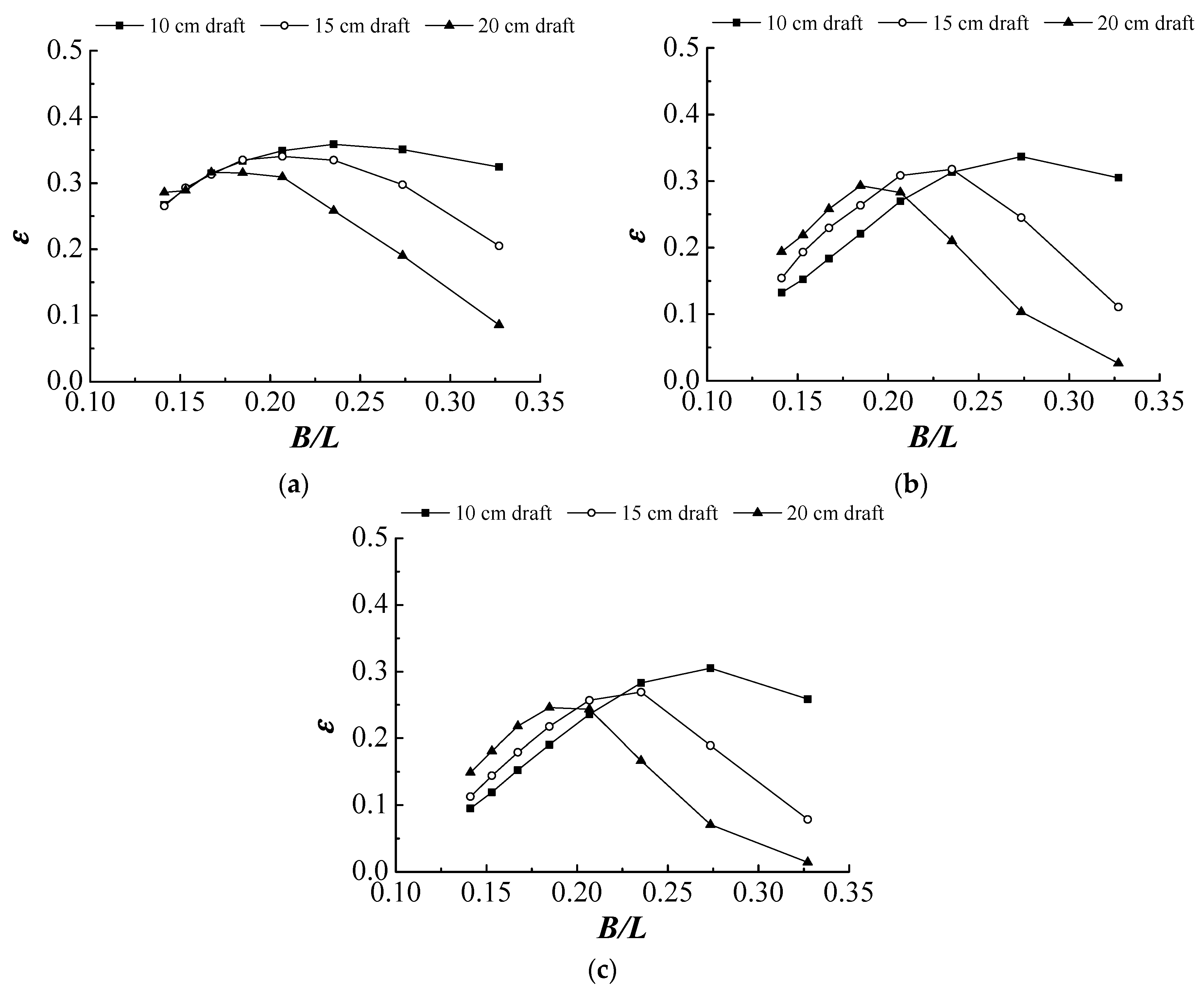
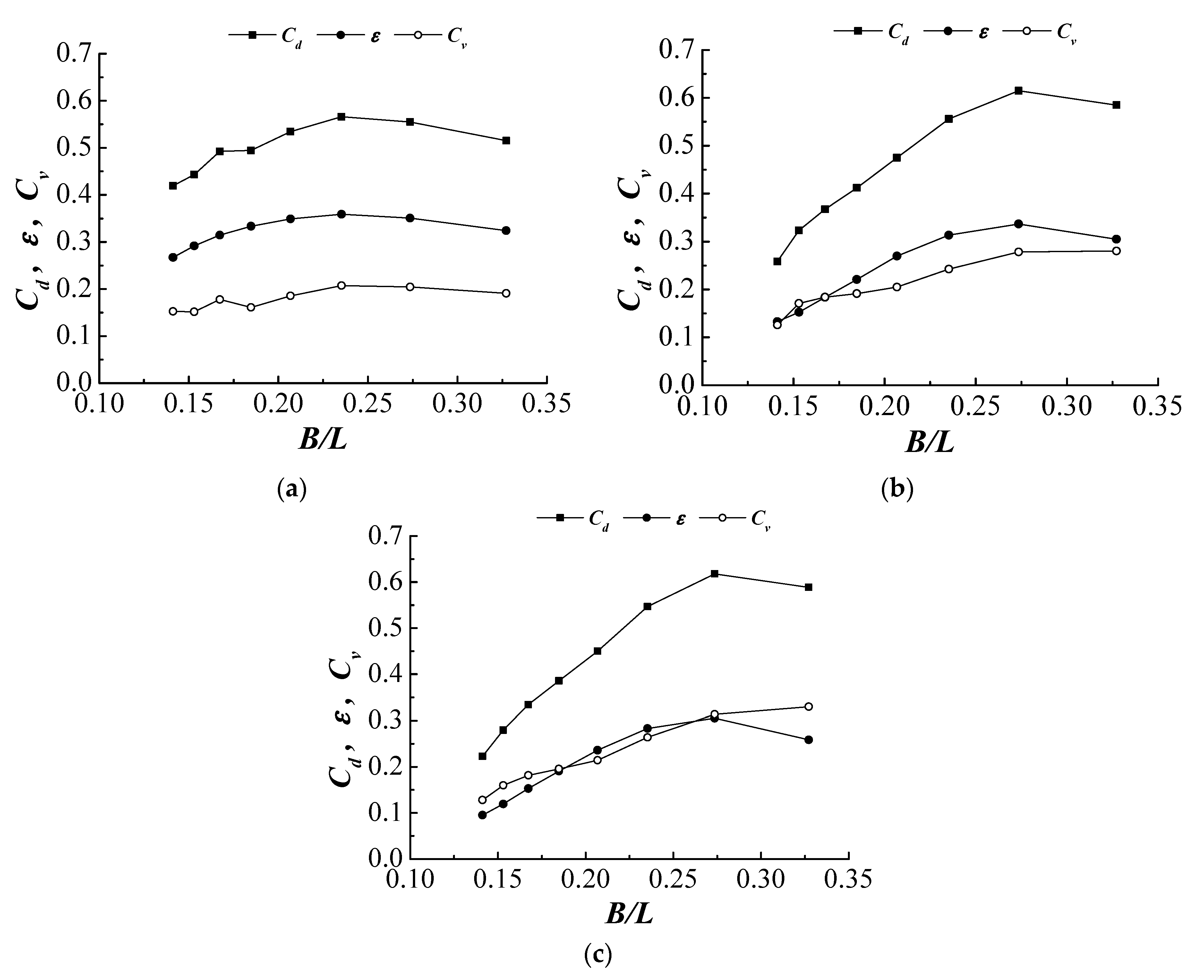
3.1. Energy Extraction
3.1.1. The Effects of Opening Characteristics
3.1.2. The Effects of Chamber Drafts
3.2. Vortex-Induced Energy Loss
3.2.1. The Effects of Opening Characteristics
3.2.2. The Effects of Chamber Drafts
3.2.3. Remarks
4. Conclusions
- The characteristics of top openings affected the energy extraction notably through the means of opening-induced pneumatic damping. A smaller opening ratio induced a larger pneumatic damping and consequently increased the damped natural period of the OWC structure. It was essentially the difference in pneumatic damping that caused the distinction of energy extraction between different opening shapes of the same opening ratio. A larger pneumatic damping can generally extract wave energy in a wider range of wave period.
- Increasing chamber draft increased the mass of water column inside the chamber, and thus increased the inertia effect and natural period of the water column. For larger pneumatic damping, a shallower draft can obtain a better overall energy extraction performance.
- The trends of energy extraction and vortex-induced energy loss were generally correlated because that they were both crucially related to the oscillation of water column. A larger pneumatic damping could induce a larger pressure fluctuation inside the chamber but suppress the surface oscillation of water column, thus the effects of pneumatic damping could affect the vortex-induced energy loss more than the energy extraction. A larger pneumatic damping was preferable for the purpose of increasing energy extraction, whereas, for a smaller pneumatic damping, the vortex-induced energy loss was more important to the energy dissipation.
- With increasing draft, the energy extraction decreased, but the vortex-induced energy loss complementally contributed to the total energy dissipation; the relative importance of vortex-induced energy loss to the energy dissipation increased with increasing draft and made the energy dissipation at the same level to that of a shallower draft.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Comparison of the Extraction Efficiencies Calculated Using Three Methods

References
- Isaacson, M.; Baldwin, J.; Premasiri, S.; Yang, G. Wave interactions with double slotted barriers. Appl. Ocean Res. 1999, 21, 81–91. [Google Scholar] [CrossRef]
- Neelamani, S.; Rajendran, R. Wave interaction with T-type breakwaters. Ocean Eng. 2002, 29, 151–175. [Google Scholar] [CrossRef]
- Brossard, J.; Jarno-Druaux, A.; Marin, F.; Tabet-Aoul, E.H. Fixed absorbing semi-immersed breakwater. Coast. Eng. 2003, 49, 25–41. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, G.; Li, G. Experimental study on the performance of the multiple-layer breakwater. Ocean Eng. 2006, 33, 1829–1839. [Google Scholar] [CrossRef]
- Guo, C.-S.; Zhang, N.-C.; Li, Y.-Y.; Li, J.-B.; Fang, Z.; Cui, C. Experimental study on the performance of twin plate breakwater. China Ocean Eng. 2011, 25, 645–656. [Google Scholar] [CrossRef]
- Teh, H.; Venugopal, V.; Bruce, T. Hydrodynamic Characteristics of a Free-Surface Semicircular Breakwater Exposed to Irregular Waves. J. Waterw. Port Coast. Eng. 2012, 138, 149–163. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.-J. Wave scattering by dual submerged horizontal porous plates: Further results. Ocean Eng. 2014, 81, 158–163. [Google Scholar] [CrossRef]
- Wang, G.; Ren, B.; Wang, Y. Experimental study on hydrodynamic performance of arc plate breakwater. Ocean Eng. 2016, 111, 593–601. [Google Scholar] [CrossRef]
- He, F.; Huang, Z. Hydrodynamic performance of pile-supported OWC-type structures as breakwaters: An experimental study. Ocean Eng. 2014, 88, 618–626. [Google Scholar] [CrossRef]
- Ojima, R.; Suzumura, S.; Goda, Y. Theory and experiments on extractable wave power by an oscillating water-column type breakwater caisson. Coast. Eng. J. 1984, 27, 315–326. [Google Scholar]
- Takahashi, S.; Nakada, H.; Ohneda, H.; Shikamori, M. Wave Power Conversion by a Prototype Wave Power Extracting Caisson in Sakata Port. In Proceedings of the 23rd International Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992; pp. 3440–3453.
- Thiruvenkatasamy, K.; Neelamani, S. On the efficiency of wave energy caissons in array. Appl. Ocean Res. 1997, 19, 61–72. [Google Scholar] [CrossRef]
- Tseng, R.-S.; Wu, R.-H.; Huang, C.-C. Model study of a shoreline wave-power system. Ocean Eng. 2000, 27, 801–821. [Google Scholar] [CrossRef]
- Boccotti, P.; Filianoti, P.; Fiamma, V.; Arena, F. Caisson breakwaters embodying an OWC with a small opening—Part II: A small-scale field experiment. Ocean Eng. 2007, 34, 820–841. [Google Scholar] [CrossRef]
- Boccotti, P. Design of breakwater for conversion of wave energy into electrical energy. Ocean Eng. 2012, 51, 106–118. [Google Scholar] [CrossRef]
- Torre-Enciso, Y.; Ortubia, I.; López de Aguileta, L.; Marqués, J. Mutriku Wave Power Plant: From the Thinking out to the Reality. In Proceedings of the 8th European Wave and Tidal Energy Conference, Uppsala, Sweden, 7–10 September 2009; pp. 319–329.
- Vijayakrishna Rapaka, E.; Natarajan, R.; Neelamani, S. Experimental investigation on the dynamic response of a moored wave energy device under regular sea waves. Ocean Eng. 2004, 31, 725–743. [Google Scholar] [CrossRef]
- Koo, W. Nonlinear time-domain analysis of motion-restrained pneumatic floating breakwater. Ocean Eng. 2009, 36, 723–731. [Google Scholar] [CrossRef]
- He, F.; Huang, Z.H.; Law, A.W.K. Hydrodynamic performance of a rectangular floating breakwater with and without pneumatic chambers: An experimental study. Ocean Eng. 2012, 51, 16–27. [Google Scholar] [CrossRef]
- He, F.; Huang, Z.; Law, A.W.-K. An experimental study of a floating breakwater with asymmetric pneumatic chambers for wave energy extraction. Appl. Energy 2013, 106, 222–231. [Google Scholar] [CrossRef]
- Heath, T.; Whittaker, T.; Boake, C. The Design, Construction and Operation of the LIMPET Wave Energy Converter (Islay, Scotland). In Proceedings of the 4th European Wave Energy Conference, Aalborg, Denmark, 4–6 December 2000; pp. 49–55.
- Falcão, A.D.O. The Shoreline OWC Wave Power Plant at the Azores. In Proceedings of the 4th European Wave Energy Conference, Aalborg, Denmark, 4–6 December 2000; pp. 42–48.
- Martinelli, L.; Pezzutto, P.; Ruol, P. Experimentally based model to size the geometry of a new OWC device, with reference to the Mediterranean Sea wave environment. Energies 2013, 6, 4696–4720. [Google Scholar] [CrossRef]
- López, I.; Pereiras, B.; Castro, F.; Iglesias, G. Optimisation of turbine-induced damping for an OWC wave energy converter using a RANS-VOF numerical model. Appl. Energy 2014, 127, 105–114. [Google Scholar] [CrossRef]
- Ning, D.-Z.; Shi, J.; Zou, Q.-P.; Teng, B. Investigation of hydrodynamic performance of an OWC (oscillating water column) wave energy device using a fully nonlinear HOBEM (higher-order boundary element method). Energy 2015, 83, 177–188. [Google Scholar] [CrossRef]
- López, I.; Pereiras, B.; Castro, F.; Iglesias, G. Holistic performance analysis and turbine-induced damping for an OWC wave energy converter. Renew. Energy 2016, 85, 1155–1163. [Google Scholar] [CrossRef]
- Xu, C.; Huang, Z.; Deng, Z. Experimental and theoretical study of a cylindrical oscillating water column device with a quadratic power take-off model. Appl. Ocean Res. 2016, 57, 19–29. [Google Scholar] [CrossRef]
- Liu, C. A tunable resonant oscillating water column wave energy converter. Ocean Eng. 2016, 116, 82–89. [Google Scholar] [CrossRef]
- Liu, Z.; Hyun, B.; Jin, J.; Hong, K.; Lee, Y. OWC air chamber performance prediction under impulse turbine damping effects. Sci. China Tech. Sci. 2016, 59, 1–10. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, Q.-P.; Greaves, D. Air–water two-phase flow modelling of hydrodynamic performance of an oscillating water column device. Renew. Energy 2012, 41, 159–170. [Google Scholar] [CrossRef]
- López, I.; Castro, A.; Iglesias, G. Hydrodynamic performance of an oscillating water column wave energy converter by means of particle imaging velocimetry. Energy 2015, 83, 89–103. [Google Scholar] [CrossRef]
- Robinson, R.W.; Murray, A. Geometric-Wavefield Influences on the Behavior of an Oscillation Water Column. In Proceedings of the International Symposium on Hydrodynamics in Ocean Engineering, Trondheim, Norway, 24–28 August 1981.
- Evans, D.V.; Porter, R. Hydrodynamic characteristics of an oscillating water column device. Appl. Ocean Res. 1995, 17, 155–164. [Google Scholar] [CrossRef]
- Wang, D.J.; Katory, M.; Li, Y.S. Analytical and experimental investigation on the hydrodynamic performance of onshore wave-power devices. Ocean Eng. 2002, 29, 871–885. [Google Scholar] [CrossRef]
- Gouaud, F.; Rey, V.; Piazzola, J.; Van Hooff, R. Experimental study of the hydrodynamic performance of an onshore wave power device in the presence of an underwater mound. Coast. Eng. 2010, 57, 996–1005. [Google Scholar] [CrossRef]
- He, F.; Huang, Z. Using an oscillating water column structure to reduce wave reflection from a vertical wall. J. Waterw. Port Coast. Eng. 2016, 142, 04015021. [Google Scholar] [CrossRef]
- Ning, D.-Z.; Wang, R.-Q.; Zou, Q.-P.; Teng, B. An experimental investigation of hydrodynamics of a fixed OWC Wave Energy Converter. Appl. Energy 2016, 168, 636–648. [Google Scholar] [CrossRef]
- Goda, Y.; Suzuki, Y. Estimation of Incident and Reflected Waves in Random Wave Experiments. In Proceedings of the 15th International Conference On Coastal Engineering ASCE, Honolulu, HI, USA, 11–17 July 1976; pp. 828–845.
- Sarmento, A.J.N.A. Wave flume experiments on two-dimensional oscillating water column wave energy devices. Exp. Fluids 1992, 12, 286–292. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Stiassnie, M.; Boguslavsky, I.; Naheer, E. Scattering and dissipation of surface wave by a bi-plate structure. Appl. Ocean Res. 1986, 8, 33–37. [Google Scholar] [CrossRef]
- Evans, D. Wave-power absorption by systems of oscillating surface pressure distributions. J. Fluid Mech. 1982, 114, 481–499. [Google Scholar] [CrossRef]
- Sarmento, A.J.; Falcão, A.d.O. Wave generation by an oscillating surface-pressure and its application in wave-energy extraction. J. Fluid Mech. 1985, 150, 467–485. [Google Scholar] [CrossRef]




| Opening Ratio | Slot-Shaped Opening | Circular-Shaped Opening |
|---|---|---|
| 0.625% opening ratio | breadth = 2.5 mm | diameter = 41.0 mm |
| 1.25% opening ratio | breadth = 5.0 mm | diameter = 58.0 mm |
| 1.875% opening ratio | breadth = 7.5 mm | diameter = 71.0 mm |
| Parameters | Range |
|---|---|
| Water depth () | 0.4 m |
| Incident wave height () | 0.035 m |
| Wave periods () | 0.9–1.6 s at 0.1 s interval |
| Wave length () | 1.22–2.84 m |
| Model breadth () | 0.4 m |
| Model draft () | 0.10, 0.15, 0.20 m |
| Relative model breadth (B/L) | 0.141–0.328 |
| Wave steepness (Hi/L) | 0.0123–0.0287 |
| Openings | Cf Range |
|---|---|
| slot-shaped opening (0.625% ratio) | 47,644–56,748 |
| slot-shaped opening (1.25% ratio) | 10,717–12,678 |
| slot-shaped opening (1.875% ratio) | 5832–6810 |
| circular-shaped opening (0.625% ratio) | 67,034–68,426 |
| circular-shaped opening (1.25% ratio) | 17,209–17,701 |
| circular-shaped opening (1.875% ratio) | 7185–7739 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, F.; Li, M.; Huang, Z. An Experimental Study of Pile-Supported OWC-Type Breakwaters: Energy Extraction and Vortex-Induced Energy Loss. Energies 2016, 9, 540. https://doi.org/10.3390/en9070540
He F, Li M, Huang Z. An Experimental Study of Pile-Supported OWC-Type Breakwaters: Energy Extraction and Vortex-Induced Energy Loss. Energies. 2016; 9(7):540. https://doi.org/10.3390/en9070540
Chicago/Turabian StyleHe, Fang, Mingjia Li, and Zhenhua Huang. 2016. "An Experimental Study of Pile-Supported OWC-Type Breakwaters: Energy Extraction and Vortex-Induced Energy Loss" Energies 9, no. 7: 540. https://doi.org/10.3390/en9070540
APA StyleHe, F., Li, M., & Huang, Z. (2016). An Experimental Study of Pile-Supported OWC-Type Breakwaters: Energy Extraction and Vortex-Induced Energy Loss. Energies, 9(7), 540. https://doi.org/10.3390/en9070540