Dynamic Prediction of Power Storage and Delivery by Data-Based Fractional Differential Models of a Lithium Iron Phosphate Battery
Abstract
:1. Introduction
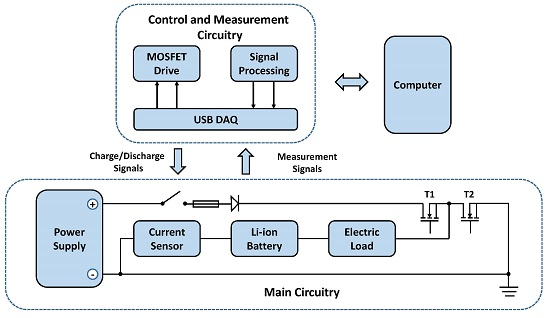
2. Experimental Setup
3. Fractional Differential Systems
3.1. Fractional Differential System Equation
3.2. Direct Least Squares Method
3.3. Least Squares-Based State-Variable Filter Method
3.4. Computation of Digitized Fractional Derivatives
4. Power-Based Modeling
4.1. Experimental Results
4.2. Voltage Model
4.3. Current Model
4.4. Experimental Data-Based Modeling
- Voltage Model
- Current Model
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kanchev, H.; Lu, D.; Colas, F.; Lazarov, V.; Francois, B. Energy Management and Operational Planning of a Microgrid with a PV-Based Active Generator for Smart Grid Applications. IEEE Trans. Ind. Electron. 2011, 58, 4583–4592. [Google Scholar] [CrossRef] [Green Version]
- Chaturvedi, N.A.; Klein, R.; Christensen, J.; Ahmed, J.; Kojic, A. Algorithms for Advanced Battery-Management Systems. IEEE Control Syst. 2010, 30, 49–68. [Google Scholar] [CrossRef]
- Perez, H.; Shahmohammadhamedani, N.; Moura, S. Enhanced Performance of Li-Ion Batteries via Modified Reference Governors and Electrochemical Models. IEEE/ASME Trans. Mechatron. 2015, 20, 1511–1520. [Google Scholar] [CrossRef]
- Guo, X.; Kang, L.; Yao, Y.; Huang, Z.; Li, W. Joint Estimation of the Electric Vehicle Power Battery State of Charge Based on the Least Squares Method and the Kalman Filter Algorithm. Energies 2016, 9, 100. [Google Scholar] [CrossRef]
- Lee, J.; Sung, W.; Choi, J.H. Metamodel for Efficient Estimation of Capacity-Fade Uncertainty in Li-Ion Batteries for Electric Vehicles. Energies 2015, 8, 5538–5554. [Google Scholar] [CrossRef]
- Hua, Y.; Xu, M.; Li, M.; Ma, C.; Zhao, C. Estimation of State of Charge for Two Types of Lithium-Ion Batteries by Nonlinear Predictive Filter for Electric Vehicles. Energies 2015, 8, 3556–3577. [Google Scholar] [CrossRef]
- Zou, Z.; Xu, J.; Mi, C.; Cao, B.; Chen, Z. Evaluation of Model Based State of Charge Estimation Methods for Lithium-Ion Batteries. Energies 2014, 7, 5065–5082. [Google Scholar] [CrossRef]
- Sidhu, A.; Izadian, A.; Anwar, S. Adaptive Nonlinear Model-Based Fault Diagnosis of Li-Ion Batteries. IEEE Trans. Ind. Electron. 2015, 62, 1002–1011. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. Battery Management Systems in Electric and Hybrid Vehicles. Energies 2011, 4, 1840–1857. [Google Scholar] [CrossRef]
- Lee, Y.S.; Cheng, M.W. Intelligent control battery equalization for series connected lithium-ion battery strings. IEEE Trans. Ind. Electron. 2005, 52, 1297–1307. [Google Scholar] [CrossRef]
- Lawder, M.T.; Suthar, B.; Northrop, P.W.C.; De, S.; Hoff, C.M.; Leitermann, O.; Crow, M.L.; Santhanagopalan, S.; Subramanian, V.R. Battery Energy Storage System (BESS) and Battery Management System (BMS) for Grid-Scale Applications. Proc. IEEE 2014, 102, 1014–1030. [Google Scholar] [CrossRef]
- Elsayed, A.T.; Lashway, C.R.; Mohammed, O.A. Advanced Battery Management and Diagnostic System for Smart Grid Infrastructure. IEEE Trans. Smart Grid 2016, 7, 897–905. [Google Scholar] [CrossRef]
- Bruen, T.; Hooper, J.M.; Marco, J.; Gama, M.; Chouchelamane, G.H. Analysis of a Battery Management System (BMS) Control Strategy for Vibration Aged Nickel Manganese Cobalt Oxide (NMC) Lithium-Ion 18650 Battery Cells. Energies 2016, 9, 255. [Google Scholar] [CrossRef]
- Xia, M.; Lai, Q.; Zhong, Y.; Li, C.; Chiang, H.D. Aggregator-Based Interactive Charging Management System for Electric Vehicle Charging. Energies 2016, 9, 159. [Google Scholar] [CrossRef]
- Xia, B.; Wang, H.; Wang, M.; Sun, W.; Xu, Z.; Lai, Y. A New Method for State of Charge Estimation of Lithium-Ion Battery Based on Strong Tracking Cubature Kalman Filter. Energies 2015, 8, 13458–13472. [Google Scholar] [CrossRef]
- Yuan, S.; Wu, H.; Ma, X.; Yin, C. Stability Analysis for Li-Ion Battery Model Parameters and State of Charge Estimation by Measurement Uncertainty Consideration. Energies 2015, 8, 7729–7751. [Google Scholar] [CrossRef]
- Scavongelli, C.; Francesco, F.; Orcioni, S.; Conti, M. Battery management system simulation using SystemC. In Proceedings of the 2015 12th International Workshop on Intelligent Solutions in Embedded Systems (WISES), Ancona, Italy, 29–30 October 2015; pp. 151–156.
- Fang, H.; Zhao, X.; Wang, Y.; Sahinoglu, Z.; Wada, T.; Hara, S.; de Callafon, R.A. Improved adaptive state-of-charge estimation for batteries using a multi-model approach. J. Power Sources 2014, 254, 258–267. [Google Scholar] [CrossRef]
- Moura, S.J.; Chaturvedi, N.A.; Krstic, M. PDE estimation techniques for advanced battery management systems—Part I: SOC estimation. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 559–565.
- Moura, S.J.; Chaturvedi, N.A.; Krstić, M. PDE estimation techniques for advanced battery management systems—Part II: SOH identification. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 566–571.
- Shiau, J.K.; Ma, C.W. Li-Ion Battery Charging with a Buck-Boost Power Converter for a Solar Powered Battery Management System. Energies 2013, 6, 1669–1699. [Google Scholar] [CrossRef]
- Zhao, X.; de Callafon, R.A. Data-based modeling of a lithium iron phosphate battery as an energy storage and delivery system. In Proceedings of the 2013 IEEE American Control Conference (ACC), Washington, DC, USA, 17–19 June 2013; pp. 1908–1913.
- Mastali, M.; Samadani, E.; Farhad, S.; Fraser, R.; Fowler, M. Three-dimensional Multi-Particle Electrochemical Model of LiFePO4 Cells based on a Resistor Network Methodology. Electrochim. Acta 2016, 190, 574–587. [Google Scholar] [CrossRef]
- Abada, S.; Marlair, G.; Lecocq, A.; Petit, M.; Sauvant-Moynot, V.; Huet, F. Safety focused modeling of lithium-ion batteries: A review. J. Power Sources 2016, 306, 178–192. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; Guo, Q.; Ramadass, P.; White, R.E. Review of models for predicting the cycling performance of lithium ion batteries. J. Power Sources 2006, 156, 620–628. [Google Scholar] [CrossRef]
- Zhang, D.; Popov, B.N.; White, R.E. Modeling Lithium Intercalation of a Single Spinel Particle under Potentiodynamic Control. J. Electrochem. Soc. 2000, 147, 831–838. [Google Scholar] [CrossRef]
- Sepasi, S.; Roose, L.R.; Matsuura, M.M. Extended Kalman Filter with a Fuzzy Method for Accurate Battery Pack State of Charge Estimation. Energies 2015, 8, 5217–5233. [Google Scholar] [CrossRef]
- Rahmoun, A.; Biechl, H. Modelling of Li-ion batteries using equivalent circuit diagrams. Available online: http://pe.org.pl/articles/2012/7b/40.pdf (accessed on 21 July 2016).
- He, H.; Xiong, R.; Fan, J. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Gao, L.; Liu, S.; Dougal, R.A. Dynamic lithium-ion battery model for system simulation. IEEE Trans. Compon. Packag. Technol. 2002, 25, 495–505. [Google Scholar]
- Klein, R.; Chaturvedi, N.A.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Electrochemical Model Based Observer Design for a Lithium-Ion Battery. IEEE Trans. Control Syst. Technol. 2013, 21, 289–301. [Google Scholar] [CrossRef]
- Eckert, M.; Kolsch, L.; Hohmann, S. Fractional algebraic identification of the distribution of relaxation times of battery cells. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Janpan, 15–18 December 2015; pp. 2101–2108.
- Malti, R.; Victor, S.; Oustaloup, A.; Garnier, H. An optimal instrumental variable method for continuous-time fractional model identification. IFAC Proc. Vol. 2008, 41, 14379–14384. [Google Scholar] [CrossRef]
- Victor, S.; Malti, R.; Oustaloup, A. Instrumental variable method with optimal fractional differentiation order for continuous-time system identification. IFAC Proc. Vol. 2009, 42, 904–909. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kaczorek, T.; Rogowski, K. Fractional Linear Systems and Electrical Circuits, Studies in Systems, Decision and Control; Springer International Publishing: Cham, Switzerland, 2015; Volume 13. [Google Scholar]
- Podlubny, I. The Laplace Transform Method for Linear Differential Equations of the Fractional Order. 1997. arXiv:funct-an/9710005. arXiv.org e-Print archive. Avaliable online: http://arxiv.org/abs/funct-an/9710005 (accessed on 21 July 2016).
- Kexue, L.; Jigen, P. Laplace transform and fractional differential equations. Appl. Math. Lett. 2011, 24, 2019–2023. [Google Scholar] [CrossRef]
- Ljung, L. System Identification. In Signal Analysis and Prediction; Procházka, A., Uhlíř, J., Rayner, P.W.J., Kingsbury, N.G., Eds.; Birkhäuser Boston: Boston, MA, USA, 1998; pp. 163–173. [Google Scholar]
- Cois, O.; Oustaloup, A.; Poinot, T.; Battaglia, J.L. Fractional state variable filter for system identification by fractional model. In Proceedings of the 2001 European Control Conference (ECC), Porto, Portugal, 4–7 September 2001; pp. 2481–2486.
- Garnier, H.; Wang, L.; Young, P.C. Direct Identification of Continuous-Time Models from Sampled Data: Issues, Basic Solutions and Relevance. In Identification of Continuous-time Models from Sampled Data; Garnier, H., Wang, L., Eds.; Springer: London, UK, 2008; pp. 1–29. [Google Scholar]
- Garnier, H.; Gilson, M.; Bastogne, T.; Mensler, M. The CONTSID Toolbox: A Software Support for Data-based Continuous-time Modelling. In Identification of Continuous-time Models from Sampled Data; Garnier, H., Wang, L., Eds.; Springer: London, UK, 2008; pp. 249–290. [Google Scholar]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. FOMCON: Fractional-order modeling and control toolbox for MATLAB. In Proceedings of the 2011 Proceedings of the 18th International Conference Mixed Design of Integrated Circuits and Systems (MIXDES), Gliwice, Poland, 16–18 June 2011; pp. 684–689.












| Model Fit Ratio | Fractional Model | Integer Model |
|---|---|---|
| Voltage Model | 98.9893% | 81.7168% |
| Current Model | 97.5721% | 97.1509% |
| Power Storage/Delivery Model | 97.9440% | 91.0754% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Zhao, X.; Valibeygi, A.; De Callafon, R.A. Dynamic Prediction of Power Storage and Delivery by Data-Based Fractional Differential Models of a Lithium Iron Phosphate Battery. Energies 2016, 9, 590. https://doi.org/10.3390/en9080590
Jiang Y, Zhao X, Valibeygi A, De Callafon RA. Dynamic Prediction of Power Storage and Delivery by Data-Based Fractional Differential Models of a Lithium Iron Phosphate Battery. Energies. 2016; 9(8):590. https://doi.org/10.3390/en9080590
Chicago/Turabian StyleJiang, Yunfeng, Xin Zhao, Amir Valibeygi, and Raymond A. De Callafon. 2016. "Dynamic Prediction of Power Storage and Delivery by Data-Based Fractional Differential Models of a Lithium Iron Phosphate Battery" Energies 9, no. 8: 590. https://doi.org/10.3390/en9080590
APA StyleJiang, Y., Zhao, X., Valibeygi, A., & De Callafon, R. A. (2016). Dynamic Prediction of Power Storage and Delivery by Data-Based Fractional Differential Models of a Lithium Iron Phosphate Battery. Energies, 9(8), 590. https://doi.org/10.3390/en9080590