Numerical Modeling and Investigation of Fluid-Driven Fracture Propagation in Reservoirs Based on a Modified Fluid-Mechanically Coupled Model in Two-Dimensional Particle Flow Code
Abstract
:1. Introduction
2. Modeling Methodology
2.1. Particle Flow Code
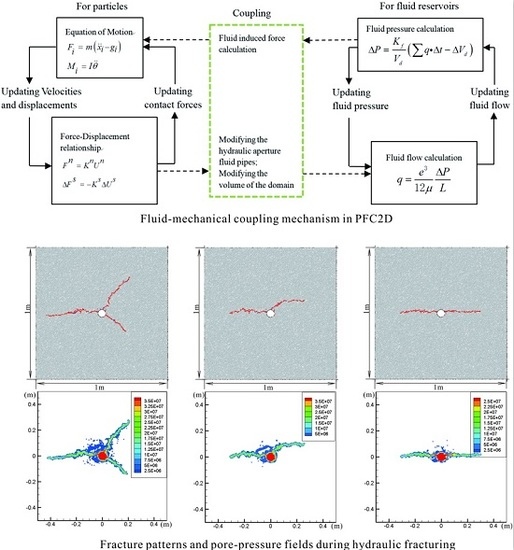
2.2. Fluid-Mechanical Coupling in Two-Dimensional Particle Flow Code
3. Modeling Validation and Some Scenarios
3.1. Model Description and Parameters
3.2. Validation of Hydraulic Fracturing Model
3.3. Modeling Scenarios
4. Modeling Results and Discussion
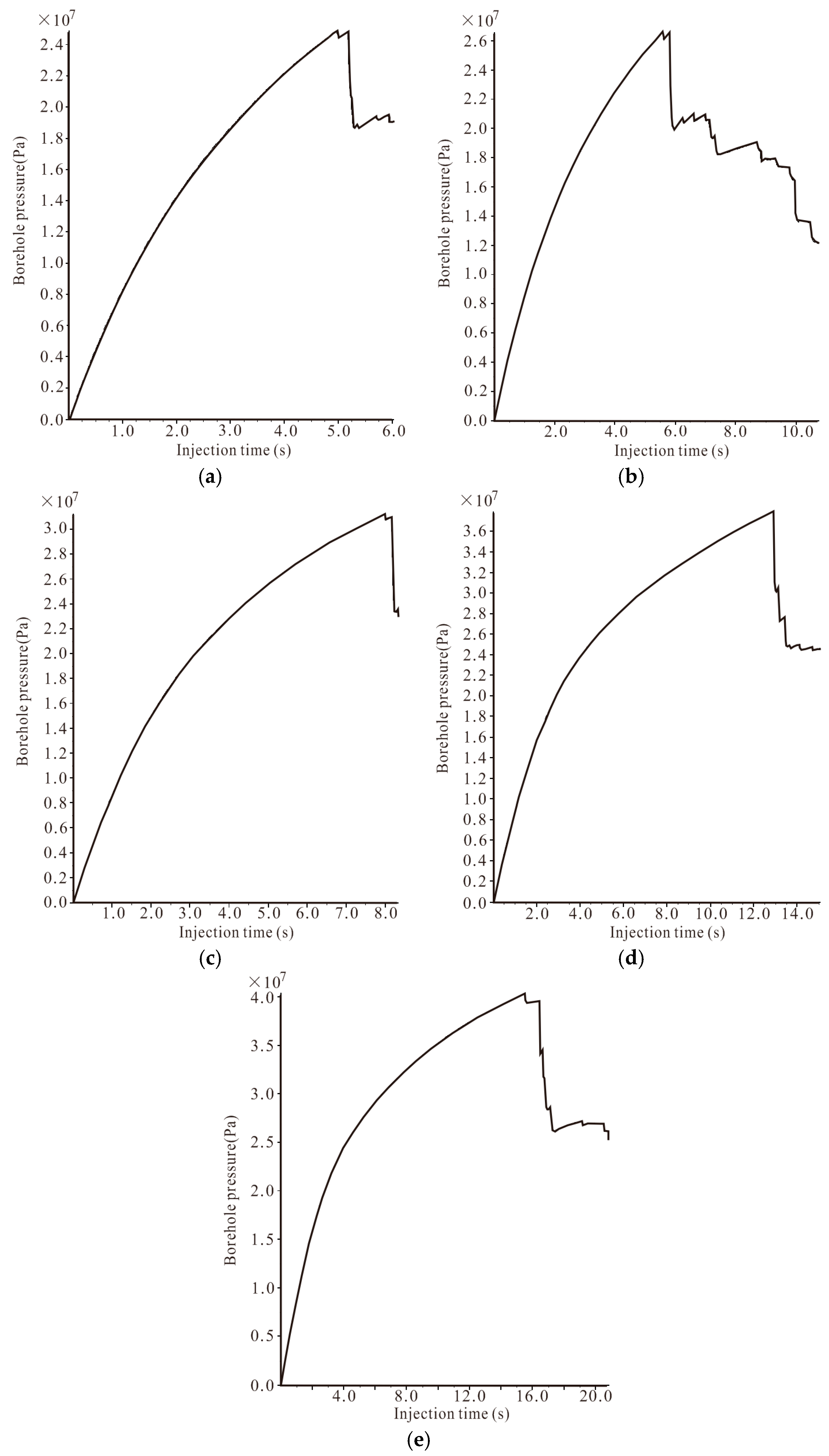
4.1. The Influence of in Situ Stress
4.2. The Influence of the Rate of Fluid Injection
4.3. The Influence of Fluid Viscosity
5. Conclusions
- (1)
- In this study, in all cases, except for the model under hydrostatic stress state (the confining pressures are equal both in x-direction and y-direction), the orientation of hydraulic fractures is parallel to the direction of maximum compressive principle stress. This result verifies that the influence of in situ stress was appropriately expressed in the PFC2D simulation.
- (2)
- Different injection rates in hydraulic fracturing represent different loading scenarios. Similar to in-rock dynamic testing, high injection rates correspond to a larger strain rate loading way. Thus, the breakdown pressure increases as the injection rate increases. When the injection rate is high, the stress in the solid skeleton caused by the borehole pressure cannot adjust instantaneously and local stress concentrations prevail, which leads to a higher breakdown pressure. In this case, complex geometry of fractures can be formed with a predomination of micro-cracks.
- (3)
- Breakdown pressure with the low viscosity fluid was lower than with high viscosity fluid. Fracturing fluid can more easily penetrate through the interconnected domains into the rock from the borehole wall, and so the pore pressure increases around the borehole, which causes the effective stress reduction. Finally, the breakdown pressure with the low viscosity fluid was lower than that with high viscosity fluid. The geometry of the fractures is found to be not very sensitive to the fluid viscosity.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rubin, A.M. Propagation of magma-filled cracks. Ann. Rev. Earth Planet. Sci. 1995, 23, 287–336. [Google Scholar] [CrossRef]
- Spence, D.A.; Turcotte, D.L. Magma-driven propagation of cracks. J. Geophys. Res. Solid Earth 1985, 90, 575–580. [Google Scholar] [CrossRef]
- Adachi, J.; Siebrits, E.; Peirce, A.; Desroches, J. Computer simulation of hydraulic fractures. Int. J. Rock Mech. Min. Sci. 2007, 44, 739–757. [Google Scholar] [CrossRef]
- Vermylen, J.; Zoback, M.D. Hydraulic fracturing, microseismic magnitudes, and stress evolution in the Barnett Shale, Texas, USA. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 24–26 January 2011.
- Fisher, K.; Warpinski, N. Hydraulic fracture height growth: Real data. SPE Prod. Oper. 2012, 27, 8–19. [Google Scholar] [CrossRef]
- De Laguna, W.; Tamura, T.; Weeren, H.O.; Struxness, E.G.; McClain, W.C.; Sexton, R.C. Engineering Development of Hydraulic Fracturing as a Method for Permanent Disposal of Radioactive Wastes; Oak Ridge National Lab.: Oak Ridge, TN, USA, 1968. [Google Scholar]
- Zimmermann, G.; Tischner, T.; Legarth, B.; Huenges, E. Pressure-dependent production efficiency of an enhanced geothermal system (EGS): Stimulation results and implications for hydraulic fracture treatments. Pure Appl. Geophys. 2009, 166, 1089–1106. [Google Scholar] [CrossRef]
- Zimmermann, G.; Moeck, I.; Blöcher, G. Cyclic waterfrac stimulation to develop an enhanced geothermal system (EGS)—Conceptual design and experimental results. Geothermics 2010, 39, 59–69. [Google Scholar] [CrossRef]
- Yokoyama, T.; Sano, O.; Hirata, A.; Ogawa, K.; Nakayama, Y.; Ishida, T.; Mizuta, Y. Development of borehole-jack fracturing technique for in situ stress measurement. Int. J. Rock Mech. Min. Sci. 2014, 67, 9–19. [Google Scholar] [CrossRef]
- King, G.E. Thirty years of gas shale fracturing: What have we learned? In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010.
- Zhang, B.; Li, X.; Zhang, Z.; Wu, Y.; Wu, Y.; Wang, Y. Numerical investigation of influence of in-situ stress ratio, injection rate and fluid viscosity on hydraulic fracture propagation using a distinct element approach. Energies 2016, 9, 140. [Google Scholar] [CrossRef]
- Perkins, T.K.; Kern, L.R. Widths of hydraulic fractures. J. Pet. Technol. 1961, 13, 937–949. [Google Scholar] [CrossRef]
- Nordgren, R.P. Propagation of a vertical hydraulic fracture. Soc. Pet. Eng. J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Khristianovic, S.; Zheltov, Y. Formation of vertical fractures by means of highly viscous fluids. In Proceedings of the 4th World Petroleum Congress, Rome, Italy, 6–15 June 1955; Volume 2, pp. 579–586.
- Geertsma, J.; De Klerk, F. A rapid method of predicting width and extent of hydraulically induced fractures. J. Pet. Technol. 1969, 21, 1571–1581. [Google Scholar] [CrossRef]
- Cleary, M.P. Comprehensive design formulae for hydraulic fracturing. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 21–24 September 1980.
- Barree, R.D. A practical numerical simulator for three-dimensional fracture propagation in heterogeneous media. In Proceedings of the SPE Reservoir Simulation Symposium, San Francisco, CA, USA, 15–18 November 1983.
- Shaffer, R.J.; Thorpe, R.K.; Heuze, F.E.; Ingraffea, A.R. Numerical and physical studies of fluid-driven fracture propagation in jointed rock. In Proceedings of the 25th US Symposium on Rock Mechanics (USRMS), Pittsburgh, PA, USA, 13–15 May 1984.
- Ventura, J.L. Slator Ranch fracture optimization study. J. Pet. Technol. 1985, 37, 1251–1262. [Google Scholar] [CrossRef]
- Meyer, B.R. Three-dimensional hydraulic fracturing simulation on personal computers: Theory and comparison studies. In Proceedings of the SPE Eastern Regional Meeting, Morgantown, WV, USA, 24–27 October 1989.
- Mohaghegh, S.; Balanb, B.; Platon, V.; Ameri, S. Hydraulic fracture design and optimization of gas storage wells. J. Pet. Sci. Eng. 1999, 23, 161–171. [Google Scholar] [CrossRef]
- Dong, C.Y.; De Pater, C.J. Numerical modeling of crack reorientation and link-up. Adv. Eng. Softw. 2002, 33, 577–587. [Google Scholar] [CrossRef]
- Reynolds, M.; Shaw, J.; Pollock, B. Hydraulic fracture design optimization for deep foothills gas wells. J. Can. Pet. Technol. 2004, 43. [Google Scholar] [CrossRef]
- Cundall, P.A. A computer model for simulating progressive, large-scale movements in blocky rock systems. In Proceedings of the International Symposium on Rock Fracture, Nancy, France, 4–6 October 1971.
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Choi, S.O. Interpretation of shut-in pressure in hydrofracturing pressure-time records using numerical modeling. Int. J. Rock Mech. Min. Sci. 2012, 50, 29–37. [Google Scholar] [CrossRef]
- Zangeneh, N.; Eberhardt, E.; Bustin, R.M. Investigation of the influence of stress shadows on multiple hydraulic fractures from adjacent horizontal wells using the distinct element method. In Proceedings of the 21st Canadian Rock Mechanics Symposium, RockEng 2012-Rock Engineering for Natural Resources, Edmonton, AB, Canada, 5–9 May 2012; pp. 445–454.
- Zangeneh, N.; Eberhardt, E.; Bustin, R.M.; Bustin, A. A numerical investigation of fault slip triggered by hydraulic fracturing. In Proceedings of the ISRM International Conference for Effective and Sustainable Hydraulic Fracturing, Brisbane, Australia, 20–22 May 2013.
- Zangeneh, N.; Eberhardt, E.; Bustin, R.M. Investigation of the influence of natural fractures and in situ stress on hydraulic fracture propagation using a distinct-element approach. Can. Geotech. J. 2015, 52, 926–946. [Google Scholar] [CrossRef]
- Hamidi, F.; Mortazavi, A. Three dimensional modeling of hydraulic fracturing process in oil reservoirs. In Proceedings of the 46th US Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012.
- Hamidi, F.; Mortazavi, A. A new three dimensional approach to numerically model hydraulic fracturing process. J. Pet. Sci. Eng. 2014, 124, 451–467. [Google Scholar] [CrossRef]
- PFC2D—Particle Flow Code in 2 Dimensions; Version 4.0; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2008.
- Hazzard, J.F.; Young, R.P.; Oates, S.J. Numerical modeling of seismicity induced by fluid injection in a fractured reservoir. In Proceedings of the 5th North American Rock Mechanics Symposium Mining and Tunnel Innovation and Opportunity, Toronto, ON, Canada, 7–10 July 2002; pp. 1023–1030.
- Al-Busaidi, A.; Hazzard, J.F.; Young, R.P. Distinct element modeling of hydraulically fractured Lac du Bonnet granite. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Zhao, X.; Young, P.R. Numerical modeling of seismicity induced by fluid injection in naturally fractured reservoirs. Geophysics 2011, 76, WC167–WC180. [Google Scholar] [CrossRef]
- Shimizu, H.; Murata, S.; Ishida, T. The distinct element analysis for hydraulic fracturing in hard rock considering fluid viscosity and particle size distribution. Int. J. Rock Mech. Min. Sci. 2011, 48, 712–727. [Google Scholar] [CrossRef]
- Eshiet, K.I.; Sheng, Y.; Ye, J. Microscopic modelling of the hydraulic fracturing process. Environ. Earth Sci. 2013, 68, 1169–1186. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zang, A.; Stephansson, O. Numerical investigation on optimized stimulation of intact and naturally fractured deep geothermal reservoirs using hydro-mechanical coupled discrete particles joints model. Geothermics 2014, 52, 165–184. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zimmermann, G.; Zang, A. Numerical investigation on stress shadowing in fluid injection-induced fracture propagation in naturally fractured geothermal reservoirs. Rock Mech. Rock Eng. 2015, 48, 1439–1454. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zimmermann, G.; Zang, A. Discrete element modeling of cyclic rate fluid injection at multiple locations in naturally fractured reservoirs. Int. J. Rock Mech. Min. Sci. 2015, 74, 15–23. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zimmermann, G.; Zang, A.; Stephansson, O. Discrete element modeling of fluid injection—Induced seismicity and activation of nearby fault 1. Can. Geotech. J. 2015, 52, 1457–1465. [Google Scholar]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Cundall, P. Fluid Formulation for PFC2D; Itasca Consulting Group: Minneapolis, MN, USA, 2000. [Google Scholar]
- Thallak, S.; Rothenburg, L.; Dusseault, M. Simulation of multiple hydraulic fractures in a discrete element system. In Proceedings of the 32nd US Symposium on Rock Mechanics (USRMS), Norman, OK, USA, 10–12 July 1991.
- Chang, M.; Huang, R.C. Observations of hydraulic fracturing in soils through field testing and numerical simulations. Can. Geotech. J. 2016, 53, 343–359. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, W.; Chen, J.; Xiao, X.; Li, Y.; Zhao, X. Simulation of hydraulic fracturing using particle flow method and application in a coal mine. Int. J. Coal Geol. 2014, 121, 1–13. [Google Scholar] [CrossRef]
- Hubbert, M.K.; Willis, D.G. Mechanics of hydraulic fracturing. Petr. Trans. AIME. 1957, 210, 153–168. [Google Scholar]
- Haimson, B.; Fairhurst, C. Initiation and extension of hydraulic fractures in rocks. Soc. Pet. Eng. J. 1967, 7, 310–318. [Google Scholar] [CrossRef]
- Fairhurst, C. Stress estimation in rock: A brief history and review. Int. J. Rock Mech. Min. Sci. 2003, 40, 957–973. [Google Scholar] [CrossRef]
- Haimson, B.C.; Cornet, F.H. ISRM suggested methods for rock stress estimation—Part 3: Hydraulic fracturing (HF) and/or hydraulic testing of pre-existing fractures (HTPF). Int. J. Rock Mech. Min. Sci. 2003, 40, 1011–1020. [Google Scholar] [CrossRef]
- Ishida, T.; Chen, Q.; Mizuta, Y.; Roegiers, J.-C. Influence of fluid viscosity on the hydraulic fracturing mechanism. J. Energy Resour. Technol. 2004, 126, 190–200. [Google Scholar] [CrossRef]
- Chen, Y.; Nagaya, Y.; Ishida, T. Observations of fractures induced by hydraulic fracturing in anisotropic granite. Rock Mech. Rock Eng. 2015, 48, 1455–1461. [Google Scholar] [CrossRef]











| Rock Properties | Notations | Values |
|---|---|---|
| UCS of rock model (MPa) | σc | 46.1 |
| Tensile strength (MPa) | σt | 4.4 |
| Young’s modulus (GPa) | E | 44.2 |
| Poisson’s ratio | ν | 0.20 |
| Porosity (%) | ϕ | 10 |
| Permeability (m2) | κ | 1 × 10−17 |
| Input micro-parameters | - | - |
| Lower bound of particle radius (mm) | Rmin | 4.0 |
| Ratio of upper bound of particle radius to lower bound of particle radius | Rmin/Rmax | 1.5 |
| Particle density (kg/m3) | ρ | 3095 |
| Young’s modulus of the particle (GPa) | Ec | 32.0 |
| Ratio of normal to shear stiffness of the particle | kn/ks | 1.6 |
| Friction coefficient of particle | μ | 0.30 |
| Young’s modulus of the parallel bond (GPa) | 32.0 | |
| Ratio of normal to shear stiffness of the parallel bond | 1.6 | |
| Tensile strength of the parallel bond (MPa) | 12.0 | |
| Cohesion of the parallel bond (MPa) | 30.0 | |
| Friction angle of the parallel bond (°) | ϕ | 45.0 |
| Radius multiplier | 1.0 | |
| Moment contribution factor | β | 0.2 |
| Hydraulic Properties | - | - |
| Initial saturation (%) | St | 100 |
| Initial hydraulic aperture (m) | e0 1 | 2.2 × 10−6 |
| Infinite hydraulic aperture (m) | einf 1 | 2.2 × 10−7 |
| Bulk modulus of the fracturing fluid (GPa) | Kf | 2.0 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Zhang, L.; Braun, A.; Han, Z. Numerical Modeling and Investigation of Fluid-Driven Fracture Propagation in Reservoirs Based on a Modified Fluid-Mechanically Coupled Model in Two-Dimensional Particle Flow Code. Energies 2016, 9, 699. https://doi.org/10.3390/en9090699
Zhou J, Zhang L, Braun A, Han Z. Numerical Modeling and Investigation of Fluid-Driven Fracture Propagation in Reservoirs Based on a Modified Fluid-Mechanically Coupled Model in Two-Dimensional Particle Flow Code. Energies. 2016; 9(9):699. https://doi.org/10.3390/en9090699
Chicago/Turabian StyleZhou, Jian, Luqing Zhang, Anika Braun, and Zhenhua Han. 2016. "Numerical Modeling and Investigation of Fluid-Driven Fracture Propagation in Reservoirs Based on a Modified Fluid-Mechanically Coupled Model in Two-Dimensional Particle Flow Code" Energies 9, no. 9: 699. https://doi.org/10.3390/en9090699
APA StyleZhou, J., Zhang, L., Braun, A., & Han, Z. (2016). Numerical Modeling and Investigation of Fluid-Driven Fracture Propagation in Reservoirs Based on a Modified Fluid-Mechanically Coupled Model in Two-Dimensional Particle Flow Code. Energies, 9(9), 699. https://doi.org/10.3390/en9090699