A Framework to Analyze the Stochastic Harmonics and Resonance of Wind Energy Grid Interconnection
Abstract
:1. Introduction
2. Statistical Modeling
2.1. Maximum Likelihood Estimation
2.2. Chi Square Test
3. Harmonic Current Generation
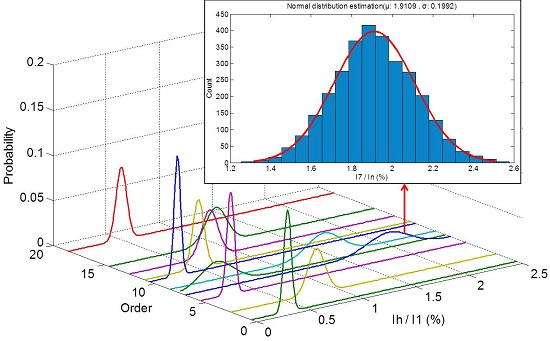
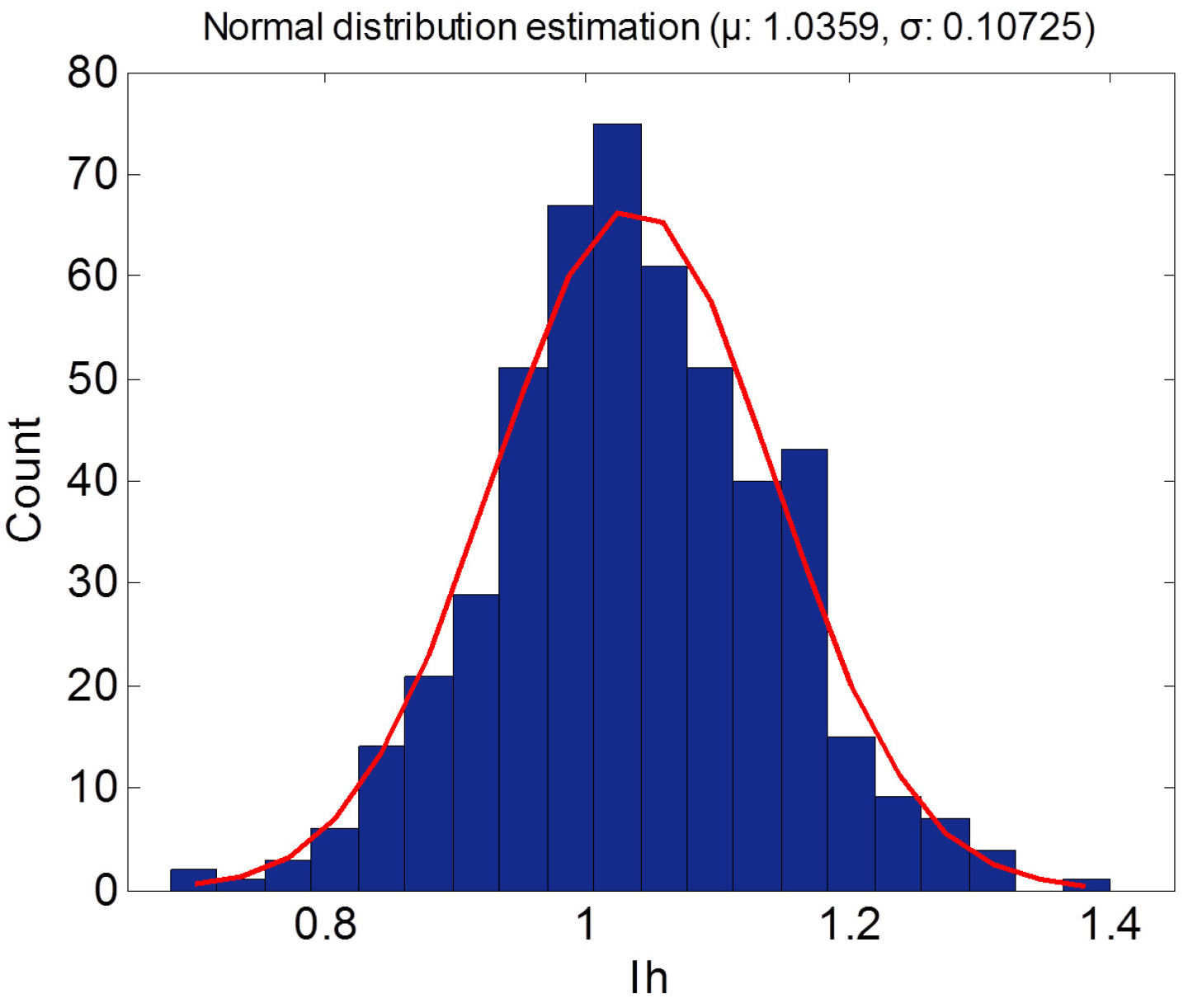
3.1. Determining the Harmonic Current Magnitudes
3.2. Determining the Harmonic Current Phase
3.3. Inverse Fast Fourier Transform Analysis
4. Modeling a Wind Power Plant
4.1. Power Conditioning System Filter Gain and Measurement Location
4.2. The Relationship Between the Wind Turbine Operating Point and the Harmonic Magnitude
4.3. Harmonics of Interest
4.4. Single Wind Turbine Modeling
5. Harmonics Assessment for a 100-MW Offshore Wind Power Plant
5.1. System Configuration
5.2. Simulation Results of a Base Case
5.3. Change of the Standard Deviation
5.4. Change of the Interval Size of the Uniform Distribution of the Phase Angle
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Simulation Parameters
| Parameters | Values | Units |
|---|---|---|
| Grid frequency | 60 | Hz |
| X/R ratio | 4.5 | - |
| Short circuit capacity | 1525 | MVA |
| Parameters | Values | Units |
|---|---|---|
| Transformer capacity | 6.14 | MVA |
| Transformer leakage reactance | 10% | - |
| Filter reactor | 1.0 | mH |
| Filter capacitor | 200 | uF |
| Damping reactor | 0.12 | mH |
| Damping resistor | 0.6 | Ω |
| Converter switching frequency | 1 | kHz |
| Types | Parameters | Values | Units |
|---|---|---|---|
| Type 1 | Resistance | 0.344 | Ω/km |
| Capacitance | 0.117 | uF/km | |
| Inductance | 0.456 | mH/km | |
| Type 2 | Resistance | 0.130 | Ω/km |
| Capacitance | 0.160 | uF/km | |
| Inductance | 0.393 | mH/km | |
| Type 3 | Resistance | 0.064 | Ω/km |
| Capacitance | 0.209 | uF/km | |
| Inductance | 0.350 | mH/km | |
| Submarine cable denoted in Figure 8 | Resistance | 0.056 | Ω/km |
| Capacitance | 0.141 | uF/km | |
| Inductance | 0.401 | mH/km |
References
- Bradt, M.; Badrzadeh, B.; Camm, E.; Mueller, D.; Schoene, J.; Siebert, T.; Smith, T.; Starke, M.; Walling, R. Harmonics and resonance issues in wind power plants. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–8.
- Bollen, M.; Meyer, J.; Amaris, H.; Blanco, A.; Castro, A.; Desmet, J.; Klatt, M.; Kocewiak, L.; Rönnberg, S.; Yang, K. Future work on harmonics—Some expert opinions Part I—Wind and solar power. In Proceedings of the IEEE 16th International Conference on Harmonics and Quality of Power, Bucharest, Romania, 25–28 May 2014; pp. 904–908.
- Negnevitsky, M.; Nguyen, D.; Piekutowski, M. Risk assessment for power system operation planning with high wind power penetration. IEEE Trans. Power Syst. 2015, 30, 1359–1368. [Google Scholar] [CrossRef]
- Zhang, S.; Tseng, K.; Choi, S. Statistical voltage quality assessment method for grids with wind power generation. IET Renew. Power Gener. 2010, 4, 43–54. [Google Scholar] [CrossRef]
- Xie, G.; Zhang, B.; Li, Y.; Mao, C. Harmonic propagation and interaction evaluation between small-scale wind farms and nonlinear loads. Energies 2013, 6, 3297–3322. [Google Scholar] [CrossRef]
- Yang, K.; Bollen, M.; Larsson, E.; Wahlberg, M. Measurement of harmonic emission versus active power from wind turbines. Electr. Power Syst. Res. 2014, 108, 304–314. [Google Scholar] [CrossRef]
- Sainz, L.; Mesas, J.; Teodorescu, R.; Rodriguez, P. Deterministic and stochastic study of wind farm harmonic currents. IEEE Trans. Energy Conver. 2010, 25, 1071–1080. [Google Scholar] [CrossRef] [Green Version]
- Tentzerakis, S.; Papathanassiou, S. An investigation of the harmonic emissions of wind turbines. IEEE Trans. Energy Conver. 2007, 22, 150–158. [Google Scholar] [CrossRef]
- Kocewiak, L. Harmonics in Large Offshore Wind Farms. Ph.D. Thesis, Deptartment of Energy Techonology, Aalborg University, Aalborg, Denmark, 2012. [Google Scholar]
- Baghzouz, Y.; Burch, R.; Capasso, A.; Cavallini, A.; Emanuel, A.; Halpin, M.; Imece, A.; Ludbrook, A.; Montanari, G.; Olejniczak, K.; et al. Time-varying harmonics. I. Characterizing measured data. IEEE Trans. Power Deliv. 1998, 13, 938–944. [Google Scholar] [CrossRef]
- Mau Teng, A.; Milanovic, J. Development of stochastic aggregate harmonic load model based on field measurements. IEEE Trans. Power Deliv. 2007, 22, 323–330. [Google Scholar]
- Foiadelli, F.; Pinato, P.; Zaninelli, D. Statistical model for harmonic propagation studies in electric traction supply systems. In Proceedings of the 11th International Conference on Harmonics and Quality of Power, Lake Placid, NY, USA, 12–15 September 2004; pp. 753–758.
- Kocewiak, L.; Bak, C.; Hjerrild, J. Statistical Analysis and Comparison of Harmonics Measured in Offshore Wind Farms. In Proceedings of the European Wind Energy Association OFFSHORE 2011, Amsterdam, The Netherlands, 29 November–1 December 2011; pp. 1–10.
- Cavallini, A.; Montanari, G. A deterministic/stochastic framework for power system harmonics modeling. IEEE Trans. Power Syst. 1997, 12, 407–415. [Google Scholar] [CrossRef]
- Teng, J.; Leou, R.; Chang, C.; Chan, S. Harmonic current predictors for wind turbines. Energies 2013, 6, 1314–1328. [Google Scholar] [CrossRef]
- Badrzadeh, B.; Gupta, M. Practical experiences and mitigation methods of harmonics in wind power plants. IEEE Trans. Ind. Appl. 2013, 49, 2279–2289. [Google Scholar] [CrossRef]
- Patel, D.; Varma, R.; Seethapathy, R.; Dang, M. Impact of wind turbine generators on network resonance and harmonic distortion. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Calgary, AB, Canada, 2–5 May 2010; pp. 1–6.
- Hasan, K.; Rauma, K.; Rodriguez, P.; Candela, J.; Munoz-Aguilar, R.; Luna, A. An overview of harmonic analysis and resonances of large wind power plant. In Proceedings of the IECON 2011—37th Annual Conference on IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 2467–2474.
- Yang, K.; Bollen, M.; Anders Larsson, E. Aggregation and amplification of wind-turbine harmonic emission in a wind park. IEEE Trans. Power Deliv. 2015, 30, 791–799. [Google Scholar] [CrossRef]
- Huan, C.X.; Tayjasanant, T. Modeling wind power plants in harmonic resonance study—A case study in Thailand. In Proceedings of the International Conference on Information Technology and Electrical Engineering, Yogyakarta, Indonesia, 7–8 October 2013; pp. 385–390.
- Baghzouz, Y.; Burch, R.; Capasso, A.; Cavallini, A.; Emanuel, A.; Halpin, M.; Langella, R.; Montanari, G.; Olejniczak, K.; Ribeiro, P.; et al. Time-varying harmonics: Part II. Harmonic summation and propagation. IEEE Trans. Power Deliv. 2002, 17, 279–285. [Google Scholar] [CrossRef]
- Wind Turbine Generator Systems-Part 21: Measurement and Assessment of Power Quality Characteristics of Grid Connected Wind Turbines; IEC 61400-21; International Electrotechnical Commission: Geneva, Switzerland, 2001.
- Papathanassiou, S.; Papadopoulos, M. Harmonic analysis in a power system with wind generation. IEEE Trans. Power Deliv. 2006, 21, 2006–2016. [Google Scholar] [CrossRef]
- Medeiros, F.; Brasil, D.; Ribeiro, P.F.; Marques, C.; Duque, C. A new approach for harmonic summation using the methodology of IEC 61400-21. In Proceedings of the 14th International Conference on Harmonics and Quality of Power, Bergamo, Italy, 26–29 September 2010; pp. 1–7.
- Yates, R.; Goodman, D. Probability and Stochastic Process, 2nd ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Myung, I. Tutorial on maximum likelihood estimation. J. Math. Psychol. 2003, 47, 90–100. [Google Scholar] [CrossRef]
- Keller, G. Managerial Statistics, 9th ed.; South-Western Cengage Learning: Mason, OH, USA, 2011. [Google Scholar]
- Electromagnetic Compatibility (EMC)-Part 4-7: Testing and Measurement Techniques-General Guide on Harmonics and Interharmonics Measurements and Instrumentation, for Power Supply Systems and Equipment Connected Thereto; IEC 61000-4-7; International Electrotechnical Commission: Geneva, Switzerland, 2002.
- Mendonça, G.; Pereira, H.; Silva, S. Wind farm and system modelling evaluation in harmonic propagation studies. In Proceedings of the International Conference on Renewable Energies and Power Quality, Santiago de Compostela, Spain, 28–30 March 2012; pp. 1–6.
- Dugan, R.; Mcgranaghan, M.; Santoso, S.; Beaty, H. Electrical Power Systems Quality, 3rd ed.; McGraw-Hill: New York, NY, USA, 2012. [Google Scholar]
- IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE Std 519; IEEE Standards Association: New York, NY, USA, 2014.












© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, Y.; Lee, C.; Hur, K.; Kang, Y.C.; Muljadi, E.; Park, S.-H.; Choy, Y.-D.; Yoon, G.-G. A Framework to Analyze the Stochastic Harmonics and Resonance of Wind Energy Grid Interconnection. Energies 2016, 9, 700. https://doi.org/10.3390/en9090700
Cho Y, Lee C, Hur K, Kang YC, Muljadi E, Park S-H, Choy Y-D, Yoon G-G. A Framework to Analyze the Stochastic Harmonics and Resonance of Wind Energy Grid Interconnection. Energies. 2016; 9(9):700. https://doi.org/10.3390/en9090700
Chicago/Turabian StyleCho, Youngho, Choongman Lee, Kyeon Hur, Yong Cheol Kang, Eduard Muljadi, Sang-Ho Park, Young-Do Choy, and Gi-Gab Yoon. 2016. "A Framework to Analyze the Stochastic Harmonics and Resonance of Wind Energy Grid Interconnection" Energies 9, no. 9: 700. https://doi.org/10.3390/en9090700
APA StyleCho, Y., Lee, C., Hur, K., Kang, Y. C., Muljadi, E., Park, S.-H., Choy, Y.-D., & Yoon, G.-G. (2016). A Framework to Analyze the Stochastic Harmonics and Resonance of Wind Energy Grid Interconnection. Energies, 9(9), 700. https://doi.org/10.3390/en9090700