Next Article in Journal
Preparation and Characterization of Extruded Composites Based on Polypropylene and Chitosan Compatibilized with Polypropylene-Graft-Maleic Anhydride
Previous Article in Journal
Au3+/Au0 Supported on Chromium(III) Terephthalate Metal Organic Framework (MIL-101) as an Efficient Heterogeneous Catalystfor Three-Component Coupling Synthesis of Propargylamines
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 10
Issue 2
10.3390/ma10020103
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

First-Principles Study of Vacancies in Ti3SiC2 and Ti3AlC2

by
Hui Wang
1,
Han Han
2,*,
Gen Yin
3,
Chang-Ying Wang
2,
Yu-Yang Hou
1,
Jun Tang
1,
Jian-Xing Dai
2,
Cui-Lan Ren
2,
Wei Zhang
2 and
Ping Huai
2,*
1
School of Physics and Engineering, Henan University of Science and Technology, Luoyang 471003, China
2
Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Shanghai 201800, China
3
Department of Electrical Engineering, University of California, Los Angeles, CA 90095, USA
*
Authors to whom correspondence should be addressed.
Materials 2017, 10(2), 103; https://doi.org/10.3390/ma10020103
Submission received: 23 December 2016 / Revised: 18 January 2017 / Accepted: 23 January 2017 / Published: 25 January 2017
Browse Figures
Versions Notes

Abstract

:
MAX phase materials have attracted increased attention due to their unique combination of ceramic and metallic properties. In this study, the properties of vacancies in Ti3AlC2 and Ti3SiC2, which are two of the most widely studied MAX phases, were investigated using first-principles calculations. Our calculations indicate that the stabilities of vacancies in Ti3SiC2 and Ti3AlC2 differ greatly from those previously reported for Cr2AlC. The order of the formation energies of vacancies is VTi(a) > VTi(b) > VC > VA for both Ti3SiC2 and Ti3AlC2. Although the diffusion barriers for Ti3SiC2 and Ti3AlC2 are similar (~0.95 eV), the properties of their vacancies are significantly different. Our results show that the vacancy–vacancy interaction is attractive in Ti3AlC2 but repulsive in Ti3SiC2. The introduction of VTi and VC vacancies results in the lattice constant c along the [0001] direction increasing for both Ti3SiC2 and Ti3AlC2. In contrast, the lattice constant c decreases significantly when VA are introduced. The different effect of VA on the lattice constants is explained by enhanced interactions of nearby Ti layers.

Graphical Abstract

1. Introduction

The MAX phases form a large family of ternary carbides/nitrides with the general formula Mn+1AXn, where n varies from 1 to 3, M is an early transition metal, A is an A-group element, and X is C or N [1,2,3]. The MAX phases have a unique combination of the properties of ceramics and metals. Similar to metals, they are electrically and thermally conductive, easy to machine, ductile at high temperatures, and exceptionally resistant to damage and thermal shock. Like ceramics, they are elastically rigid, lightweight, and oxidation resistant.
Titanium aluminum carbide (Ti3AlC2) and titanium silicon carbide (Ti3SiC2) are 312 MAX phases. Like most MAX phases, Ti3SiC2 is stiff (Young’s modulus 352 GPa [4], tough (toughness 9 MPa m1/2 [5]), thermally conductive (37 W·m−1·K−1 [6]), and electrically conductive (4.5 × 106 Ω−1·m−1 [7]). The properties of Ti3AlC2 differ slightly from those of Ti3SiC2; for example, it has a lower Young’s modulus (297 GPa) and electrical conductivity (2.9 × 106 Ω−1·m−1). Both materials are readily machinable and tolerant to damage and thermal shock [8]. Ti3SiC2, has two polymorphs, i.e., α and β phases [9]. α-Ti3SiC2 has the same structure as Ti3AlC2, but the Si layer in β-Ti3SiC2 is shifted. β-Ti3SiC2 is a metastable phase, therefore α-Ti3SiC2 has been more widely studied [8,10]. For simplicity, only α-Ti3SiC2 is considered in this work.
On one hand, defects can be unintentionally introduced into Ti3SiC2 and Ti3AlC2 during their synthesis. These materials are refractory ceramics and considerable concentrations of vacancies and impurities are introduced during their multi-component nanolaminate formation. On the other hand, Ti3SiC2 and Ti3AlC2 are potential structural materials for nuclear applications. Defects are created in the lattices of Ti3SiC2 and Ti3AlC2 by irradiation when the incident particles displace atoms from their substitutional positions. As mentioned above, their unique properties make Ti3SiC2 and Ti3AlC2 suitable candidates to be adopted in applications where materials are subject to extreme environments, such as nuclear reactors [11,12,13,14]. Amorphization is an important factor to evaluate the irradiation-resistant of a material. The resistance of amorphization is dependent on the competing effects between the defect production and annihilation rate. Vacancies are the simplest defects in MAX phases. A deeper knowledge of the properties of them in Ti3SiC2 and Ti3AlC2 is crucial for the understanding of the defect production, annihilation process, and phase stability [15,16,17,18,19,20,21,22,23].
A large number of experimental studies [11,12,13,14,24,25,26,27,28,29,30,31] have investigated the properties of Ti3SiC2 and Ti3AlC2 when subjected to irradiation with heavy ions and neutrons. Nappé et al. [11] studied the defect properties of Ti3SiC2 under Au-, Kr-, and Xe-ion irradiation. They observed generation of many defects in the structure and an expansion along the c axis. Liu et al. [12] reported that atomic disorder appeared in Ti3(Si,Al)C2 after Kr-ion irradiation, but the typical layered structure was preserved. Whittle et al. [13] reported that Ti3AlC2 and Ti3SiC2 showed high tolerance to damage from Xe-ion irradiation. Hoffman et al. [14] compared the neutron irradiation tolerances of Ti3SiC2 and Ti3AlC2 with those of SiC and alloy 617. They concluded that Ti3SiC2 and Ti3AlC2 have good irradiation tolerances.
Compared with experimental methods, first-principles calculations have the advantage of enabling the study of materials at the atomic scale. Such calculations have frequently been used to predict the crystal structures and stabilities of MAX phases, and to model their defects and related properties. Wang et al. [15,16,17] systematically studied the effects of vacancies and impurities in the Ti2AlC phase. They calculated the stabilities of Ti2AlC samples with different types of vacancies. Music et al. [18] studied the vacancies in Ti4AlN3, and reported that the introduction of about 25% N vacancies in Ti4AlN3 is energetically favorable. Tan et al. [19] studied vacancy diffusion in Ti2AlC and its impurity phase Ti3AlC. Du et al. [20] studied the C vacancies in Ta4AlC3, and suggested that the introducing of C vacancies decreases the phase stability. Han et al. [21] studied defect stabilities in Cr2AlC under different magnetic orderings.
However, although Ti3SiC2 and Ti3AlC2 are the most extensively studied MAX phases experimentally, theoretical investigations of their defect properties are rare. Medvedev at al. [22] studied the influence of disorder associated with the presence of vacancies on the electronic properties of Ti3SiC2. They found that the presence of C vacancies in Ti3SiC2 caused local perturbations of the electronic structures. Zhao et al. [23] studied the formation energies of different defects in Ti3SiC2 and Ti3AlC2. They found that replacement of Ti by Al in Ti3AlC2 was more energetically favorable than replacement of Ti by Si in Ti3SiC2. These previous theoretical works mainly investigated point defect stabilities. In this work, we focus on the formation, stability, geometry, and diffusion properties of vacancies in Ti3SiC2 and Ti3AlC2.

2. Theoretical Method

Our calculations were performed under the framework of density functional theory as implemented in the Vienna ab initio simulation package (VASP) [32,33]. The projected augmented wave method (PAW) [34] and the generalized gradient approximation (GGA) [35] were used. According to our previous study on MAX phases [19,21], the exchange and correlation energies were calculated using the Perdew−Burke−Ernzerhof (PBE) functional [36]. The wave functions were expanded in a plane-wave basis set with an energy cutoff of 400 eV. The lattice constants and internal freedom of the unit cell were fully optimized until the Hellman-Feynman forces on the atoms were less than 0.01 eV/Å. The effective charge for each atom (charge difference after bonding) is given using Bader charge analysis [37].
In order to simulate a single vacancy structure, we employed a 2 × 2 × 1 supercell, which contains 48 atoms. According to our previous studies on defects properties of MAX phases [19,21,38], the supercell has been proved to be sufficient to reproduce the defect structures. The special k-point sampling integration was used over the Brillouin zone by using the Γ-centered 5 × 5 × 5 for this supercell [39]. All these calculation setups were checked using a larger energy cutoff and k-mesh; the results of total energy and Hellmann-Feynman forces are convergent within 0.01 eV and 0.01 eV/Å, respectively.
To evaluate the energy barrier of an Al-vacancy, the climbing image nudged elastic band method (cNEB) [40,41] was employed to investigate the saddle points and minimum energy paths for vacancy diffusion from the initial state to the final state. In all transition state search calculations performed in this paper, a total of eight images were used (not including the initial and final images of each transition).

3. Results and Discussion

3.1. Properties of Perfect Ti3SiC2 and Ti3AlC2

Ti3SiC2 and Ti3AlC2 are both belonging to 312 phases with the same crystal symmetries, as shown in Figure 1. They are based on layers of hexagonally close-packed Ti and Al/Si layers with C occupying octahedral centers between the Ti layers. The structures of Ti3SiC2 and Ti3AlC2 can also be regarded as alternating stacks of two layers of edge-sharing Ti6C octahedra and a planar close-packed Al/Si layer. The Si/Al atoms are located in the Wyckoff 2b (0, 0, 1/4) positions and the C atoms are in 4f (1/3, 2/3, zC) positions. There are two types of non-equivalent Ti atoms, denoted by Ti(a) and Ti(b), which are located at 4f (1/3, 2/3, zTi) and 2a (0, 0, 0), respectively. The calculated structural parameters for Ti3SiC2 and Ti3AlC2 are listed in Table 1; the experimental results are also listed for comparison. The differences between the calculated and experimental values of the lattice constants are all smaller than 1%, indicating reliable predictions by our PBE calculations.
After optimization of the crystal structures, the mechanical property parameters were calculated. In the Voigt–Reuss–Hill approximation [43,44,45], the bulk modulus B, and the shear modulus G are the average of the values obtained by Voigt and Reuss approximations [43]. The Young’s modulus (E), the Poisson ratio (v), the transverse (Vt), longitudinal (Vl), and average (Va) acoustic wave velocities, and the Debye temperature (ΘD) can be obtained. Experimental values for Ti3AlC2 have not been reported, therefore only the calculated values for Ti3SiC2 are listed in Table 2 and compared with the experimental values. The results show that the calculated values are reasonably consistent with the experimental results.

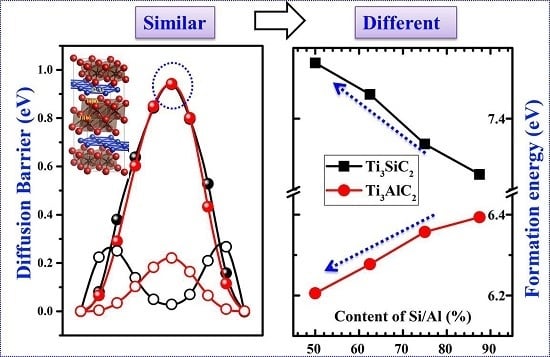
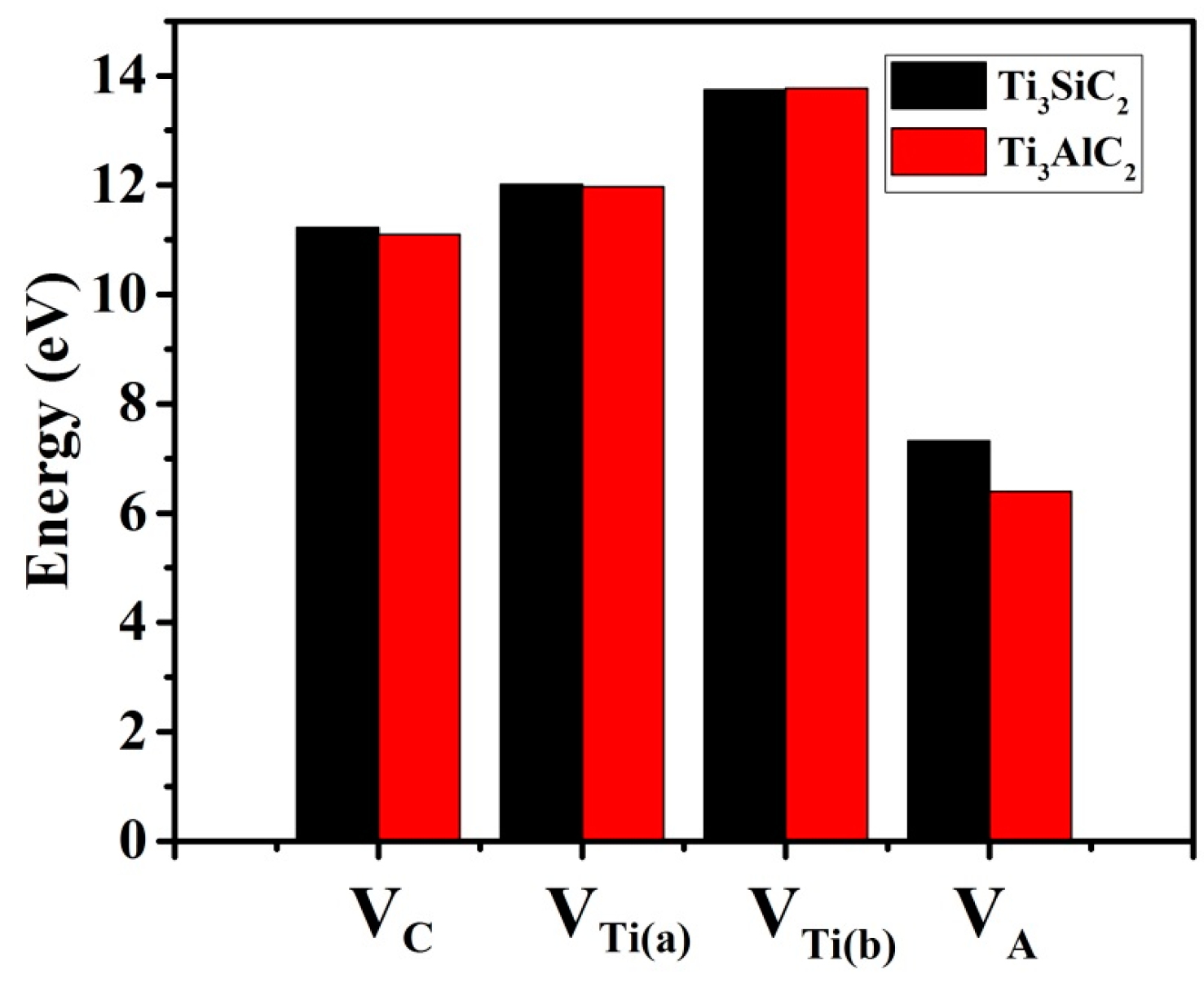
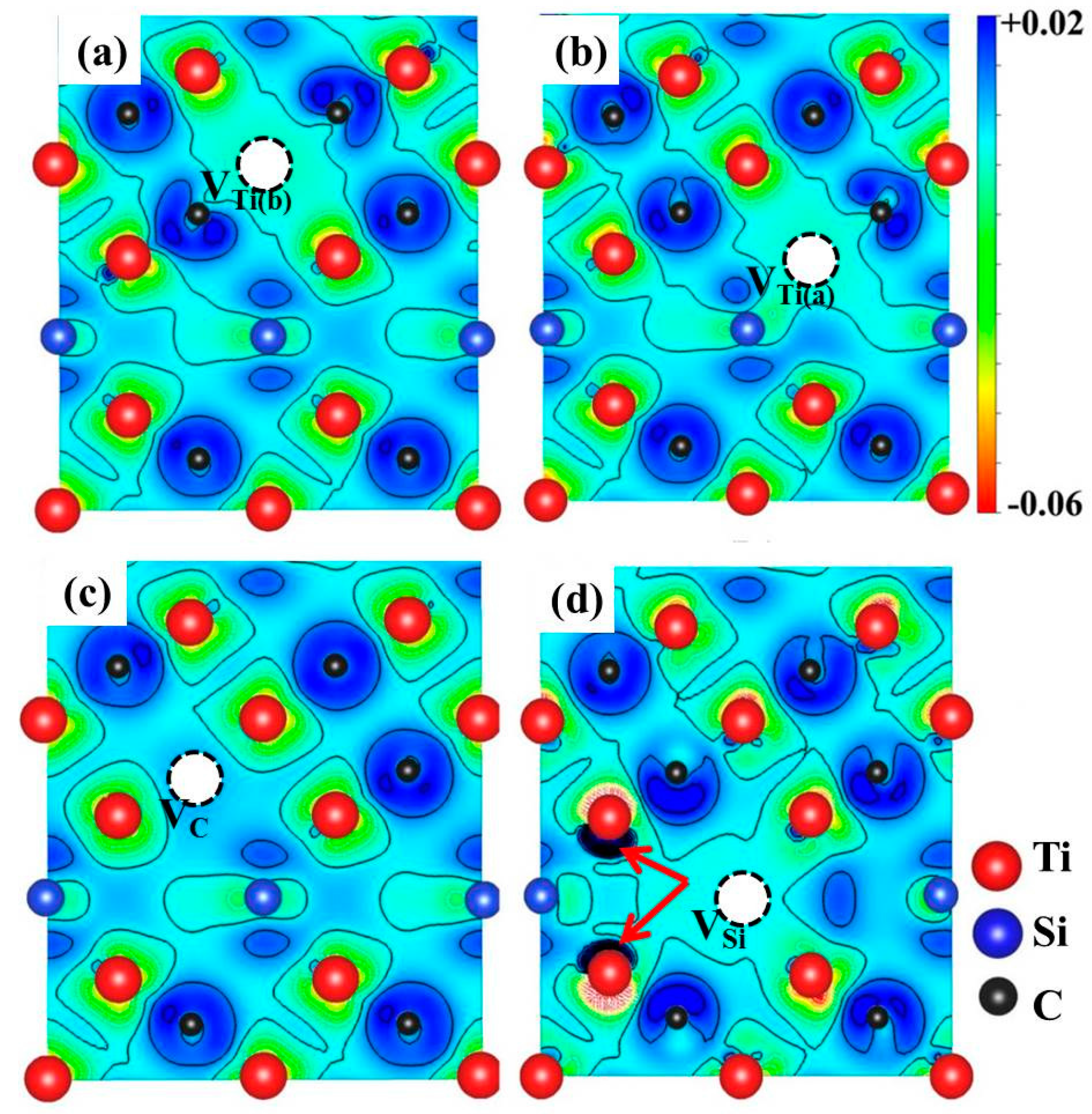
3.2. Formation Energies of Vacancies in Ti3SiC2 and Ti3AlC2

The stabilities of vacancies at different atomic sites in crystals can be evaluated by the vacancy formation energy, which is defined as follows:
Evac(VX) = Etot(VX) − Etot(perf) + μX,
where Evac(VX) is the vacancy formation energy of atom X (X = Ti, Al, C), Etot(VX) is the calculated total energy of a cell with defect X, Etot(perf) is the total energy of a perfect crystal without defects, and μX is the chemical potential of X. Here, μX is chosen as the energy of an isolated X atom for simplicity.
As shown in Figure 2, for both Ti3SiC2 and Ti3AlC2, A-group element vacancies have the lowest formation energies, indicating that they are easily formed. The non-equivalent Ti(a) and Ti(b) atoms have different vacancy formation energies. Figure 1 shows that the Ti(a) atoms are located between Al and C layers. Ti(a) forms covalent bonds with C atoms, but forms weak metallic bonds with Al atoms. In contrast, the Ti(b) atoms are located at the center of [Ti6C] octahedra, and have stronger interactions with surrounding atoms. The vacancy formation energies of the Ti(b) atoms are therefore larger than those of the Ti(a) atoms. The order of the vacancy formation energies is VTi(a) > VTi(b) > VC > VA. These results for Ti3SiC2 and Ti3AlC2 differ greatly from our previously reported results for Cr2AlC, in which the Al vacancies were predicted to have high formation energies and the Cr vacancies were predicted to have low formation energies [21]. The formation energy of VAl is 0.9 eV lower than that of VSi, indicating that an A-group element mono-vacancy is more easily formed in Ti3AlC2.

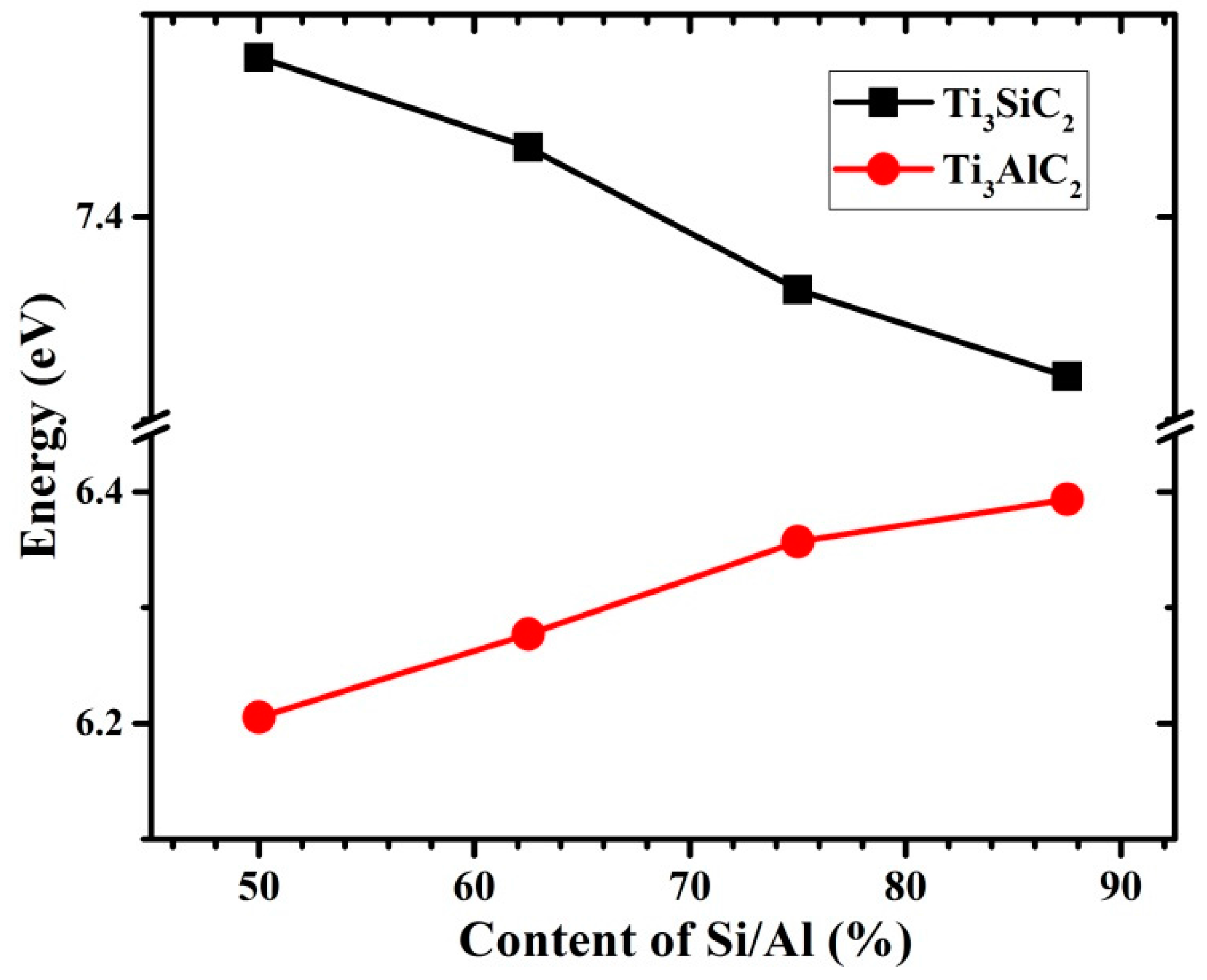
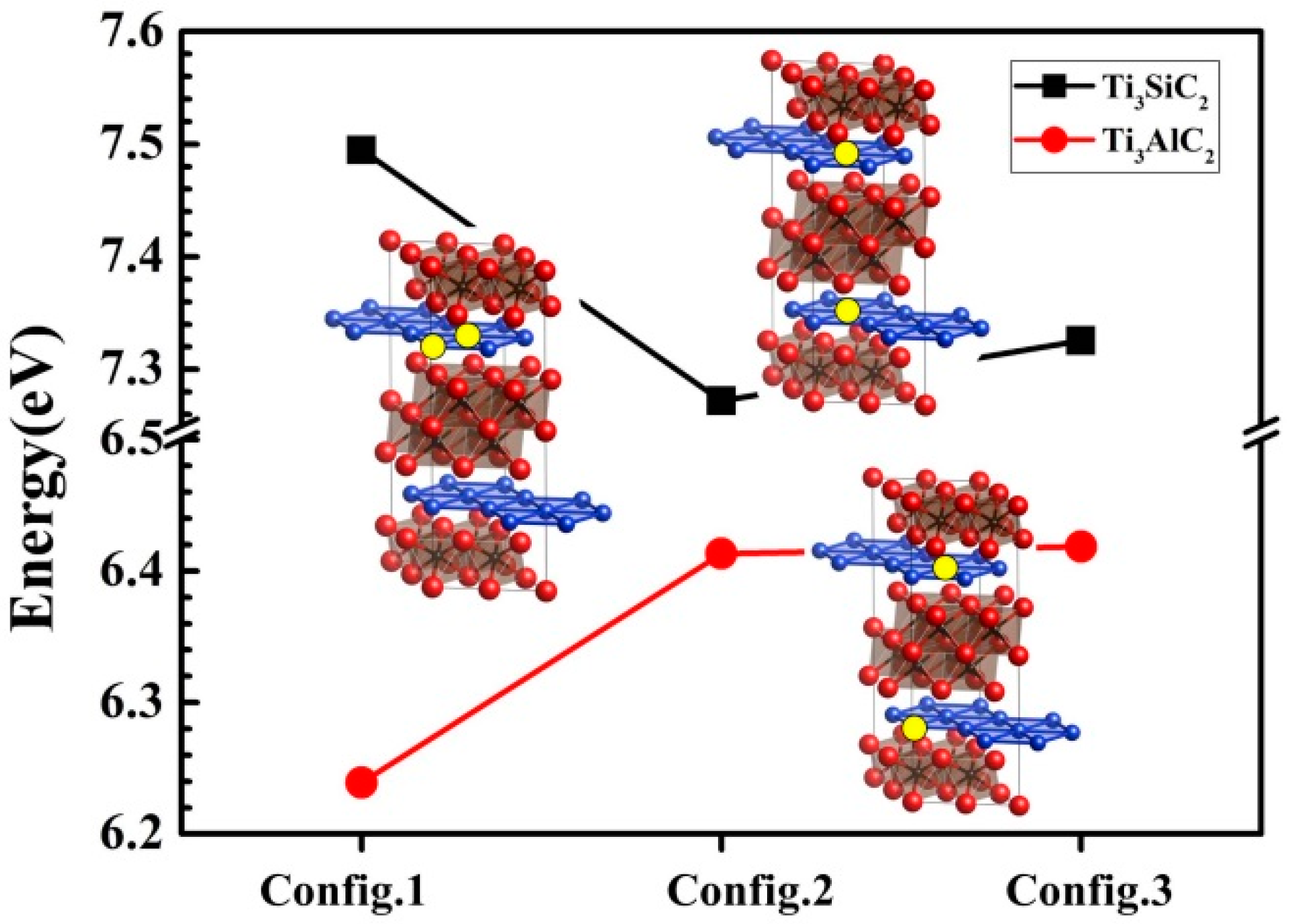
3.3. Vacancy–Vacancy Interactions of VA

These above calculation results indicate that VA vacancies are easily formed when Ti3SiC2 and Ti3AlC2 are in oxidizing, corrosive, and irradiation environments. The effects of VA vacancies on the phase stabilities of Ti3SiC2 and Ti3AlC2 were explored by introducing more vacancies and calculating their vacancy formation energies:
Evac(VX) = Etot(VX) − Etot(perf) + μX,
where n is the concentration of VA vacancies in Ti3SiC2 and Ti3AlC2. Figure 3 shows that for Ti3AlC2 the vacancy formation energy decreases as the number of vacancies increases, indicating that existing vacancies can accelerate the formation of new vacancies. Therefore, decomposition of Ti3AlC2 can be caused by formation of a large number of vacancies in the Al layers. In contrast, the relationship between the VA content and the vacancy formation energy is different for Ti3SiC2; the vacancy formation energy increases significantly with the increasing number of vacancies. This indicates that it is difficult to introduce a new VSi near the original one because of the increased vacancy formation energy. Based on these results, it is reasonable to conclude that the interactions between nearby vacancies in Ti3AlC2 are attractive, but are repulsive in Ti3SiC2. The vacancies therefore tend to disperse in Ti3SiC2 but are accommodated in Ti3AlC2.
In order to verify this conclusion, we calculated and compared the vacancy formation energies for three configurations with two vacancies introduced at different locations. The results are shown in Figure 4. For Ti3SiC2, the configuration with two vacancies located in different layers has a low formation energy. Vacancy pair formation (config.1) increases the energy by ~0.2 eV compared with the other two configurations (config.2 and config.3). In contrast, config.1 is energetically more favorable for Ti3AlC2. Therefore, Ti3SiC2 should be more stable than Ti3AlC2 in a corrosive environment.

3.4. Diffusion of VA Vacancies

It is well known that the Al/Si atoms move in MAX phases predominantly by vacancy-mediated diffusion [19,21]. To ensure that the supercell was sufficiently large to avoid the influence of adjacent cells, a √3 × 2√3 × 1 supercell was used to calculate the diffusion barrier. The obtained values are consistent with those obtained using a 2 × 2 × 1 supercell.
The calculated diffusion barriers (Bdiff) for Si/Al in Ti3SiC2 and Ti3AlC2 are less than 1 eV; these are close to the self-diffusion barriers of many metals, as shown in Table 3. The diffusion of vacancies along the (0001) plane can therefore occur frequently in these two materials. As mentioned previously, the interactions of vacancies in Ti3SiC2 are repulsive, whereas they are attractive in Ti3AlC2. A new vacancy will therefore diffuse away from an existing vacancy in Ti3SiC2; this does not greatly affect the stability of the material. In contrast, the low diffusion barrier indicates that vacancies in Ti3AlC2 tend to be accommodated. A large number of vacancies may therefore lead to decomposition of the material. The diffusion of atoms in the corresponding free-standing Si/Al layers was also studied using the same method shown in Figure 5. The diffusion barriers in free-standing layers (~0.2 eV) are clearly different from those in the Si/Al layers of MAX phases (~0.95 eV). These results indicate that the main contribution to the barrier is the interaction between the Al/Si and Ti layers, rather than the interaction in the Si/Al layers.

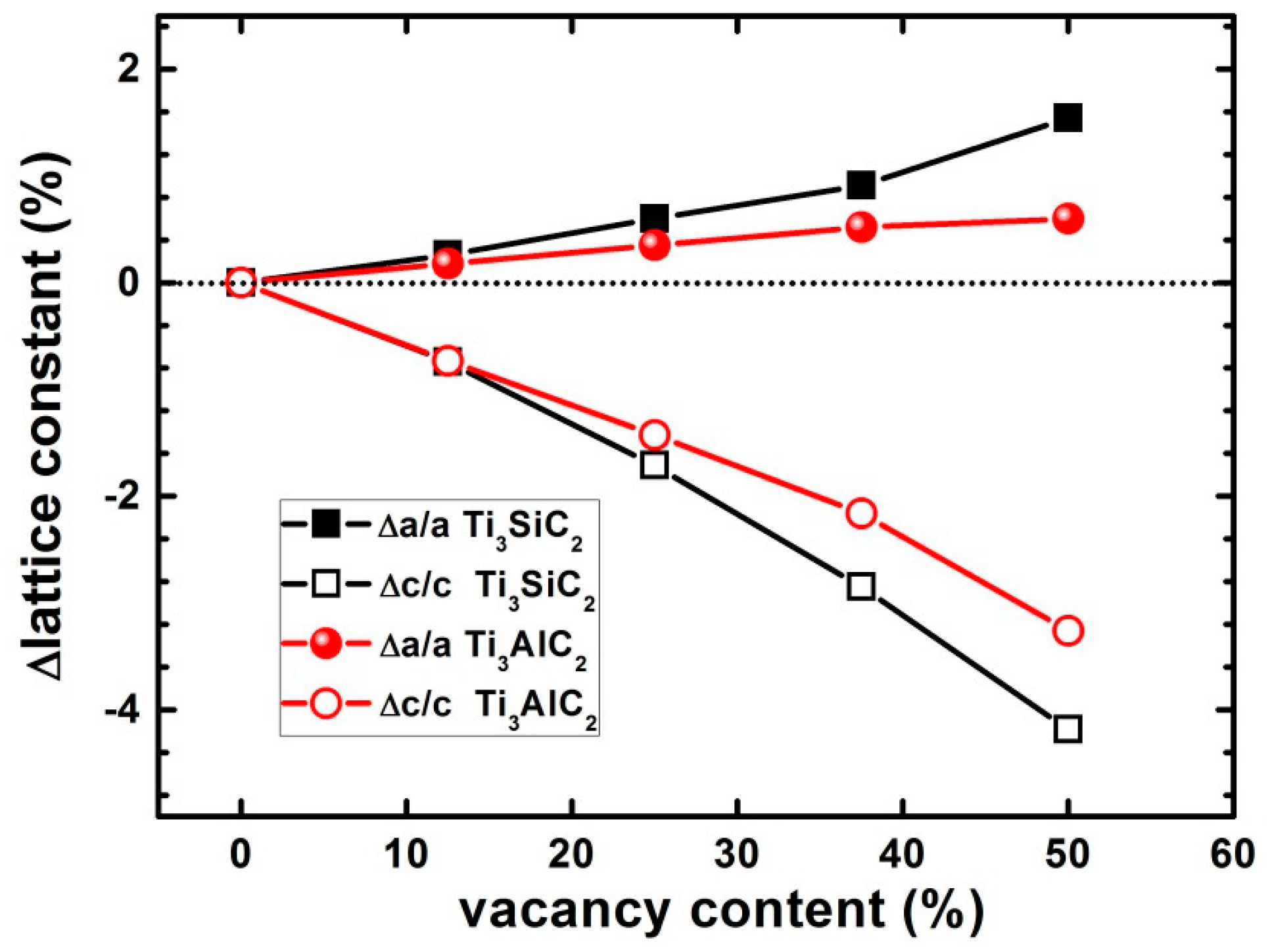
3.5. Effects of Vacancies on Lattice Constants

Defects in a material can lead to changes in the lattice constants. For example, irradiation of nuclear graphite increases the lattice constant c along the [0001] direction, and decreases the lattice constants a and b in the (0001) plane. This is because of the large numbers of interstitial carbons in the graphite interlayers. In this work, the effects of vacancies on the lattice constants of Ti3SiC2 and Ti3AlC2 were investigated. Figure 6 shows the trends in the changes in the lattice constants of Ti3SiC2 and Ti3AlC2 with increasing the number of vacancies in the supercell. The introduction of vacancies increases the lattice constant a and decreases c. The change in a is negligible, but a significant change in c is observed along the [0001] direction. The lattice constant changes for Ti3SiC2 are larger than those for Ti3AlC2.
The lattice constant changes induced by other types of vacancies were also calculated. The results for VTi and VC are the opposite of those for VA. As shown in Figure 7, when VTi and VC vacancies are introduced, the lattice constant a decreases and c increases. The effects of VA and VTi/VC on the lattice constants differ because the interactions between the corresponding atoms and their surrounding atoms are different. In the formation of VTi and VC, the strong Ti–C covalent bond is broken; this is the driving force behind the decrease in the lattice constant in the (0001) plane. In the formation of VA, the bonds between Al/Si atoms and the surrounding atoms are broken. According to our previous analysis of diffusion barriers, the interactions between the Al/Si layer and the two neighboring Ti layers are stronger than the in-plane interactions for VA. The formation of VA therefore contracts the materials along the [0001] direction.
To verify this conclusion, the interactions between atoms in Ti3SiC2 with vacancies were analyzed based on the deformation charge densities. As shown in Figure 8, unlike the electron density distributions in the configurations of VTi and VC, there is an electron accumulation area around the two Ti atoms neighboring VA. The electron accumulation of these two Ti atoms along the [0001] direction indicates that the interaction between them is enhanced by the Si vacancy. The effects of VSi on the lattice constants are therefore different from those of VTi and VC.

4. Conclusions

In this study, the properties of vacancies in Ti3AlC2 and Ti3SiC2, which are two of the most widely studied MAX phases, were investigated using first-principles calculations. Our results show that an A-group element vacancy (VA) has the lowest formation energy, therefore the vacancy–vacancy interactions, the effects of VA on the lattice constants, and the charge redistribution of VA were studied. The formation energy of VAl is 0.9 eV lower than that of VSi, indicating that an A-group element mono-vacancy is more easily formed in Ti3AlC2. Although the diffusion barriers for Ti3SiC2 and Ti3AlC2 are similar (~0.95 eV), the vacancy properties are different. Our results show that the vacancy–vacancy interaction is attractive in Ti3AlC2 but repulsive in Ti3SiC2. The vacancies therefore tend to disperse in Ti3SiC2 but are accommodated in Ti3AlC2. Based on these results, we conclude that Ti3SiC2 should be more stable than Ti3AlC2 in a corrosive environment. The introduction of VTi and VC vacancies causes the lattice constant c along the [0001] direction to increase for both Ti3SiC2 and Ti3AlC2. The changes in the lattice constants caused by VA are opposite. The effect of VA on the lattice constants is explained by enhanced interactions of nearby Ti layers.

Acknowledgments

This work was supported by the Program of International S&T Cooperation (Grant No. 2014DFG60230), National Natural Science Foundation of China (Nos. 11605273, 91326105, U1404111, 11504089, 21501189, 21676291), the Shanghai Municipal Science and Technology Commission (16ZR1443100), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDA02040104). We also thank the Supercomputing Center of Chinese Academy of Sciences (SCCAS) and the Shanghai Supercomputing Center for computer resources.

Author Contributions

Han Han and Ping Huai conceived and designed the whole study. Hui Wang, Han Han, Yu-Yang Hou, and Jun Tang performed DFT calculations. Chang-Ying Wang, Jian-Xing Dai, Cui-Lan Ren, and Wei Zhang analyzed the data. Han Han and Hui Wang co-wrote the manuscript. Ping Huai and Gen Yin helped with correction, modification, and revision of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ghidiu, M.; Lukatskaya, M.R.; Zhao, M.-Q.; Gogotsi, Y.; Barsoum, M.W. Conductive two-dimensional titanium carbide ‘clay’ with high volumetric capacitance. Nature 2014, 516, 78–81. [Google Scholar] [CrossRef] [PubMed]
  2. Naguib, M.; Mochalin, V.N.; Barsoum, M.W.; Gogotsi, Y. 25th Anniversary Article: Mxenes: A New Family of Two-Dimensional Materials. Adv. Mater. 2014, 26, 992–1005. [Google Scholar] [CrossRef] [PubMed]
  3. Radovic, M.; Barsoum, M.W. Max phases: Bridging the gap between metals and ceramics. Am. Ceram. Soc. Bull. 2013, 92, 20–27. [Google Scholar]
  4. Barsoum, M.W.; El-Raghy, T. Synthesis and Characterization of a Remarkable Ceramic: Ti3SiC2. J. Am. Ceram. Soc. 1996, 79, 1953–1956. [Google Scholar] [CrossRef]
  5. Barsoum, M.W. The MN+1AXN Phases: A New Class of Solids: Thermodynamically stable nanolaminates. Prog. Solid State Chem. 2000, 28, 201–281. [Google Scholar] [CrossRef]
  6. Barsoum, M.W.; El-Raghy, T.; Rawn, C.J.; Porter, W.D.; Wang, H.; Payzant, E.A.; Hubbard, C.R. Thermal properties of Ti3SiC2. J. Phys. Chem. Solids 1999, 60, 429–439. [Google Scholar] [CrossRef]
  7. Kisi, E.H.; Crossley, J.A.A.; Myhra, S.; Barsoum, M.W. Structure and Crystal Chemistry of Ti3SiC2. J. Phys. Chem. Solids 1998, 59, 1437–1443. [Google Scholar] [CrossRef]
  8. Zhang, H.; Bao, Y.; Zhou, Y. Current Status in Layered Ternary Carbide Ti3SiC2, a Review. J. Mater. Sci. Technol. 2009, 25, 1–38. [Google Scholar]
  9. Farber, L.; Levin, I.; Barsoum, M.W.; El-Raghy, T.; Tzenov, T. High-resolution transmission electron microscopy of some Tin+1AXn compounds (n = 1, 2; A = Al or Si; X = C or N). J. Appl. Phys. 1999, 86, 2540–2543. [Google Scholar] [CrossRef]
  10. Wang, J.-Y.; Zhou, Y.-C. Polymorphism of Ti3SiC2 ceramic: First-principles investigations. Phys. Rev. B 2004, 69, 144108. [Google Scholar] [CrossRef]
  11. Nappé, J.C.; Monnet, I.; Grosseau, P.; Audubert, F.; Guilhot, B.; Beauvy, M.; Benabdesselam, M.; Thomé, L. Structural changes induced by heavy ion irradiation in titanium silicon carbide. J. Nucl. Mater. 2011, 409, 53–61. [Google Scholar] [CrossRef] [Green Version]
  12. Liu, X.M.; Le Flem, M.; Béchade, J.L.; Monnet, I. Nanoindentation investigation of heavy ion irradiated Ti3(Si,Al)C2. J. Nucl. Mater. 2010, 401, 149–153. [Google Scholar] [CrossRef]
  13. Whittle, K.R.; Blackford, M.G.; Aughterson, R.D.; Moricca, S.; Lumpkin, G.R.; Riley, D.P.; Zaluzec, N.J. Radiation tolerance of Mn+1AXn phases, Ti3AlC2 and Ti3SiC2. Acta Mater. 2010, 58, 4362–4368. [Google Scholar] [CrossRef]
  14. Hoffman, E.N.; Vinson, D.W.; Sindelar, R.L.; Tallman, D.J.; Kohse, G.; Barsoum, M.W. MAX phase carbides and nitrides: Properties for future nuclear power plant in-core applications and neutron transmutation analysis. Nucl. Eng. Des. 2012, 244, 17–24. [Google Scholar] [CrossRef]
  15. Wang, J.; Zhou, Y.; Liao, T.; Zhang, J.; Lin, Z. A first-principles investigation of the phase stability of Ti2AlC with Al vacancies. Scr. Mater. 2008, 58, 227–230. [Google Scholar] [CrossRef]
  16. Liao, T.; Wang, J.; Zhou, Y. Ab initio modeling of the formation and migration of monovacancies in Ti2AlC. Scr. Mater. 2008, 59, 854–857. [Google Scholar] [CrossRef]
  17. Liao, T.; Wang, J.; Zhou, Y. First-principles investigation of intrinsic defects and (N, O) impurity atom stimulated Al vacancy in Ti2AlC. Appl. Phys. Lett. 2008, 93, 261911. [Google Scholar] [CrossRef]
  18. Music, D.; Ahuja, R.; Schneider, J.M. Theoretical study of nitrogen vacancies in Ti4AlN3. Appl. Phys. Lett. 2005, 86, 031911. [Google Scholar] [CrossRef]
  19. Jie, T.; Han, H.; Darshana, W.; Wenguan, L.; Mingwen, Z.; Ping, H. A comparative first-principles study of the electronic, mechanical, defect and acoustic properties of Ti2AlC and Ti3AlC. J. Phys. D Appl. Phys. 2014, 47, 215301. [Google Scholar]
  20. Du, Y.L.; Sun, Z.M.; Hashimoto, H.; Tian, W.B. First-Principles Study of Carbon Vacancy in Ta4AlC3. Mater. Trans. 2008, 49, 1934–1936. [Google Scholar] [CrossRef]
  21. Han, H.; Wickramaratne, D.; Huang, Q.; Dai, J.; Li, T.; Wang, H.; Zhang, W.; Huai, P. A first-principles study on the defective properties of MAX phase Cr2AlC: The magnetic ordering and strong correlation effect. RSC Adv. 2016, 6, 84262–84268. [Google Scholar] [CrossRef]
  22. Medvedeva, N.I.; Novikov, D.L.; Ivanovsky, A.L.; Kuznetsov, M.V.; Freeman, A.J. Electronic properties of Ti3SiC2-based solid solutions. Phys. Rev. B 1998, 58, 16042–16050. [Google Scholar] [CrossRef]
  23. Zhao, S.; Xue, J.; Wang, Y.; Huang, Q. Ab initio study of irradiation tolerance for different Mn+1AXn phases: Ti3SiC2 and Ti3AlC2. J. Appl. Phys. 2014, 115, 023503. [Google Scholar] [CrossRef]
  24. Liu, X.; Le Flem, M.; Béchade, J.-L.; Onimus, F.; Cozzika, T.; Monnet, I. XRD investigation of ion irradiated Ti3Si0.90Al0.10C2. Nucl. Instrum. Methods B 2010, 268, 506–512. [Google Scholar] [CrossRef]
  25. Nappé, J.C.; Monnet, I.; Audubert, F.; Grosseau, P.; Beauvy, M.; Benabdesselam, M. Formation of nanosized hills on Ti3SiC2 oxide layer irradiated with swift heavy ions. Nucl. Instrum. Methods B 2012, 270, 36–43. [Google Scholar] [CrossRef] [Green Version]
  26. Marion, L.F.; Monnet, I. Saturation of irradiation damage in (Ti,Zr)3(Si,Al)C2 compounds. J. Nucl. Mater. 2013, 433, 534–537. [Google Scholar] [CrossRef]
  27. Song, P.; Sun, J.; Wang, Z.; Cui, M.; Shen, T.; Li, Y.; Pang, L.; Zhu, Y.; Huang, Q.; Lü, J. Irradiation resistance properties studies on helium ions irradiated MAX phase Ti3AlC2. Nucl. Instrum. Methods B 2014, 326, 332–336. [Google Scholar] [CrossRef]
  28. Zhang, L.; Qi, Q.; Shi, L.Q.; O’Connor, D.J.; King, B.V.; Kisi, E.H.; Venkatachalam, D.K. Damage tolerance of Ti3SiC2 to high energy iodine irradiation. Appl. Surf. Sci. 2012, 258, 6281–6287. [Google Scholar] [CrossRef]
  29. Huang, Q.; Liu, R.; Lei, G.; Huang, H.; Li, J.; He, S.; Li, D.; Yan, L.; Zhou, J.; Huang, Q. Irradiation resistance of MAX phases Ti3SiC2 and Ti3AlC2: Characterization and comparison. J. Nucl. Mater. 2015, 465, 640–647. [Google Scholar] [CrossRef]
  30. Wang, C.; Yang, T.; Kong, S.; Xiao, J.; Xue, J.; Wang, Q.; Hu, C.; Huang, Q.; Wang, Y. Effects of He irradiation on Ti3AlC2: Damage evolution and behavior of He bubbles. J. Nucl. Mater. 2013, 440, 606–611. [Google Scholar] [CrossRef]
  31. Yang, T.; Wang, C.; Taylor, C.A.; Huang, X.; Huang, Q.; Li, F.; Shen, L.; Zhou, X.; Xue, J.; Yan, S.; et al. The structural transitions of Ti3AlC2 induced by ion irradiation. Acta Mater. 2014, 65, 351–359. [Google Scholar] [CrossRef]
  32. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  33. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  34. Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  35. Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
  36. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  37. Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for bader decomposition of charge density. Comp. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
  38. Huang, Q.; Han, H.; Liu, R.; Lei, G.; Yan, L.; Zhou, J.; Huang, Q. Saturation of ion irradiation effects in MAX phase Cr2AlC. Acta Mater. 2016, 110, 1–7. [Google Scholar] [CrossRef]
  39. Pack, J.D.; Monkhorst, H.J. “Special points for Brillouin-zone integrations”—A reply. Phys. Rev. B 1977, 16, 1748–1749. [Google Scholar] [CrossRef]
  40. Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
  41. Henkelman, G.; Jónsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. [Google Scholar] [CrossRef]
  42. Onodera, A.; Hirano, H.; Yuasa, T.; Gao, N.F.; Miyamoto, Y. Static compression of Ti3SiC2 to 61 GPa. Appl. Phys. Lett. 1999, 74, 3782–3784. [Google Scholar] [CrossRef]
  43. Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A 1952, 65, 349. [Google Scholar] [CrossRef]
  44. Han, H.; Cheng, C.; Xiong, X.-G.; Su, J.; Dai, J.-X.; Wang, H.; Yin, G.; Huai, P. Piezoelectric, Mechanical and Acoustic Properties of KNaNbOF5 from First-Principles Calculations. Materials 2015, 8, 8578–8589. [Google Scholar] [CrossRef]
  45. Han, H.; Yin, G.; Wickramaratne, D. A first-principles investigation of the electronic, elastic, piezoelectric and acoustic properties of K3B6O10Cl. Comput. Mater. Sci. 2013, 69, 81–86. [Google Scholar] [CrossRef]
  46. Pietzka, M.A.; Schuster, J.C. Summary of Constitutional Data on the Aluminum-Carbon-Titanium System. J. Phase Equilib. 1994, 15, 392–400. [Google Scholar] [CrossRef]
  47. Kornblit, L.; Pelleg, J.; Rabinovitch, A. Self-diffusion calculation for fcc metals. Phys. Rev. B 1977, 16, 1164–1167. [Google Scholar] [CrossRef]
  48. García Ortega, M.; Ramos de Debiaggi, S.; Monti, A. Self-Diffusion in FCC Metals: Static and Dynamic Simulations in Aluminium and Nickel. Phys. Stat. Sol. (b) 2002, 234, 506–521. [Google Scholar] [CrossRef]
  49. Atkinson, A.; Taylor, R.I. The diffusion of Ni in the bulk and along dislocations in NiO single crystals. Philos. Mag. A 1979, 39, 581–595. [Google Scholar] [CrossRef]
  50. Debiaggi, S.; Decorte, P.; Monti, A. Diffusion by Vacancy Mechanism in Ni, Al, and Ni3Al: Calculation Based on Many-Body Potentials. Phys. Stat. Sol. (b) 1996, 195, 37–54. [Google Scholar] [CrossRef]
Materials 10 00103 g001 550
Figure 1. Crystal structures of Ti3SiC2 and Ti3AlC2: (a) conventional cell and (b) supercell used to model defect configurations. Red, blue, and black balls represent Ti, Si/Al, and C atoms, respectively. Two types of non-equivalent Ti atoms are identified.
Figure 1. Crystal structures of Ti3SiC2 and Ti3AlC2: (a) conventional cell and (b) supercell used to model defect configurations. Red, blue, and black balls represent Ti, Si/Al, and C atoms, respectively. Two types of non-equivalent Ti atoms are identified.
Materials 10 00103 g001
Materials 10 00103 g002 550
Figure 2. Vacancy formation energies (Evac, eV) of VC, VTi(a), VTi(b), and VA (VSi/VAl) in Ti3SiC2 and Ti3AlC2.
Figure 2. Vacancy formation energies (Evac, eV) of VC, VTi(a), VTi(b), and VA (VSi/VAl) in Ti3SiC2 and Ti3AlC2.
Materials 10 00103 g002
Materials 10 00103 g003 550
Figure 3. Vacancy formation energy (Evac, eV) of VA (VSi/VAl) dependences on A-group element atomic content of Ti3SiC2 and Ti3AlC2.
Figure 3. Vacancy formation energy (Evac, eV) of VA (VSi/VAl) dependences on A-group element atomic content of Ti3SiC2 and Ti3AlC2.
Materials 10 00103 g003
Materials 10 00103 g004 550
Figure 4. Vacancy formation energies (Evac, eV) for VA (VSi/VAl) in three defect configurations of Ti3SiC2 and Ti3AlC2. Yellow circles represent vacancies in Si/Al layers.
Figure 4. Vacancy formation energies (Evac, eV) for VA (VSi/VAl) in three defect configurations of Ti3SiC2 and Ti3AlC2. Yellow circles represent vacancies in Si/Al layers.
Materials 10 00103 g004
Materials 10 00103 g005 550
Figure 5. Calculated energy plots for diffusion of Si/Al vacancy in Ti3SiC2 and Ti3AlC2 using cNEB method. Energy barriers (Bdiff) for Ti3SiC2 and Ti3AlC2 are both 0.95 eV. Empty squares/circles denote energies for Si/Al vacancy diffusion in free-standing Si/Al layers; these indicate a low barrier of ~0.2 eV.
Figure 5. Calculated energy plots for diffusion of Si/Al vacancy in Ti3SiC2 and Ti3AlC2 using cNEB method. Energy barriers (Bdiff) for Ti3SiC2 and Ti3AlC2 are both 0.95 eV. Empty squares/circles denote energies for Si/Al vacancy diffusion in free-standing Si/Al layers; these indicate a low barrier of ~0.2 eV.
Materials 10 00103 g005
Materials 10 00103 g006 550
Figure 6. Changes in lattice constants of Ti3SiC2 and Ti3AlC2 with respect to concentration of Si/Al vacancies. Black and red lines indicate results for Ti3SiC2 and Ti3AlC2, respectively.
Figure 6. Changes in lattice constants of Ti3SiC2 and Ti3AlC2 with respect to concentration of Si/Al vacancies. Black and red lines indicate results for Ti3SiC2 and Ti3AlC2, respectively.
Materials 10 00103 g006
Materials 10 00103 g007 550
Figure 7. Lattice constant changes for Ti3SiC2 (black bar) and Ti3AlC2 (red bar) with respect to three types of on-site vacancies at a concentration of 12.5%. The difference between the results for Ti(a) and Ti(b) is very small, therefore the values are averaged as VTi for clarity.
Figure 7. Lattice constant changes for Ti3SiC2 (black bar) and Ti3AlC2 (red bar) with respect to three types of on-site vacancies at a concentration of 12.5%. The difference between the results for Ti(a) and Ti(b) is very small, therefore the values are averaged as VTi for clarity.
Materials 10 00103 g007
Materials 10 00103 g008 550
Figure 8. Deformation charge density (difference between crystal charge and atomic charge distribution) on (1, 1, 2 − , 0) plane of Ti3SiC2 with (a) VTi(b); (b) VTi(a); (c) VC; and (d) VSi vacancies. Contours added with intervals of 0.005 electrons/Bohr3. Red and blue isosurfaces correspond to electron-depleted and electron-enriched zones, respectively. White circles indicate positions of vacancies. Electron accumulation areas around two Ti atoms neighboring VA in (d) are indicated by red arrows.
Figure 8. Deformation charge density (difference between crystal charge and atomic charge distribution) on (1, 1, 2 − , 0) plane of Ti3SiC2 with (a) VTi(b); (b) VTi(a); (c) VC; and (d) VSi vacancies. Contours added with intervals of 0.005 electrons/Bohr3. Red and blue isosurfaces correspond to electron-depleted and electron-enriched zones, respectively. White circles indicate positions of vacancies. Electron accumulation areas around two Ti atoms neighboring VA in (d) are indicated by red arrows.
Materials 10 00103 g008
Table
Table 1. Calculated (Cal.) lattice constants a and c (Å), c/a ratio, and internal structural parameters zTi and zC for Ti3SiC2 and Ti3AlC2. Experimental values (Exp.) are also listed.
Table 1. Calculated (Cal.) lattice constants a and c (Å), c/a ratio, and internal structural parameters zTi and zC for Ti3SiC2 and Ti3AlC2. Experimental values (Exp.) are also listed.
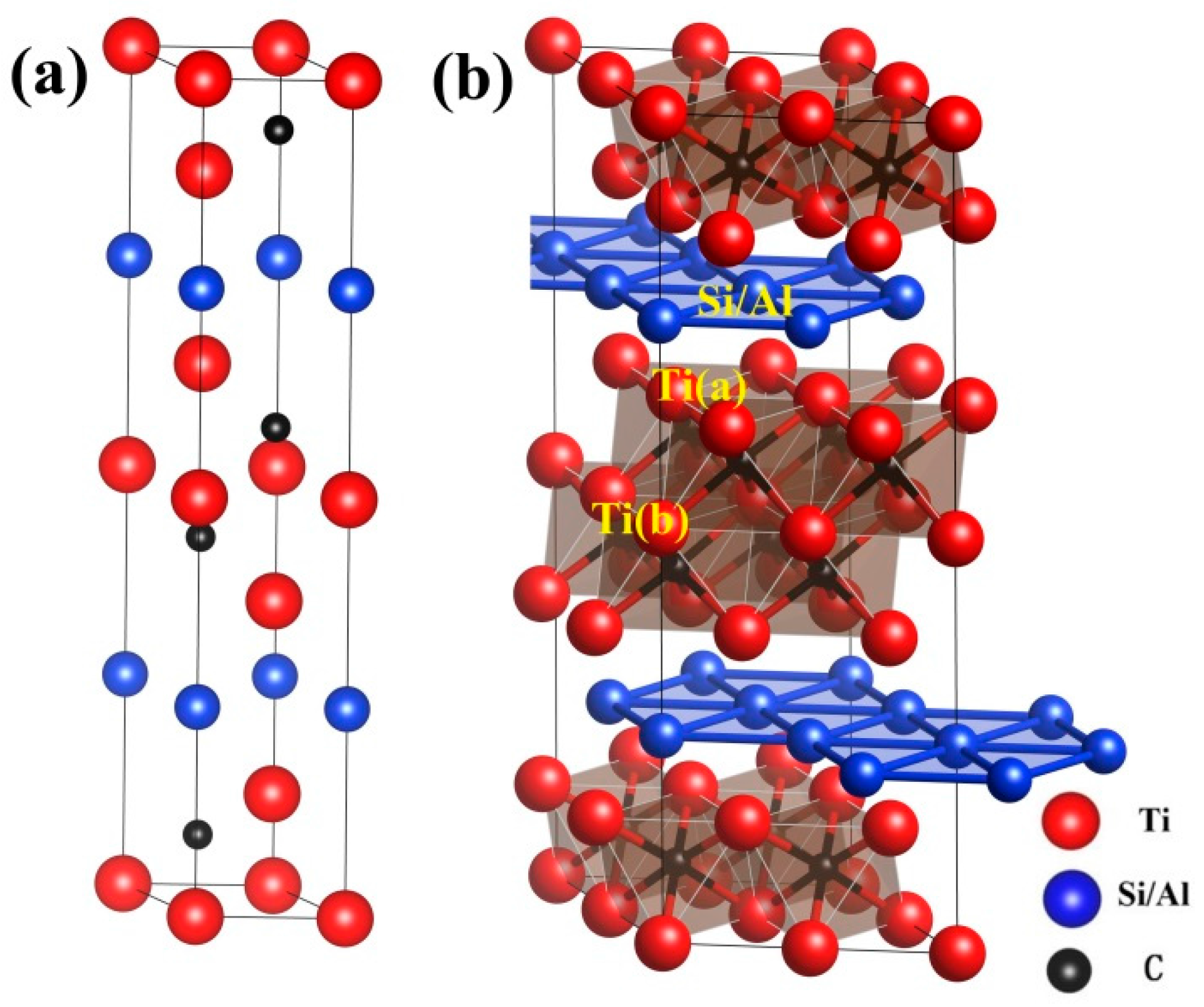
MaterialMethoda (Å)c (Å)c/azTizC
Ti3SiC2Cal.3.07517.7345.7670.1350.572
Exp. [42]3.0717.675.760.1350.568
Ti3AlC2Cal.3.08218.6420.6480.1270.569
Exp. [6]3.07518.5780.6410.1280.564
Table
Table 2. Calculated elastic properties of Ti3SiC2, including the bulk modulus B, the shear modulus G, the Young’s modulus E, the Poisson ration v, the acoustic wave velocities (Vl, Vt, Va), and the Debye temperature ΘD. The experimental values [46] are also listed for comparison.
Table 2. Calculated elastic properties of Ti3SiC2, including the bulk modulus B, the shear modulus G, the Young’s modulus E, the Poisson ration v, the acoustic wave velocities (Vl, Vt, Va), and the Debye temperature ΘD. The experimental values [46] are also listed for comparison.
PropertiesB (GPa)G (GPa)E (GPa)v
Cal.200.3132.3325.20.23
Exp.1871423390.2
PropertiesVl (Km/s)Vt (Km/s)Va (Km/s)ΘD (K)
Cal.9.175.436.0780
Exp.9.145.616.2804
Table
Table 3. Diffusion barriers for VA in Ti3SiC2 and Ti3AlC2. Self-diffusion barriers of Al, C, and Ni are also listed for comparison.
Table 3. Diffusion barriers for VA in Ti3SiC2 and Ti3AlC2. Self-diffusion barriers of Al, C, and Ni are also listed for comparison.
MaterialTi3SiC2/Ti3AlCCuAlNi
Barrier (eV)0.950.92 [47]0.61 [48]1.4–1.8 [49,50]

Share and Cite

MDPI and ACS Style

Wang, H.; Han, H.; Yin, G.; Wang, C.-Y.; Hou, Y.-Y.; Tang, J.; Dai, J.-X.; Ren, C.-L.; Zhang, W.; Huai, P. First-Principles Study of Vacancies in Ti3SiC2 and Ti3AlC2. Materials 2017, 10, 103. https://doi.org/10.3390/ma10020103

AMA Style

Wang H, Han H, Yin G, Wang C-Y, Hou Y-Y, Tang J, Dai J-X, Ren C-L, Zhang W, Huai P. First-Principles Study of Vacancies in Ti3SiC2 and Ti3AlC2. Materials. 2017; 10(2):103. https://doi.org/10.3390/ma10020103

Chicago/Turabian Style

Wang, Hui, Han Han, Gen Yin, Chang-Ying Wang, Yu-Yang Hou, Jun Tang, Jian-Xing Dai, Cui-Lan Ren, Wei Zhang, and Ping Huai. 2017. "First-Principles Study of Vacancies in Ti3SiC2 and Ti3AlC2" Materials 10, no. 2: 103. https://doi.org/10.3390/ma10020103

APA Style

Wang, H., Han, H., Yin, G., Wang, C. -Y., Hou, Y. -Y., Tang, J., Dai, J. -X., Ren, C. -L., Zhang, W., & Huai, P. (2017). First-Principles Study of Vacancies in Ti3SiC2 and Ti3AlC2. Materials, 10(2), 103. https://doi.org/10.3390/ma10020103

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop