Mesoscale Fracture Analysis of Multiphase Cementitious Composites Using Peridynamics
Abstract
:1. Introduction
1.1. Mesoscale Modeling
1.2. Analysis Methods Available for Fracture Modeling
1.3. Summary of Work Presented in the Remaining Sections
1.4. Novel Aspects of the Research
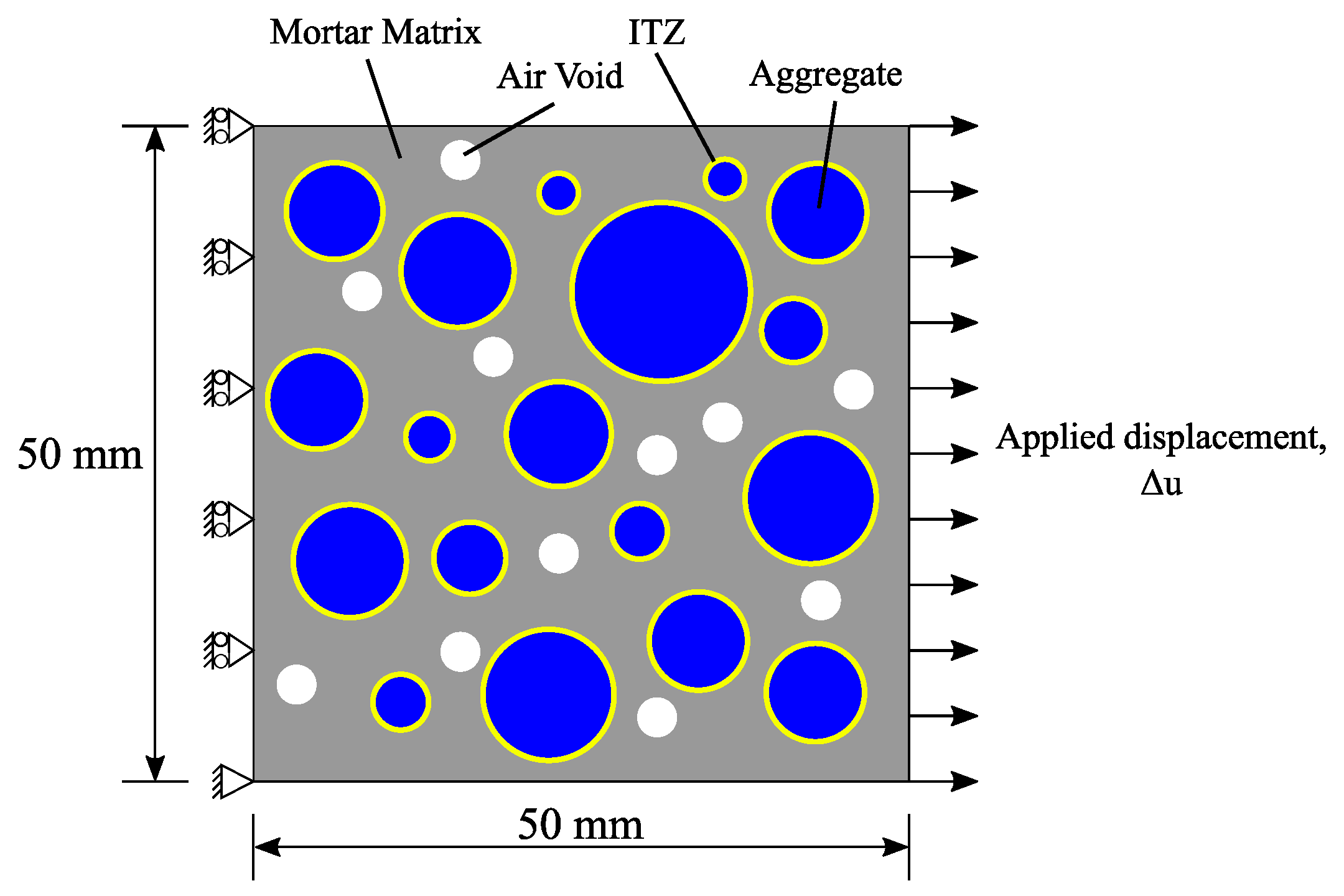
2. Proposed Mesoscale Concrete Model
2.1. Mesoscopic Constituent Materials
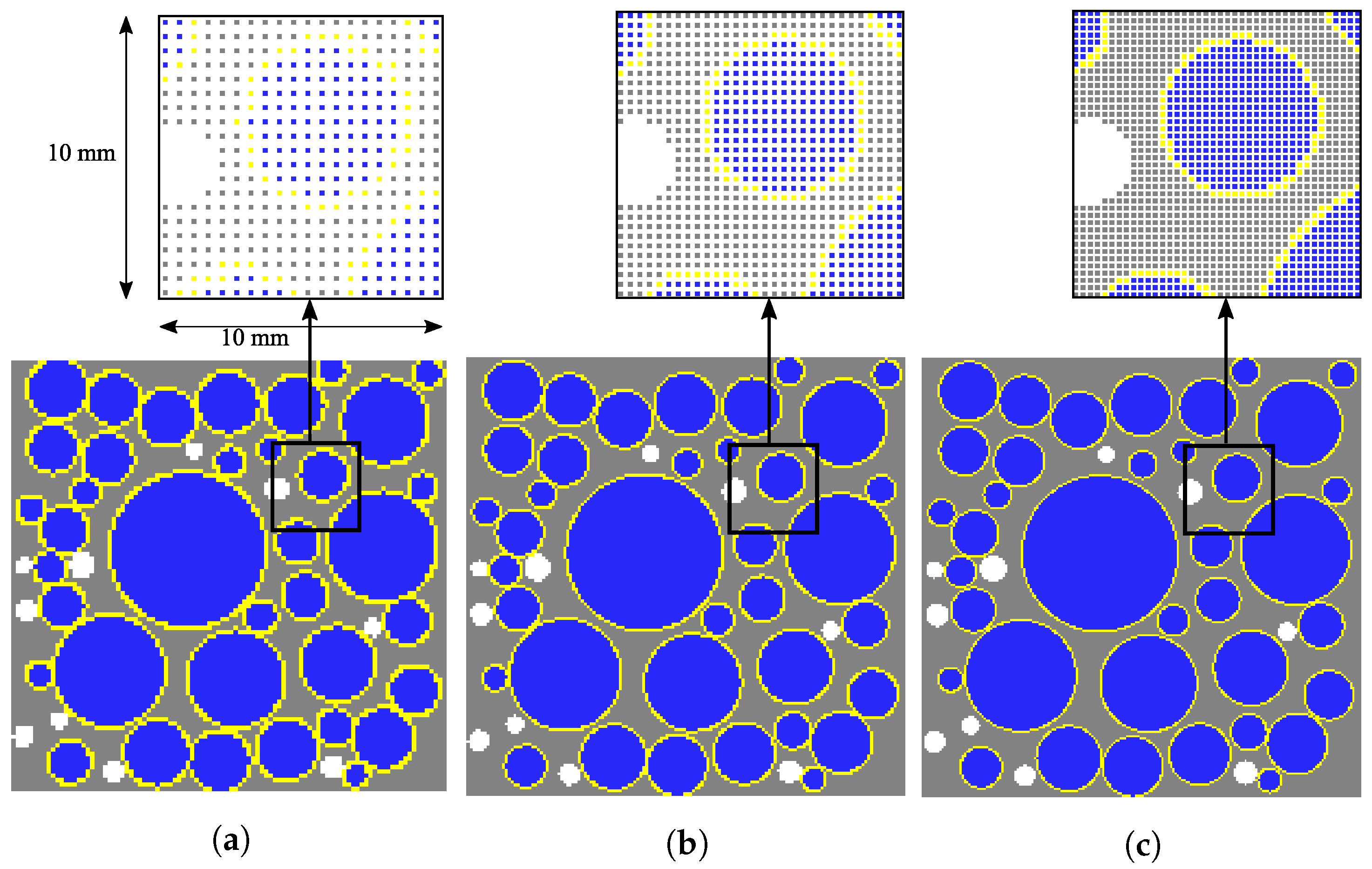
2.2. Distribution of Constituent Materials into Multi-Phases
- Determine the total area of the coarse aggregate, , with the aggregate size between and , using Equation (1).
- Generate a random number, which defines the aggregate diameter, d, within the segment . The aggregate diameter, d, is obtained by , where is a variable selected from a uniform distribution of numbers between zero and one by using the “” command in FORTRAN.
- Generate two sets of random numbers to define the location of current aggregate. Two numbers are selected from a uniform distribution, with equal probability for all values, of the random variables between zero and one.
- Check the placement of aggregate: Two conditions must be met to position the aggregate. First, the aggregate must be located within the analytical specimen boundary with a minimum clearance distance from the specimen boundary, . There must be no overlapping area between current aggregate and previously-placed aggregate, if any. A minimum distance of between the two aggregates must be considered. These two conditions assure that the current aggregate is reasonably surrounded by the cementitious matrix. For the coarse aggregate distribution, and are used for and , respectively. d is the diameter of the current aggregate being positioned, and is the diameter of previously-positioned aggregate.
- Repeat the random placement in Steps 2–3 until the conditions in Step 4 are satisfied.
- Determine the total area of generated aggregates, , in this segment, and find the remaining aggregate area by subtracting from the total aggregate area, , determined in Step 1.
- Repeat Steps 2–6 until the remaining area is no longer available to generate additional aggregate in the grading segment.
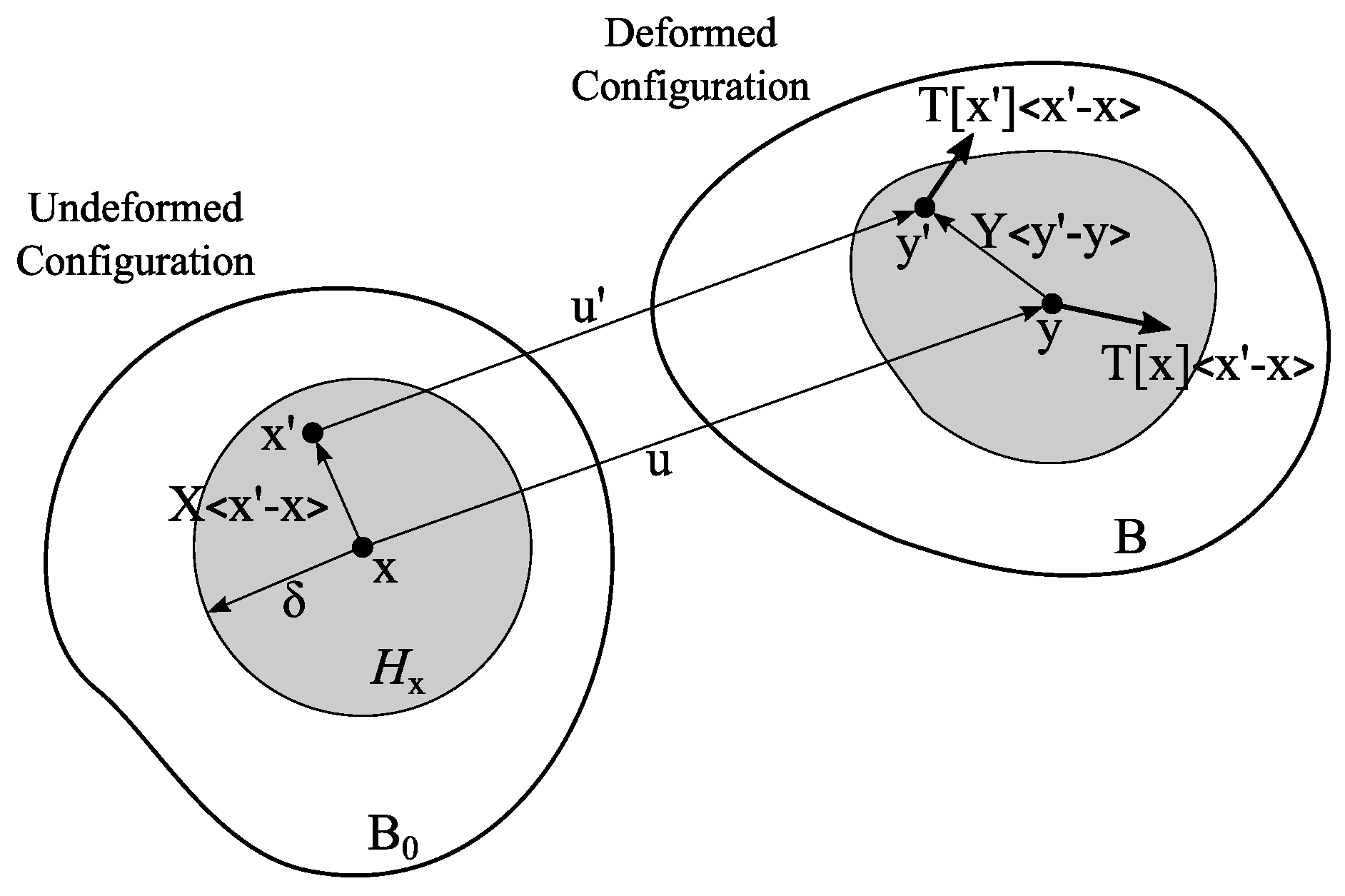
2.3. Formulation of the Proposed Analysis Framework
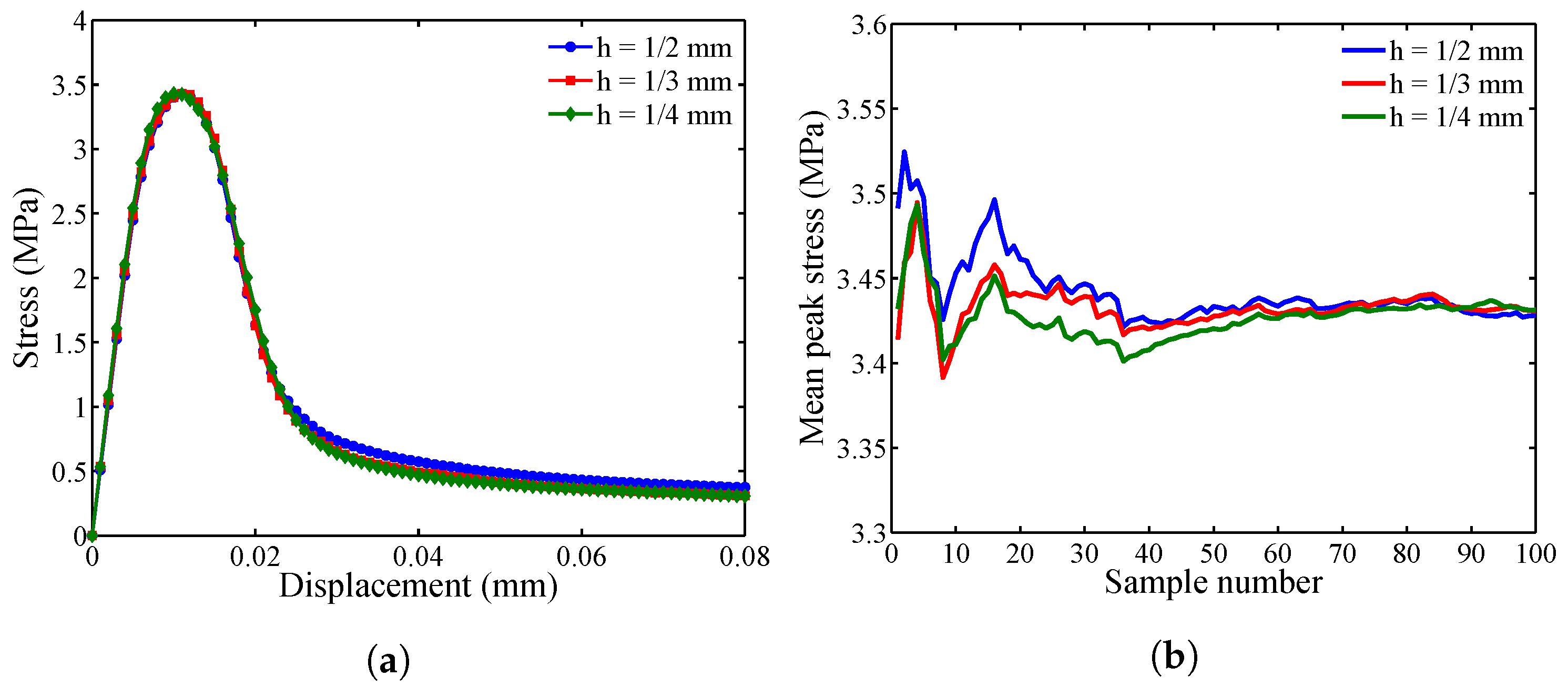
2.4. Determination of Statistically-Significant Sample Size
3. Analysis of a Concrete Specimen in Tension
3.1. Description of a Numerical Model
3.2. Material Models
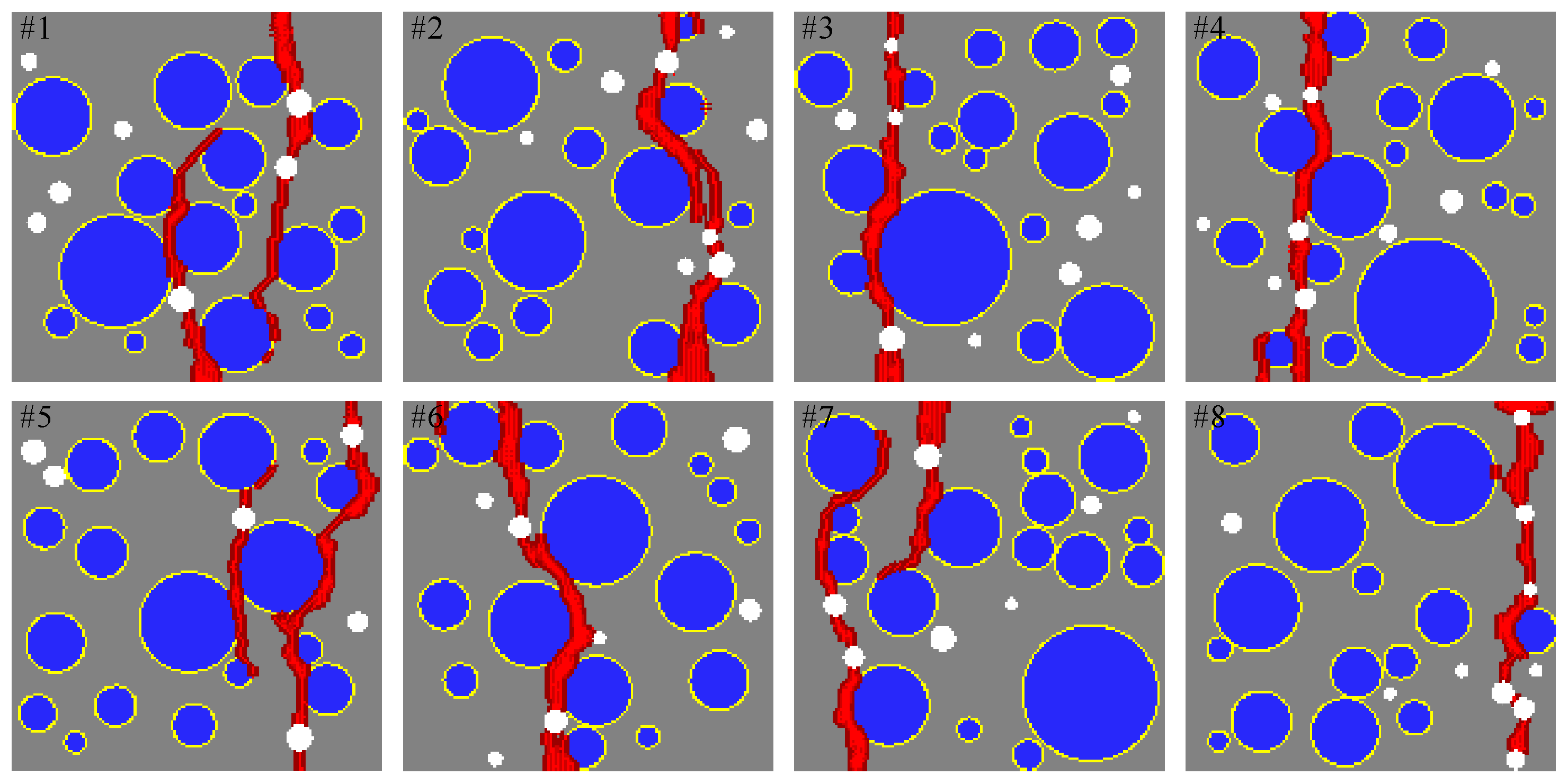
4. Analysis Results and Discussion of the Results
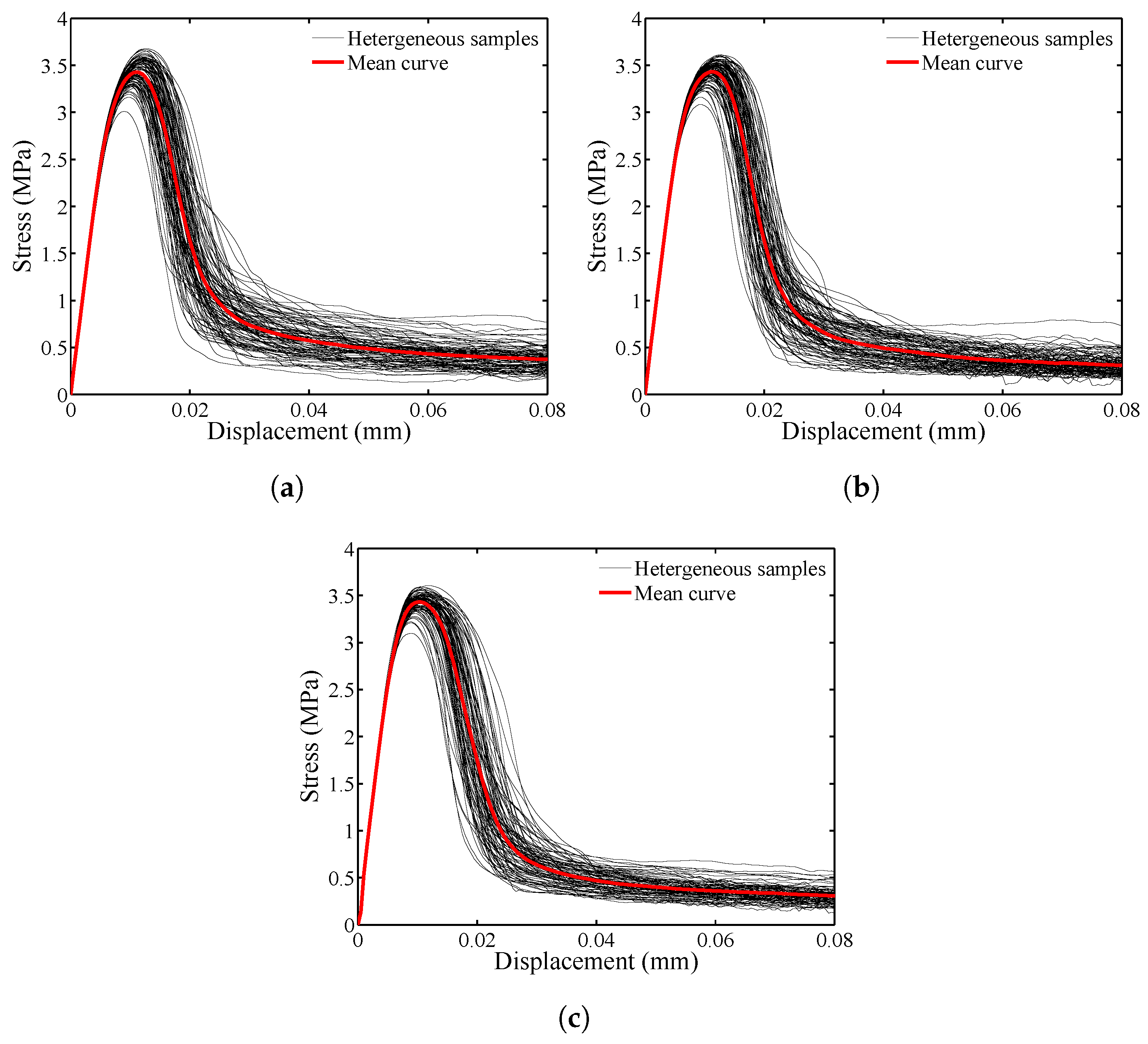
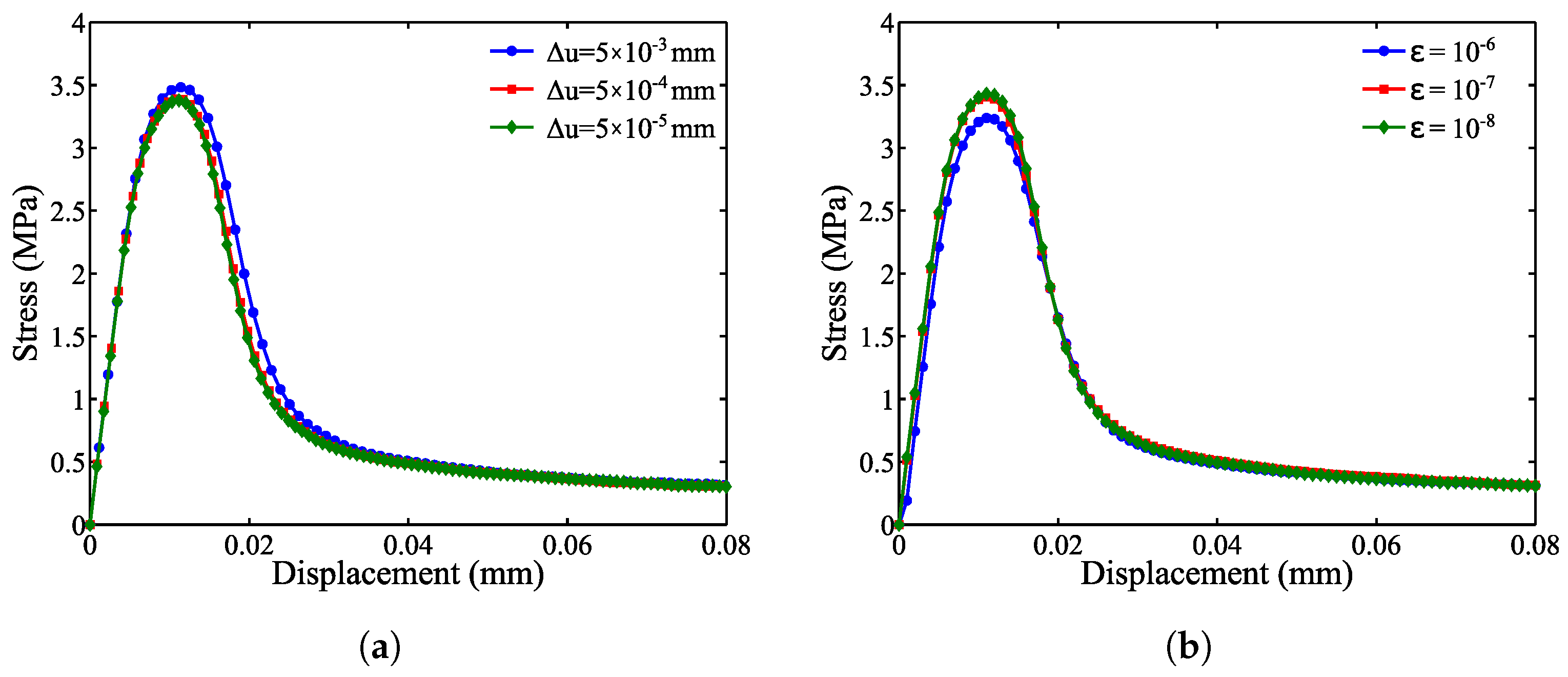
4.1. Effect of Particle Spacing and Convergence
4.2. Effect of Loading Increment and Dynamic Relaxation Threshold
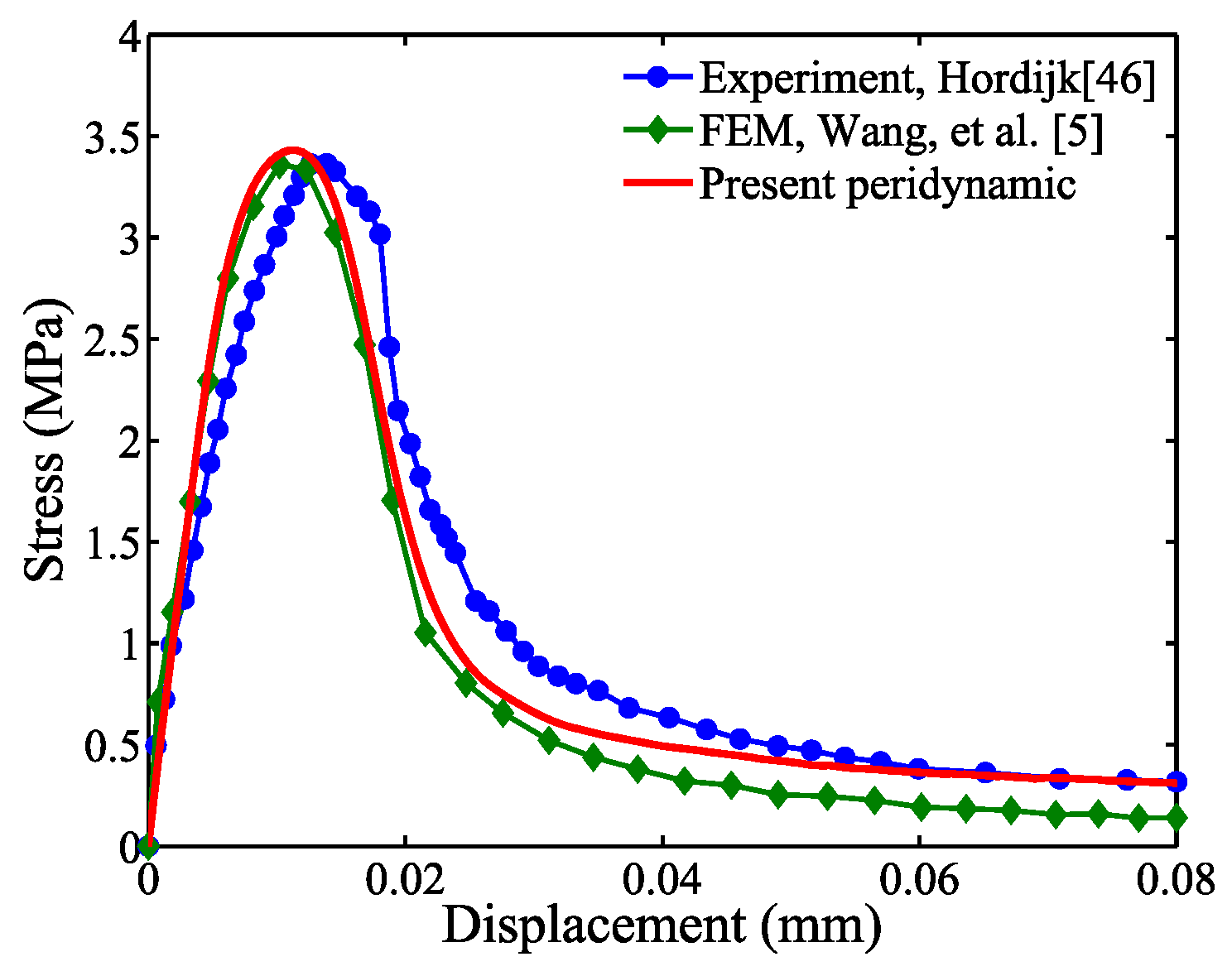
4.3. Comparison with Available Finite Element Analysis Results
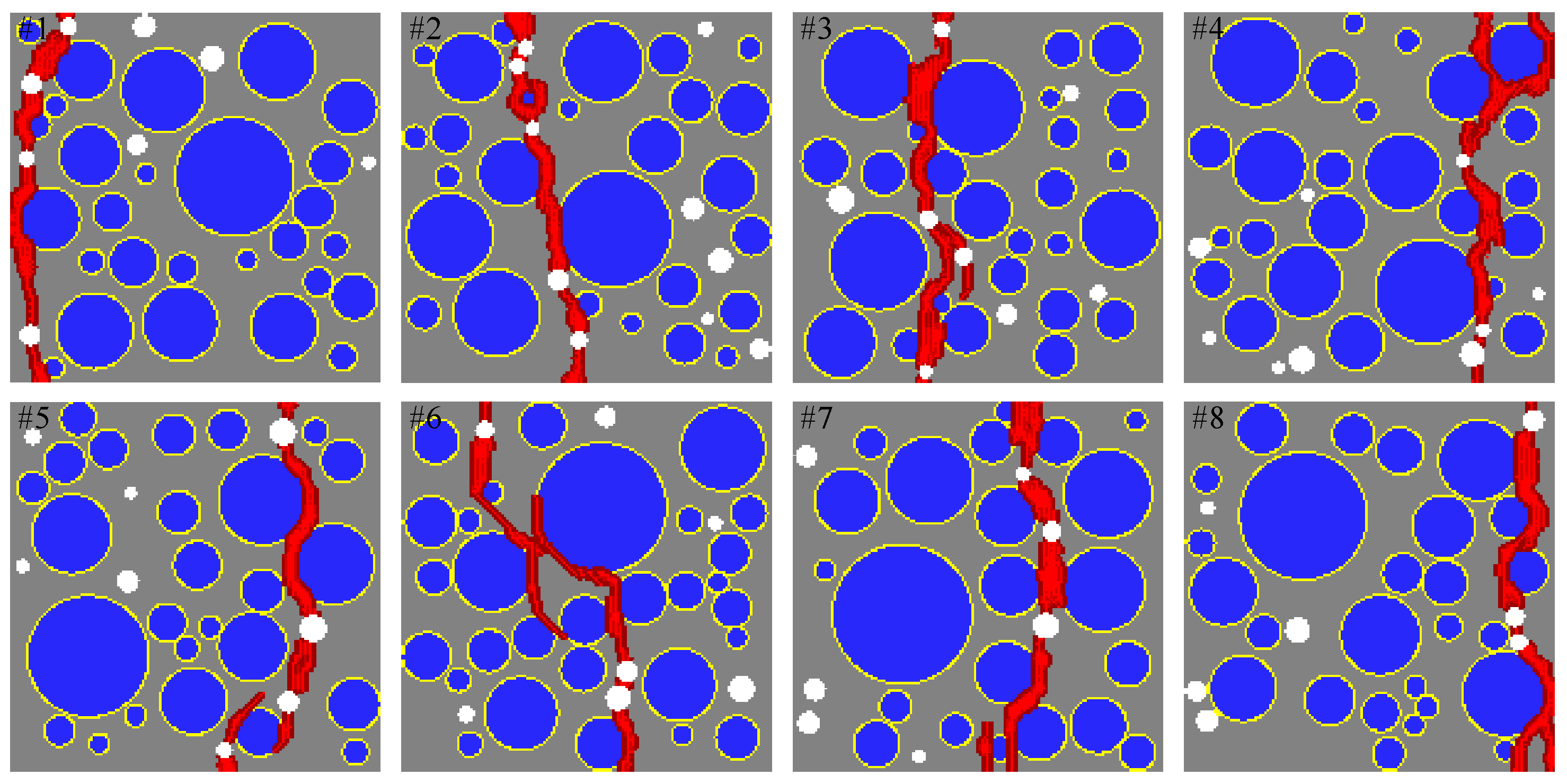
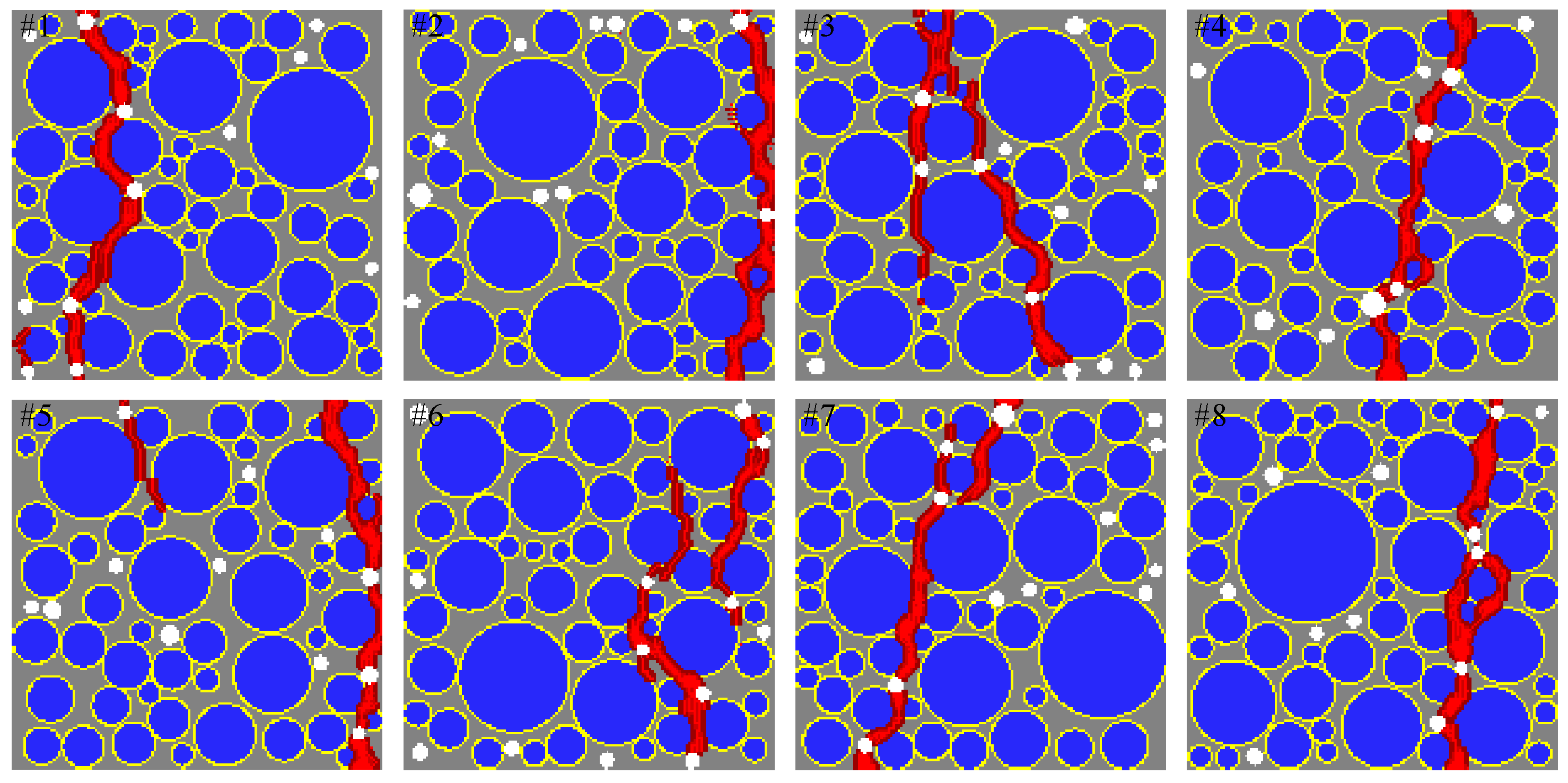
5. Sensitivity Study
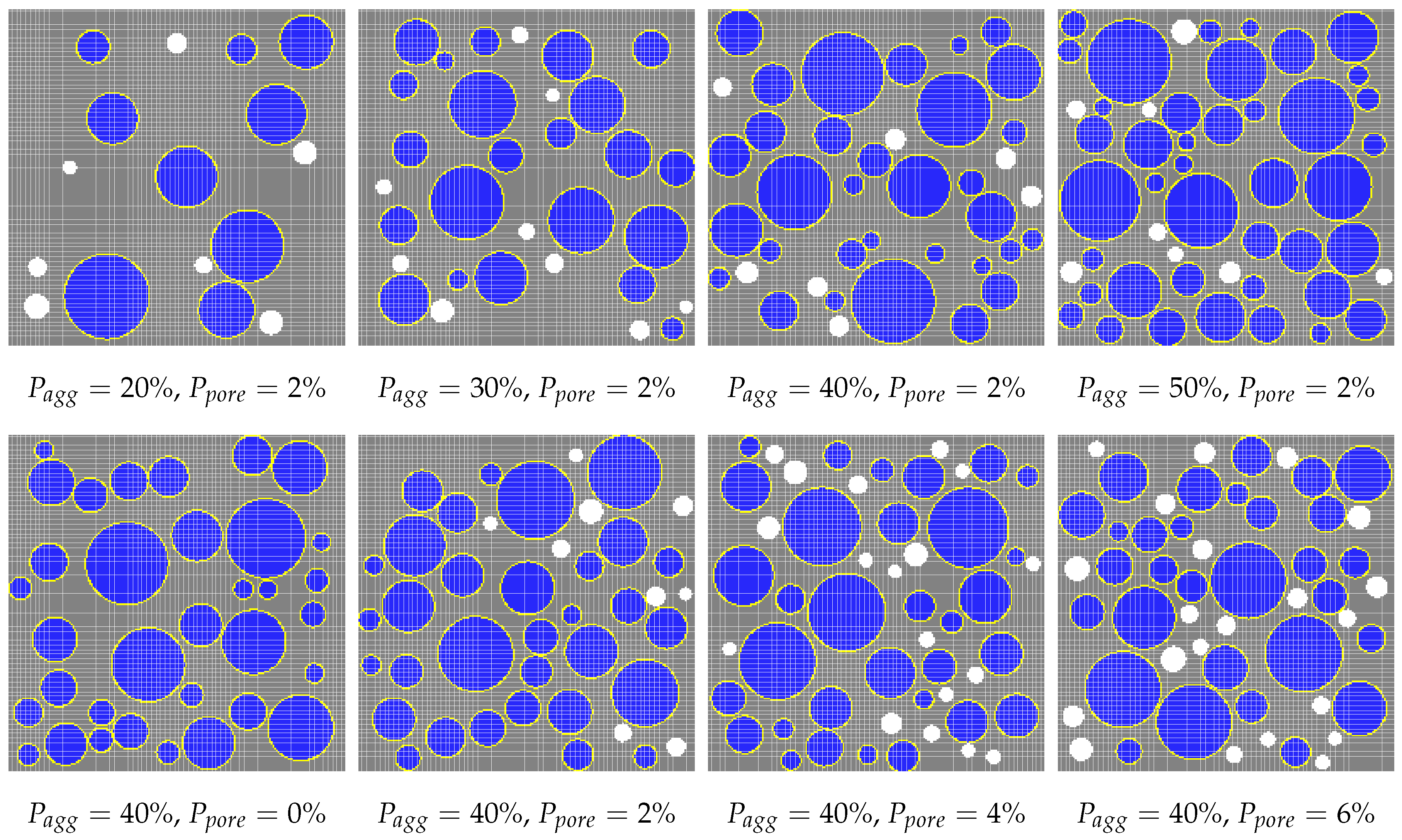
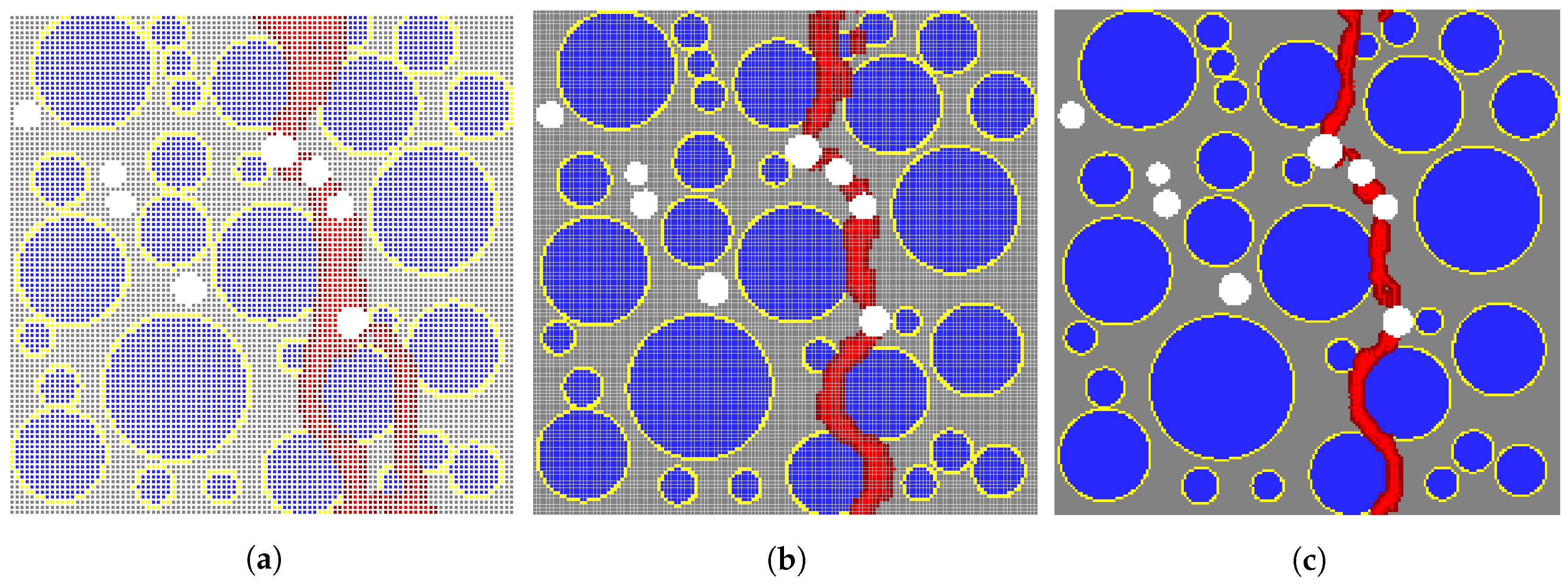
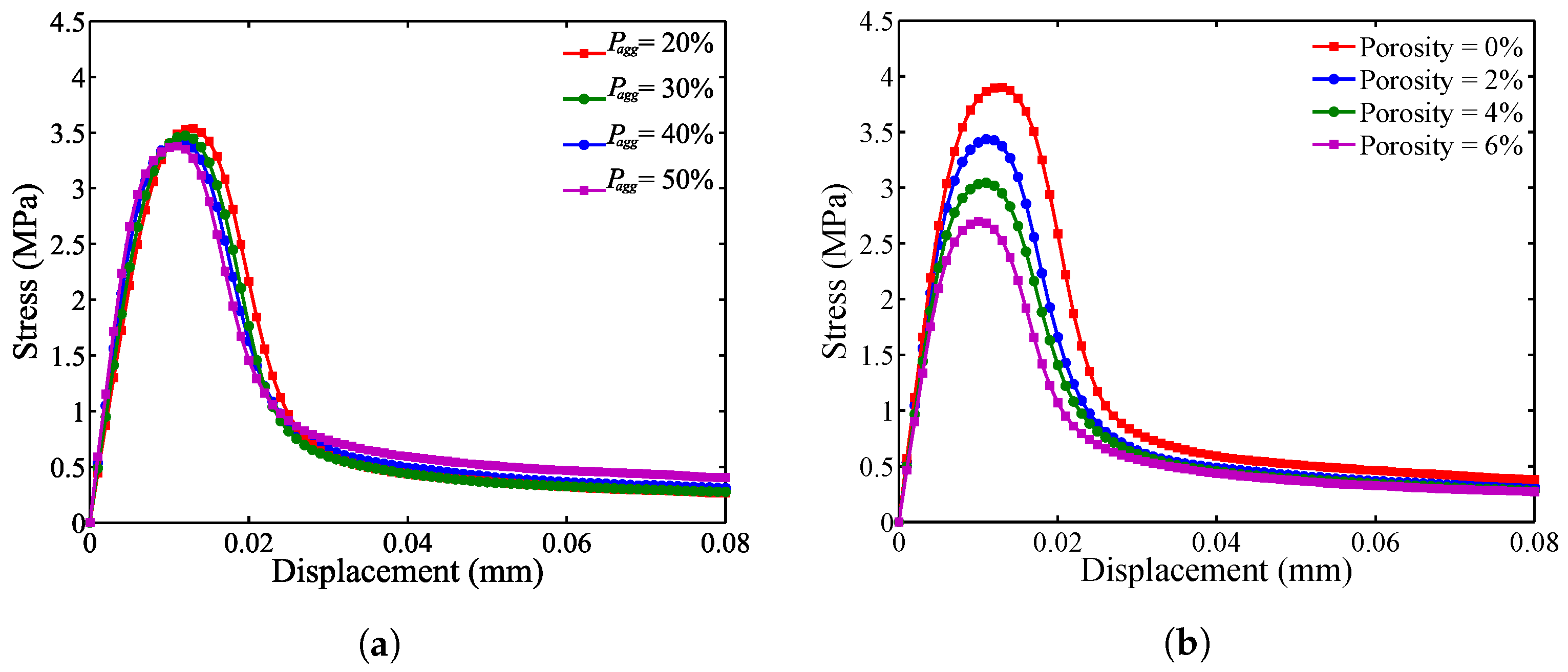
5.1. Effect of Aggregate Volume Fraction
5.2. Effect of Porosity
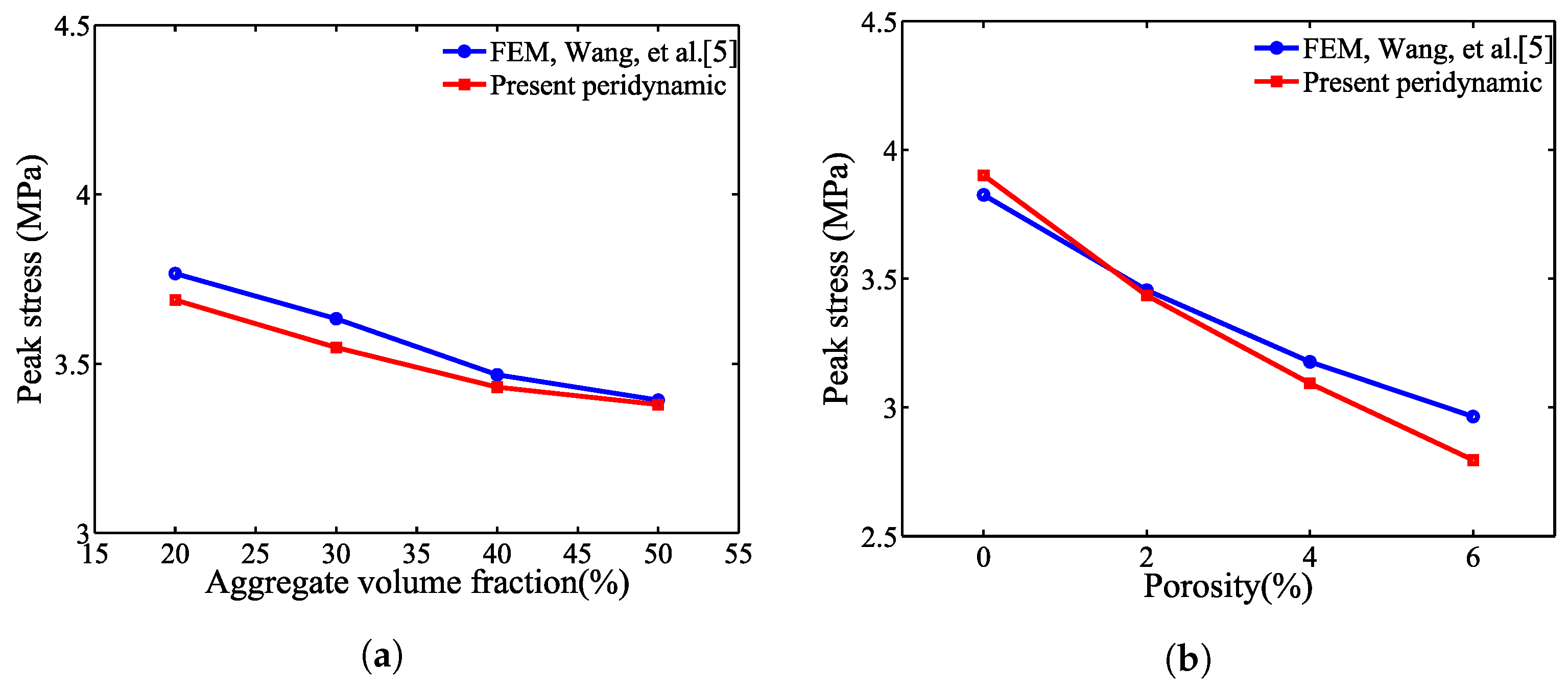
5.3. Comparison with the FEM Results and Damage Patterns
6. Discussion
- Studying the influence of particle shape and surface texture of the coarse aggregate.
- Refinement in particle spacing and/or horizon size in ITZs to reduce the computational time while providing accuracy.
- Enhancing material models and damaged parameters for complex loading conditions, such as shear.
- Extending the proposed analysis approach to three-dimensional (3D) models in which, for instance, non-planar (or 3D) fracture surfaces are characterized.
- Advanced computational techniques to optimize computational expense.
7. Conclusions
- The results indicate that particle spacing affects the stress convergence, as well as crack patterns. For the tensile loading condition considered herein, the particle spacing of mm provides the most effective discretization with a reasonable computational effort.
- The results of the mesoscale analysis show that the simulation time is sensitive to the displacement loading increment used for dynamic relaxation. Based on the analysis results reported in this paper, the optimal displacement increment and DR threshold is mm and , respectively, for tensile loading.
- By means of interfacial transition zones (ITZs) characterized in the proposed mesoscale model, it is capable of reflecting the effect of varying coarse aggregate volume fractions on the load carrying capacity.
- It is concluded that the strength reduction due to increased air content is reflected in the proposed model, by removing particle points from the areas of voids.
- Finally, in the proposed mesoscale peridynamics analysis, it is possible to identify a statistically-significant sample size for reasonably representing coarse aggregate gradation and distribution and to predict the fracture mechanism in concrete specimens.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Young, P.; Beresford-West, T.; Coward, S.; Notarberardino, B.; Walker, B.; Abdul-Aziz, A. An efficient approach to converting three-dimensional image data into highly accurate computational models. Philos. Trans. A Math. Phys. Eng. Sci. 2008, 366, 3155–3173. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.; Yang, Z.; Sharma, R.; Zhang, C.; Withers, P.J. Two-dimensional X-ray CT image based meso-scale fracture modelling of concrete. Eng. Fract. Mech. 2015, 133, 24–39. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, Z.; Ren, W.; Liu, G.; Zhang, C. 3D meso-scale fracture modelling and validation of concrete based on in-situ X-ray Computed Tomography images using damage plasticity model. Int. J. Solids Struct. 2015, 67, 340–352. [Google Scholar] [CrossRef]
- Wang, Z.; Kwan, A.; Chan, H. Mesoscopic study of concrete I: Generation of random aggregate structure and finite element mesh. Comput. Struct. 1999, 70, 533–544. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Z.; Yates, J.; Jivkov, A.; Zhang, C. Monte Carlo simulations of mesoscale fracture modelling of concrete with random aggregates and pores. Constr. Build. Mater. 2015, 75, 35–45. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, M.; Jivkov, A.P. Computational technology for analysis of 3D meso-structure effects on damage and failure of concrete. Int. J. Solids Struct. 2016, 80, 310–333. [Google Scholar] [CrossRef]
- Leite, J.; Slowik, V.; Mihashi, H. Computer simulation of fracture processes of concrete using mesolevel models of lattice structures. Cem. Concr. Res. 2004, 34, 1025–1033. [Google Scholar] [CrossRef]
- Jivkov, A.P.; Xiong, Q. A network model for diffusion in media with partially resolvable pore space characteristics. Transp. Porous Media 2014, 105, 83–104. [Google Scholar] [CrossRef]
- Xiong, Q.; Jivkov, A.P.; Yates, J.R. Discrete modelling of contaminant diffusion in porous media with sorption. Microporous Mesoporous Mater. 2014, 185, 51–60. [Google Scholar] [CrossRef]
- Shahbeyk, S.; Hosseini, M.; Yaghoobi, M. Mesoscale finite element prediction of concrete failure. Comput. Mater. Sci. 2011, 50, 1973–1990. [Google Scholar] [CrossRef]
- Van Mier, J.; van Vliet, M. Influence of microstructure of concrete on size/scale effects in tensile fracture. Eng. Fract. Mech. 2003, 70, 2281–2306. [Google Scholar] [CrossRef]
- Unger, J.F.; Eckardt, S.; Könke, C. Modelling of cohesive crack growth in concrete structures with the extended finite element method. Comput. Methods Appl. Mech. Eng. 2007, 196, 4087–4100. [Google Scholar] [CrossRef]
- Vořechovskỳ, M.; Sadílek, V. Computational modeling of size effects in concrete specimens under uniaxial tension. Int. J. Fract. 2008, 154, 27–49. [Google Scholar] [CrossRef]
- Patzák, B.; Jirásek, M. Process zone resolution by extended finite elements. Eng. Fract. Mech. 2003, 70, 957–977. [Google Scholar] [CrossRef]
- Roubin, E.; Vallade, A.; Benkemoun, N.; Colliat, J.B. Multi-scale failure of heterogeneous materials: A double kinematics enhancement for Embedded Finite Element Method. Int. J. Solids Struct. 2015, 52, 180–196. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Tabbara, M.R.; Kazemi, M.T.; Pijaudier-Cabot, G. Random particle model for fracture of aggregate or fiber composites. J. Eng. Mech. 1990, 116, 1686–1705. [Google Scholar] [CrossRef]
- Cusatis, G.; Pelessone, D.; Mencarelli, A. Lattice Discrete Particle Model (LDPM) for failure behavior of concrete. I: Theory. Cem. Concr. Compos. 2011, 33, 881–890. [Google Scholar] [CrossRef]
- Schlangen, E.; van Mier, J. Experimental and numerical analysis of micromechanisms of fracture of cement-based composites. Cem. Concr. Compos. 1992, 14, 105–118. [Google Scholar] [CrossRef]
- Schlangen, E.; van Mier, J. Simple lattice model for numerical simulation of fracture of concrete materials and structures. Mater. Struct. 1992, 25, 534–542. [Google Scholar] [CrossRef]
- Schlangen, E.; van Mier, J. Micromechanical analysis of fracture of concrete. Int. J. Damage Mech. 1992, 1, 435–454. [Google Scholar] [CrossRef]
- Schlangen, E.; Garboczi, E. Fracture simulations of concrete using lattice models: Computational aspects. Eng. Fract. Mech. 1997, 57, 319–332. [Google Scholar] [CrossRef]
- Lilliu, G.; van Mier, J.G. 3D lattice type fracture model for concrete. Eng. Fract. Mech. 2003, 70, 927–941. [Google Scholar] [CrossRef]
- Grassl, P.; Jirásek, M. Damage-plastic model for concrete failure. Int. J. Solids Struct. 2006, 43, 7166–7196. [Google Scholar] [CrossRef]
- Khalili, A.; Samaratunga, D.; Jha, R.; Lacy, T.E.; Gopalakrishnanrth, S. Wavelet spectral finite element based user-defined element in abaqus for modeling delamination in Composite Beams. In Proceedings of the 23nd AIAA/ASME/AHS Adaptive Structures Conference, Kissimmee, FL, USA, 5–9 January 2015.
- Khalili, A.; Jha, R.; Samaratunga, D. Spectrally Formulated User-Defined Element in Conventional Finite Element Environment for Wave Motion Analysis in 2-D Composite Structures. Eur. J. Comput. Mech. 2016, 25, 446–474. [Google Scholar]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Silling, S.A.; Askari, E. A meshfree method based on the peridynamic model of solid mechanics. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Gerstle, W.; Sau, N.; Silling, S. Peridynamic modeling of concrete structures. Nucl. Eng. Des. 2007, 237, 1250–1258. [Google Scholar] [CrossRef]
- Yaghoobi, A.; Chorzepa, M.G. Fracture analysis of fiber reinforced concrete structures in the micropolar peridynamic analysis framework. Eng. Fract. Mech. 2017, 169, 238–250. [Google Scholar] [CrossRef]
- Silling, S.; Lehoucq, R. Peridynamic theory of solid mechanics. Adv. Appl. Mech. 2010, 44, 73–168. [Google Scholar]
- Warren, T.L.; Silling, S.A.; Askari, A.; Weckner, O.; Epton, M.A.; Xu, J. A non-ordinary state-based peridynamic method to model solid material deformation and fracture. Int. J. Solids Struct. 2009, 46, 1186–1195. [Google Scholar] [CrossRef]
- Silling, S.A.; Epton, M.; Weckner, O.; Xu, J.; Askari, E. Peridynamic states and constitutive modeling. J. Elast. 2007, 88, 151–184. [Google Scholar] [CrossRef]
- Breitenfeld, M.; Geubelle, P.; Weckner, O.; Silling, S. Non-ordinary state-based peridynamic analysis of stationary crack problems. Comput. Methods Appl. Mech. Eng. 2014, 272, 233–250. [Google Scholar] [CrossRef]
- Chorzepa, M.G.; Yaghoobi, A. Innovative Meshless Computational Method for the Analysis of Fiber-Reinforced Concrete (FRC) Structures. In Proceedings of the Geotechnical and Structural Engineering Congress 2016, Phoenix, AZ, USA, 14–17 February 2016; pp. 1209–1221.
- Unger, J.F.; Eckardt, S. Multiscale modeling of concrete. Arch. Comput. Methods Eng. 2011, 18, 341–393. [Google Scholar] [CrossRef]
- Wriggers, P.; Moftah, S. Mesoscale models for concrete: Homogenisation and damage behaviour. Finite Elem. Anal. Des. 2006, 42, 623–636. [Google Scholar] [CrossRef]
- Rao, G.A.; Prasad, B.R. Influence of the roughness of aggregate surface on the interface bond strength. Cem. Concr. Res. 2002, 32, 253–257. [Google Scholar] [CrossRef]
- Guinea, G.; El-Sayed, K.; Rocco, C.; Elices, M.; Planas, J. The effect of the bond between the matrix and the aggregates on the cracking mechanism and fracture parameters of concrete. Cem. Concr. Res. 2002, 32, 1961–1970. [Google Scholar] [CrossRef]
- Häfner, S.; Eckardt, S.; Luther, T.; Könke, C. Mesoscale modeling of concrete: Geometry and numerics. Comput. Struct. 2006, 84, 450–461. [Google Scholar] [CrossRef]
- Yaghoobi, A.; Chorzepa, M.G. Higher-order approximation to suppress the zero-energy mode in non-ordinary state-based peridynamics. Comput. Struct. 2017, in press. [Google Scholar]
- Underwood, P. Dynamic relaxation(in structural transient analysis). In Computational Methods for Transient Analysis (A 84-29160 12-64); North-Holland Publishing Co.: Amsterdam, The Netherlands, 1983; pp. 245–265. [Google Scholar]
- Yaghoobi, A.; Chorzepa, M.G. Meshless modeling framework for fiber reinforced concrete structures. Comput. Struct. 2015, 161, 43–54. [Google Scholar] [CrossRef]
- Hu, W.; Ha, Y.D.; Bobaru, F.; Silling, S.A. The formulation and computation of the nonlocal J-integral in bond-based peridynamics. Int. J. Fract. 2012, 176, 195–206. [Google Scholar] [CrossRef]
- Tupek, M.; Rimoli, J.; Radovitzky, R. An approach for incorporating classical continuum damage models in state-based peridynamics. Comput. Methods Appl. Mech. Eng. 2013, 263, 20–26. [Google Scholar] [CrossRef]
- O’Grady, J.; Foster, J. Peridynamic plates and flat shells: A non-ordinary, state-based model. Int. J. Solids Struct. 2014, 51, 4572–4579. [Google Scholar] [CrossRef]
- Hordijk, D.A. Tensile and tensile fatigue behaviour of concrete; experiments, modelling and analyses. Heron 1992, 37. [Google Scholar]
- Tasdemir, M.A.; Karihaloo, B.L. Effect of type and volume fraction of aggregate on the fracture properties of concrete. In Fracture Mechanics of Concrete Structures; Swets & Zeitlinger: Lisse, The Netherlands, 2001; Volume 90, p. 825. [Google Scholar]
- Akcay, B.; Agar-Ozbek, A.S.; Bayramov, F.; Atahan, H.N.; Sengul, C.; Tasdemir, M.A. Interpretation of aggregate volume fraction effects on fracture behavior of concrete. Constr. Build. Mater. 2012, 28, 437–443. [Google Scholar] [CrossRef]
- Sengul, O.; Tasdemir, C.; Tasdemir, M.A. Influence of aggregate type on mechanical behavior of normal-and high-strength concretes. Mater. J. 2002, 99, 528–533. [Google Scholar]
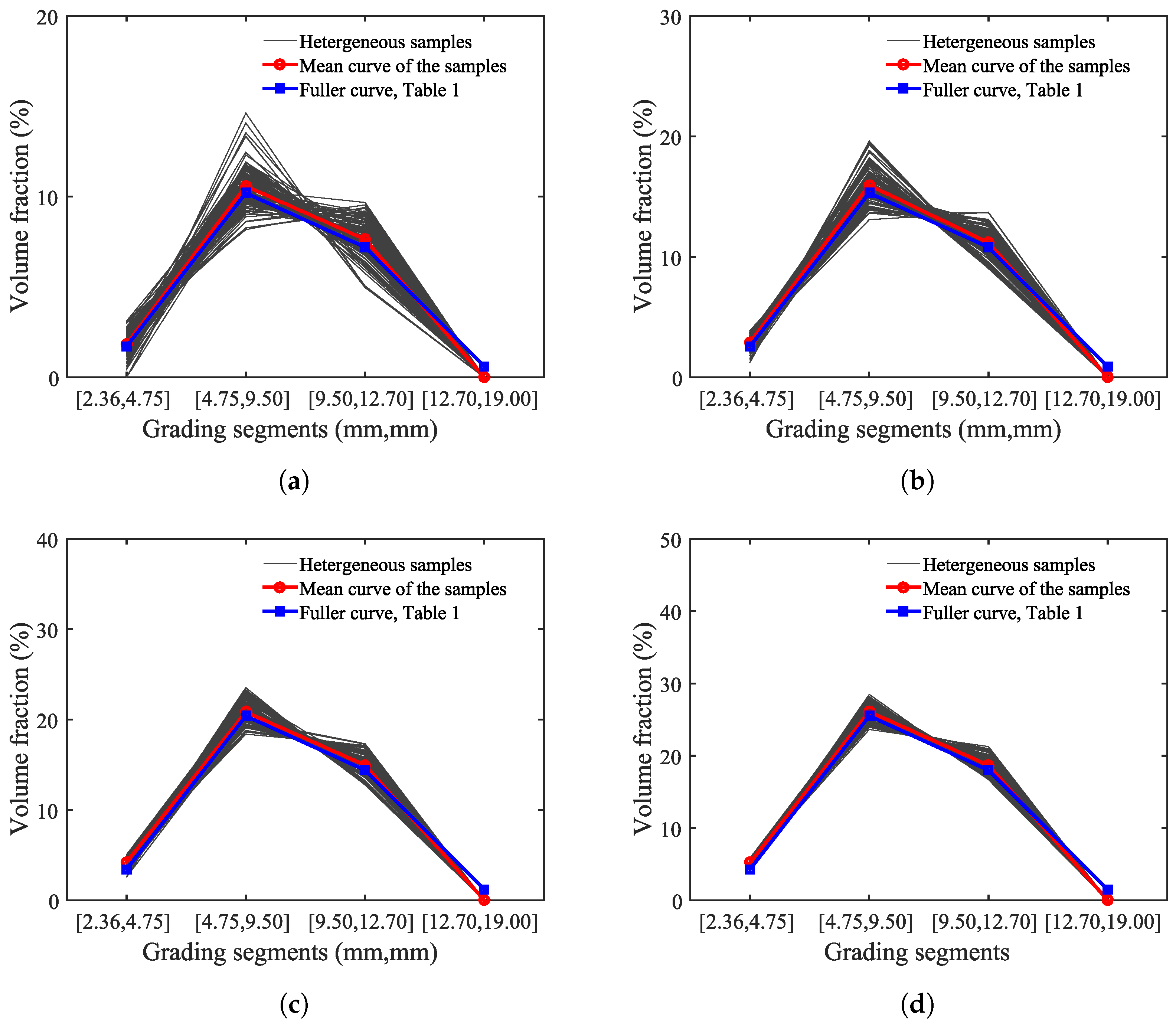






| Sieve size (mm) | 19.00 | 12.70 | 9.50 | 4.75 | 2.36 |
| Total percentage passing (%) | 100 | 97 | 61 | 10 | 1.4 |
| Constituent | Young’s Modulus, E (MPa) | Poisson’s Ratio, | Fracture Energy, (N/mm) |
|---|---|---|---|
| Aggregate | 70,000 | 0.2 | - |
| Mortar | 25,000 | 0.2 | 0.06 |
| ITZ | 25,000 | 0.2 | 0.03 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaghoobi, A.; Chorzepa, M.G.; Kim, S.S.; A., S. Mesoscale Fracture Analysis of Multiphase Cementitious Composites Using Peridynamics. Materials 2017, 10, 162. https://doi.org/10.3390/ma10020162
Yaghoobi A, Chorzepa MG, Kim SS, A. S. Mesoscale Fracture Analysis of Multiphase Cementitious Composites Using Peridynamics. Materials. 2017; 10(2):162. https://doi.org/10.3390/ma10020162
Chicago/Turabian StyleYaghoobi, Amin, Mi G. Chorzepa, S. Sonny Kim, and Stephan A. 2017. "Mesoscale Fracture Analysis of Multiphase Cementitious Composites Using Peridynamics" Materials 10, no. 2: 162. https://doi.org/10.3390/ma10020162
APA StyleYaghoobi, A., Chorzepa, M. G., Kim, S. S., & A., S. (2017). Mesoscale Fracture Analysis of Multiphase Cementitious Composites Using Peridynamics. Materials, 10(2), 162. https://doi.org/10.3390/ma10020162







