Lamb Wave-Based Structural Health Monitoring on Composite Bolted Joints under Tensile Load
Abstract
:1. Introduction
2. Experimental Details
2.1. Materials and Processing
2.2. Fundamental Mechanical Tests
2.3. Lamb Wave Inspection System
3. Fundamental Theory and Dispersion Feature of Lamb Wave in Composite Laminates
4. Experimental Works on SHM of the Composite Bolted Joints Using Lamb Wave
4.1. Lamb Wave in Composite Bolted Joints Before Tensile Test
4.2. Lamb Waves Inspection of the Composite Bolted Joints after Tensile Test
4.3. Lamb Wave Inspection of the Composite Bolted Joints during Tensile Test
5. Simulation Works on Lamb Waves in Composite Bolted Joints
5.1. 3D FE Model Description
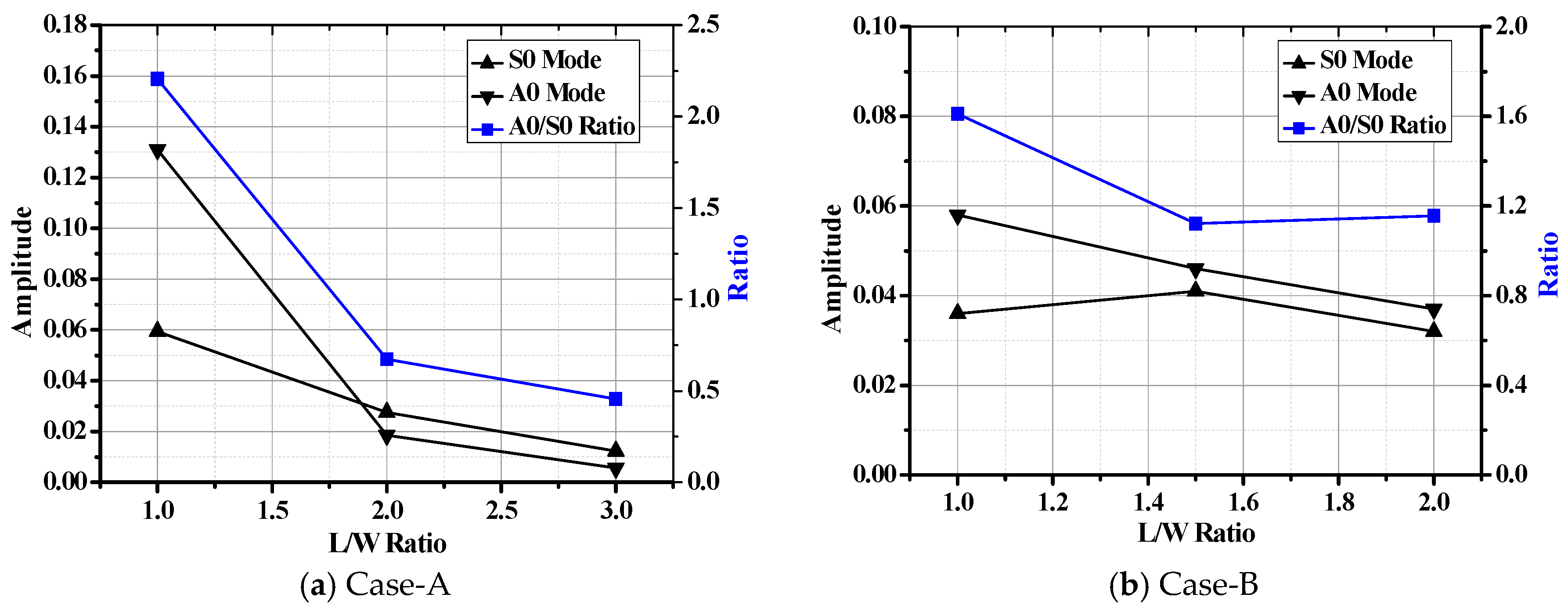
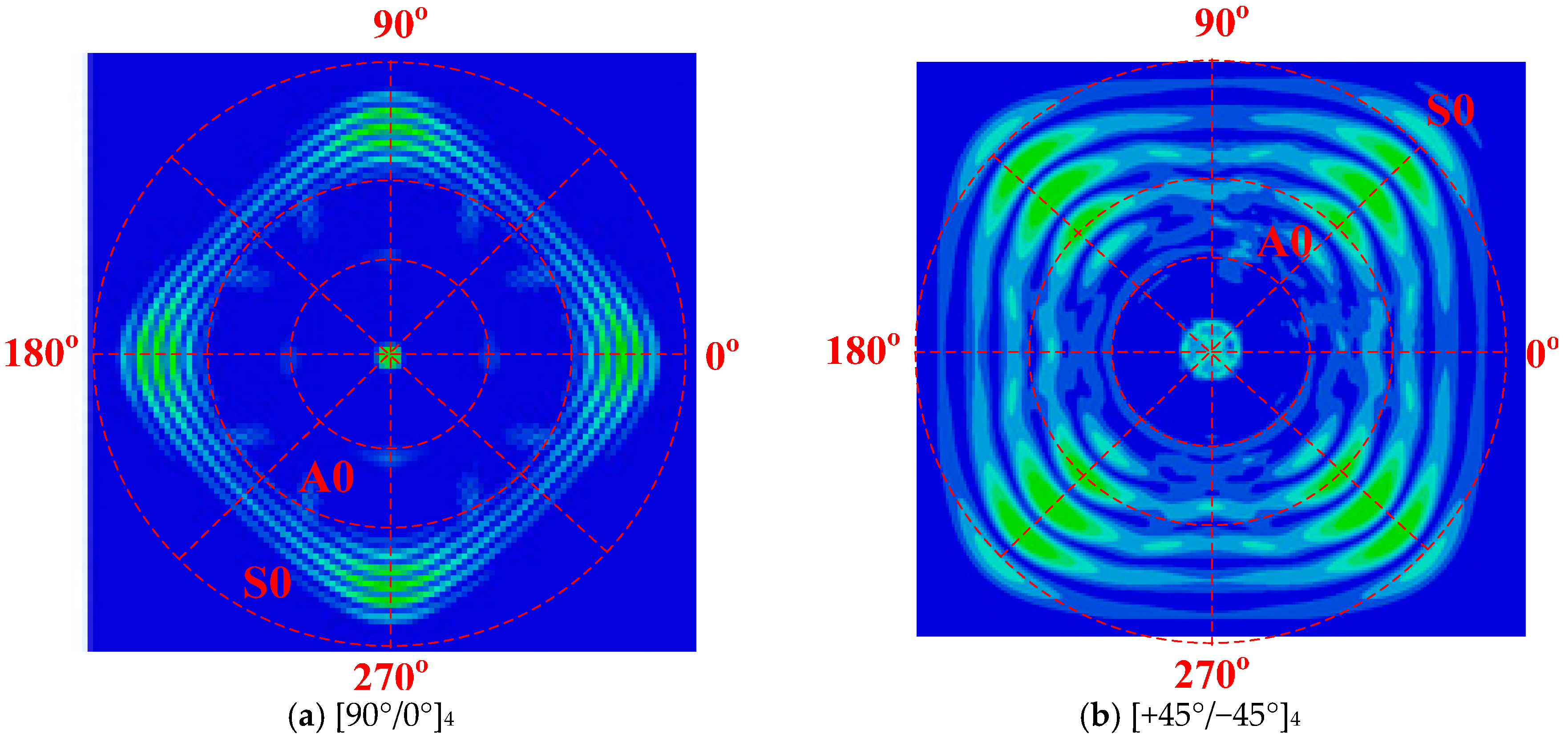
5.2. Simulation Results
6. Conclusions
- Relationships between S0/A0 wave and the failure mode of the composite bolted joints were found. Damages in the joints mainly affected the amplitude of the Lamb wave, and the difference in S0/A0 amplitude could be adopted to identify the failure mode of the joints after tensile load.
- The amplitude of the Lamb wave varied with the applied torque on the joints. The S0/A0 wave amplitudes showed a decrease in tendency with the increasing of tensile load, and this was mainly caused by the increased specimen length and the weakened contact property in the joint region during the tensile test.
- The built 3D FE model could capture the slowness profiles of Lamb waves well when they were propagating in multi-layered composite laminates. The captured wave in the simulation matched the experiment results, and wave expansion and reflection phenomenon were observed in the overlapped joint region.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lobel, T.; Holzhuter, D.; Sinapius, M.; Huhne, C. A hybrid bondline concept for bonded composite joints. Int. J. Adhes. Adhes. 2016, 68, 229–238. [Google Scholar] [CrossRef]
- Fu, M.; Mallick, P.K. Fatigue of hybrid (adhesive/bolted) joints in SRIM composites. Int. J. Adhes. Adhes. 2001, 21, 145–159. [Google Scholar] [CrossRef]
- Vallee, T.; Tannert, T.; Meena, R.; Hehl, S. Dimensioning method for bolted, adhesively bonded, and hybrid joints involving fiber reinforced polymers. Compos. Part B 2013, 46, 179–187. [Google Scholar] [CrossRef]
- Esmaeili, F.; Chakherlou, T.N.; Zehsaz, M. Investigation of bolt clamping force on the fatigue life of double lap simple bolted and hybrid (bolted/bonded) joints via experimental and numerical analysis. Eng. Fail. Anal. 2014, 45, 406–420. [Google Scholar] [CrossRef]
- Samaei, M.; Zehsaz, M.; Chakherlou, T.N. Experimental and numerical study of fatigue crack growth of aluminum alloy 2024-T3 single lap simple bolted and hybrid (adhesive/bolted) joints. Eng. Fail. Anal. 2016, 59, 253–268. [Google Scholar] [CrossRef]
- Vijaya Kumar, R.L.; Bhat, M.R.; Murthy, C.R.L. Evaluation of kissing bond in composite adhesive lap joints using digital image correlation: Preliminary studies. Int. J. Adhes. Adhes. 2013, 42, 60–68. [Google Scholar] [CrossRef]
- Ostachowicz, W.M. Damage detection of structures using spectral finite element method. Comput. Struct. 2008, 86, 454–462. [Google Scholar] [CrossRef]
- Su, Z.Q.; Ye, L. Identification of Damage Using Lamb Waves; Springer: Berlin, Germany, 2009. [Google Scholar]
- Harb, M.S.; Yuan, F.G. Non-contact ultrasonic technique for Lamb wave characterization in composite plates. Ultrasonics 2016, 64, 162–169. [Google Scholar] [CrossRef] [PubMed]
- Kang, T.; Lee, D.H.; Song, S.J.; Kim, H.J.; Jo, Y.D.; Cho, H.J. Enhancement of detecting defects in pipes with focusing techniques. NDT E Int. 2011, 44, 178–187. [Google Scholar] [CrossRef]
- Gianneo, A.; Carboni, M.; Giglio, M. Feasibility study of a multi-parameter probability of detection formulation for a Lamb waves-based structural health monitoring approach to light alloy aeronautical plates. Struct. Health Monit. 2017, 16, 225–249. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Wave Propagation in Layered Anisotropic Media: With Applications to Composites; Elsevier: New York, NY, USA, 1995. [Google Scholar]
- Yu, L.; Bottai-Santoni, G.; Giurgiutiu, V. Shear lag solution for tuning ultrasonic piezoelectric wafer active sensors with applications to Lamb wave array imaging. Int. J. Eng. Sci. 2010, 48, 848–861. [Google Scholar] [CrossRef]
- Yu, X.D.; Ratassepp, M.; Rajagopal, P.; Fan, Z. Anisotropic effects on ultrasonic guided waves propagation in composite bends. Ultrasonics 2016, 72, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Pant, S.; Laliberte, J.; Martinez, M.; Rocha, B. Derivation and experimental validation of Lamb wave equations for an n-layered anisotropic composite laminate. Compos. Struct. 2014, 111, 566–579. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, Z.Q.; Zhou, J.S.; Wu, X.D. Experimental and numerical investigation on bolted composite joint made by vacuum assisted resin injection. Compos. Part B 2013, 45, 1620–1628. [Google Scholar] [CrossRef]
- Ascione, F.; Feo, L.; Maceri, F. An experimental investigation on the bearing failure load of glass fiber/epoxy laminates. Compos. Part B 2009, 40, 197–205. [Google Scholar] [CrossRef]
- Ascione, F.; Feo, L.; Maceri, F. On the pin-bearing failure load of GFRP bolted laminates: An experimental analysis on the influence of bolt diameter. Compos. Part B 2010, 41, 482–490. [Google Scholar] [CrossRef]
- Feo, L.; Marra, G.; Mosallam, A.S. Stress analysis of multi-bolted joints for FRP pultruded composite structures. Compos. Struct. 2012, 94, 3769–3780. [Google Scholar] [CrossRef]
- Ahmad, H.; Crocombe, A.D.; Smith, P.A. Strength prediction in CFRP woven laminate bolted double-lap joints under quasi-static loading using XFEM. Compos. Part A 2014, 56, 192–202. [Google Scholar] [CrossRef]
- Matt, H.; Bartoli, I.; Lanza di Scalea, F. Ultrasonic guided wave monitoring of composite wing skin-to-spar bonded joints in aerospace structures. J. Acoust. Soc. Am. 2005, 118, 2240–2253. [Google Scholar] [CrossRef]
- Sherafat, M.H.; Guitel, R.; Quaegebeur, N.; Lessard, L.; Hubert, P.; Masson, P. Guided wave scattering behavior in composite bonded assemblies. Compos. Struct. 2016, 136, 696–705. [Google Scholar] [CrossRef]
- Ren, B.; Lissenden, C.L. Ultrasonic guided wave inspection of adhesive bonds between composite laminates. Int. J. Adhes. Adhes. 2013, 45, 59–68. [Google Scholar] [CrossRef]
- Samaratunga, D.; Jha, R.; Gopalakrishnan, S. Wave propagation analysis in adhesively bonded composite joints using the wavelet spectral finite element method. Compos. Struct. 2015, 122, 271–283. [Google Scholar] [CrossRef]
- Deng, Q.T.; Yang, Z.C. Propagation of guided waves in bonded composite structures with tapered adhesive layer. Appl. Math. Model. 2011, 35, 5369–5381. [Google Scholar] [CrossRef]
- Geetha, G.K.; Mahapatra, D.R.; Gopalakrishnan, S.; Hanagud, S. Laser Doppler imaging of delamination in a composite T-joint with remotely located ultrasonic actuators. Compos. Struct. 2016, 147, 197–210. [Google Scholar] [CrossRef]
- Rucka, M. Experimental and numerical study on damage detection in an L-joint using guided wave propagation. J. Sound Vib. 2010, 329, 1760–1779. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, J.F.; Zhou, L.M.; Lu, M.K.; Liang, W.Y.; Wang, Z.Q. Effect of fiber surface modification on water absorption and hydrothermal aging behaviors of GF/pCBT composites. Compos. Part B 2015, 82, 84–91. [Google Scholar] [CrossRef]
- Yang, B.; Wang, Z.Q.; Zhou, L.M.; Zhang, J.F.; Tong, L.L.; Liang, W.Y. Study on the low-velocity impact response and CAI behavior of foam-filled sandwich panels with hybrid facesheet. Compos. Struct. 2015, 132, 1129–1140. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: New York, NY, USA, 1999. [Google Scholar]
- Pavlakovic, B.; Lowe, M. Disperse User’s Manual, version 2.0; Imperial College London: London, UK, 2003. [Google Scholar]
- Staszewski, W.J.; Lee, B.C.; Mallet, L.; Scarpa, F. Structural health monitoring using scanning laser vibrometry: I. Lamb wave sensing. Smart Mater. Struct. 2004, 13, 251–260. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Predictive methodologies for the design of lamb-wave piezoelectric wafer active sensors for structural health monitoring, damage detection and failure prevention. In Proceedings of the 2009 NSF Engineering Research and Innovation Conference, Honolulu, HI, USA, 22–25 June 2009. [Google Scholar]
- Yu, L.; Momeni, S.; Godinez, V.; Giurgiutiu, V.; Ziehl, P.; Yu, J. Dual mode sensing with low-profile piezoelectric thin wafer sensors for steel bridge crack detection and diagnosis. Adv. Civ. Eng. 2012. [Google Scholar] [CrossRef]
- Ng, C.T.; Veidt, M. A Lamb-wave-based technique for damage detection in composite laminates. Smart Mater. Struct. 2009, 18, 074006. [Google Scholar] [CrossRef]
- Veidt, M.; Ng, C.T. Influence of stacking sequence on scattering characteristics of the fundamental anti-symmetric Lamb wave at through holes in composite laminates. J. Acoust. Soc. Am. 2011, 129, 1280–1287. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Wang, Z.Q.; Zhou, L.M.; Zhang, J.F.; Liang, W.Y. Experimental and numerical investigation of interply hybrid composites based on woven fabrics and PCBT resin subjected to low-velocity impact. Compos. Struct. 2015, 132, 464–476. [Google Scholar] [CrossRef]
- Yang, B.; Xuan, F.Z.; Chen, S.J.; Zhou, S.P.; Gao, Y.; Xiao, B. Damage localization and identification in WGF/epoxy composite laminates by using Lamb waves: Experiment and simulation. Compos. Struct. 2017, 165, 138–147. [Google Scholar] [CrossRef]
- Yelve, N.P.; Mitra, M.; Mujumdar, P.M. Detection of delamination in composite laminates using Lamb wave based nonlinear method. Compos. Struct. 2017, 159, 257–266. [Google Scholar] [CrossRef]
- Wandowski, T.; Malinowski, P.H.; Ostachowicz, W.M. Circular sensing networks for guided waves based structural health monitoring. Mech. Syst. Signal Process. 2016, 66–67, 248–267. [Google Scholar] [CrossRef]
- Su, Z.Q.; Ye, L.; Lu, Y. Guided Lamb waves for identification of damage in composite structures: A review. J. Sound Vib. 2006, 295, 753–780. [Google Scholar] [CrossRef]















| Parameter | Case A | Case B | ||||
|---|---|---|---|---|---|---|
| W | 40 | 40 | 40 | 60 | 60 | 60 |
| L | 40 | 80 | 120 | 60 | 90 | 120 |
| L/W | 1:1 | 2:1 | 3:1 | 1:1 | 3:2 | 2:1 |
| Ltotal | 450 | 410 | 380 | 450 | 410 | 380 |
| Bolt location | (L/2, W/2) | (L/2, W/2) | (L/2, W/2) | (L/2, W/4) | (L/2, W/4) | (L/2, W/4) |
| Test Method | ASTM Standard | Dimension (L × W × T, mm3) | Calibrating Length (mm) |
|---|---|---|---|
| 90°/0° tensile | D3039/D3039M-08 | 220 × 20 × 2.5 | 140 |
| ±45° tensile | D3518/D3518M-13 | 180 × 20 × 2.5 | 100 |
| ±45°/90°/0° compression | D3410/D3410M-95 | 160 × 20 × 2.5 | 80 |
| DCB | D5528-13 | 220 × 25 × 2.5 | 25 (precrack) |
| 3ENF | D7905/D7905M-14 | 100 × 25 × 2.5 | 80 |
| Mode III | E1922-04 | 100 × 25 × 2.5 | 25 (precrack) |
| E11/GPa | E22/GPa | E33/GPa | G12/GPa | G13/GPa | G23/GPa | µ12 | µ13 | µ23 | ρ/(g/cm3) |
|---|---|---|---|---|---|---|---|---|---|
| 11.8 ± 0.23 | 11.8 ± 0.25 | 0.58 ± 0.02 | 4.82 ± 0.08 | 4.82 ± 0.08 | 4.82 ± 0.08 | 0.05 ± 0.01 | 0.24 ± 0.01 | 0.23 ± 0.01 | 1.65 |
| XT | XC | YT | YC | ZT | ZC | S12 | S13 | S23 |
|---|---|---|---|---|---|---|---|---|
| 485.05 ± 12.54 | 59.94 ± 2.37 | 488.91 ± 15.29 | 59.58 ± 1.27 | 52.14 ± 0.98 | 180.24 ± 1.89 | 108.4 ± 5.34 | 108.4 ± 5.34 | 108.4 ± 5.34 |
| Test Method | Maximum Load/N | Failure Displacement/mm | Strain Energy Release Rate/(kJ/m2) |
|---|---|---|---|
| Mode-I | 112.5 ± 3.24 | 5.45 ± 0.05 | 1.65 ± 0.05 |
| Mode-II | 1628.4 ± 20.05 | 8.78 ± 0.32 | 2.71 ± 0.03 |
| Mode-III | 512.3 ± 4.34 | 10.67 ± 1.12 | 1.22 ± 0.01 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Xuan, F.-Z.; Xiang, Y.; Li, D.; Zhu, W.; Tang, X.; Xu, J.; Yang, K.; Luo, C. Lamb Wave-Based Structural Health Monitoring on Composite Bolted Joints under Tensile Load. Materials 2017, 10, 652. https://doi.org/10.3390/ma10060652
Yang B, Xuan F-Z, Xiang Y, Li D, Zhu W, Tang X, Xu J, Yang K, Luo C. Lamb Wave-Based Structural Health Monitoring on Composite Bolted Joints under Tensile Load. Materials. 2017; 10(6):652. https://doi.org/10.3390/ma10060652
Chicago/Turabian StyleYang, Bin, Fu-Zhen Xuan, Yanxun Xiang, Dan Li, Wujun Zhu, Xiaojun Tang, Jichao Xu, Kang Yang, and Chengqiang Luo. 2017. "Lamb Wave-Based Structural Health Monitoring on Composite Bolted Joints under Tensile Load" Materials 10, no. 6: 652. https://doi.org/10.3390/ma10060652
APA StyleYang, B., Xuan, F.-Z., Xiang, Y., Li, D., Zhu, W., Tang, X., Xu, J., Yang, K., & Luo, C. (2017). Lamb Wave-Based Structural Health Monitoring on Composite Bolted Joints under Tensile Load. Materials, 10(6), 652. https://doi.org/10.3390/ma10060652




