Output-Based Structural Damage Detection by Using Correlation Analysis Together with Transmissibility
Abstract
:1. Introduction
2. Theoretical Background
2.1. Transmissibility
2.2. Damage Sensitive Feature
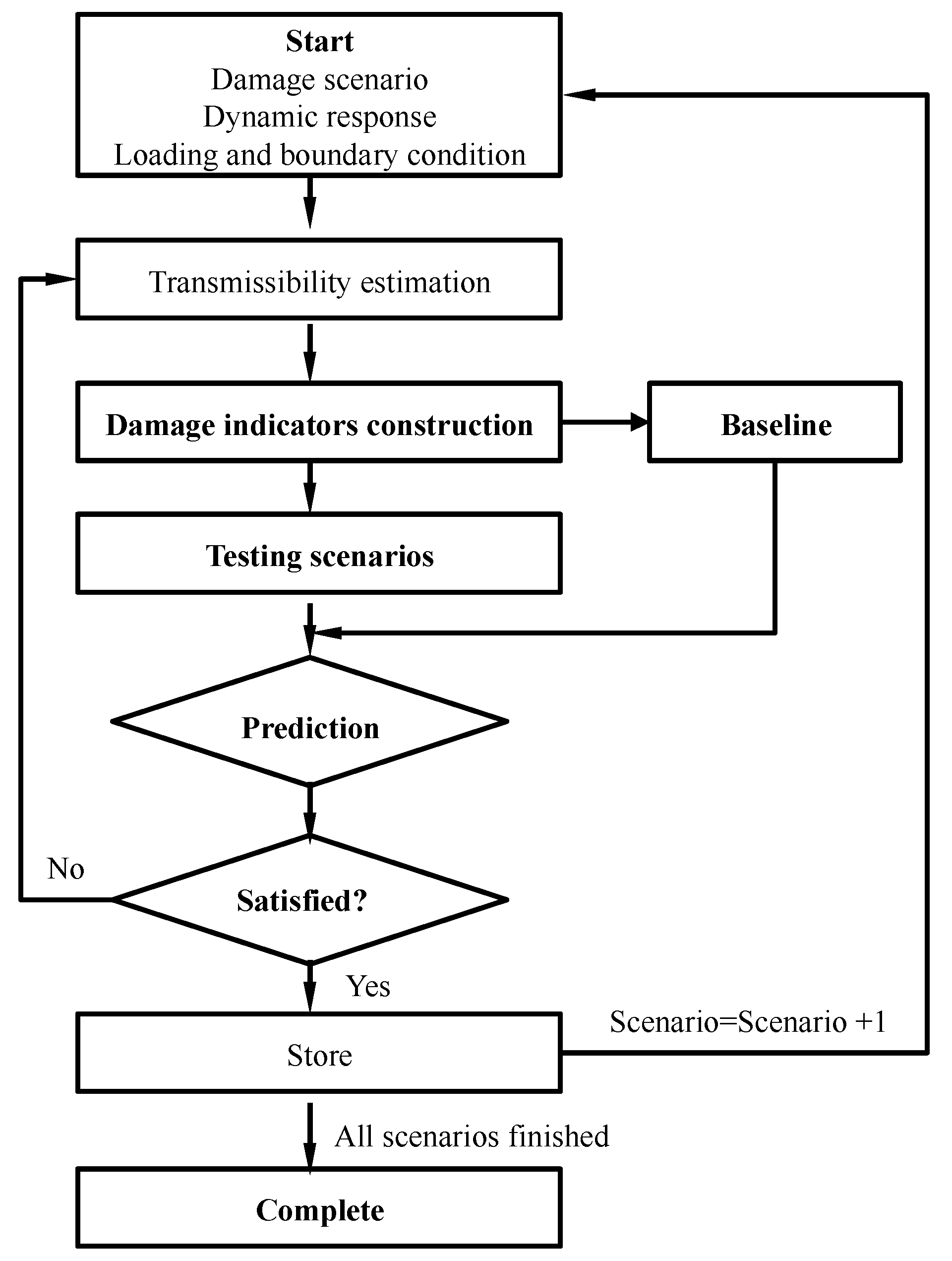
2.3. Damage Detection Procedure
3. Numerical Analysis
3.1. Model Description
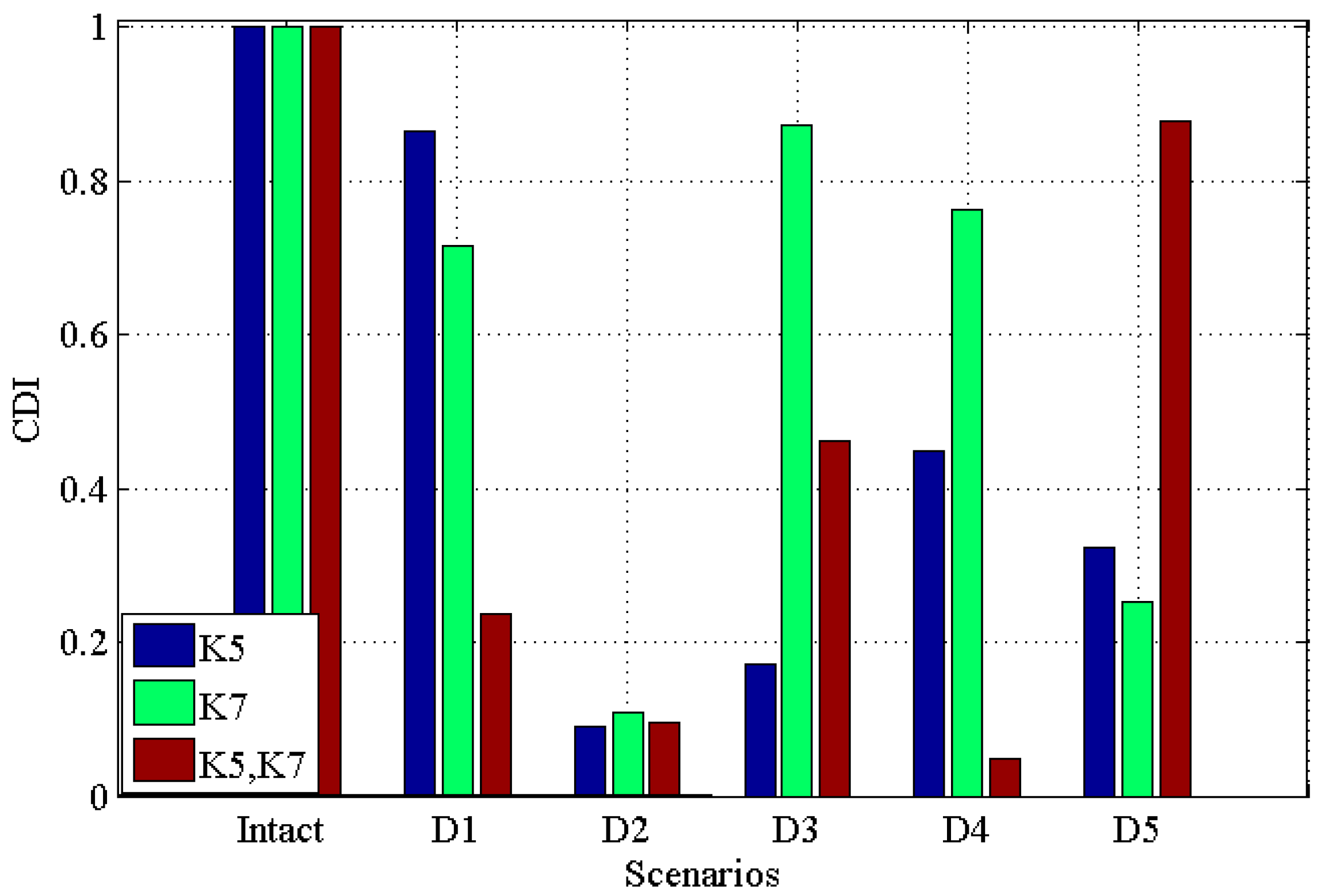
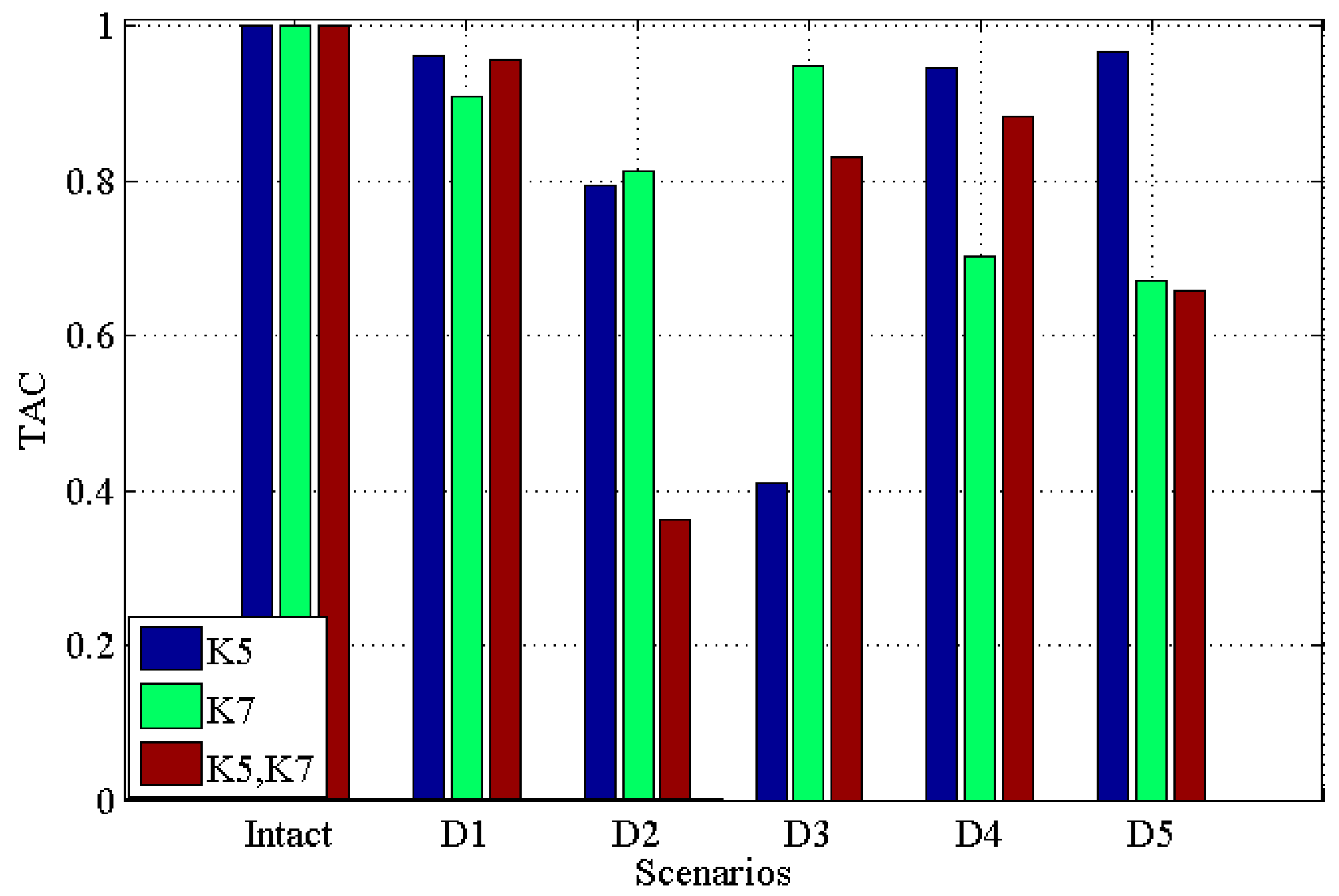
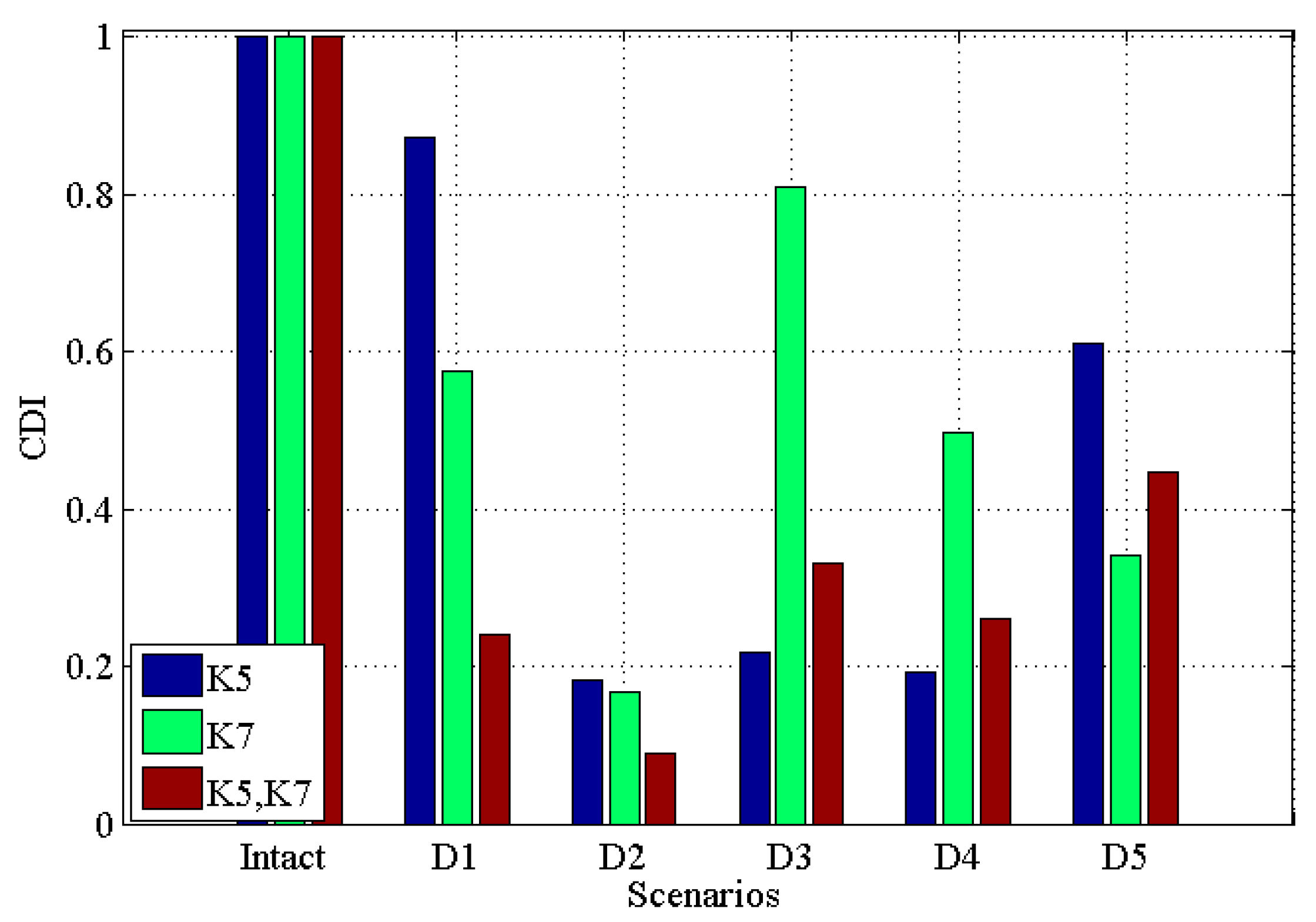
3.2. Results Analysis
3.2.1. Noisy Free Scenarios
3.2.2. Noisy Scenarios
4. Experimental Validation
4.1. Model Description
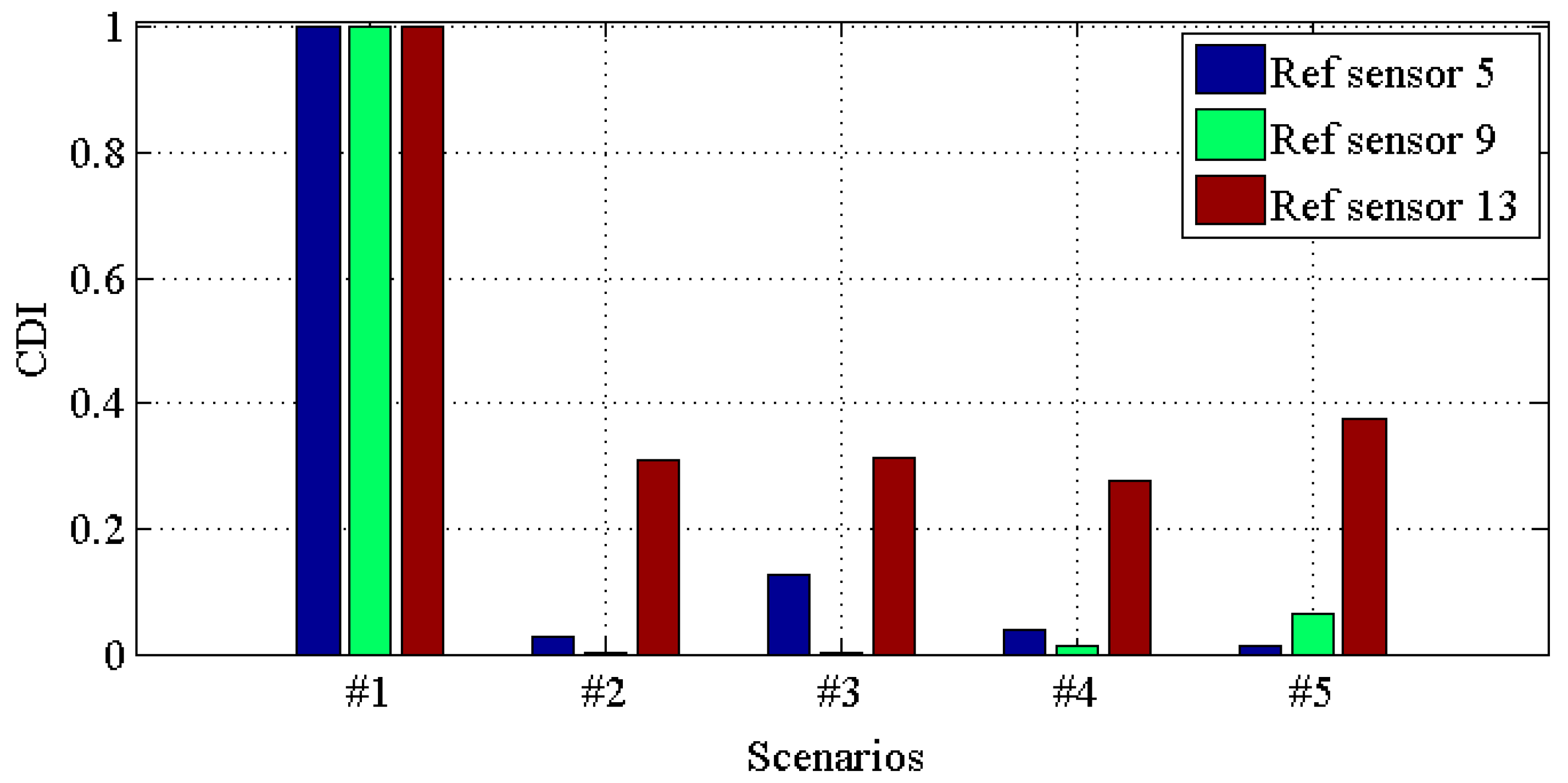
4.2. Result Analysis
5. Conclusions
- (1)
- This study contributed an alternative criteria—CDI—in addition to the conventional damage sensitive indicators, and the correlation coefficient-based indicator CDI proved to be efficient and effective in detecting the structural damages, and it has a good tolerance to noise from the numerical analysis;
- (2)
- The comparison between CDI and TAC proved that both features have a good capacity for identifying structural damages; namely, discriminating structural damages from the baseline—the undamaged scenario—while locating and quantifying the damages would be challenging for both of them;
- (3)
- The proposed approach performs very well in distinguishing minor structural damage, which might be used in real-time SHM. Further investigation with more accurate experiment data is needed to achieve the potential for the locating and quantifying of damages;
- (4)
- For a nonlinear problem such as hysteretic damping, complex geometry and so on, further investigation by extending the proposed approach, such as using further accurate measured damping sensitive data, would give a potential satisfactary solution;
- (5)
- For damage type recognition, i.e., to determine the damage type such as corrosion and cracking, further investigation awaits to unveil the kernel and the potentail application of transmissibiltiy.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Abdelghani, M.; Goursat, M.; Biolchini, T. On-line modal monitoring of aircraft structures under unknown excitation. Mech. Syst. Signal Process. 1999, 13, 839–853. [Google Scholar]
- Sohn, H.; Farrar, C.R.; Hemez, F.M.; Shunk, D.D.; Stinemates, S.W.; Nadler, B.R.; Czarnecki, J.J. A review of structural health monitoring literature from 1996–2001. In Technical Report LA-13976-MS; Los Alamos National Laboratory: Los Alamos, NM, USA, 2004. [Google Scholar]
- Staszewski, W.J.; Boller, C.; Tomlinson, G.R. Health Monitoring of Aerospace Structures; John Wiley & Sons, Ltd.: Chichester, UK, 2004; ISBN 0-470-84340-3. [Google Scholar]
- Ser’eznov, A.N.; Stepanova, L.N.; Tikhonravov, A.B.; Kulikov, E.N.; Kabanov, S.I.; Lebedev, E.Y.; Kozhemyakin, V.L.; Kareev, A.E. Application of the Acoustic-Emission and Strain-Gaging Methods to Testing of the Residual Strength of Airplanes. Russ. J. Nondestruct. Test. 2008, 44, 95–101. [Google Scholar] [CrossRef]
- Dickinson, L.P.; Fletcher, N.H. Acoustic detection of invisible damage in aircraft composite panels. Appl. Acoust. 2009, 70, 110–119. [Google Scholar]
- Jovancevic, I.; Larnier, S.; Orteu, J.-J.; Sentenac, T. Automated exterior inspection of an aircraft with a pan-tilt-zoom camera mounted on a mobile robot. J. Electron. Imaging 2015, 24, 061110. [Google Scholar] [CrossRef]
- Senyurek, V.Y. Detection of cuts and impact damage at the aircraft wing slat by using Lamb wave method. Measurement 2015, 67, 10–23. [Google Scholar]
- Zhou, Y.-L.; Maia, N.M.M.; Wahab, M.A. Damage detection using transmissibility compressed by principal component analysis enhanced with distance measure. J. Vib. Control 2016. [Google Scholar] [CrossRef]
- Zhou, Y.-L.; Wahab, M.A. Rapid early damage detection using transmissibility with distance measure analysis under unknown excitation in long-term health monitoring. J. Vib. 2016, 18, 4491–4499. [Google Scholar]
- Zhou, Y.-L. Structural Health Monitoring by Using Transmissibility. Ph.D. Thesis, Escuela Técnica Superior de Ingenieros Industriales, Madrid, Spain, 2015. [Google Scholar]
- Zhou, Y.-L.; Figueiredo, E.; Maia, N.; Perera, R. Damage detection and quantification using transmissibility coherence analysis. Shock. Vib. 2015, 2015. [Google Scholar] [CrossRef]
- Zhou, Y.-L.; Figueiredo, E.; Maia, N.M.M.; Sampaio, R.; Perera, R. Damage Detection in Structures using a Transmissibility-based Mahalanobis Distance. Struct. Control. Health Monit. 2015, 22, 1209–1222. [Google Scholar]
- Zhou, Y.-L.; Maia, N.M.M.; Sampaio, R.; Wahab, M.A. Structural damage detection using transmissibility together with hierarchical clustering analysis and similarity measure. Struct. Health Monit. 2016. [Google Scholar] [CrossRef]
- Zhou, Y.-L.; Wahab, M.A. Damage detection using vibration data and dynamic transmissibility ensemble with auto-associative neural network. Mechanika 2017, in press. [Google Scholar]
- Zhou, Y.-L.; Wahab, M.A. Cosine based extended transmissibility damage indicators for structural damage detection. Eng. Struct. 2017, 141, 175–183. [Google Scholar] [CrossRef]
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, University of Aalborg, Aalborg, Danemark, 1993. [Google Scholar]
- Chen, S.; Qian, X.D.; Ahmed, A. Cleavage fracture assessment for surface-cracked plates fabricated from high strength steels. Eng. Fract. Mech. 2016, 161, 1–20. [Google Scholar] [CrossRef]
- Qian, X.D.; Li, Y. A compliance-based approach to measure fracture resistance curve for surface cracked steel plates. Int. J. Fract. 2013, 182, 1–19. [Google Scholar] [CrossRef]
- Qian, X.D.; Li, T.P. Effect of residual stresses on the linear-elastic KI–T field for circumferential surface flaws in pipes. Eng. Fract. Mech. 2010, 77, 2682–2697. [Google Scholar] [CrossRef]
- Qian, X.D. KI-T estimations for embedded flaws in pipes e Part I: Axially oriented cracks. Int. J. Press. Vessel. Pip. 2010, 87, 134–149. [Google Scholar] [CrossRef]
- Ahmed, A.; Qian, X.D. A deformation limit based on failure assessment diagram for fatigue-cracked X-joints under in-plane bending. Ships Offshore Struct. 2016, 11, 182–197. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Penna, A.; Magenes, G. Seismic damage diagnosis of a masonry building using short-term damping measurements. J. Sound Vib. 2017, 394, 366–391. [Google Scholar] [CrossRef]
- Cha, Y.-J.; Choi, W.; Büyüköztürk, O. Deep Learning-Based Crack Damage Detection Using Convolutional Neural Networks. Comput.-Aided Civ. Infrastruct. Eng. 2017, 32, 361–378. [Google Scholar] [CrossRef]
- Ribeiro, A.M.R.; Silva, J.M.M.; Maia, N.M.M. On the generalization of the transmissibility concept. Mech. Syst. Signal Process. 2000, 14, 29–35. [Google Scholar] [CrossRef]
- Maia, N.M.M.; Silva, J.M.M.; Ribeiro, A.M.R. The transmissibility concept in multi-degree-of-freedom systems. Mech. Syst. Signal Process. 2001, 15, 129–137. [Google Scholar] [CrossRef]
- Maia, N.; Almeida, R.; Urgueira, A.; Sampaio, R. Damage detection and quantification using transmissibility. Mech. Syst. Signal Process. 2011, 25, 2475–2483. [Google Scholar] [CrossRef]
- Manson, G.; Worden, K.; Allman, D.J. Experimental validation of a structural health monitoring methodology: Part III. Novelty detection on an aircraft wing. J. Sound Vib. 2003, 259, 345–363. [Google Scholar] [CrossRef]
- Maia, N.M.M.; Urgueira, A.P.V.; Almeida, R.A.B. Whys and Wherefores of Transmissibility. In Vibration Analysis and Control—New Trends and Developments; Beltran-Carbajal, F., Ed.; InTech: Munich, Germany, 2011; ISBN 978-953-307-433-7. [Google Scholar]
- Devriendt, C.; de Sitter, G.; Guillaume, P. An operational modal analysis approach based on parametrically identified multivariable transmissibilities. Mech. Syst. Signal Process. 2010, 24, 1250–1259. [Google Scholar] [CrossRef]
- Urgueira, A.P.V.; lmeida, R.A.B.; Maia, N.M.M. On the use of the transmissibility concept for the evaluation of frequency response functions. Mech. Syst. Signal Process. 2011, 25, 940–951. [Google Scholar] [CrossRef]
- Devriendt, C.; Guillaume, P. Identification of modal parameters from transmissibility measurements. J. Sound Vib. 2008, 314, 343–356. [Google Scholar] [CrossRef]
- Devriendt, C.; de Sitter, G.; Vanlanduit, S.; Guillaume, P. Operational modal analysis in the presence of harmonic excitations by the use of transmissibility measurements. Mech. Syst. Signal Process. 2009, 23, 621–635. [Google Scholar] [CrossRef]
- Seki, D. A Novel Damage Index for Fatigue Damage Detection in a Laminated Composites in a Laminated Composites Using Lamb Waves. Master’s Thesis, The University of Alabama, Tuscaloosa, AL, USA, 2015. [Google Scholar]
- Gao, H.; Shi, Y.; Rose, J.L. Guided Wave Tomography on an Aircraft Wing with Leave in Place Sensors. 25–30 July 2004, Golden, Colorado (USA); AIP: College Park, MD, USA, 2005. [Google Scholar]
- Yan, F.; Royer, R.L.; Rose, J.L. Ultrasonic guided wave imaging techniques in structural health monitoring. Intell. Mater. Syst. Struct. 2010, 21, 377–384. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Wahab, M.A.; Perera, R.; Maia, N.; Sampaio, R.; Figueiredo, E. Single side damage simulations and detection in beam-like structures. J. Phys. 2015, 628. [Google Scholar] [CrossRef]
- IASC-ASCE SHM Task Group. Task Group website. Available online: http://bc029049.cityu.edu.hk/asce.shm/wp_home.aspS (accessed on 15 May 2010).
- Johnson, E.A.; Lam, H.F.; Katafygiotis, L.S.; Beck, J.L. A benchmark problem for structural health monitoring and damage detection. In Proceedings of the 14th Engineering Mechanics Conference ASCE, Austin, TX, USA, 21–24 May 2000; Caltech: Pasadena, CA, USA, 2000. [Google Scholar]
- Johnson, E.A.; Lam, H.F.; Katafygiotis, L.S.; Beck, J.L. Phase I IASC-ASCE structural health monitoring benchmark problem using simulated data. J. Eng. Mech. 2004, 130, 3–15. [Google Scholar] [CrossRef]
- Dyke, S.J.; Bernal, D.; Beck, J.L.; Ventura, C. An experimental benchmark problem in structural health monitoring. In Proceedings of the 3rd International Workshop on Structural Health Monitoring, Stanford University, Stanford, CA, USA, 8–10 September 1999; Wiley: New York, NY, USA, 2001. [Google Scholar]

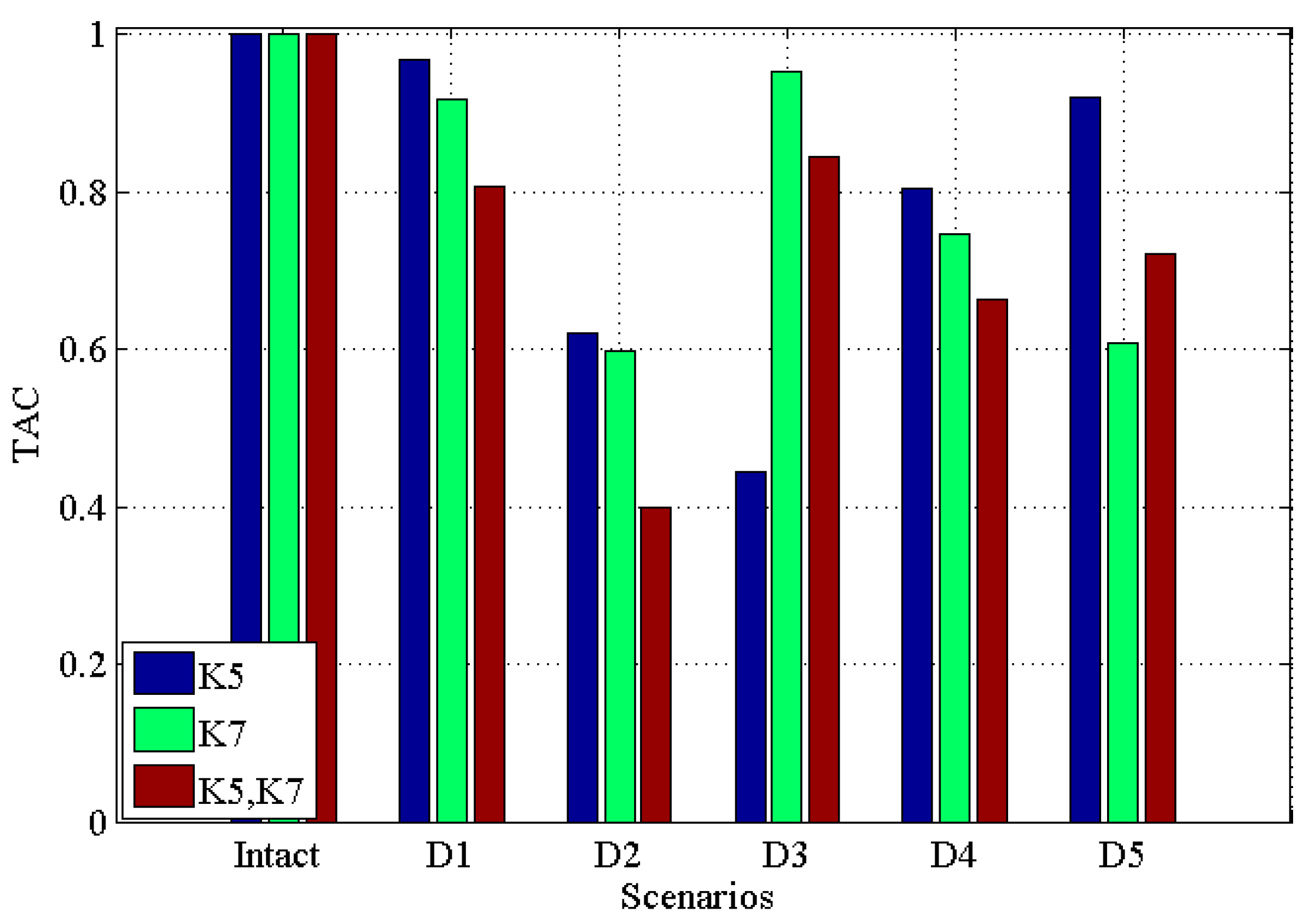
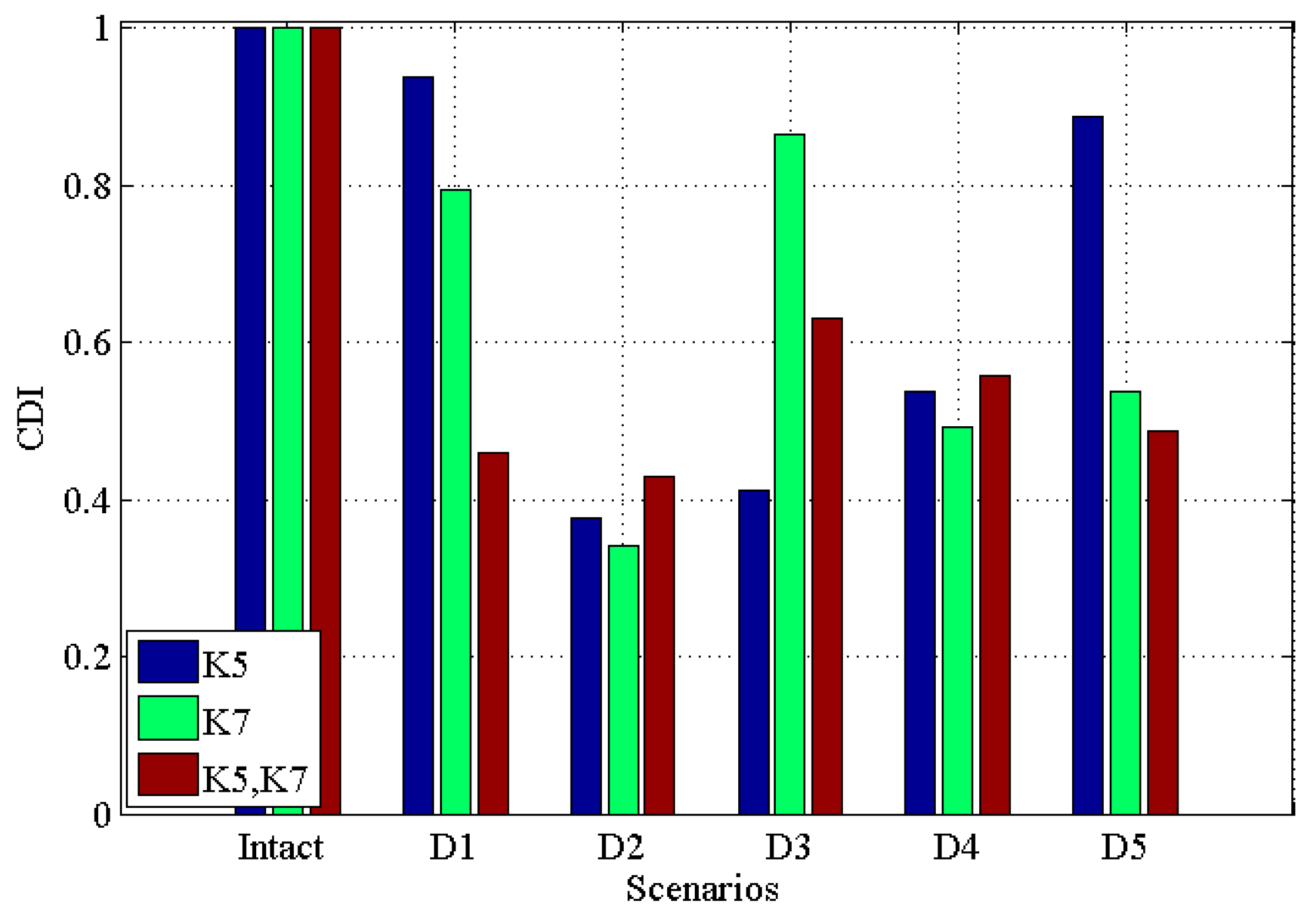
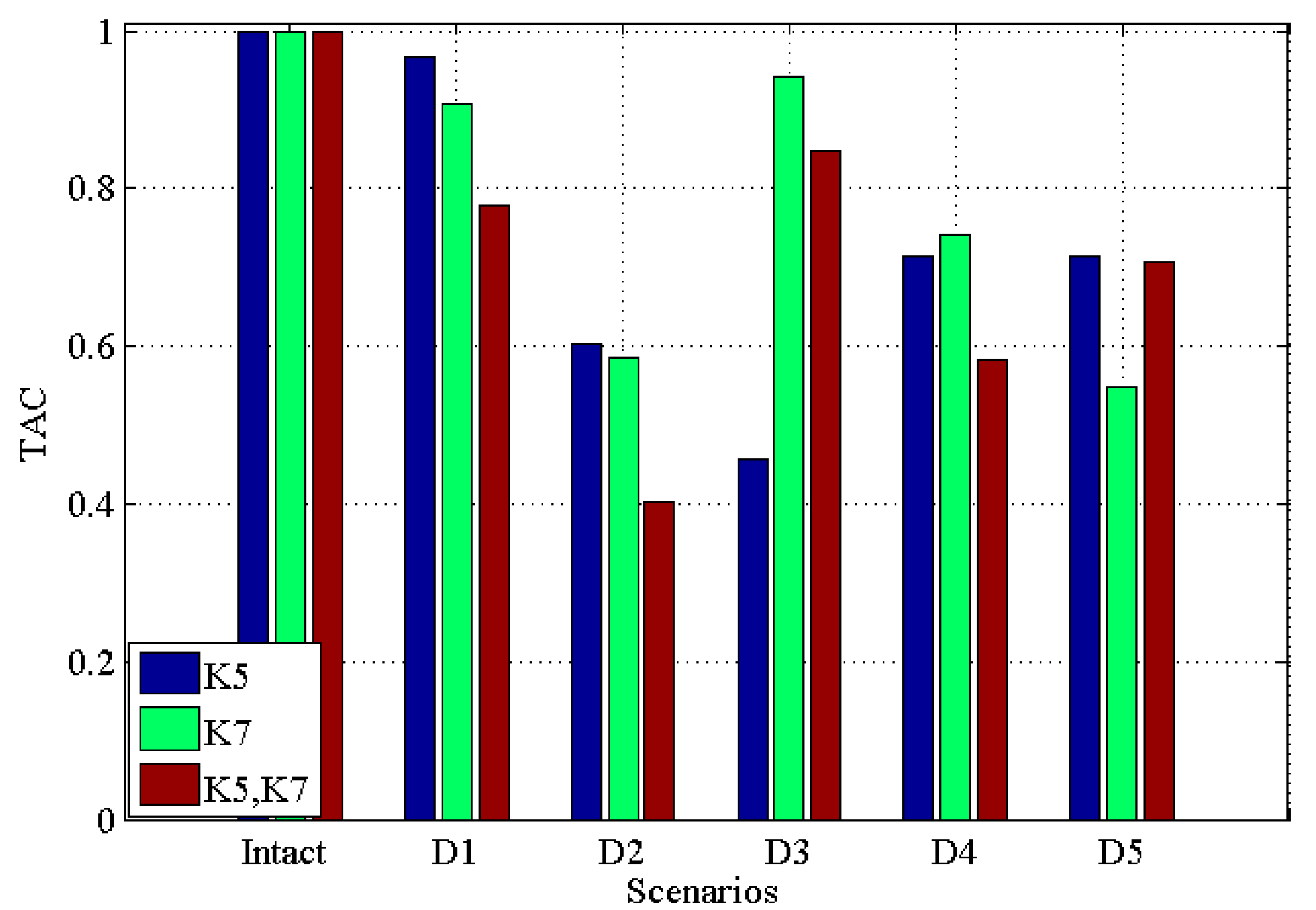


| Damage Scenario | Single Damage | Multiple Damages | |
|---|---|---|---|
| Stiffness Reduction K5 | Stiffness Reduction K7 | Stiffness Reduction K5 and K7 | |
| Intact | 0 | - | - |
| D1 | 2% | 2% | 2% |
| D2 | 5% | 5% | 5% |
| D3 | 10% | 10% | 10% |
| D4 | 15% | 15% | 15% |
| D5 | 20% | 20% | 20% |
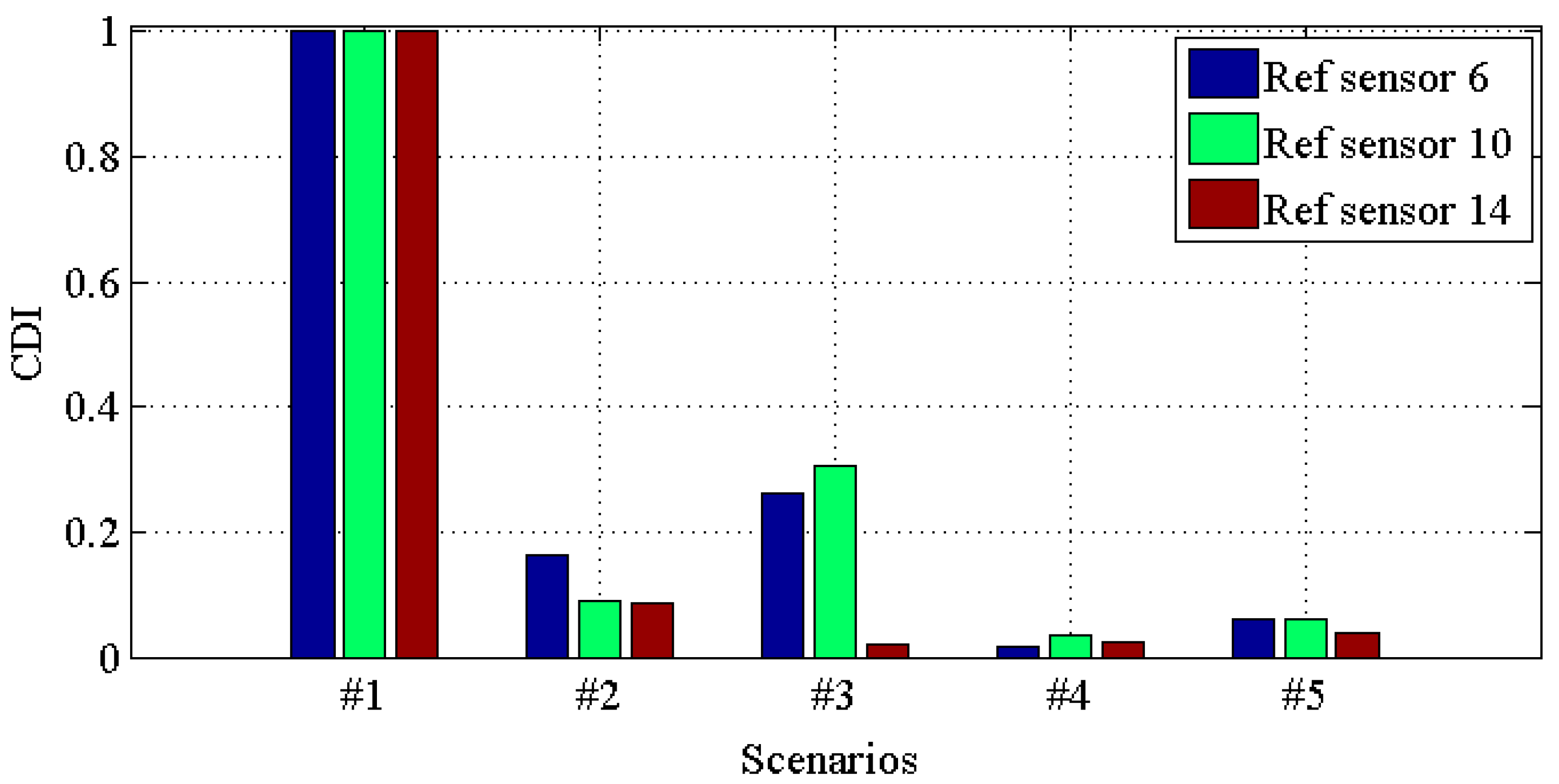
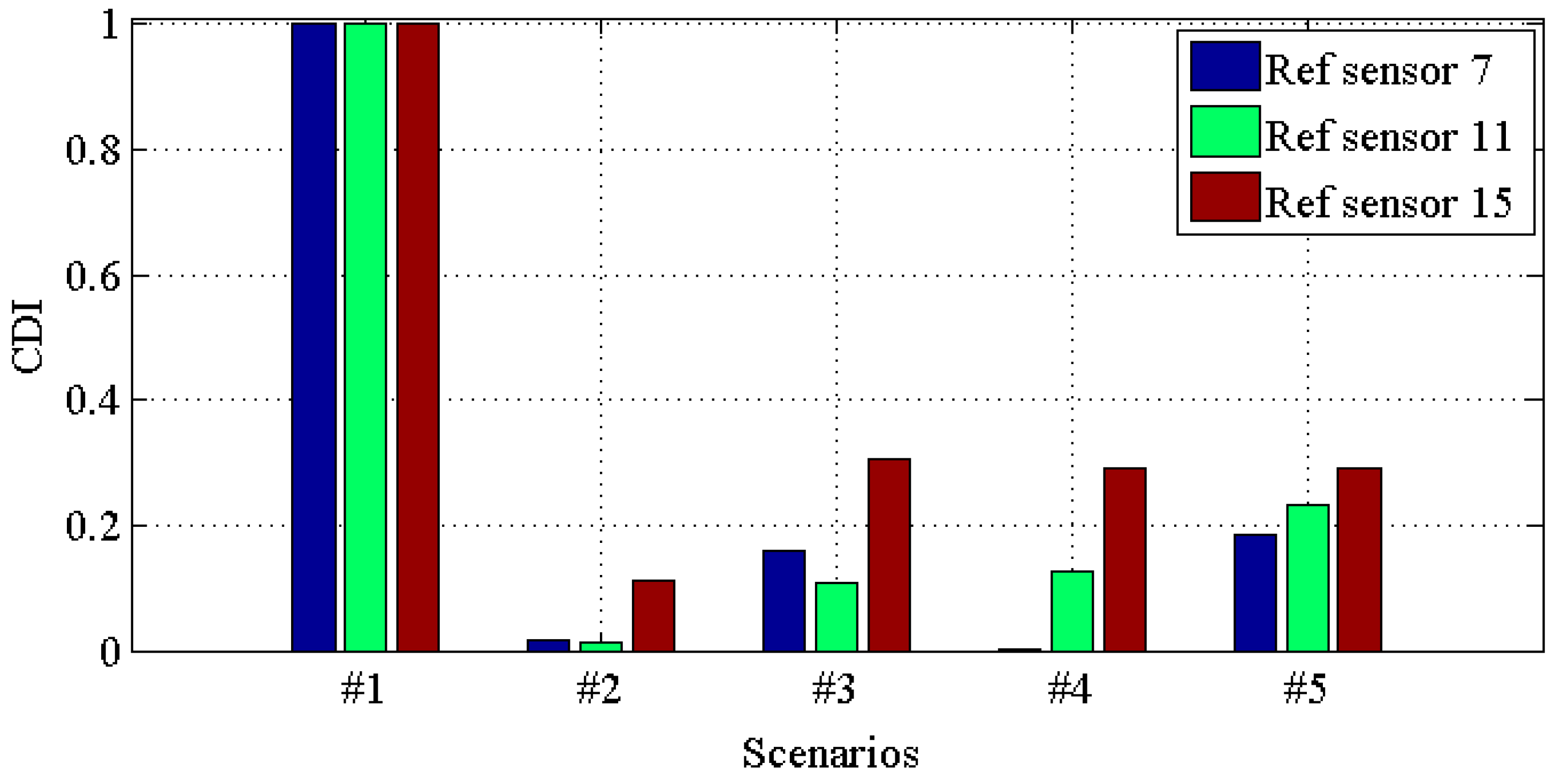
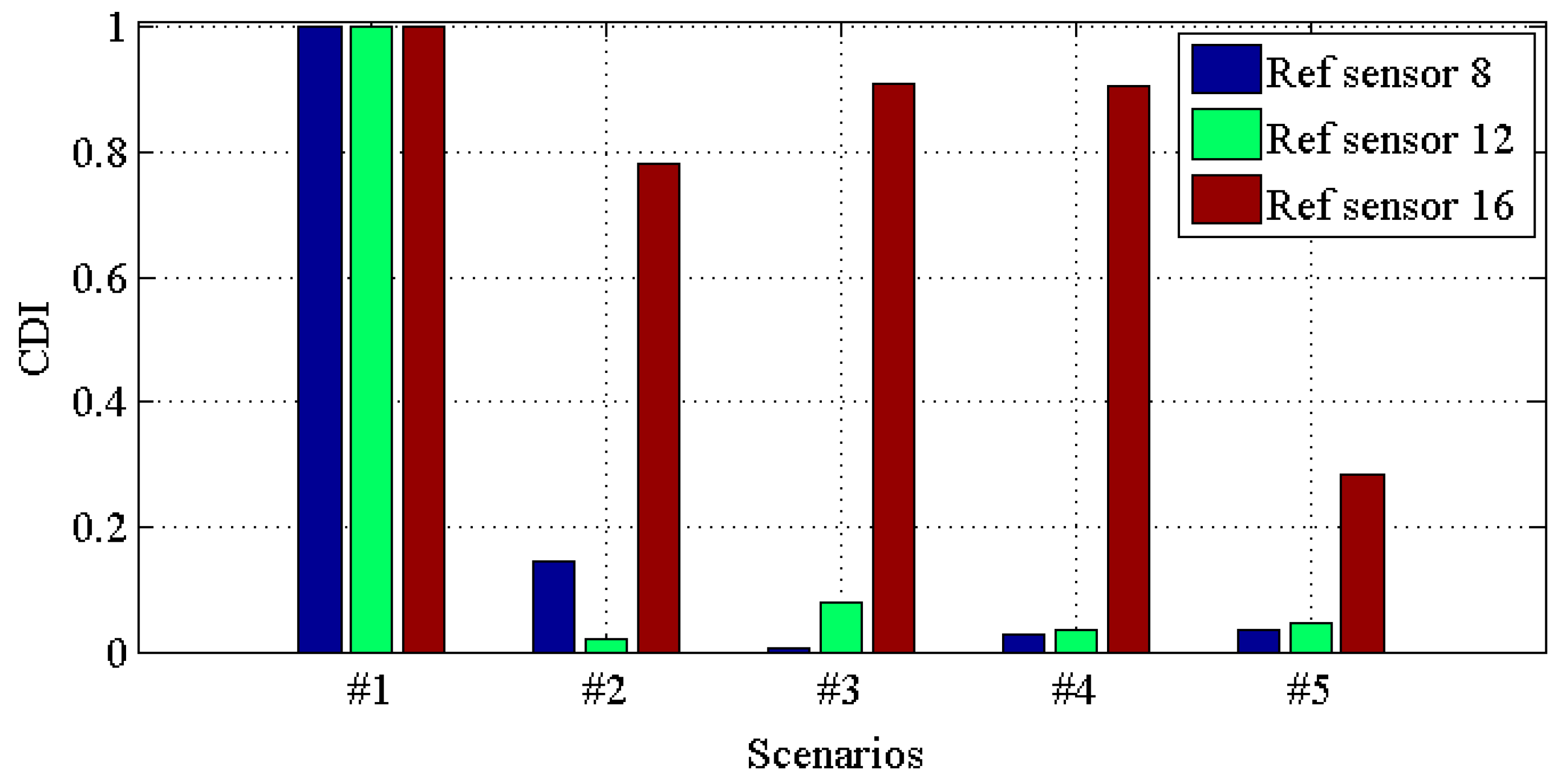
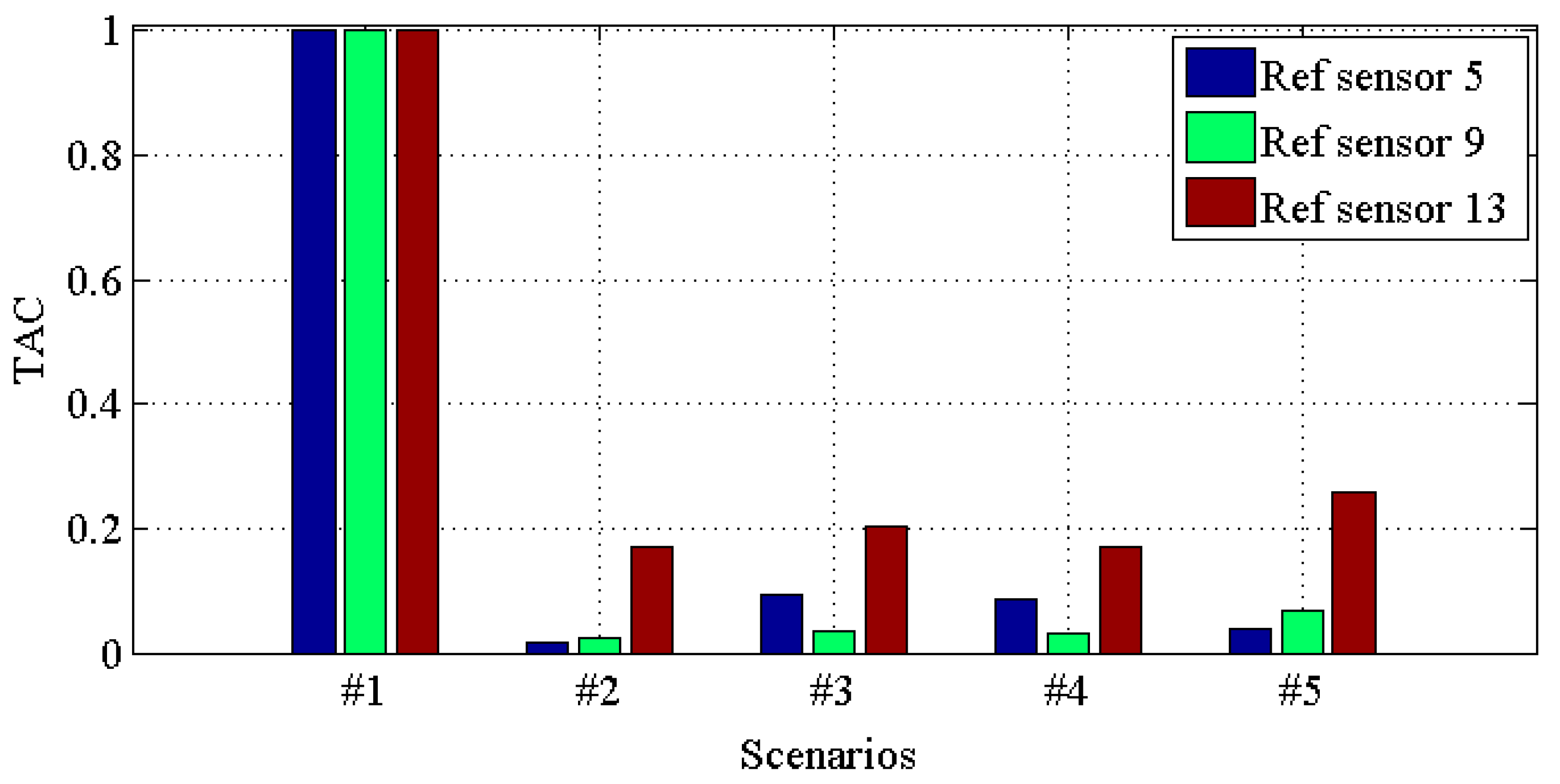
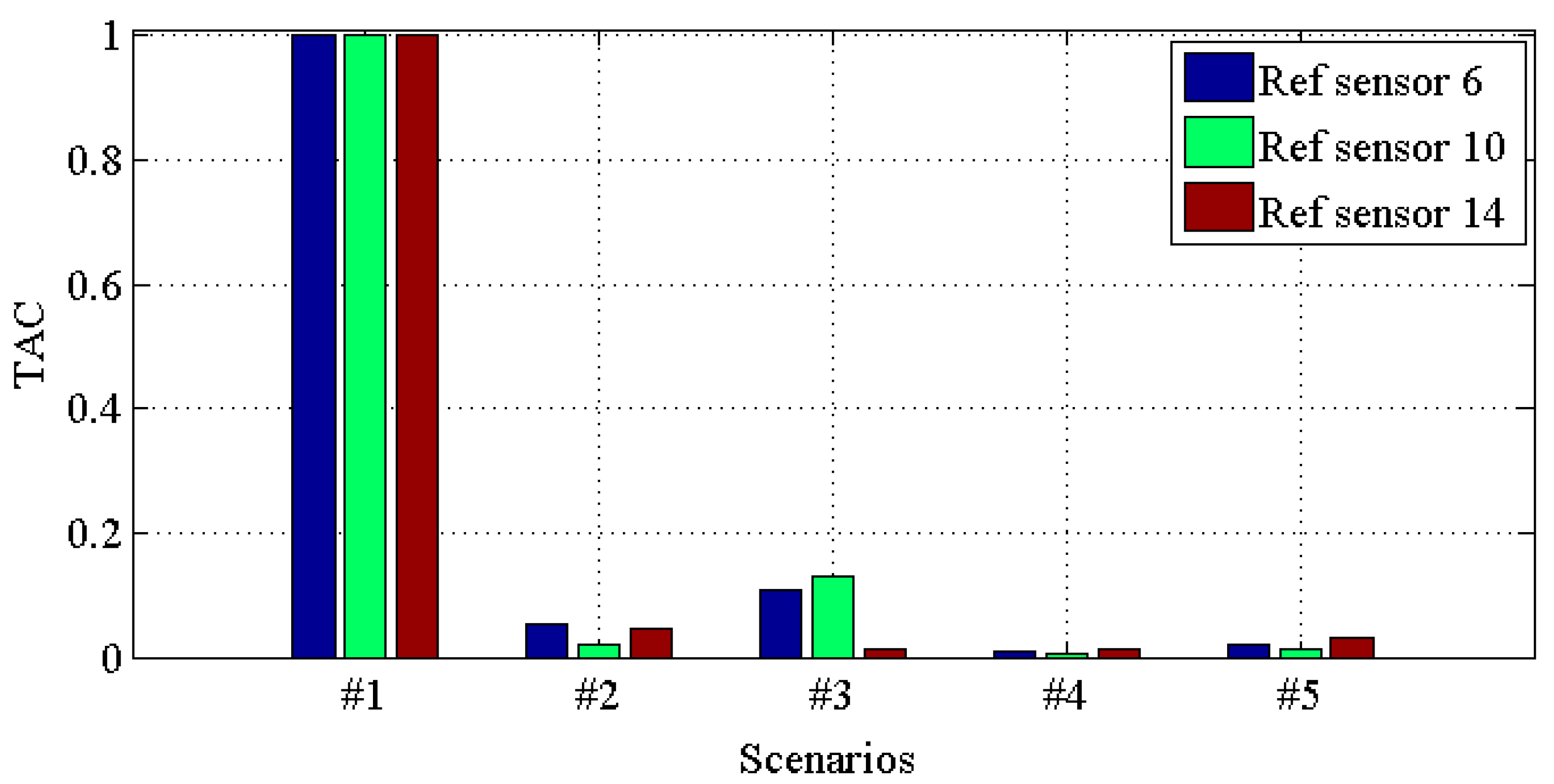
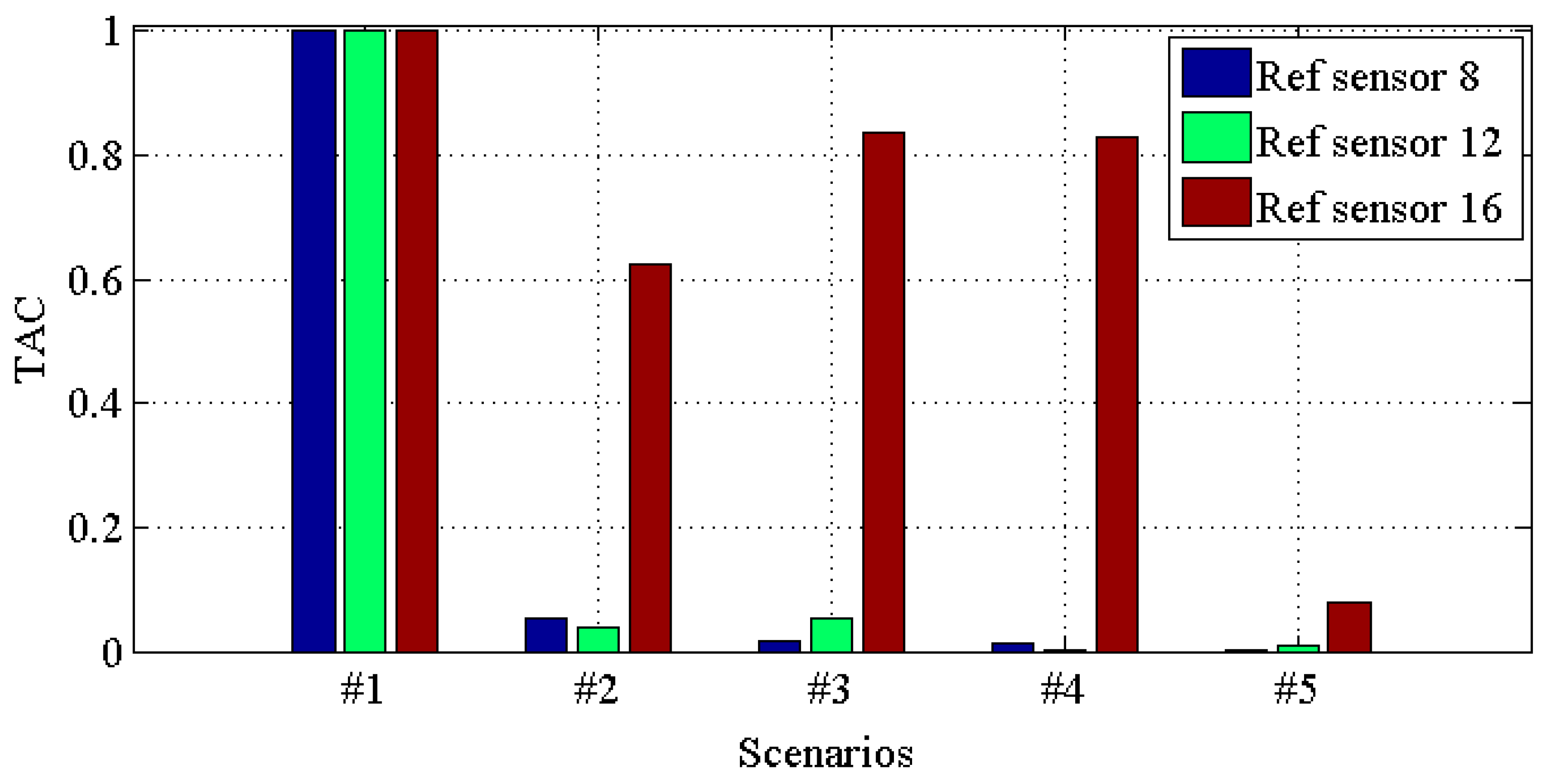
| Damage Scenario | Case Description |
|---|---|
| #1 | All braces |
| #2 | Missing all east side braces |
| #3 | Case #2 + remove one brace on floor 1 |
| #4 | Case #3 + remove one brace on floor 3 |
| #5 | Case #4 + loosen one connection |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.-L.; Cao, H.; Liu, Q.; Wahab, M.A. Output-Based Structural Damage Detection by Using Correlation Analysis Together with Transmissibility. Materials 2017, 10, 866. https://doi.org/10.3390/ma10080866
Zhou Y-L, Cao H, Liu Q, Wahab MA. Output-Based Structural Damage Detection by Using Correlation Analysis Together with Transmissibility. Materials. 2017; 10(8):866. https://doi.org/10.3390/ma10080866
Chicago/Turabian StyleZhou, Yun-Lai, Hongyou Cao, Quanmin Liu, and Magd Abdel Wahab. 2017. "Output-Based Structural Damage Detection by Using Correlation Analysis Together with Transmissibility" Materials 10, no. 8: 866. https://doi.org/10.3390/ma10080866
APA StyleZhou, Y.-L., Cao, H., Liu, Q., & Wahab, M. A. (2017). Output-Based Structural Damage Detection by Using Correlation Analysis Together with Transmissibility. Materials, 10(8), 866. https://doi.org/10.3390/ma10080866






