Fatigue Damage Evaluation Using Nonlinear Lamb Waves with Quasi Phase-Velocity Matching at Low Frequency
Abstract
1. Introduction
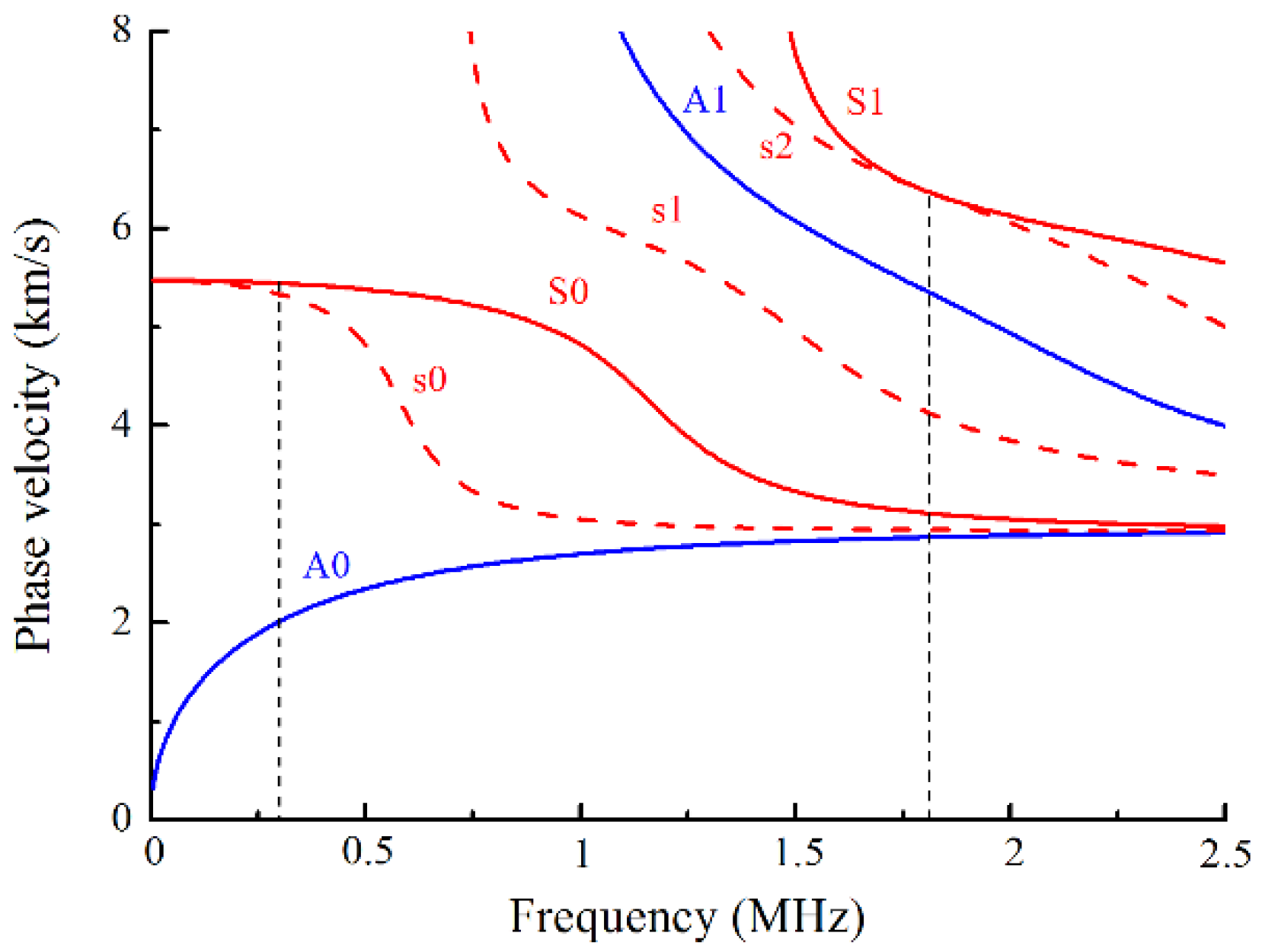
2. Theoretical Considerations
3. Experimental Details
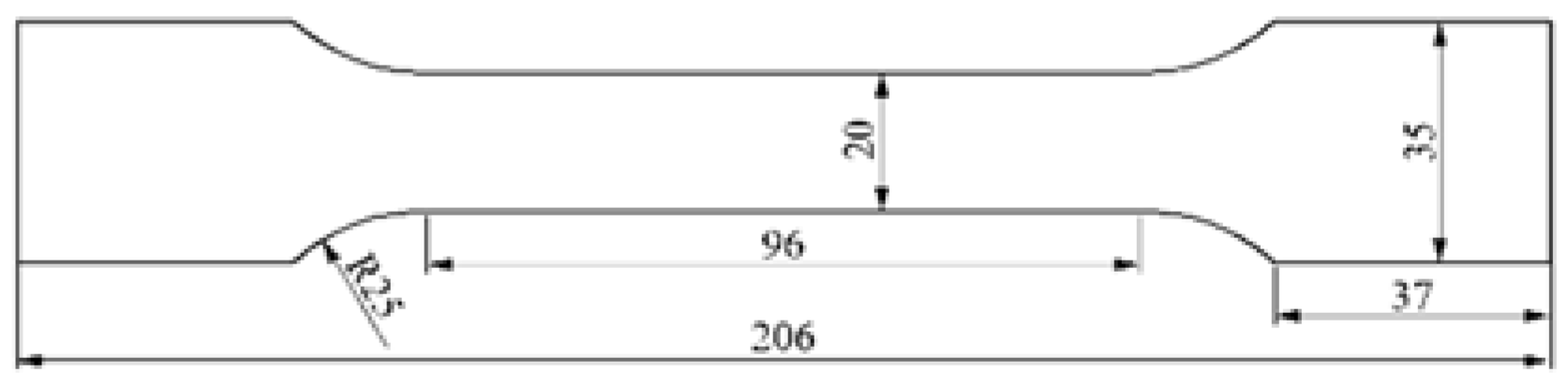
3.1. Low Cycle Fatigue Test
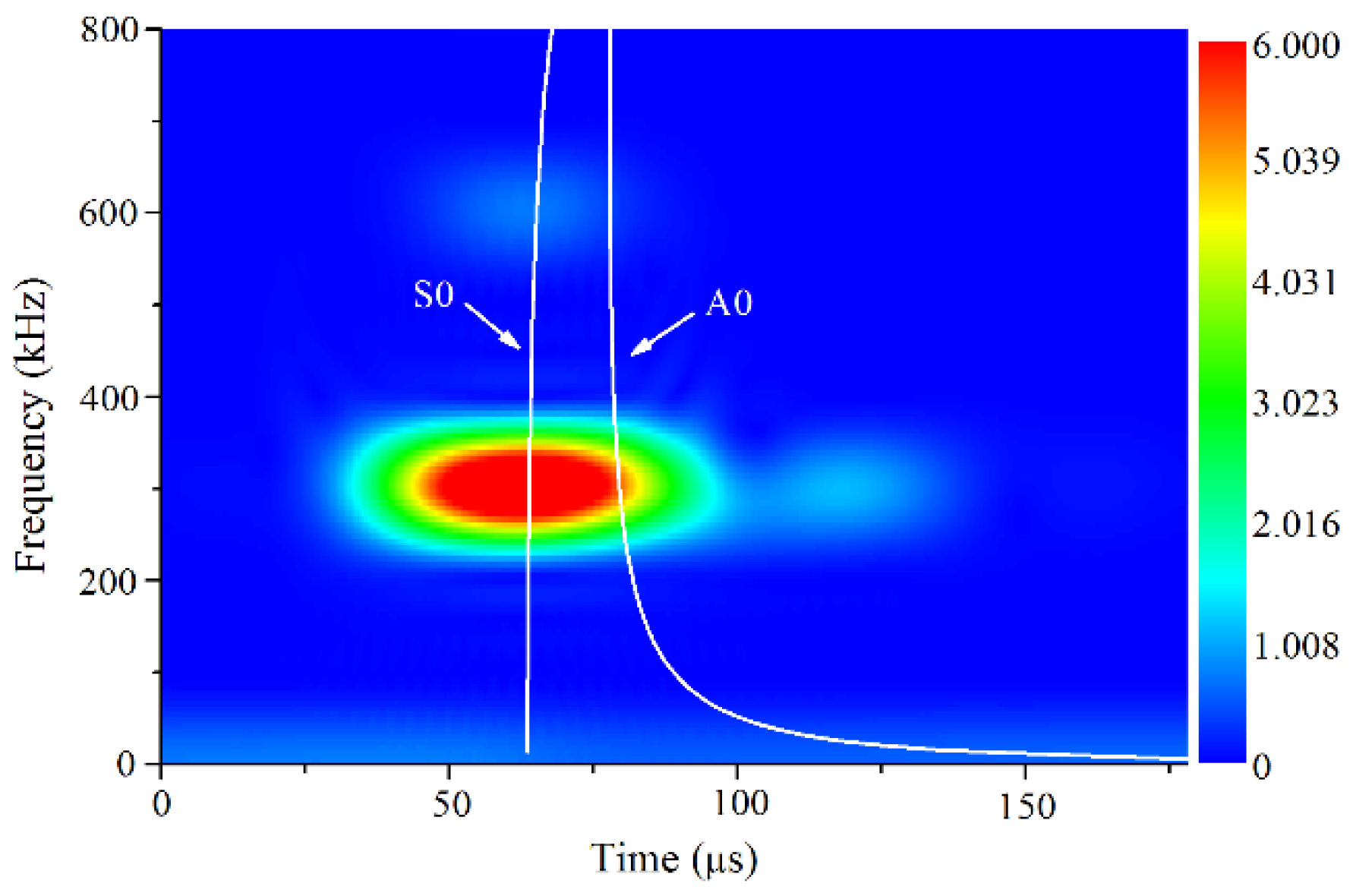
3.2. Nonlinear Lamb Wave Measurements
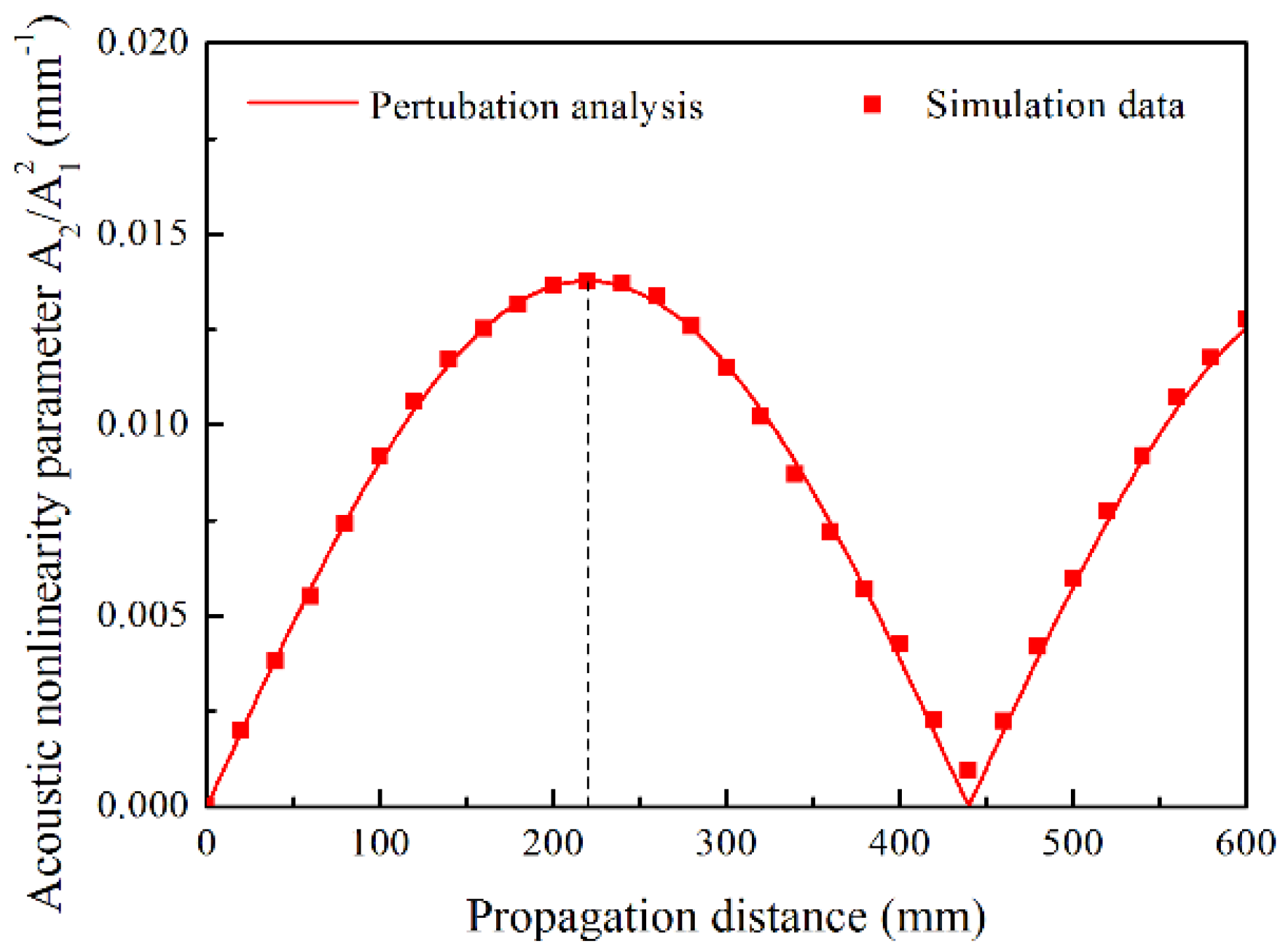
4. Simulation Deployments
5. Results and Discussions
5.1. Cumulative Generation of Second Harmonics
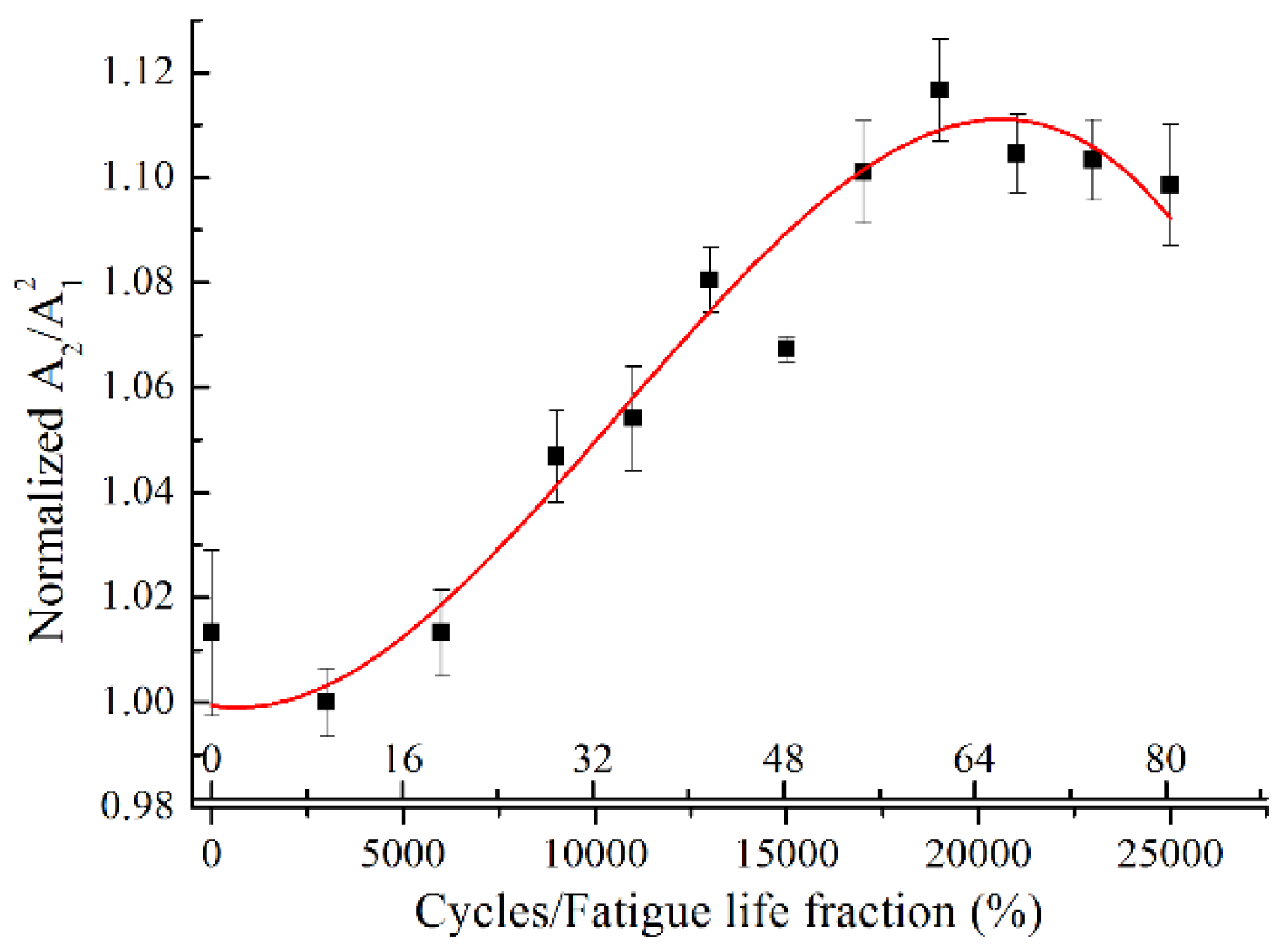
5.2. Fatigue Damage Evaluation
5.3. Analyses of Sensitivity
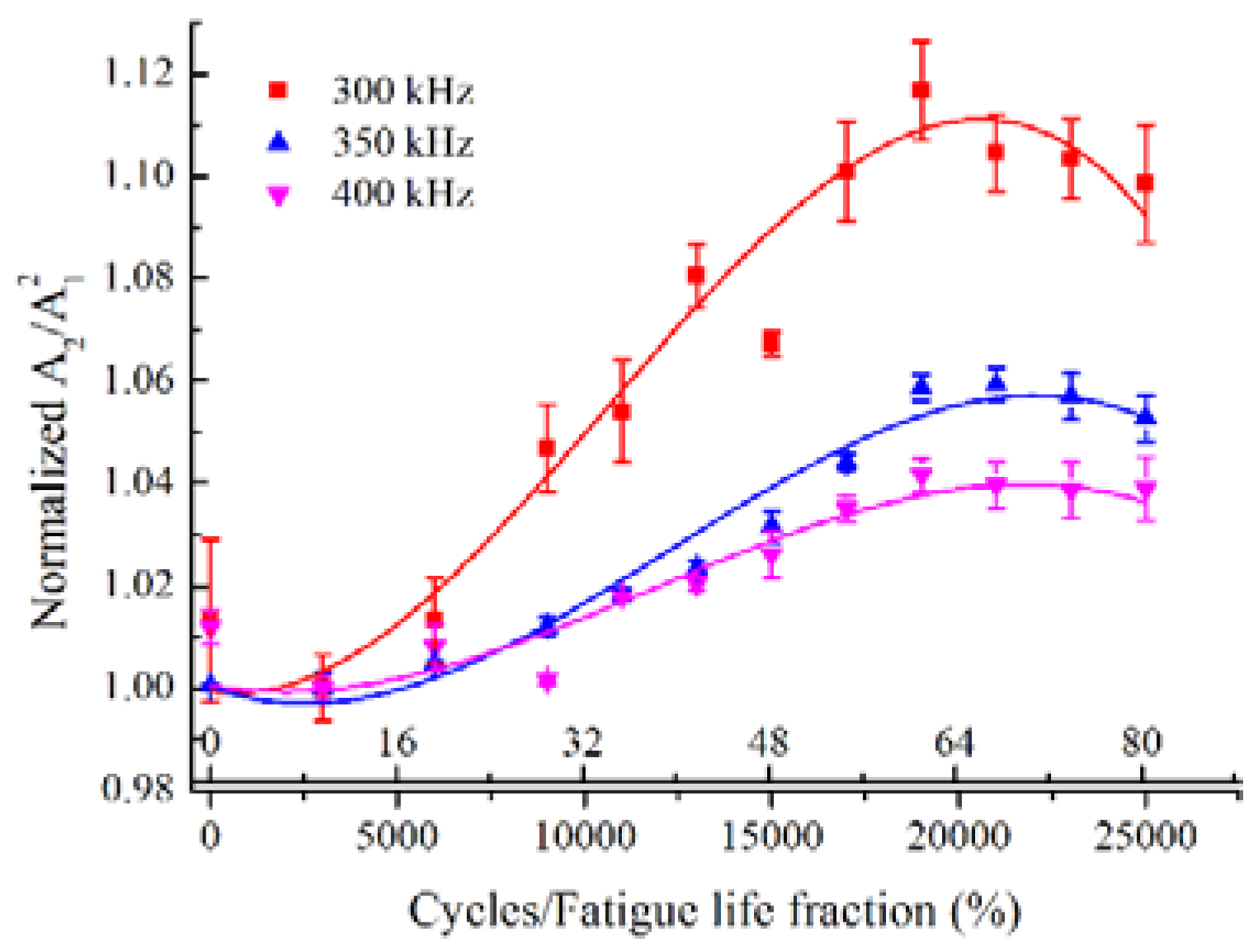
5.4. Effect of Frequency
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations/Nomenclature
| Nomenclature | |||
| A/B/C | third order elastic constants | k | wave number |
| A1 | amplitude of primary wave | N | fatigue cycles |
| A2 | amplitude of second harmonic wave | R | stress ratio |
| magnitude of nth double frequency Lamb wave | U0 | excitation displacement amplitude | |
| A(t) | temporal waveform | w | angular velocity |
| B(Y) | thickness profile | v | Poisson’s ratio |
| c | group velocity | z | propagation distance |
| cl | longitudinal wave velocity | zn | half the oscillation spatial period |
| phase velocity of primary wave | α | scale factor | |
| phase velocity of second harmonic wave | β | absolute nonlinearity parameter | |
| ct | transverse wave velocity | ρ | density |
| Δd | element size | σmax | maximum stress |
| E | elasticity modulus | σ0.2 | yield stress |
| Abbreviations | |||
| SHG | second harmonic generation | FE | finite element |
| DFLW | double frequency Lamb wave | STFT | short time Fourier transform |
References
- Chillara, V.K.; Lissenden, C.J. Review of nonlinear ultrasonic guided wave nondestructive evaluation: Theory, numerics, and experiments. Opt. Eng. 2016, 55, 011002. [Google Scholar] [CrossRef]
- Jhang, K.-Y. Nonlinear ultrasonic techniques for nondestructive assessment of micro damage in material: A review. Int. J. Precis. Eng. Manuf. 2009, 10, 123–135. [Google Scholar] [CrossRef]
- Deng, M. Analysis of second-harmonic generation of Lamb modes using a modal analysis approach. J. Appl. Phys. 2003, 94, 4152. [Google Scholar] [CrossRef]
- De Lima, W.J.N.; Hamilton, M.F. Finite-amplitude waves in isotropic elastic plates. J. Sound Vib. 2003, 265, 819–839. [Google Scholar] [CrossRef]
- De Lima, W.J. Harmonic Generation in Isotropic Elastic Waveguides. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, January 2000. [Google Scholar]
- Zhao, J.; Chillara, V.K.; Ren, B.; Cho, H.; Qiu, J.; Lissenden, C.J. Second harmonic generation in composites: Theoretical and numerical analyses. J. Appl. Phys. 2016, 119, 064902. [Google Scholar] [CrossRef]
- Matsuda, N.; Biwa, S. Phase and group velocity matching for cumulative harmonic generation in Lamb waves. J. Appl. Phys. 2011, 109, 094903. [Google Scholar] [CrossRef]
- Chillara, V.K.; Lissenden, C.J. Interaction of guided wave modes in isotropic weakly nonlinear elastic plates: Higher harmonic generation. J. Appl. Phys. 2012, 111, 124909. [Google Scholar] [CrossRef]
- Bender, F.A.; Kim, J.-Y.; Jacobs, L.J.; Qu, J. The generation of second harmonic waves in an isotropic solid with quadratic nonlinearity under the presence of a stress-free boundary. Wave Motion 2013, 50, 146–161. [Google Scholar] [CrossRef]
- Liu, M.; Wang, K.; Lissenden, C.; Wang, Q.; Zhang, Q.; Long, R.; Su, Z.; Cui, F. Characterizing hypervelocity impact (HVI)-induced pitting damage using active guided ultrasonic waves: From linear to nonlinear. Materials 2017, 10, 547. [Google Scholar] [CrossRef] [PubMed]
- Rauter, N.; Lammering, R.; Kühnrich, T. On the detection of fatigue damage in composites by use of second harmonic guided waves. Compos. Struct. 2016, 152, 247–258. [Google Scholar] [CrossRef]
- Metya, A.K.; Ghosh, M.; Parida, N.; Balasubramaniam, K. Effect of tempering temperatures on nonlinear Lamb wave signal of modified 9Cr-1Mo steel. Mater. Charact. 2015, 107, 14–22. [Google Scholar] [CrossRef]
- Lim, H.; Sohn, H. Necessary conditions for nonlinear ultrasonic modulation generation given a localized fatigue crack in a plate-like structure. Materials 2017, 10, 248. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.; Lanza di Scalea, F. On the existence of antisymmetric or symmetric Lamb waves at nonlinear higher harmonics. J. Sound Vib. 2009, 323, 932–943. [Google Scholar] [CrossRef]
- Sun, X.; Liu, X.; Liu, Y.; Hu, N.; Zhao, Y.; Ding, X.; Qin, S.; Zhang, J.; Zhang, J.; Liu, F.; et al. Simulations on Monitoring and Evaluation of Plasticity-Driven Material Damage Based on Second Harmonic of S0 Mode Lamb Waves in Metallic Plates. Materials 2017, 10, 827. [Google Scholar] [CrossRef] [PubMed]
- Wan, X.; Tse, P.W.; Xu, G.H.; Tao, T.F.; Zhang, Q. Analytical and numerical studies of approximate phase velocity matching based nonlinear S0 mode Lamb waves for the detection of evenly distributed microstructural changes. Smart Mater. Struct. 2016, 25, 045023. [Google Scholar] [CrossRef]
- Zuo, P.; Zhou, Y.; Fan, Z. Numerical and experimental investigation of nonlinear ultrasonic Lamb waves at low frequency. Appl. Phys. Lett. 2016, 109, 021902. [Google Scholar] [CrossRef]
- Matsuda, N.; Biwa, S. Frequency dependence of second-harmonic generation in Lamb waves. J. Nondestruct. Eval. 2014, 33, 169–177. [Google Scholar] [CrossRef]
- Chillara, V.K.; Lissenden, C.J. Nonlinear guided waves in plates: A numerical perspective. Ultrasonics 2014, 54, 1553–1558. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Xiang, Y.; Liu, C.J.; Deng, M.; Xuan, F.Z. Symmetry properties of second harmonics generated by antisymmetric Lamb waves. J. Appl. Phys. 2018, 123, 104902. [Google Scholar] [CrossRef]
- Xiao, H.; Shen, Y.; Xiao, L.; Qu, W.; Lu, Y. Damage detection in composite structures with high-damping materials using time reversal method. Nondestruct. Test. Eval. 2018, 33, 329–345. [Google Scholar] [CrossRef]
- Chronopoulos, D. Calculation of guided wave interaction with nonlinearities and generation of harmonics in composite structures through a wave finite element method. Compos. Struct. 2018, 186, 375–384. [Google Scholar] [CrossRef]
- Gomes, G.F.; Mendéz, Y.A.D.; da Silva Lopes Alexandrino, P.; da Cunha, S.S.; Ancelotti, A.C. The use of intelligent computational tools for damage detection and identification with an emphasis on composites—A review. Compos. Struct. 2018, 196, 44–54. [Google Scholar] [CrossRef]
- Nagy, P.B. Fatigue damage assessment by nonlinear ultrasonic materials characterization. Ultrasonics 1998, 36, 375–381. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Nonlinear ultrasonic characterization of fatigue microstructures. Int. J. Fatigue 2001, 23, 487–490. [Google Scholar] [CrossRef]
- Zhang, J.; Xuan, F.-Z. Fatigue damage evaluation of austenitic stainless steel using nonlinear ultrasonic waves in low cycle regime. J. Appl. Phys. 2014, 115, 204906. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Jacobs, L.J.; Qu, J.; Littles, J.W. Experimental characterization of fatigue damage in a nickel-base superalloy using nonlinear ultrasonic waves. J. Acoust. Soc. Am. 2006, 120, 1266. [Google Scholar] [CrossRef]
- Jhang, K.-Y.; Kim, K.-C. Evaluation of material degradation using nonlinear acoustic effect. Ultrasonics 1999, 37, 39–44. [Google Scholar] [CrossRef]
- Cantrell, J.H. Dependence of microelastic-plastic nonlinearity of martensitic stainless steel on fatigue damage accumulation. J. Appl. Phys. 2006, 100, 063508. [Google Scholar] [CrossRef]
- Deng, M.; Pei, J. Assessment of accumulated fatigue damage in solid plates using nonlinear Lamb wave approach. Appl. Phys. Lett. 2007, 90, 121902. [Google Scholar] [CrossRef]
- Pruell, C.; Kim, J.-Y.; Qu, J.; Jacobs, L.J. Evaluation of fatigue damage using nonlinear guided waves. Smart Mater. Struct. 2009, 18, 035003. [Google Scholar] [CrossRef]
- Zhu, W.; Xiang, Y.; Liu, C.J.; Deng, M.; Xuan, F.Z. A feasibility study on fatigue damage evaluation using nonlinear Lamb waves with group-velocity mismatching. Ultrasonics 2018, 90, 18–22. [Google Scholar] [CrossRef] [PubMed]
- Auld, B.A. Acoustic Fields and Waves in Solids; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Sewell, G. The Numerical Solution of Ordinary and Partial Differential Equations; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Matlack, K.H.; Kim, J.Y.; Jacobs, L.J.; Qu, J. Review of second harmonic generation measurement techniques for material state determination in metals. J. Nondestruct. Eval. 2014, 34, 273. [Google Scholar] [CrossRef]
- Cantrell, J.H. Substructural organization, dislocation plasticity and harmonic generation in cyclically stressed wavy slip metals. Proc. R. Soc. A 2004, 460, 757–780. [Google Scholar] [CrossRef]
- Hikata, A.; Chick, B.B.; Elbaum, C. Dislocation contribution to the second harmonic generation of ultrasonic waves. J. Appl. Phys. 1965, 36, 229. [Google Scholar] [CrossRef]
- Wan, X.; Zhang, Q.; Xu, G.; Tse, P.W. Numerical simulation of nonlinear Lamb waves used in a thin plate for detecting buried micro-cracks. Sensors 2014, 14, 8528–8546. [Google Scholar] [CrossRef] [PubMed]
- Jiao, J.; Meng, X.; He, C.; Wu, B. Nonlinear Lamb wave-mixing technique for micro-crack detection in plates. NDT E Int. 2017, 85, 63–71. [Google Scholar] [CrossRef]
- Bermes, C.; Kim, J.-Y.; Qu, J.; Jacobs, L.J. Nonlinear Lamb waves for the detection of material nonlinearity. Mech. Syst. Signal Process. 2008, 22, 638–646. [Google Scholar] [CrossRef]
- Xiang, Y.; Deng, M.; Xuan, F.Z.; Liu, C.J. Effect of precipitate-dislocation interactions on generation of nonlinear Lamb waves in creep-damaged metallic alloys. J. Appl. Phys. 2012, 111, 104905. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhu, W.; Deng, M.; Xuan, F.Z.; Liu, C.J. Generation of cumulative second-harmonic ultrasonic guided waves with group velocity mismatching Numerical analysis and experimental validation. Europhys. Lett. 2016, 116, 34001. [Google Scholar] [CrossRef]

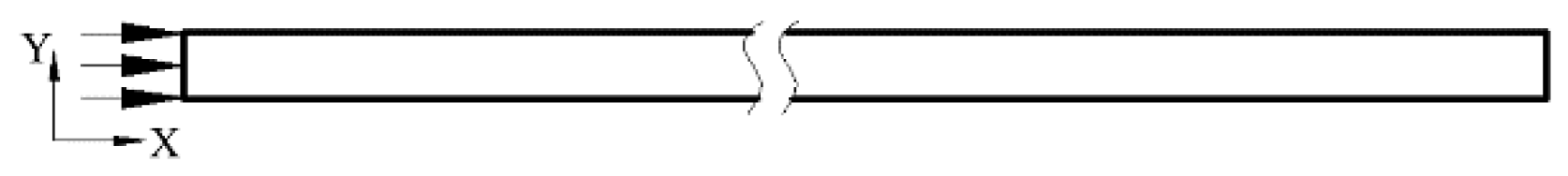



| Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti | Al |
|---|---|---|---|---|---|---|---|---|
| 0.085 | 0.176 | 1.654 | 0.069 | 2.611 | 0.200 | 5.768 | 0.0438 | Bal. |
| Specimen | σmax (MPa) | R | N (cycles) | Life Fraction (%) |
|---|---|---|---|---|
| 1 | 349.8 | 0.1 | 3000 | 9.65 |
| 2 | 349.8 | 0.1 | 6000 | 19.29 |
| 3 | 349.8 | 0.1 | 9000 | 28.94 |
| 4 | 349.8 | 0.1 | 11,000 | 35.37 |
| 5 | 349.8 | 0.1 | 13,000 | 41.80 |
| 6 | 349.8 | 0.1 | 15,000 | 48.23 |
| 7 | 349.8 | 0.1 | 17,000 | 54.67 |
| 8 | 349.8 | 0.1 | 19,000 | 61.10 |
| 9 | 349.8 | 0.1 | 21,000 | 67.53 |
| 10 | 349.8 | 0.1 | 23,000 | 73.96 |
| 11 | 349.8 | 0.1 | 25,000 | 80.39 |
| ρ (kg/m3) | E (GPa) | v | σ0.2 (GPa) | cl (m/s) | ct (m/s) | A (GPa) | B (GPa) | C (GPa) |
|---|---|---|---|---|---|---|---|---|
| 2757.82 | 73.1 | 0.34 | 318 | 6372.70 | 3146.18 | −351.2 | −149.4 | −102.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Xiang, Y.; Liu, C.-j.; Deng, M.; Ma, C.; Xuan, F.-z. Fatigue Damage Evaluation Using Nonlinear Lamb Waves with Quasi Phase-Velocity Matching at Low Frequency. Materials 2018, 11, 1920. https://doi.org/10.3390/ma11101920
Zhu W, Xiang Y, Liu C-j, Deng M, Ma C, Xuan F-z. Fatigue Damage Evaluation Using Nonlinear Lamb Waves with Quasi Phase-Velocity Matching at Low Frequency. Materials. 2018; 11(10):1920. https://doi.org/10.3390/ma11101920
Chicago/Turabian StyleZhu, Wujun, Yanxun Xiang, Chang-jun Liu, Mingxi Deng, Congyun Ma, and Fu-zhen Xuan. 2018. "Fatigue Damage Evaluation Using Nonlinear Lamb Waves with Quasi Phase-Velocity Matching at Low Frequency" Materials 11, no. 10: 1920. https://doi.org/10.3390/ma11101920
APA StyleZhu, W., Xiang, Y., Liu, C.-j., Deng, M., Ma, C., & Xuan, F.-z. (2018). Fatigue Damage Evaluation Using Nonlinear Lamb Waves with Quasi Phase-Velocity Matching at Low Frequency. Materials, 11(10), 1920. https://doi.org/10.3390/ma11101920





