Estimation of the Onset of Crack Growth in Ductile Materials
Abstract
:1. Introduction
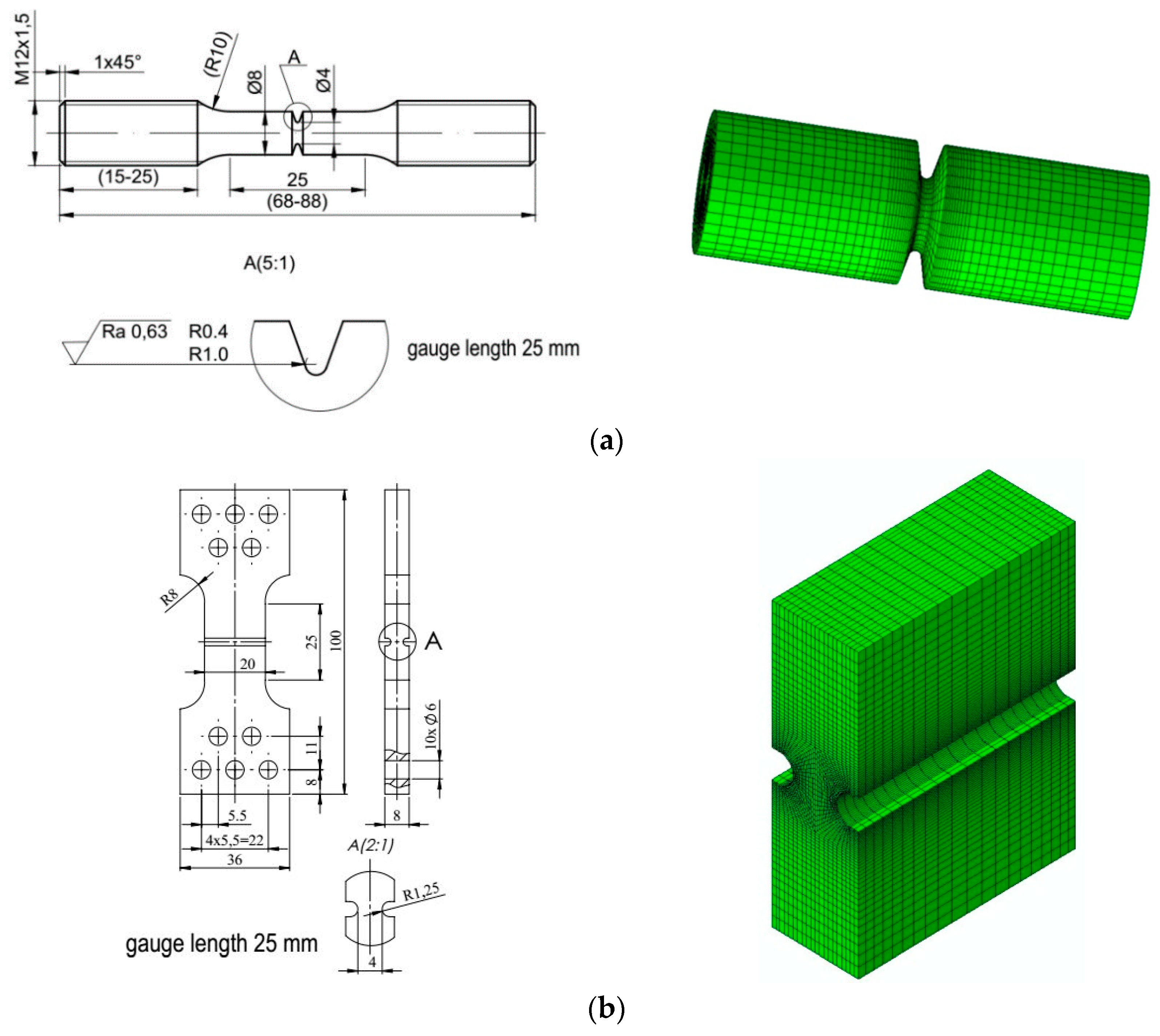
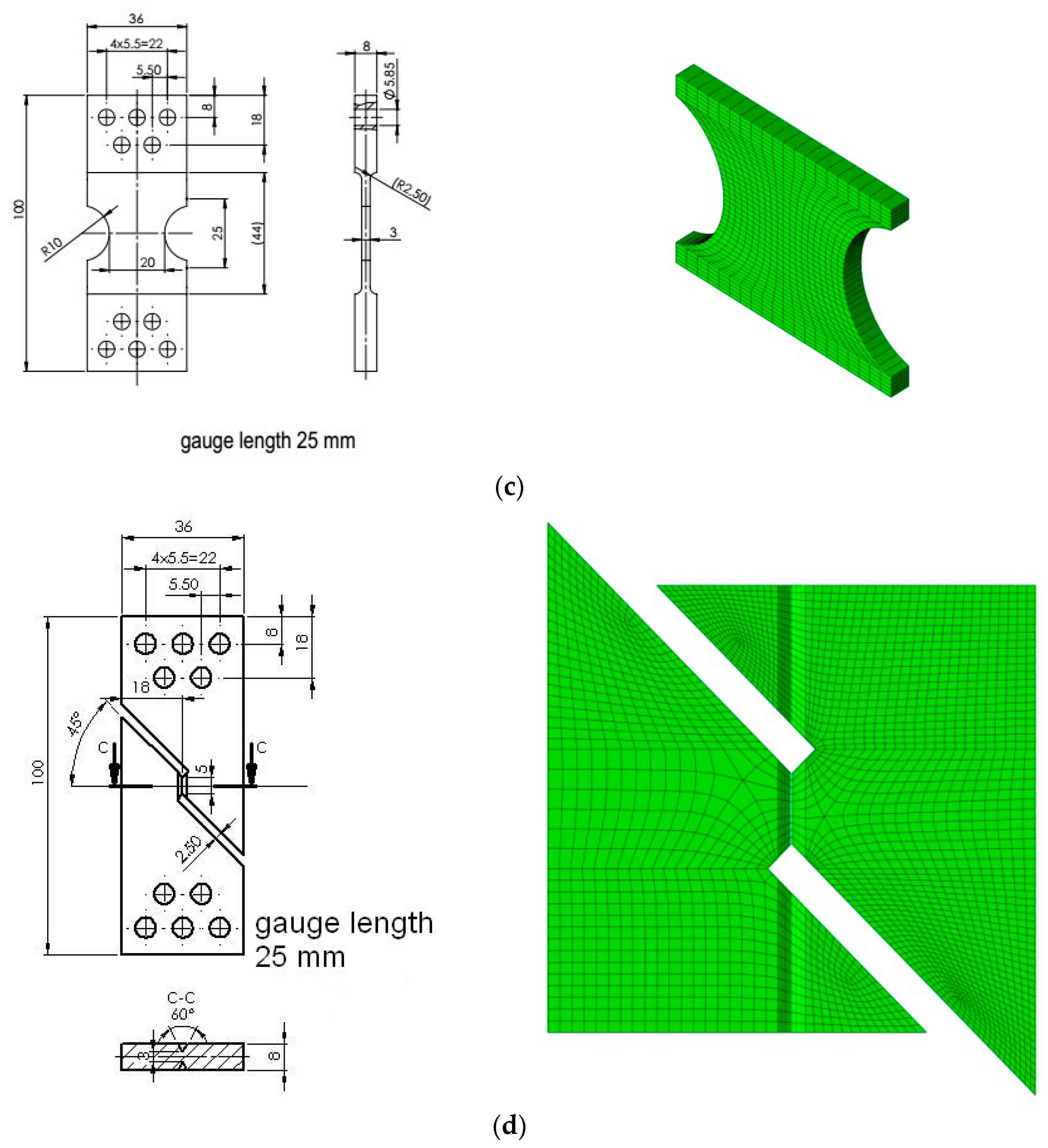
2. Materials and Tested Specimens
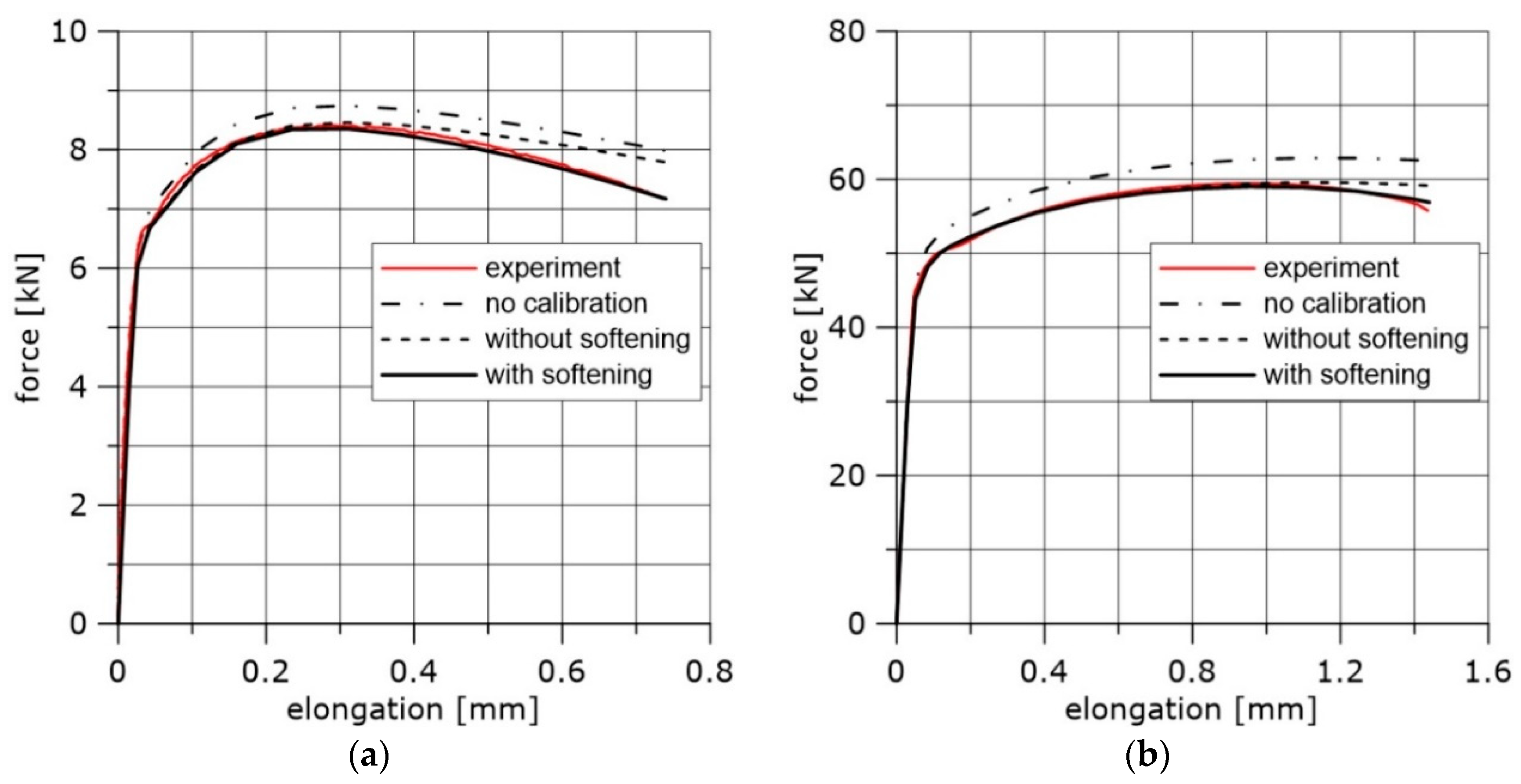
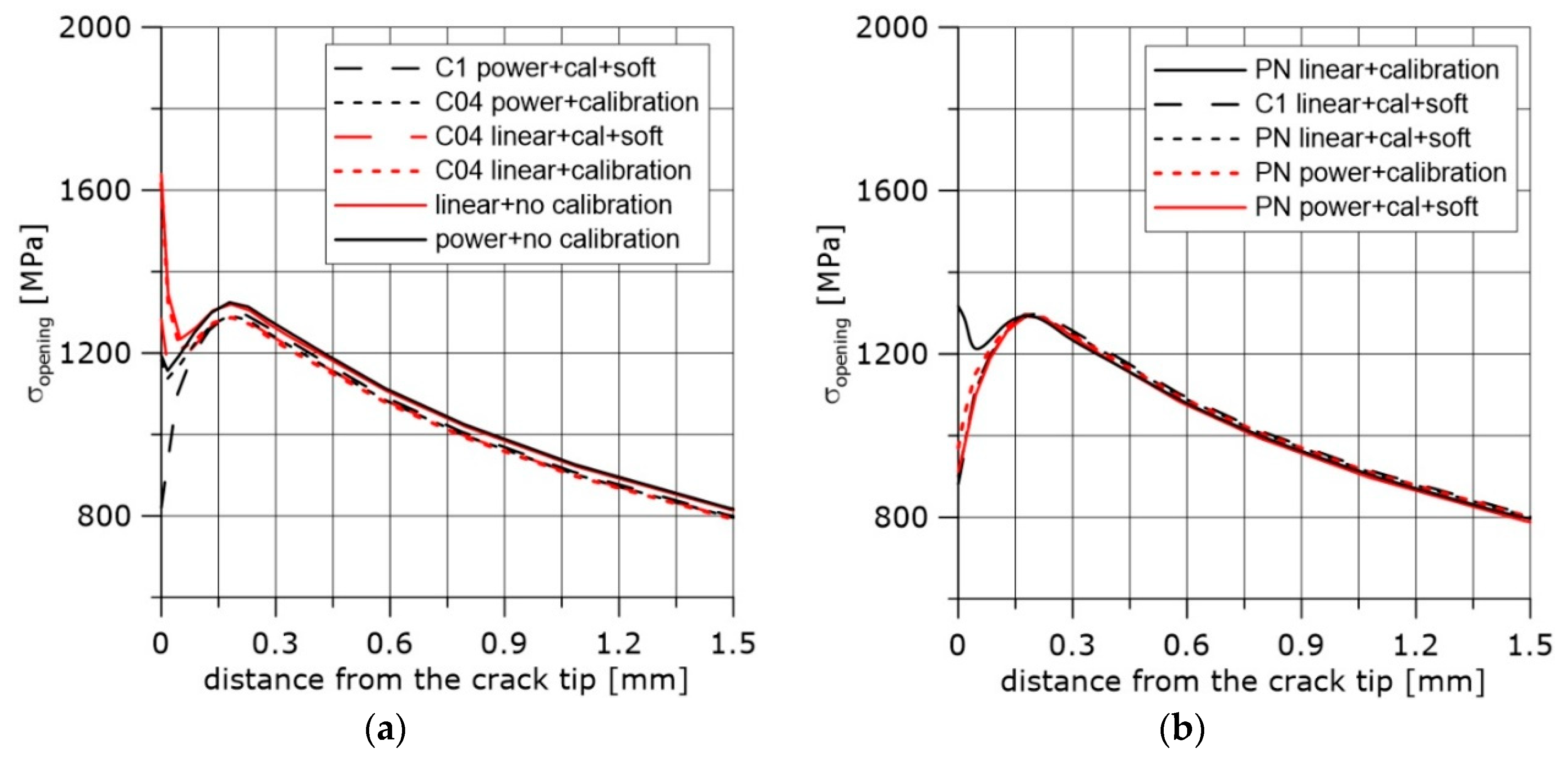
3. Calibration of the Constitutive Relationships
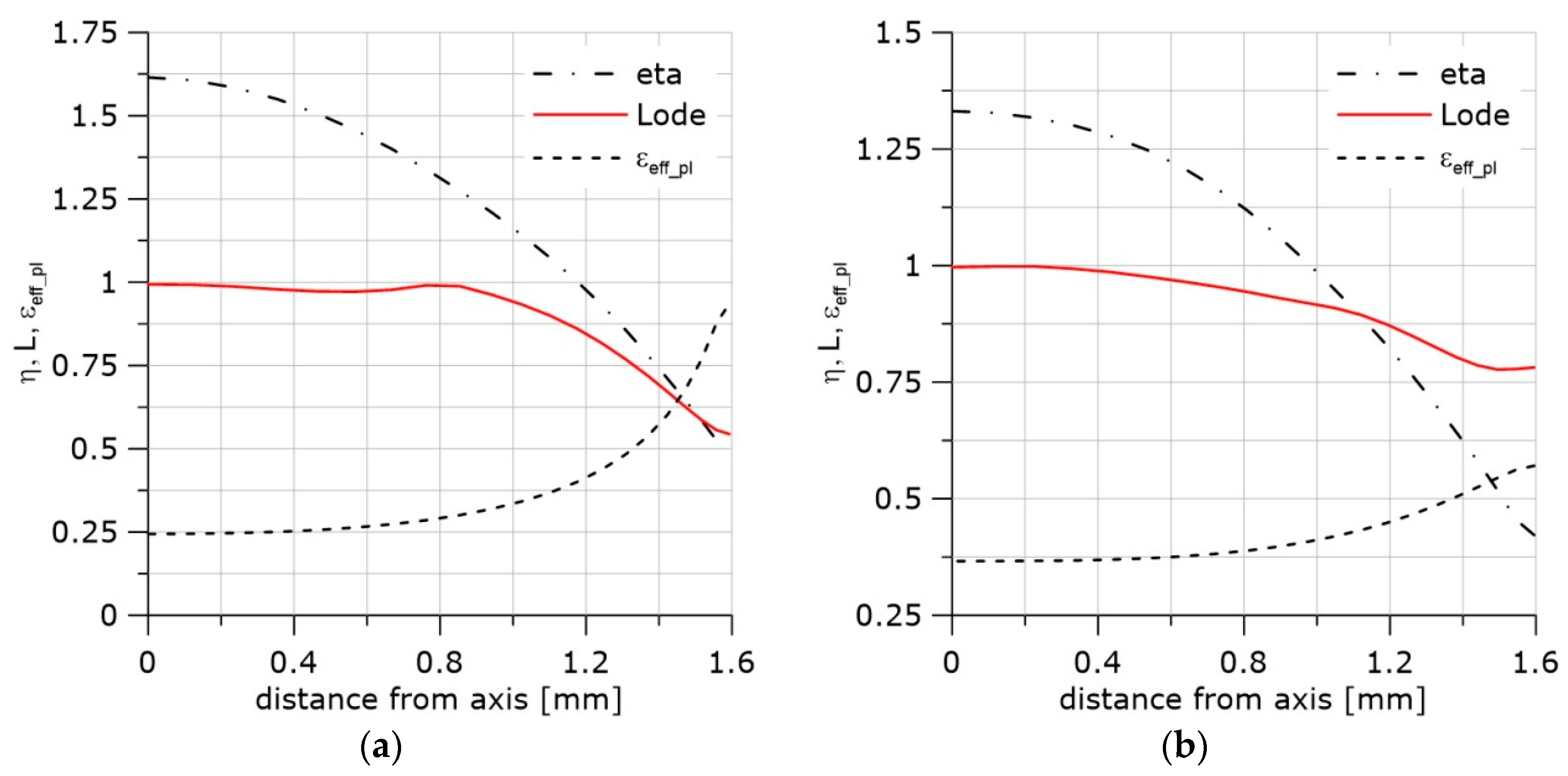
4. Critical Accumulated Effective Plastic Strain
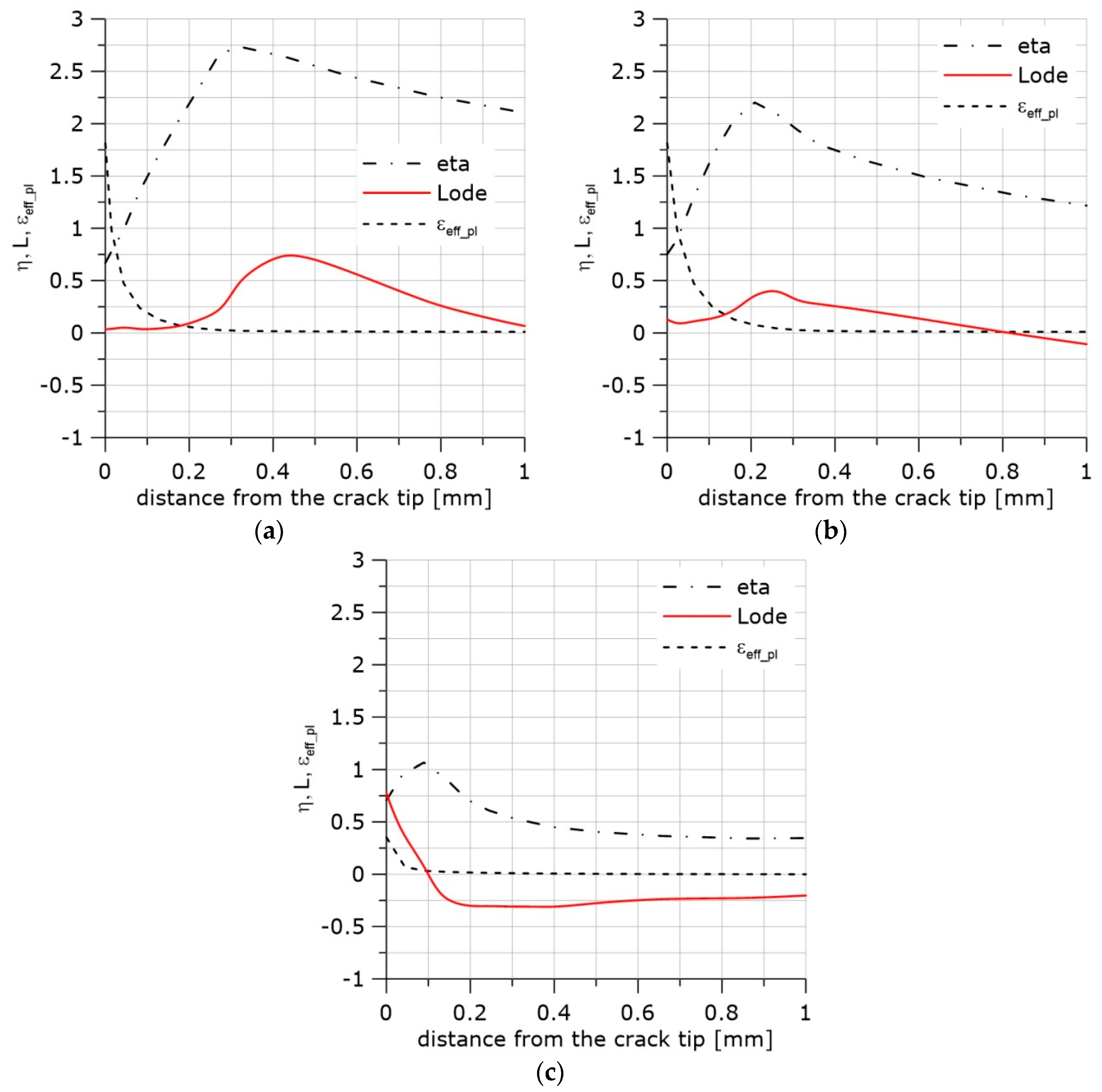
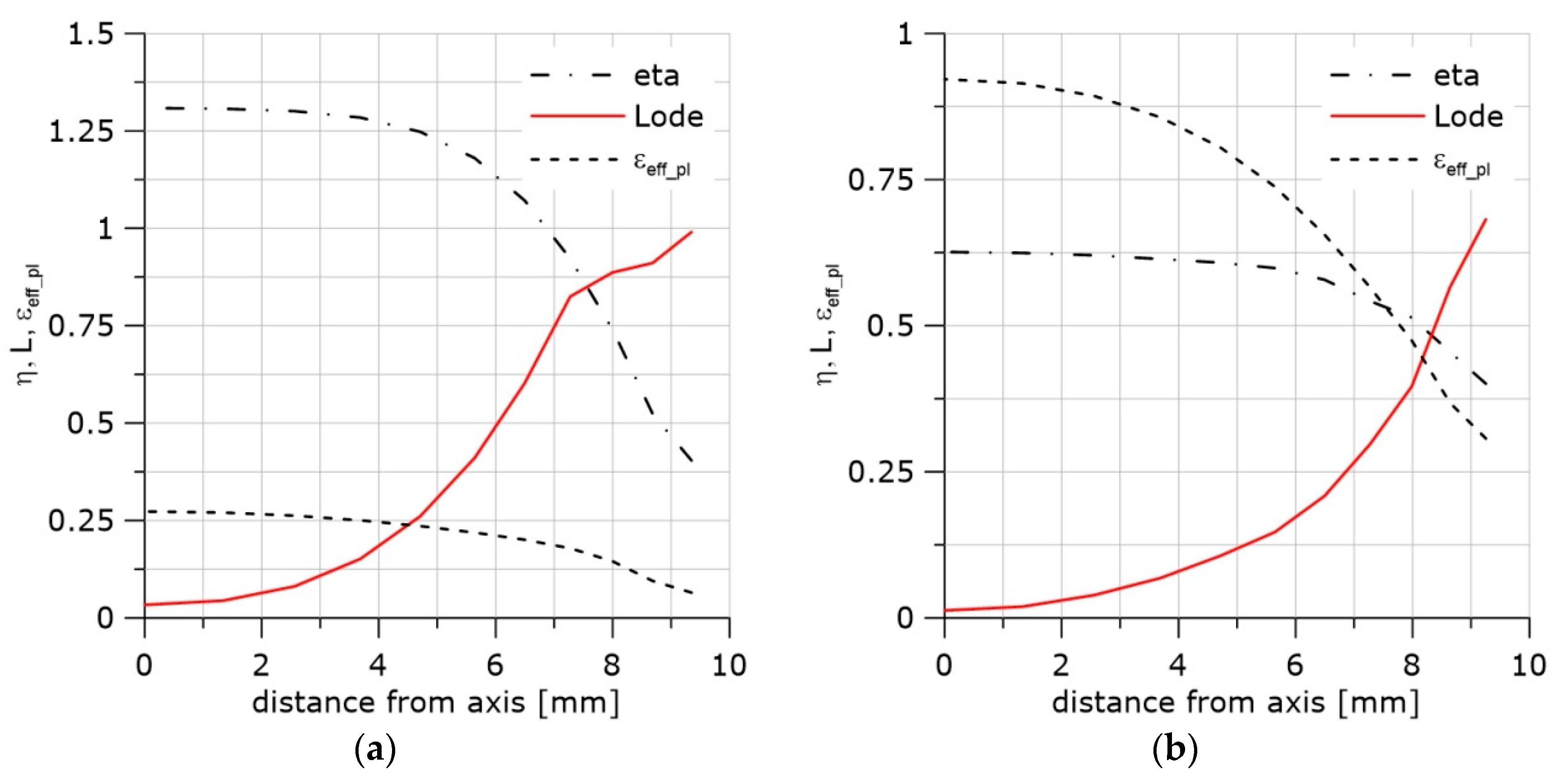
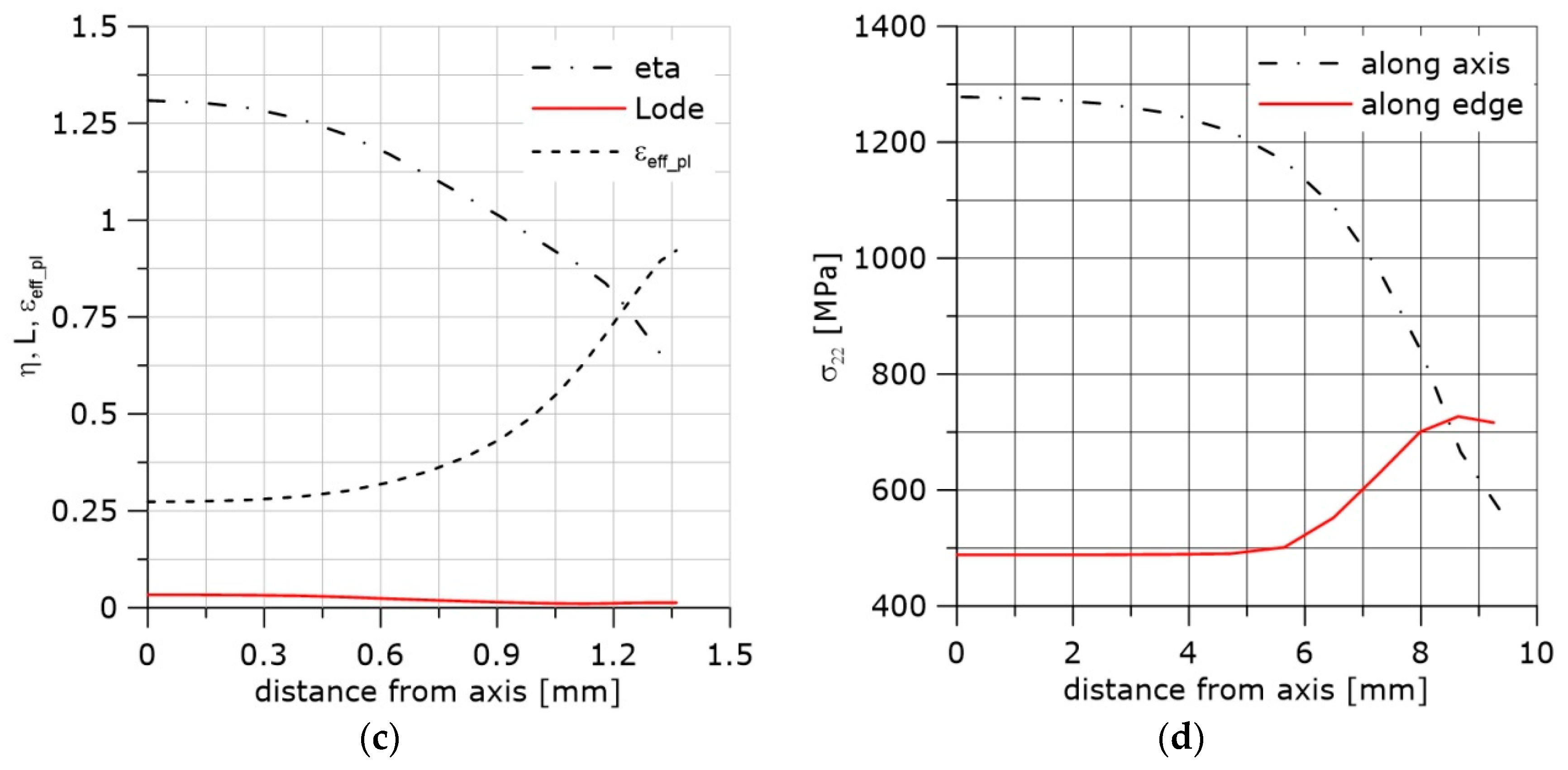
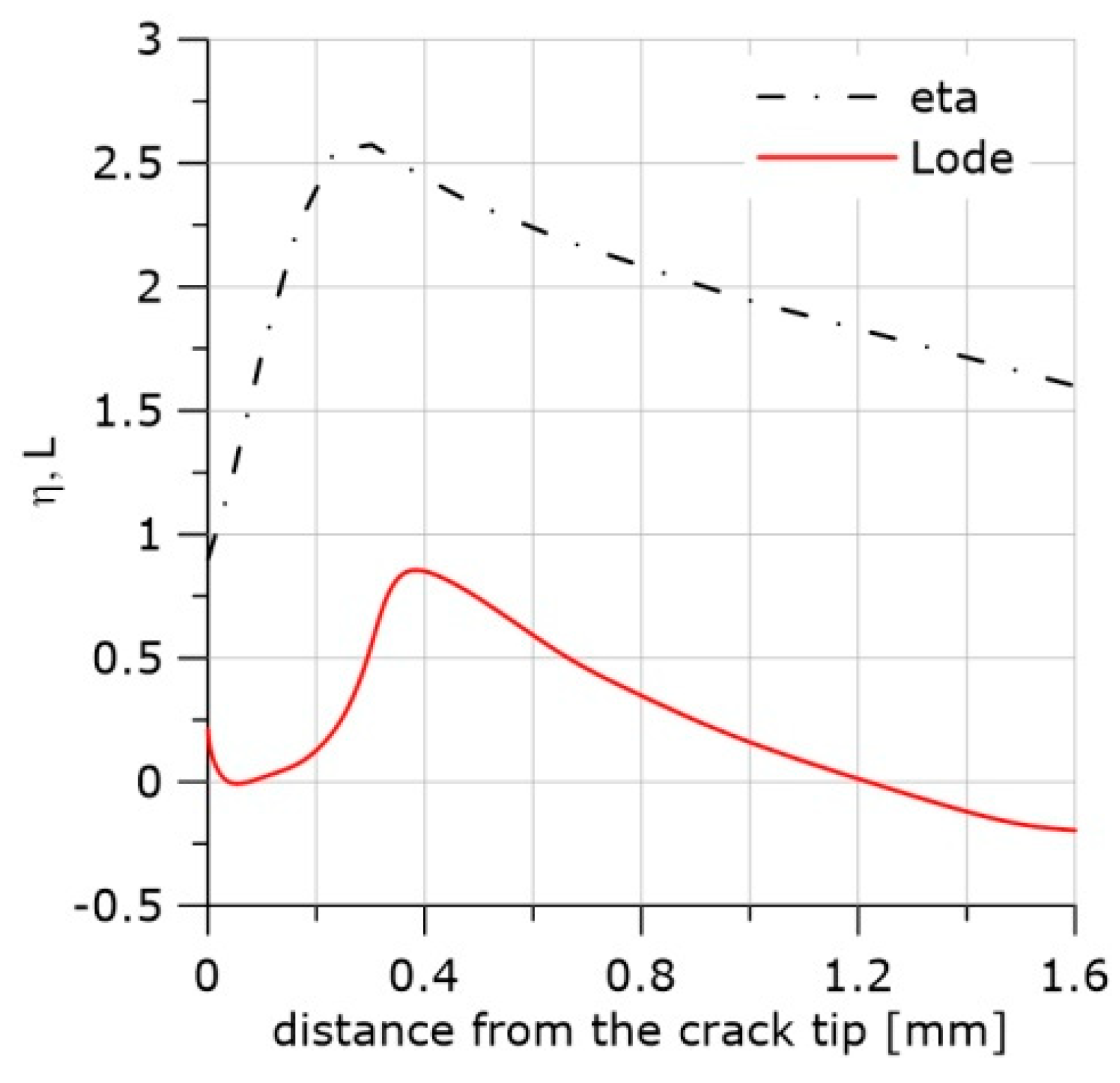
5. Stress Distribution in Front of the Crack
6. Accumulated Effective Plastic Strain Distributions in Front of the Crack
7. Discussion, Summary and Conclusions
- selection of the material;
- calibration of the constitutive equations, including material softening before the final specimen break;
- machining of the specimens of at least five different shapes to generate a wide range of η and L factors;
- loading of the specimens to failure;
- localization of the critical spot;
- computations at the critical spot, by finite element method, the values of η and L parameters and effective plastic strain;
- computation of the εeff_pl_cr = f(η,L) function;
- computation of the mechanical field parameters in front of the crack in the specimen or structural member; and
- using criterion εeff_pl = εeff_pl_cr to estimate the onset of ductile crack growth.
Author Contributions
Funding
Conflicts of Interest
References
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Bao, Y.; Lee, Y.-W.; Bai, Y. Calibration of seven fracture models. Int. J. Mech. Sci. 2005, 47, 719–743. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. Application of extended Mohr–Coulomb criterion to ductile fracture. Int. J. Fract. 2010, 161, 1. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. A new model of metal plasticity and fracture with pressure and Lode dependence. Int. J. Plast. 2008, 24, 1071–1096. [Google Scholar] [CrossRef]
- Algarni, M.; Bai, Y.; Choi, Y. A study of Inconel 718 dependency on stress triaxiality and Lode angle in plastic deformation and ductile fracture. Eng. Fract. Mech. 2015, 147, 140–157. [Google Scholar] [CrossRef]
- Bai, Y.; Teng, X.; Wierzbicki, T. On the application of stress triaxiality formula for plane strain fracture testing. J. Eng. Mater. Technol. 2009, 131, 021002. [Google Scholar] [CrossRef]
- Kofiani, K.; Nonn, A.; Wierzbicki, T. New calibration method for high and low triaxiality and validation on SENT specimens of API X70. Int. J. Press. Vessels Pip. 2013, 111, 187–201. [Google Scholar] [CrossRef]
- Mohr, D.; Marcadet, S.J. Micromechanically–motivated phenomenological Hasford–Coulomb model for predicting ductile fracture initiation at low stress triaxialities. Int. J. Solids Struct. 2015, 67, 40–45. [Google Scholar] [CrossRef]
- Faleskog, J.; Barsoum, I. Tension-torsion fracture experiments-Part I; Experiments and a procedure to evaluate the equivalent plastic strain. Int. J. Solids Struct. 2013, 50, 4241–4257. [Google Scholar] [CrossRef]
- Dunand, M.; Mohr, D. Hybrid experimental-numerical analysis of basic ductile fracture experiments for sheet metals. Int. J. Solids Struct. 2010, 47, 1130–1143. [Google Scholar] [CrossRef]
- Dunand, M.; Mohr, D. On predictive capabilities of the shear modified Gurson and the modified Mohr-Coulomb fracture models over a wide range of stress triaxialities and Lode angles. J. Mech. Phys. Solids 2011, 59, 1374–1394. [Google Scholar] [CrossRef]
- Barsoum, I.; Faleskog, J.; Pingle, S. The effect of stress state on ductility in moderate stress triaxiality regime of medium and high strength steels. Int. J. Mech. Sci. 2012, 65, 203–212. [Google Scholar] [CrossRef]
- Barsoum, I.; Faleskog, J.; Pingle, S. The Influence of the Lode parameter on ductile failure strain in steel. Procedia Eng. 2011, 10, 69–75. [Google Scholar] [CrossRef]
- Papisidero, J.; Doquet, V.; Mohr, D. Ductile fracture of aluminium 2024-T351 under proportional and non-proportional multi-axial loading: Bao-Wierzbicki results revisited. Int. J. Solids Struct. 2015, 69, 459–474. [Google Scholar]
- Xue, L. Damage accumulation and fracture initiation in uncracked ductile solids subject to triaxial loading. Int. J. Solids Struct. 2007, 44, 5163–5181. [Google Scholar] [CrossRef]
- Erice, B.; Galvez, F. A coupled elastoplastic-damage constitutive model with Lode angle dependent failure criterion. Int. J. Solids Struct. 2014, 51, 93–110. [Google Scholar] [CrossRef]
- Neimitz, A.; Galkiewicz, J.; Dzioba, I. Calibration of constitutive equations under conditions of large strains and stress triaxiality. Arch. Civ. Mech. Eng. 2018, 18, 1123–1135. [Google Scholar] [CrossRef]
- McClintock, F.A. A Criterion for Ductile Fracture by Growth of Holes. J. Appl. Mech. 1968, 4, 363–371. [Google Scholar] [CrossRef]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]





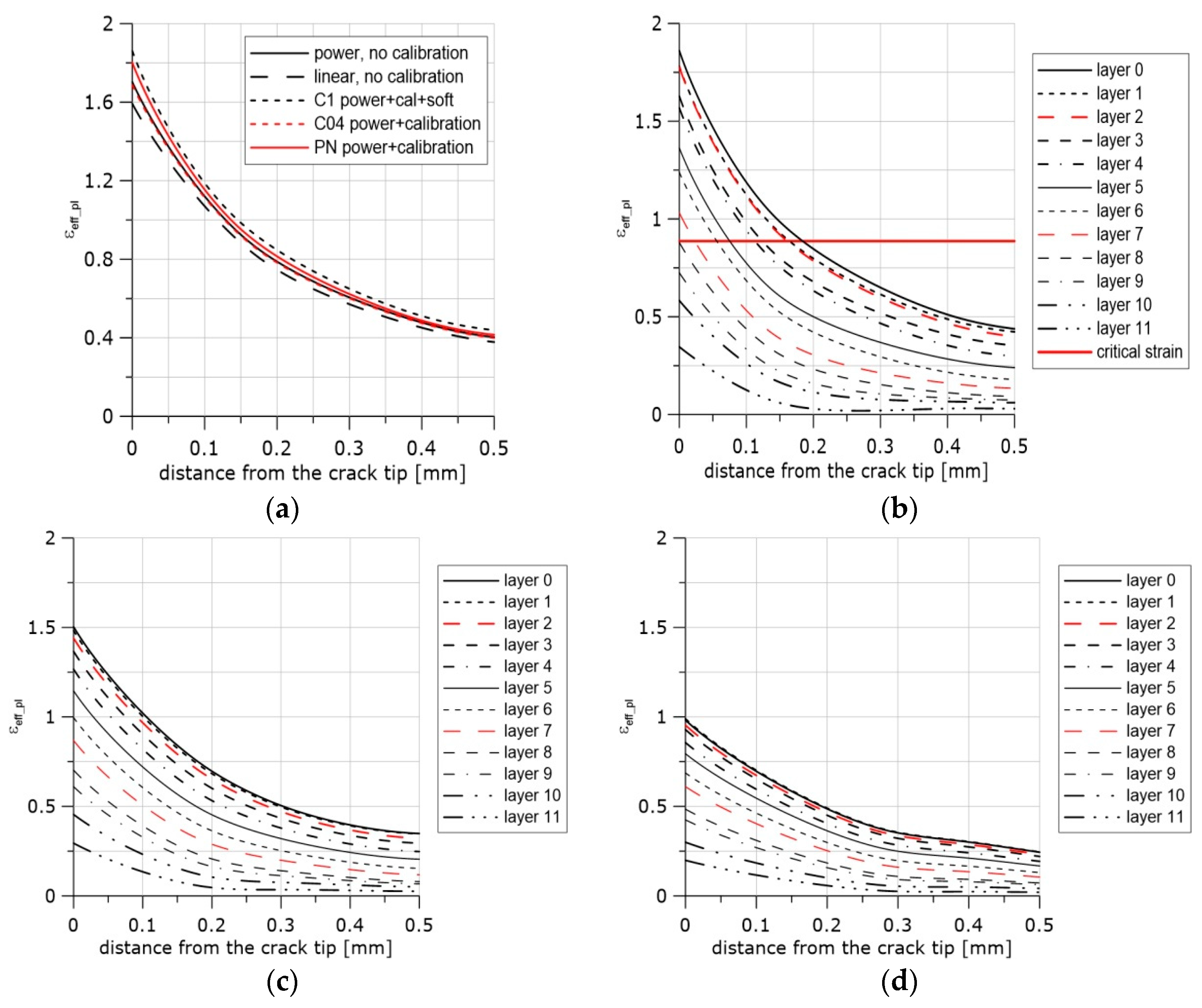

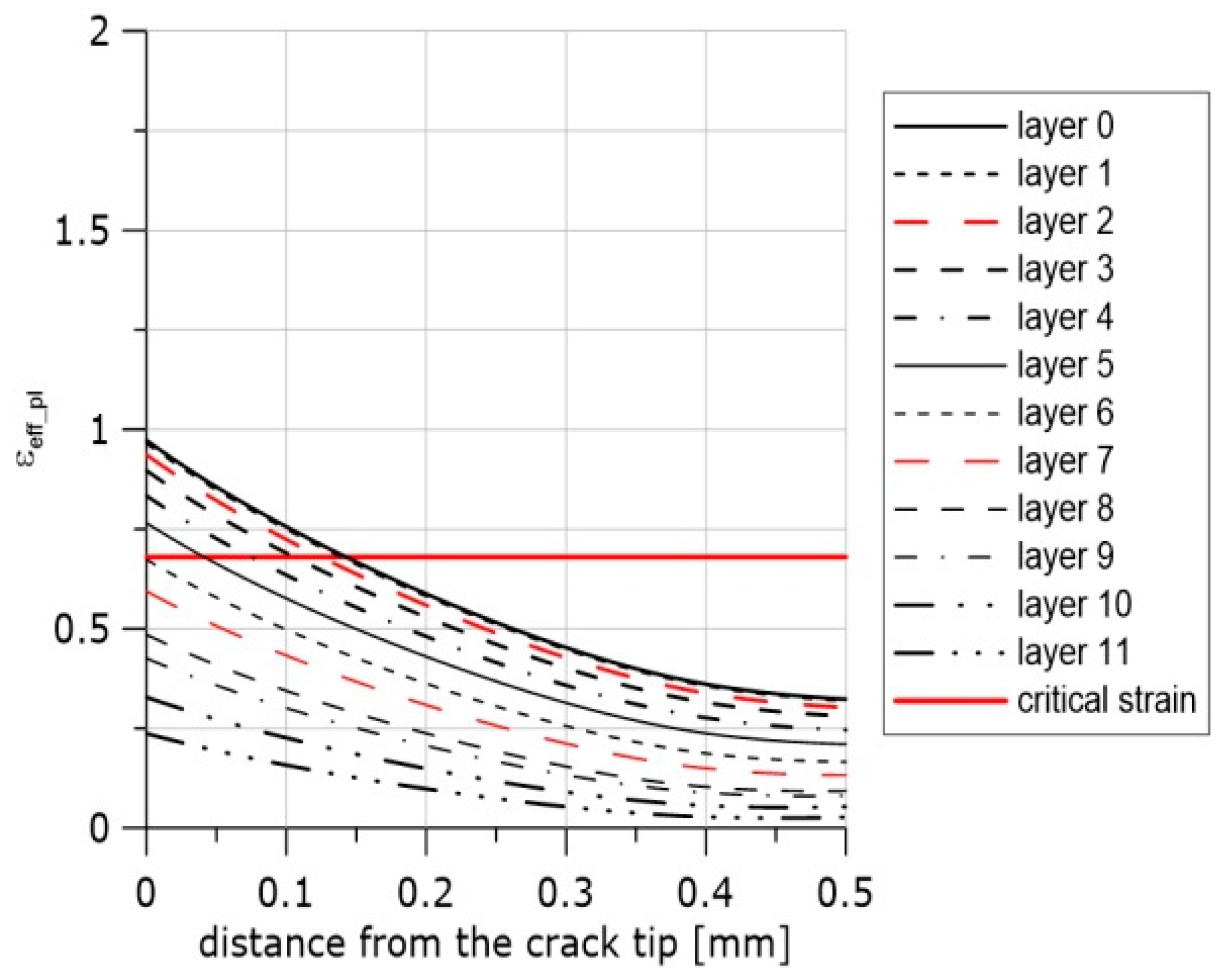
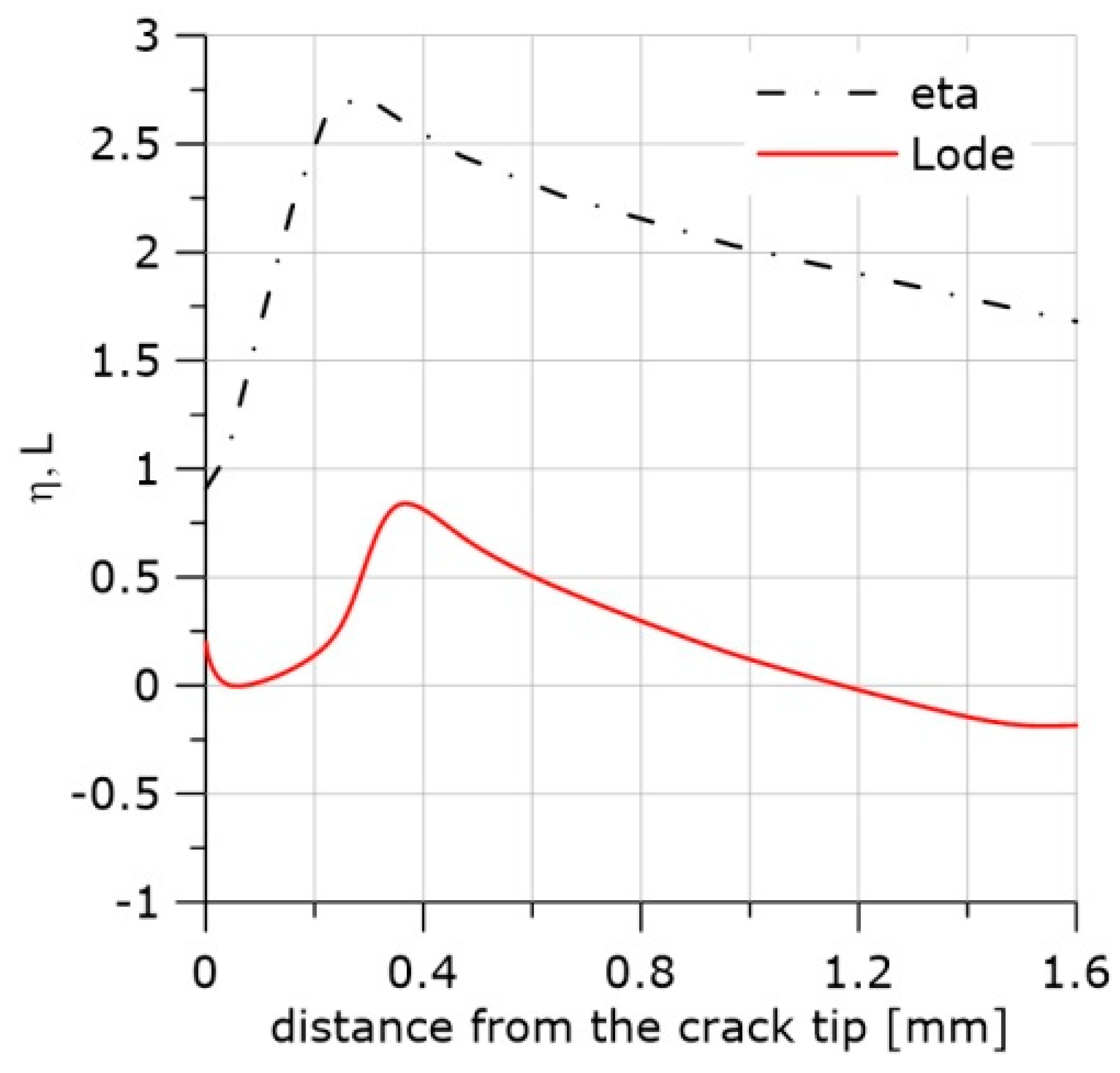

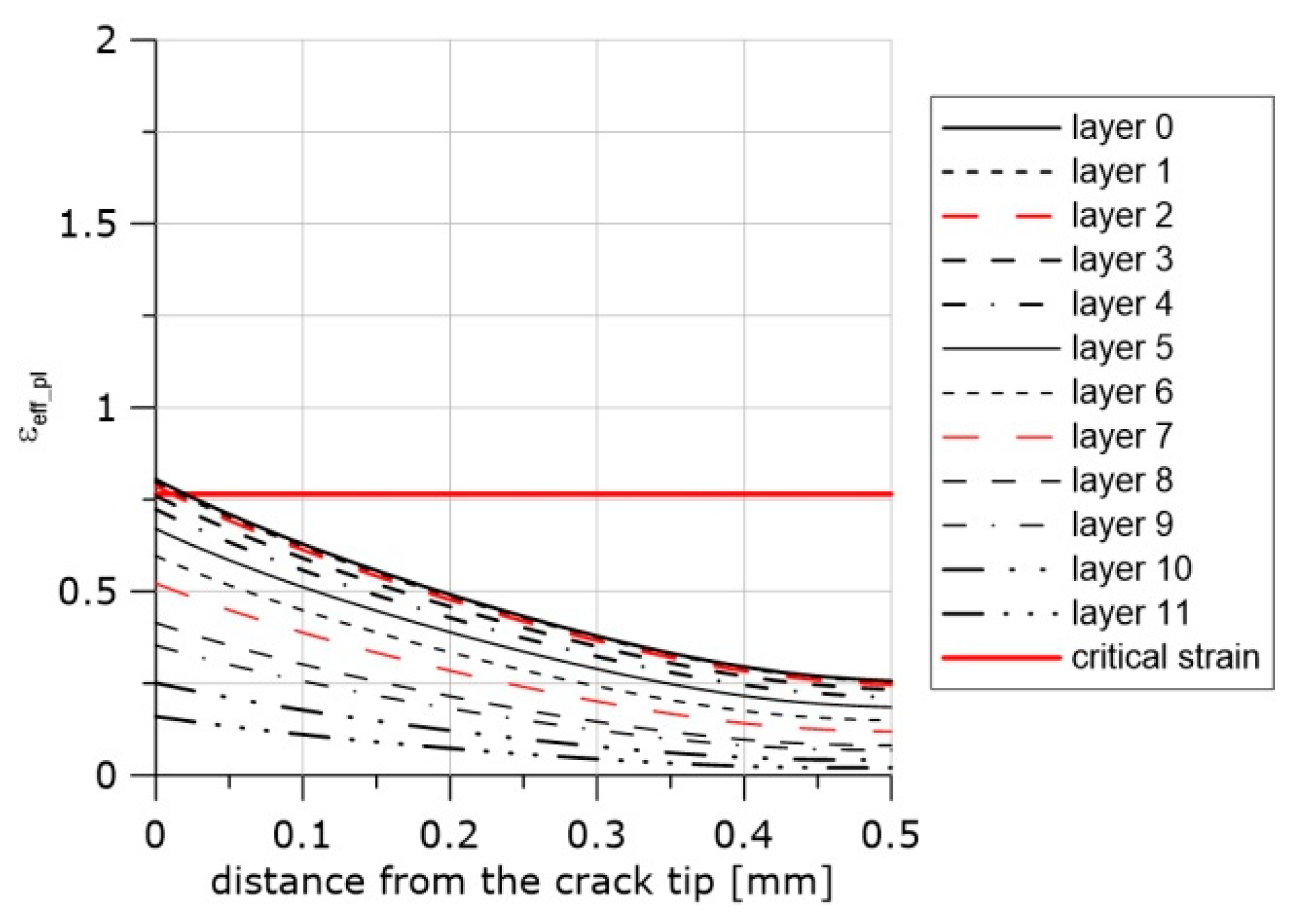

| Materials | Heat Treatment | Microstructure | Temp. (°C) | E (GPa) | ReL (MPa) | ReH (MPa) | Rm (MPa) |
|---|---|---|---|---|---|---|---|
| S355JR steel, symbol NW | Normalized and annealed (600 °C, 150 h) | Ferrite containing spheroidal carbide particles | +20 | 210 | 382 | 368 | 470 |
| −20 | 200 | 376 | 419 | 502 | |||
| −50 | 212 | 390 | 396 | 526 | |||
| S355JR steel, symbol HW | Quenching in oil and annealed (600 °C, 150 h) | Ferrite containing spheroidal carbide particles | +20 | 197 | 412 | 406 | 511 |
| −20 | 191 | 437 | 444 | 555 | |||
| −50 | 210 | 463 | 488 | 581 | |||
| S355JR steel, symbol N | Normalized at 950 °C | Ferrite–pearlite | +20 | 197 | 367 | 375 | 496 |
| −20 | 202 | 402 | 407 | 526 | |||
| −50 | 220 | 401 | 428 | 553 |
| Spot Where the Measurements were Performed | εeff_pl_cr | η | L | σmax | εeff_pl_cr·exp(η) | |
|---|---|---|---|---|---|---|
| R = 0.4 | Specimen center | 0.24 | 1.6 | 0.99 | 1443 | 1.19 |
| Next to the notch | 0.93 | 0.497 | 0.54 | 789 | 1.53 | |
| R = 1.0 | Specimen center | 0.36 | 1.33 | 0.996 | 1298 | 1.36 |
| Next to the notch | 0.57 | 0.42 | 0.78 | 619 | 0.86 | |
| Spot Where the Measurements were Performed | εeff_pl_cr | η | L | σmax | εeff_pl_cr·exp(η) | |
|---|---|---|---|---|---|---|
| PN specimen | Central part next to the axis | 0.27 | 1.3 | 0.033 | 1278 | 0.99 |
| Central part next to the notch | 0.92 | 0.626 | 0.013 | 477 | 1.16 | |
| Material | HW | HW | HW | N | N | N | NW | NW | NW |
|---|---|---|---|---|---|---|---|---|---|
| Temp. | −20 | −50 | 20 | −20 | −50 | 20 | −20 | −50 | 20 |
| a | −0.065 | −0.016 | −0.099 | −0.038 | −0.01 | −0.07 | −0.04 | −0.030 | −0.12 |
| b | 0.121 | 0.036 | 0.25 | 0.113 | 0.018 | 0.23 | 0.11 | 0.097 | 0.33 |
| c | −0.046 | −0.02 | −0.118 | −0.07 | −0.026 | −0.07 | −0.087 | −0.01 | −0.015 |
| d | 0.135 | 0.032 | 0.227 | 0.14 | 0.064 | 0.126 | 0.21 | 0.0024 | −0.0027 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neimitz, A.; Galkiewicz, J.; Lipiec, S.; Dzioba, I. Estimation of the Onset of Crack Growth in Ductile Materials. Materials 2018, 11, 2026. https://doi.org/10.3390/ma11102026
Neimitz A, Galkiewicz J, Lipiec S, Dzioba I. Estimation of the Onset of Crack Growth in Ductile Materials. Materials. 2018; 11(10):2026. https://doi.org/10.3390/ma11102026
Chicago/Turabian StyleNeimitz, Andrzej, Jaroslaw Galkiewicz, Sebastian Lipiec, and Ihor Dzioba. 2018. "Estimation of the Onset of Crack Growth in Ductile Materials" Materials 11, no. 10: 2026. https://doi.org/10.3390/ma11102026






