Multi-Scale Modeling for Predicting the Stiffness and Strength of Hollow-Structured Metal Foams with Structural Hierarchy
Abstract
:1. Introduction
2. Simulation Methods
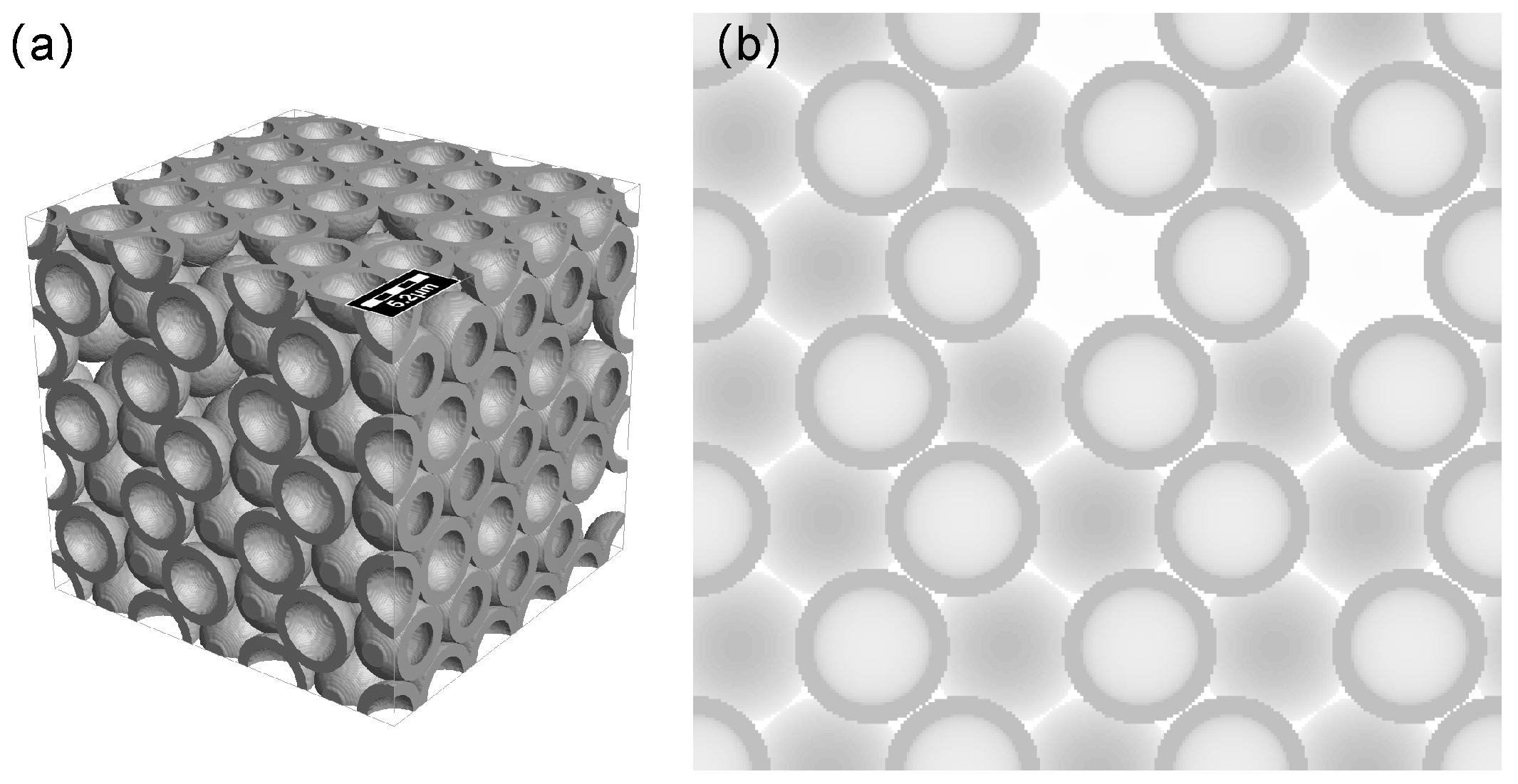
2.1. Modeling
2.2. Finite Volume Simulation
3. Results and Discussion
3.1. Mechanical Properties of Nanoporous Gold
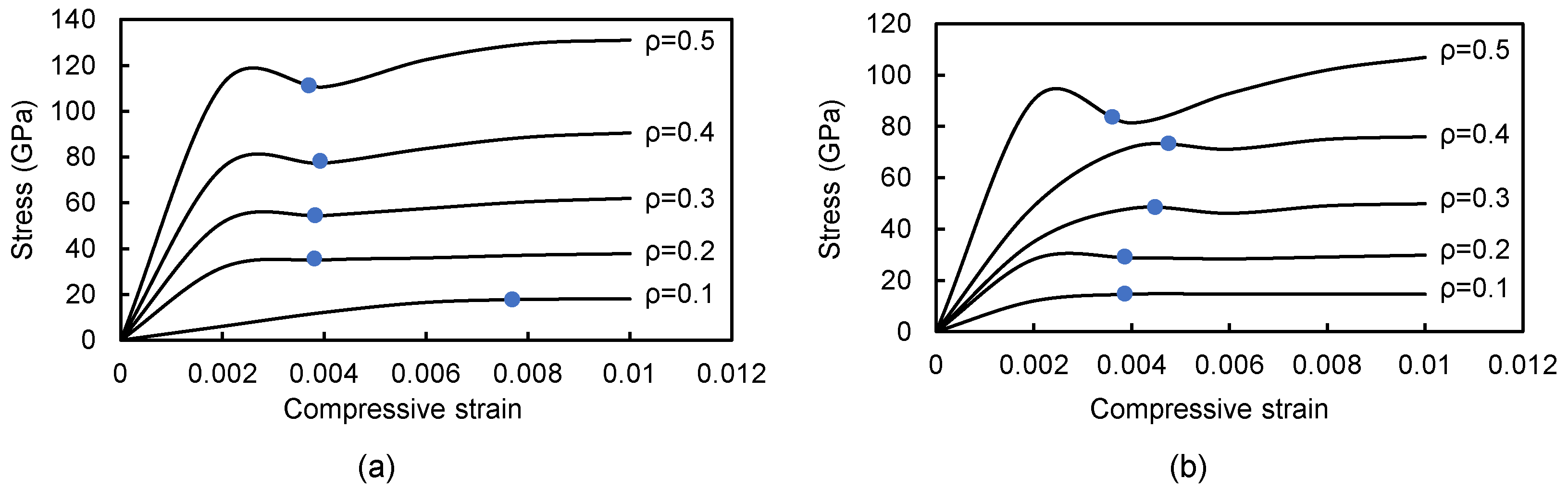
3.1.1. Compression Behavior
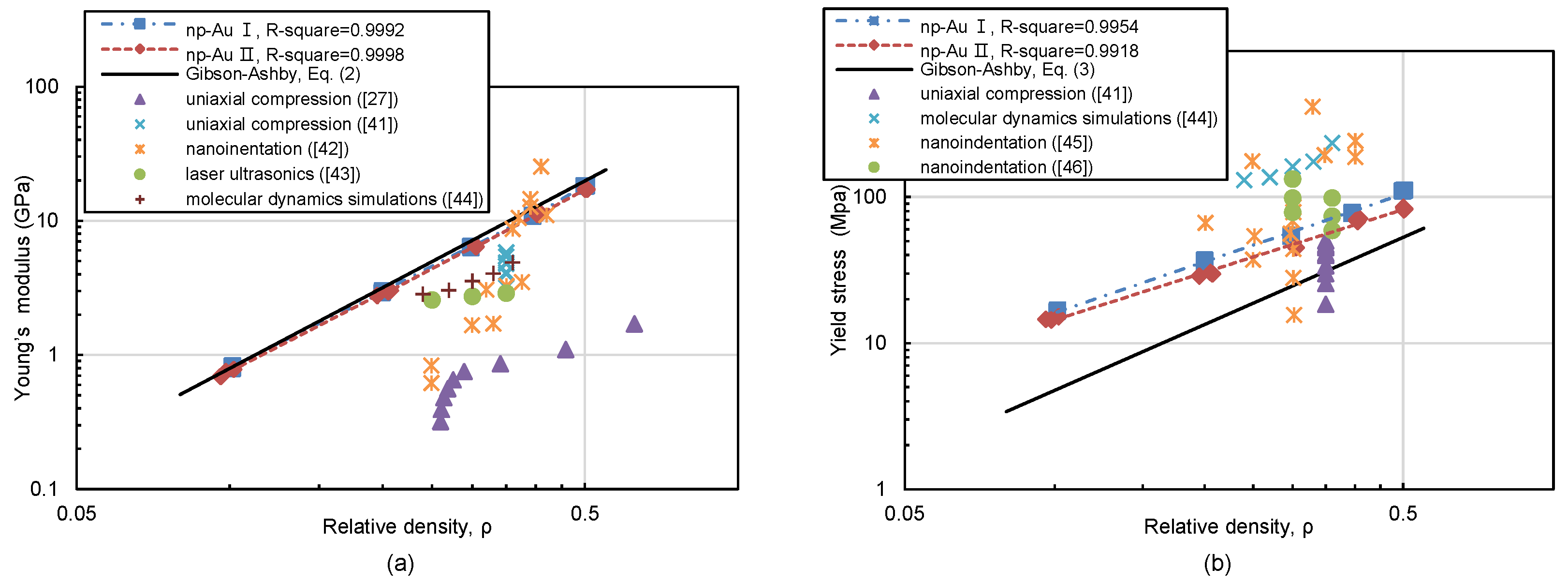
3.1.2. Young’s Modulus and Yield Strength
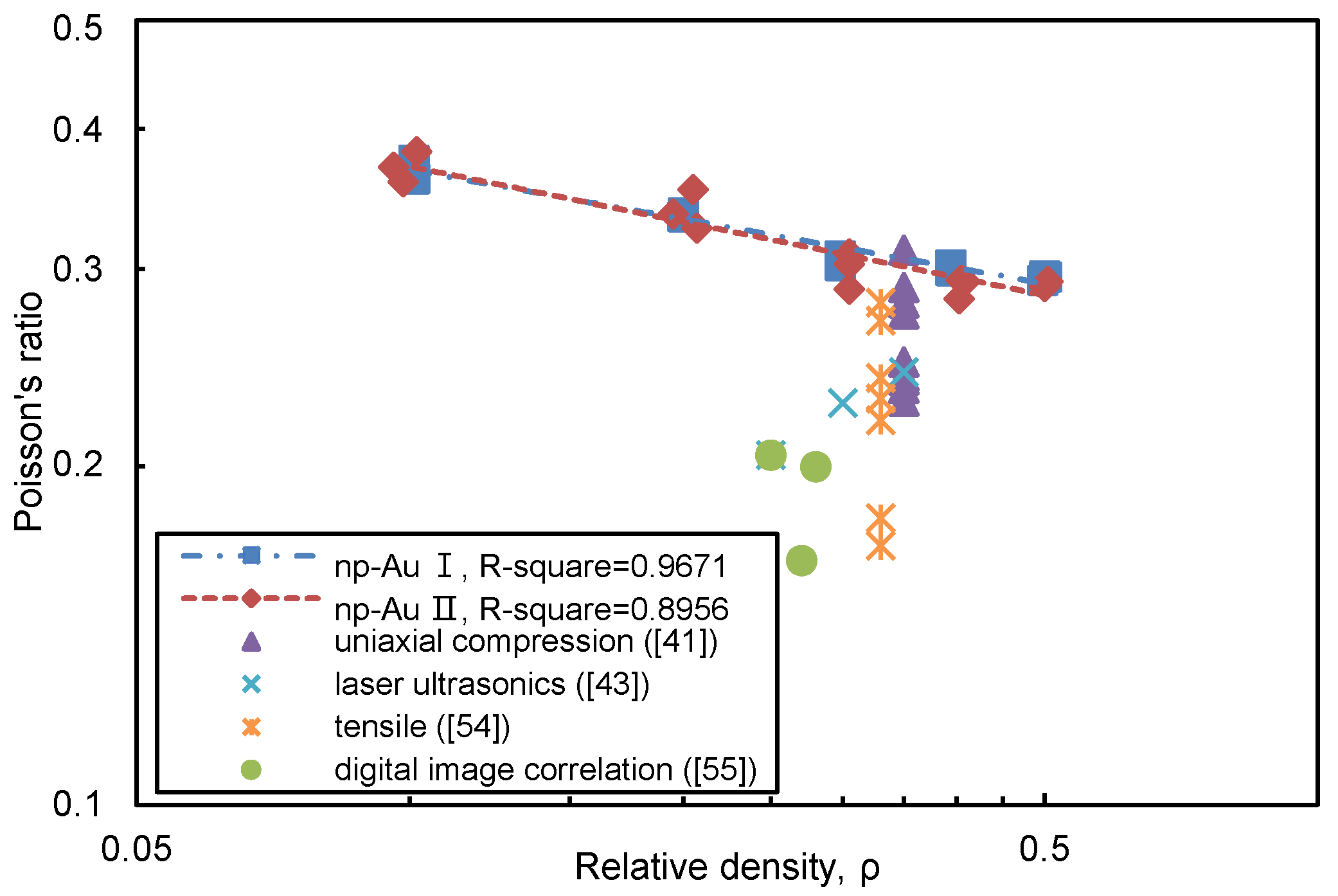
3.1.3. Poisson’s Ratio
3.2. Mechanical Properties of Gold Foam
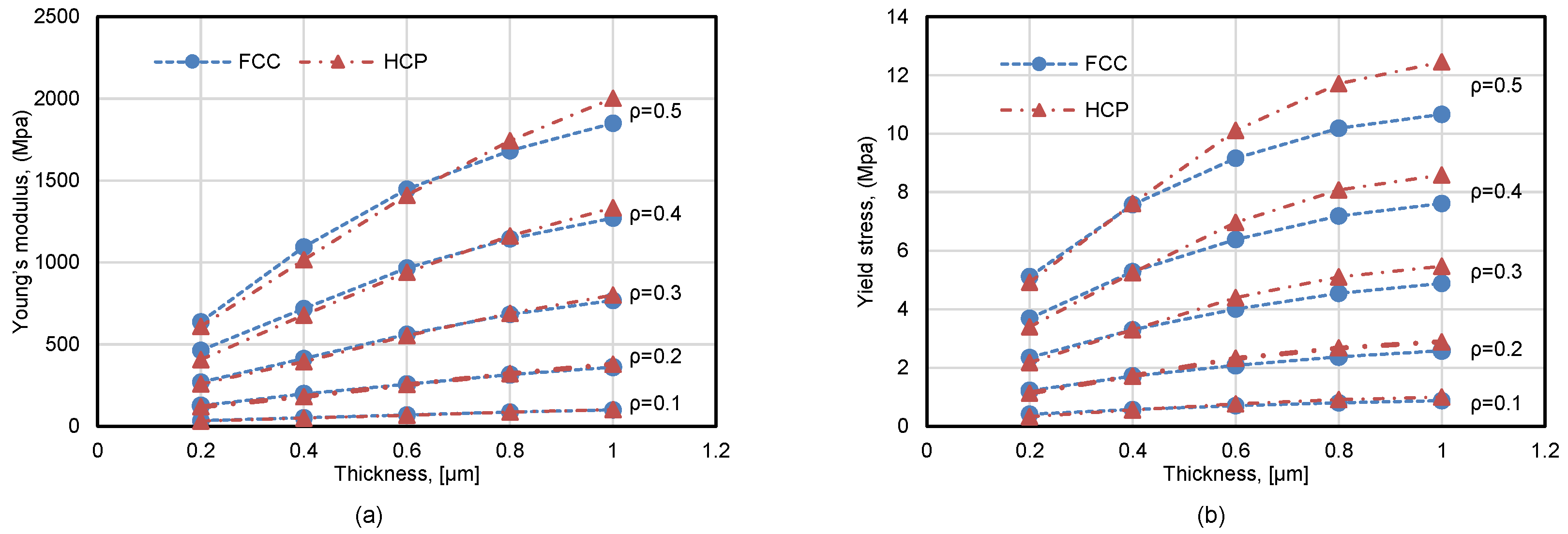
3.2.1. Young’s Modulus and Yield Strength
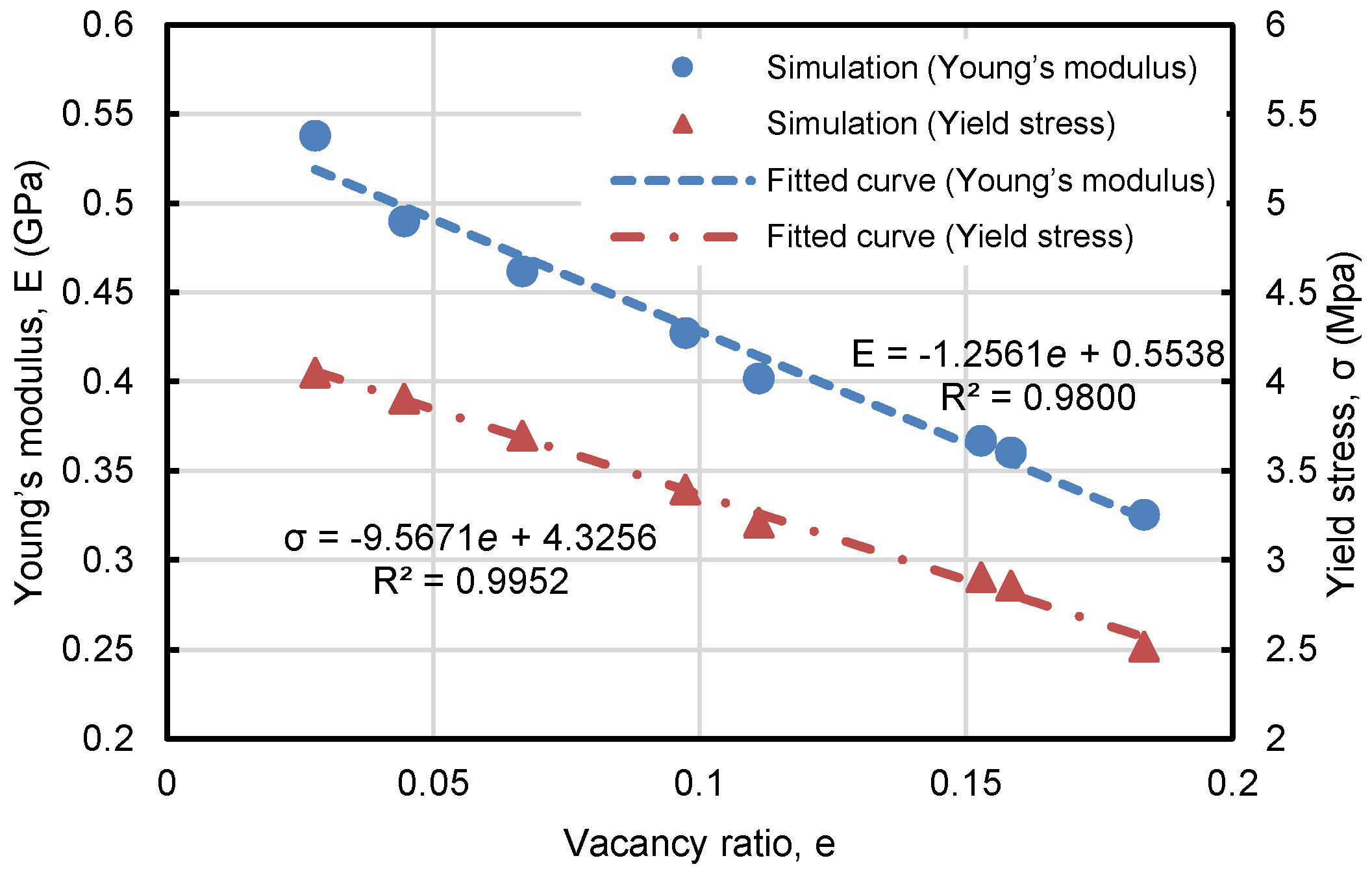
3.2.2. Effect of Defects
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Juarez, T.; Biener, J.; Weissmüller, J.; Hodge, A.M. Nanoporous metals with structural hierarchy: A review. Adv. Eng. Mater. 2017, 19. [Google Scholar] [CrossRef]
- Fujita, T. Hierarchical nanoporous metals as a path toward the ultimate three-dimensional functionality. Sci. Technol. Adv. Mater. 2017, 18, 724–740. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Shi, J. Hollow-Structured Mesoporous Materials: Chemical Synthesis, Functionalization and Applications. Adv. Mater. 2014, 26, 3176–3205. [Google Scholar] [CrossRef] [PubMed]
- You, B.; Sun, Y. Hierarchically porous nickel sulfide multifunctional superstructures. Adv. Energy Mater. 2016, 6. [Google Scholar] [CrossRef]
- Parlett, C.M.; Wilson, K.; Lee, A.F. Hierarchical porous materials: catalytic applications. Chem. Soc. Rev. 2013, 42, 3876–3893. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhang, J.; Wang, L.; Yang, T.; Guo, X.; Wu, S.; Wang, S. 3D hierarchically porous ZnO structures and their functionalization by Au nanoparticles for gas sensors. J. Mater. Chem. 2011, 21, 349–356. [Google Scholar] [CrossRef]
- Tiginyanu, I.; Ghimpu, L.; Gröttrup, J.; Postolache, V.; Mecklenburg, M.; Stevens-Kalceff, M.A.; Ursaki, V.; Payami, N.; Feidenhansl, R.; Schulte, K.; et al. Strong light scattering and broadband (UV to IR) photoabsorption in stretchable 3D hybrid architectures based on Aerographite decorated by ZnO nanocrystallites. Sci. Rep. 2016, 6, 32913. [Google Scholar] [CrossRef] [PubMed]
- Drisko, G.L.; Luca, V.; Sizgek, E.; Scales, N.; Caruso, R.A. Template synthesis and adsorption properties of hierarchically porous zirconium titanium oxides. Langmuir 2009, 25, 5286–5293. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Lee, P.; Jones, J.; Poologasundarampillai, G.; Post, T.; Lindley, T.; Dashwood, R. Hierarchically structured titanium foams for tissue scaffold applications. Acta Biomater. 2010, 6, 4596–4604. [Google Scholar] [CrossRef] [PubMed]
- Mecklenburg, M.; Schuchardt, A.; Mishra, Y.K.; Kaps, S.; Adelung, R.; Lotnyk, A.; Kienle, L.; Schulte, K. Aerographite: Ultra lightweight, flexible nanowall, carbon microtube material with outstanding mechanical performance. Adv. Mater. 2012, 24, 3486–3490. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.Y.; Chen, L.H.; Li, Y.; Rooke, J.C.; Sanchez, C.; Su, B.L. Hierarchically porous materials: Synthesis strategies and structure design. Chem. Soc. Rev. 2017, 46, 481–558. [Google Scholar] [CrossRef] [PubMed]
- Mishra, Y.K.; Adelung, R. ZnO tetrapod materials for functional applications. Mater. Today 2017. [Google Scholar] [CrossRef]
- Young, P.; Rosen, M.; Hammer, J.; Hsing, W.; Glendinning, S.; Turner, R.; Kirkwood, R.; Schein, J.; Sorce, C.; Satcher, J., Jr.; et al. Demonstration of the density dependence of X-ray flux in a laser-driven hohlraum. Phys. Rev. Lett. 2008, 101, 035001. [Google Scholar] [CrossRef] [PubMed]
- Schein, J.; Jones, O.; Rosen, M.; Dewald, E.; Glenzer, S.; Gunther, J.; Hammel, B.; Landen, O.; Suter, L.; Wallace, R. Demonstration of enhanced radiation drive in hohlraums made from a mixture of high-Z wall materials. Phys. Rev. Lett. 2007, 98, 175003. [Google Scholar] [CrossRef]
- Rosen, M.D.; Hammer, J.H. Analytic expressions for optimal inertial-confinement-fusion hohlraum wall density and wall loss. Phys. Rev. E 2005, 72, 056403. [Google Scholar] [CrossRef] [PubMed]
- Schütt, F.; Signetti, S.; Krüger, H.; Röder, S.; Smazna, D.; Kaps, S.; Gorb, S.N.; Mishra, Y.K.; Pugno, N.M.; Adelung, R. Hierarchical self-entangled carbon nanotube tube networks. Nat. Commun. 2017, 8, 1215. [Google Scholar] [CrossRef] [PubMed]
- Mishra, Y.K.; Kaps, S.; Schuchardt, A.; Paulowicz, I.; Jin, X.; Gedamu, D.; Freitag, S.; Claus, M.; Wille, S.; Kovalev, A.; et al. Fabrication of macroscopically flexible and highly porous 3D semiconductor networks from interpenetrating nanostructures by a simple flame transport approach. Part. Part. Syst. Charact. 2013, 30, 775–783. [Google Scholar] [CrossRef]
- Nyce, G.W.; Hayes, J.R.; Hamza, A.V.; Satcher, J.H. Synthesis and characterization of hierarchical porous gold materials. Chem. Mater. 2007, 19, 344–346. [Google Scholar] [CrossRef]
- Zhang, K.; Tan, X.; Zhang, J.; Wu, W.; Tang, Y. Template-dealloying synthesis of ultralow density Au foams with bimodal porous structure. RSC Adv. 2014, 4, 7196–7201. [Google Scholar] [CrossRef]
- Zhang, K.; Tan, X.; Wu, W.; Tang, Y. Template synthesis of low-density gold foams: Density, microstructure and compressive strength. Mater. Res. Bull. 2013, 48, 3499–3504. [Google Scholar] [CrossRef]
- Komini Babu, S.; Chung, H.T.; Zelenay, P.; Litster, S. Resolving Electrode Morphology’s Impact on Platinum Group Metal-Free Cathode Performance Using Nano-CT of 3D Hierarchical Pore and Ionomer Distribution. ACS Appl. Mater. Interfaces 2016, 8, 32764–32777. [Google Scholar] [CrossRef] [PubMed]
- Takano, N.; Fukasawa, K.; Nishiyabu, K. Structural strength prediction for porous titanium based on micro-stress concentration by micro-CT image-based multiscale simulation. Int. J. Mech. Sci. 2010, 52, 229–235. [Google Scholar] [CrossRef]
- Carraro, T.; Joos, J.; Rüger, B.; Weber, A.; Ivers-Tiffée, E. 3D finite element model for reconstructed mixed-conducting cathodes: I. Performance quantification. Electrochim. Acta 2012, 77, 315–323. [Google Scholar] [CrossRef]
- Hu, K.; Ziehmer, M.; Wang, K.; Lilleodden, E.T. Nanoporous gold: 3D structural analyses of representative volumes and their implications on scaling relations of mechanical behaviour. Philos. Mag. 2016, 96, 3322–3335. [Google Scholar] [CrossRef]
- Cho, Y.J.; Lee, W.; Park, Y.H. Finite Element Modeling of Tensile Deformation Behaviors of Iron Syntactic Foam with Hollow Glass Microspheres. Materials 2017, 10, 1201. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.J.; Kang, Y.; Lee, Y.C.; Park, Y.; Lee, W. Influence of Partially Debonded Interface on Elasticity of Syntactic Foam: A Numerical Study. Materials 2017, 10, 911. [Google Scholar] [CrossRef] [PubMed]
- Huber, N.; Viswanath, R.; Mameka, N.; Markmann, J.; Weißmüller, J. Scaling laws of nanoporous metals under uniaxial compression. Acta Mater. 2014, 67, 252–265. [Google Scholar] [CrossRef]
- Mangipudi, K.; Epler, E.; Volkert, C. Topology-dependent scaling laws for the stiffness and strength of nanoporous gold. Acta Mater. 2016, 119, 115–122. [Google Scholar] [CrossRef]
- Ngô, B.N.D.; Stukowski, A.; Mameka, N.; Markmann, J.; Albe, K.; Weissmüller, J. Anomalous compliance and early yielding of nanoporous gold. Acta Mater. 2015, 93, 144–155. [Google Scholar] [CrossRef]
- Rodriguez-Nieva, J.; Ruestes, C.; Tang, Y.; Bringa, E. Atomistic simulation of the mechanical properties of nanoporous gold. Acta Mater. 2014, 80, 67–76. [Google Scholar] [CrossRef]
- Coudert, F.X.; Fuchs, A.H. Computational characterization and prediction of metal–organic framework properties. Coord. Chem. Rev. 2016, 307, 211–236. [Google Scholar] [CrossRef]
- Eymard, R.; Gallouët, T.; Herbin, R. Finite volume methods. Handb. Numer. Anal. 2000, 7, 713–1018. [Google Scholar]
- Kabel, M.; Andrä, H. Fast numerical computation of precise bounds of effective elastic moduli. Berichte Fraunhofer ITWM 2012, 224, 1–16. [Google Scholar]
- Rutka, V.; Wiegmann, A. Explicit jump immersed interface method for virtual material design of the effective elastic moduli of composite materials. Numer. Algorithms 2006, 43, 309–330. [Google Scholar] [CrossRef]
- Rutka, V.; Andrä, H.; Wiegmann, A. EJIIM for Calculation of Effective Elastic Moduli in 3D Linear Elasticity; Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM: Kaiserslautern, Germany, 2006; Volume 1. [Google Scholar]
- GeoDict. Available online: https://www.geodict.com/ (accessed on 1 January 2018).
- Lautensack, C.; Giertzsch, M.; Godehardt, M.; Schladitz, K. Modelling a ceramic foam using locally adaptable morphology. J. Microsc. 2008, 230, 396–404. [Google Scholar] [CrossRef] [PubMed]
- Redenbach, C.; Wirjadi, O.; Rief, S.; Wiegmann, A. Modeling of ceramic foams for filtration simulation. Adv. Eng. Mater. 2011, 13, 171–177. [Google Scholar] [CrossRef]
- Onck, P.; Andrews, E.; Gibson, L. Size effects in ductile cellular solids. Part I: modeling. Int. J. Mech. Sci. 2001, 43, 681–699. [Google Scholar] [CrossRef]
- Andrews, E.; Gioux, G.; Onck, P.; Gibson, L. Size effects in ductile cellular solids. Part II: Experimental results. Int. J. Mech. Sci. 2001, 43, 701–713. [Google Scholar] [CrossRef]
- Bürckert, M.; Briot, N.J.; Balk, T.J. Uniaxial compression testing of bulk nanoporous gold. Philos. Mag. 2017, 97, 1157–1178. [Google Scholar] [CrossRef]
- Uchic, M.D.; Dimiduk, D.M.; Florando, J.N.; Nix, W.D. Sample dimensions influence strength and crystal plasticity. Science 2004, 305, 986–989. [Google Scholar] [CrossRef] [PubMed]
- Mameka, N.; Wang, K.; Markmann, J.; Lilleodden, E.T.; Weissmüller, J. Nanoporous gold—Testing macro-scale samples to probe small-scale mechanical behavior. Mater. Res. Lett. 2016, 4, 27–36. [Google Scholar] [CrossRef]
- Liu, L.Z.; Ye, X.L.; Jin, H.J. Interpreting anomalous low-strength and low-stiffness of nanoporous gold: Quantification of network connectivity. Acta Mater. 2016, 118, 77–87. [Google Scholar] [CrossRef]
- Liu, L.Z.; Jin, H.J. Scaling equation for the elastic modulus of nanoporous gold with “fixed” network connectivity. Appl. Phys. Lett. 2017, 110, 211902. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Ashby, M. The properties of foams and lattices. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, V.; Ashby, M.; Fleck, N. Foam topology: Bending versus stretching dominated architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar] [CrossRef]
- Hodge, A.; Doucette, R.; Biener, M.; Biener, J.; Cervantes, O.; Hamza, A. Ag effects on the elastic modulus values of nanoporous Au foams. J. Mater. Res. 2009, 24, 1600–1606. [Google Scholar] [CrossRef]
- Ahn, P.; Balogun, O. Elastic characterization of nanoporous gold foams using laser based ultrasonics. Ultrasonics 2014, 54, 795–800. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.Y.; Xu, G.K.; Li, X.; Feng, X.Q.; Gao, H. Mechanical properties and scaling laws of nanoporous gold. J. Appl. Phys. 2013, 113, 023505. [Google Scholar] [CrossRef]
- Hodge, A.; Biener, J.; Hayes, J.; Bythrow, P.; Volkert, C.; Hamza, A. Scaling equation for yield strength of nanoporous open-cell foams. Acta Mater. 2007, 55, 1343–1349. [Google Scholar] [CrossRef]
- Sun, Y.; Ye, J.; Shan, Z.; Minor, A.M.; Balk, T.J. The mechanical behavior of nanoporous gold thin films. J. Miner. Met. Mater. Soc. 2007, 59, 54–58. [Google Scholar] [CrossRef]
- Briot, N.J.; Kennerknecht, T.; Eberl, C.; Balk, T.J. Mechanical properties of bulk single crystalline nanoporous gold investigated by millimetre-scale tension and compression testing. Philos. Mag. 2014, 94, 847–866. [Google Scholar] [CrossRef]
- Lührs, L.; Soyarslan, C.; Markmann, J.; Bargmann, S.; Weissmüller, J. Elastic and plastic Poisson’s ratios of nanoporous gold. Scr. Mater. 2016, 110, 65–69. [Google Scholar] [CrossRef]


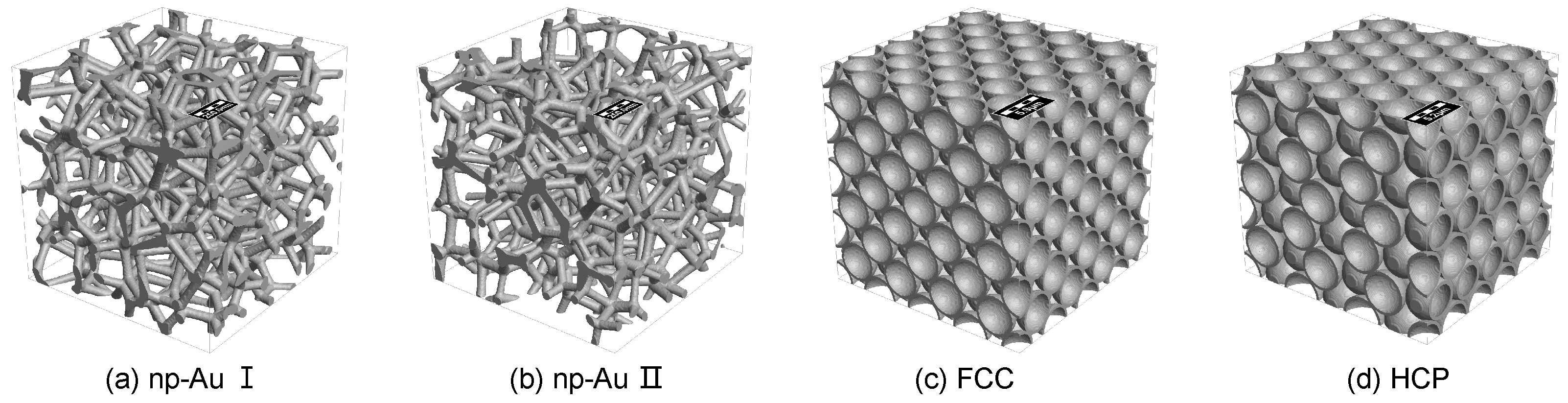
| - | Relative Density | Pore Size (nm) | Ligament Diameter (nm) | ||||
|---|---|---|---|---|---|---|---|
| Mean Value | Standard Deviation | Distribution Bound | Mean Value | Standard Deviation | Distribution Bound | ||
| np-Au I | 0.1 | 250 | 0 | 0 | 50 | 0 | 0 |
| 0.2 | 170 | 0 | 0 | 50 | 0 | 0 | |
| 0.3 | 132 | 0 | 0 | 50 | 0 | 0 | |
| 0.4 | 112 | 0 | 0 | 50 | 0 | 0 | |
| 0.5 | 95 | 0 | 0 | 50 | 0 | 0 | |
| np-Au II | 0.1 | 250 | 50 | 100 | 50 | 10 | 20 |
| 0.2 | 170 | 34 | 68 | 50 | 10 | 20 | |
| 0.3 | 132 | 26.4 | 52.8 | 50 | 10 | 20 | |
| 0.4 | 112 | 22.4 | 44.8 | 50 | 10 | 20 | |
| 0.5 | 95 | 19 | 38 | 50 | 10 | 20 | |
| Relative Density | Young’s Modulus (GPa) | Yield Stress (MPa) | Poisson’s Ratio |
|---|---|---|---|
| 0.1 | 0.724 | 13.511 | 0.371 |
| 0.2 | 2.815 | 29.694 | 0.331 |
| 0.3 | 6.230 | 47.067 | 0.309 |
| 0.4 | 10.946 | 65.259 | 0.295 |
| 0.5 | 16.947 | 84.087 | 0.284 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, Y.; Zheng, X.; Fu, Z.; Wang, C.; Xu, X.; Tan, X. Multi-Scale Modeling for Predicting the Stiffness and Strength of Hollow-Structured Metal Foams with Structural Hierarchy. Materials 2018, 11, 380. https://doi.org/10.3390/ma11030380
Yi Y, Zheng X, Fu Z, Wang C, Xu X, Tan X. Multi-Scale Modeling for Predicting the Stiffness and Strength of Hollow-Structured Metal Foams with Structural Hierarchy. Materials. 2018; 11(3):380. https://doi.org/10.3390/ma11030380
Chicago/Turabian StyleYi, Yong, Xiaoyang Zheng, Zhibing Fu, Chaoyang Wang, Xibin Xu, and Xiulan Tan. 2018. "Multi-Scale Modeling for Predicting the Stiffness and Strength of Hollow-Structured Metal Foams with Structural Hierarchy" Materials 11, no. 3: 380. https://doi.org/10.3390/ma11030380
APA StyleYi, Y., Zheng, X., Fu, Z., Wang, C., Xu, X., & Tan, X. (2018). Multi-Scale Modeling for Predicting the Stiffness and Strength of Hollow-Structured Metal Foams with Structural Hierarchy. Materials, 11(3), 380. https://doi.org/10.3390/ma11030380





