Rupture Predictions of Notched Ti-6Al-4V Using Local Approaches
Abstract
:1. Introduction
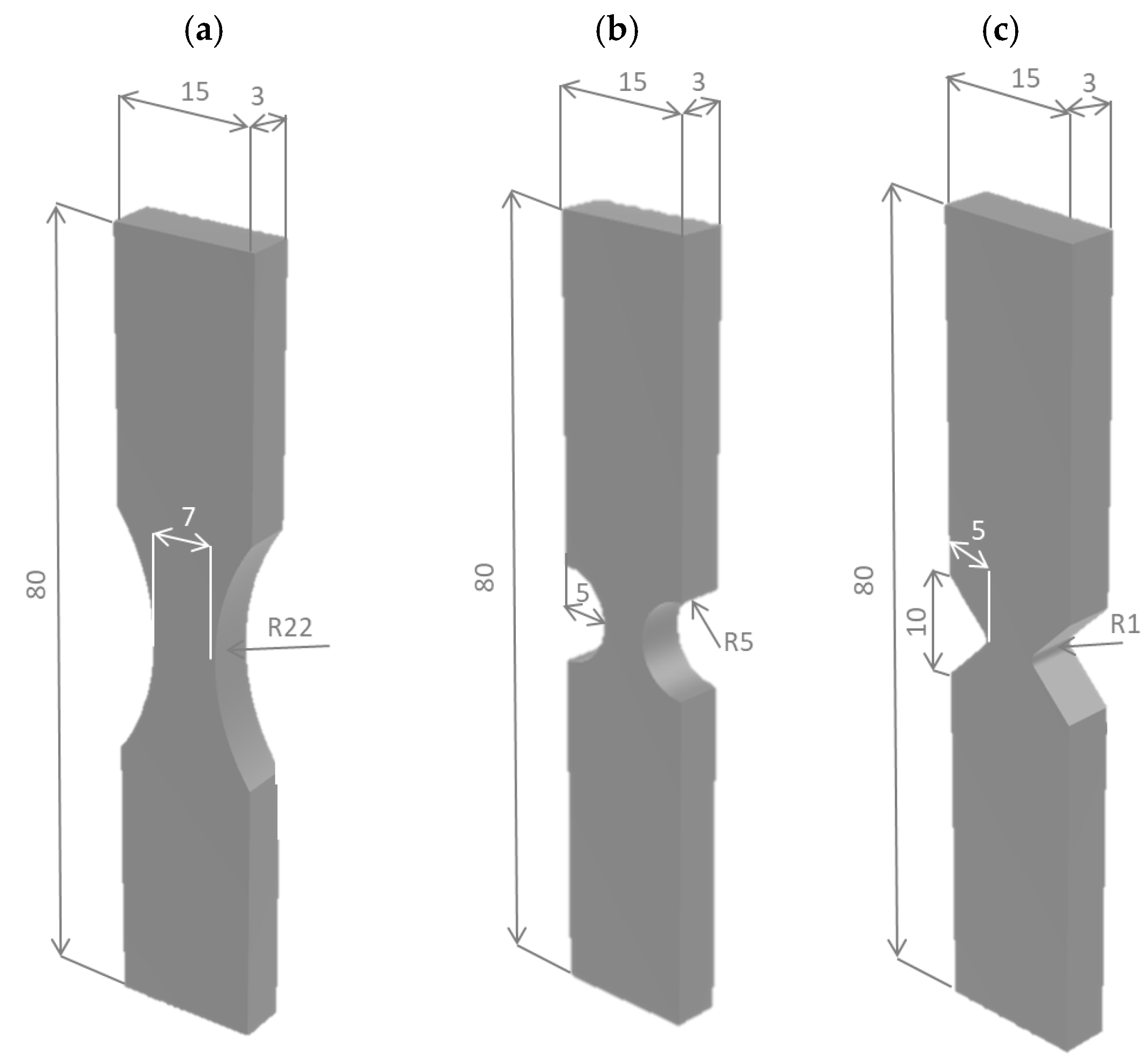
2. Materials and Methods
3. Theoretical Background
3.1. Strain Energy Density Criterion
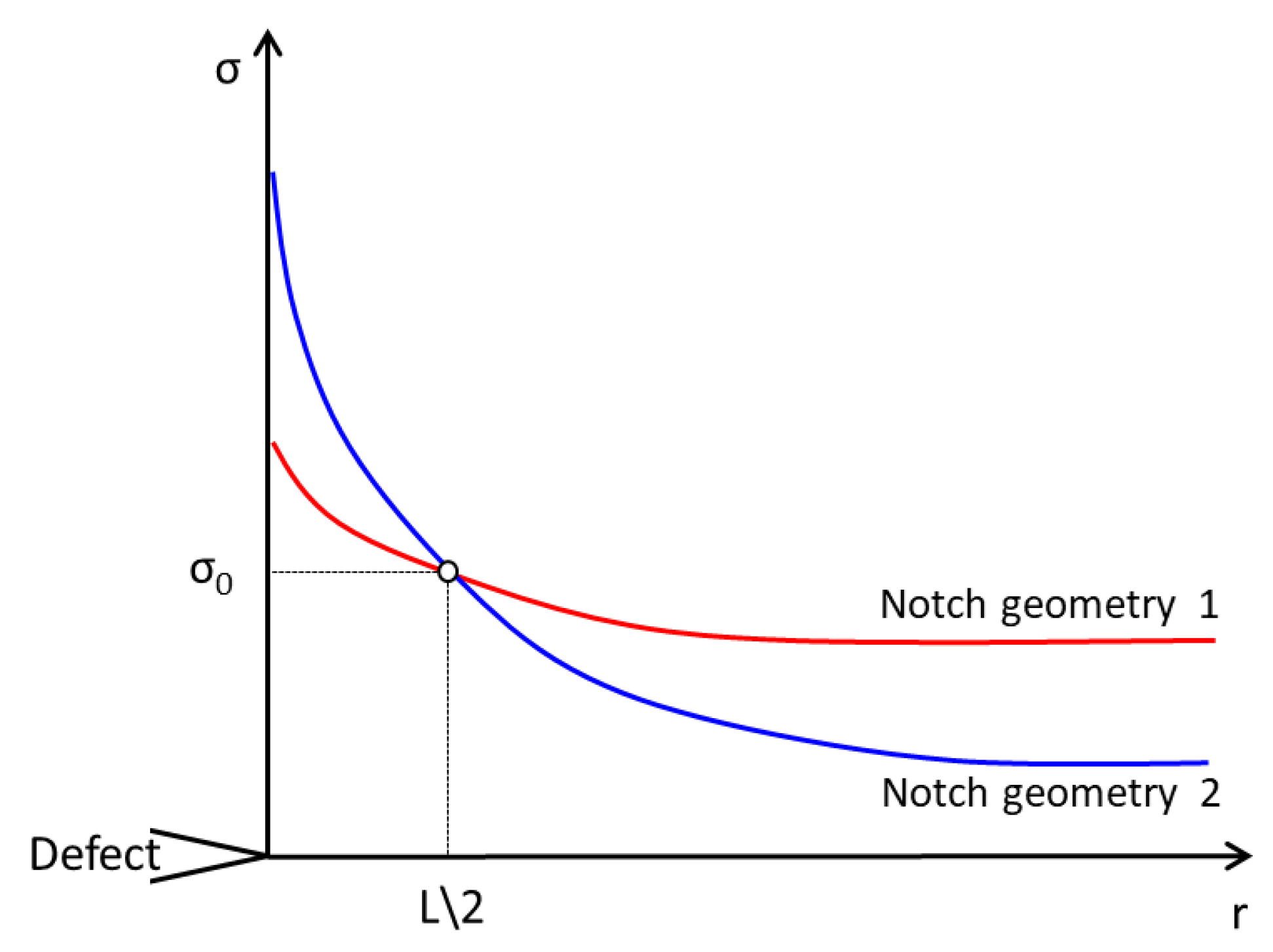
3.2. Theory of Critical Distances
4. Results
4.1. Tensile Tests
4.2. Critical SED Parameters and Synthesis of Tensile Data in Terms of SED
4.3. TCD Critical Parameters Evaluation and Tensile Strength Prediction According to the Line Method (LM)
5. Discussions
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Leyens, C.; Peters, M. Titanium and Titanium Alloys: Fundamentals and Applications; Wiley-VCH: Weinheim, Germany, 2003. [Google Scholar]
- Lütjering, G.; Williams, J.C. Titanium; Springer: Berlin, Germany, 2007. [Google Scholar]
- Elias, C.N.; Lima, J.H.C.; Valiev, R.; Meyers, M.A. Biomedical applications of titanium and its alloys. JOM 2008, 60, 46–49. [Google Scholar] [CrossRef]
- Berto, F.; Lazzarin, P. Recent developments in brittle and quasi-brittle failure assessment of engineering materials by means of local approaches. Mater. Sci. Eng. R 2014, 75, 1–48. [Google Scholar] [CrossRef]
- Berto, F.; Lazzarin, P. The volume-based Strain Energy Density approach applied to static and fatigue strength assessments of notched and welded structures. Procedia Eng. 2009, 1, 155–158. [Google Scholar] [CrossRef]
- Maragoni, L.; Carraro, P.A.; Peron, M.; Quaresimin, M. Fatigue behaviour of glass/epoxy laminates in the presence of voids. Int. J. Fatigue 2017, 95, 18–28. [Google Scholar] [CrossRef]
- Peron, M.; Razavi, S.; Torgersen, J.; Berto, F. Fracture Assessment of PEEK under Static Loading by Means of the Local Strain Energy Density. Materials 2017, 10, 1423. [Google Scholar] [CrossRef] [PubMed]
- Carpinteri, A. Stress-singularity and generalized fracture toughness at the vertex of re-entrant corners. Eng. Fract. Mech. 1987, 26, 143–155. [Google Scholar] [CrossRef]
- Seweryn, A.; Łukaszewicz, A. Verification of brittle fracture criteria for elements with V-shaped notches. Eng. Fract. Mech. 2002, 69, 1487–1510. [Google Scholar] [CrossRef]
- Seweryn, A.; Poskrobko, S.; Mróz, Z. Brittle Fracture in Plane Elements with Sharp Notches under Mixed-Mode Loading. J. Eng. Mech. 1997, 123, 535–543. [Google Scholar] [CrossRef]
- Knesl, Z. A criterion of V-notch stability. Int. J. Fract. 1991, 48, 79–83. [Google Scholar] [CrossRef]
- Seweryn, A. Brittle fracture criterion for structures with sharp notches. Eng. Fract. Mech. 1994, 47, 673–681. [Google Scholar] [CrossRef]
- Dunn, M.L.; Suwito, W.; Cunningham, S.; May, C.W. Fracture initiation at sharp notches under mode I, mode II, and mild mixed mode loading. Int. J. Fract. 1997, 84, 367–381. [Google Scholar] [CrossRef]
- Dunn, M.L.; Suwito, W.; Cunningham, S. Fracture initiation at sharp notches: Correlation using critical stress intensities. Int. J. Solids Struct. 1997, 34, 3873–3883. [Google Scholar] [CrossRef]
- Lazzarin, P.; Filippi, S. A generalized stress intensity factor to be applied to rounded V-shaped notches. Int. J. Solids Struct. 2006, 43, 2461–2478. [Google Scholar] [CrossRef]
- Williams, M.L. Stress singularities resulting from various boundary conditions in angular corners on plates in extension. J. Appl. Mech. 1952, 19, 526–528. [Google Scholar]
- Lazzarin, P.; Zambardi, R. A finite-volume-energy based approach to predict the static and fatigue behavior of components with sharp V-shaped notches. Int. J. Fract. 2001, 112, 275–298. [Google Scholar] [CrossRef]
- Gillemot, F.; Czoboly, E.; Havas, I. Fracture mechanics applications of absorbed specific fracture energy: Notch and unnotched specimens. Theor. Appl. Fract. Mech. 1985, 5, 39–45. [Google Scholar] [CrossRef]
- Sih, G.C.; Ho, J.W. Sharp notch fracture strength characterized by critical energy density. Theor. Appl. Fract. Mech. 1991, 16, 179–214. [Google Scholar] [CrossRef]
- Sih, G.C. Strain-energy-density factor applied to mixed mode crack problems. Int. J. Fract. 1974, 10, 305–321. [Google Scholar] [CrossRef]
- Sih, G.C. Some basic problems in fracture mechanics and new concepts. Eng. Fract. Mech. 1973, 5, 365–377. [Google Scholar] [CrossRef]
- Razavi, S.M.J.; Peron, M.; Torgersen, J.; Berto, F.; Mutignani, F. Effect of hot dip galvanization on the fatigue strength of steel bolted connections. Fract. Int. Struct. 2017, 41, 432–439. [Google Scholar]
- Peron, M.; Razavi, S.M.J.; Berto, F.; Torgersen, J.; Marsavina, L. Local strain energy density for the fracture assessment of polyurethane specimens weakened by notches of different shape. Fract. Int. Struct. 2017, 42, 214–222. [Google Scholar]
- Campagnolo, A.; Razavi, S.M.J.; Peron, M.; Torgersen, J.; Berto, F. Mode II brittle fracture: Recent developments. Fract. Int. Struct. 2017, 42, 181–188. [Google Scholar]
- Razavi, S.M.J.; Peron, M.; Torgersen, J.; Berto, F. Static Multiaxial Fracture Behavior of Graphite Components: A Review of Recent Results. Key Eng. Mater. 2017, 754, 35–38. [Google Scholar] [CrossRef]
- Razavi, S.M.J.; Peron, M.; Torgersen, J.; Berto, F.; Welo, T. 40CrMoV13.9 notched specimens under multiaxial fatigue: An overview of recent results. Fract. Int. Struct. 2017, 41, 440–446. [Google Scholar]
- Peron, M.; Razavi, S.M.J.; Berto, F.; Torgersen, J.; Mutignani, F. Local strain energy density for the fatigue assessment of hot dip galvanized welded joints: Some recent outcomes. Fract. Int. Struct. 2017, 42, 205–213. [Google Scholar]
- Peron, M.; Razavi, S.M.J.; Berto, F.; Torgersen, J.; Colussi, M. Fracture assessment of magnetostrictive materials. Fract. Int. Struct. 2017, 42, 223–230. [Google Scholar]
- Gallo, P.; Razavi, S.M.J.; Peron, M.; Torgersen, J.; Berto, F. Creep behavior of V-notched components. Fract. Int. Struct. 2017, 41, 456–463. [Google Scholar]
- Ferro, P.; Peron, M.; Razavi, S.M.J.; Berto, F.; Torgersen, J. The fatigue behavior of V-notches in presence of residual stresses: Recent developments and future outcomes. Fract. Int. Struct. 2017, 42, 189–195. [Google Scholar]
- Berto, F.; Campagnolo, A.; Lazzarin, P. Fatigue strength of severely notched specimens made of Ti-6Al-4V under multiaxial loading. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 503–517. [Google Scholar] [CrossRef]
- Piccotin, A.; Marsavina, L.; Berto, F.; Negru, R. Fracture parameters determination of polyurethane materials for application of SED criteria to notched components. Procedia Struct. Integr. 2016, 2, 1861–1869. [Google Scholar] [CrossRef]
- Taylor, D. Geometrical effects in fatigue: A unifying theoretical model. Int. J. Fatigue 1999, 21, 413–420. [Google Scholar] [CrossRef]
- Taylor, D. The theory of critical distances. Eng. Fract. Mech. 2008, 75, 1696–1705. [Google Scholar] [CrossRef]
- Neuber, H. Theory of Notch Stresses: Principles for Exact Calculation of Strength with Reference to Structural Form and Material, 2nd ed.; Springer: Berlin, Germany, 1958; p. 292. [Google Scholar]
- Peterson, R. Notch-sensitivity. In Metal Fatigue; Sines, G., Waisman, J.L., Eds.; McGraw Hill: New York, NY, USA, 1959; pp. 293–306. [Google Scholar]
- Taylor, D.; Merlo, M.; Pegley, R.; Cavatorta, M.P. The effect of stress concentrations on the fracture strength of polymethylmethacrylate. Mater. Sci. Eng. A 2004, 382, 288–294. [Google Scholar] [CrossRef]
- Taylor, D. Predicting the fracture strength of ceramic materials using the theory of critical distances. Eng. Fract. Mech. 2004, 71, 2407–2416. [Google Scholar] [CrossRef]
- Taylor, D. The theory of critical distances: A review of its applications in fatigue. Eng. Fract. Mech. 2008, 75, 1706–1724. [Google Scholar] [CrossRef]
- Berto, F.; Lazzarin, P. A review of the volume-based strain energy density approach applied to V-notches and welded structures. Theor. Appl. Fract. Mech. 2009, 52, 183–194. [Google Scholar] [CrossRef]
- Berto, F.; Campagnolo, A.; Gallo, P. Brittle Failure of Graphite Weakened by V-Notches: A Review of Some Recent Results Under Different Loading Modes. Strength Mater. 2015, 47, 488–506. [Google Scholar] [CrossRef]
- Beltrami, E. Sulle condizioni di resistenza dei corpi elastici. Il Nuovo Cimento 1885, 18, 145–155. [Google Scholar] [CrossRef]
- Taylor, D. The Theory of Critical Distances: A New Perspective in Fracture Mechanics, 1st ed.; Elsevier: New York, NY, USA, 2007. [Google Scholar]
- Taylor, D. The Theory of Critical Distances Applied to the Prediction of Brittle Fracture in Metallic. Materials 2005, 1, 145–154. [Google Scholar]
- Nasa Technical Report Center. Strength, Fatigue, and Fracture Toughness of Ti-6Al-4V Liner from a Composite Over-Wrapped Pressure Vessel; Nasa Technical Report Center: Cleveland, OH, USA, 2013. [Google Scholar]
- Lazzarin, P.; Berto, F.; Zappalorto, M. Rapid calculations of notch stress intensity factors based on averaged strain energy density from coarse meshes: Theoretical bases and applications. Int. J. Fatigue 2010, 32, 1559–1567. [Google Scholar] [CrossRef]
- Taylor, D.; Kasiri, S.; Brazel, E. The theory of critical distances applied to problems in fracture and fatigue of bone. Fract. Int. Struct. 2009, 10, 12–20. [Google Scholar]
- Fuentes, J.; Cicero, S.; Berto, F.; Torabi, A.R.; Madrazo, V.; Azizi, P. Estimation of Fracture Loads in AL7075-T651 Notched Specimens Using the Equivalent Material Concept Combined with the Strain Energy Density Criterion and with the Theory of Critical Distances. Metals 2018, 8, 87. [Google Scholar] [CrossRef]




| E (MPa) | ν | σ0.2 (MPa) | σUTS (MPa) |
|---|---|---|---|
| 113,000 (678) | 0.342 (0.016) | 1035 (7.5) | 1058 (4.3) |
| Specimen Geometry | Tensile Strength (MPa) |
|---|---|
| Semi-circular | 1132.89 (4.82) |
| Blunt V-notch | 1053.08 (10.79) |
| Specimen Geometry | Experimental Data (MPa) | SED Prediction (MPa) | SED Deviation | Line Method Prediction (MPa) | LM Deviation |
|---|---|---|---|---|---|
| Semi-circular notch | 1132.89 | 1142.37 | +0.84% | 1227.37 | +8.42% |
| Blunt V-notch | 1053.08 | 1065.97 | +1.27% | 1056.56 | +0.33% |
| Specimen Geometry | Experimental Data (MPa) | SED Prediction, Rc = 1.19 (MPa) | SED Prediction, Rc = 1.15 (MPa) |
|---|---|---|---|
| Semi-circular notch | 1132.89 | 1142.37 (+0.84%) | 1141.84 (+0.79%) |
| Blunt V-notch | 1053.08 | 1065.97 (+1.27%) | 1053.08 (+1.22%) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peron, M.; Torgersen, J.; Berto, F. Rupture Predictions of Notched Ti-6Al-4V Using Local Approaches. Materials 2018, 11, 663. https://doi.org/10.3390/ma11050663
Peron M, Torgersen J, Berto F. Rupture Predictions of Notched Ti-6Al-4V Using Local Approaches. Materials. 2018; 11(5):663. https://doi.org/10.3390/ma11050663
Chicago/Turabian StylePeron, Mirco, Jan Torgersen, and Filippo Berto. 2018. "Rupture Predictions of Notched Ti-6Al-4V Using Local Approaches" Materials 11, no. 5: 663. https://doi.org/10.3390/ma11050663






