Research on the Crushing Process of PELE Casing Material Based on the Crack-Softening Algorithm and Stochastic Failure Algorithm
Abstract
:1. Introduction
2. Theoretical Foundations
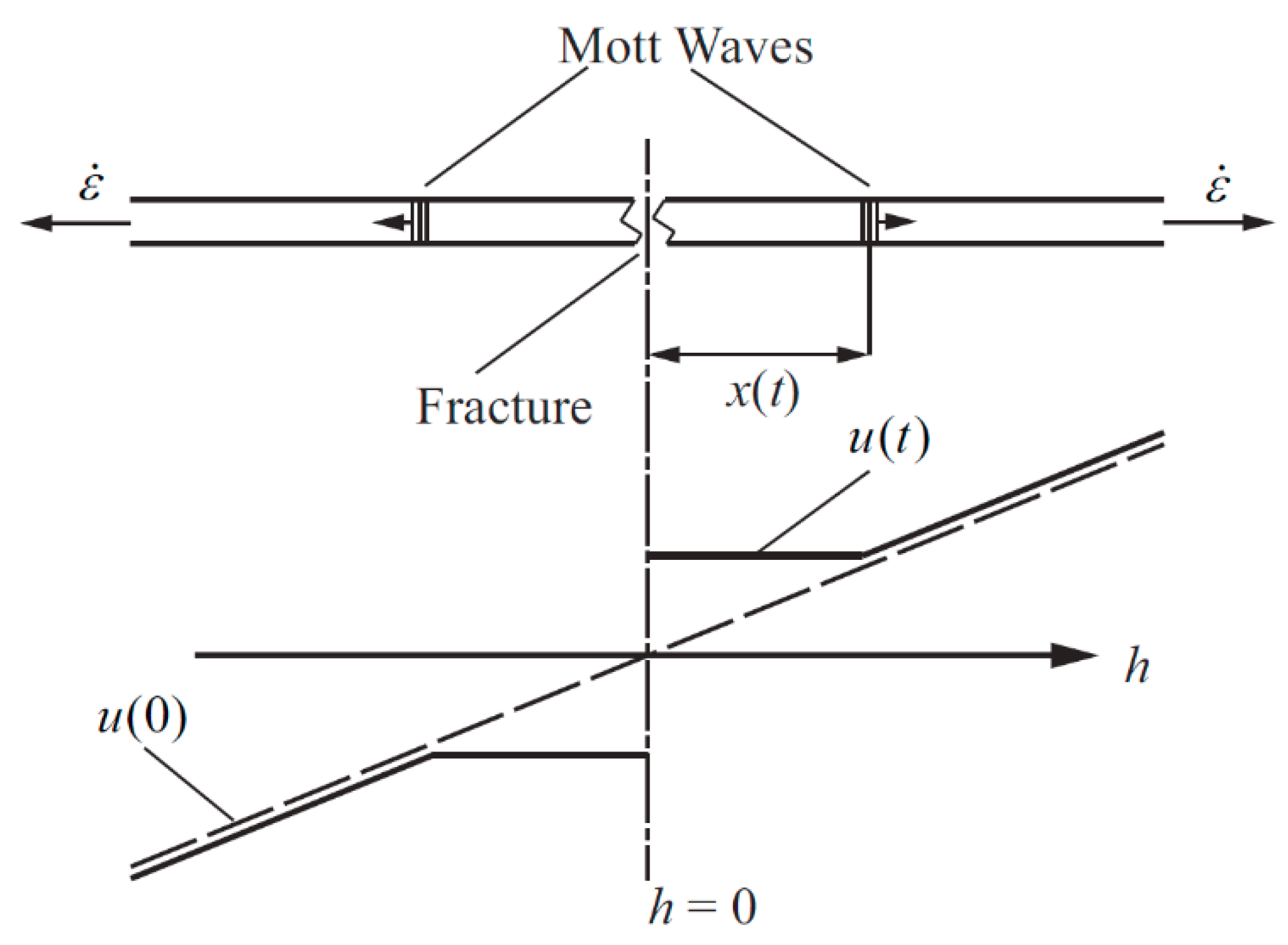
2.1. Basic Theory of Mott Ring
2.2. Grady One-Dimensional Fracture Theory and the Crack-Softening Algorithm
- Dam = 0: it represents the grid does not reach the failure condition.
- Dam = 1: it represents the grid has gone through the unloading process and completely invalid.
2.3. Grady Spallation Theory and Spall Strength of Materials
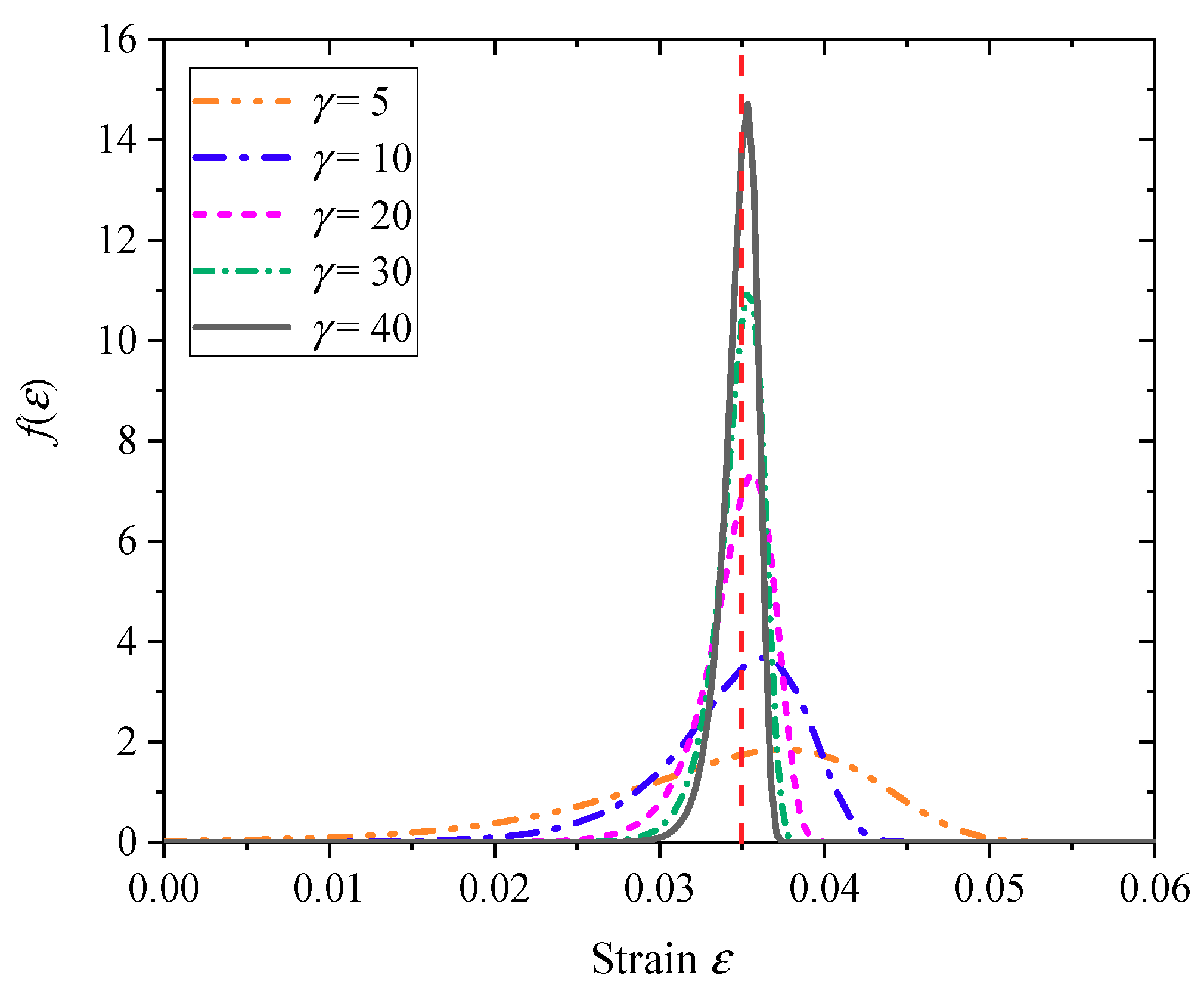
2.4. Mott Fracture Probability Density Function and Stochastic Failure Algorithm
3. Numerical Simulation
3.1. Finite Element Model
3.2. Determination of Key Parameters in the Material Failure Model
3.3. Material Model and Parameters
4. Analysis and Discussion of the Simulation Results
4.1. Influence of the Crack-Softening Algorithm and Stochastic Failure Algorithm on the Simulation Results
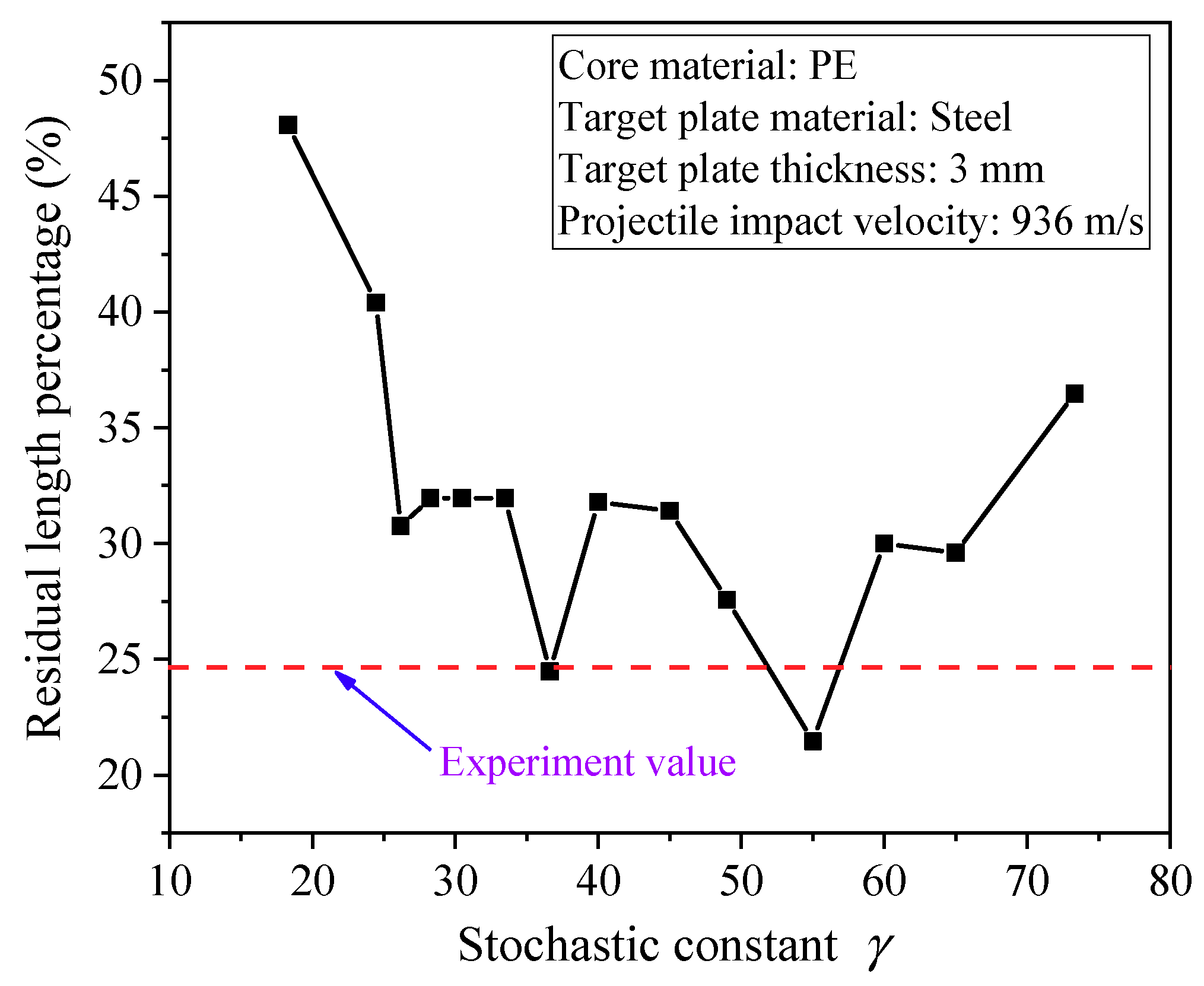
4.2. Quantitative Comparison of the Simulation Results and Experimental Results
- (1)
- Comparing the following four sets of working conditions (#3–#9; #4–#10; #5–#7; #6–#8), the following conclusions can be obtained intuitively from Figure 14 and Table 3. When the core material was aluminum, the residual length of the projectile was larger, the size of fragments was smaller, and the radial velocity of fragments was higher than when the core material was polyethylene.
- (2)
- Comparing the following two sets of working conditions (#1–#5; #2–#6) from Table 3, for the same core material and the target plate thickness, when the target material changed from aluminum to steel, the residual velocity of projectile decreases and the radial velocity of fragments increased. Comparing the following two sets of working conditions (#1–#3; #2–#4) from Table 3, for the same core material and the target plate material, when the target plate thickness increased, the residual velocity of the projectile decreased and the radial velocity of the fragments increased.
5. Conclusions
- (1)
- Based on the qualitative analysis designed in this paper, the crack-softening algorithm was beneficial for controlling the distortion of failure grids, and the stochastic-failure algorithm was beneficial to control the length and shape of fragments. After adding the two algorithms, the simulation results were more consistent with the actual situation.
- (2)
- Several sets of simulation conditions were designed to quantitatively analyze the coincidence degree between the simulation and experiment by means of the residual velocity of the projectile and the maximum radial velocity of fragments. The results indicated that the simulation results were in good agreement with the experimental results and the errors were small. Specifically, the radial velocity error of fragments was within 8.5%, and the axial residual velocity error of the projectile was within 2%.
- (3)
- According to the four sets of working conditions (#3–#9; #4–#10; #5–#7; #6–#8) shown in Figure 14 and Table 3, the following conclusion could be obtained intuitively: when the inner core material was aluminum, the residual length of projectile was larger, the size of fragments was smaller, and the radial velocity of fragments was higher than the situation where the inner core material was polyethylene.
- (4)
- For the same core material and target plate thickness, when the target material changed from aluminum to steel, the residual velocity of the projectile decreased and the radial velocity of the fragments increased, which could be explained intuitively by the two groups of working conditions (#1–#5; #2–#6) in Table 3. Similarly, for the same core material and target plate material, when the target plate thickness increased, the residual velocity of the projectile decreased and the radial velocity of the fragments increased, which could also be explained intuitively by the two groups of working conditions (#1–#3; #2–#4) in Table 3.
Author Contributions
Funding
Conflicts of Interest
References
- Kesberg, G.; Schirm, V.; Kerk, S. PELE: The future ammunition concept. In Proceedings of the 21st International Symposium on Ballistics (ISB’21), Adelaide, Australia, 19–23 April 2004. [Google Scholar]
- Paulus, G.; Chanteret, P.Y.; Wollmann, E. PELE: A new penetrator concept for generating lateral effects. In Proceedings of the 21st International Symposium on Ballistics (ISB’21), Adelaide, Australia, 19–23 April 2004. [Google Scholar]
- Rheinmetall Waffe Munition. 105/120/125 mm PELE Firing Results. Available online: https://ndiastorage.blob.core.usgovcloudapi.net/ndia/2005/garm/wednesday/borngen.pdf (accessed on 29 August 2018).
- Gloude, D. Capabilities of Penetrator with Enhanced Lateral Efficiency. Available online: https://ndiastorage.blob.core.usgovcloudapi.net/ndia/2007/gun_missile/GMTueAM1/GloudePresentation.pdf (accessed on 29 August 2018).
- Paulus, G.; Schirm, V. Impact behavior of PELE projectiles perforating thin target plates. Int. J. Impact Eng. 2006, 33, 566–579. [Google Scholar] [CrossRef]
- Zhu, J.; Zhao, G.; Du, Z.; Wang, X. Mechanism of PELE projectiles perpendicularly impacting on thin target plates. Explos. Shock Waves 2009, 29, 281–288. [Google Scholar]
- Zhu, J.; Zhao, G.; Du, Z.; Li, D. Experimental study of the influence factors on small caliber PELE impacting thin target. Chin. J. Exp. Mech. 2007, 22, 505–510. [Google Scholar]
- Jiang, J.; Zhang, M.; Men, J.; Wang, S. Experimental study on multi-layered target penetration of PELE with different cores. Trans. Beijing Inst. Technol. 2010, 30, 1009–1012. [Google Scholar]
- Tu, S.; Wang, J.; An, Z.; Chang, Y. Influence of thickness of armor on the burst-effect of steel shell PELE. In Proceedings of the 9th International Conference on Electronic Measurement & Instruments, Beijing, China, 16–19 August 2009. [Google Scholar]
- Du, Z.; Song, L. Theoretical model of penetrator with enhanced lateral effect impacting thin metal target. J. Nanjing Univ. Sci. Technol. 2011, 35, 821–826. [Google Scholar]
- Fan, Z.; Ran, X.; Tang, W.; Ke, Y.; Li, Z. The model to calculate the radial velocities of fragments after PELE penetrator perforating a thin plate. Int. J. Impact Eng. 2016, 95, 12–16. [Google Scholar] [CrossRef]
- Verreault, J.; Hinsberg, V.N.; Abadjieva, E. PELE fragmentation dynamics. In Proceedings of the 27th International Symposium on Ballistics (ISB’27), Freiburg, Germany, 22–26 April 2013. [Google Scholar]
- Wang, H.; Ji, P.; Yu, Q.; Zheng, Y. Numerical simulation of oblique penetration of PELE into finite thickness plates. Trans. Beijing Inst. Technol. 2010, 30, 1017–1019. [Google Scholar]
- Verreault, J. Analytical and numerical description of the PELE fragmentation upon impact with thin target plates. Int. J. Impact Eng. 2015, 76, 196–206. [Google Scholar] [CrossRef]
- Grady, D. Fragmentation of Rings and Shells: The Legacy of NF Mott; Springer: Heidelberg, Germany, 2006. [Google Scholar]
- Grady, D.; Kipp, M. Fragmentation properties of metals. Int. J. Impact Eng. 1997, 20, 293–308. [Google Scholar] [CrossRef] [Green Version]
- Kipp, M.E.; Grady, D. Dynamic fracture growth and interaction in one dimension. J. Mech. Phys. Solids 1985, 33, 399–415. [Google Scholar] [CrossRef]
- Century Dynamics Inc. AUTODYN Theory Manual; Revision 4.3; Century Dynamics Inc.: Houston, TX, USA, 2003. [Google Scholar]
- Grady, D. The spall strength of condensed matter. J. Mech. Phys. Solids 1988, 36, 353–384. [Google Scholar] [CrossRef]
- Grady, D.; Olsen, M. A statistics and energy based theory of dynamic fragmentation. Int. J. Impact Eng. 2003, 29, 293–306. [Google Scholar] [CrossRef]
- Livingstone, I.; Verolme, K.; Hayhurst, C. Predicting the fragmentation onset velocity for different metallic projectiles using numerical simulations. Int. J. Impact Eng. 2001, 26, 453–464. [Google Scholar] [CrossRef]
- Century Dynamics Inc. Interactive Non-Linear Dynamic Analysis Software AUTODYN User Manual; Century Dynamics Inc.: Oakland, CA, USA, 2003. [Google Scholar]
- Grady, D. Impact failure and fragmentation properties of tungsten carbide. Int. J. Impact Eng. 1999, 23, 307–317. [Google Scholar] [CrossRef]
- Rosenberg, Z.; Dekel, E. On the deep penetration and plate perforation by rigid projectiles. Int. J. Solids Struct. 2009, 46, 4169–4180. [Google Scholar] [CrossRef]
- Rosenberg, Z.; Dekel, E. On the deep penetration of deforming long rods. Int. J. Solids Struct. 2010, 47, 238–250. [Google Scholar] [CrossRef]













| Variable | Material | ||||
|---|---|---|---|---|---|
| Tungsten | Al-6061 | PE | Al-7075 | Steel-4340 | |
| ρ0 (g/cm3) | 18 | 2.65 | 0.92 | 2.8 | 7.823 |
| c0 (km/s) | 4.03 | 5.24 | 2.9 | 5.2 | 4.57 |
| s | 1.237 | 1.4 | 1.48 | 1.36 | 1.49 |
| Grüneisen Coefficient | - | 1.97 | 1.6 | - | - |
| Cp (J/kg∙K) | - | 885 | 2300 | - | - |
| Shear Modulus G (GPa) | 139.02 | 27.5 | 0.13 | 26.7 | 77 |
| Yield Stress Y (GPa) | 1.5 | 0.3 | 0.02 | 0.4 | 0.8 |
| Principle Tensile Stress σT (GPa) | 2.8 | 0.5 | - | - | - |
| Principle Tensile Strain εT | 0.035 | - | - | - | - |
| Fracture Energy Gf (J/m2) | 45 | - | - | - | - |
| Stochastic Variance γ | 36.5 | - | - | - | - |
| Inst. Geometric Strain | 0.6 | 0.8 | 1.8 | Failure | Failure |
| Condition Number | Inner Core Material | Target Plate Material | Target Plate Thickness (mm) | Projectile Impact Velocity (m/s) |
|---|---|---|---|---|
| #1 | Al | Al | 3 | 929 |
| #2 | Al | Al | 3 | 1275 |
| #3 | Al | Al | 8 | 937 |
| #4 | Al | Al | 8 | 1254 |
| #5 | Al | Steel | 3 | 925 |
| #6 | Al | Steel | 3 | 1261 |
| #7 | PE | Steel | 3 | 936 |
| #8 | PE | Steel | 3 | 1262 |
| #9 | PE | Al | 8 | 939 |
| #10 | PE | Al | 8 | 1258 |
| Condition Number | Maximum Radial Velocity of Fragments (m/s) | Error | Axial Residual Velocity of Projectile (m/s) | Error | ||
|---|---|---|---|---|---|---|
| Experiment | Simulation | Experiment | Simulation | |||
| #1 | 112 | 114 | 1.8% | 914 | 921 | 0.7% |
| #2 | 158 | 149 | −5.7% | 1261 | 1259 | −0.2% |
| #3 | 143 | 139 | −2.7% | 900 | 907 | 0.8% |
| #4 | 221 | 207 | −6.3% | 1208 | 1219 | 0.9% |
| #5 | 184 | 192 | 4.3% | 895 | 904 | 1.0% |
| #6 | 243 | 229 | −5.8% | 1231 | 1246 | 1.2% |
| #7 | 94 | 102 | 8.5% | 889 | 907 | 2.0% |
| #8 | 145 | 134 | −7.5% | 1206 | 1221 | 1.2% |
| #9 | 112 | 116 | 3.6% | 887 | 904 | 1.9% |
| #10 | 184 | 171 | −7.1% | 1203 | 1224 | 1.7% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, L.; Zhou, J.; Tang, W.; Ran, X.; Cheng, Y. Research on the Crushing Process of PELE Casing Material Based on the Crack-Softening Algorithm and Stochastic Failure Algorithm. Materials 2018, 11, 1561. https://doi.org/10.3390/ma11091561
Ding L, Zhou J, Tang W, Ran X, Cheng Y. Research on the Crushing Process of PELE Casing Material Based on the Crack-Softening Algorithm and Stochastic Failure Algorithm. Materials. 2018; 11(9):1561. https://doi.org/10.3390/ma11091561
Chicago/Turabian StyleDing, Liangliang, Jingyuan Zhou, Wenhui Tang, Xianwen Ran, and Ye Cheng. 2018. "Research on the Crushing Process of PELE Casing Material Based on the Crack-Softening Algorithm and Stochastic Failure Algorithm" Materials 11, no. 9: 1561. https://doi.org/10.3390/ma11091561





