Freeze–Thaw Durability of Strain-Hardening Cement-Based Composites under Combined Flexural Load and Chloride Environment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material and Specimen Preparation
2.2. Loading Device and Stress Level
2.3. Test Methods
3. Results and Discussion
3.1. Freezing and Thawing Resistance
3.1.1. Surface Damage and Mass Loss
3.1.2. Relative Dynamic Elasticity Modulus
3.1.3. Microstructure Characteristics
3.2. Residual Flexural Performance
3.3. Chloride Diffusion Performance
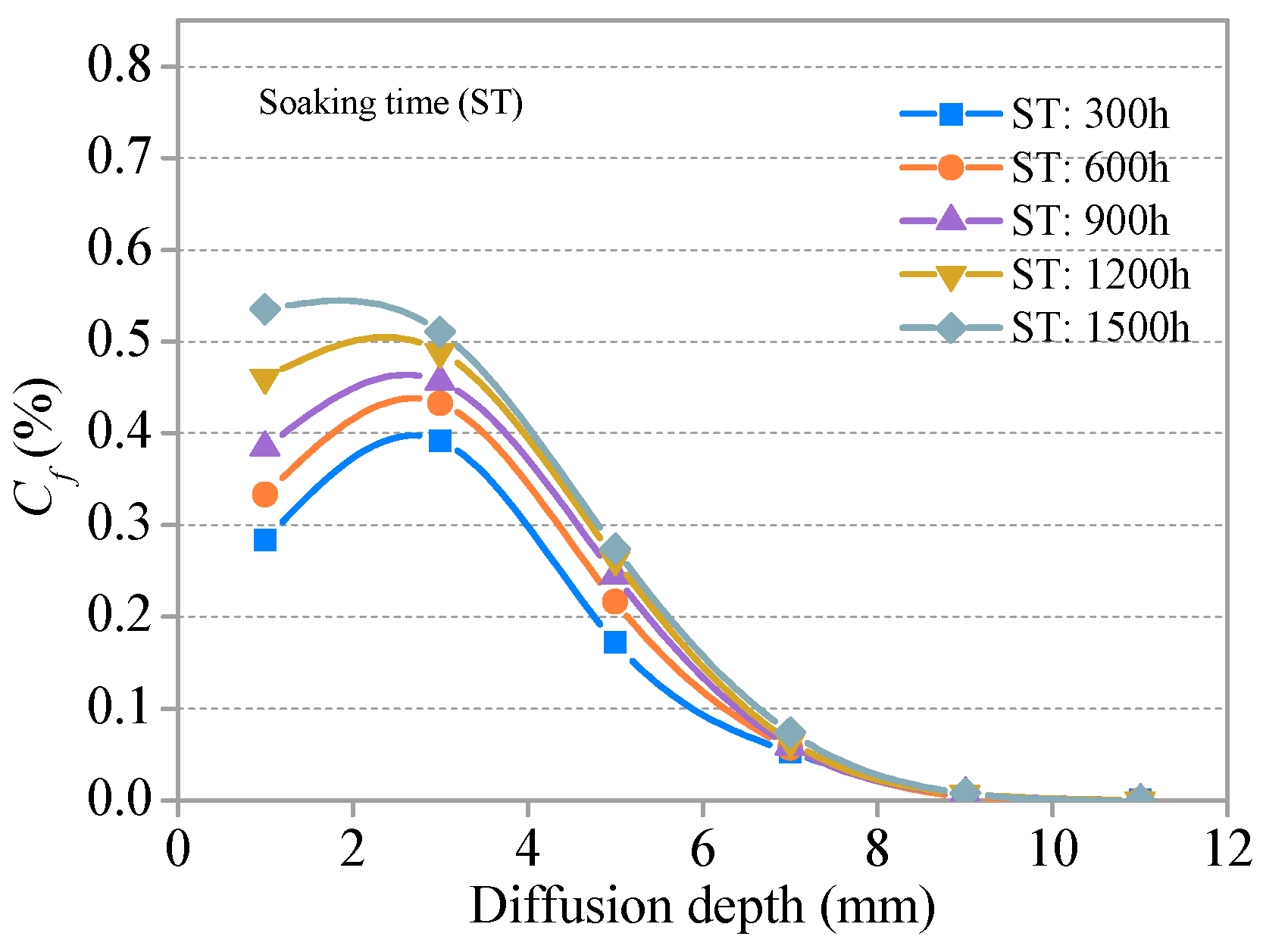
3.3.1. Distribution and Relationship of Cf and Ct
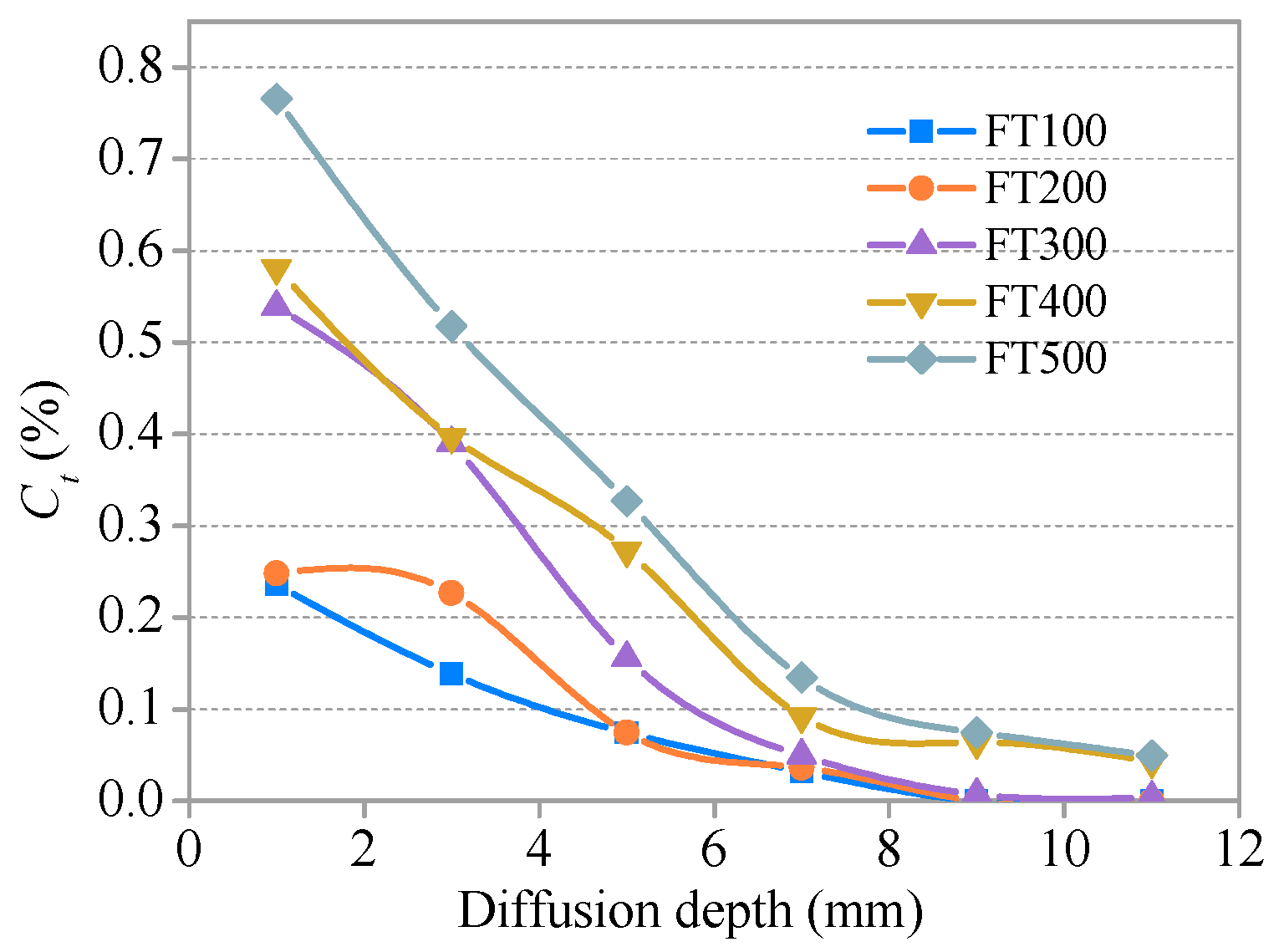
3.3.2. Effects of Freeze–thaw Cycles on Total Cf and Ct
3.3.3. Chloride Diffusion Coefficient
4. Conclusions
- (1)
- Four different flexural loading levels had little effect on surface damage and mass loss, and the mass loss of SHCC specimens experienced several freeze–thaw cycles under combined loads from −0.6% to 0.6%. Compared to no flexural loading (S = 0), the reduction of RDEM of SHCC specimens accelerated after sustained flexural loading was applied (S = 0.36, 0.54, 0.72). A higher loading level led to greater freeze–thaw damage, and the RDEM of the corresponding specimen decreased significantly.
- (2)
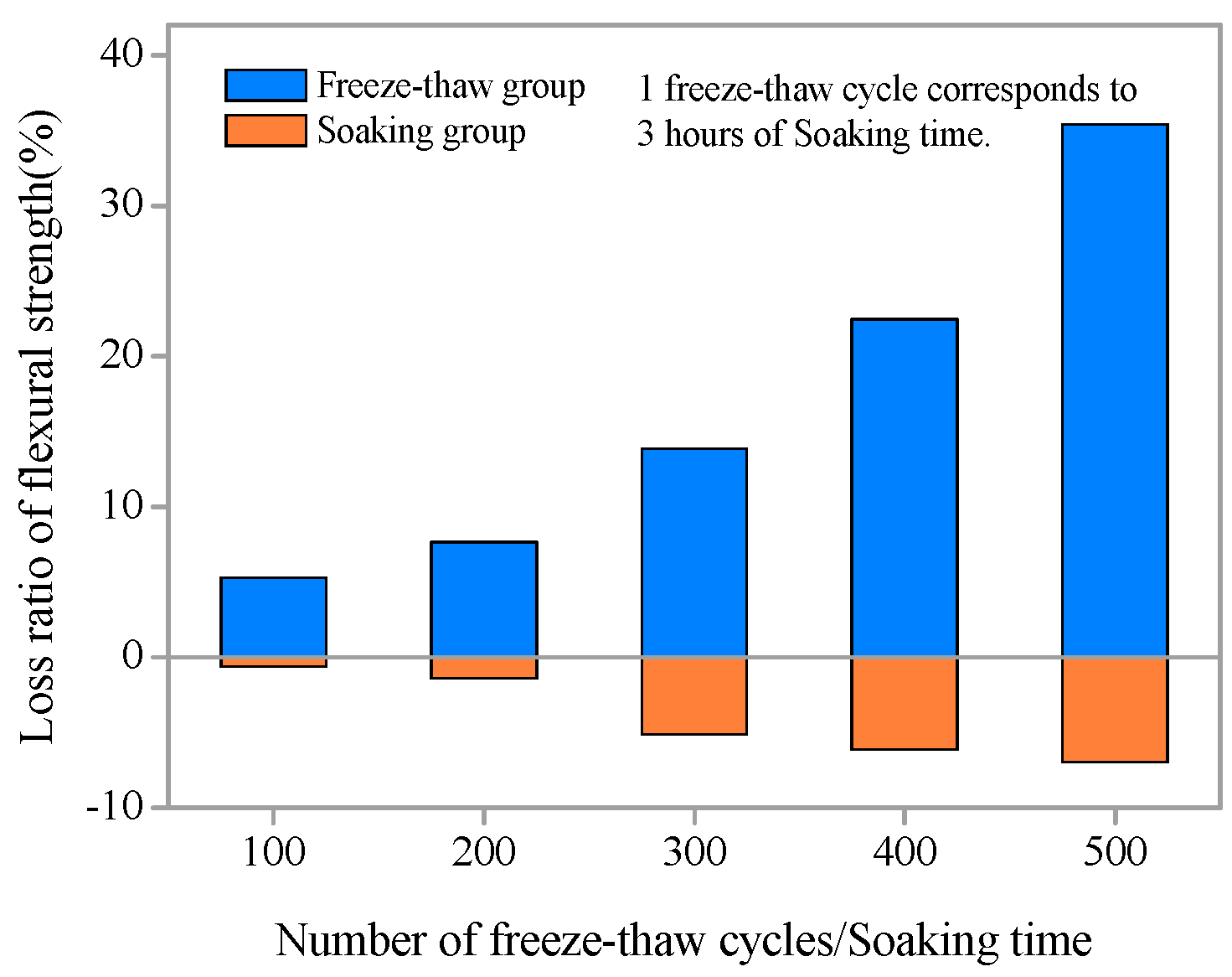
- With increasing freeze–thaw cycles, the flexural strength of SHCC specimens decreases gradually. After 300 cycles, flexural strength decreased only by 13.87%. The residual flexural strength degradation model of SHCC specimens under the coupling action of salt freezing cycles and flexural loading (S = 0.36) was obtained using nonlinear fitting regression.
- (3)
- Cf and Ct increase with the development of freezing and thawing at the same diffusion depth, and a bilinear relationship was found between the chloride diffusion coefficient Dc and the number of freeze–thaw cycles. Comparative analysis shows that the Dc of the freeze–thaw cycle group was greater than for the immersion environment corresponding to the same soaking time.
Author Contributions
Funding
Conflicts of Interest
References
- Tang, S.W.; Yao, Y.; Andrade, C.; Li, Z.J. Recent durability studies on concrete structure. Cem. Concr. Res. 2015, 78, 143–154. [Google Scholar] [CrossRef]
- Shi, X.; Xie, N.; Fortune, K.; Gong, J. Durability of steel reinforced concrete in chloride environments: An overview. Constr. Build. Mater. 2012, 30, 125–138. [Google Scholar] [CrossRef]
- Li, V.C.; Mishra, D.K.; Wu, H.C. Matrix design for pseudo-strain-hardening fibre reinforced cementitious composites. Mater. Struct. 1995, 28, 586–595. [Google Scholar] [CrossRef]
- Li, V.C. On engineered cementitious composites (ECC). J. Adv. Concr. Technol. 2003, 1, 215–230. [Google Scholar] [CrossRef]
- Rokugo, K.; Kanda, T.; Yokota, H.; Sakata, N. Applications and recommendations of high performance fiber reinforced cement composites with multiple fine cracking (HPFRCC) in Japan. Mater. Struct. 2009, 42, 1197. [Google Scholar] [CrossRef]
- Choi, J.I.; Lee, B.Y.; Ranade, R.; Li, V.C.; Lee, Y. Ultra-high-ductile behavior of a polyethylene fiber-reinforced alkali-activated slag-based composite. Cem. Concr. Compos. 2016, 70, 153–158. [Google Scholar] [CrossRef]
- Altmann, F.; Mechtcherine, V. Durability design strategies for new cementitious materials. Cem. Concr. Res. 2013, 54, 114–125. [Google Scholar] [CrossRef]
- Paul, S.C.; Babafemi, A.J. A review of the mechanical and durability properties of strain hardening cement-based composite (SHCC). J. Sustain. Cem.-Based Mater. 2018, 7, 57–78. [Google Scholar] [CrossRef]
- Zhang, Y.; Johnson, A.E.; White, D.J. Laboratory freeze–thaw assessment of cement, fly ash, and fiber stabilized pavement foundation materials. Cold Reg. Sci. Technol. 2016, 122, 50–57. [Google Scholar] [CrossRef]
- Şahmaran, M.; Lachemi, M.; Li, V.C. Assessing the durability of engineered cementitious composites under freezing and thawing cycles. J. ASTM Int. 2009, 6, 1–13. [Google Scholar]
- Şahmaran, M.; Özbay, E.; Yücel, H.E.; Lachemi, M.; Li, V.C. Frost resistance and microstructure of engineered cementitious composites: influence of fly ash and micro poly-vinyl-alcohol fiber. Cem. Concr. Compos. 2012, 34, 156–165. [Google Scholar] [CrossRef]
- Li, M.; Li, V.C. Cracking and healing of engineered cementitious composites under chloride environment. ACI Mater. J. 2011, 108, 333–340. [Google Scholar]
- Zijl, G.P.A.G.V.; Wittmann, F.H.; Oh, B.H.; Kabele, P.; Filho, R.D.T.; Fairbairn, E.M.R.; Slowik, V.; Ogawa, A.; Hoshiro, H.; Mechtcherine, V.; et al. Durability of strain-hardening cement-based composites (SHCC). Mater. Struct. 2012, 45, 1447–1463. [Google Scholar] [CrossRef]
- Nam, J.; Kim, G.; Lee, B.; Hasegawa, R.; Hama, Y. Frost resistance of polyvinyl alcohol fiber and polypropylene fiber reinforced cementitious composites under freeze thaw cycling. Compos. Part B Eng. 2016, 90, 241–250. [Google Scholar] [CrossRef]
- Yun, H.D. Effect of accelerated freeze–thaw cycling on mechanical properties of hybrid PVA and PE fiber-reinforced strain-hardening cement-based composites (SHCCs). Compos. Part B Eng. 2013, 52, 11–20. [Google Scholar] [CrossRef]
- Jang, S.J.; Rokugo, K.; Park, W.S.; Yun, H.D. Influence of rapid freeze-thaw cycling on the mechanical properties of sustainable strain-hardening cement composite (2SHCC). Materials 2014, 7, 1422–1440. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, K.; Ahn, D.L.; Rokugo, K. Effects of crack properties and water-cement ratio on the chloride proofing performance of cracked SHCC suffering from chloride attack. Cem. Concr. Compos. 2016, 69, 18–27. [Google Scholar] [CrossRef]
- Shaikh, F.U.A.; Mihashi, H.; Kobayakawa, A. Corrosion durability of reinforcing steel in cracked high-performance fiber-reinforced cementitious composite beams. J. Mater. Civ. Eng. 2014, 27, 04014228. [Google Scholar] [CrossRef]
- Miyazato, S.; Hiraishi, Y. Durability against Steel Corrosion of HPFRCC with Bending Cracks. J. Adv. Concr. Technol. 2013, 11, 135–143. [Google Scholar] [CrossRef] [Green Version]
- Şahmaran, M.; Li, V.C. Durability properties of micro-cracked ECC containing high volumes fly ash. Cem. Concr. Res. 2009, 39, 1033–1043. [Google Scholar] [CrossRef]
- Paul, S.C.; van Zijl, G.P.A.G.; Babafemi, A.J.; Tan, M.J. Chloride ingress in cracked and uncracked SHCC under cyclic wetting-drying exposure. Constr. Build. Mater. 2016, 114, 232–240. [Google Scholar] [CrossRef]
- Ahmed, S.F.U.; Mihashi, H. Corrosion durability of strain hardening fibre-reinforced cementitious composites. Aust. J. Civ. Eng. 2010, 8, 27–39. [Google Scholar] [CrossRef]
- Wittmann, F.H.; Zhang, P.; Zhao, T. Influence of combined environmental loads on durability of reinforced concrete structures. Restor. Build. Monum. 2006, 12, 349–362. [Google Scholar]
- Paul, S.C.; Babafemi, A.J. Performance of strain hardening cement-based composite (SHCC) under various exposure conditions. Cogent Eng. 2017, 4, 1345608. [Google Scholar] [CrossRef]
- Ma, Z.; Zhao, T.; Xiao, J.; Wang, P. Effect of applied loads on water and chloride penetrations of strain hardening cement-based composites. J. Mater. Civ. Eng. 2016, 28, 04016069. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, D.; Yan, C.; Deng, Y. Experimental study on the tensile properties of pva-ecc with high-calcium fly ash. Bull. Chin. Ceram. Soc. 2016, 35, 52–60. [Google Scholar]
- Gao, R.; Li, Q.; Zhao, S. Concrete deterioration mechanisms under combined sulfate attack and flexural loading. J. Mater. Civ. Eng. 2013, 25, 39–44. [Google Scholar] [CrossRef]
- Standard for Test Methods of Long-Term Performance and Durability of Ordinary Concrete; GB/T50082-2009; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010.
- Test Code for Hydraulic Concrete; SL352-2006; Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2006.
- Stark, J. Recent advances in the field of cement hydration and microstructure analysis. Cem. Concr. Res. 2011, 41, 666–678. [Google Scholar] [CrossRef]
- Liu, S.G.; Yan, M.; Yan, C.W.; Guo, R.Y. Deicing salt resistance of PVA fiber reinforced cementitious composite. J. Jilin Univ. Eng. Technol. Ed. 2012, 42, 63–67. [Google Scholar]
- Jin, S.; Zhang, J.; Huang, B. Fractal analysis of effect of air void on freeze–thaw resistance of concrete. Constr. Build. Mater. 2013, 47, 126–130. [Google Scholar] [CrossRef]
- Mu, R.; Miao, C.; Luo, X.; Sun, W. Combined deterioration of concrete subjected to loading, freeze—Thaw cycles and chloride salt attack. Mag. Concr. Res. 2002, 54, 175–180. [Google Scholar] [CrossRef]














| Components/Property | Unit | Measurement |
|---|---|---|
| Cement | kg/m3 | 745 |
| Fly ash | 319 | |
| Water | 319 | |
| Silica sand | 639 | |
| Water-RAE | 30 | |
| PVA fiber | 26 | |
| Compressive strength, 28d | MPa | 56 |
| Tensile strain, 28d | - | 0.034 |
| Tensile strength, 28d | MPa | 5.2 |
| Flexural strength, 28d | MPa | 13.05 |
| Specimen | No. 1 | No. 2 | No. 3 | Mean |
|---|---|---|---|---|
| Air content (%) | 1.35 | 1.03 | 1.18 | 1.19 |
| Specific surface (mm−1) | 50.33 | 58.77 | 58.11 | 55.74 |
| Spacing factor (mm) | 0.176 | 0.169 | 0.203 | 0.183 |
| Void frequency (mm−1) | 0.170 | 0.151 | 0.098 | 0.140 |
| Average chord length (mm) | 0.079 | 0.068 | 0.069 | 0.072 |
| Measure | S = 0 | S = 0.36 | S = 0.54 | S = 0.72 |
|---|---|---|---|---|
| No. of cycles completed | 500 | 500 | 250 | 50 |
| Mass loss ratio (%) | –0.56 | –0.07 | 0.53 | –0.06 |
| Relative dynamic elasticity modulus | 94.77 | 93.26 | 72.09 | 0 |
| No. | FT100 | FT200 | FT300 | FT400 | FT500 | ST300 | ST600 | ST900 | ST1200 | ST1500 |
|---|---|---|---|---|---|---|---|---|---|---|
| a | 0.296 | 0.520 | 0.677 | 0.645 | 0.928 | 0.008 | 1.239 | 1.253 | 1.346 | 1.402 |
| b | 4.649 | 10.017 | 4.038 | 4.075 | 3.449 | 0.058 | 3.639 | 3.943 | 4.113 | 4.558 |
| c | –0.043 | –0.229 | –0.059 | –0.009 | 0.005 | 0.006 | –0.108 | –0.130 | –0.155 | –0.200 |
| R2 | 0.999 | 0.943 | 0.984 | 0.992 | 0.996 | 0.999 | 0.998 | 0.995 | 0.995 | 0.989 |
| Cs | 0.253 | 0.291 | 0.619 | 0.406 | 0.933 | 1.206 | 1.131 | 1.123 | 1.191 | 1.221 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, L.; Yan, C.; Liu, S. Freeze–Thaw Durability of Strain-Hardening Cement-Based Composites under Combined Flexural Load and Chloride Environment. Materials 2018, 11, 1721. https://doi.org/10.3390/ma11091721
Yin L, Yan C, Liu S. Freeze–Thaw Durability of Strain-Hardening Cement-Based Composites under Combined Flexural Load and Chloride Environment. Materials. 2018; 11(9):1721. https://doi.org/10.3390/ma11091721
Chicago/Turabian StyleYin, Liqiang, Changwang Yan, and Shuguang Liu. 2018. "Freeze–Thaw Durability of Strain-Hardening Cement-Based Composites under Combined Flexural Load and Chloride Environment" Materials 11, no. 9: 1721. https://doi.org/10.3390/ma11091721
APA StyleYin, L., Yan, C., & Liu, S. (2018). Freeze–Thaw Durability of Strain-Hardening Cement-Based Composites under Combined Flexural Load and Chloride Environment. Materials, 11(9), 1721. https://doi.org/10.3390/ma11091721




