Numerical Validation of Two-Parameter Weibull Model for Assessing Failure Fatigue Lives of Laminated Cementitious Composites—Comparative Assessment of Modeling Approaches
Abstract
:1. Introduction
2. Experimental Work
2.1. Fabrication of LCC Specimens
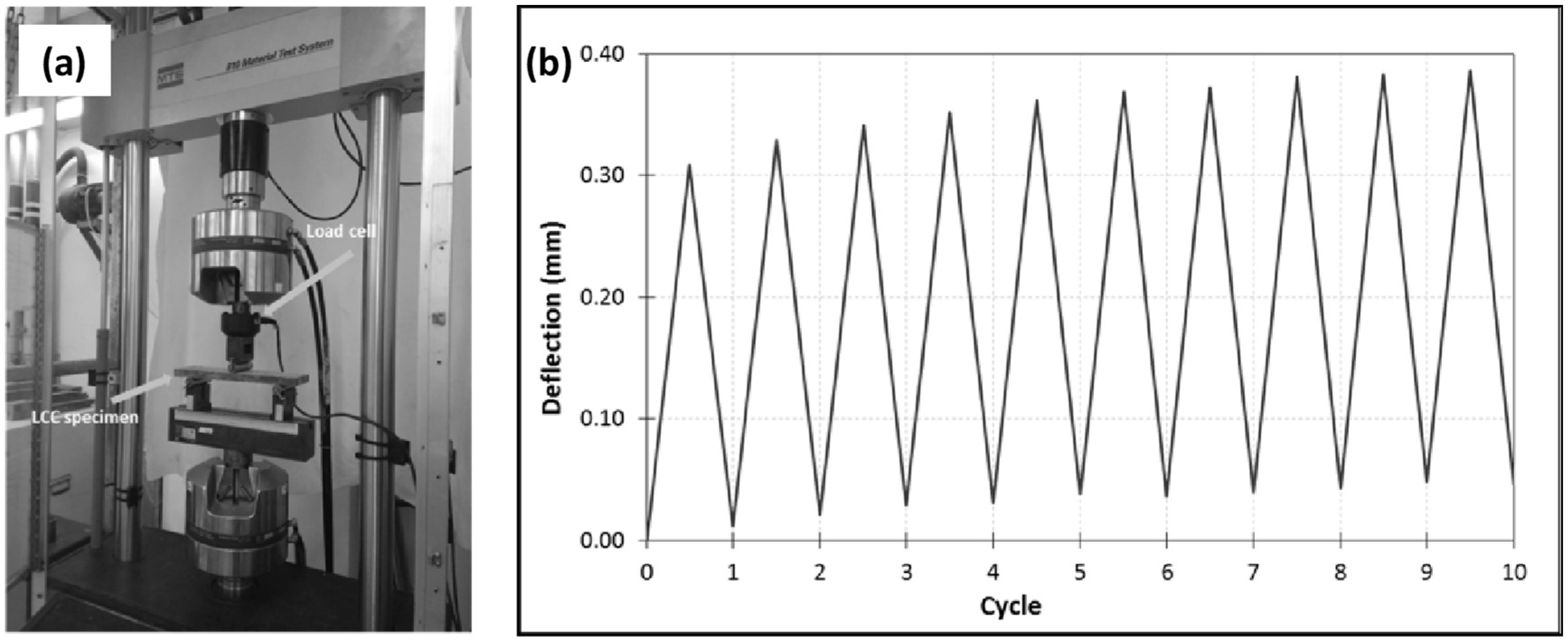
2.2. Fatigue Test Program
3. Fatigue Modeling Approaches for Cementitious Composites
3.1. Two-Parameter Weibull Distribution Model
3.2. Three-Parameter Weibull Distribution Model
4. Results and Discussion
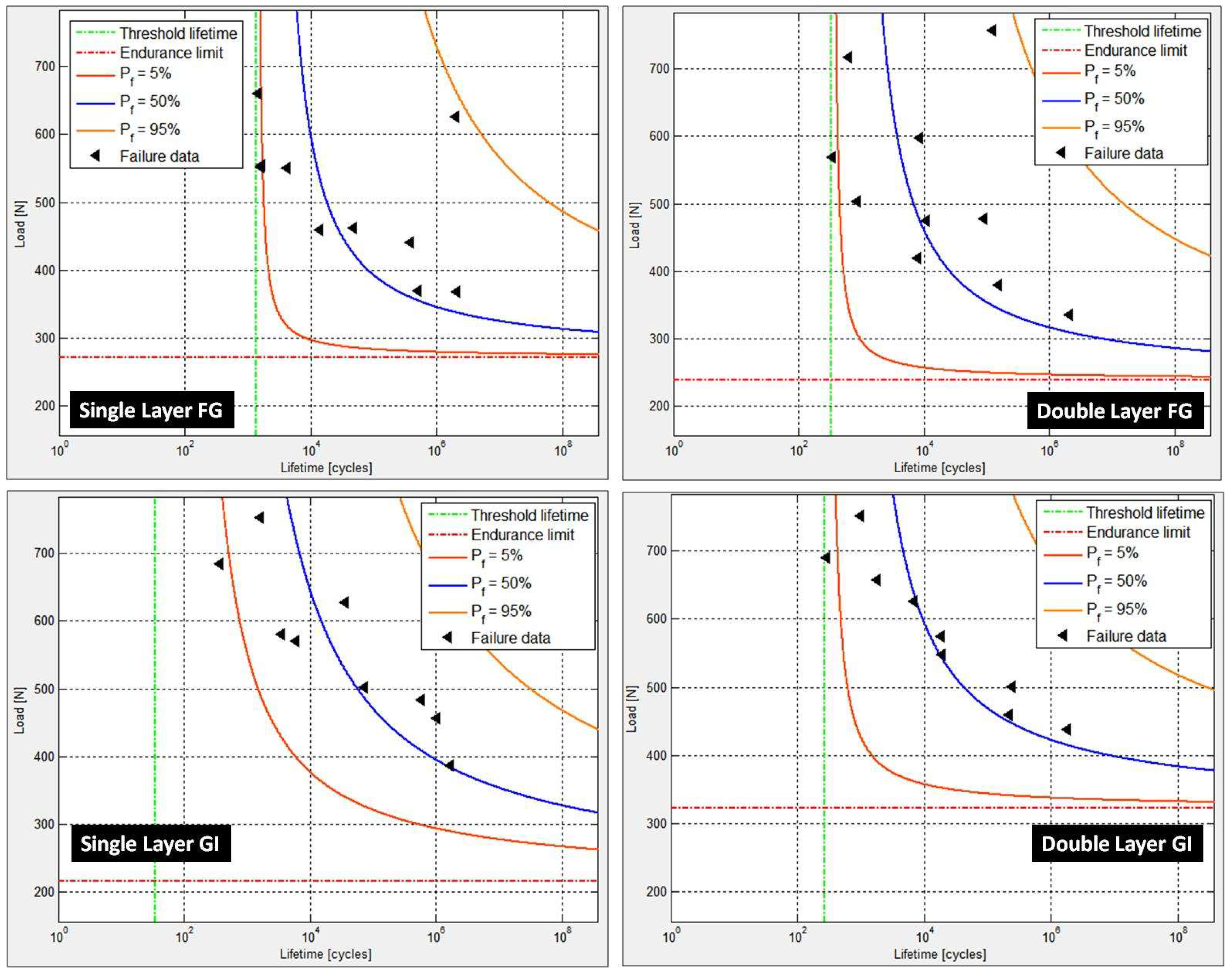
4.1. Two-Parameter Weibull Distribution Model
4.2. Three-Parameter Weibull Distribution Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- American Concrete Institute. Report on Thin Reinforced Cementitious Products; ACI 549.2R-04; American Concrete Institute: Farmington Hills, MI, USA, 2004. [Google Scholar]
- Naaman, A.E. Ferrocement and Laminated Cementitious Composites, 1st ed.; Technopress: Ann Arbor, MI, USA, 2000; ISBN 0967493900. [Google Scholar]
- Naaman, A.E. Ferrocement: International Revival. ACI Spec. Publ. 2002, 206, 323–340. [Google Scholar]
- Hanif, A.; Cheng, Y.; Lu, Z.; Li, Z. Mechanical Behavior of Thin-Laminated Cementitious Composites Incorporating Cenosphere Fillers. ACI Mater. J. 2018, 115, 117–127. [Google Scholar] [CrossRef]
- Hanif, A.; Lu, Z.; Sun, M.; Parthasarathy, P.; Li, Z. Green lightweight ferrocement incorporating fly ash cenosphere based fibrous mortar matrix. J. Clean. Prod. 2017, 159, 326–335. [Google Scholar] [CrossRef]
- Yerramala, A.; Ramachandurdu, C.; Bhaskar Desai, V. Flexural strength of metakaolin ferrocement. Compos. Part B Eng. 2013, 55, 176–183. [Google Scholar] [CrossRef]
- Memon, N.A.; Sumadi, S.R.; Ramli, M. Performance of high wokability slag-cement mortar for ferrocement. Build. Environ. 2007, 42, 2710–2717. [Google Scholar] [CrossRef]
- Desayi, P.; Reddy, V. Strength of Lightweight Ferrocement in Flexure. Cem. Concr. Compos. 1991, 13, 13–20. [Google Scholar] [CrossRef]
- Memon, N.A.; Sumadi, S.R.; Ramli, M. Ferrocement encased lightweight aerated concrete: A novel approach to produce sandwich composite. Mater. Lett. 2007, 61, 4035–4038. [Google Scholar] [CrossRef]
- Hanif, A. Development and Application of High Performance Lightweight Cementitious Composite for Wind Energy Harvesting; The Hong Kong University of Science and Technology: Hong Kong, China, 2017. [Google Scholar]
- Paskova, T.; Meyer, C. Low-cycle Fatigue of Plain and Fiber-Reinforced Concrete. ACI Mater. J. 1997, 94, 273–285. [Google Scholar]
- Hsu, T.T.C. Fatigue of Plain Concrete. ACI J. 1981, 78, 292–305. [Google Scholar]
- Tepfers, R.; Hedberg, B.; Szczekocki, G. Absorption of energy in fatigue loading of plain concrete. Mateiraux Constr. 1984, 17, 59–64. [Google Scholar] [CrossRef]
- Byung, H.O. Fatigue Analysis of Plain Concrete in Flexure. ASCE J. Struct. Eng. 1986, 112, 273–288. [Google Scholar]
- Naik, T.R.; Singh, S.S.; Ye, C. Fatigue Behavior of Plain Concrete Made with or Without Fly Ash; The Department of Civil Engineering and Mechanics, University of Wisconsin-Milwaukee for Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2015. [Google Scholar]
- Singh, S.R.; Kaushik, S.K. Flexural fatigue life distributions and failure probability of steel fibrous concrete. ACI Struct. J. 2000, 97, 658–667. [Google Scholar]
- Saleh, M.F.; Yeow, T.; Macrae, G.; Scott, A. Effect of steel fibre content on the fatigue behaviour of steel fibre reinforced concrete. RILEM Bookseries 2012, 4, 815–825. [Google Scholar]
- Yan, H.; Sun, W.; Chen, H. The effect of silica fume and steel fiber on the dynamic mechanical performance of high-strength concrete. Cem. Concr. Res. 1999, 29, 423–426. [Google Scholar] [CrossRef]
- Behbahani, H.P. Flexural Behavior of Steel Fibers Reinforced Concrete Beams. Master’s Thesis, Universiti Teknologi Malaysia, Johor, Malaysia, 2010. [Google Scholar]
- Chang, D.I.; Chai, W.K. Flexural fracture and fatigue behavior of steel-fiber-reinforced concrete structures. Nucl. Eng. Des. 1995, 156, 201–207. [Google Scholar] [CrossRef]
- Batson, B.G.; Ball, C.; Bailey, L.; Landers, E.; Hooks, J. Flexural Fatigue Strength of Steel Fiber Reinforced Concrete Beams. J. Proc. 1972, 69, 673–677. [Google Scholar]
- Jang, J.G.; Kim, H.K.; Kim, T.S.; Min, B.J.; Lee, H.K. Improved flexural fatigue resistance of PVA fiber-reinforced concrete subjected to freezing and thawing cycles. Constr. Build. Mater. 2014, 59, 129–135. [Google Scholar] [CrossRef]
- Ranjbarian, M.; Mechtcherine, V. A novel test setup for the characterization of bridging behaviour of single microfibres embedded in a mineral-based matrix. Cem. Concr. Compos. 2018, 92, 92–101. [Google Scholar] [CrossRef]
- Hanif, A.; Kim, Y.; Parthasarathy, P.; Usman, M.; Li, Z. Flexural Fatigue Behavior of Lightweight Ferrocement: Experimental Investigation & Numerical Modeling. In Proceedings of the International Federation for Structural Concrete 5th International FIB Congress 2018, Melbourne, Australia, 7–11 October 2018. [Google Scholar]
- Hanif, A.; Usman, M.; Lu, Z.; Cheng, Y.; Li, Z. Flexural Fatigue Behaviour of Thin Laminated Cementitious Composites Incorporating Cenosphere Fillers. Mater. Des. 2018, 140, 267–277. [Google Scholar] [CrossRef]
- Huang, B.; Li, Q.; Xu, S.; Zhou, B. Investigation on Compressive Fatigue Damage Process of Ultra-High Toughness Cementitious Composites. In Proceedings of the 9th International Conference on Fracture Mechanics of Concrete and Concrete Structures, Berkeley, CA, USA, 22–25 May 2016. [Google Scholar]
- Huang, B.-T.; Li, Q.-H.; Xu, S.-L.; Liu, W.; Wang, H.-T. Fatigue deformation behavior and fiber failure mechanism of ultra-high toughness cementitious composites in compression. Mater. Des. 2018, 157, 457–468. [Google Scholar] [CrossRef]
- Huang, B.-T.; Li, Q.-H.; Xu, S.-L.; Zhou, B.-M. Tensile fatigue behavior of fiber-reinforced cementitious material with high ductility: Experimental study and novel P-S-N model. Constr. Build. Mater. 2018, 178, 349–359. [Google Scholar] [CrossRef]
- Huang, B.-T.; Li, Q.-H.; Xu, S.-L.; Zhou, B.-M. Frequency Effect on the Compressive Fatigue Behavior of Ultrahigh Toughness Cementitious Composites: Experimental Study and Probabilistic Analysis. J. Struct. Eng. 2017, 143, 04017073. [Google Scholar] [CrossRef]
- Huang, B.-T.; Li, Q.-H.; Xu, S.-L. Fatigue Deformation Model of Plain and Fiber-Reinforced Concrete Based on Weibull Function. J. Struct. Eng. 2019, 145, 04018234. [Google Scholar] [CrossRef]
- Singh, S.P.; Mohammadi, Y.; Kaushik, S.K. Flexural Fatigue Analysis of Steel Fibrous Concrete Containing Mixed Fibers. ACI Mater. J. 2005, 102, 306–312. [Google Scholar]
- Behloul, M.; Chanvillard, G.; Pimienta, P.; Pineaud, A.; Rivillon, P. Fatigue Flexural Behavior of Pre-cracked Specimens of Special UHPFRC. In Proceedings of the Seventh International Symposium on the Utilization of High Strength/High-Performance Concrete, Washington, DC, USA, 20–24 June 2005; pp. 1253–1268. [Google Scholar]
- Mohamadi, M.R.; Mohandesi, J.A.; Homayonifar, M. Fatigue behavior of polypropylene fiber reinforced concrete under constant and variable amplitude loading. J. Compos. Mater. 2013, 47, 3331–3342. [Google Scholar] [CrossRef]
- Castillo, E.; Ramos, A.; Koller, R.; López-Aenlle, M.; Fernández-Canteli, A. A critical comparison of two models for assessment of fatigue data. Int. J. Fatigue 2008, 30, 45–57. [Google Scholar] [CrossRef]
- Castillo, E.; Fernendez-Canteli, A. A Unified Statistical Methodology for Modeling Fatigue Damage; Springer: Dordrecht, The Netherlands, 2009; ISBN 978-1-4020-9181-0. [Google Scholar]
- Fernández-Canteli, A.; Przybilla, C.; Nogal, M.; Aenlle, M.L.; Castillo, E. ProFatigue: A Software Program for Probabilistic Assessment of Experimental Fatigue Data Sets. Procedia Eng. 2014, 74, 236–241. [Google Scholar] [CrossRef]
- Hanif, A.; Parthasarathy, P.; Ma, H.; Fan, T.; Li, Z. Properties Improvement of Fly Ash Cenosphere Modified Cement Pastes Using Nano-Silica. Cem. Concr. Compos. 2017, 81, 35–48. [Google Scholar] [CrossRef]
- Goel, S.; Singh, S.P.; Singh, P. Fatigue Analysis of Plain and Fiber-Reinforced Self Consolidating Concrete. ACI Mater. J. 2013, 573–582. [Google Scholar]
- Oh, B.H. Fatigue Life Distributions of Concrete for Various Stress Levels. ACI Mater. J. 1991, 88, 122–128. [Google Scholar]
- Singh, S.P.; Mohammadi, Y.; Madan, S.K. Flexural fatigue analysis of steel fibrous concrete containing mixed fibers. J. Zhejiang Univ. Sci. A 2006, 7, 1329–1335. [Google Scholar] [CrossRef]
- Singh, S.P.; Kaushik, S.K. Fatigue strength of steel fibre reinforced concrete in flexure. Cem. Concr. Compos. 2003, 25, 779–786. [Google Scholar] [CrossRef]
- Przybilla, C.; Fernández-Canteli, A.; Castillo, E. Maximum likelihood estimation for the three-parameter Weibull cdf of strength in presence of concurrent flaw populations. J. Eur. Ceram. Soc. 2013, 33, 1721–1727. [Google Scholar] [CrossRef] [Green Version]
- Pyttel, B.; Canteli, A.F.; Ripoll, A.A. Comparison of different statistical models for description of fatigue including very high cycle fatigue. Int. J. Fatigue 2016, 93, 435–442. [Google Scholar] [CrossRef]



| Reinforcement Type | Manufacturer | Thickness (µm) | Opening (mm) | Yield Strength (Mpa) | Elastic Modulus (GPa) | Density (g/cm3) | Elongation (%) |
|---|---|---|---|---|---|---|---|
| Fiber Glass Mesh (FG) | HaoXin hardware mesh Co. Ltd., Wuxi, China | 250 | 5 × 5 | 1100 | 75 | 2.6 | 3.9 |
| Galvanized Iron Welded Wire Mesh (GI) | Xing Meng Zinc Steel Guardrail Co. Ltd., Chengdu, China | 750 | 5 × 5 | 250 | 300 | 7.8 | 7 |
| PVA Fibers | Kuraray Co., Ltd., Okayama, Japan | 15 | NA | 1600 | 41 | 1.3 | 6 |
| Series | Matrix | Mesh Type | No. of Layers | Mesh Volume Fraction, Vr (%) | PVA Fibers Volume Fraction, Vf (%) | Total Reinforcement Ratio, (%) |
|---|---|---|---|---|---|---|
| No. 1 | Mix 1 | GI | 1 | 1.00% | 0.50% | 1.50% |
| No. 2 | Mix 1 | GI | 2 | 2.00% | 0.50% | 2.50% |
| No. 3 | Mix 1 | FG | 1 | 0.70% | 0.50% | 1.20% |
| No. 4 | Mix 1 | FG | 2 | 1.40% | 0.50% | 1.90% |
| No. 5 | Mix 2 | GI | 1 | 1.00% | 0.50% | 1.50% |
| No. 6 | Mix 2 | GI | 2 | 2.00% | 0.50% | 2.50% |
| No. 7 | Mix 2 | FG | 1 | 0.70% | 0.50% | 1.20% |
| No. 8 | Mix 2 | FG | 2 | 1.40% | 0.50% | 1.90% |
| No. 9 | Mix 3 | GI | 1 | 1.00% | 0.50% | 1.50% |
| No. 10 | Mix 3 | GI | 2 | 2.00% | 0.50% | 2.50% |
| No. 11 | Mix 3 | FG | 1 | 0.70% | 0.50% | 1.20% |
| No. 12 | Mix 3 | FG | 2 | 1.40% | 0.50% | 1.90% |
| No. 13 | Mix 4 | GI | 1 | 1.00% | 0.50% | 1.50% |
| No. 14 | Mix 4 | GI | 2 | 2.00% | 0.50% | 2.50% |
| No. 15 | Mix 4 | FG | 1 | 0.70% | 0.50% | 1.20% |
| No. 16 | Mix 4 | FG | 2 | 1.40% | 0.50% | 1.90% |
| Series | Cyclic Test (Number of Cycles, N) | Cyclic Test, log10(N) | ||||
|---|---|---|---|---|---|---|
| Stress Range (0.10–0.60) | Stress Range (0.10–0.75) | Stress Range (0.10–0.90) | Stress Range (0.10–0.60) | Stress Range (0.10–0.75) | Stress Range (0.10–0.90) | |
| Series 1 | 73,214 | 35,925 | 1646 | 4.86 | 4.56 | 3.22 |
| Series 2 | 240,772 | 6916 | 975 | 5.38 | 3.84 | 2.99 |
| Series 3 | 380,751 | 4144 | 1455 | 5.58 | 3.62 | 3.16 |
| Series 4 | 89,960 | 8450 | 630 | 4.95 | 3.93 | 2.80 |
| Series 5 | 1,016,836 | 5944 | 372 | 6.01 | 3.77 | 2.57 |
| Series 6 | 214,647 | 18,446 | 283 | 5.33 | 4.27 | 2.45 |
| Series 7 | 504,847 | 47,101 | 1695 | 5.70 | 4.67 | 3.23 |
| Series 8 | 155,944 | 10,918 | 346 | 5.19 | 4.04 | 2.54 |
| Series 9 | 1,703,252 | 584,742 | 3523 | 6.23 | 5.77 | 3.55 |
| Series 10 | 1,808,915 | 19,458 | 1816 | 6.26 | 4.29 | 3.26 |
| Series 11 | 2,112,929 | 14,022 | 1596 | 6.32 | 4.15 | 3.20 |
| Series 12 | 2,097,152 | 7904 | 858 | 6.32 | 3.90 | 2.93 |
| Series 13 | 2,000,000 | 10,649 | 773 | 6.30 | 4.03 | 2.89 |
| Series 14 | 2,000,000 | 72,045 | 2867 | 6.30 | 4.86 | 3.46 |
| Series 15 | 2,000,000 | 323,705 | 33,263 | 6.30 | 5.51 | 4.52 |
| Series 16 | 2,000,000 | 126,156 | 1469 | 6.30 | 5.10 | 3.17 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hanif, A.; Kim, Y.; Park, C. Numerical Validation of Two-Parameter Weibull Model for Assessing Failure Fatigue Lives of Laminated Cementitious Composites—Comparative Assessment of Modeling Approaches. Materials 2019, 12, 110. https://doi.org/10.3390/ma12010110
Hanif A, Kim Y, Park C. Numerical Validation of Two-Parameter Weibull Model for Assessing Failure Fatigue Lives of Laminated Cementitious Composites—Comparative Assessment of Modeling Approaches. Materials. 2019; 12(1):110. https://doi.org/10.3390/ma12010110
Chicago/Turabian StyleHanif, Asad, Yongjae Kim, and Cheolwoo Park. 2019. "Numerical Validation of Two-Parameter Weibull Model for Assessing Failure Fatigue Lives of Laminated Cementitious Composites—Comparative Assessment of Modeling Approaches" Materials 12, no. 1: 110. https://doi.org/10.3390/ma12010110
APA StyleHanif, A., Kim, Y., & Park, C. (2019). Numerical Validation of Two-Parameter Weibull Model for Assessing Failure Fatigue Lives of Laminated Cementitious Composites—Comparative Assessment of Modeling Approaches. Materials, 12(1), 110. https://doi.org/10.3390/ma12010110






