Study on the Geometric Design of Supports for Overhanging Structures Fabricated by Selective Laser Melting
Abstract
:1. Introduction
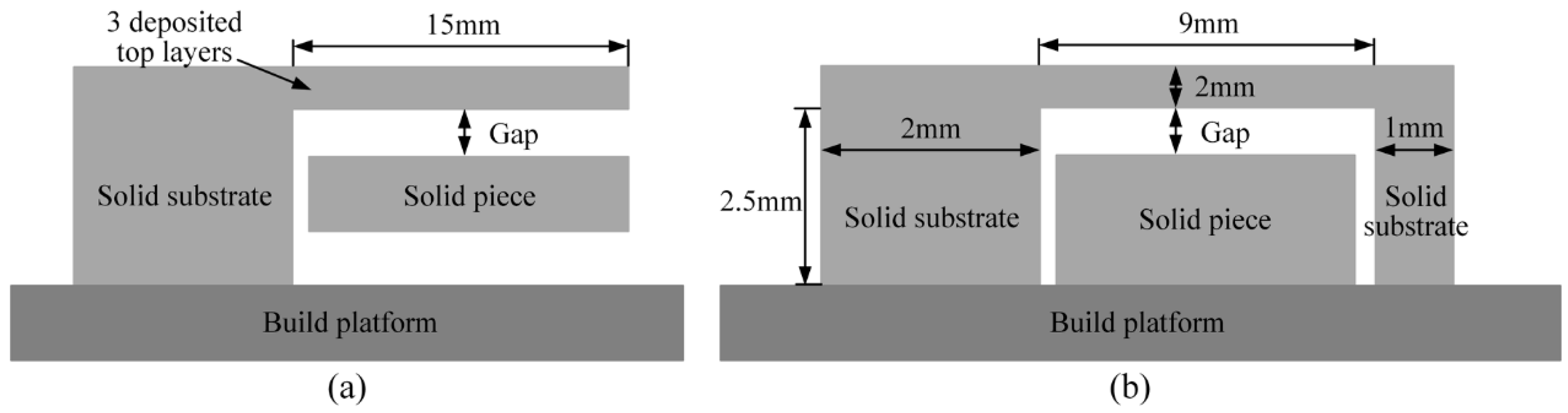
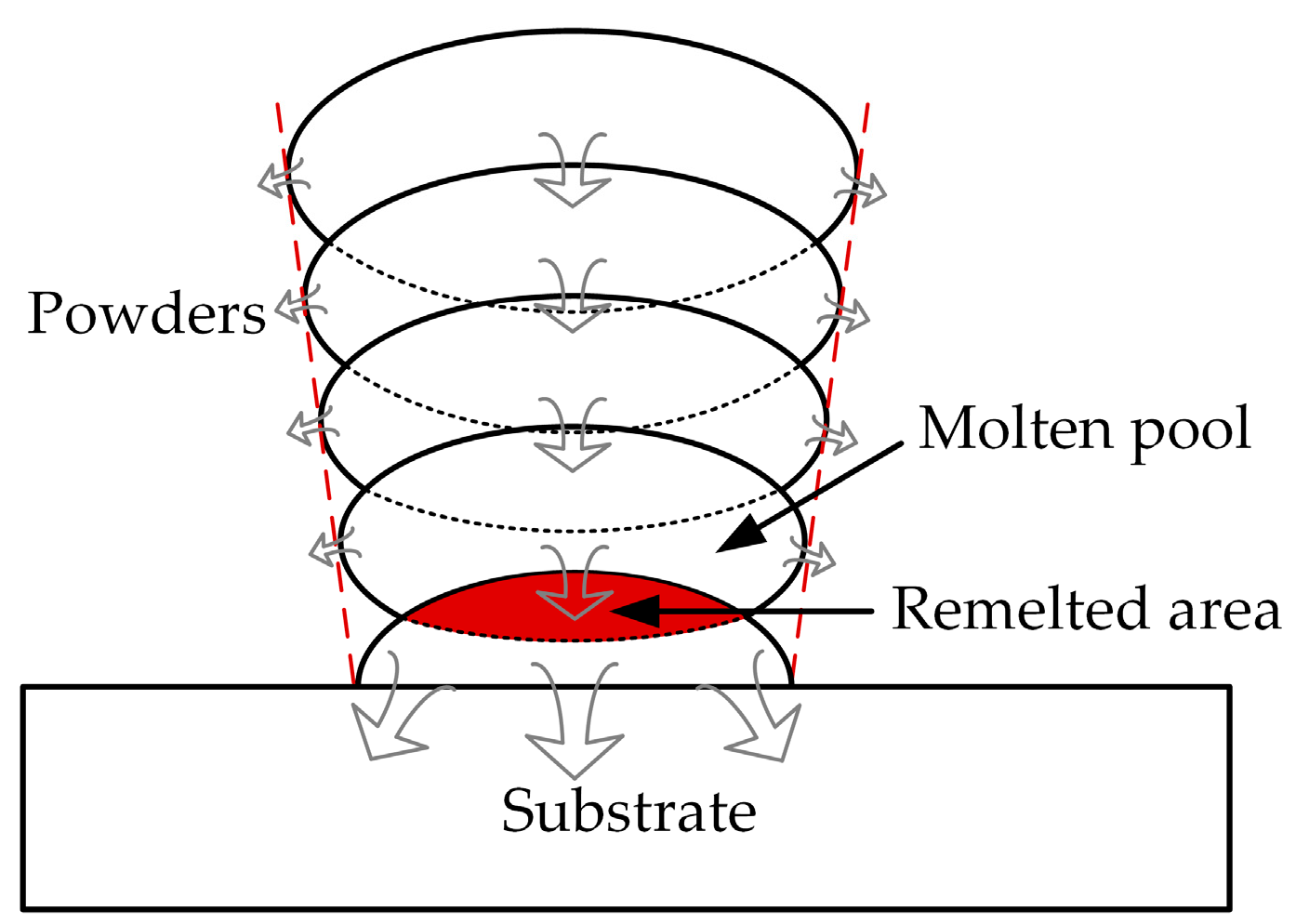
2. Solid Piece as Support Structure for Heat Dissipation
3. Experimental Methods
3.1. Equipment and Material
3.2. Experimental Design
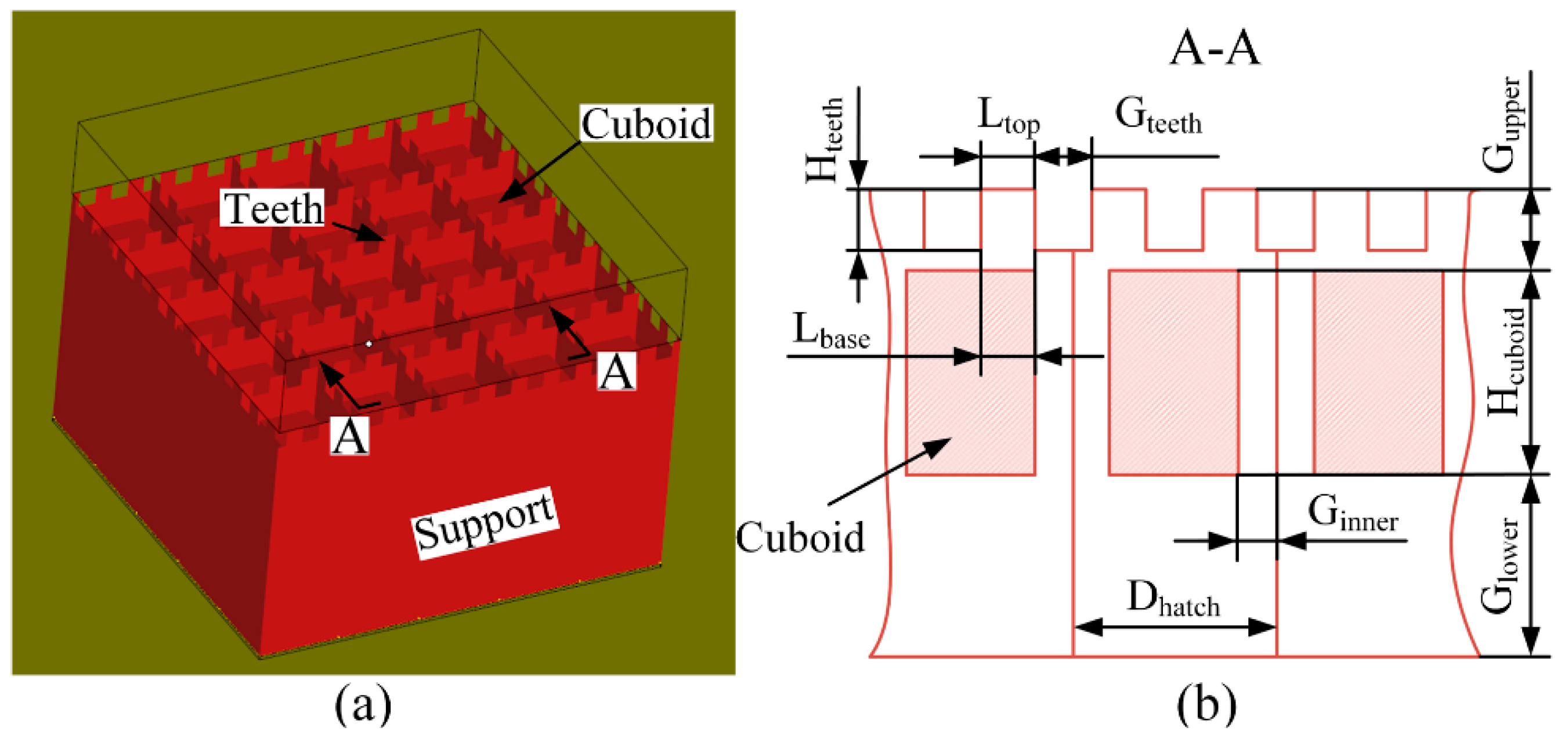
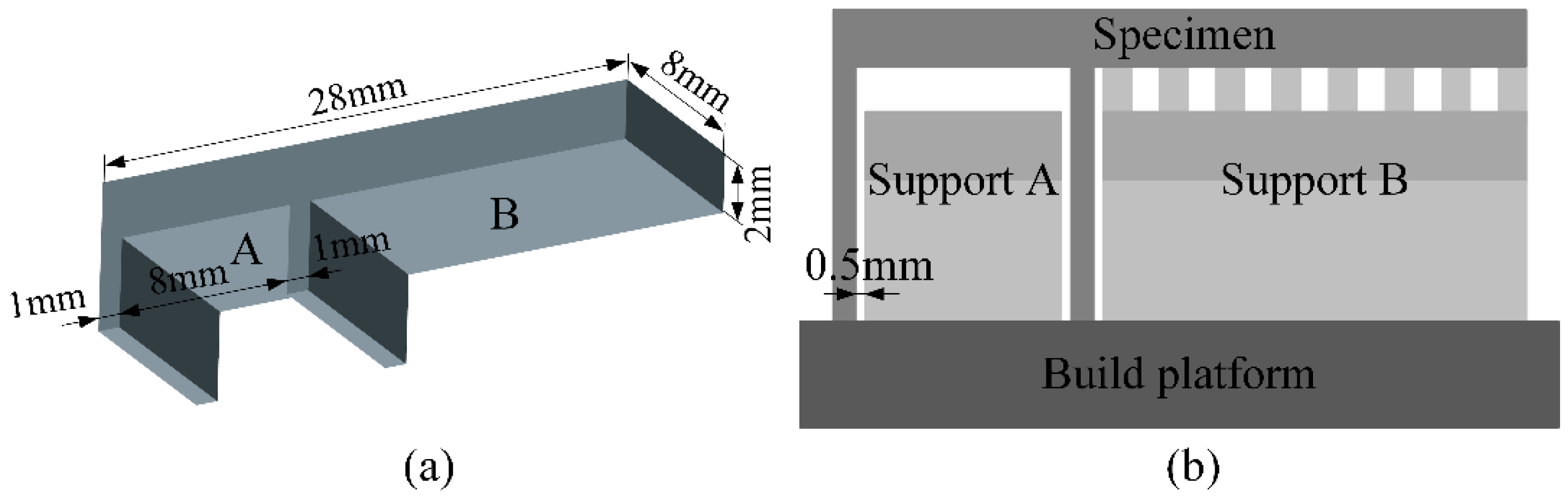
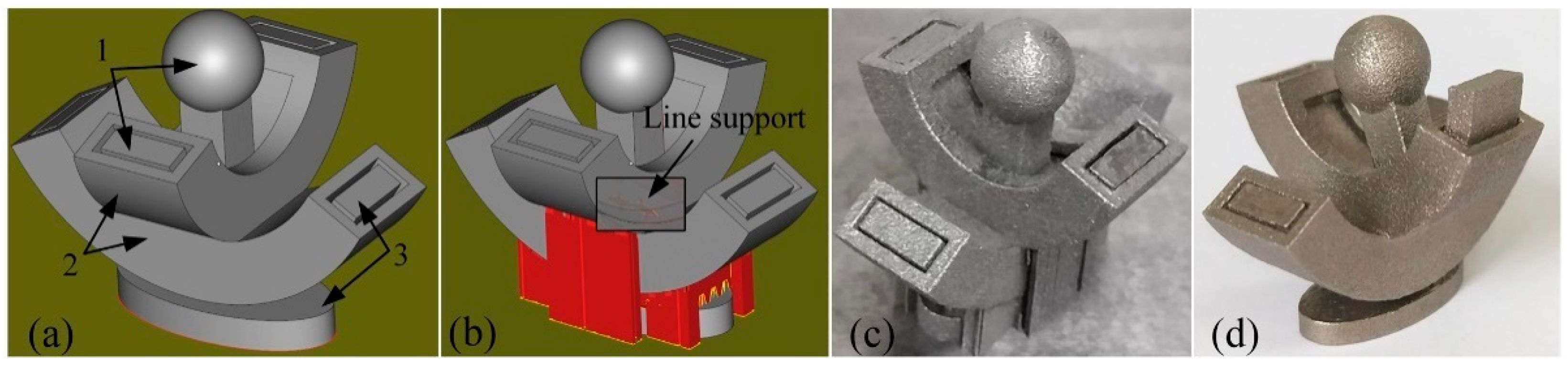
3.2.1. Design of Specimens
3.2.2. The Taguchi Method
3.2.3. Evaluation of Deformation and Surface Roughness
4. Results and Discussion
4.1. Effect of Supports on the Deformation
4.2. Tensile Property, Morphology and Microstructure
4.3. Effect of Supports on the Roughness
5. Example of Support Addition
6. Conclusions
- Solid pieces or cuboids as support structures can reduce the deformation and then increase the forming property of SLMed overhanging structure through improving the heat dissipation condition;
- The teeth connecting supports and part are more effective than the added solid cuboids at resisting the deformation of part. Therefore, when designing the support structure, the parameters related to the tooth geometry should be mainly considered;
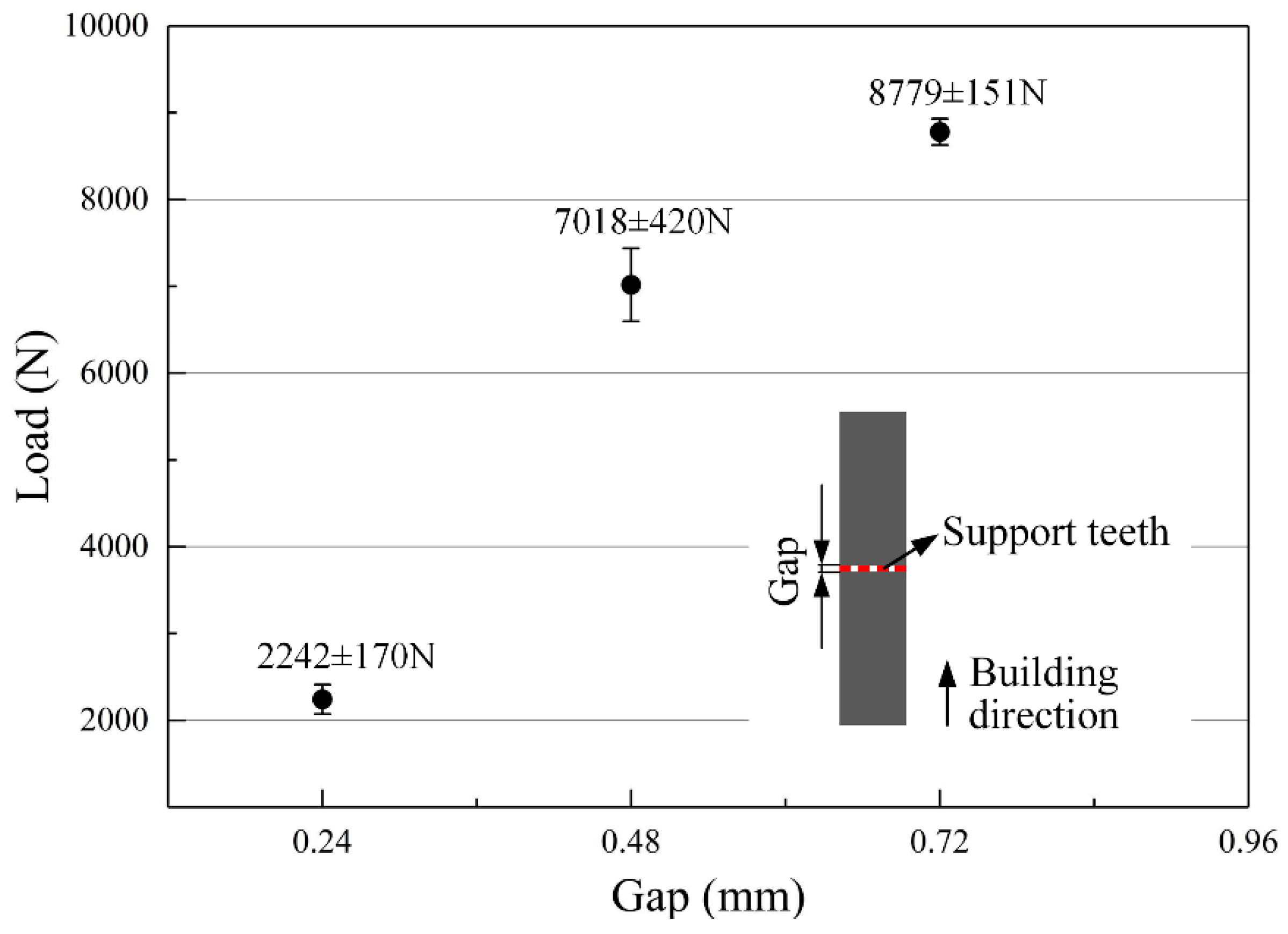
- The strength of the support teeth can be weakened approximately from 495 MPa to 396 MPa and then to 127 MPa by narrowing the gap between the cuboids and the overhang from 0.72 mm to 0.48 mm and then to 0.24 mm. Similar to the main body of the tensile specimen, small amount of martensite α’ can also be found in the support teeth. The thickness of support teeth is unstable along the building direction and increases layer-by-layer;
- The distance between every two adjacent walls of support and the gap between the cuboids and the overhang, respectively, most influence the part’s deformation and surface quality. As the gap between the cuboids and the overhang decreases, the bottom surface of part has a better quality.
- Absolutely, the gap between the cuboids and the overhang cannot be too small. A gap of 0.3 mm is preferred to form a non-assembly mechanical structure in this work.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hitzler, L.; Hirsch, J.; Heine, B.; Merkel, M.; Hall, W.; Ochsner, A. On the anisotropic mechanical properties of selective laser-melted stainless steel. Materials 2017, 10, 1136. [Google Scholar] [CrossRef] [PubMed]
- Boschetto, A.; Bottini, L.; Veniali, F. Roughness modeling of AlSi10Mg parts fabricated by selective laser melting. J. Mater. Process. Technol. 2017, 241, 154–163. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Strano, G.; Hao, L.; Everson, R.M.; Evans, K.E. Surface roughness analysis, modelling and prediction in selective laser melting. J. Mater. Process. Technol. 2013, 213, 589–597. [Google Scholar] [CrossRef]
- Tian, Y.; Tomus, D.; Rometsch, P.; Wu, X. Influences of processing parameters on surface roughness of Hastelloy X produced by selective laser melting. Addit. Manuf. 2017, 13, 103–112. [Google Scholar] [CrossRef]
- Wang, L.-Z.; Wang, S.; Wu, J.-J. Experimental investigation on densification behavior and surface roughness of AlSi10Mg powders produced by selective laser melting. Opt. Laser Technol. 2017, 96, 88–96. [Google Scholar] [CrossRef]
- Sing, S.L.; Wiria, F.E.; Yeong, W.Y. Selective laser melting of titanium alloy with 50 wt % tantalum: Effect of laser process parameters on part quality. Int. J. Refract. Met. Hard Mater. 2018, 77, 120–127. [Google Scholar] [CrossRef]
- Alrbaey, K.; Wimpenny, D.; Tosi, R.; Manning, W.; Moroz, A. On Optimization of surface roughness of selective laser melted stainless steel parts: A statistical study. J. Mater. Eng. Perform. 2014, 23, 2139–2148. [Google Scholar] [CrossRef]
- Matsumoto, M.; Shiomi, M.; Osakada, K.; Abe, F. Finite element analysis of single layer forming on metallic powder bed in rapid prototyping by selective laser processing. Int. J. Mach. Tool Manuf. 2002, 42, 61–67. [Google Scholar] [CrossRef]
- Parry, L.; Ashcroft, I.A.; Wildman, R.D. Understanding the effect of laser scan strategy on residual stress in selective laser melting through thermo-mechanical simulation. Addit. Manuf. 2016, 12, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Gu, D.; Xiong, J.; Xia, M. Improving additive manufacturing processability of hard-to-process overhanging structure by selective laser melting. J. Mater. Process. Technol. 2017, 250, 99–108. [Google Scholar] [CrossRef]
- Buchbinder, D.; Meiners, W.; Pirch, N.; Wissenbach, K.; Schrage, J. Investigation on reducing distortion by preheating during manufacture of aluminum components using selective laser melting. J. Laser Appl. 2014, 26, 012004. [Google Scholar] [CrossRef]
- Strano, G.; Hao, L.; Everson, R.M.; Evans, K.E. A new approach to the design and optimisation of support structures in additive manufacturing. Int. J. Adv. Manuf. Technol. 2012, 66, 1247–1254. [Google Scholar] [CrossRef]
- Vanek, J.; Galicia, J.A.G.; Benes, B. Clever support: Efficient support structure generation for digital fabrication. Comput. Graph. Forum 2014, 33, 117–125. [Google Scholar] [CrossRef]
- Gan, M.X.; Wong, C.H. Practical support structures for selective laser melting. J. Mater. Process. Technol. 2016, 238, 474–484. [Google Scholar] [CrossRef]
- Mumtaz, K.A.; Vora, P.; Hopkinson, N. A Method to eliminate anchors/supports from directly laser melted metal powder bed processes. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2011. [Google Scholar]
- Jhabvala, J.; Boillat, E.; André, C.; Glardon, R. An innovative method to build support structures with a pulsed laser in the selective laser melting process. Int. J. Adv. Manuf. Technol. 2011, 59, 137–142. [Google Scholar] [CrossRef]
- Kuo, Y.-H.; Cheng, C.-C.; Lin, Y.-S.; San, C.-H. Support structure design in additive manufacturing based on topology optimization. Struct. Multidiscip. Optim. 2017, 57, 183–195. [Google Scholar] [CrossRef]
- Morgan, H.D.; Cherry, J.A.; Jonnalagadda, S.; Ewing, D.; Sienz, J. Part orientation optimisation for the additive layer manufacture of metal components. Int. J. Adv. Manuf. Technol. 2016, 86, 1679–1687. [Google Scholar] [CrossRef] [Green Version]
- Calignano, F. Design optimization of supports for overhanging structures in aluminum and titanium alloys by selective laser melting. Mater. Des. 2014, 64, 203–213. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, L.-C.; Mo, J.-H.; Qian, B. New method of improving parts accuracy by adding heat balance support in selective laser sintering. J. Zhejiang Univ.-Sci. A 2009, 10, 361–369. [Google Scholar] [CrossRef]
- Nadammal, N.; Kromm, A.; Saliwan-Neumann, R.; Farahbod, L.; Haberland, C.; Portella, P.D. Influence of support configurations on the characteristics of selective laser-melted inconel 718. JOM 2018, 70, 343–348. [Google Scholar] [CrossRef]
- Krol, T.A.; Zaeh, M.F.; Seidel, C. Optimization of supports in metal-based additive manufacturing by means of finite element models. Int. J. Robust Nonlinear Control 2012, 25, 3349–3366. [Google Scholar]
- Cheng, B.; Chou, K. Geometric consideration of support structures in part overhang fabrications by electron beam additive manufacturing. Comput. Aided Des. 2015, 69, 102–111. [Google Scholar] [CrossRef] [Green Version]
- Fousová, M.; Vojtěch, D.; Doubrava, K.; Daniel, M.; Lin, C.-F. Influence of inherent surface and internal defects on mechanical properties of additively manufactured Ti6Al4V alloy: Comparison between selective laser melting and electron beam melting. Materials 2018, 11, 537. [Google Scholar] [CrossRef] [PubMed]
- Cheng, B.; Shrestha, S.; Chou, K. Stress and deformation evaluations of scanning strategy effect in selective laser melting. Addit. Manuf. 2016, 12, 240–251. [Google Scholar] [CrossRef]
- Mertens, R.; Clijsters, S.; Kempen, K.; Kruth, J.-P. Optimization of scan strategies in selective laser melting of aluminum parts with downfacing areas. J. Manuf. Sci. Eng. 2014, 136, 061012. [Google Scholar] [CrossRef]
- Li, Z.; Xu, R.; Zhang, Z.; Kucukkoc, I. The influence of scan length on fabricating thin-walled components in selective laser melting. Int. J. Mach. Tool Manuf. 2018, 126, 1–12. [Google Scholar] [CrossRef]
- Xing, W.; Ouyang, D.; Li, N.; Liu, L. Estimation of residual stress in selective laser melting of a zr-based amorphous alloy. Materials 2018, 11, 1480. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Yang, Y.; Wang, D. Parametric optimization of selective laser melting for forming Ti6Al4V samples by Taguchi method. Opt. Laser Technol. 2013, 49, 118–124. [Google Scholar] [CrossRef]
- Launhardt, M.; Wörz, A.; Loderer, A.; Laumer, T.; Drummer, D.; Hausotte, T.; Schmidt, M. Detecting surface roughness on SLS parts with various measuring techniques. Polym. Test. 2016, 53, 217–226. [Google Scholar] [CrossRef]
- Vrancken, B.; Thijs, L.; Kruth, J.P.; Humbeeck, J.V. Heat treatment of Ti6Al4V produced by selective laser melting: Microstructure and mechanical properties. J. Alloys Compd. 2012, 541, 177–185. [Google Scholar] [CrossRef]
- Casalino, G.; Campanelli, S.L.; Contuzzi, N.; Ludovico, A.D. Experimental investigation and statistical optimisation of the selective laser melting process of a maraging steel. Opt. Laser Technol. 2015, 65, 151–158. [Google Scholar] [CrossRef]
- Thijs, L.; Verhaeghe, F.; Craeghs, T.; Humbeeck, J.V.; Kruth, J.P. A study of the microstructural evolution during selective laser melting of Ti–6Al–4V. Acta Mater. 2010, 58, 3303–3312. [Google Scholar] [CrossRef]
- Shi, W.; Liu, Y.; Shi, X.; Hou, Y.; Wang, P.; Song, G. Beam diameter dependence of performance in thick-layer and high-power selective laser melting of Ti-6Al-4V. Materials 2018, 11, 1237. [Google Scholar] [CrossRef]
- Lee, Y.; Farson, D.F. Simulation of transport phenomena and melt pool shape for multiplelayer additive manufacturing. J. Laser Appl. 2016, 28, 012006. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Y.; Yi, Z.; Su, X. Research on the fabricating quality optimization of the overhanging surface in SLM process. Int. J. Adv. Manuf. Technol. 2013, 65, 1471–1484. [Google Scholar] [CrossRef]







| Elements | Al | V | Fe | O | C | N | H | Ti |
|---|---|---|---|---|---|---|---|---|
| Content (wt. %) | 5.5–6.75 | 3.5–4.5 | <0.3 | <0.2 | <0.08 | <0.05 | <0.015 | Balance |
| Process Parameter | Value |
|---|---|
| Laser power | 170 W |
| Scanning speed | 1250 mm/s |
| Hatch distance | 100 µm |
| Spot diameter | 100 µm |
| Layer thickness | 30 µm |
| Preheating temperature | 35 °C |
| Atmosphere | Ar (Oxygen level <0.1%) |
| Level | Gupper (mm) | Hcuboid (mm) | Glower (mm) | Dhatch (mm) | Ltop (mm) | Gteeth (mm) |
|---|---|---|---|---|---|---|
| 1 | 0.30 | 0 | 0 | 0.5 | 0.3 | 0.3 |
| 2 | 0.45 | 0.6 | 0.6 | 1.0 | 0.6 | 0.6 |
| 3 | 0.75 | 3.0 | 3.0 | 1.5 | 1.0 | 1.0 |
| N | Gupper (mm) | Hcuboid (mm) | Glower (mm) | Dhatch (mm) | Ltop (mm) | Gteeth (mm) | Warp (–) | Roughness (µm) | S/NW (dB) | S/NR (dB) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.3 | 0 | 0 | 0.5 | 0.3 | 0.3 | 3 | 16.9 | −9.54 | −24.56 |
| 2 | 0.3 | 0 | 0 | 1 | 0.6 | 0.6 | 4 | 17.3 | −12.04 | −24.76 |
| 3 | 0.3 | 0 | 0 | 1.5 | 1 | 1 | 4 | 17.1 | −12.04 | −24.66 |
| 4 | 0.45 | 0.6 | 0.6 | 0.5 | 0.3 | 0.3 | 1 | 20.9 | 0.00 | −26.40 |
| 5 | 0.45 | 0.6 | 0.6 | 1 | 0.6 | 0.6 | 3 | 21.2 | −9.54 | −26.53 |
| 6 | 0.45 | 0.6 | 0.6 | 1.5 | 1 | 1 | 4 | 21.7 | −12.04 | −26.73 |
| 7 | 0.75 | 3 | 3 | 0.5 | 0.3 | 0.3 | 1 | 23.4 | 0.00 | −27.38 |
| 8 | 0.75 | 3 | 3 | 1 | 0.6 | 0.6 | 1 | 24.1 | 0.00 | −27.64 |
| 9 | 0.75 | 3 | 3 | 1.5 | 1 | 1 | 2 | 23.8 | −6.02 | −27.53 |
| 10 | 0.3 | 0.6 | 3 | 0.5 | 0.6 | 1 | 3 | 16.5 | −9.54 | −24.35 |
| 11 | 0.3 | 0.6 | 3 | 1 | 1 | 0.3 | 1 | 16.1 | 0.00 | −24.14 |
| 12 | 0.3 | 0.6 | 3 | 1.5 | 0.3 | 0.6 | 4 | 15.8 | −12.04 | −23.97 |
| 13 | 0.45 | 3 | 0 | 0.5 | 0.6 | 1 | 1 | 17.6 | 0.00 | −24.91 |
| 14 | 0.45 | 3 | 0 | 1 | 1 | 0.3 | 1 | 16.8 | 0.00 | −24.51 |
| 15 | 0.45 | 3 | 0 | 1.5 | 0.3 | 0.6 | 4 | 17.1 | −12.04 | −24.66 |
| 16 | 0.75 | 0 | 0.6 | 0.5 | 0.6 | 1 | 1 | 22.3 | 0.00 | −26.97 |
| 17 | 0.75 | 0 | 0.6 | 1 | 1 | 0.3 | 1 | 20.1 | 0.00 | −26.06 |
| 18 | 0.75 | 0 | 0.6 | 1.5 | 0.3 | 0.6 | 4 | 21.5 | −12.04 | −26.65 |
| 19 | 0.3 | 3 | 0.6 | 0.5 | 1 | 0.6 | 1 | 13.8 | 0.00 | −22.80 |
| 20 | 0.3 | 3 | 0.6 | 1 | 0.3 | 1 | 3 | 13.3 | −9.54 | −22.48 |
| 21 | 0.3 | 3 | 0.6 | 1.5 | 0.6 | 0.3 | 2 | 14.7 | −6.02 | −23.35 |
| 22 | 0.45 | 0 | 3 | 0.5 | 1 | 0.6 | 1 | 18.2 | 0.00 | −25.20 |
| 23 | 0.45 | 0 | 3 | 1 | 0.3 | 1 | 4 | 18.5 | −12.04 | −25.34 |
| 24 | 0.45 | 0 | 3 | 1.5 | 0.6 | 0.3 | 1 | 19 | 0.00 | −25.58 |
| 25 | 0.75 | 0.6 | 0 | 0.5 | 1 | 0.6 | 1 | 19.8 | 0.00 | −25.93 |
| 26 | 0.75 | 0.6 | 0 | 1 | 0.3 | 1 | 4 | 18.6 | −12.04 | −25.39 |
| 27 | 0.75 | 0.6 | 0 | 1.5 | 0.6 | 0.3 | 3 | 19 | −9.54 | −25.58 |
 Warp 1 |  Warp 2 |  Warp 3 |  Warp 4 | |||||||
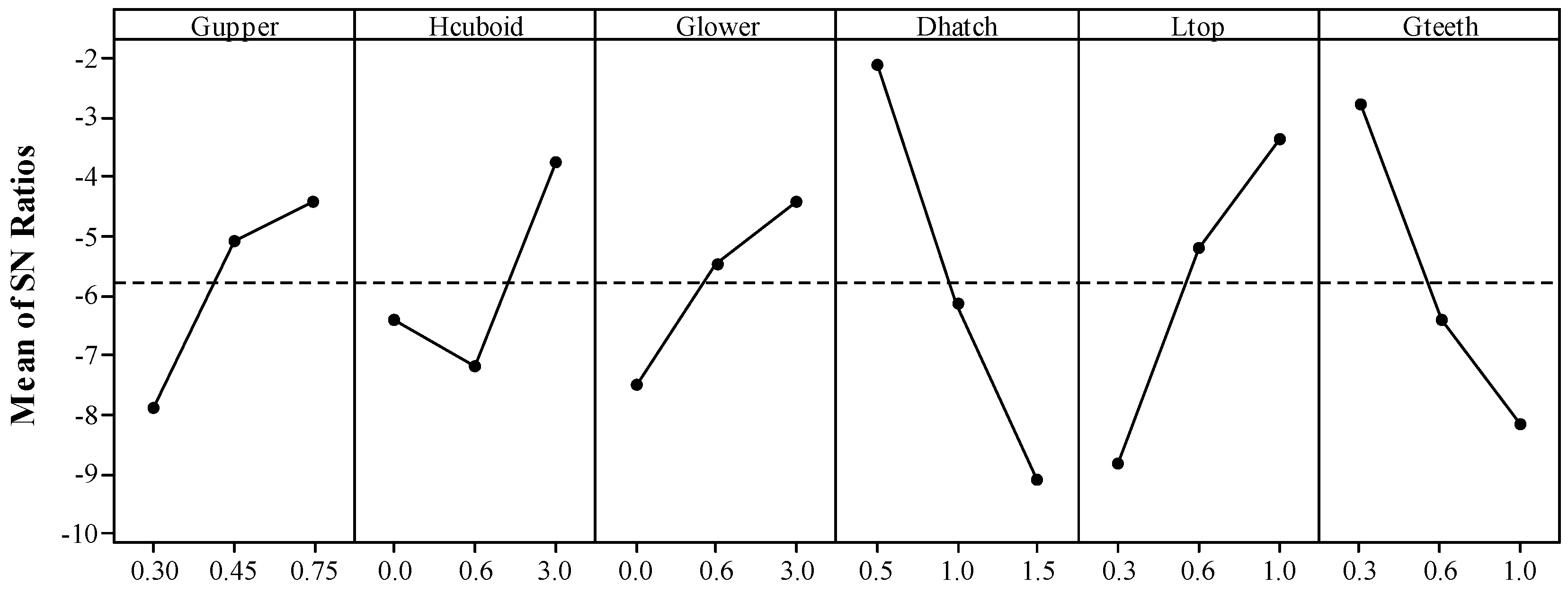
| Level | Gupper | Hcuboid | Glower | Dhatch | Ltop | Gteeth |
|---|---|---|---|---|---|---|
| 1 | −7.863 | −6.412 | −7.472 | −2.121 | −8.810 | −2.789 |
| 2 | −5.074 | −7.195 | −5.465 | −6.134 | −5.188 | −6.412 |
| 3 | −4.405 | −3.736 | −4.405 | −9.088 | −3.345 | −8.141 |
| Delta | 3.458 | 3.458 | 3.067 | 6.967 | 5.465 | 5.352 |
| Rank | 4.5 | 4.5 | 6 | 1 | 2 | 3 |
| Source | DOF | Seq SS | MS | F | p | Contribution (%) |
|---|---|---|---|---|---|---|
| Gupper | 2 | 60.57 | 30.284 | 3.30 | 0.067 | 7.71 |
| Hcuboid | 2 | 59.20 | 29.600 | 3.23 | 0.070 | 7.54 |
| Glower | 2 | 43.68 | 21.839 | 2.38 | 0.129 | 5.56 |
| Dhatch | 2 | 220.12 | 110.062 | 12.00 | 0.001 | 28.03 |
| Ltop | 2 | 139.16 | 69.582 | 7.59 | 0.006 | 17.72 |
| Gteeth | 2 | 134.26 | 67.128 | 7.32 | 0.007 | 17.09 |
| Error | 14 | 128.43 | 9.173 | – | – | 16.35 |
| Total | 26 | 785.42 | – | – | – | 100 |
| Level | Gupper | Hcuboid | Glower | Dhatch |
|---|---|---|---|---|
| 1 | −23.90 | −25.53 | −24.99 | −25.39 |
| 2 | −25.54 | −25.45 | −25.33 | −25.21 |
| 3 | −26.57 | −25.03 | −25.68 | −25.41 |
| Delta | 2.67 | 0.50 | 0.69 | 0.21 |
| Rank | 1 | 3 | 2 | 4 |
| Source | DOF | Seq SS | MS | F | p | Contribution (%) |
|---|---|---|---|---|---|---|
| Gupper | 2 | 32.7634 | 16.3817 | 22.06 | 0.000 | 65.80 |
| Hcuboid | 2 | 1.3039 | 0.6519 | 0.88 | 0.433 | 2.62 |
| Glower | 2 | 2.1236 | 1.0618 | 1.43 | 0.265 | 4.27 |
| Dhatch | 2 | 0.2305 | 0.1152 | 0.16 | 0.857 | 0.46 |
| Error | 18 | 13.3696 | 0.7428 | – | – | 26.85 |
| Total | 26 | 49.7911 | – | – | – | 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Fu, G.; Zhang, P.; Ma, Z.; Mao, Z.; Zhang, D.Z. Study on the Geometric Design of Supports for Overhanging Structures Fabricated by Selective Laser Melting. Materials 2019, 12, 27. https://doi.org/10.3390/ma12010027
Zhang K, Fu G, Zhang P, Ma Z, Mao Z, Zhang DZ. Study on the Geometric Design of Supports for Overhanging Structures Fabricated by Selective Laser Melting. Materials. 2019; 12(1):27. https://doi.org/10.3390/ma12010027
Chicago/Turabian StyleZhang, Kaifei, Guang Fu, Peng Zhang, Zhibo Ma, Zhongfa Mao, and David Z. Zhang. 2019. "Study on the Geometric Design of Supports for Overhanging Structures Fabricated by Selective Laser Melting" Materials 12, no. 1: 27. https://doi.org/10.3390/ma12010027
APA StyleZhang, K., Fu, G., Zhang, P., Ma, Z., Mao, Z., & Zhang, D. Z. (2019). Study on the Geometric Design of Supports for Overhanging Structures Fabricated by Selective Laser Melting. Materials, 12(1), 27. https://doi.org/10.3390/ma12010027





