Micro–Macro Relationships in the Simulation of Wave Propagation Phenomenon Using the Discrete Element Method
Abstract
:1. Introduction
2. Basic Notions of Elastic Wave Propagation
3. Formulation of the Discrete Element Method
3.1. Equations of Motion
3.2. Time Integration Scheme
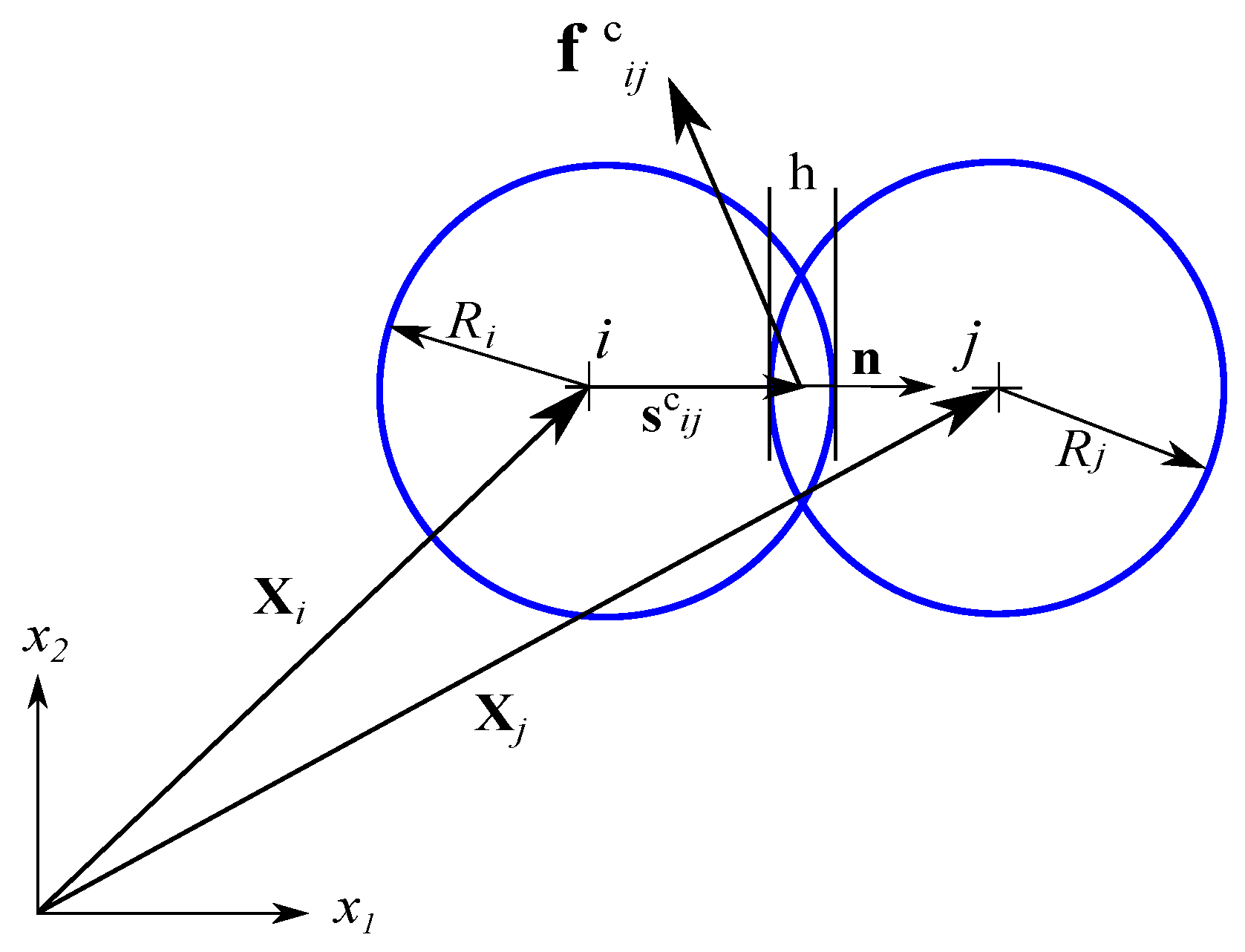
3.3. Contact Model
4. Micro–Macro Relationships
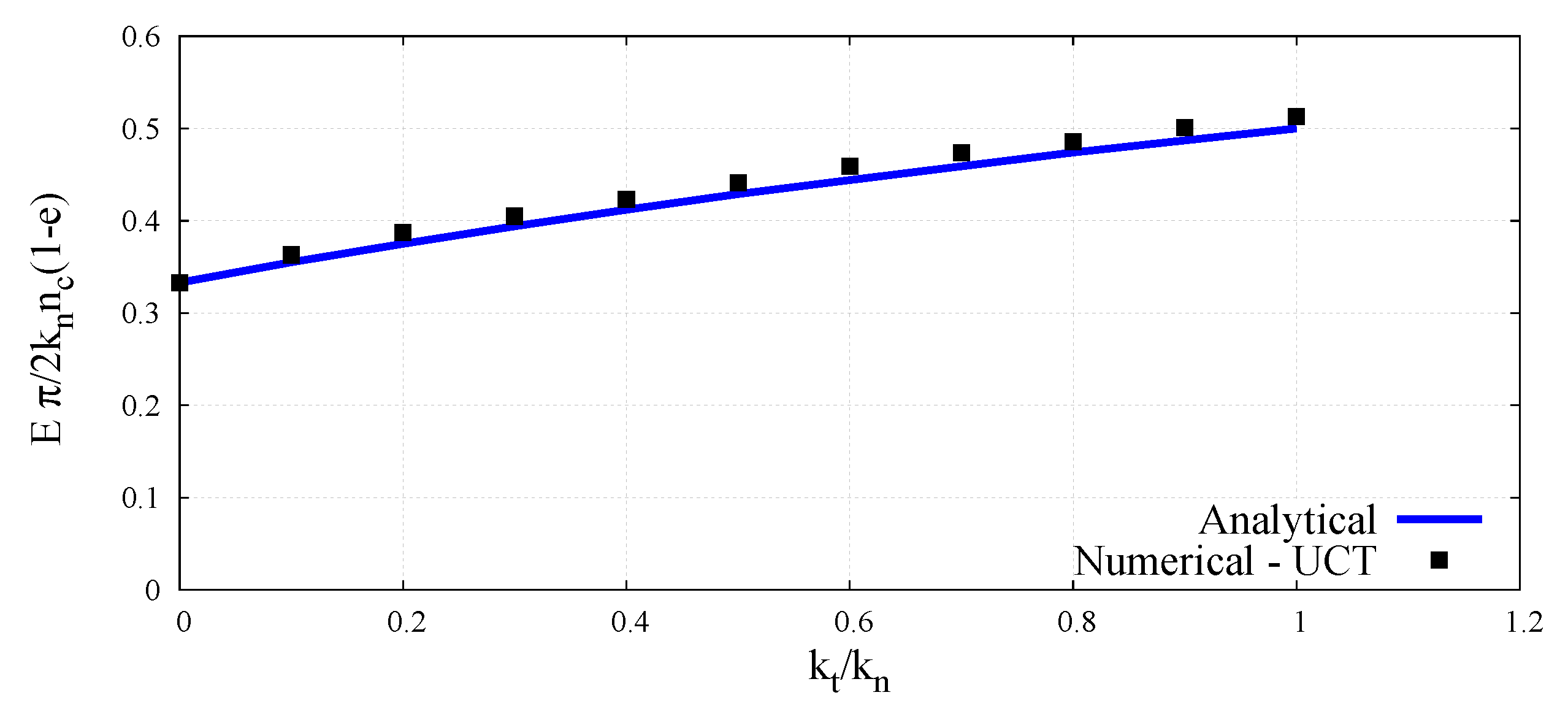
4.1. Analytical Micro–Macro Relationships
4.2. Numerical Micro–Macro Constitutive Relationships
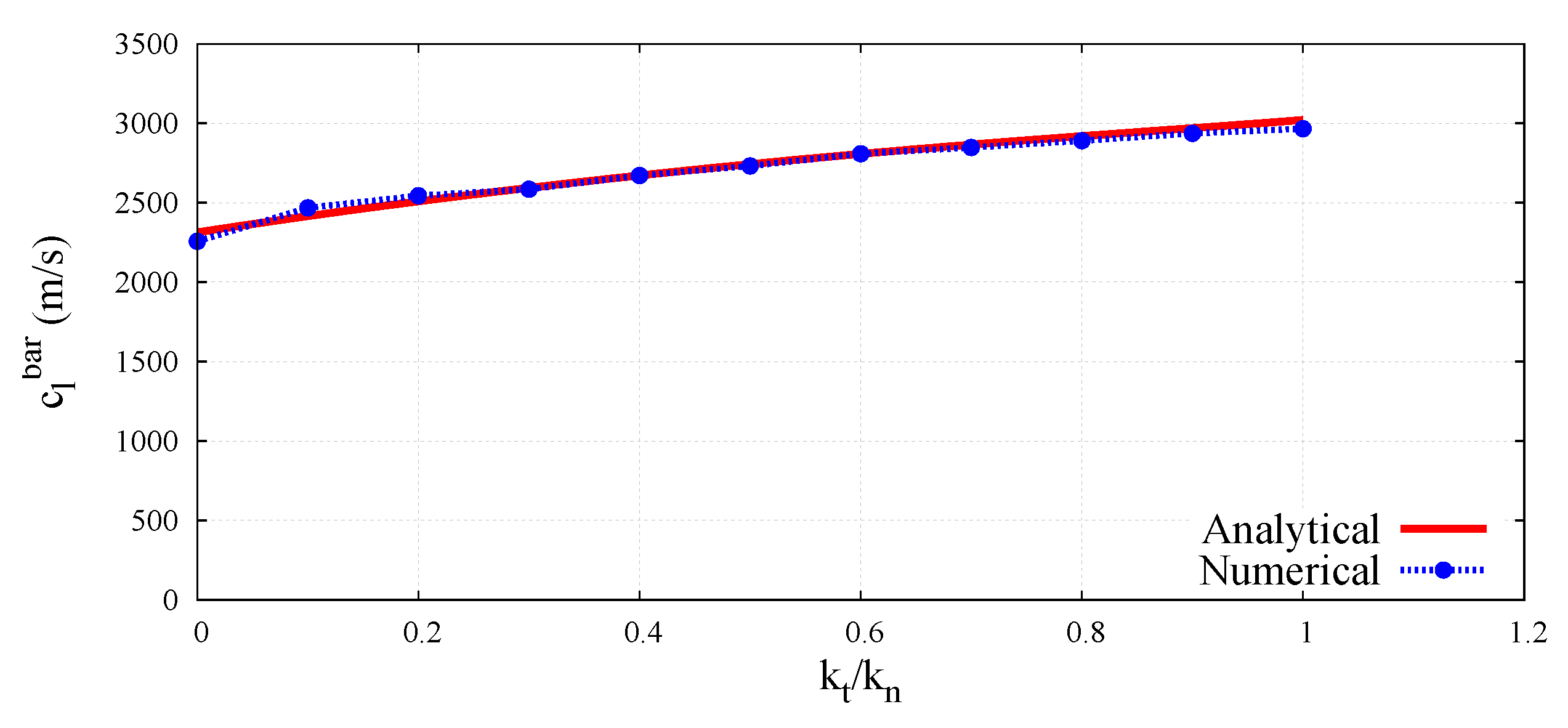
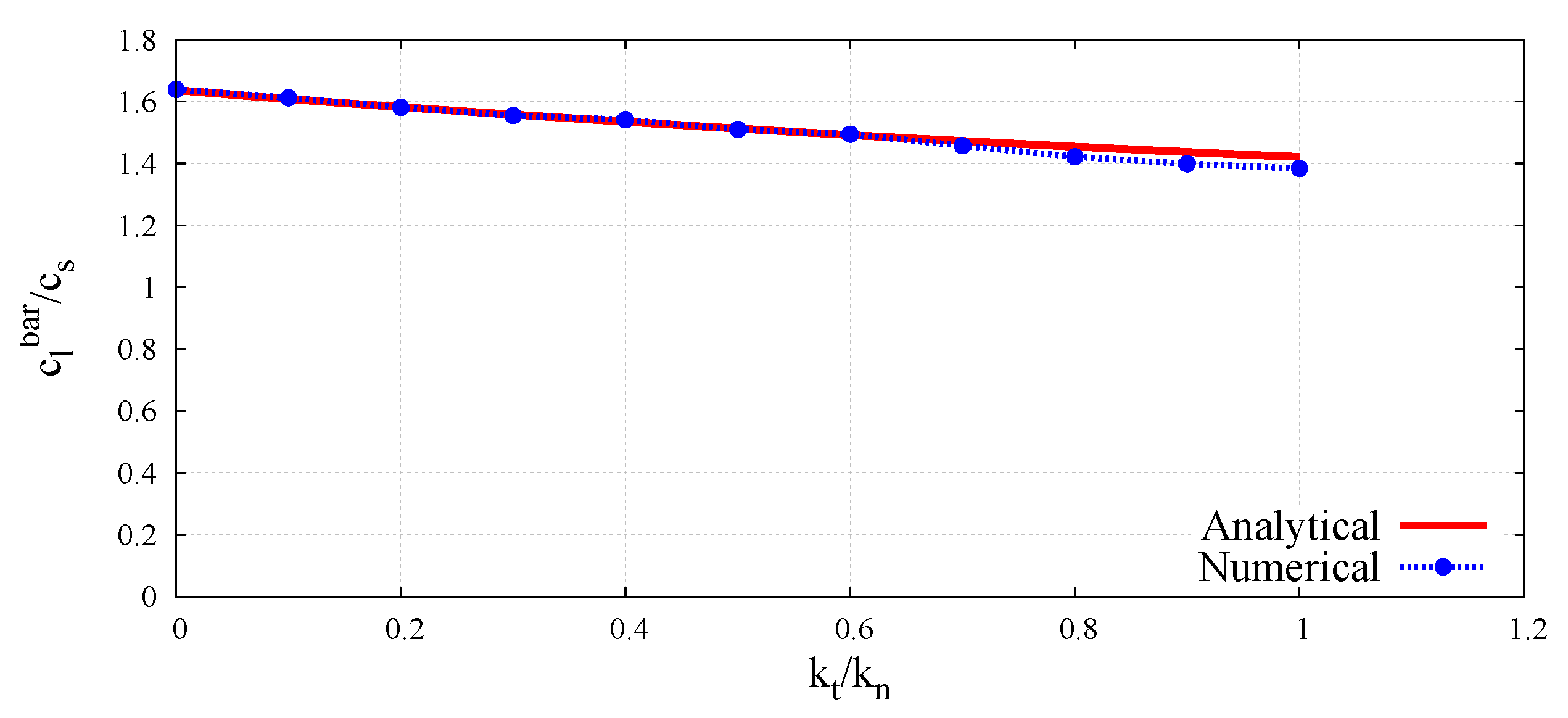
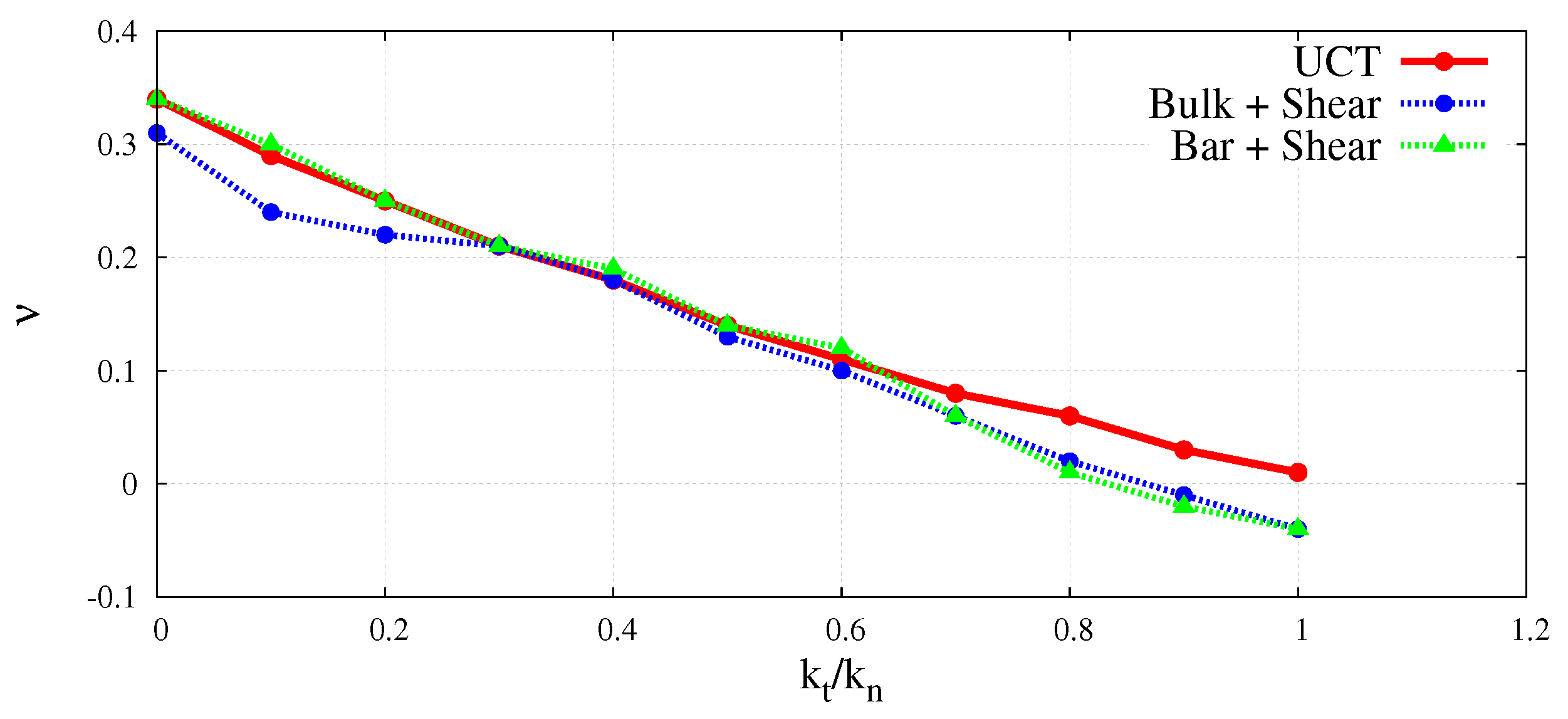
5. Determination of the Micro–Macro Relationships
6. Simulation of the Wave Propagation
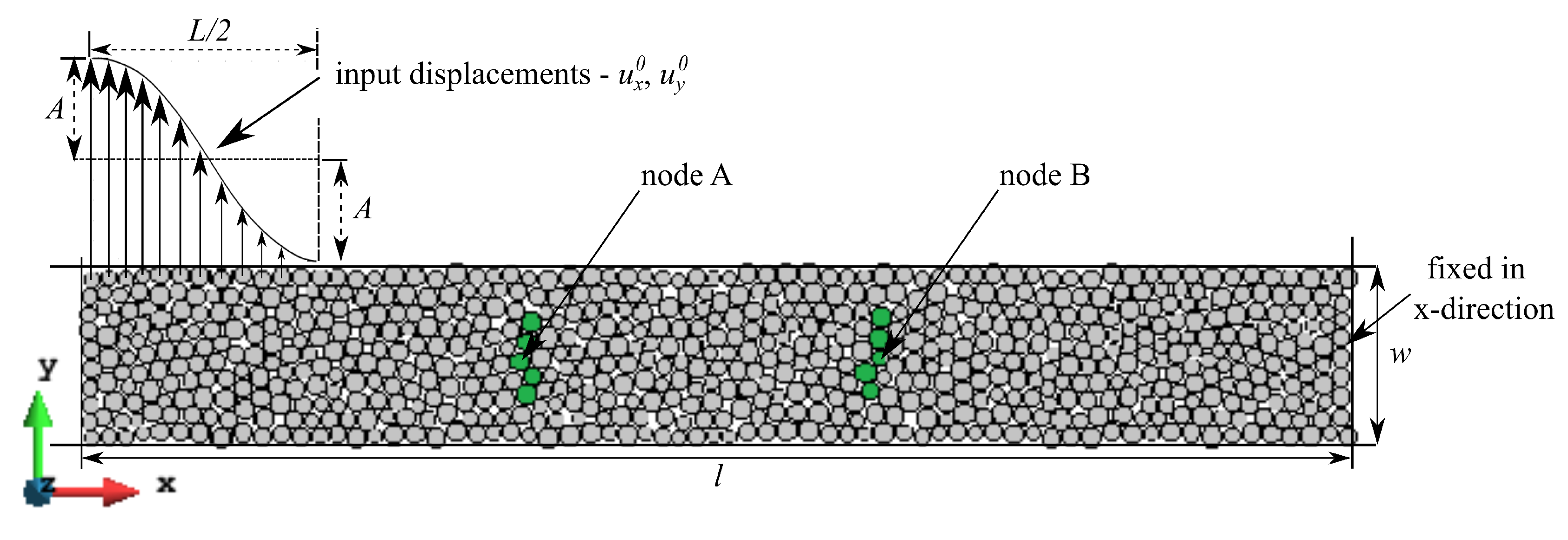
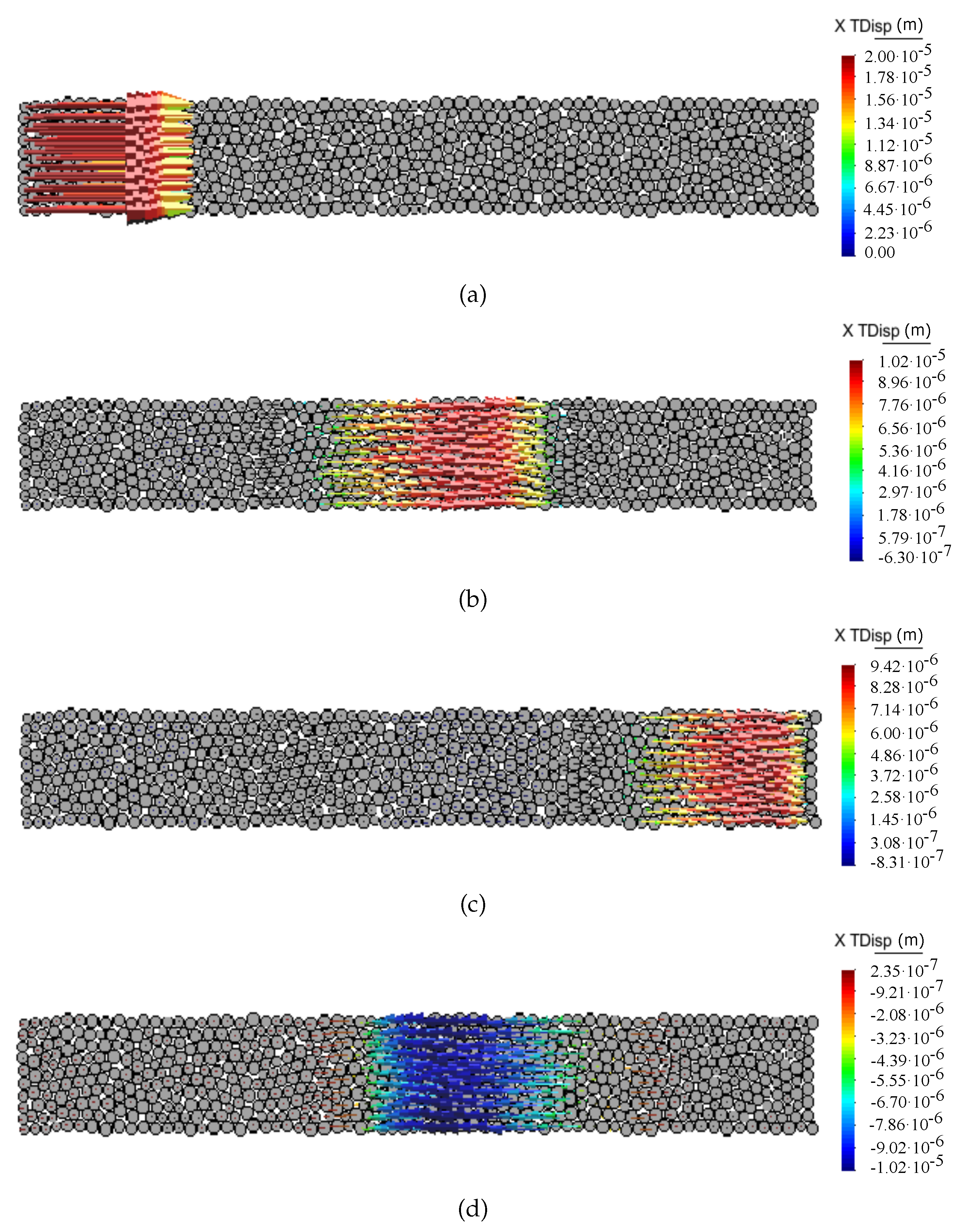
6.1. Discrete Element Simulation Setup
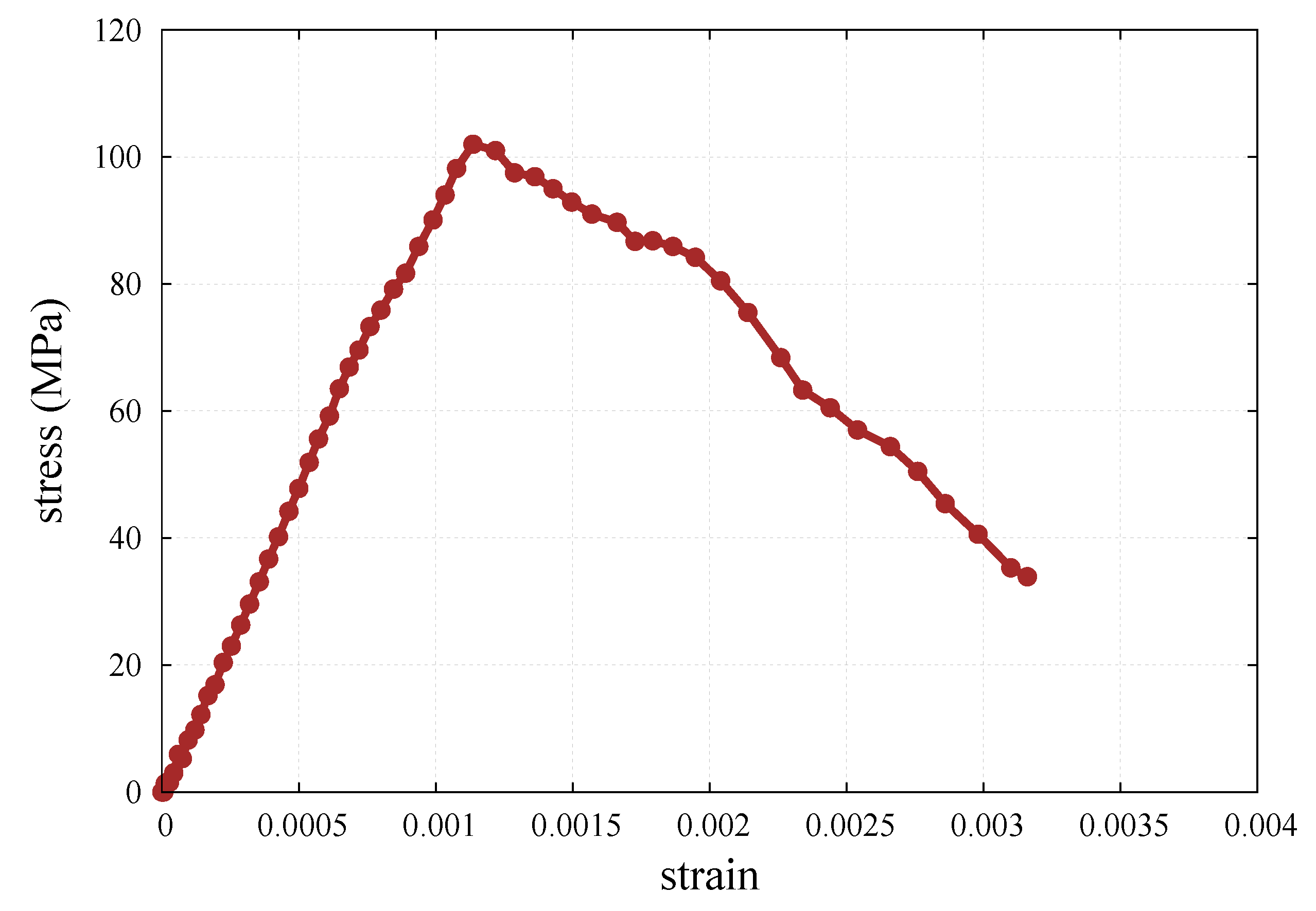
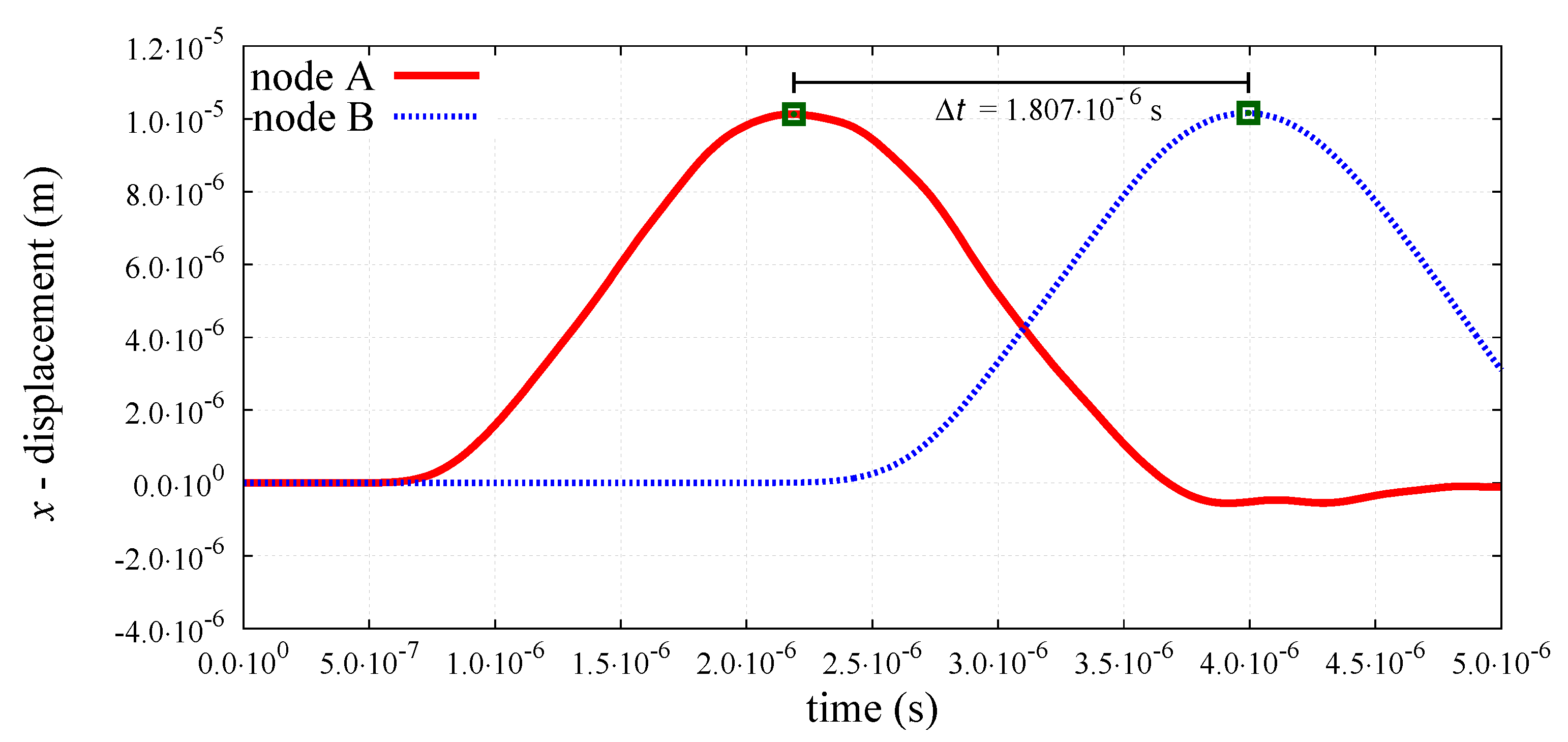
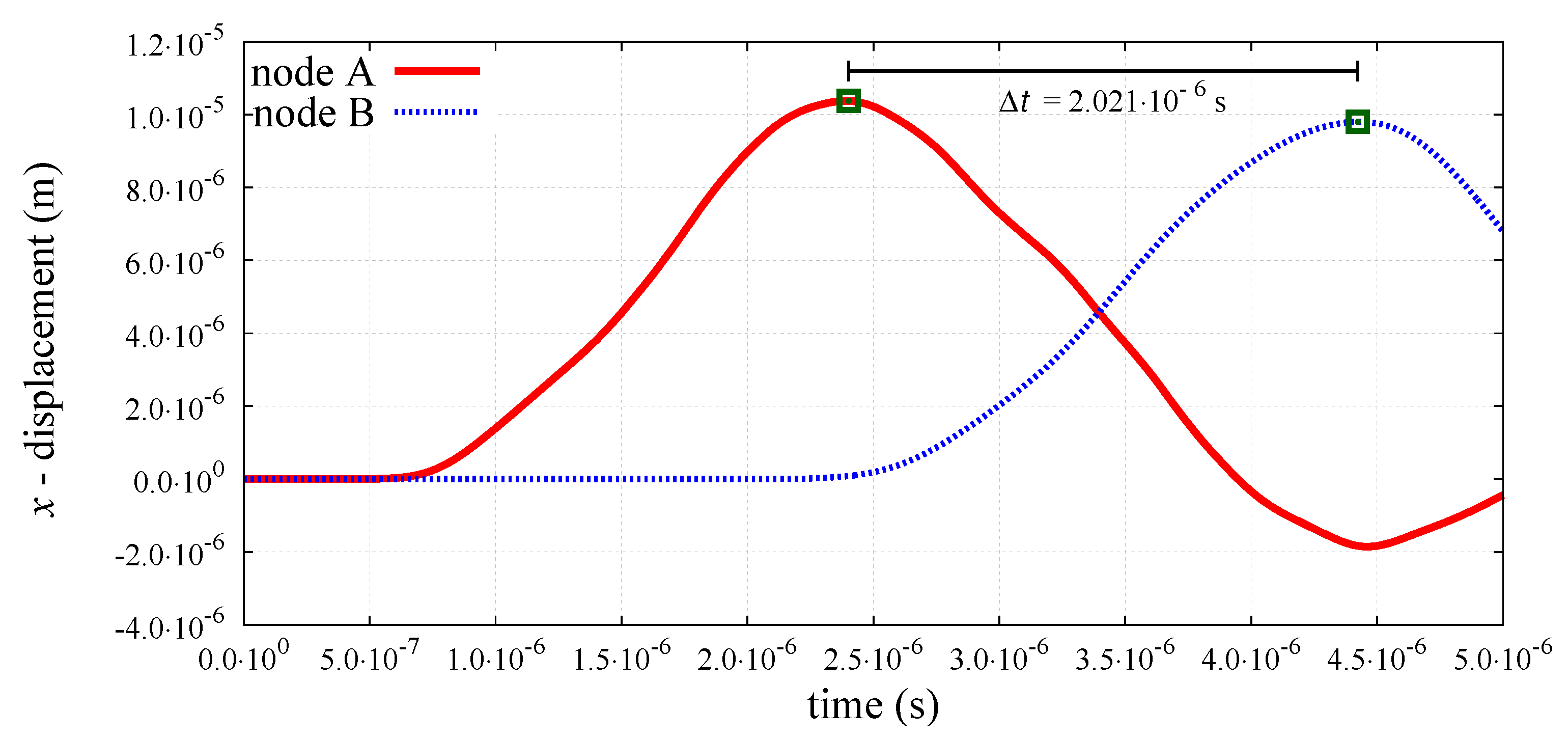
6.2. Numerical Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fellinger, P.; Marklein, R.; Langenberg, K.; Klaholz, S. Numerical modeling of elastic wave propagation and scattering with EFIT—Elastodynamic finite integration technique. Wave Motion 1995, 21, 47–66. [Google Scholar] [CrossRef]
- Raley, S.; Dieckman, E.A. Application of Elastodynamic Finite Integration Technique (EFIT) to three-dimensional wave propagation and scattering in arbitrary geometries. J. Acoust. Soc. Am. 2019, 145, 1781. [Google Scholar] [CrossRef]
- Nadella, K.S.; Cesnik, C.E.S. Local interaction simulation approach for modeling wave propagation in composite structures. CEAS Aeronaut. J. 2013, 4, 35–48. [Google Scholar] [CrossRef]
- Diaz, J. Modelling and Advanced Simulation of Wave Propagation Phenomena in 3D Geophysical Media; Habilitation à diriger des recherches, Université de Pau et des Pays de l’Adour: Pau, France, 2016. [Google Scholar]
- Komatitsch, D.; Tromp, J. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophys. J. Int. 1999, 139, 806–822. [Google Scholar] [CrossRef]
- Grote, M.J.; Schneebeli, A.; Schötzau, D. Discontinuous Galerkin Finite Element Method for the Wave Equation. SIAM J. Numer. Anal. 2006, 44, 2408–2431. [Google Scholar] [CrossRef] [Green Version]
- Mansur, W.; Brebbia, C. Numerical implementation of the boundary element method for two dimensional transient scalar wave propagation problems. Appl. Math. Model. 1982, 6, 299–306. [Google Scholar] [CrossRef]
- Sadd, M.H.; Tai, Q.; Shukla, A. Contact law effects on wave propagation in particulate materials using distinct element modeling. Int. J. Non-Linear Mech. 1993, 28, 251–265. [Google Scholar] [CrossRef]
- Sadd, M.H.; Adhikari, G.; Cardoso, F. DEM simulation of wave propagation in granular materials. Powder Technol. 2000, 109, 222–233. [Google Scholar] [CrossRef]
- Mouraille, O.; Luding, S. Sound wave propagation in weakly polydisperse granular materials. Ultrasonics 2008, 48, 498–505. [Google Scholar] [CrossRef] [Green Version]
- Donze, F.; Richefeu, V.; Magnier, S. Advances in discrete element method applied to soil, rock and concrete mechanics. Electron. J. Geotech. Eng. 2009, 8, 1–44. [Google Scholar]
- Kruggel-Emden, H.; Wirtz, S.; Scherer, V. A study on tangential force laws applicable to the discrete element method (DEM) for materials with viscoelastic or plastic behavior. Chem. Eng. Sci. 2008, 63, 1523–1541. [Google Scholar] [CrossRef]
- Luding, S. Cohesive, frictional powders: Contact models for tension. Granul. Matter 2008, 10, 235–246. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.; Hicher, P. An elasto-plastic model for granular materials with microstructural consideration. Int. J. Solids Struct. 2005, 42, 4258–4277. [Google Scholar] [CrossRef] [Green Version]
- Luding, S. Micro-Macro Transition for anisotropic, aperiodic, granular materials. In preparation.
- O’Donovan, J.; O’Sullivan, C.; Marketos, G. Two-dimensional discrete element modelling of bender element tests on an idealised granular material. Granul. Matter 2012, 14, 733–747. [Google Scholar] [CrossRef] [Green Version]
- O’Donovan, J.; Ibraim, E.; O’Sullivan, C.; Hamlin, S.; Muir Wood, D.; Marketos, G. Micromechanics of seismic wave propagation in granular materials. Granul. Matter 2016, 18, 56. [Google Scholar] [CrossRef] [Green Version]
- Toomey, A.; Bean, C. Numerical simulation of seismic waves using a discrete particle scheme. Geophys. J. Int. 2000, 141, 595–604. [Google Scholar] [CrossRef] [Green Version]
- Resende, R.; Fortunato, E.; Andrade, C.; Miranda, T. Vibration propagation in discrete element particle models of rock. In Rock Engineering and Rock Mechanics: Structures in and on Rock Masses; Alejano, R., Perucho, A., Olalla, C., Jiménez, R., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 871–876. [Google Scholar]
- Yoon, J.; Jeon, S. Use of a modified particle-based method in simulating blast-induced rock fracture. In Rock Fragmentation by Blasting; Sanchidrian, J., Ed.; CRC Press: Boca Raton, FL, USA, 2010; pp. 371–380. [Google Scholar]
- Rojek, J.; Oñate, E.; Labra, C.; Kargl, H. Discrete element simulation of rock cutting. Int. J. Rock Mech. Min. Sci. 2011, 48, 996–1010. [Google Scholar] [CrossRef]
- Labra, C.; Rojek, J.; Oñate, E. Discrete/Finite Element Modelling of Rock Cutting with a TBM Disc Cutter. Rock Mech. Rock Eng. 2017, 50, 621–638. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Tonon, F. Discrete Element Modeling of Rock Fragmentation upon Impact in Rock Fall Analysis. Rock Mech. Rock Eng. 2011, 44, 23–35. [Google Scholar] [CrossRef]
- Hu, E.; Wang, W. The Elastic Constants Measurement of Metal Alloy by Using Ultrasonic Nondestructive Method at Different Temperature. Math. Probl. Eng. 2016, 2016, 6762076. [Google Scholar] [CrossRef] [Green Version]
- Achenbach, J. Chapter 4—Elastic Waves in an Unbounded Medium. In Wave Propagation in Elastic Solids; Achenbach, J., Ed.; North-Holland Series in Applied Mathematics and Mechanics; Elsevier: Amsterdam, The Netherlands, 1975; pp. 122–164. [Google Scholar]
- DEMpack. Discrete/Finite Element Simulation Software. CIMNE. Available online: http://www.cimne.com/dem/ (accessed on 7 November 2019).
- Rojek, J.; Oñate, E. Multiscale analysis using a coupled discrete/finite element model. Interact. Multiscale Mech. 2007, 1, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Rojek, J.; Nosewicz, S.; Jurczak, K.; Chmielewski, M.; Bochenek, K.; Pietrzak, K. Discrete element simulation of powder compaction in cold uniaxial pressing with low pressure. Comput. Part. Mech. 2016, 3, 513–524. [Google Scholar] [CrossRef]
- Rojek, J.; Labra, C.; Su, O.; Onate, E. Comparative study of different discrete element models and evaluation of equivalent micromechanical parameters. Int. J. Solids Struct. 2012, 49, 1497–1517. [Google Scholar] [CrossRef] [Green Version]
- Cundall, P.; Strack, O. A discrete numerical method for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers, 7th ed.; McGraw-Hill, Inc.: New York, NY, USA, 2015. [Google Scholar]
- Belytschko, T.; Smolinski, P.; Liu, W. Stability of multi-time step partitioned integrators for the first order finite element systems. Comput. Meth. Appl. Mech. Eng. 1985, 49, 281–297. [Google Scholar] [CrossRef]
- O’Sullivan, C.; Bray, J. Selecting a suitable time step for discrete element simulations that use the central difference time integration scheme. Eng. Comput. 2004, 21, 278–303. [Google Scholar] [CrossRef]
- Otsubo, M.; O’Sullivan, C.; Shire, T. Empirical assessment of the critical time increment in explicit particulate discrete element method simulations. Comput. Geotech. 2017, 86, 67–79. [Google Scholar] [CrossRef] [Green Version]
- Kruggel-Emden, H.; Simsek, E.; Rickelt, S.; Wirtz, S.; Scherer, V. Review and extension of normal force models for the Discrete Element Method. Powder Technol. 2007, 171, 157–173. [Google Scholar] [CrossRef]
- Fortin, J.; Millet, O.; de Saxcé, G. Numerical simulation of granular materials by an improved discrete element method. Int. J. Numer. Meth. Eng. 2004, 62, 639–663. [Google Scholar] [CrossRef]
- Cambou, B.; Danescu, A. Multiscale Techniques for Granular Materials. In Micromechanics of Granular Materials; Cambou, B., Jean, M., Radjai, F., Eds.; ISTE Ltd and John Wiley & Sons: London, UK, 2009. [Google Scholar]
- Kruyt, N.; Rothenburg, L. Kinematic and static assumptions for homogenization in micromechanics of granular materials. Mech. Mater. 2004, 6, 1157–1173. [Google Scholar] [CrossRef]
- Hsieh, Y.M.; Li, H.H.; Huang, T.H.; Jeng, F.S. Interpretations on how the macroscopic mechanical behavior of sandstone affected by microscopic properties—Revealed by bonded-particle model. Eng. Geol. 2008, 99, 1–10. [Google Scholar] [CrossRef]
- Bagi, K. Analysis of microstructural strain tensors for granular assemblies. Int. J. Solids Struct. 2006, 43, 3166–3184. [Google Scholar] [CrossRef] [Green Version]
- Liao, C.L.; Chang, T.P.; Young, D.H.; Chang, C. Stress strain relationship for granular materials based on the hypothesis of best fit. Int. J. Solids Struct. 1997, 34, 4087–4100. [Google Scholar] [CrossRef]
- Huang, H.; Lecampion, B.; Detournay, E. Discrete element modeling of tool-rock interaction I: Rock cutting. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1913–1929. [Google Scholar] [CrossRef]
- Chang, C.S.; Chao, S.J.; Chang, Y. Estimates of elastic moduli for granular material with anisotropic random packing structure. Int. J. Solids Struct. 1995, 32, 1989–2008. [Google Scholar] [CrossRef]
- Fakhimi, A.; Villegas, T. Application of Dimensional Analysis in Calibration of a Discrete Element Model for Rock Deformation and Fracture. Rock Mech. Rock Engng. 2007, 40, 193–211. [Google Scholar] [CrossRef]
- Marczewska, I.; Rojek, J.; Kačianauskas, R. Investigation of the effective elastic parameters in the discrete element model of granular material by the triaxial compression test. Arch. Civ. Mech. Eng. 2016, 16, 64–75. [Google Scholar] [CrossRef]
- Rojek, J.; Zubelewicz, A.; Madan, N.; Nosewicz, S. The discrete element method with deformable particles. Int. J. Numer. Methods Eng. 2018, 114, 828–860. [Google Scholar] [CrossRef]
- Huang, H. Discrete Element Modeling of Tool-Rock Interaction. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 1999. [Google Scholar]
- Labra, C.; Oñate, E.; Rojek, J. Advances in the Development of the Discrete Element Method for Excavation Processes; CIMNE: Barcelona, Spain, 2012; Monograph M132. [Google Scholar]
- Moser, F.; Jacobs, L.J.; Qu, J. Modeling elastic wave propagation in waveguides with the finite element method. NDT E Int. 1999, 32, 225–234. [Google Scholar] [CrossRef]










| Symbol | Parameter | Value | Units |
|---|---|---|---|
| no. of particles | 682 | - | |
| max. radius | 0.145 | mm | |
| min. radius | 0.1 | mm | |
| l | sample length | 16.54 | mm |
| w | sample width | 2.3 | mm |
| e | porosity | 0.11 | - |
| particle density | 2000.0 | kg/m | |
| sample average density | 1784.26 | kg/m | |
| normal contact stiffness | 1 × | N/m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rojek, J.; Madan, N.; Nosewicz, S. Micro–Macro Relationships in the Simulation of Wave Propagation Phenomenon Using the Discrete Element Method. Materials 2019, 12, 4241. https://doi.org/10.3390/ma12244241
Rojek J, Madan N, Nosewicz S. Micro–Macro Relationships in the Simulation of Wave Propagation Phenomenon Using the Discrete Element Method. Materials. 2019; 12(24):4241. https://doi.org/10.3390/ma12244241
Chicago/Turabian StyleRojek, Jerzy, Nikhil Madan, and Szymon Nosewicz. 2019. "Micro–Macro Relationships in the Simulation of Wave Propagation Phenomenon Using the Discrete Element Method" Materials 12, no. 24: 4241. https://doi.org/10.3390/ma12244241





