Probabilistic Prediction of Strength and Fracture Toughness Scatters for Ceramics Using Normal Distribution

Abstract

Tensile strength f_t and fracture toughness K_IC of ceramic are not deterministic properties or fixed values, but fluctuate within certain ranges. A nonlinear elastic fracture mechanics model was developed in this study and combined with the common normal distribution to predict ceramic’s f_t and K_IC with consideration of their scatters in a statistical sense. In the model, the relative characteristic crack size a*_ch/G (characteristic crack size a*_ch, average grain size G) was determined based on the fracture measurements on five types of ceramics with different G from 2 to 20 μm in the reference (Usami S, et al., Eng. Fract Mech. 1986, 23, 745). The combined application of the model and normal distribution has two functions: (i) probabilistic f_t and K_IC can be derived from seemingly randomly varied fracture tests on small ceramic specimens containing different initial defects/cracks, and (ii) with f_t or K_IC values (corresponding mean and standard deviation), fracture strength of heterogeneous samples with and without cracks can be predicted by considering scatter described by specified reliability. For the fine ceramics, the predicted results containing the mean and the upper and lower bounds with 96% reliability gained with the model, match very well with the experimental results (a, σ_N).

1. Introduction

One of the biggest challenges in material sensitive design is to accurately and reliably predict the fundamental mechanical properties of materials. However, the physical properties such as tensile strength f_t and fracture toughness K_IC are not fixed or deterministic, and fluctuate in certain range, which has been well recognized recently [1,2,3].

The inevitable variation in mechanical property of materials is mainly due to the heterogeneity of microstructure, defects like pores and the activation of various fracture mechanisms during the crack-microstructure interactions [4]. For polycrystalline brittle materials such as fine-grained ceramics [5,6,7] and coarse-grained rocks [8,9,10], the average grain size G has a profound influence on material properties including f_t and K_IC. For composites and 3D-printed scaffolds [11], their unit cells have a similar role as that of G.

Nonlinear elastic fracture of those solids initiated from shallow defects comparable to their grain sizes can bring out significant information on the inherent relationship between microstructure and material properties. Besides separate influence on f_t and K_IC, the effect of G on the combined parameter 0.25*(K_IC/f_t)², commonly known as characteristic crack size a*_ch indicating the transition from f_t-controlled to K_IC-controlled fracture of brittle solid [12,13], is becoming increasingly important. Taylor has done numerous studies on characteristic length l_ch, proportional to a*_ch, and proposed the world-renowned theory of critical distance (TCD) [14,15,16,17,18,19]. It has been found that the l_ch varies from 1 to 10 times of grain size G depending on the materials. Generally speaking, l_ch = (3–4)G can be adopted for various fine-grained ceramics. More recently, we reanalysed the fracture measurements data on four fine-grained ceramics with G from 2 to 20 μm and on two coarse-grained rocks with G = 2.5 and 10 mm, and also found a semi-quantitative relation of a*_ch ≥ 3G [7,10].Therefore, an explicit relationship between a*_ch and G is an urgency need not only for the fundamental knowledge of microstructure-driven material research, but also for the safe design application.

For fracture data analysis methods, the common practice is that fracture strength is first obtained from experiment and then fitted by various fracture models, and the scatters are usually indicated by the maximum and minimum values but rarely described with a specified reliability [20,21,22,23,24,25,26]. The problem is that the models cannot describe the scatter of physical properties or fracture strength with specified reliability. In addition, many parameters in the models are fitting parameters which carry little physical significance.

In this study, five groups of fracture measurements on ceramics specimens with G from 2 to 20 μm and containing different initial defects from 100 nm to 800 μm [27,28] were reanalyzed to determine the relative characteristic crack size C = a*_ch/G. Based on this, a non- linear elastic fracture mechanics (non-LEFM) analytical model is proposed to predict f_t and K_IC of ceramics as function of grain size G from common fracture measurements, and to predict fracture strength of specimens with and without small defects if f_t or K_IC are available. Instead of curve fitting, the common normal distribution was used to analyse the fracture behaviour of ceramics to consider the scatters of physical and mechanical properties.

2. Determination of the Relative Characteristic Crack Size in Non-LEFM Model

Based on our previous work [7], fracture strength of ceramic specimens containing small flaws/cracks can be assessed by the following formula,

$${\sigma }_N=f_t·\frac{1}{\sqrt{1+\frac{a}{C·G}}}$$

(1a)

where the combined parameter C⋅G = a*_ch = 0.25(K_IC/f_t)² is a material constant defined by the intersection of two fracture criteria K_IC and f_t, and σ_N is the engineering stress without consideration of the influence of initial crack size a.

Although Weibull distribution has been widely used to determine the fracture behavior of materials, its role has usually been confined to fit experimental data rather than providing predictive insight into material properties (e.g., f_t and K_IC) and their experimental scatters [4]. In our previous study [7,10], another common statistical analysis method of normal distribution has been used to analyze experimental data of ceramic fracture after roughly assessing the relative characteristic crack size C (= a*_ch/G) at intervals of 0.25. In this study, we accurately determine the C value by continuously changing its value instead of interval.

The average grain size G is the microstructure characteristic of a polycrystalline material which can be statistically measured separately.If the C is a fixed value, Equation (1a) can be linearized by considering σ_N and 1/[1 + a/(C⋅G)]^0.5 as ordinate and abscissa respectively, then it can be used in conjunction with the common normal distribution to make probabilistic analysis on f_t with 96% reliability. That is, if an experimental data (σ_N, a) is measured, the f_t from Equation (1a) becomes a single parameter after giving C a fixed value. Having numerous pairs of values of original crack a and engineering stress σ_N obtained from specimens with different α ratio (= a/W, W is the beam/specimen height), the data points (σ_N, 1/[1 + a/(C⋅G)]^0.5) obtained can be plotted with these quantities considered as ordinate and abscissa respectively. Using Equation (1a), a group of f_t values can be easily statistically analysed by normal distribution mehthodology.

Similarly, the following equation can be obtained by substituing the relation C⋅G = 0.25(K_IC/f_t)² into Equation (1a), which is used to calculate K_IC value from fracture measurement (σ_N, a). Similarly, Equation (1b) combined with normal distribution can be used to do statistical analyses of K_IC values from experimental measurements data if the C is a fixed value.

$${\sigma }_N=K_{IC}·\frac{1}{2\sqrt{a+C·G}}$$

(1b)

Therefore, a determined value of C urgently needs to be included in the two formulas of Equation (1). For this reason, the ralative characteristic crack sizeC (= a*_ch/G) independent of grain size G is assessed based on the experimental data (σ_N, a) on five ceramics with different G from 2 to 20 μm. In total, 14 experimental data points (σ_N, a) of the Sialon with average grain size G = 2 μm, 29 points of the SiC with G = 3 μm, 25 points of Si₃N₄ with G = 3 μm, 16 points of Si₃N₄ with G = 4 μm, and 42 points of Al₂O₃ with G = 20 μm, were digitized from the reference [28].

Based on the fracture measurements (σ_N, a) of the five ceramics considered in this study, each group of f_t values from Equation (1a) and K_IC values from Equation (1b) was analyzed using two ways respectively to ensure reliability of analyzed results.

Figure 1 illustrates the evolution of standard deviation σ_f of tensile strength f_t from Equation (1) as the relative characteristic crack size C (= a*_ch/G) varies continuously. C₀ is defined as the critical value of C signifying the σ_f transitioned from decrease to increase. That is the C₀ value is determined by the condition that the σ_f value is minimum. When the relative characteristic crack size C gradually deviates from the C₀ value, σ_f increases accordingly. According to the analyzed results of the five ceramics with different G from 2 to 20 μm, it can be found that C₀ value is not dependent on grain size and fluctuates in a range from 2.8 to 4.7.

The largest number of experimental data points selected in this analysis is 42 from Al₂O₃ fracture, and the minimum number is mere 14 from Sialon. Considering the effect of the fewer number of data points (14 to 42 points) in each group of fracture measurements, we take the average of C₀ values (i.e., 3.380 in this analysis) obtained from the fracture measurements of the five ceramics as the determined value of C, which at least should be one of the accepted and reasonable ways.

For the analysis of f_t distribution in Figure 1, f_t is derived from fracture measurement data (σ_N, a) through Equation (1a), in which σ_N and 1/[1 + a/(C⋅G)]^0.5 follow a linear relation and f_t in MPa is the slope of the straigth line through the origin. For each data point (σ_N, a), the angle between the abscissa and the straight line through the origin and the considered point approaches 90° because the tangent of angle indicating f_t value is usually around several hundred. Therefore, any tiny error in the degitization of data point (a, σ_N) can result in significant fluctuation in the corresponding f_t value.

For this reason, we tried another statistic method to determine the C value based on the same five groups of ceramic fracture measurements. Figure 2 illustrates the evolution of the sum of distances of all the experimental points to the mean line indicating the average of f_t values from Equation (1a) as C varies continuously. C₀ value is determined by the condition that the sum of distances by normal to the mean line is minimum. It is evident that the sum of the distances gradually increases when the C deviates from C₀. It can also be found that C₀ value is not dependent on the grain size G and flucturates in a range from 2.6 to 4.3. Again, we took the average of C₀ values obtained from the five different ceramics fracture as the determined C value, i.e., 3.1788 in this analysis.

Figure 3 illustrates the evolution of standard deviation σ_k of K_IC from Equation (1b) determined by normal distribution as the relative characteristic crack size C (= a*_ch/G) varies continuously for the five ceramics, and the C₀ value is determined by the condition the σ_k is minimum. The same as above, C₀ value is not dependent on the grain size G and flucturates in narrower range from 2.7 to 4.1 in comparison to the results of f_t distribution. The average of C₀ values obtained from the five different ceramics fracture is 3.1426 in this analysis.

Figure 4 illustrates the evolution of the range of (K_IC)_max–(K_IC)_min from Equation (1b) as the relative characteristic crack size C (= a*_ch/G) varies continuously for the five ceramics, and the C₀ value is determined by the condition the range is minimum. Again, the C₀ value is not dependent on the grain size G and flucturates in narrower range from 2.6 to 4.0 in comparison to the results of f_t distribution. The average of C₀ values obtained from the five different ceramics fracture is 3.1288 in this analysis.

According to the above analyses based on the fracture measurements of the five ceramic with largely different G, the relative charateristic crack C (= a*_ch/G) value is indeed not dependent on the grain size G, and is eaual to 3.380 and 3.1788 obtained from f_t distribution, and 3.1426 and 3.1288 from K_IC distribution. It should be noted that the characteristic crack size a*_ch = C⋅G is a specified crack indicating the transition from f_t-controlled fracture to K_IC-controlled fracture. Furthermore, the dominant non-LEFM mechanism of brittle materials such as ceramic should have relation to the defects in solids, which may be linked to microstructure characteristic G. If one quantitatively links the specified crack length a*_ch to the material microstructure characteristic G, from the perspectives of mathematics and physics the relation of a*_ch = π⋅G between the two should be a good choice under condition of C ≈ 3.1–3.4 from the above f_t and K_IC distribution analyses. In addtion, the C values from K_IC distribution is more stable than those from f_t distribution, which will be proved in the following section. For simplicity and consistency between f_t distribution and K_IC distribution, C₀ = a*_ch/G = π is selected in this study.

3. Probabilistic Strength and Fracture Toughness Analyses

Following the determination of the relative characteristic crack size C = π based on the fracture behaviour of five ceramics with G from 2 to 20 μm, Equation (1) can now be rewritten as follows.

$${\sigma }_N=f_t·\frac{1}{\sqrt{1+\frac{a}{\pi ·G}}}=f_t·\eta \left(a,G\right)$$

(2a)

$${\sigma }_N=K_{IC}·\frac{1}{2\sqrt{a+\pi ·G}}=K_{IC}·L_{\mathrm{e}}\left(a,G\right)$$

(2b)

The dimensionless η(a, G) and equivalent length L_e (a, G) in Equation (2) are wholly determined for a specified sample. For any group of ceramic specimens, the seemingly randomly varied fracture measurements data (σ_N, a) can be used to obtain a group of f_t value using Equation (2a) and K_IC values using Equation (2b) which can be easily analysed by normal distribution to get corresponding mean and standard deviation. With the mean μ_f and standard deviation σ_f of f_t distribution, Equation (2a) can be rewritten to include the mean and upper and lower bounds with 96% reliability indicating f_t scatter during fracture behaviour.

$${\sigma }_N=\left({\mathsf{\mu }}_f\pm 2{\sigma }_f\right)·\frac{1}{\sqrt{1+\frac{a}{\pi ·G}}}=\left({\mathsf{\mu }}_f\pm 2{\sigma }_f\right)·\eta \left(a,G\right)$$

(3a)

Similarly, Equation (2b) can be rewritten as follows.

$${\sigma }_N=\left({\mathsf{\mu }}_k\pm 2{\sigma }_k\right)·\frac{1}{2\sqrt{a+\pi ·G}}=\left({\mathsf{\mu }}_k\pm 2{\sigma }_k\right)·L_{\mathrm{e}}\left(a,G\right)$$

(3b)

The problem of the most existing probabilistic models is that they do not consider the scatters of f_t, K_IC and fracture strengthσ_N prior to experimental measurements [4]. After determinations of the corresponding mean and standard deviation, three σ_N–η(a, G) linear relations from f_t distribution and three σ_N–L_e(a, G) straight lines based on K_IC distribution, can be plotted together including the mean line and upper and lower bounds indicating both f_t and K_IC scatters.

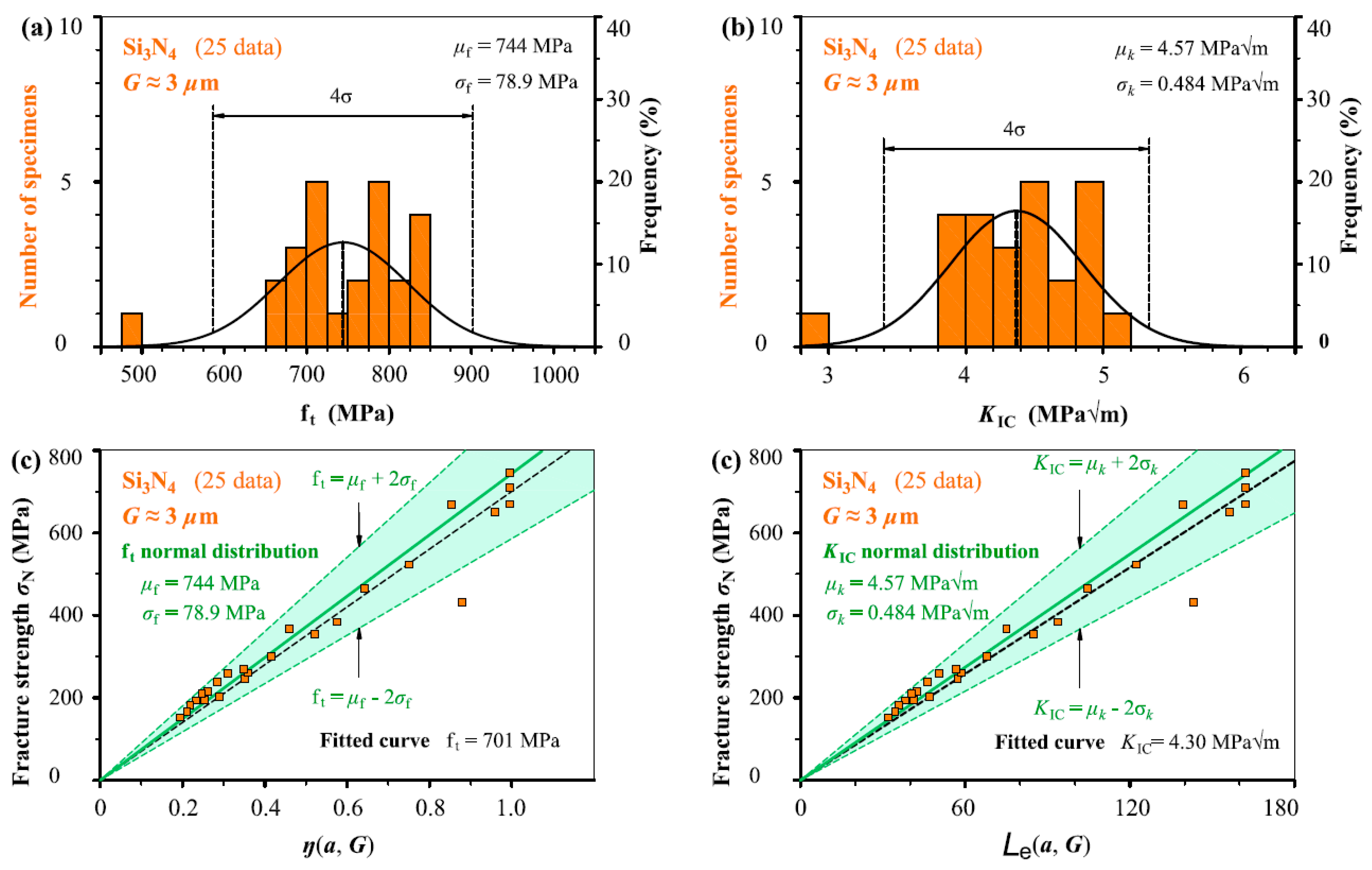
In Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, we take the five ceramic-fracture cases as examples to illustrate the combined application of the non-LEFM model Equation (3) and the normal distribution, and to check the validity and reliability of the C = π. For each group of ceramic fracture, f_t normal distribution illustrated in Figure 5a–Figure 9a and K_IC normal distribution in Figure 5b–Figure 9b are evaluated from the same experimental measurements (σ_N, a). Then the three predicted linear relations from Equation (3a) using μ_f and σ_f of f_t distribution are shown in Figure 5c–Figure 9c, and the three predicted straight lines from Equation (3b) with the μ_k and μ_k ± 2σ_k from K_IC distribution are illustrated in Figure 5d–Figure 9d.

Obviously, both f_t and K_IC with 96% reliability can be successfully deduced from the seemingly randomly varied experimental data points (σ_N, a). It can also be seen that the middle straight lines indicating the mean values of f_t or K_IC are almost the same as the corresponding fitted curves respectively. As we all know, the commonly used curve fitting methodology cannot describe the experimental scatter of fracture behaviour, but the proposed model can provide more scientific descriptions. This adds a significant understanding for the fracture of ceramic with and without small defects. Similarly, the scatters of fracture strength σ_N due to the stochastic characteristic of microstructure and the activation of various fracture mechanisms during the crack-microstructure interaction cannot be identified by the common curve fitting methodology.

Because the μ_f and σ_f values are constants, the corresponding slopes of the three straight lines of σ_N–η(a, G) relation indicating mean and upper and lower bounds are kept as constants as η(a, G) increases in Figure 5c–Figure 9c, leading to more σ_N scatter, which matches very well the experimental results reported in the literature [27,28]. This indicates that a specimen with higher η(a, G) value will have larger fluctuation of σ_N during fracture. That is larger specimen has larger σ_N scatter which is absolutely reasonable in physics concept. Here, it should be noted that the percentage of σ_N variation keeps constant in theory for various specimens with different η(a₀, G) as the mean and standard deviation are constant. The same conclusions can also be observed from the corresponding results obtained from K_IC distribution in Figure 5d–Figure 9d.

It should be noted that the two linear relations of σ_N–η(a, G) and σ_N–L_e (a, G) pass through their respective origins, which are fixed points from perspectives of mathematics and physics. During the process of application, this is very useful to helping determine the slopes of the linear relations, which indicate the f_t or K_IC values. In addition, it can be seen that K_IC normal distribution is better than the f_t normal distribution from the histograms for Sialon, SiC and Al₂O₃ cases, and K_IC and f_t normal distribution are similar for the other two cases. Thus, it is reasonable that the determination of C value (=π) in Section 2 thought more of the K_IC analyses.

4. Probabilistic Prediction of Ceramic Facture

By employing the two concepts of dimensionless η(a, G) and equivalent length L_e (a, G), the nonlinear relation in Equation (1) for assessing the fracture strength of ceramic specimen is linearized in relation as listed in Equation (2). The non-LEFM model combined with the common normal distribution can easily deduce ceramic’s f_t and K_IC with a specified reliability from the seemingly randomly varied fracture measurements (σ_N, a) as shown in Equation (3).

In fact, the linearized non-LEFM model with a specified reliability or Equation (3) can be conveniently transformed to an application model in nor-linear relation of σ_N–a for finally predicting the fracture strength σ_N. If corresponding mean and standard deviation of material strength f_t or fracture toughness K_IC are available, the fracture strength of notched specimens with and without small defects can be easily predicted with a specified reliability through Equation (3). Using the values of f_t property obtained and shown in Figure 5a–Figure 9a, here we take Equation (3a) as an example to show how to apply the model in nonlinear relation for predicting σ_N with a specified reliability.

The three predicted σ_N–a curves with mean and upper and lower bounds are shown in Figure 10 together with the experimental data points. For comparison, the fitted curves for the nonlinear relationship of σ_N–a using Equation (3a) are also added to the figure. A direct comparison between the experimental results and the predicted curves shows that the non-LEFM model or Equation (3a) can reliably predict the fracture of notch ceramics as the predicted curves with 96% reliability cover all the data points. In addition, the middle curve indicating the mean of f_t value is more appropriate than the best fitted curve in each case. More importantly, those σ_N variations are inevitable for ceramic fracture. The proposed model can describe the σ_N scatter with a specified reliability, which is beyond the job of common curve fitting.

5. Discussion

In most of the existing probabilistic models, the fracture measurements data (a,σ_N) is usually first obtained from experiment and then fitted by linearized formula to get f_t and K_IC values. The problem of the most existing models is that they do not allow the scatters of f_t and K_IC data to be predicted before the experimental testing. As we all known, it is easy to establish a normal distribution for a group of data (e.g., f_t or K_IC values) with a specified reliability if a group of samples without defects or cracks are tested. But such a practical application soon becomes impractical for a wide crack range from the f_t-controlled fracture over non-LEFM to finally the K_IC-controlled fracture. The non-LEFM model in Equation (3) removes the need of curve fitting for fracture measurements data, and considers the scatters of mechanical properties f_t and K_IC through the upper and lower bounds with 96% reliability.

In the model, the microstructure characteristic G of ceramic is explicitly linked to both f_t and K_IC. In the present study, the five ceramics, Sialon, SiC, Si₃N₄ with G = 3 μm, Si₃N₄ with G = 4 μm and Al₂O₃, were considered, and they have hugely different grain size G ranged from 2 to 20 μm. Since a*_ch = 0.25(K_IC/f_t)², they also have different characteristic crack size a*_ch values due to obvious difference in material properties f_t and K_IC. Most recently, we studied the relative characteristic crack size C = a*_ch/G at an interval of 0.25 from 2 to 4.5, and found C ≥ 3.0 [7,10]. Following the conclusion, the present study further found the C = π (or a*_ch = π⋅G) is appropriate to consider the effect of microstructure characteristic G on the a*_ch value indicating the transition from f_t-controlled fracture to K_IC-controlled fracture.

Equation (3) can be easily used in either linear relations [σ_N–η(a, G), σ_N–L_e (a, G)] or nonlinear relations (σ_N–a) as required. It should be noted that the predicted results (e.g., f_t, K_IC and σ_N) with 96% reliability do not change with the different forms of non-LEFM model, which makes the combined use of the proposed model and normal distribution more meaningful and easier in practical applications and data analysis. Furthermore, the σ_N–η(a, G) and σ_N–L(a, G) linear relations through the respective origins make the non-LEFM model easier to determine f_t and K_IC values as the origin is absolutely fixed.

Substituting Equation (1a) into Equation (1b), the mechanical properties f_t and K_IC can be linked together through the average grain size G and the relative characteristic crack size C = π as shown in Equation (4). In another word, the microstructure characteristic G has direct influence on f_t and K_IC of ceramic.

$$K_{IC}=f_t·2\sqrt{\pi ·G}$$

(4)

To have a better understanding, the σ_N–η(a, G) linear relations in Figure 5c–Figure 9c were plotted together to show the influnce of microstructure characteristic G on f_t value. To make it clearer, three different ceramics with different G are shown in Figure 11a, and two types of Si₃N₄ ceramic with slightly different G are illustrated in Figure 11b in which only mean lines are given because the experimental points get close each other due to that the two materials are Si₃N₄ and have similar G values. Obviously, both f_t and K_IC have been explicitly linked together through the average grain size, in which the fracture toughness K_IC is determined from Equation (4) based on the f_t value and G value. Grain size G has significant influence on f_t and K_IC, and can explicitly link the two properties.

In this study, five groups of fracture data on ceramics with average grain size G from 2 to 20 μm have been analyzed. Using the fracture data, it has been proven the proposed non-LEFM model and normal distribution can be combined used to (i) deduce both f_t and K_IC with a specified reliability from the seeming randomly varied fracture measurement and (ii) probabilistic predict σ_N of ceramic specimens with and without defects if f_t or K_IC values (corresponding mean and standard deviation) are available. The predictions including mean and upper and lower bounds can be either linear relation as shown in Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, or nonlinear relation in Figure 10 as required.

6. Conclusions

A non-LEFM model for ceramic fracture is proposed and combined with normal distribution, which is applicable to predictions of f_t, K_IC and σ_N with consideration of their scatters. The relative characteristic crack size C (= a*_ch/G) indicating the transition from f_t- to K_IC- controlled fracture was determined based on the five groups of fracture data on ceramics with different G from 2 to 20 μm reported in the literature and the dominant fracture mechanism of brittle materials. The main conclusions are as follows:

(1)

The proposed non-LEFM model combined with normal distribution can be conveniently used either in linear relation to deduce ceramic’s f_t and K_IC with a specified reliability from seemingly randomly varied fracture data (σ_N, a) shown in Equation (2), or in nonlinear relation to predict fracture strength σ_N including upper and lower bounds if f_t and K_IC ranges are available shown in Equation (2).

(2)

From perspectives of mathematics and physics, the relative characteristic crack size C = a*_ch/G = π independent of the grain size G is determined based on the fracture measurements.

(3)

Basic mechanical properties of ceramic, f_t and K_IC, have been linked to the microstructure characteristic G and the relative characteristic crack size C = π shown in Equation (2), and f_t and K_IC are explicitly linked together through the G and C = π in Equation (4).

(4)

The upper and lower bounds with 96% reliability for predicting f_t, K_IC and σ_N scatters in the present study can provide effective insight to design application, which is beyond the job of the commonly used curve fitting.

Although the quantification is specific to fine-grained ceramics, the proposed non-LEFM model and normal distribution analysed approach can also be applied to other polycrystalline solids such as rock.