Theoretical and Experimental Analysis of a New Process for Forming Flanges on Hollow Parts
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
- σmax is the maximum principal stress,
- σHMH is the reduced stress according to the Huber–Mises–Hencky hypothesis,
- ε is the strain,
- C is the material constant.
- Dp is the inside diameter of the limit ring,
- F(Dp) is the force as a function of limit ring diameter,
- a, b are coefficients,
- ΩF is the objective function,
- Fi is the value of force at i-th measurement (Table 3).
4. Conclusions
- the incremental radial extrusion process for hollow parts makes it possible to form flanges with their diameter bigger by 30% than that of flanges produced by extrusion without the use of rings;
- due to the favorable stress pattern, the proposed method makes it possible to produce flanges with uniform thickness, which cannot be done by the extrusion process without rings wherein the flange thickness decreases with the distance from the workpiece axis;
- due to the use of rings for limiting a free radial flow of material in flange extrusion, three-axial compressive stresses occur in the flange during filling of the closed die cavity, which is desired in terms of cracking;
- flange cracking occurs in the plane of maximum shear stresses; this plane is oriented at an angle of ±45° relative to the direction of the maximum principal stress, this direction being similar to that of circumferential stresses; in the performed research, the crack always occur in the same direction;
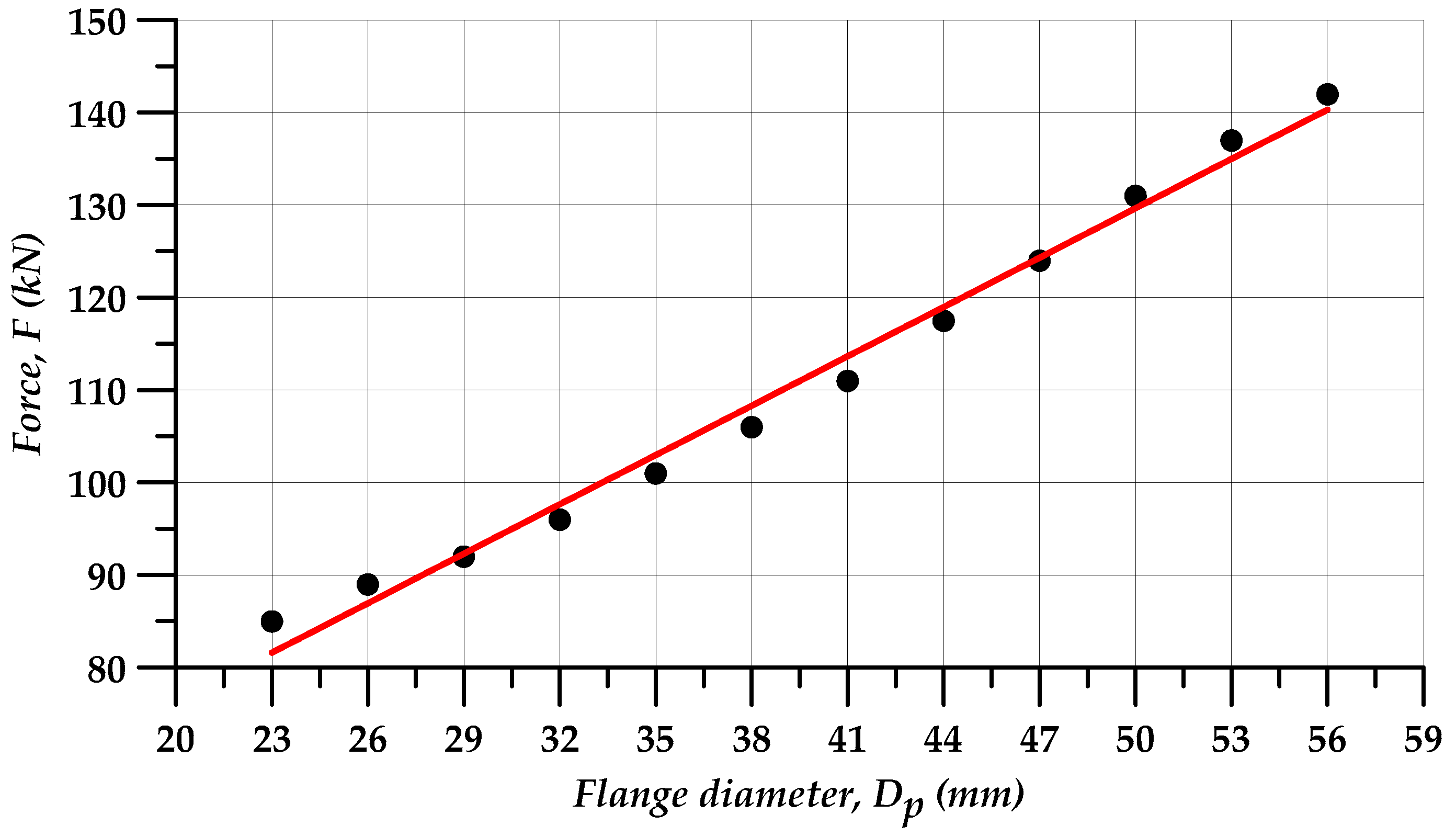
- the maximum forming forces increase almost linearly with increasing flange diameter.
Author Contributions
Funding
Conflicts of Interest
References
- Janicek, L.; Petruska, J.; Maros, B.; Rusz, S. Cold forming of bolts without thermal treatment. J. Mater. Process. Tech. 2002, 125–126, 341–346. [Google Scholar] [CrossRef]
- Aliiev, I.; Aliieva, L.; Grudkina, N.; Zhbankov, I. Prediction of the variation of the form in the processes of extrusion. Metall. Min. Ind. 2011, 3, 17–22. [Google Scholar]
- Schiemann, T.; Liewald, M.; Beiermeister, C.; Till, M. Influence of process chain on fold formation during flange upsetting of tubular cold forged parts. Procedia Eng. 2014, 81, 352–357. [Google Scholar] [CrossRef]
- Alves, L.M.; Afonso, R.M.; Silva, C.M.A.; Martins, P.A.F. Boss forming of annular flanges in thin-walled tubes. J. Mater. Process. Tech. 2017, 250, 182–189. [Google Scholar] [CrossRef]
- Winiarski, G.; Gontarz, A.; Dziubińska, A. The influence of tool geometry on the course of flanges radial extrusion in hollow parts. Arch. Civ. Mech. Eng. 2017, 17, 986–996. [Google Scholar] [CrossRef]
- Winiarski, G.; Gontarz, A.; Samołyk, G. Flange formation in aluminium alloy EN AW 6060 tubes by radial extrusion with the use of a limit ring. Arch. Civ. Mech. Eng. 2019, 19, 1020–1028. [Google Scholar] [CrossRef]
- Winiarski, G.; Gontarz, A. Numerical and experimental study of producing two-step flanges by extrusion with a movable sleeve. Arch. Metall. Mater. 2017, 62, 495–499. [Google Scholar] [CrossRef] [Green Version]
- Winiarski, G.; Bulzak, T.; Wojcik, Ł.; Szala, M. Effect of tool kinematics on tube flanging by extrusion with a moving sleeve. Adv. Sci. Technol. Res. J. 2019, 13, 210–216. [Google Scholar] [CrossRef]
- Winiarski, G.; Bulzak, T.; Wojcik, Ł.; Szala, M. Numerical analysis of a six stage forging process for producing hollow flanged parts from tubular blanks. Adv. Sci. Technol. Res. J. 2020, 14, 201–208. [Google Scholar] [CrossRef]
- Zhu, S.; Zhuang, X.; Xu, D.; Zhu, Y.; Zhao, Z. Flange forming at an arbitrary tube location through upsetting with a controllable deformation zone. J. Mater. Process. Tech. 2019, 273, 116230. [Google Scholar] [CrossRef]
- Wang, Z.G.; Dong, W.Z.; Yato, H. A new forming method of flange on a drawn cup by plate forging. Procedia Manuf. 2018, 15, 955–960. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, J.; Wang, Z.R. Numerical and experimental research of the cold upsetting-extruding of tube flanges. J. Mater. Process. Tech. 2001, 110, 28–35. [Google Scholar] [CrossRef]
- Hu, X.L.; Wang, H. Numerical simulation and experimental study on the multi-step upsetting of a thick and wide flange on the end of a pipe. J. Mater. Process. Tech. 2004, 151, 321–327. [Google Scholar] [CrossRef]
- Ortiz, M.; Penalva, M.L.; Puerto, M.J.; Homola, P.; Kafka, V. Hot single point incremental forming of Ti-6Al-4V alloy. Key Eng. Mater. 2014, 611–612, 1079–1087. [Google Scholar] [CrossRef]
- Ortiz, M.; Penalva, M.; Iriondo, E.; López de Lacalle, L.N. Accuracy and surface quality improvements in the manufacturing of Ti-6Al-4V parts using hot single point incremental forming. Metals 2019, 9, 697. [Google Scholar] [CrossRef] [Green Version]
- Ji, H.; Liu, J.; Wang, B.; Zheng, Z.; Huang, J.; Hu, Z. Cross-wedge rolling of a 4Cr9Si2 hollow valve: Explorative experiment and finite element simulation. Int. J. Adv. Manuf. Tech. 2015, 77, 15–26. [Google Scholar] [CrossRef]
- Yang, C.; Ma, J.; Hu, Z. Analysis and design of cross wedge rolling hollow axle sleeve with mandrel. J. Mater. Process. Tech. 2017, 239, 346–358. [Google Scholar] [CrossRef]
- Pater, Z.; Tomczak, J.; Bulzak, T. New forming possibilities in cross wedge rolling processes. Arch. Civ. Mech. Eng. 2018, 18, 149–161. [Google Scholar] [CrossRef]
- Murillo-Marrodan, A.; Garcia, E.; Cortes, F. A study of friction model performance in a skew rolling process numerical simulation. Int. J. Simul. Model. 2018, 17, 569–582. [Google Scholar] [CrossRef]
- Murillo-Marrodan, A.; Garcia, E.; Barco, J.; Cortes, F. Analysis of wall thickness eccentricity in the rotary tube piercing process using a strain correlated FE model. Metals 2020, 10, 1045. [Google Scholar] [CrossRef]
- Tomczak, J.; Bulzak, T.; Pater, Z. A method for producing hollow shafts by rotary compression using a specially designed forging machine. Arch. Metall. Mater. 2015, 60, 1745–1753. [Google Scholar] [CrossRef]
- Tomczak, J.; Bulzak, T.; Pater, Z. The effect of billet wall thickness on the rotary compression process for hollow parts. Stroj. Vestn.-J. Mech. E 2015, 61, 149–156. [Google Scholar] [CrossRef] [Green Version]
- Tomczak, J.; Pater, Z.; Bulzak, T. The influence of hollow billet thickness in rotary compression. Int. J. Adv. Manuf. Tech. 2016, 82, 1281–1291. [Google Scholar] [CrossRef] [Green Version]
- Pater, Z.; Tomczak, J.; Bulzak, T. Experimental study of rotary compression for hollow parts. Metalurgija 2015, 54, 419–422. [Google Scholar]
- Tomczak, J.; Pater, Z.; Bulzak, T. A theoretical and experimental analysis of rotary compression of hollow forgings formed over a mandrel. Strength Mater. 2017, 49, 555–564. [Google Scholar] [CrossRef]
- Tomczak, J.; Bulzak, T.; Pater, Z. Theoretical and experimental analysis of rotary compression of ball pins hollow forgings. Adv. Sci. Technol. Res. J. 2016, 10, 109–117. [Google Scholar] [CrossRef]
- Tomczak, J. Rotary compression process for producing toothed hollow shafts. Metalurgija 2014, 53, 649–652. [Google Scholar]
- Tomczak, J.; Pater, Z.; Bulzak, T. Forming of hollow shaft forging from titanium alloy Ti6Al4V by means of rotary compression. Arch. Metall. Mater. 2015, 60, 419–425. [Google Scholar] [CrossRef]
- Rosa, P.A.R.; Rodrigues, J.M.C.; Martins, P.A.F. External inversion of thin-walled tubes using a die: Experimental and theoretical investigation. Int. J. Mach. Tool Manuf. 2003, 43, 787–796. [Google Scholar] [CrossRef]
- Rosa, P.A.; Rodrigues, J.M.C.; Martins, P.A.F. Internal inversion of thin-walled tubes using a die: Experimental and theoretical investigation. Int. J. Mach. Tools Manuf. 2004, 44, 775–784. [Google Scholar] [CrossRef]
- Niknejad, A.; Moeinifard, M. Theoretical and experimental studies of the external inversion process in the circular metal tubes. Mater. Des. 2012, 40, 324–330. [Google Scholar] [CrossRef]
- Qiu, X.M.; He, L.H.; Gu, J.; Yu, X.H. An improved theoretical model of a metal tube under free external inversion. Thin-Walled Struct. 2014, 80, 32–37. [Google Scholar] [CrossRef]
- Mohamed, F.A.; El-Abden, S.Z.; Abdel-Rahman, M. A rotary flange forming process on the lathe using a ball-shaped tool. J. Mater. Process. Tech. 2005, 170, 501–508. [Google Scholar] [CrossRef]
- Kadkhodayan, M.; Erfani-Moghadam, A. An investigation of the optimal load paths for the hydroforming of T-shaped tubes. Int. J. Adv. Manuf. Tech. 2012, 61, 73–85. [Google Scholar] [CrossRef]
- Kim, C.; Yang, S.H.; Kim, Y.S. Analysis of forming limit in tube hydroforming. J. Mech. Sci. Technol. 2013, 27, 3817–3823. [Google Scholar] [CrossRef]
- Alzahrani, B.; Ngaile, G. Analytical and numerical modeling of thick tube hydroforging. Procedia Eng. 2014, 81, 2223–2229. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Hu, G.; Liu, J. Investigation of forming limit diagram for tube hydroforming considering effect of changing strain path. Int. J. Adv. Manuf. Technol. 2015, 79, 793–803. [Google Scholar] [CrossRef]
- Xu, Y.; Ma, Y.; Zhang, S.; Chen, D.; Zhang, X.; Li, J.; Zhao, C. Numerical and experimental study on large deformation of thin-walled tube through hydroforging process. Int. J. Adv. Manuf. Technol. 2016, 87, 1885–1890. [Google Scholar] [CrossRef]
- Samołyk, G.; Winiarski, G.; Gontarz, A. A cold forging process for producing thin-walled hollow balls from tube using a plastic insert. Int. J. Adv. Manuf. Technol. 2020, 108, 1429–1446. [Google Scholar] [CrossRef]
- Zhang, Q.; Jin, K.; Mu, D.; Ma, P.; Tian, J. Rotary swaging forming process of tube workpieces. Procedia Eng. 2014, 81, 2336–2341. [Google Scholar] [CrossRef] [Green Version]
- Şchiopu, V.; Luca, D. A new net-shape plating technology for axisymmetric metallic parts using rotary swaging. Int. J. Adv. Manuf. Technol. 2016, 85, 2471–2482. [Google Scholar] [CrossRef]


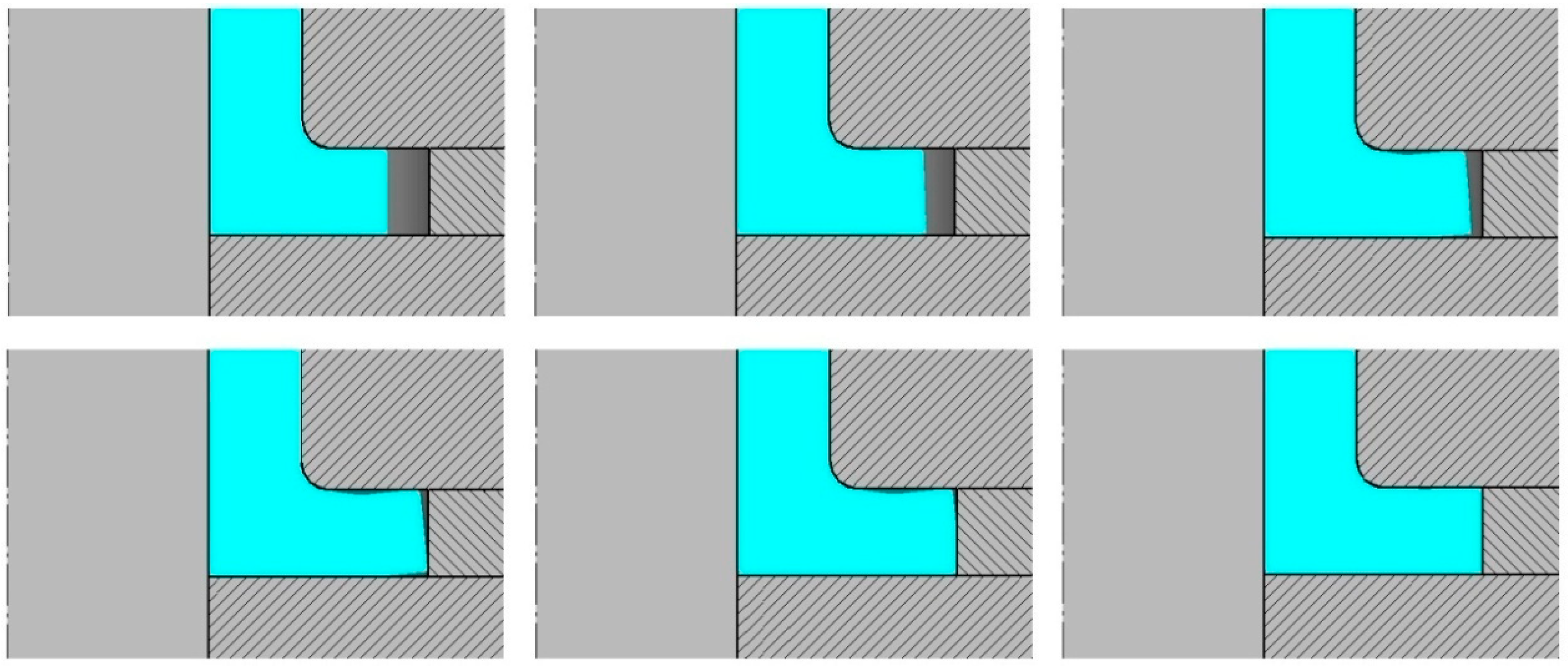



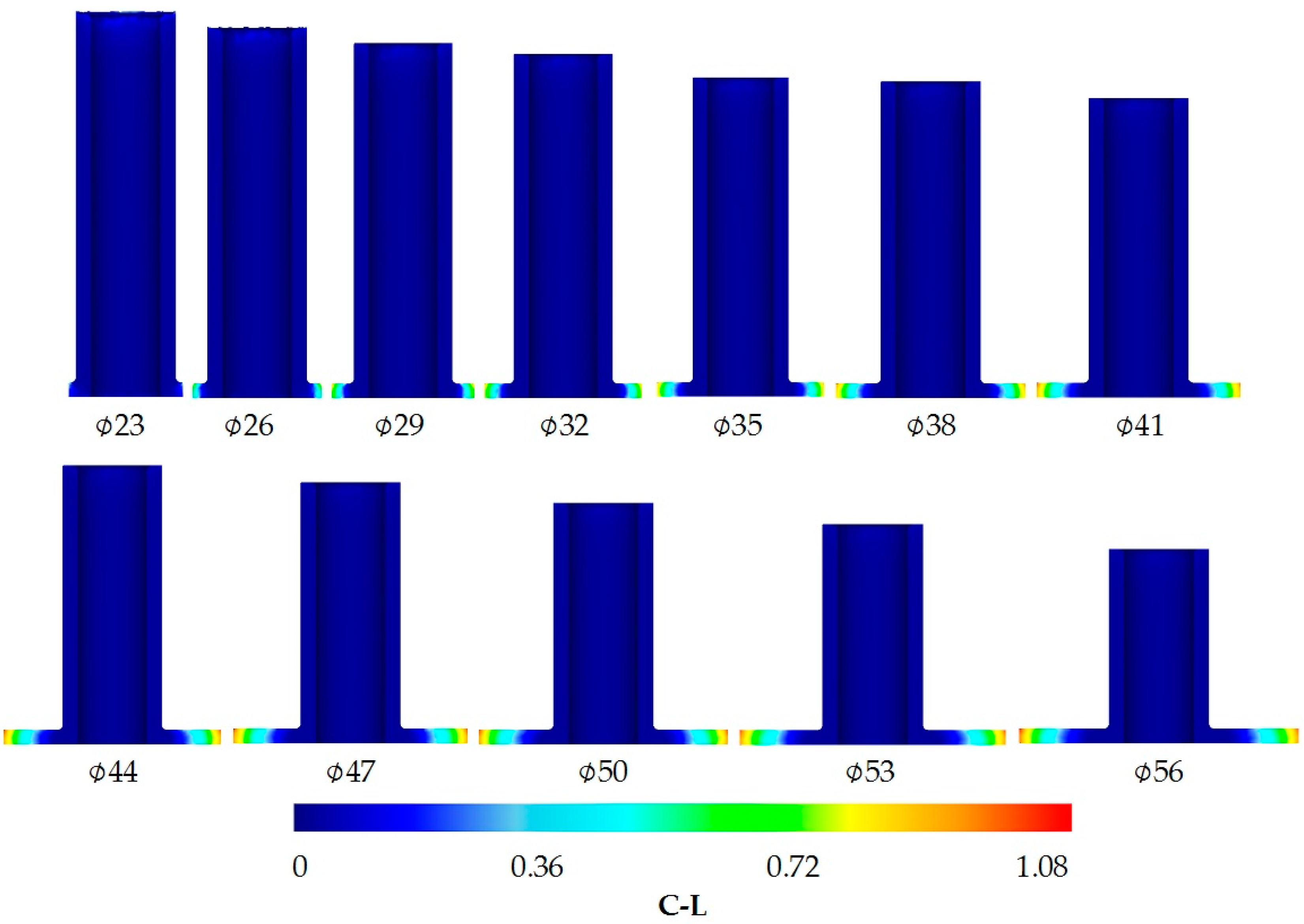


| D (mm) | g (mm) | l (mm) | R (mm) | h (mm) | Dpi (mm) | Dz (mm) |
|---|---|---|---|---|---|---|
| 20 | 3 | 80 | 1 | 3 | 23, 26, 29, 32, 35, 38, 41, 44, 47, 50, 53, 56 | 70 |
| σx (MPa) | σy (MPa) | σz (MPa) | τxy (MPa) | τxz (MPa) | τyz (MPa) | σ1 (MPa) | σ2 (MPa) | σ3 (MPa) |
| 171.60 | −4.74 | 10.51 | −7.71 | 0.25 | 2.74 | 171.93 | 10.98 | −5.54 |
| α1 (°) | β1 (°) | γ1 (°) | α2 (°) | β2 (°) | γ2 (°) | α3 (°) | β3 (°) | γ3 (°) |
| 2.49 | 92.49 | 89.95 | 89.62 | 80.29 | 9.71 | 92.47 | 169.97 | 80.28 |
| Measurement No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Dpi (mm) | 23 | 26 | 29 | 32 | 35 | 38 | 41 | 44 | 47 | 50 | 53 | 56 |
| Fi (kN) | 85 | 89 | 92 | 96 | 101 | 106 | 111 | 117.5 | 124 | 131 | 137 | 142 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winiarski, G.; Gontarz, A.; Samołyk, G. Theoretical and Experimental Analysis of a New Process for Forming Flanges on Hollow Parts. Materials 2020, 13, 4088. https://doi.org/10.3390/ma13184088
Winiarski G, Gontarz A, Samołyk G. Theoretical and Experimental Analysis of a New Process for Forming Flanges on Hollow Parts. Materials. 2020; 13(18):4088. https://doi.org/10.3390/ma13184088
Chicago/Turabian StyleWiniarski, Grzegorz, Andrzej Gontarz, and Grzegorz Samołyk. 2020. "Theoretical and Experimental Analysis of a New Process for Forming Flanges on Hollow Parts" Materials 13, no. 18: 4088. https://doi.org/10.3390/ma13184088






