Structure, Magnetocaloric Effect and Critical Behavior of the Fe60Co12Gd4Mo3B21 Amorphous Ribbons
Abstract
:1. Introduction
2. Materials and Methods
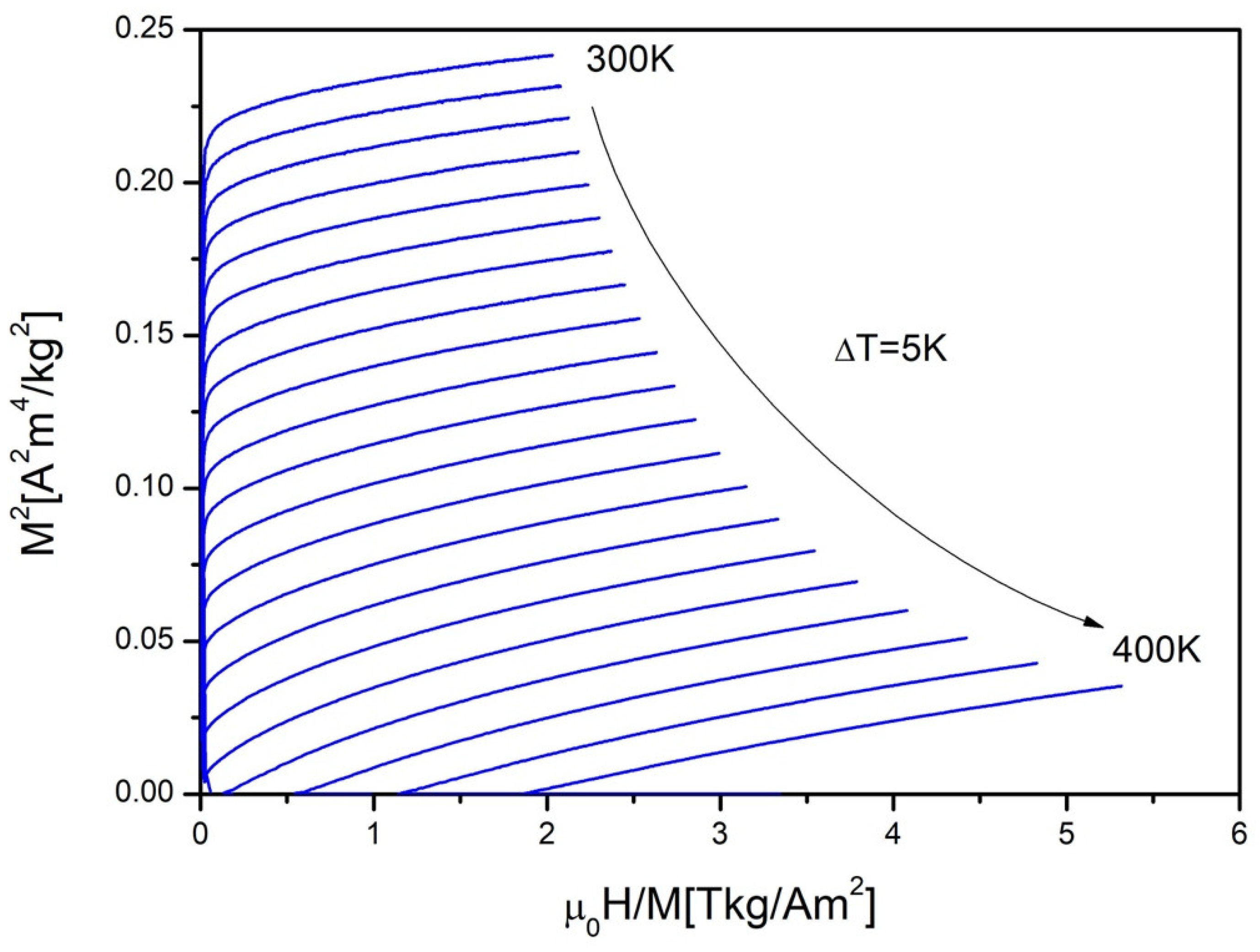
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, F.; Inoue, A.; Han, Y.; Zhu, S.L.; Kong, F.L.; Zanaeva, E.; Liu, G.D.; Shalaan, E.; Al-Marzouki, F.; Obaid, A. Soft magnetic Fe-Co-based amorphous alloys with extremely high saturation magnetization exceeding 1.9 T and low coercivity of 2 A /m. J. Alloys Compd. 2017, 723, 376–384. [Google Scholar] [CrossRef]
- Herzer, G. Modern soft magnets: Amorphous and nanocrystalline materials. Acta Mater. 2013, 61, 718–734. [Google Scholar] [CrossRef]
- McHenry, M.E.; Willard, M.A.; Laughlin, D.E. Amorphous and nanocrystalline materials for applications as soft magnets. Prog. Mater. Sci. 1999, 44, 291–433. [Google Scholar] [CrossRef]
- Panahi, S.L.; Ramasamy, P.; Masdeu, F.; Stoica, M.; Torrens-Serra, J.; Bruna, P. Ewaluation of the effect of minor additions in the crystallization path of [(Fe0.5Co0.5)0.75B0.2Si0.05]100−xMx metallic glasses by means of Mössbauer spectroscopy. Metals 2021, 11, 1293. [Google Scholar] [CrossRef]
- Kupczyk, A.; JŚwierczek, J.; Hasiak, M.; Prusik, K.; Zbroszczyk, J.; Gębara, P. Microstructure and some thermomagnetic properties of amorphous Fe-(Co)-Mn-Mo-B alloys. J. Alloys Compd. 2018, 735, 253–260. [Google Scholar] [CrossRef]
- O’Handley, R.C. Physics of ferromagnetic amorphous alloys. J. Appl. Phys. 1987, 62, R15–R49. [Google Scholar] [CrossRef]
- Zhang, Y. Review of the structural, magnetic and magnetocaloric properties in ternary rare earth RE2T2X type intermetallic compounds. J. Alloys Compd. 2019, 787, 1173–1186. [Google Scholar] [CrossRef]
- Li, L.; Yan, M. Recent progresses in exploring the rare earth based intermetallic compounds for cryogenic magnetic refrigeration. J. Alloys Compd. 2020, 823, 153810. [Google Scholar] [CrossRef]
- Law, J.; Ramanujan, R.V.; Franco, V. Tunable Curie temperatures in Gd alloyed Fe–B–Cr magnetocaloric materials. J. Alloys Compd. 2010, 508, 14–19. [Google Scholar] [CrossRef]
- Brand, R.A. Improving the validity of hyperfine field distributions from magnetic alloys. Nucl. Instrum. Methods Phys. Res. B 1987, 28, 398–416. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A. Magnetocaloric effect and magnetic refrigeration. J. Magn. Magn. Mater. 1999, 200, 44–56. [Google Scholar] [CrossRef]
- Świerczek, J. Medium range ordering and some magnetic properties of amorphous Fe90Zr7B3 alloy. J. Magn. Magn. Mater. 2010, 322, 2696–2702. [Google Scholar] [CrossRef]
- Świerczek, J.; Kupczyk, A.; Hasiak, M. Flattening of isothermal magnetic entropy change versus temperature curve in amorphous Fe–Mn–Mo–B ribbons. J. Alloys Compd. 2019, 808, 151496. [Google Scholar] [CrossRef]
- Świerczek, J.; Kupczyk, A.; Hasiak, M. Structure and some magnetic properties of amorphous and partially crystallized Fe-(Co)-Mn-Mo-B alloys. J. Magn. Magn. Mater. 2020, 499, 166269. [Google Scholar] [CrossRef]
- Banerjee, S.K. On a generalized approach to first and second order magnetic transition. Phys. Lett. 1964, 12, 16–17. [Google Scholar] [CrossRef]
- Franco, V.; Blasquez, J.S.; Conde, A. Field dependence of the magnetocaloric effect in materials with a second order phase transition: A master curve for the magnetic entropy change. Appl. Phys. Lett. 2006, 89, 222512. [Google Scholar] [CrossRef]
- Świerczek, J. Superparamagnetic behavior and magnetic entropy change in partially crystallized Fe-Mo-Cu-B. Phys. Status Solidi A 2014, 211, 1567–1576. [Google Scholar] [CrossRef]
- Gębara, P.; Hasiak, M. Determination of Phase Transition and Critical Behavior of the As-Cast GdGeSi-(X) Type Alloys (Where X = Ni, Nd and Pr). Materials 2021, 14, 185. [Google Scholar] [CrossRef]
- Fisher, M.E. The theory of equilibrium critical phenomena. Rep. Prog. Phys. 1967, 30, 615. [Google Scholar] [CrossRef]
- Widom, B. Equation of State in the Neighborhood of the Critical Point. J. Chem. Phys. 1965, 43, 3898–3905. [Google Scholar] [CrossRef]
- Gębara, P.; Hasiak, M. Investigation of critical behavior in the vicinity of ferromagnetic to paramagnetic phase transition in the Fe75Mo8Cu1B16 alloy. J. Appl. Phys. 2018, 124, 083904. [Google Scholar] [CrossRef]


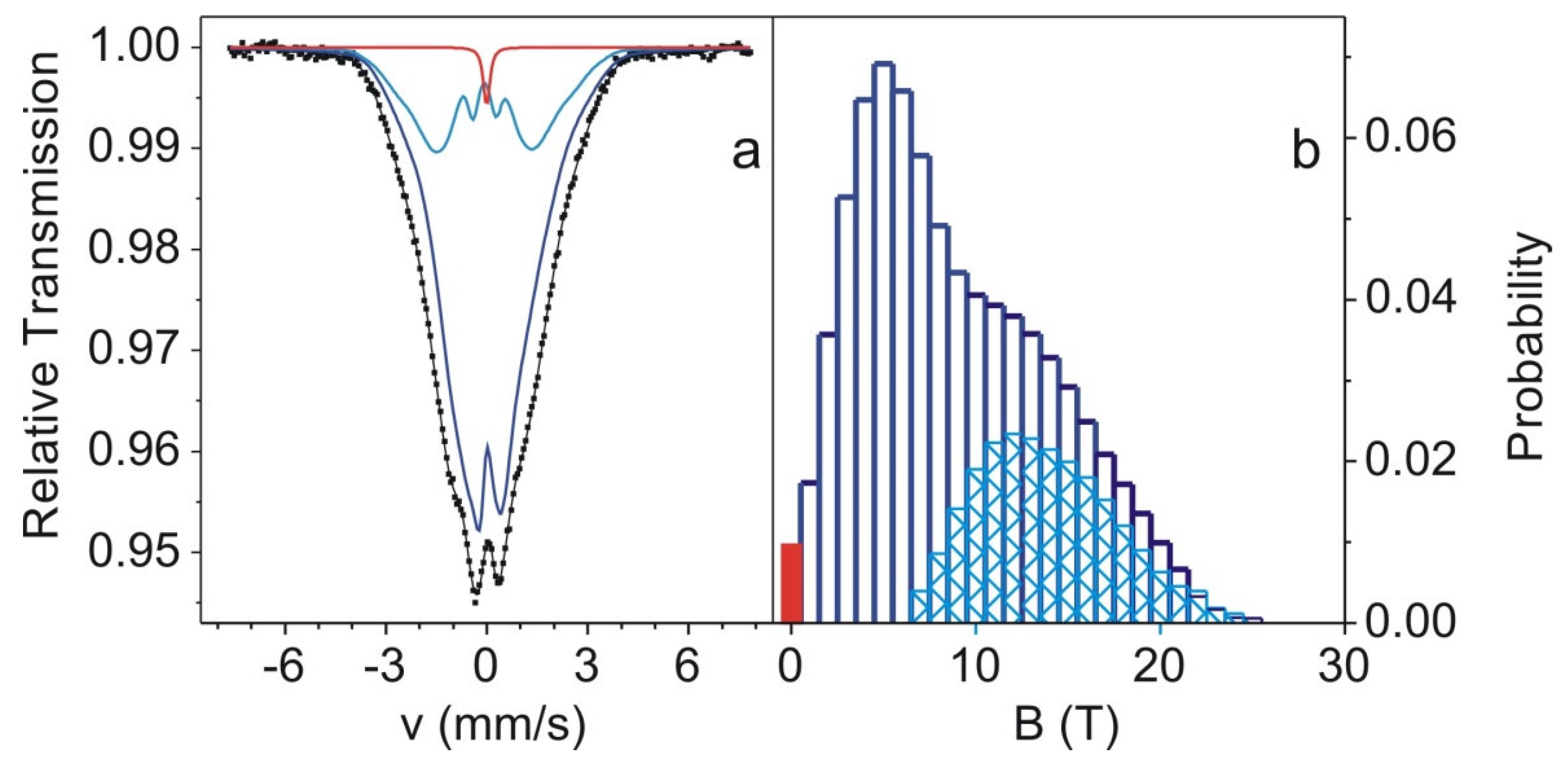



| Fe60Co12Gd4Mo3B21 | |
|---|---|
| Amorphous | |
| I1 | 0.95 |
| (A2;5)1 | 3.0(1) |
| <Bhf>1 [T] | 9.66(7) |
| Δ(Bhf)1 [T] | 5.30(5) |
| (IS0)1 [mm/s] | −0.036(7) |
| a1 [mm/s−1T−1] | 0.0019(6) |
| <Bhf>2 [T] | 15.4(5) |
| Δ(Bhf)2 [T] | 3.1(5) |
| (IS0)2 [mm/s] | 0.32(8) |
| a2 [mm/s−1T−1] | −0.016(9) |
| <Bhf> [T] | 9.97(3) |
| Crystalline | |
| IC1 | 0.01 |
| QS1 [mm/s] | 0.07(2) |
| IS1 [mm/s] | 0.017(7) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łukiewska, A.; Gębara, P. Structure, Magnetocaloric Effect and Critical Behavior of the Fe60Co12Gd4Mo3B21 Amorphous Ribbons. Materials 2022, 15, 34. https://doi.org/10.3390/ma15010034
Łukiewska A, Gębara P. Structure, Magnetocaloric Effect and Critical Behavior of the Fe60Co12Gd4Mo3B21 Amorphous Ribbons. Materials. 2022; 15(1):34. https://doi.org/10.3390/ma15010034
Chicago/Turabian StyleŁukiewska, Agnieszka, and Piotr Gębara. 2022. "Structure, Magnetocaloric Effect and Critical Behavior of the Fe60Co12Gd4Mo3B21 Amorphous Ribbons" Materials 15, no. 1: 34. https://doi.org/10.3390/ma15010034






