Mechanical Properties and Acoustic Emission Characteristics of Anchored Structure Plane with Different JRC under Direct Shear Test
Abstract
:1. Introduction
2. Experiment
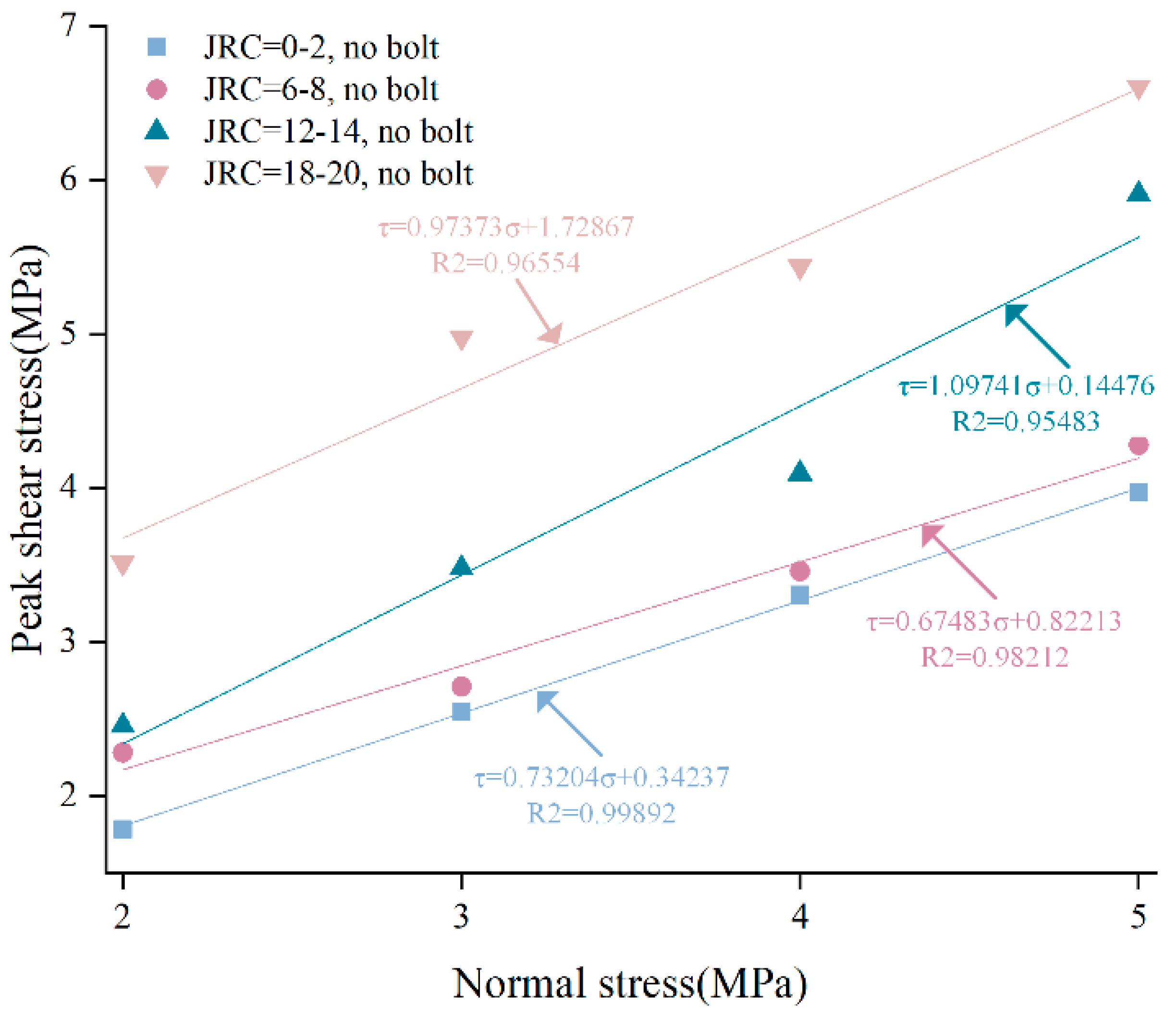
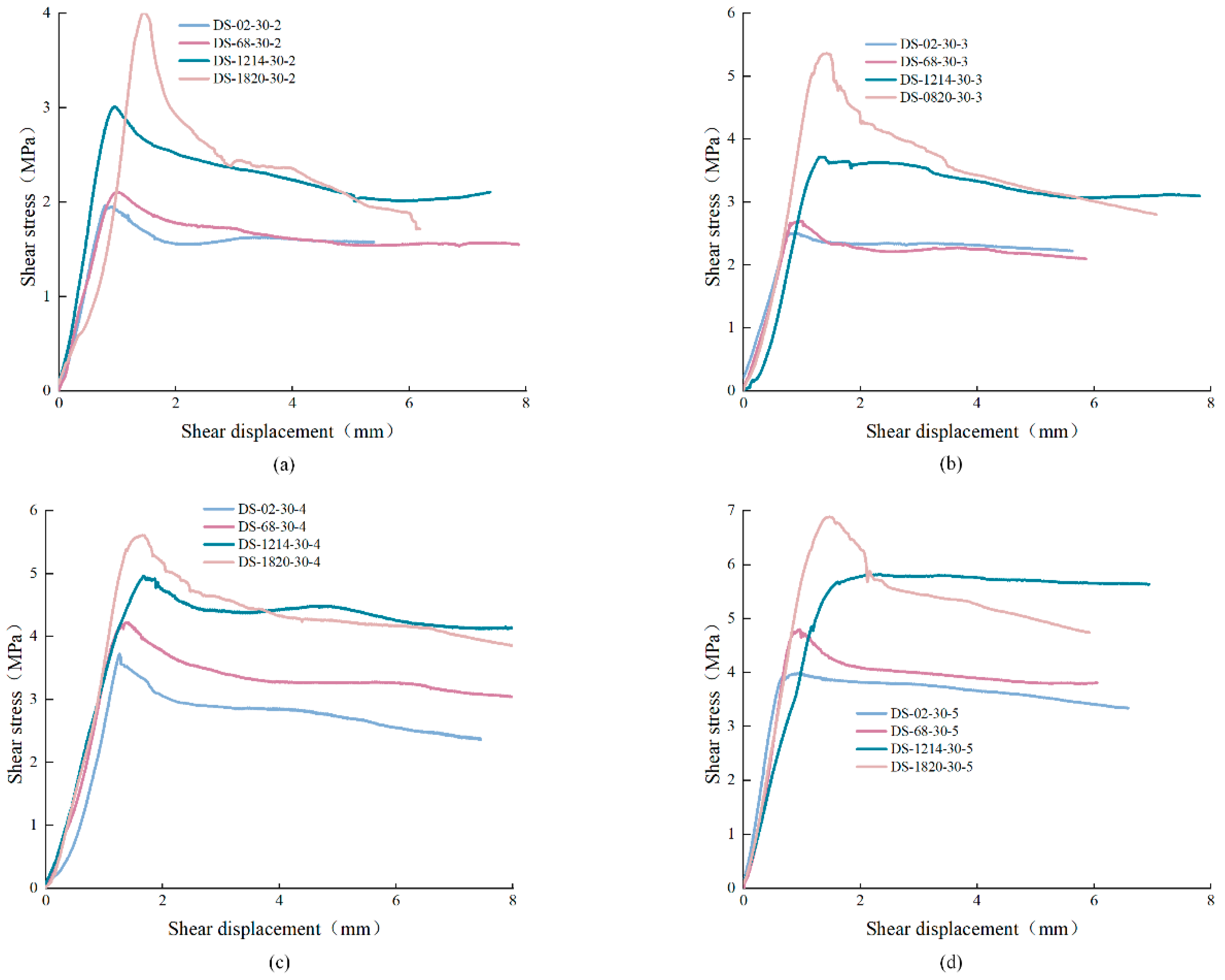
3. Mechanical Properties
4. AE Characteristics
4.1. Ring-Down Count
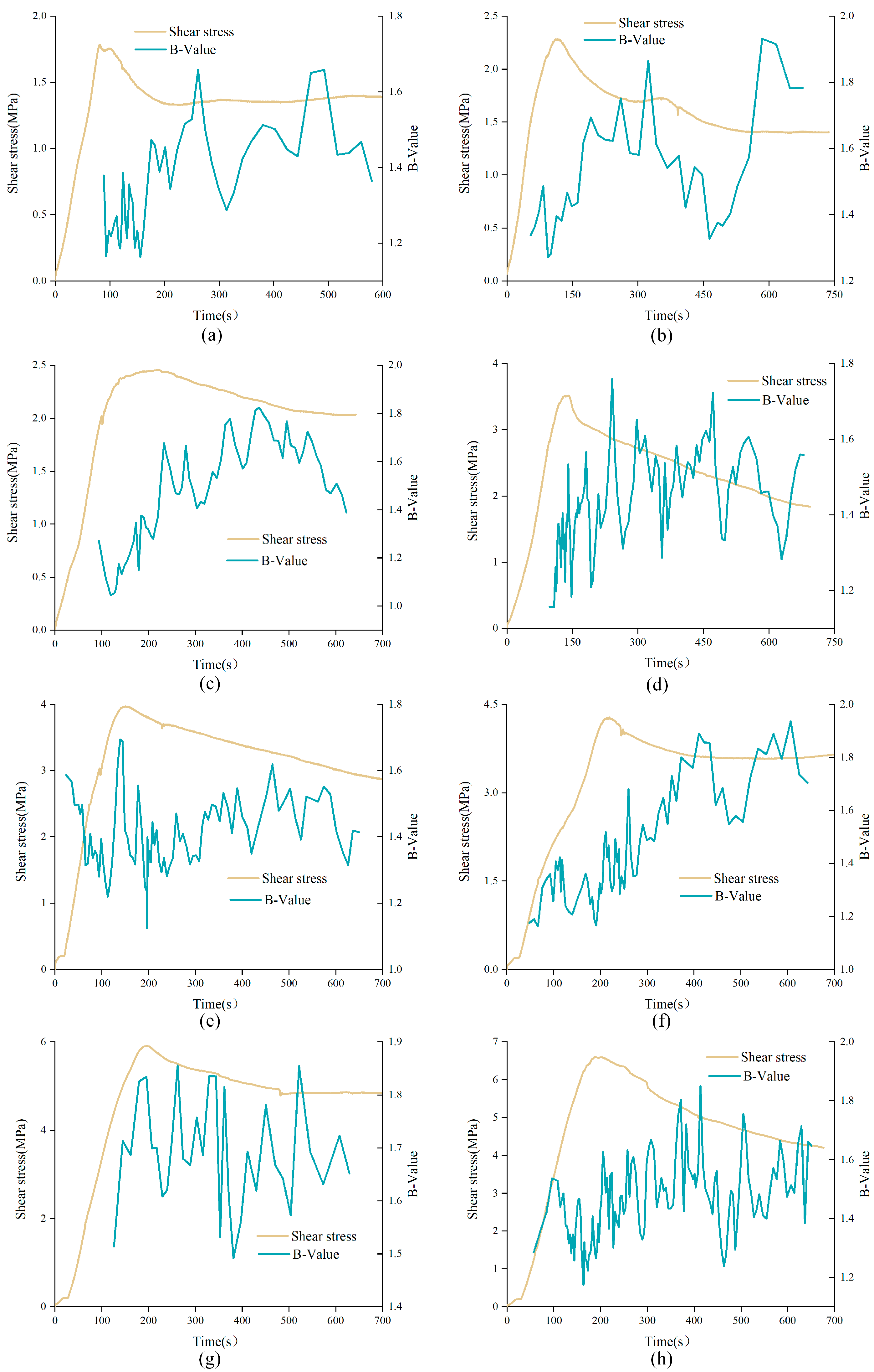
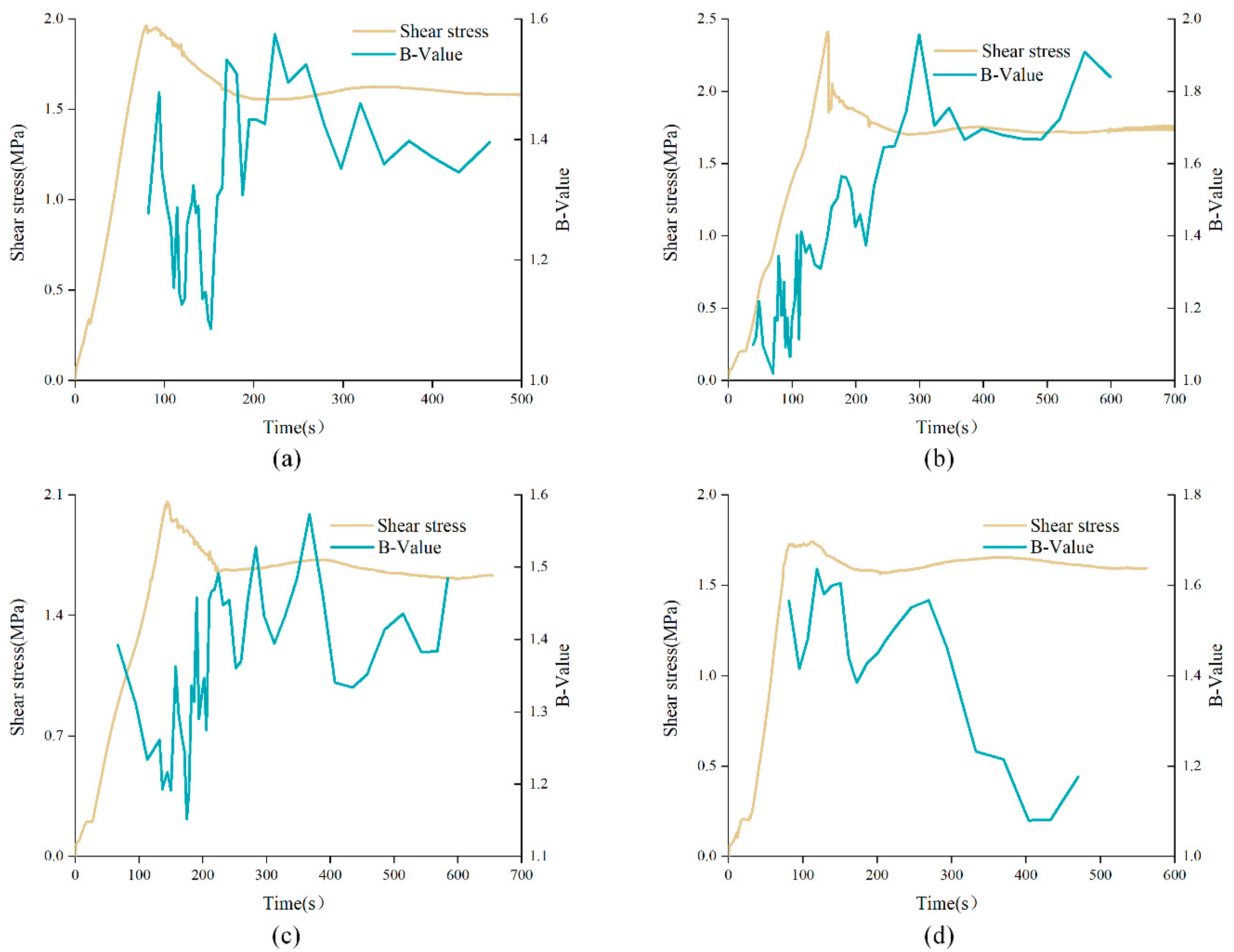
4.2. B-value
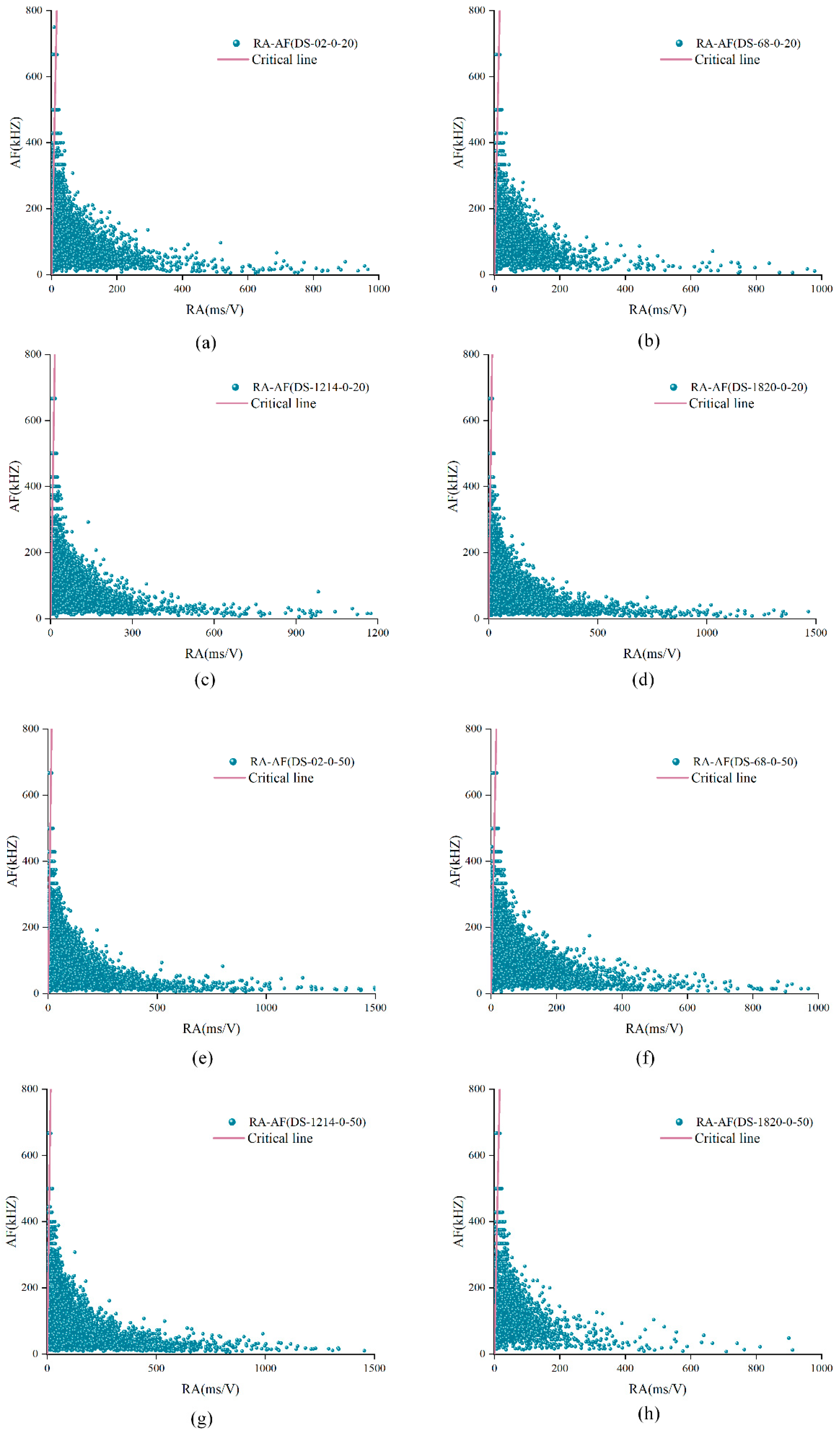
4.3. Analysis of RA-AF
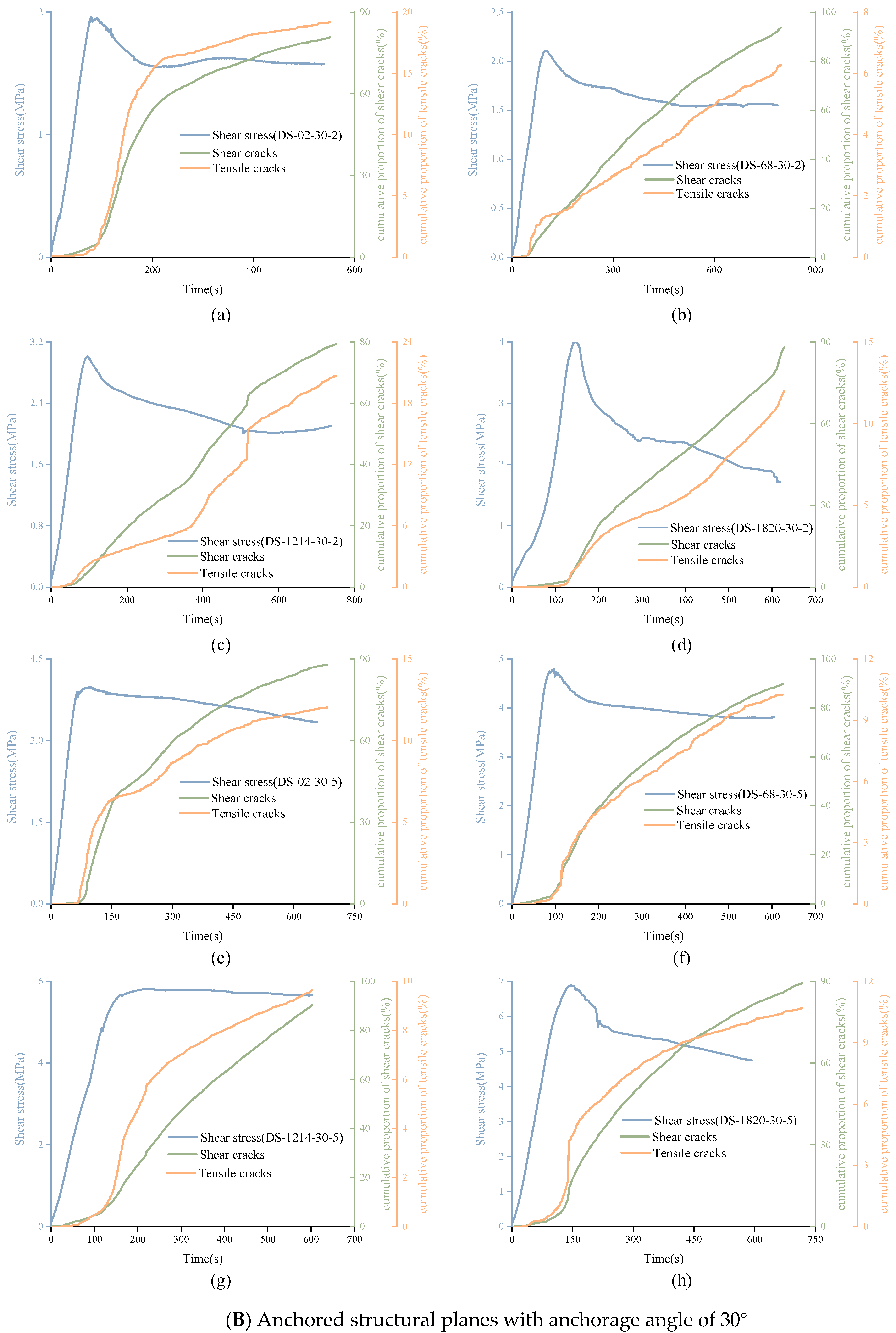
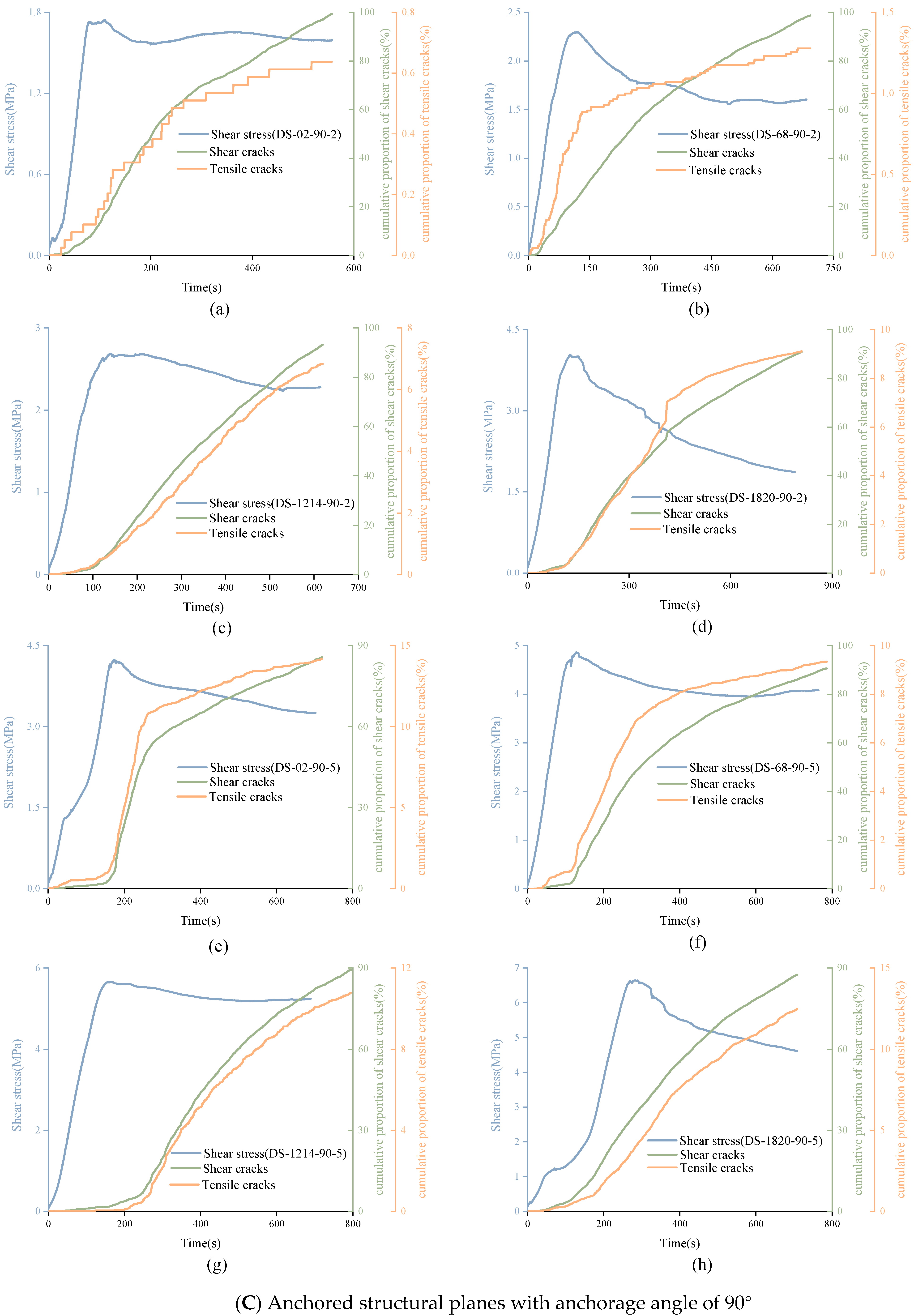
4.3.1. Variation of Cumulative Proportion of Shear-Tensile Cracks
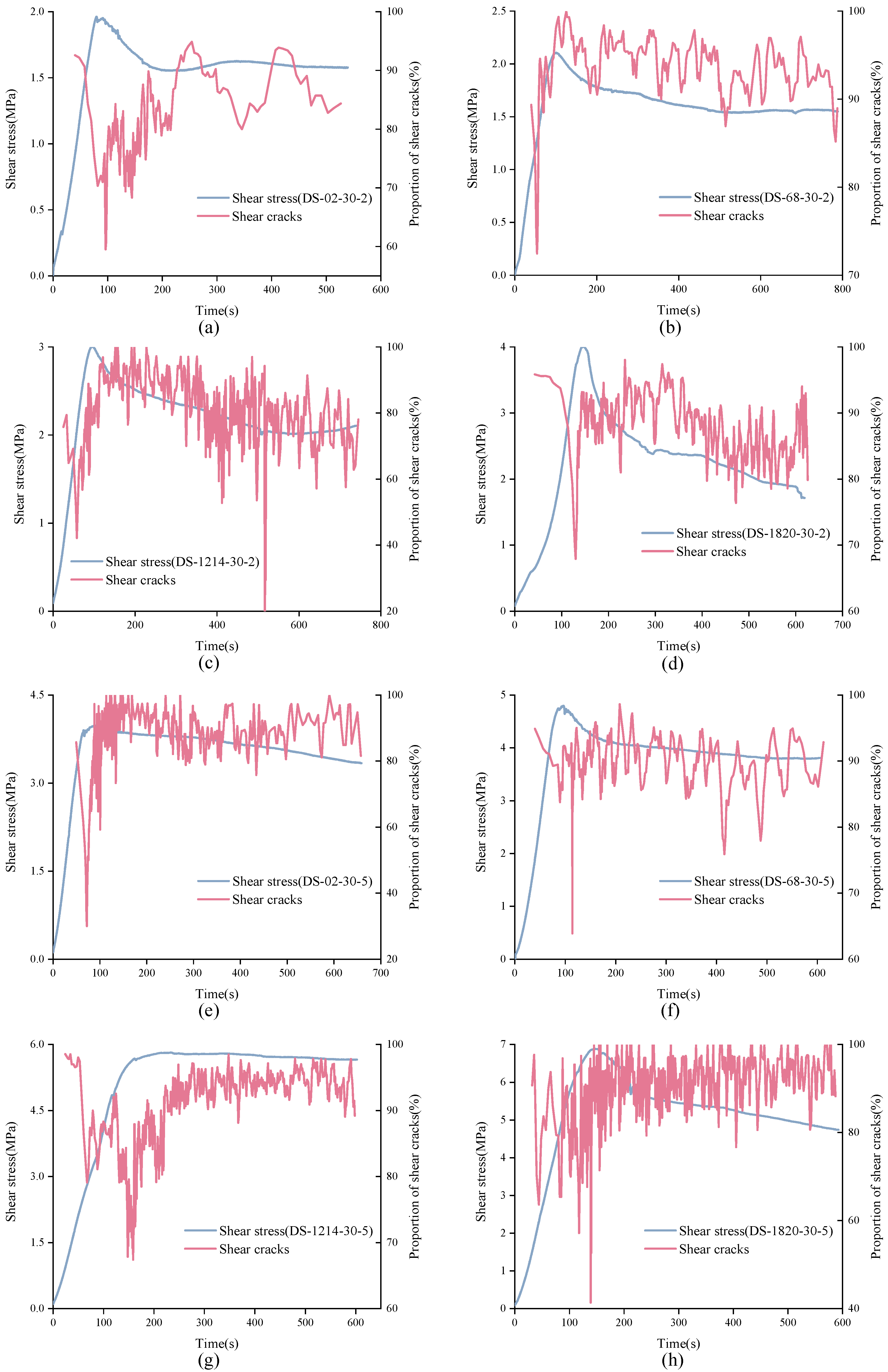
4.3.2. Variation of Real-Time Proportion of Shear Cracks
5. Conclusions
- (1)
- The larger the normal stress, the larger the peak shear strength of the anchored structural plane. Under the same normal stress, compared with the peak shear strength, the residual strength of structural planes with JRC of 6–8 and 18–20 decreased more, and that of structural planes with JRC of 0–2 and 12–14 decreased less. The peak shear strength of the anchored structural plane increased and then decreased with the variation of anchorage angle, and always reached the maximum value at 45° or 60°, which means the optimal installation angle of the bolt is in the range of [45°, 60°].
- (2)
- According to the AE monitoring results, the ring-down count rises first, then decreases and finally flattens, showing an obvious correlation with the shear stress curve. The ring-down count still kept a certain degree in the residual stage, which was about 60. The cumulative ring-down count curve was characterized by three-stage and the increase of normal stress accelerated the curve entering the rapid growth stage. The b-value curve was dense at the initial loading stage and tended to be sparse in the residual stage. Its variation trend mainly depended on the topography of structural plane, not only affected by the value of JRC. The influence of anchorage angle on b-value variation characteristics mainly depended on whether the bolt would be deformed during shearing.
- (3)
- Through AE experiments, the cumulative ratio of shear cracks could reach 85%, which is much higher than that of tensile cracks. The cumulative proportion curve of tensile cracks showed a three-stage pattern and the correlation with the shear stress curve was more significant. Besides, the higher the normal stress, the easier the signal cumulative proportion curve appearing in three-stage form. The proportion of shear cracks and tensile cracks in the experiment changed dynamically. For unanchored structural planes, the proportion of shear cracks was more than 50% in the whole experiment. For anchored structural planes, the proportion of tensile cracks may exceed that of shear cracks, sometimes even up to 80%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, S.J.; Lin, H.; Chen, Y.F.; Wang, Y.X. A new nonlinear empirical strength criterion for rocks under conventional triaxial compression. J. Cent. South Univ. 2021, 28, 1448–1458. [Google Scholar] [CrossRef]
- Yang, H.; Lin, H.; Chen, Y.; Wang, Y.; Zhao, Y.; Yong, W.; Gao, F. Influence of wing crack propagation on the failure process and strength of fractured specimens. Bull. Eng. Geol. Environ. 2022, 81, 1–19. [Google Scholar] [CrossRef]
- Asadizadeh, M.; Moosavi, M.; Hossaini, M.F. Investigation of mechanical behaviour of non-persistent jointed blocks under uniaxial compression. Geomech. Eng. 2018, 14, 29–42. [Google Scholar]
- Zhao, Y.; Zhang, C.; Wang, Y.; Lin, H. Shear-related roughness classification and strength model of natural rock joint based on fuzzy comprehensive evaluation. Int. J. Rock Mech. Min. Sci. 2021, 137, 104550. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Q.; Zhang, C.; Liao, J.; Lin, H.; Wang, Y. Coupled seepage-damage effect in fractured rock masses: Model development and a case study. Int. J. Rock Mech. Min. Sci. 2021, 144, 104822. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Y.; Yang, Y.; Sun, Q.; Luo, T.; Zhang, H. Influence of surface roughness and hydrophilicity on bonding strength of concrete-rock interface. Constr. Build. Mater. 2019, 213, 156–166. [Google Scholar] [CrossRef]
- Lei, D.; Lin, H.; Wang, Y. Damage characteristics of shear strength of joints under freeze–Thaw cycles. Arch. Appl. Mech. 2022, 92, 1615–1631. [Google Scholar] [CrossRef]
- Du, S.G.; Lin, H.; Yong, R.; Liu, G.J. Characterization of Joint Roughness Heterogeneity and Its Application in Representative Sample Investigations. Rock Mech. Rock Eng. 2022, 55, 1–25. [Google Scholar] [CrossRef]
- Asadizadeha, M.; Hossainia, M.F.; Moosavia, M.; Mohammadia, S. A laboratory study on mix design to properly resemble a brittle jointed rock. Int. J. Min. Geo-Eng. 2016, 50, 201–210. [Google Scholar]
- Uotinen, L.; Torkan, M.; Baghbanan, A.; Hernández, E.C.; Rinne, M. Photogrammetric Prediction of Rock Fracture Properties and Validation with Metric Shear Tests. Geosciences 2021, 11, 293. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, H.; Xie, S.; Ding, X.; He, D.; Yong, W.; Gao, F. Effect of joint microcharacteristics on macroshear behavior of single-bolted rock joints by the numerical modelling with PFC. Environ. Earth Sci. 2022, 81, 276. [Google Scholar] [CrossRef]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. Rock Eng. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Abolfazli, M.; Fahimifar, A. An investigation on the correlation between the joint roughness coefficient (JRC) and joint roughness parameters. Constr. Build. Mater. 2020, 259, 120415. [Google Scholar] [CrossRef]
- Tang, Z.C.; Zhang, Z.F.; Zuo, C.Q.; Jiao, Y.Y. Peak shear strength criterion for mismatched rock joints: Revisiting JRC-JMC criterion. Int. J. Rock Mech. Min. Sci. 2021, 147, 104894. [Google Scholar] [CrossRef]
- Xie, S.; Lin, H.; Cheng, C.; Chen, Y.; Wang, Y.; Zhao, Y.; Yong, W. Shear strength model of joints based on Gaussian smoothing method and macro-micro roughness. Comput. Geotech. 2022, 143, 104605. [Google Scholar] [CrossRef]
- Tang, W.; Lin, H.; Chen, Y.; Feng, J.; Hu, H. Mechanical Characteristics and Acoustic Emission Characteristics of Mortar-Rock Binary Medium. Buildings 2022, 12, 665. [Google Scholar] [CrossRef]
- Li, Y.; Tannant, D.D.; Pang, J.; Su, G. Experimental and analytical investigation of the shear resistance of a rock joint held by a fully-grouted bolt and subject to large deformations. Transp. Geotech. 2021, 31, 100671. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, L.; Zhu, L.; Fan, B.; Dong, M.; Sun, Z.; An, C. Analytical model of the shear behaviors of bolted rough joints based on the dilation effect and surface abrasion. Eng. Geol. 2021, 294, 106399. [Google Scholar] [CrossRef]
- Meng, B.; Jing, H.; Yang, S.; Cui, T.; Li, B. Experimental Study on Shear Behavior of Bolted Cement Mortar Blocks under Constant Normal Stiffness. KSCE J. Civ. Eng. 2019, 23, 3724–3734. [Google Scholar] [CrossRef]
- Fan, X.; Yang, Z.; Li, K. Effects of the lining structure on mechanical and fracturing behaviors of four-arc shaped tunnels in a jointed rock mass under uniaxial compression. Theor. Appl. Fract. Mech. 2021, 112, 102887. [Google Scholar] [CrossRef]
- Fan, X.; Yu, H.; Deng, Z.; He, Z.; Zhao, Y. Cracking and deformation of cuboidal sandstone with a single nonpenetrating flaw under uniaxial compression. Theor. Appl. Fract. Mech. 2022, 119, 103284. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, H.; Zhao, Y.; Liu, Q.; Luo, S. Numerical Analysis of the Mud Inflow Model of Fractured Rock Mass Based on Particle Flow. Geofluids 2021, 2021, 5599748. [Google Scholar] [CrossRef]
- Jalalifar, H.; Aziz, N.; Hadi, M. The effect of surface profile, rock strength and pretension load on bending behaviour of fully grouted bolts. Geotech. Geol. Eng. 2006, 24, 1203–1227. [Google Scholar] [CrossRef]
- Li, X.; Yang, G.; Nemcik, J.; Mirzaghorbanali, A.; Aziz, N. Numerical investigation of the shear behaviour of a cable bolt in single shear test. Tunn. Undergr. Space Technol. 2019, 84, 227–236. [Google Scholar] [CrossRef]
- Chen, Y.; Li, C.C. Performance of fully encapsulated rebar bolts and D-Bolts under combined pull-and-shear loading, Tunn. Undergr. Space Technol. 2015, 45, 99–106. [Google Scholar]
- Liu, C.H.; Li, Y.Z. Analytical Study of the Mechanical Behavior of Fully Grouted Bolts in Bedding Rock Slopes. Rock Mech. Rock Eng. 2017, 50, 2413–2423. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, Y.; Li, B. Influence of Joint Roughness on the Shear Behaviour of Fully Encapsulated Rock Bolt. Rock Mech. Rock Eng. 2017, 51, 953–959. [Google Scholar] [CrossRef]
- Liu, B.; Lin, H.; Chen, Y. Deformation Characteristics of Bolted Rock Joints under Compression-Shear Load. Appl. Sci. 2022, 12, 5226. [Google Scholar] [CrossRef]
- Lin, H.; Sun, P.; Chen, Y.; Zhu, Y.; Fan, X.; Zhao, Y. Analytical and experimental analysis of the shear strength of bolted saw-tooth joints. Eur. J. Environ. Civ. Eng. 2022, 26, 1639–1653. [Google Scholar] [CrossRef]
- Wu, Q.; Jiang, Y.; Tang, H.; Luo, H.; Wang, X.; Kang, J.; Zhang, S.; Yi, X.; Fan, L. Experimental and Numerical Studies on the Evolution of Shear Behaviour and Damage of Natural Discontinuities at the Interface Between Different Rock Types. Rock Mech. Rock Eng. 2020, 53, 3721–3744. [Google Scholar] [CrossRef]
- Yoshinaka, R.; Sakaguchi, S.; Shimizu, T.; Arai, H.; Kato, E. Experimental study on the rock bolt reinforcement in discontinuous rocks. Electron. Commun. Japan 1987, 133, 117–127. [Google Scholar]
- Wang, G.; Zhang, Y.; Jiang, Y.; Liu, P.; Guo, Y.; Liu, J.; Ma, M.; Wang, K.; Wang, S. Shear Behaviour and Acoustic Emission Characteristics of Bolted Rock Joints with Different Roughnesses. Rock Mech. Rock Eng. 2018, 51, 1885–1906. [Google Scholar] [CrossRef]
- Chen, N.; Zhang, X.; Jiang, Q.; Feng, X.; Wei, W.; Yi, B. Shear Behavior of Rough Rock Joints Reinforced by Bolts. Int. J. Geomech. 2018, 18, 04017130. [Google Scholar] [CrossRef]
- Liu, J.; Wang, J.; Wan, W. Numerical study of crack propagation in an indented rock specimen. Comput. Geotech. 2018, 96, 1–11. [Google Scholar] [CrossRef]
- Aliabadian, Z.; Sharafisafa, M.; Tahmasebinia, F.; Shen, L. Experimental and numerical investigations on crack development in 3D printed rock-like specimens with pre-existing flaws. Eng. Fract. Mech. 2021, 241, 107396. [Google Scholar] [CrossRef]
- Liu, R.; Lou, S.; Li, X.; Han, G.; Jiang, Y. Anisotropic surface roughness and shear behaviors of rough-walled plaster joints under constant normal load and constant normal stiffness conditions. J. Rock Mech. Geotech. Eng. 2020, 12, 338–352. [Google Scholar] [CrossRef]
- Meng, Y.; Jing, H.; Zhou, Z.; Zhang, L.; Sun, S. Experimental investigation on the mixed-mode fracture behavior of rock-like material with bedding plane. Theor. Appl. Fract. Mech. 2022, 117, 103159. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Hagan, P.C.; Mitra, R.; Khosravi, M.H. Experimental and numerical study of asperity degradation in the direct shear test. Eng. Geol. 2016, 204, 41–52. [Google Scholar] [CrossRef]
- Ma, H.; Tian, Y.; Liu, Q.; Pan, Y. Experimental study on the influence of height and dip angle of asperity on the mechanical properties of rock joints. Bull. Eng. Geol. Environ. 2020, 80, 443–471. [Google Scholar] [CrossRef]
- ISRM. Suggested methods for determining the uniaxial compressive strength and deformability of rock materials. Int. J. Rock Mech. Min. Sci. 1979, 16, 138–140. [Google Scholar] [CrossRef]
- ISRM. Suggested method for the complete stress-strain curve for intact rock in uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 279–289. [Google Scholar]
- Luo, X.; Cao, P.; Liu, T.; Zhao, Q.; Meng, G.; Fan, Z.; Xie, W. Mechanical Behaviour of Anchored Rock Containing Weak Interlayer under Uniaxial Compression: Laboratory Test and Coupled DEM–FEM Simulation. Minerals 2022, 12, 492. [Google Scholar] [CrossRef]
- Dong, X.; Yang, G.; Liu, S. Experimental study on AE response and damage evolution characteristics of frozen sandstone under uniaxial compression. Cold Reg. Sci. Technol. 2022, 193, 103424. [Google Scholar] [CrossRef]
- Xiong, F.; Liu, X.; Zhou, X.; Lin, G.; Liu, D.; Han, Y.; Xu, B.; He, C.; Wang, Z. Mechanical behaviours of sandstone containing intersecting fissures under uniaxial compression. J. Rock Mech. Geotech. Eng. 2022, 14, 460–476. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1994, 34, 185–188. [Google Scholar] [CrossRef]
- Xu, J.; Niu, X.; Yao, Z. Mechanical properties and acoustic emission data analyses of crumb rubber concrete under biaxial compression stress states. Constr. Build. Mater. 2021, 298, 123778. [Google Scholar] [CrossRef]
- Jiao, Y.; Zhang, Y.; Zhang, M.; Fu, L.; Zhang, L. Investigation of fracture modes in pervious asphalt under splitting and compression based on acoustic emission monitoring. Eng. Fract. Mech. 2019, 211, 209–220. [Google Scholar] [CrossRef]
- Ma, G.; Wu, C.; Hwang, H.J.; Li, B. Crack monitoring and damage assessment of BFRP-jacketed concrete cylinders under compression load based on acoustic emission techniques. Constr. Build. Mater. 2021, 272, 121936. [Google Scholar] [CrossRef]

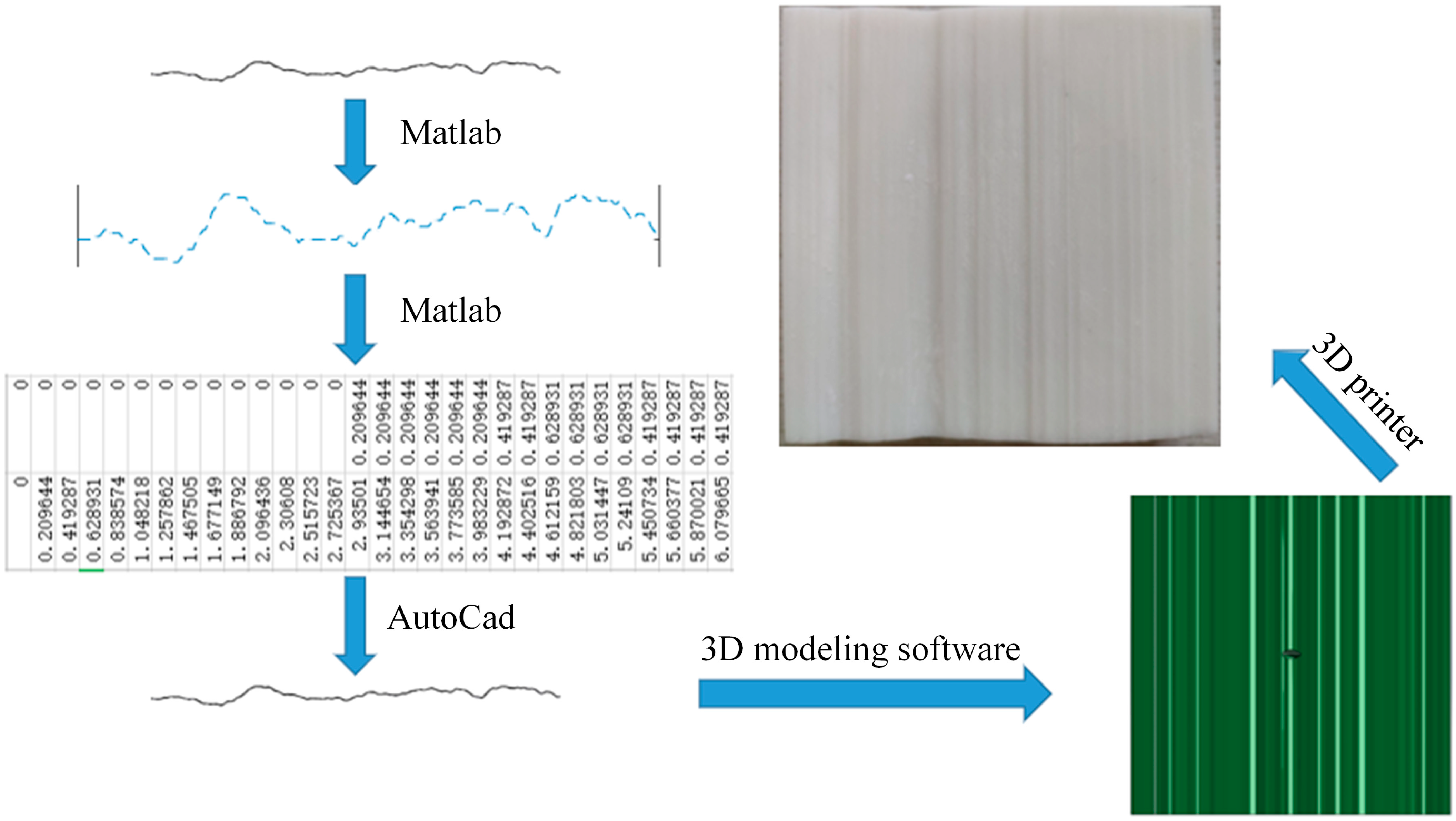

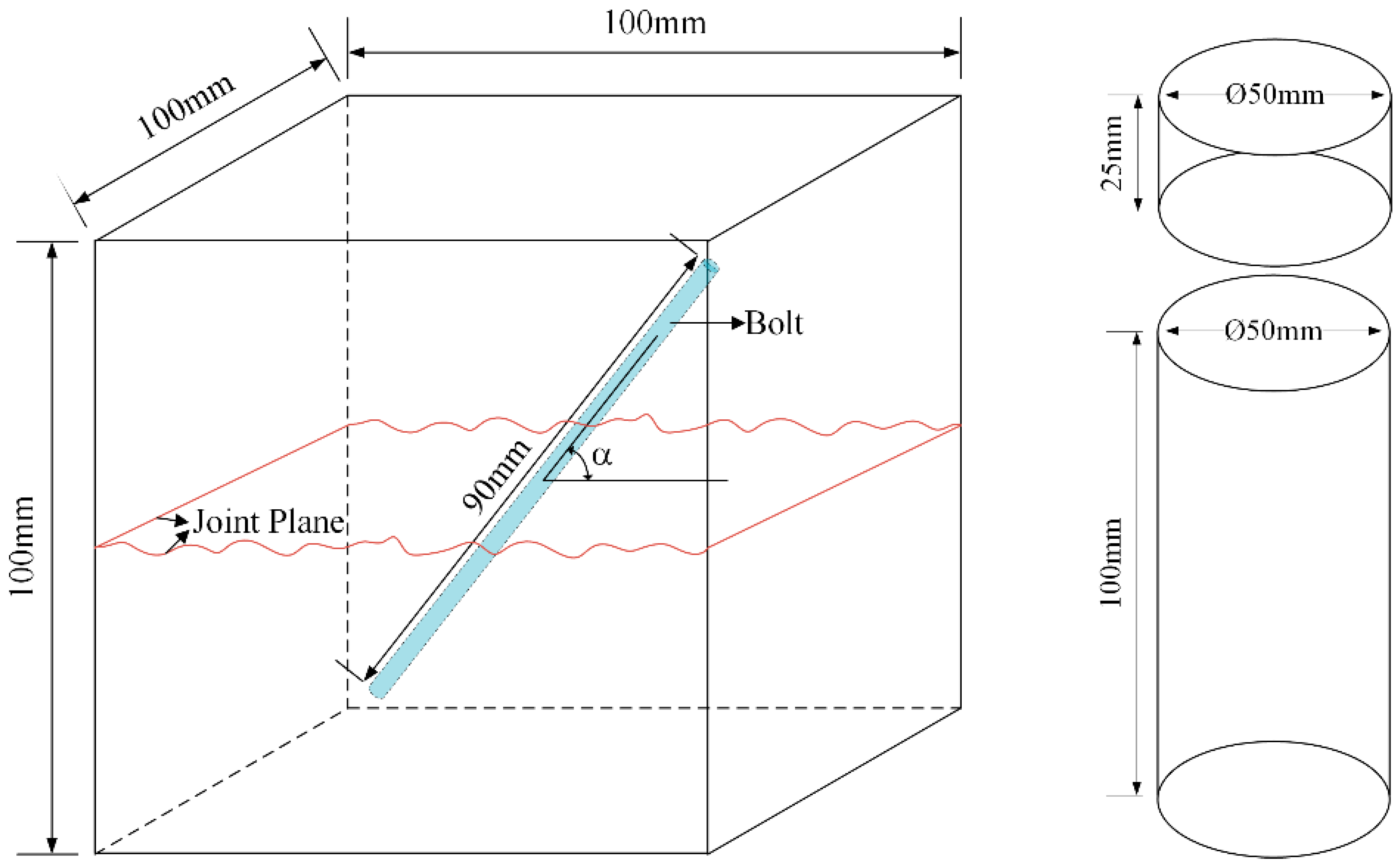









| Mechanical Parameters | Value |
|---|---|
| Unconfined compression strength (MPa) | 34.13 |
| Elastic modulus (GPa) | 5.27 |
| Tensile strength (MPa) | 2.98 |
| Cohesion (MPa) | 13.79 |
| Friction angle (°) | 27.92 |
| Poisson’s ratio | 0.21 |
| Parameters | JRC = 0–2 | JRC = 6–8 | JRC = 12–14 | JRC = 18–20 |
|---|---|---|---|---|
| Cohesion-like stress (Mpa) | 0.34 | 0.82 | 0.14 | 1.73 |
| Friction angle (°) | 36.2 | 34.0 | 47.7 | 44.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Lin, H.; Feng, J.; Cao, R.; Hu, H. Mechanical Properties and Acoustic Emission Characteristics of Anchored Structure Plane with Different JRC under Direct Shear Test. Materials 2022, 15, 4169. https://doi.org/10.3390/ma15124169
Li S, Lin H, Feng J, Cao R, Hu H. Mechanical Properties and Acoustic Emission Characteristics of Anchored Structure Plane with Different JRC under Direct Shear Test. Materials. 2022; 15(12):4169. https://doi.org/10.3390/ma15124169
Chicago/Turabian StyleLi, Su, Hang Lin, Jingjing Feng, Rihong Cao, and Huihua Hu. 2022. "Mechanical Properties and Acoustic Emission Characteristics of Anchored Structure Plane with Different JRC under Direct Shear Test" Materials 15, no. 12: 4169. https://doi.org/10.3390/ma15124169
APA StyleLi, S., Lin, H., Feng, J., Cao, R., & Hu, H. (2022). Mechanical Properties and Acoustic Emission Characteristics of Anchored Structure Plane with Different JRC under Direct Shear Test. Materials, 15(12), 4169. https://doi.org/10.3390/ma15124169








