A Study on the Design Depth of Permeable Road Pavement through Dynamic Load Experiment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Monitoring Instruments
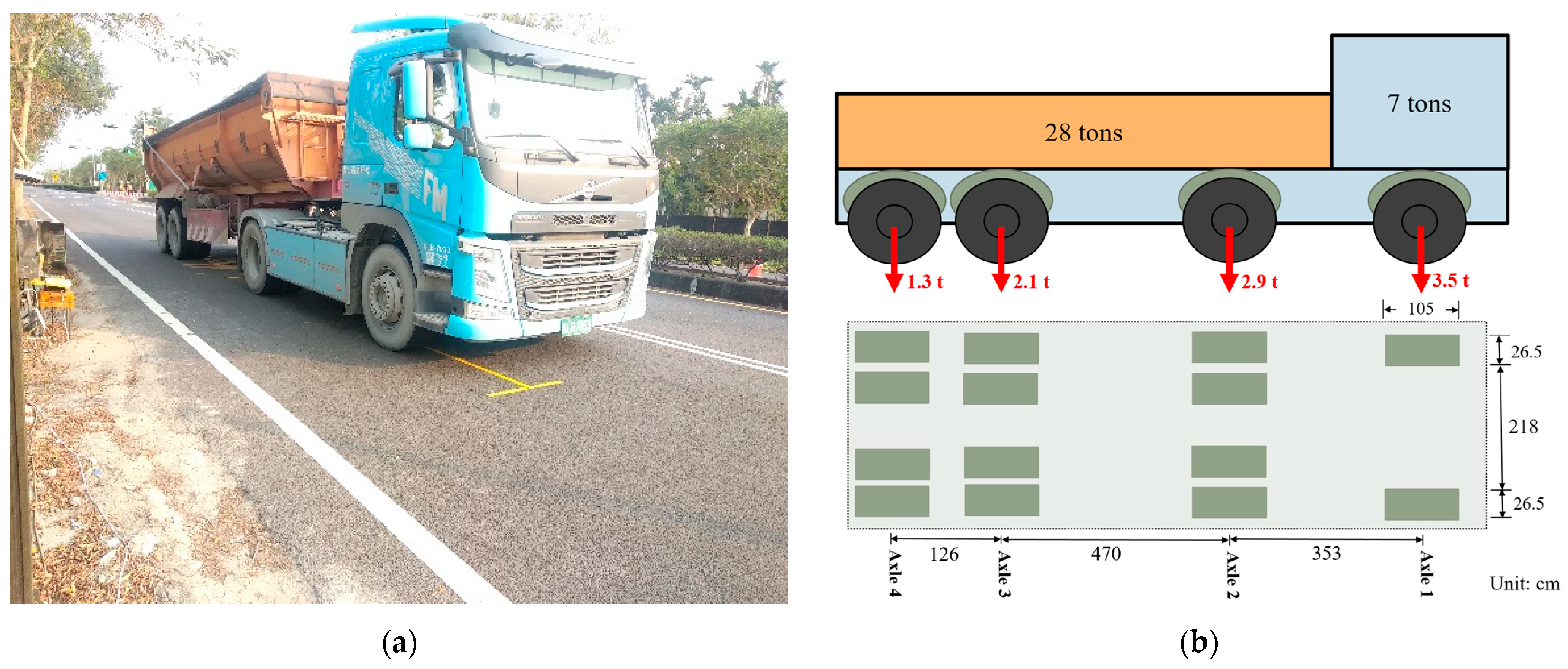
2.3. Dynamic Load Experiment
2.4. Data Process
- Four peaks in the strain and stress of the permeable road pavement must be detected by the instrument. The four peaks indicate that the wheel pressed against the instrument;
- The detected values have to have positive pressure and positive tension;
- The stress and strain responses of the surface layer have to be larger than those of the base layer;
- The time difference between the two truck axles should be calculated to determine if the trial is acceptable for the consideration of speed.
2.5. Relationship between Permeable Road Pavement Strain and Stress with Respect to Pavement Depths
3. Results and Discussion
3.1. Dynamic Responses of Permeable Road Pavement
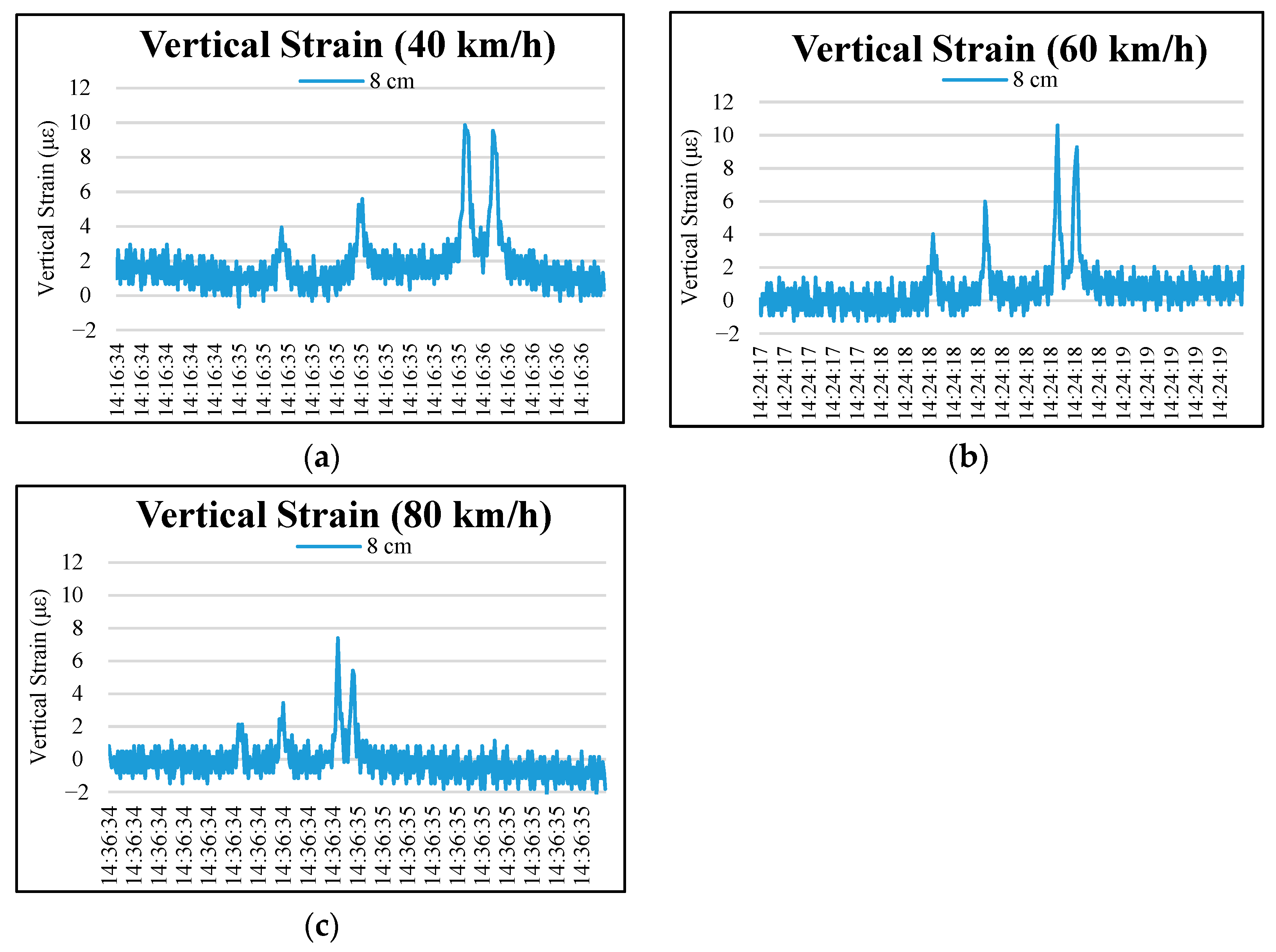
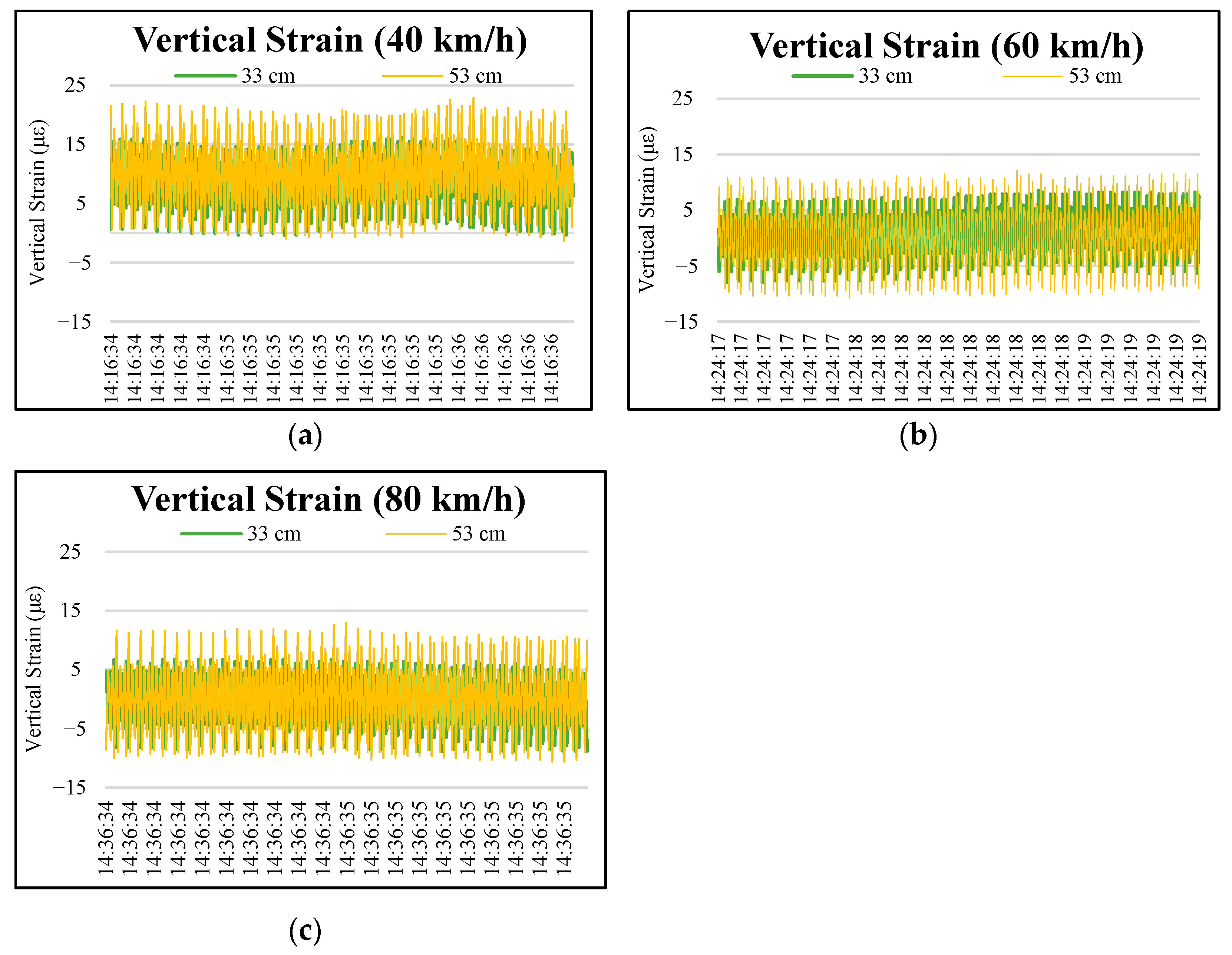
3.1.1. Vertical Strain
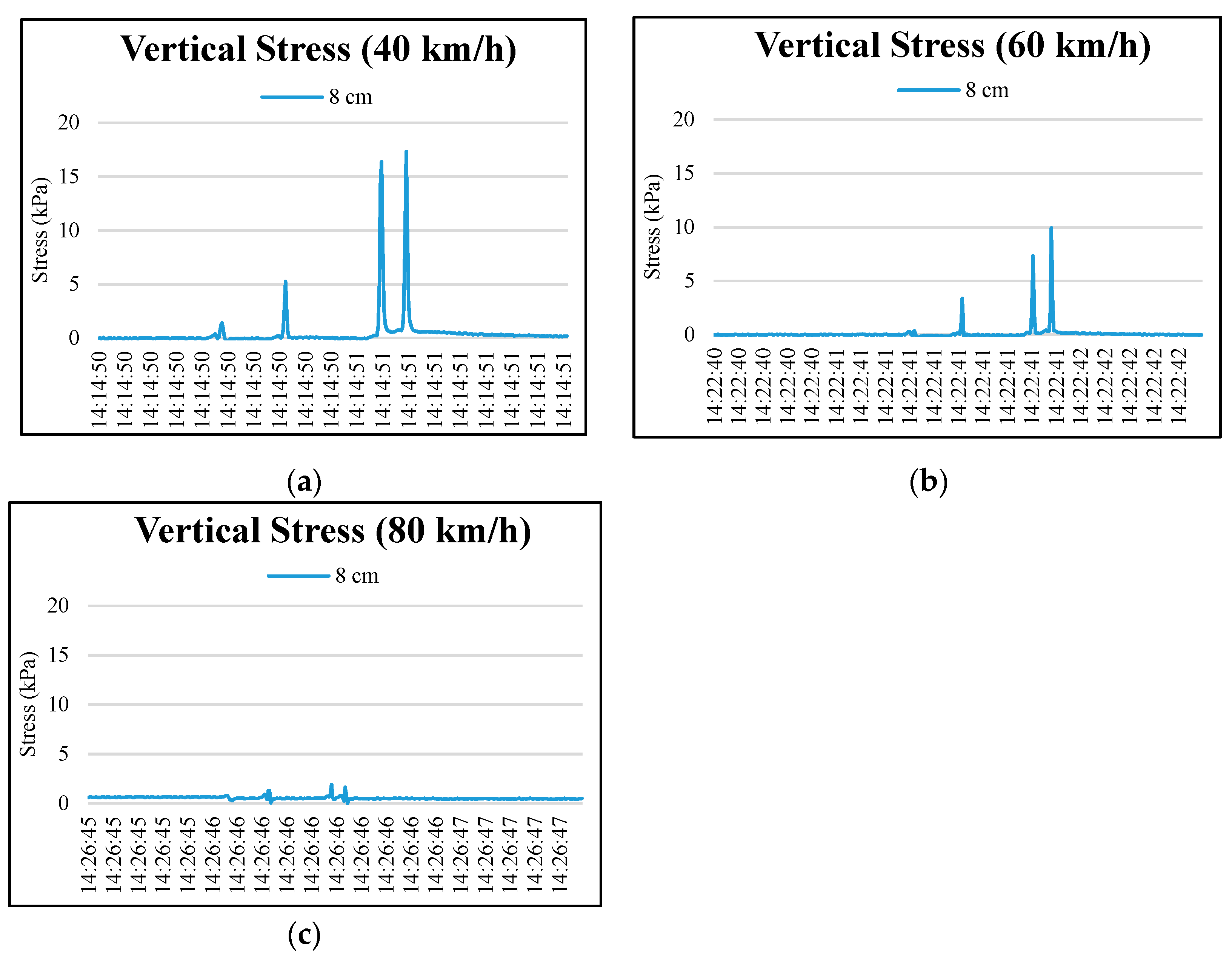
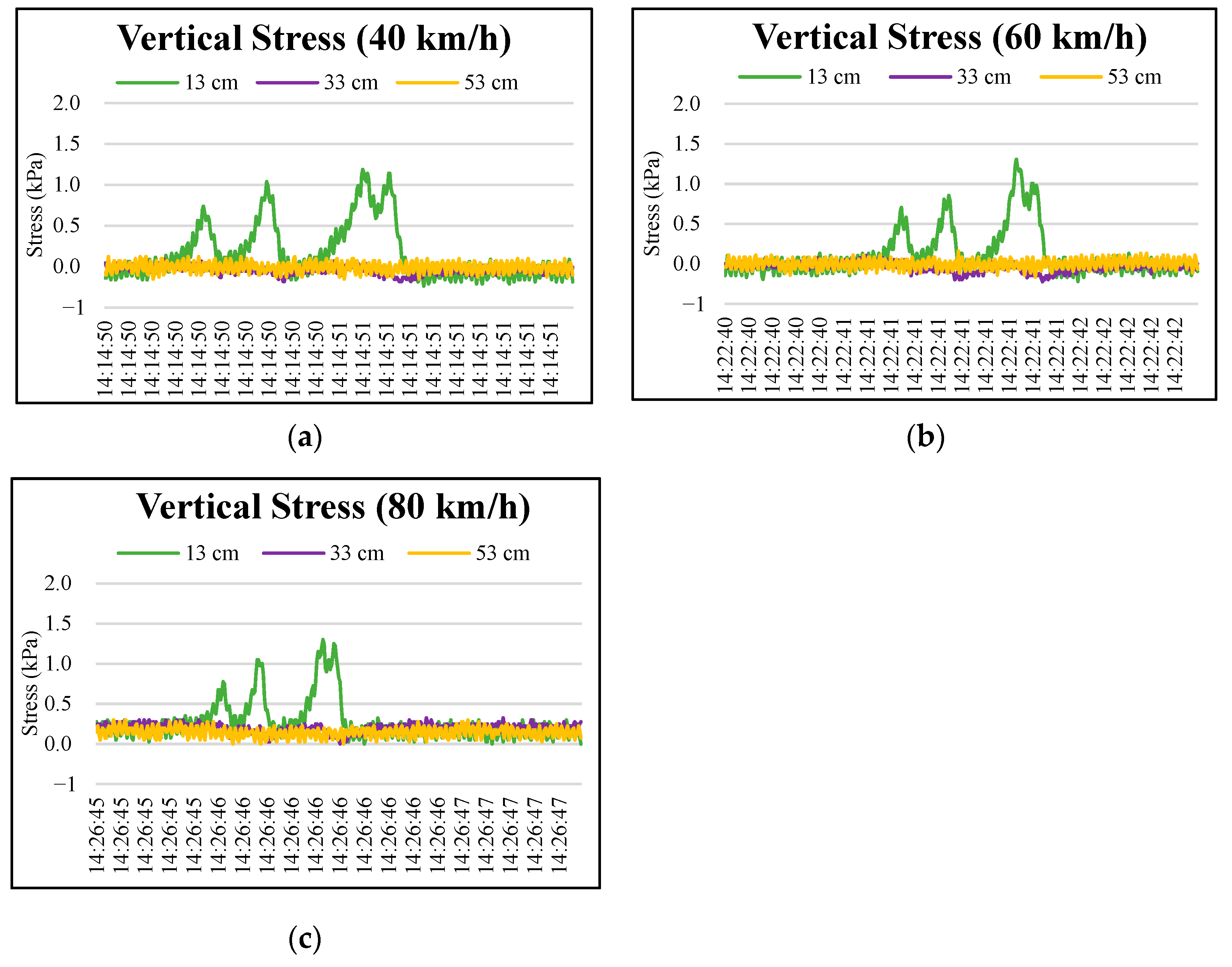
3.1.2. Vertical Stress
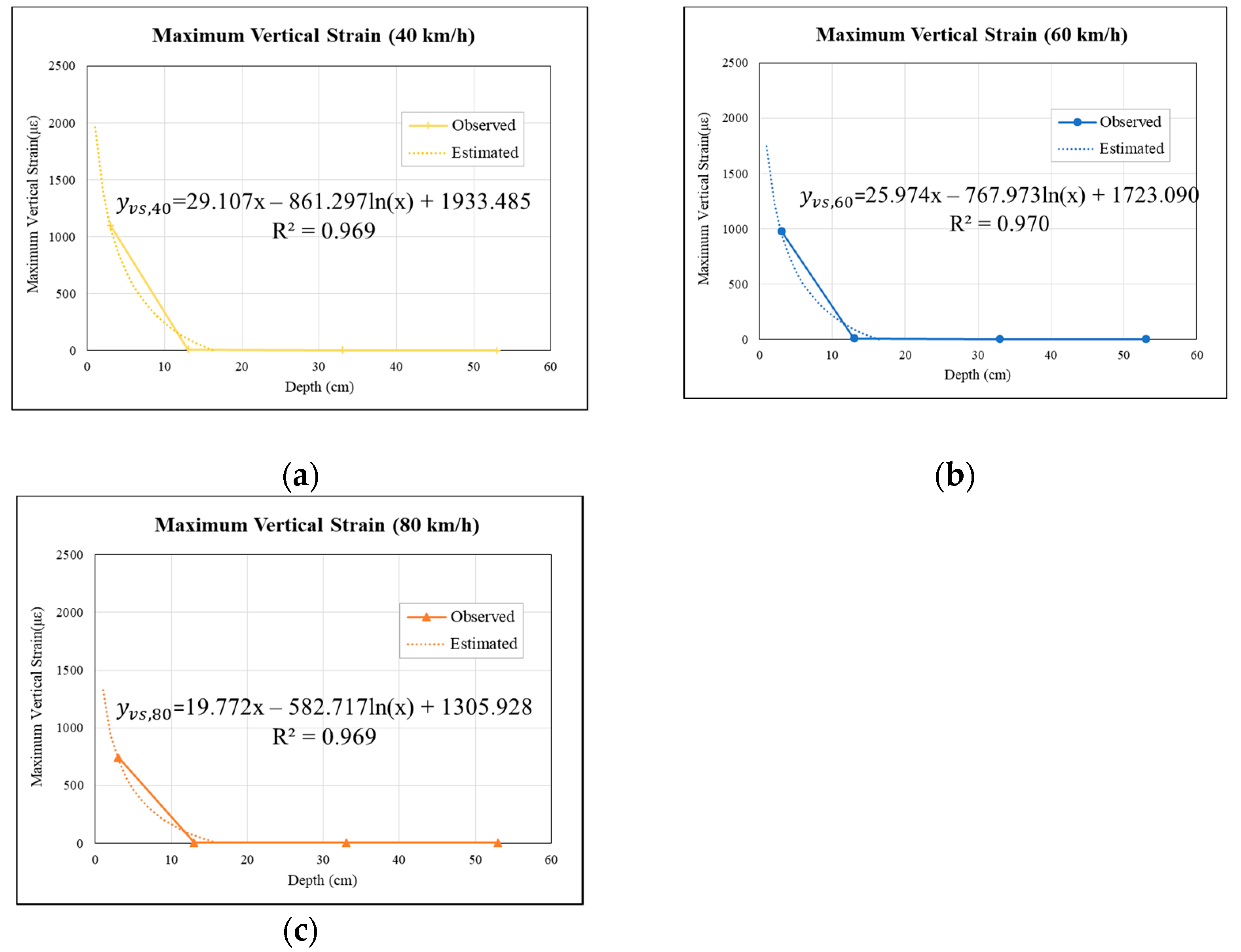
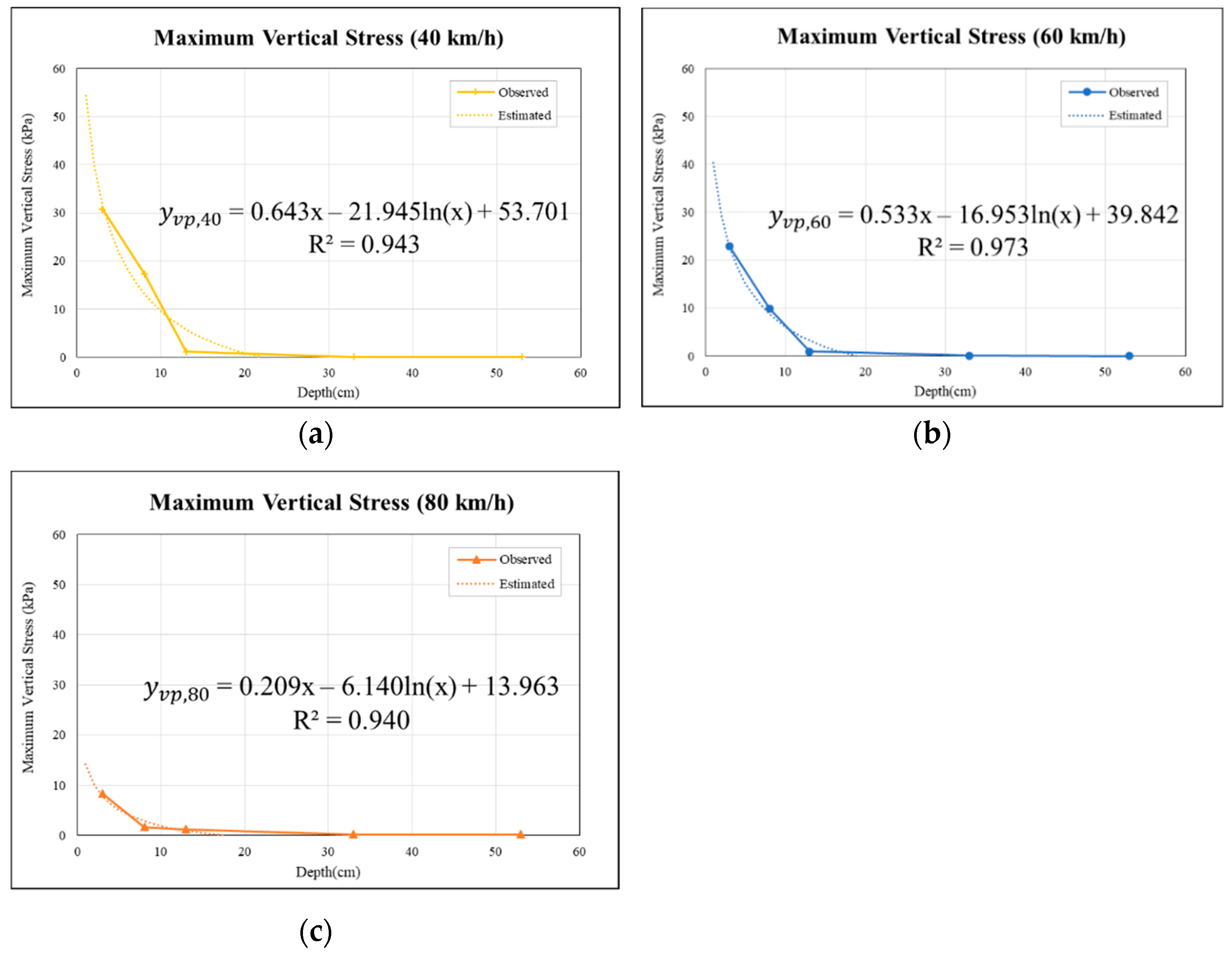
3.2. Relationship of Permeable Road Pavement Strain and Stress with Respect to Pavement Depths
4. Conclusions
- The result of vertical strains and vertical stresses in permeable road pavement indicated that the stresses and strains did not return to 0 after the truck wheel moved away from the instrumented position, and the single-curve response performs asymmetrically due to the viscoelastic property of the OGFC.
- The vertical strains and vertical stresses at the OGFC and the PAC showed an accumulating effect from the third to fourth axle from the collected data. Thus, the axle configuration significantly influences the strain and stress values of the permeable road pavement.
- Vertical strains and stresses of the permeable road pavement were strongly influenced by the truck driving speeds. An increase in truck speed decreases the reaction time of a point on the pavement, which reduces the pavement strain. This indicates that it is possible to extend the service life of a permeable road pavement at reasonably higher traffic speeds.
- By using the ANOVA F-test and t-test, from these models, the multiple logarithmic regression models of vertical stresses vs. vehicle speeds of 40, 60, and 80 km/h are meaningful. The estimated depths of the permeable road pavements are 22, 19, and 18 cm at speeds of 40, 60 and 80 km/h, respectively. Considering the results and the construction uncertainty, the recommended design thickness of the permeable pavement is 30 cm under the OGFC, PAC, and PC combination reported in Table 1 and Table 2, while the dynamic impacting force is not under consideration.
Author Contributions
Funding
Conflicts of Interest
References
- Chandrappa, A.K.; Biligiri, K.P. Influence of mix parameters on pore properties and modulus of pervious concrete: An application of ultrasonic pulse velocity. Mater. Struct. 2016, 49, 5255–5271. [Google Scholar] [CrossRef]
- Zhong, R.; Wille, K. Material design and characterization of high performance pervious concrete. Constr. Build. Mater. 2015, 98, 51–60. [Google Scholar] [CrossRef]
- Kia, A.; Wong, H.S.; Cheeseman, C.R. High-strength clogging resistant permeable pavement. Int. J. Pavement Eng. 2021, 22, 271–282. [Google Scholar] [CrossRef] [Green Version]
- Ge, N.; Li, H.; Yang, B.; Fu, K.; Yu, B.; Zhu, Y. Mechanical responses analysis and modulus inverse calculation of permeable asphalt pavement under dynamic load. Transp. Sci. 2021, in press. [CrossRef]
- Huang, B.; Wu, H.; Shu, X.; Burdette, E.G. Laboratory evaluation of permeability and strength of polymer-modified pervious concrete. Constr. Build. Mater. 2010, 24, 818–823. [Google Scholar] [CrossRef]
- Li, H.; Jones, D.; Harvey, J. Development of mechanistic–empirical design procedure for fully permeable pavement under heavy traffic. Transp. Res. Rec. 2012, 2305, 83–94. [Google Scholar] [CrossRef]
- El-Hakim, M. Instrumentation and Overall Evaluation of Perpetual and Conventional Flexible Pavement Designs. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2009. [Google Scholar]
- Al-Qadi, I.L.; Loulizi, A.; Elseifi, M.; Lahouar, S. The Virginia Smart Road: The impact of pavement instrumentation on understanding pavement performance. J. Assoc. Asphalt. Paving Technol. 2004, 73, 427–465. [Google Scholar]
- Yin, H. An analytical procedure for strain response prediction of flexible pavement. Int. J. Pavement Eng. 2013, 14, 486–497. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, J.; Wang, X. Full-scale field testing on a highway composite pavement dynamic responses. J. Transp. Geotech. 2015, 4, 13–27. [Google Scholar] [CrossRef]
- Imjai, T.; Pilakoutas, K.; Guadagnini, M. Performance of geosynthetic-reinforced flexible pavements in full-scale field trials. Geotext. Geomembr. 2019, 47, 217–229. [Google Scholar] [CrossRef]
- Lu, G.; Wang, H.; Törzs, T.; Liu, P.; Zhang, Y.; Wang, D.; Oeser, M.; Grabe, J. In-situ and numerical investigation on the dynamic response of unbounded granular material in permeable pavement. J. Transp. Geotech. 2020, 25, 100396. [Google Scholar] [CrossRef]
- Tabatabaee, N.; Al-Qadi, I.L.; Sebaaly, P.E. Field evaluation of pavement instrumentation methods. J. Test. Eval. 1992, 20, 144–151. [Google Scholar]
- Ling, J.; Wei, F.; Zhao, H.; Tian, Y.; Han, B. Analysis of airfield composite pavement responses using full-scale accelerated pavement testing and finite element method. Constr. Build. Mater. 2019, 212, 596–606. [Google Scholar] [CrossRef]
- Loulizi, A.; Al-Qadi, I.L.; Elseifi, M. Difference between in situ flexible pavement measured and calculated stresses and strains. J. Transp. Eng. 2006, 132, 574–579. [Google Scholar] [CrossRef]
- Xue, W.; Wang, L.; Wang, D.; Druta, C. Pavement health monitoring system based on an embedded sensing network. J. Mater. Civil Eng. 2014, 6, 04014072. [Google Scholar] [CrossRef]
- Wang, Y.; Norouzi, A.; Kim, Y.R. Comparison of fatigue cracking performance of asphalt pavements predicted by pavement ME and LVECD programs. J. Transp. Res. Rec. 2016, 2590, 44–55. [Google Scholar] [CrossRef]
- Zafir, Z.; Siddharthan, R.; Sebaaly, P.E. Dynamic pavement-strain histories from moving traffic load. J. Transp. Eng. 1994, 120, 821–842. [Google Scholar] [CrossRef]
- Siddharthan, R.V.; Krishnamenon, N.; El-Mously, M.; Sebaaly, P.E. Investigation of tire contact stress distributions on pavement response. J. Transp. Eng. 2002, 128, 136–144. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Rahman, A.S.M.A.; Islam, M.R.; Tarefder, R.A. Combined effect of asphalt concrete cross-anisotropy and temperature variation on pavement stress–strain under dynamic loading. Constr. Build. Mater. 2015, 93, 685–694. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, R.; Wang, X.; Ning, X. Dynamic response characteristics of permeable asphalt pavement based on unsaturated seepage. Int. J. Transp. Sci. Technol. 2019, 8, 403–417. [Google Scholar] [CrossRef]
- Al-Qadi, I.L.; Yoo, P.J. Effect of surface tangential contact stresses on flexible pavement response. J. Assoc. Asphalt. Paving Technol. 2007, 76, 663–692. [Google Scholar]
- Jaritngam, S.; Prachasaree, W.; Somchainuek, O.; Thongchim, P.; Yandell, W.O.; Taneerananon, P. Analysis of stress, strain and deflection of pavements using finite element method. J. Soc. Transp. Traf. Stud. 2010, 1, 51–59. [Google Scholar]
- Yoo, P.J.; Al-Qadi, I.L.; Elseifi, M.A.; Janajreh, I. Flexible pavement responses to different loading amplitudes considering layer interface condition and lateral shear forces. Int. J. Pavement Eng. 2006, 7, 73–86. [Google Scholar] [CrossRef]
- Alavi, A.H.; Hasni, H.; Lajnef, N.; Chatti, K. Continuous health monitoring of pavement systems using smart sensing technology. Constr. Build. Mater. 2016, 114, 719–736. [Google Scholar] [CrossRef]
- Lu, G.; Liu, P.; Toerzs, T.; Wang, D.; Oeser, M.; Grabe, J. Numerical analysis for the influence of saturation on the base course of permeable pavement with a novel polyurethane binder. J. Constr. Build. Mater. 2020, 240, 117930. [Google Scholar] [CrossRef]
- Sebaaly, P.E.; Tabatabaee, N.; Kulakowski, B.T.; Scullion, T. Instrumentation for Flexible Pavements–Field Performance of Selected Sensors; Final Report; Federal Highway Admiration: Washington, DC, USA, 1992. [Google Scholar]
- Iwański, M.; Chomicz-Kowalska, A. Evaluation of the pavement performance. Bull. Pol. Acad. Sci. 2015, 63, 97–105. [Google Scholar] [CrossRef]
- Assogba, O.C.; Tan, Y.; Zhou, X.; Zhang, C.; Anato, J.N. Numerical investigation of the mechanical response of semi-rigid base asphalt pavement under traffic load and nonlinear temperature gradient effect. J. Constr. Build. Mater. 2020, 235, 117406. [Google Scholar] [CrossRef]
- Buhari, R.; Rohani, M.M.; Abdullah, M.E. Dynamic load coefficient of tyre forces from truck axles. Appl. Mech. Mater. 2013, 405, 1900–1911. [Google Scholar] [CrossRef] [Green Version]
- Scholz, M.; Grabowiecki, P. Review of permeable pavement systems. Build. Environ. 2007, 42, 3830–3836. [Google Scholar] [CrossRef]
- Laws and Regulation Database of The Republic of China (Taiwan). Available online: https://law.moj.gov.tw/ENG/ (accessed on 8 June 2022).
- Shadman, M.; Ziari, H. Laboratory evaluation of fatigue life characteristics of polymer modified porous asphalt: A dissipated energy approach. Constr. Build. Mater. 2017, 138, 434–440. [Google Scholar] [CrossRef]
- Ferrotti, G.; Pasquini, E.; Canestrari, F. Experimental characterization of high-performance fiber-reinforced cold mix asphalt mixtures. Constr. Build. Mater. 2014, 57, 117–125. [Google Scholar] [CrossRef]
- Salama, H.K.; Chatti, K.; Lyles, R.W. Effect of heavy multiple axle trucks on flexible pavement damage using in-service pavement performance data. J. Transp. Eng. 2006, 132, 763–770. [Google Scholar] [CrossRef] [Green Version]
- Chandra, S.; Sekhar, C.R.; Bharti, A.K.; Kangadurai, B. Relationship between pavement roughness and distress parameters for Indian highways. J. Transp. Eng. 2013, 139, 467–475. [Google Scholar] [CrossRef]
- Yang, C.C.; Siao, J.H.; Yeh, W.C.; Wang, Y.M. A Study on Heat Storage and Dissipation Efficiency at Permeable Road Pavements. Materials 2021, 14, 3431. [Google Scholar] [CrossRef] [PubMed]



| Sieve No. | Opening (mm) | Percent Passing (%) | ||
|---|---|---|---|---|
| OGFC | PAC | PC | ||
| ″ | 37.5 | 100 | 100 | 100.0 |
| 1″ | 25.0 | 100 | 100 | 100.0 |
| 3/4″ | 19.0 | 100 | 95 | 89.5 |
| 1/2″ | 12.5 | 100 | 72 | 50.0 |
| 3/8″ | 9.5 | 86 | 52 | 27.8 |
| No. 4 | 4.750 | 38 | 18 | 1.6 |
| No. 8 | 2.360 | 15 | 12 | - |
| No. 10 | 2.000 | 8 | 9 | - |
| No. 30 | 0.600 | 5 | 8 | - |
| No. 50 | 0.300 | 4 | 6 | - |
| No. 100 | 0.150 | 3 | 5 | - |
| No. 200 | 0.075 | 2.0 | 3.6 | - |
| Type | Thickness (m) | Asphalt Content (%) | Maximum Specific Gravity (25 °C/25 °C) | Maximum Density (Unit Weight) (kg/m3) | Porosity, N (%) | Permeability (cm/s) | Stability (N) | Retained Strength Index (%) |
|---|---|---|---|---|---|---|---|---|
| OGFC | 0.03 | 4.5 | 1.021 | 1018 | 16.4 | - | 4446 | 93.5 |
| PAC | 0.10 | 4.9 | 2.442 | 2435 | 17.1 | 0.21 | 3329 | 80.2 |
| Cement Adjust, C (kg) | Water Adjust, W (kg) | Amount of Aggregate, G (kg) | Total Material Amount, WT (kg) | Average Compressive Strength (kg/cm2) | Permeability (cm/s) | Porosity, N (%) | ||
|---|---|---|---|---|---|---|---|---|
| 19.0 mm | 9.5 mm | 7 days | 28 days | |||||
| 261 | 135 | 980 | 653 | 2029 | 112.8 | 142.2 | 1.642 | 17.6 |
| Area | Sensor | Sensor Location (cm) | Instrument Serial Number | Calibration Coefficient |
|---|---|---|---|---|
| A | Vertical strain transducer | 3 | EKD150270 | 0.804 |
| 8 | EKD180339 | 0.828 | ||
| 33 | EKD180338 | 0.822 | ||
| 53 | EKD150276 | 0.816 | ||
| B | Vertical strain transducer | 3 | EKD180342 | 0.808 |
| 8 | EKD180342 | 0.822 | ||
| 33 | EKD180341 | 0.826 | ||
| 53 | EKD180340 | 0.829 |
| Area | Sensor Location (cm) | Instrument Serial Number | Gage Factor |
|---|---|---|---|
| A | 3 | 1743901 | 25.034 |
| 8 | 1743902 | 25.041 | |
| 13 | 1743903 | 25.053 | |
| 33 | 1743904 | 25.010 | |
| 53 | 1743905 | 25.030 | |
| B | 3 | 1743906 | 25.046 |
| 8 | 1743907 | 24.658 | |
| 13 | 1743908 | 25.009 | |
| 33 | 1743909 | 25.009 | |
| 53 | 1743910 | 25.027 |
| Type of Axle | Truck-Axle Configuration | Number of Wheels | Weight of Outer Wheel (ton) | Weight of Inner Wheel (ton) | Tire Pressure (MPa) |
|---|---|---|---|---|---|
| Single | Axle 1 | 2 | 3.5 | - | 0.85 |
| Single | Axle 2 | 4 | 2.9 | 3.5 | |
| Tandem | Axle 3 | 4 | 2.1 | 2.6 | |
| Axle 4 | 4 | 1.3 | 1.6 |
| Maximum Values of Vertical Strains (με) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Speed | At 40 km/h | At 60 km/h | At 80 km/h | ||||||||||
| Peak | First | Second | Third | Fourth | First | Second | Third | Fourth | First | Second | Third | Fourth | |
| Depth (cm) | |||||||||||||
| 3 | 235.29 | 729.79 | 1074.96 | 1099.85 | 295.89 | 666.60 | 922.90 | 979.46 | 73.11 | 359.14 | 713.37 | 742.13 | |
| 8 | 3.95 | 5.59 | 9.86 | 9.54 | 4.03 | 6.00 | 10.60 | 9.29 | 2.13 | 3.45 | 7.39 | 5.42 | |
| 33 | 3.97 | 1.98 | 5.95 | 5.62 | 1.61 | 2.27 | 5.24 | 2.93 | 6.04 | 6.04 | 6.04 | 4.06 | |
| 53 | 0.00 | 1.33 | 2.98 | 1.33 | 1.56 | 1.56 | 2.88 | 2.22 | 1.32 | 1.65 | 2.64 | 2.97 | |
| Maximum Values of Vertical Stress (KPa) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Speed | At 40 km/h | At 60 km/h | At 80 km/h | ||||||||||
| Peak | First | Second | Third | Fourth | First | Second | Third | Fourth | First | Second | Third | Fourth | |
| Depth (cm) | |||||||||||||
| 3 | 9.39 | 18.96 | 23.32 | 30.76 | 5.39 | 11.17 | 16.13 | 22.91 | 1.75 | 8.49 | 6.71 | 8.36 | |
| 8 | 1.42 | 5.28 | 16.39 | 17.34 | 0.37 | 3.37 | 7.35 | 9.93 | 0.83 | 1.3 | 1.93 | 1.63 | |
| 13 | 0.74 | 1.04 | 1.19 | 1.14 | 0.71 | 0.86 | 1.31 | 1.01 | 0.78 | 1.05 | 1.3 | 1.25 | |
| 33 | 0.07 | 0.05 | 0.07 | 0.07 | 0.06 | 0.06 | 0.08 | 0.08 | 0.18 | 0.23 | 0.18 | 0.00 | |
| 53 | 0.04 | 0.00 | 0.04 | 0.04 | 0.05 | 0.00 | 0.03 | 0.00 | 0.08 | 0.00 | 0.03 | 0.18 | |
| Models for Specific Speeds (km/h) | Source of Variation | Df | Sum of Squares | Mean Squares | F | Sig. | Fcrit |
|---|---|---|---|---|---|---|---|
| 40 | Regression | 2 | 870,716.304 | 435,358.152 | 15.815 | 0.175 | 18.513 |
| Residuals | 1 | 27,528.198 | 27,528.198 | ― | ― | ||
| Total | 3 | 898,244.501 | ― | ― | ― | ||
| 60 | Regression | 2 | 691,336.794 | 345,668.397 | 16.345 | 0.172 | 18.513 |
| Residuals | 1 | 21,148.071 | 21,148.071 | ― | ― | ||
| Total | 3 | 712,484.865 | ― | ― | ― | ||
| 80 | Regression | 2 | 395,911.518 | 197,955.759 | 15.772 | 0.175 | 18.513 |
| Residuals | 1 | 12,551.242 | 12,551.242 | ― | ― | ||
| Total | 3 | 408,462.760 | ― | ― | ― |
| Model for Specific Speed (km/h) | Source of Variation | Df | Sum of Squares | Mean Squares | F | Sig. | Fcrit |
|---|---|---|---|---|---|---|---|
| 40 | Regression | 2 | 717.958 | 358.979 | 16.697 | 0.057 | 10.128 |
| Residuals | 2 | 42.999 | 21.500 | ― | ― | ||
| Total | 4 | 760.957 | ― | ― | ― | ||
| 60 | Regression | 2 | 383.609 | 191.804 | 35.853 | 0.027 | 10.128 |
| Residuals | 2 | 10.700 | 5.350 | ― | ― | ||
| Total | 4 | 394.308 | ― | ― | ― | ||
| 80 | Regression | 2 | 44.179 | 22.089 | 15.742 | 0.060 | 10.128 |
| Residuals | 2 | 2.806 | 1.403 | ― | ― | ||
| Total | 4 | 46.985 | ― | ― | ― |
| Model for Specific Speed (km/h) | Source | Coefficient | Std.Error | t-Value | p-Value | Lower Bound (95%) | Upper Bound (95%) | T0.1 |
|---|---|---|---|---|---|---|---|---|
| 40 | Intercept | 53.7011 | 9.2729 | 5.7912 | 0.0285 | 13.8030 | 93.5992 | 1.886 |
| Depth | 0.6431 | 0.3166 | 2.0315 | 0.1793 | −0.7190 | 2.0053 | ||
| ln(x) | −21.9454 | 5.7582 | −3.8112 | 0.0625 | −46.7209 | 2.8301 | ||
| 60 | Intercept | 39.842 | 4.6256 | 8.6134 | 0.0132 | 19.9400 | 59.7448 | 1.886 |
| Depth | 0.533 | 0.1579 | 3.3775 | 0.0776 | −0.1461 | 1.2128 | ||
| ln(x) | −16.953 | 2.8724 | −5.9022 | 0.0275 | −29.3120 | −4.5945 | ||
| 80 | Intercept | 13.9630 | 2.3690 | 5.8942 | 0.0276 | 3.7702 | 24.1559 | 1.886 |
| Depth | 0.2087 | 0.0809 | 2.5805 | 0.1231 | −0.1393 | 0.5567 | ||
| ln(x) | −6.1399 | 1.4711 | −4.1738 | 0.0529 | −12.4694 | 0.1895 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsing, C.-H.; Siao, J.-H.; Wang, Y.-M. A Study on the Design Depth of Permeable Road Pavement through Dynamic Load Experiment. Materials 2022, 15, 4391. https://doi.org/10.3390/ma15134391
Hsing C-H, Siao J-H, Wang Y-M. A Study on the Design Depth of Permeable Road Pavement through Dynamic Load Experiment. Materials. 2022; 15(13):4391. https://doi.org/10.3390/ma15134391
Chicago/Turabian StyleHsing, Chun-Hua, Jun-Han Siao, and Yu-Min Wang. 2022. "A Study on the Design Depth of Permeable Road Pavement through Dynamic Load Experiment" Materials 15, no. 13: 4391. https://doi.org/10.3390/ma15134391






