Transient Phase-Driven Cyclic Deformation in Additively Manufactured 15-5 PH Steel
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Cyclic Stress-Strain Curves
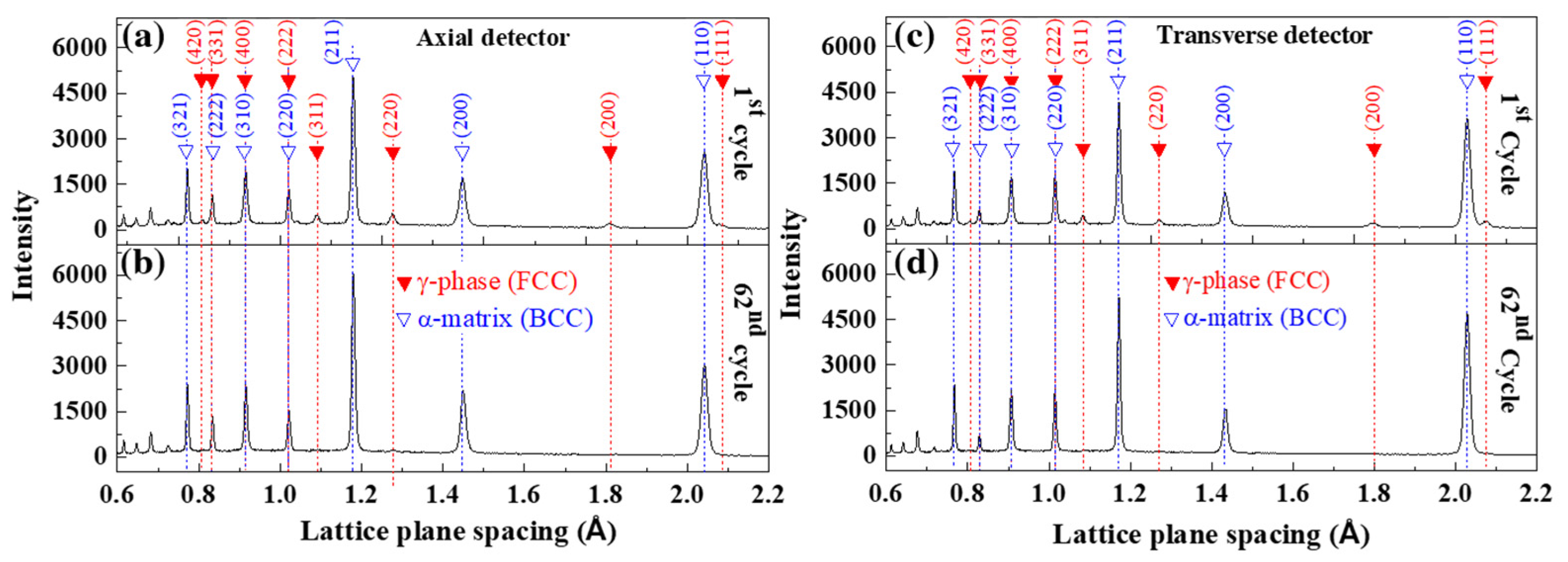
3.2. Cyclic-Induced Martensitic Transformation
3.3. Tension-Compression Asymmetry Behavior
3.4. Effect of Porous Structure on the Tension-Compression Asymmetry Behavior
3.5. Effect of Microscopic Change on the Tension-Compression Asymmetry Behavior
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Selective laser melting | SLM |
| Low-cycle fatigue | LCF |
| Additive manufacturing | AM |
| Spallation Neutron Source | SNS |
| Oak Ridge National Laboratory | ORNL |
| General structure analysis system II | GSAS-II |
| Body-centered cubic | BCC |
| Face-centered cubic | FCC |
| ○ | Measured tensile stress |
| □ | Measured compressive stress |
| ○ | Calculated tensile stress |
| □ | Calculated compressive stress |
| ○ | Reference calculated tensile stress |
| □ | Reference calculated compressive stress |
| □ | Calibrated compressive stress |
| E | Young’s modulus |
| Poisson’s ratio | |
| Stress along the axial loading direction | |
| Strain along the axial loading direction | |
| Stress components in the transverse direction | |
| Stress components in the transverse direction | |
| Strain components in the transverse direction | |
| Strain components in the transverse direction | |
| α | BCC α-matrix |
| γ | FCC γ-phase |
| Calculated stress | |
| f | Volume fraction of FCC γ-phase |
| Stress components of BCC α-matrix | |
| Stress components of FCC γ-phase | |
| Yield strength of porous material | |
| Effective modulus of porous material | |
| Yield strength of bulk material | |
| Elastic modulus of bulk material | |
| Relative density of porous material | |
| P(%) | Porosity |
| Measured density | |
| Theoretical density |
References
- Thompson, S.M.; Bian, L.; Shamsaei, N.; Yadollahi, A. An overview of Direct Laser Deposition for additive manufacturing; Part I: Transport phenomena, modeling and diagnostics. Addit. Manuf. 2015, 8, 36–62. [Google Scholar] [CrossRef]
- Shamsaei, N.; Yadollahi, A.; Bian, L.; Thompson, S.M. An overview of Direct Laser Deposition for additive manufacturing; Part II: Mechanical behavior, process parameter optimization and control. Addit. Manuf. 2015, 8, 12–35. [Google Scholar] [CrossRef]
- Kok, Y.; Tan, X.P.; Wang, P.; Nai, M.L.S.; Loh, N.H.; Liu, E.; Tor, S.B. Anisotropy and heterogeneity of microstructure and mechanical properties in metal additive manufacturing: A critical review. Mater. Des. 2018, 139, 565–586. [Google Scholar] [CrossRef]
- Huang, E.W.; Lee, S.Y.; Jain, J.; Tong, Y.; An, K.; Tsou, N.-T.; Lam, T.-N.; Yu, D.; Chae, H.; Chen, S.-W.; et al. Hardening steels by the generation of transient phase using additive manufacturing. Intermetallics 2019, 109, 60–67. [Google Scholar] [CrossRef]
- Tseng, J.C.; Huang, W.C.; Chang, W.; Jeromin, A.; Keller, T.F.; Shen, J.; Chuang, A.C.; Wang, C.C.; Lin, B.H.; Amalia, L.; et al. Deformations of Ti-6Al-4V additive-manufacturing-induced isotropic and anisotropic columnar structures: Insitu measurements and underlying mechanisms. Addit. Manuf. 2020, 35, 101322. [Google Scholar] [CrossRef] [PubMed]
- Starr, T.; Rafi, H.; Stucker, B.; Scherzer, C.M. Controlling Phase Composition in Selective Laser Melted Stainless Steels; International Solid Freeform Fabrication Symposium: Austin, TX, USA, 2012; pp. 439–446. [Google Scholar]
- Yadollahi, A.; Shamsaei, N.; Thompson, S.M.; Elwany, A.; Bian, L. Effects of building orientation and heat treatment on fatigue behavior of selective laser melted 17-4 PH stainless steel. Int. J. Fatigue 2017, 94, 218–235. [Google Scholar] [CrossRef]
- Song, B.; Zhao, X.; Li, S.; Han, C.; Wei, Q.; Wen, S.; Liu, J.; Shi, Y. Differences in microstructure and properties between selective laser melting and traditional manufacturing for fabrication of metal parts: A review. Front. Mech. Eng. 2015, 10, 111–125. [Google Scholar] [CrossRef]
- Herzog, D.; Seyda, V.; Wycisk, E.; Emmelmann, C. Additive manufacturing of metals. Acta Mater. 2016, 117, 371–392. [Google Scholar] [CrossRef]
- Kim, J.S.; LaGrange, T.; Reed, B.W.; Taheri, M.L.; Armstrong, M.R.; King, W.E.; Browning, N.D.; Campbell, G.H. Imaging of Transient Structures Using Nanosecond in Situ TEM. Science 2008, 321, 1472–1475. [Google Scholar] [CrossRef] [PubMed]
- Tomkow, J.; Janeczek, A.; Rogalski, G.; Wolski, A. Underwater Local Cavity Welding of S460N Steel. Material 2020, 13, 5535. [Google Scholar] [CrossRef]
- Garcias, J.F.; Martins, R.F.; Branco, R.; Marciniak, Z.; Macek, W.; Pereira, C.; Santos, C. Quasistatic and fatigue behavior of an AISI H13 steel obtained by additive manufacturing and conventional method. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 3384–3398. [Google Scholar] [CrossRef]
- Hunt, J.; Derguti, F.; Todd, I. Selection of steels suitable for additive layer manufacturing. Ironmak. Steelmak. 2014, 41, 254–256. [Google Scholar] [CrossRef]
- Facchini, L.; Vicente, N., Jr.; Lonardelli, I.; Magalini, E.; Robotti, P.; Molinari, A. Metastable Austenite in 17–4 Precipitation-Hardening Stainless Steel Produced by Selective Laser Melting. Adv. Eng. Mater. 2010, 12, 184–188. [Google Scholar] [CrossRef]
- Haghdadi, N.; Laleh, M.; Moyle, M.; Primig, S. Additive manufacturing of steels: A review of achievements and challenges. J. Mater. Sci. 2020, 56, 64–107. [Google Scholar] [CrossRef]
- Lum, E.; Palazotto, A.N.; Dempsey, A. Analysis of the Effects of Additive Manufacturing on the Material Properties of 15-5PH Stainless Steel. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Lass, E.A.; Stoudt, M.R.; Williams, M.E. Additively Manufactured Nitrogen-Atomized 17-4 PH Stainless Steel with Mechanical Properties Comparable to Wrought. Metall. Mater. Trans. A 2019, 50, 1619–1624. [Google Scholar] [CrossRef]
- LeBrun, T.; Nakamoto, T.; Horikawa, K.; Kobayashi, H. Effect of retained austenite on subsequent thermal processing and resultant mechanical properties of selective laser melted 17–4 PH stainless steel. Mater. Des. 2015, 81, 44–53. [Google Scholar] [CrossRef]
- Mahmoudi, M.; Elwany, A.; Yadollahi, A.; Thompson, S.M.; Bian, L.; Shamsaei, N. Mechanical properties and microstructural characterization of selective laser melted 17-4 PH stainless steel. Rapid Prototyp. J. 2017, 23, 280–294. [Google Scholar] [CrossRef] [Green Version]
- Rafi, H.K.; Starr, T.L.; Stucker, B.E. A comparison of the tensile, fatigue, and fracture behavior of Ti–6Al–4V and 15-5 PH stainless steel parts made by selective laser melting. Int. J. Adv. Manuf. Technol. 2013, 69, 1299–1309. [Google Scholar] [CrossRef]
- AlMangour, B.; Yang, J.-M. Improving the surface quality and mechanical properties by shot-peening of 17-4 stainless steel fabricated by additive manufacturing. Mater. Des. 2016, 110, 914–924. [Google Scholar] [CrossRef]
- Hsu, T.-H.; Chang, Y.-J.; Huang, C.-Y.; Yen, H.-W.; Chen, C.-P.; Jen, K.-K.; Yeh, A.-C. Microstructure and property of a selective laser melting process induced oxide dispersion strengthened 17-4 PH stainless steel. J. Alloys Compd. 2019, 803, 30–41. [Google Scholar] [CrossRef]
- Nong, X.D.; Zhou, X.L.; Wang, Y.D.; Yu, L.; Li, J.H. Effects of geometry, location, and direction on microstructure and mechanical properties of 15–5PH stainless steel fabricated by directed energy deposition. Mater. Sci. Eng. A 2021, 821, 141587. [Google Scholar] [CrossRef]
- Chae, H.; Huang, E.W.; Jain, J.; Wang, H.; Woo, W.; Chen, S.-W.; Harjo, S.; Kawasaki, T.; Lee, S.Y. Plastic anisotropy and deformation-induced phase transformation of additive manufactured stainless steel. Mater. Sci. Eng. A 2019, 762, 138065. [Google Scholar] [CrossRef]
- Carneiro, L.; Jalalahmadi, B.; Ashtekar, A.; Jiang, Y. Cyclic deformation and fatigue behavior of additively manufactured 17–4 PH stainless steel. Int. J. Fatigue 2019, 123, 22–30. [Google Scholar] [CrossRef]
- Chae, H.; Luo, M.Y.; Huang, E.W.; Shin, E.; Do, C.; Hong, S.-K.; Woo, W.; Lee, S.Y. Unearthing principal strengthening factors tuning the additive manufactured 15-5 PH stainless steel. Mater. Charact. 2022, 184, 111645. [Google Scholar] [CrossRef]
- Benson, M.L.; Liaw, P.K.; Saleh, T.A.; Choo, H.; Brown, D.W.; Daymond, M.R.; Huang, E.W.; Wang, X.L.; Stoica, A.D.; Buchanan, R.A.; et al. Deformation-induced phase development in a cobalt-based superalloy during monotonic and cyclic deformation. Phys. B Condens. Matter 2006, 385–386, 523–525. [Google Scholar] [CrossRef]
- Chae, H.; Huang, E.W.; Woo, W.; Kang, S.H.; Jain, J.; An, K.; Lee, S.Y. Unravelling thermal history during additive manufacturing of martensitic stainless steel. J. Alloys Compd. 2021, 857, 157555. [Google Scholar] [CrossRef] [PubMed]
- Huang, E.W.; Chang, C.K.; Liaw, P.K.; Suei, T.R. Fatigue induced deformation and thermodynamics evolution in a nano particle strengthened nickel base superalloy. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 675–685. [Google Scholar] [CrossRef]
- Huang, E.W.; Barabash, R.I.; Ice, G.E.; Liu, W.; Liu, Y.-L.; Kai, J.-J.; Liaw, P.K. Cyclic-loading-induced accumulation of geometrically necessary dislocations near grain boundaries in an Ni-based superalloy. JOM 2009, 61, 53. [Google Scholar] [CrossRef]
- An, K.; Chen, Y.; Stoica, A.D. VULCAN: A “hammer” for high-temperature materials research. MRS Bull. 2019, 44, 878–885. [Google Scholar] [CrossRef]
- An, K.; Skorpenske, H.D.; Stoica, A.D.; Ma, D.; Wang, X.-L.; Cakmak, E. First In Situ Lattice Strains Measurements Under Load at VULCAN. Metall. Mater. Trans. A 2010, 42, 95–99. [Google Scholar] [CrossRef]
- Huang, E.W.; Lee, S.Y.; Woo, W.; Lee, K.-W. Three-Orthogonal-Direction Stress Mapping around a Fatigue-Crack Tip Using Neutron Diffraction. Metall. Mater. Trans. A 2011, 43, 2785–2791. [Google Scholar] [CrossRef]
- Lam, T.-N.; Wu, S.-C.; Chae, H.; Chen, S.-W.; Jain, J.; Lee, S.Y.; An, K.; Vogel, S.C.; Chiu, S.-M.; Yu, D.; et al. Phase Stress Partition in Gray Cast Iron Using In Situ Neutron Diffraction Measurements. Metall. Mater. Trans. A 2020, 51, 5029–5035. [Google Scholar] [CrossRef]
- Toby, B.H.; Von Dreele, R.B. GSAS-II: The genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystallogr. 2013, 46, 544–549. [Google Scholar] [CrossRef]
- Morooka, S.; Tomota, Y.; Kamiyama, T. Heterogeneous Deformation Behavior Studied by in Situ Neutron Diffraction during Tensile Deformation for Ferrite, Martensite and Pearlite Steels. ISIJ Int. 2008, 48, 525–530. [Google Scholar] [CrossRef] [Green Version]
- Cyr, E.; Lloyd, A.; Mohammadi, M. Tension-compression asymmetry of additively manufactured Maraging steel. J. Manuf. Processes 2018, 35, 289–294. [Google Scholar] [CrossRef]
- Chen, W.; Voisin, T.; Zhang, Y.; Florien, J.B.; Spadaccini, C.M.; McDowell, D.L.; Zhu, T.; Wang, Y.M. Microscale residual stresses in additively manufactured stainless steel. Nat. Commun. 2019, 10, 4338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Tomota, Y.; Harjo, S.; Gong, W.; Ohmura, T. In-situ neutron diffraction during tension-compression cyclic deformation of a pearlite steel. Mater. Sci. Eng. A 2016, 676, 522–530. [Google Scholar] [CrossRef]
- Young, M.L.; Almer, J.D.; Daymond, M.R.; Haeffner, D.R.; Dunand, D.C. Load partitioning between ferrite and cementite during elasto-plastic deformation of an ultrahigh-carbon steel. Acta Mater. 2007, 55, 1999–2011. [Google Scholar] [CrossRef]
- Shen, C.J.L.H. 3D finite element analysis of particle-reinforced aluminum. Mater. Sci. Eng. A 2002, 338, 271–281. [Google Scholar] [CrossRef] [Green Version]
- Dakhlaoui, R.; Baczmański, A.; Braham, C.; Wroński, S.; Wierzbanowski, K.; Oliver, E.C. Effect of residual stresses on individual phase mechanical properties of austeno-ferritic duplex stainless steel. Acta Mater. 2006, 54, 5027–5039. [Google Scholar] [CrossRef]
- Jagle, E.A.; Sheng, Z.; Kurnsteiner, P.; Ocylok, S.; Weisheit, A.; Raabe, D. Comparison of Maraging Steel Micro- and Nanostructure Produced Conventionally and by Laser Additive Manufacturing. Material 2016, 10, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asgari, H.; Mohammadi, M. Microstructure and mechanical properties of stainless steel CX manufactured by Direct Metal Laser Sintering. Mater. Sci. Eng. A 2018, 709, 82–89. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A.T.; Rubenchik, A.; King, W.E. Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. Acta Mater. 2016, 108, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Sallica-Leva, E.; Jardini, A.L.; Fogagnolo, J.B. Microstructure and mechanical behavior of porous Ti-6Al-4V parts obtained by selective laser melting. J. Mech. Behav. Biomed. Mater. 2013, 26, 98–108. [Google Scholar] [CrossRef]
- de Terris, T.; Andreau, O.; Peyre, P.; Adamski, F.; Koutiri, I.; Gorny, C.; Dupuy, C. Optimization and comparison of porosity rate measurement methods of Selective Laser Melted metallic parts. Addit. Manuf. 2019, 28, 802–813. [Google Scholar] [CrossRef]
- Gu, H.; Pal, D.; Rafi, K.; Starr, T.; Stucker, B. Influences of Energy Density on Porosity and Microstructure of Selective Laser Melted 17-4PH Stainless Steel. In Proceedings of the 24th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 12–14 August 2013. [Google Scholar]
- Wits, W.W.; Carmignato, S.; Zanini, F.; Vaneker, T.H.J. Porosity testing methods for the quality assessment of selective laser melted parts. CIRP Ann. 2016, 65, 201–204. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, S.H.; Cheng, M.; Song, H.W. In situ X-ray diffraction study of martensitic transformation in austenitic stainless steel during cyclic tensile loading and unloading. Scr. Mater. 2012, 67, 771–774. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lam, T.-N.; Wu, Y.-H.; Liu, C.-J.; Chae, H.; Lee, S.-Y.; Jain, J.; An, K.; Huang, E.-W. Transient Phase-Driven Cyclic Deformation in Additively Manufactured 15-5 PH Steel. Materials 2022, 15, 777. https://doi.org/10.3390/ma15030777
Lam T-N, Wu Y-H, Liu C-J, Chae H, Lee S-Y, Jain J, An K, Huang E-W. Transient Phase-Driven Cyclic Deformation in Additively Manufactured 15-5 PH Steel. Materials. 2022; 15(3):777. https://doi.org/10.3390/ma15030777
Chicago/Turabian StyleLam, Tu-Ngoc, Yu-Hao Wu, Chia-Jou Liu, Hobyung Chae, Soo-Yeol Lee, Jayant Jain, Ke An, and E-Wen Huang. 2022. "Transient Phase-Driven Cyclic Deformation in Additively Manufactured 15-5 PH Steel" Materials 15, no. 3: 777. https://doi.org/10.3390/ma15030777







