Evaluation of the Equivalent Mechanical Properties of Lattice Structures Based on the Finite Element Method
Abstract
:1. Introduction
2. Modeling and Validation
2.1. Mechanical Reduced-Order Model
2.2. Accuracy Verification
3. Equivalent Mechanical Properties
3.1. Method of Numerical Experiments
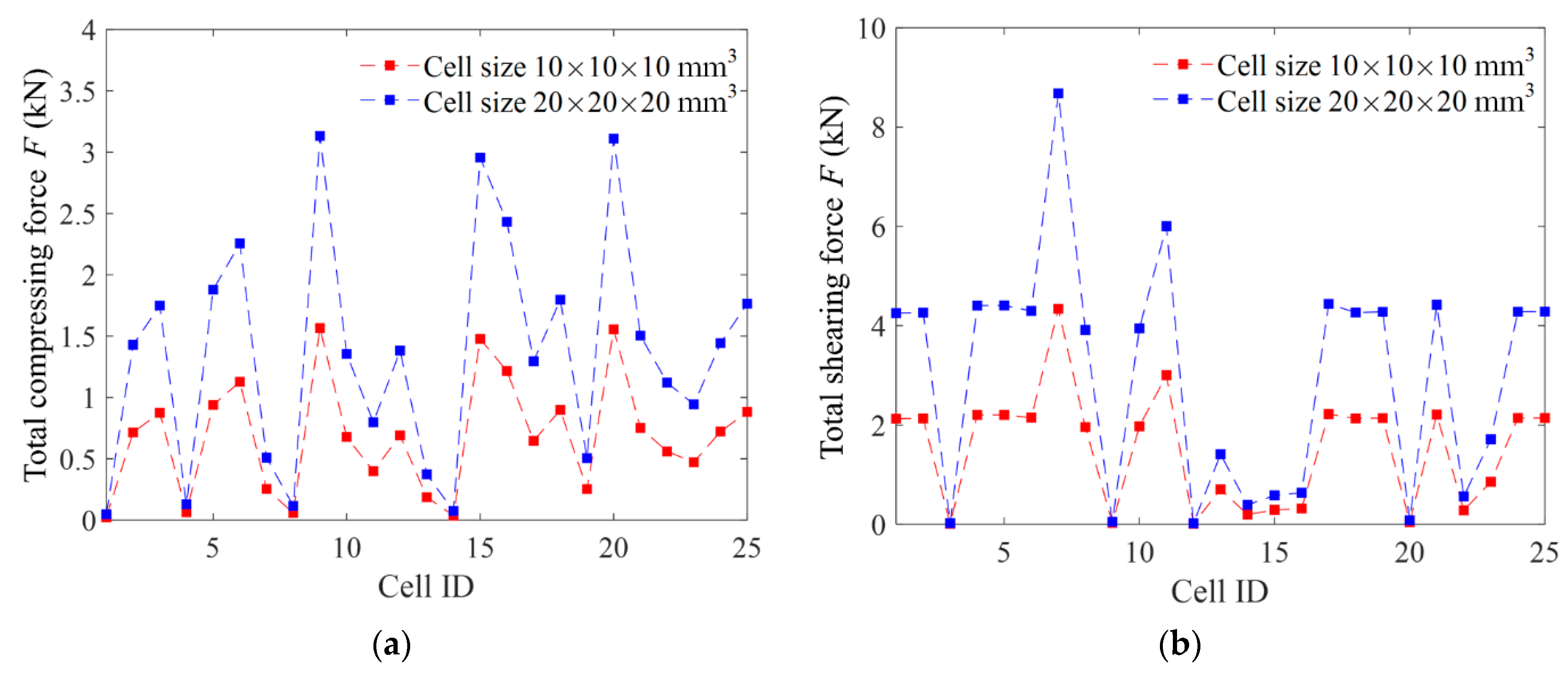
3.2. Effect of the Number of Lattice Cells
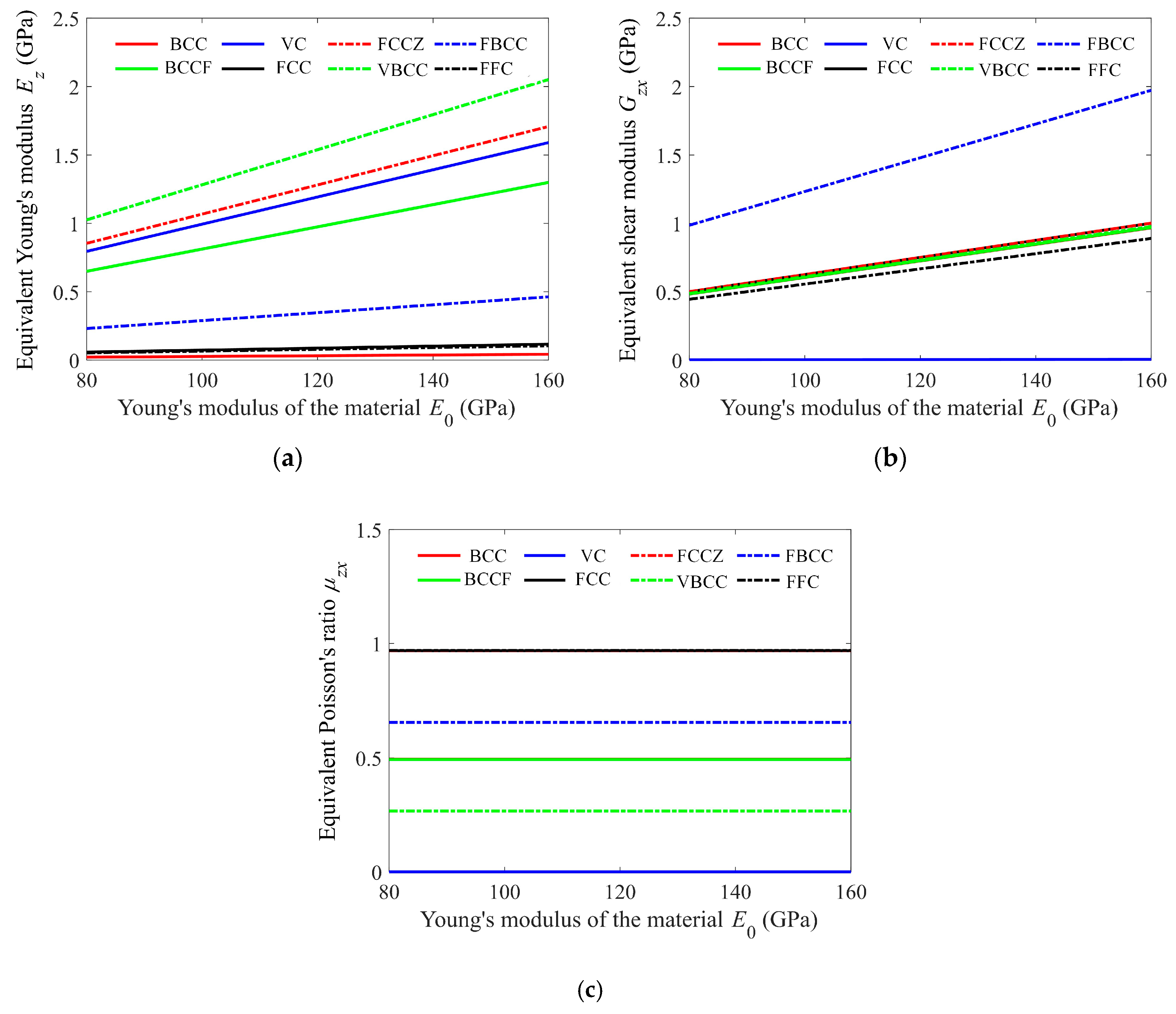
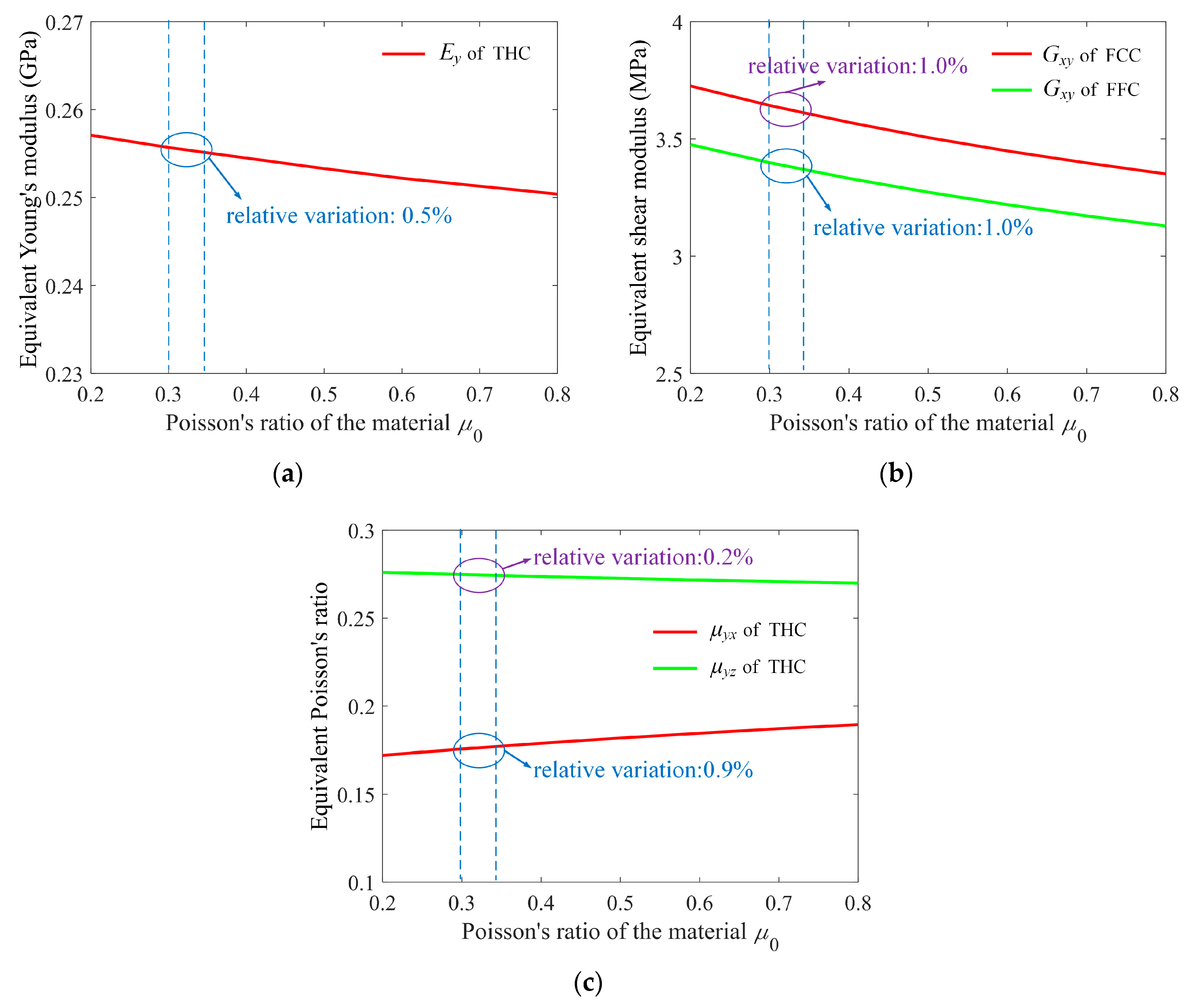
3.3. Effect of Material Properties
3.4. Effect of Cell Dimensions
3.5. Summary of Equivalent Mechanical Properties
4. Conclusions
- (1)
- A reduced-order mechanical model for a rod-like lattice structure was developed, and its accuracy was validated by comparing it with the solid-element full model, showing a relative difference smaller than 1.25% at the aspect ratio larger than 10.
- (2)
- The values of the equivalent mechanical properties change with the increase in the number of cells but tend to be stable at about 8 × 8 × 8 cells.
- (3)
- The equivalent Young’s modulus and shear modulus are linearly dependent on the material Young’s modulus but insensitive to the material Poisson’s ratio.
- (4)
- The equivalent Young’s modulus and shear modulus are the functions of the strut diameter, and the power of which is 2 to 4.
- (5)
- Analytical-fitting formulas of the equivalent Young’s modulus, shear modulus, and Poisson’s ratio of the 25 types of lattice cells were systematically given, which would be very useful to expedite the design and optimization procedures of structures containing a huge number of lattice cells.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbols and abbreviations | Denotation and full name |
| E | Young’s modulus (GPa/MPa) |
| μ | Poisson’s ratio |
| G | Shear modulus (GPa/MPa) |
| L | Size of the lattice structures (m) |
| u | Displacement in x direction (m) |
| v | Displacement in y direction (m) |
| w | Displacement in z direction (m) |
| θ | Flexural angle (rad) |
| P | Nodal load (N) |
| M | Nodal moment (N/m) |
| D | Strut diameter (mm) |
| a | Cell size (mm) |
| γ | Ratio of strut diameter to cell size |
| BCC | Body-centered cubic |
| BCCF | BCC with face-center |
| VC | vertex cubic |
| FCC | face-centered cubic |
| FCCZ | FCC with vertical strut in z-axis |
| VBCC | VC with BCC |
| FBCC | FCC with BCC |
| FFC | Face-face center cubic |
| VFC | Vertex-face center cubic |
| OC | Octahedron cubic |
| FC2R | Face center cubic with 2 rectangles |
| TAC | Tri-axis cubic |
| TCC | Tetrahedral center cubic |
| RD | Rhombic dodecahedron |
| RC | Rhombicuboctahedron |
| FPT | Flat-plate tesseract |
| ECC | Truncated hexagonal cubic |
| BCCZ | BCC with vertical strut in z-axis |
| BCCE | BCC with the edge |
| FECC | Face-edge-centered cubic |
| AFCC | All face-centered cubic |
| THC | Truncated hexagonal cubic |
| TC | Truncated cuboctahedron |
| BCCD | BCC with double-axis |
| BCCT | BCC with tri-axis |
References
- Wang, X.; Wang, C.; Zhou, X.; Wang, D.; Zhang, M.; Gao, Y.; Wang, L.; Zhang, P. Evaluating lattice mechanical properties for lightweight heat-resistant load-bearing structure design. Materials 2020, 13, 4786. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.X.; Cai, J.Q.; Xia, H.X.; Ao, X.H.; Liu, J.H. A reduced-order model based on finite element method for fast 390 prediction of thermal performance of lattice structures. Int. Commun. Heat Mass Transf. 2021, 126, 105347. [Google Scholar] [CrossRef]
- Wang, P.; Yang, F.; Zhao, J. Compression behaviors and mechanical properties of modified face-centered cubic lattice structures under quasi-static and high-speed loading. Materials 2022, 15, 1949. [Google Scholar] [CrossRef] [PubMed]
- Seharing, A.; Azman, A.H.; Abdullah, S. Finite element analysis of gradient lattice structure patterns for bone implant design. Int. J. Struct. Integr. 2020, 11, 535–545. [Google Scholar] [CrossRef]
- Chen, H.; Han, Q.; Wang, C.Y.; Liu, Y.; Chen, B.P.; Wang, J.C. Porous scaffold design for additive manufacturing in orthopedics: A review. Front. Bioeng. Biotechnol. 2020, 8, 609. [Google Scholar] [CrossRef]
- Pratama, L.K.; Santosa, S.P.; Dirgantara, T.; Widagdo, D. Design and numerical analysis of electric vehicle Li-Ion battery protections using lattice structure undergoing ground impact. World Electr. Veh. J. 2022, 13, 10. [Google Scholar] [CrossRef]
- Ren, X.; Xiao, L.; Hao, Z. Multi-property cellular material design approach based on the mechanical behaviour analysis of the reinforced lattice structure. Mater. Des. 2019, 174, 107785. [Google Scholar] [CrossRef]
- Kumar, A.; Collini, L.; Daurel, A.; Jeng, J.Y. Design and Additive Manufacturing of Closed Cells from Supportless Lattice Structure. Addit. Manuf. 2020, 33, 101168. [Google Scholar] [CrossRef]
- Yang, C.X.; Xu, K.; Xie, S.C. Comparative Study on the Uniaxial Behaviour of Topology-Optimised and Crystal-Inspired Lattice Materials. Metals 2020, 10, 491. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Banerjee, A.; Hoe, A.; Tamraparni, A.; Felts, J.R.; Shamberger, P.J.; Elwany, A. Design for laser powder bed additive manufacturing of AlSi12 periodic mesoscale lattice structures. Int. J. Adv. Manuf. Technol. 2021, 113, 3599–3612. [Google Scholar] [CrossRef]
- Hazeli, K.; Babamiri, B.B.; Indeck, J.; Minor, A.; Askari, H. Microstructure-topology relationship effects on the quasi-static and dynamic behavior of additively manufactured lattice structures. Mater. Des. 2019, 176, 107826. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, J.F.; Xiong, Y.; Chen, X.H.; Sun, Y.X.; Gong, C.; Pu, H.Y.; Wu, X.Y.; Luo, J. Influence of unit cell pose on the mechanical properties of Ti6Al4V lattice structures manufactured by selective laser melting. Addit. Manuf. 2020, 34, 101222. [Google Scholar] [CrossRef]
- Fernandes, R.; Tamijani, A. Design optimization of lattice structures with stress constraints. Mater. Des. 2021, 210, 110026. [Google Scholar] [CrossRef]
- Hajnys, J.; Pagac, M.; Zlamal, T.; Petru, J.; Kousal, L. Stiffness of 316L stainless steel support structures proposed for the SLM process. MATEC Web Conf. 2018, 244, 01008. [Google Scholar] [CrossRef]
- Han, C.J.; Yan, C.Z.; Wen, S.F.; Xu, T.; Li, S.; Liu, J.; Wei, Q.S.; Shi, Y.S. Effects of the unit cell topology on the compression properties of porous CoCr scaffolds fabricated via selective laser melting. Rapid Prototyp. J. 2017, 23, 16–27. [Google Scholar] [CrossRef]
- Dhiman, S.; Singh, M.; Sidhu, S.S.; Bahraminasab, M.; Pimenov, D.Y.; Mikolajczyk, T. Cubic lattice structures of Ti6Al4V under compressive loading: Towards assessing the performance for hard tissue implants alternative. Materials 2021, 14, 3866. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Yu, A.; Lu, X.; Tamaddon, M.; Wang, M.D.; Zhang, J.Z.; Zhang, J.L.; Qu, X.H.; Liu, C.Z.; Su, B. Design and performance evaluation of additively manufactured composite lattice structures of commercially pure Ti (CP–Ti). Bioact. Mater. 2021, 6, 1215–1222. [Google Scholar] [CrossRef]
- Liu, X.Y.; Wada, T.; Suzki, A.; Takata, N.; Kobashi, M.; Kato, M. Understanding and suppressing shear band formation in strut-based lattice structures manufactured by laser powder bed fusion. Mater. Des. 2021, 199, 109416. [Google Scholar] [CrossRef]
- Han, C.J.; Li, Y.; Wang, Q.; Wen, S.F.; Wei, Q.S.; Yan, C.Z.; Hao, L.; Liu, J.; Shi, Y.S. Continuous functionally graded porous titanium scaffolds manufactured by selective laser melting for bone implants. J. Mech. Behav. Biomed. Mater. 2018, 80, 119–127. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, J.F.; Chen, X.H.; Yi, C.Y.; Chen, R.; Zhang, Z.X. Configuration optimization design of Ti6Al4V lattice structure formed by SLM. Materials 2018, 11, 1856. [Google Scholar] [CrossRef] [Green Version]
- Zhong, T.L.; He, K.T.; Li, H.X.; Yang, L.C. Mechanical properties of lightweight 316L stainless steel lattice structures fabricated by selective laser melting. Mater. Des. 2019, 181, 108076. [Google Scholar] [CrossRef]
- Bai, L.; Yi, C.Y.; Chen, X.H.; Sun, Y.X.; Zhang, J.F. Effective Design of the Graded Strut of BCC Lattice Structure for Improving Mechanical Properties. Materials 2019, 12, 2192. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, W.M.; Liu, Y.F.; Jiang, X.F.; Dong, X.T.; Jun, J.; Baur, D.A.; Xu, J.J.; Pan, H.; Xu, X. Bionic mechanical design and 3D printing of novel porous Ti6Al4V implants for biomedical applications. J. Zhejiang Univ. Sci. B 2019, 20, 647–659. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Mertens, R.; Ferrucci, M.; Yan, C.Z.; Shi, Y.S.; Yang, S.F. Continuous graded Gyroid cellular structures fabricated by selective laser melting: Design, manufacturing and mechanical properties. Mater. Des. 2019, 162, 394–404. [Google Scholar] [CrossRef]
- Alaña, M.; Lopez-Arancibia, A.; Pradera-Mallabiabarrena, A.; Galarreta, S.R.D. Analytical model of the elastic behavior of a modified face-centered cubic lattice structure. J. Mech. Behav. Biomed. Mater. 2019, 98, 357–368. [Google Scholar] [CrossRef]
- Zhao, C.; Li, G.X.; Zhang, M.; Luo, W.P. A discretization method for predicting the equivalent elastic parameters of the graded lattice structure. Adv. Mech. Eng. 2020, 12, 1687814020984375. [Google Scholar] [CrossRef]
- Shi, X.; Liao, W.H.; Liu, T.T.; Zhang, C.D.; Li, D.W.; Jiang, W.M.; Wang, C.; Ren, F.X. Design optimization of multimorphology surface-based lattice structures with density gradients. Int. J. Adv. Manuf. Technol. 2021, 117, 2013–2028. [Google Scholar] [CrossRef]
- Dejean, T.T.; Mohr, D. Stiffness and specific energy absorption of additively-manufactured metallic BCC metamaterials composed of tapered beams. Int. J. Mech. Sci. 2018, 141, 101–116. [Google Scholar] [CrossRef]
- Červinek, O.; Werner, B.; Koutný, D.; Vaverka, O.; Pantělejev, L.; Paloušek, D. Computational approaches of quasi-static compression loading of SS316L lattice structures made by selective laser melting. Materials 2021, 14, 2462. [Google Scholar] [CrossRef]
- Wang, S.; Liu, L.L.; Li, K.; Zhu, L.C.; Chen, J.; Hao, Y.Q. Pore functionally graded Ti6Al4V scaffolds for bone tissue engineering application. Mater. Des. 2019, 168, 107643. [Google Scholar] [CrossRef]
- Zhang, W.J.; Zhao, S.Y.; Sun, R.J.; Scarpa, F.; Wang, J.W. In-plane mechanical behavior of a new star-re-entrant hierarchical metamaterial. Polymers 2019, 11, 1132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quan, C.; Han, B.; Hou, Z.H.; Lu, T.J. 3D printed continuous fiber reinforced composite auxetic honeycomb structures. Compos. Part B Eng. 2020, 187, 107858. [Google Scholar] [CrossRef]
- Libonati, F.; Graziosi, S.; Ballo, F.; Mognato, M.; Sala, G. 3D-Printed Architected Materials Inspired by Cubic Bravais Lattices. ACS Biomater. Sci. Eng. 2021. [Google Scholar] [CrossRef]
- De Galarreta, S.R.; Jeffers, J.R.T.; Ghouse, S. A validated finite element analysis procedure for porous structures. Mater. Des. 2020, 189, 108546. [Google Scholar] [CrossRef]
- Qi, C.; Jiang, F.; Yang, S. Advanced honeycomb designs for improving mechanical properties: A review. Compos. Part B Eng. 2021, 227, 109393. [Google Scholar] [CrossRef]
- Tao, R.; Ji, L.T.; Li, Y.; Wan, Z.; Hu, W.; Wu, W.; Liao, B.; Ma, L.; Fang, D. 4D printed origami metamaterials with tunable compression twist behavior and stress-strain curves. Compos. Part B Eng. 2020, 201, 108344. [Google Scholar] [CrossRef]
- Pan, C.; Han, Y.F.; Lu, J.P. Design and optimization of lattice structures: A review. Appl. Sci. 2020, 10, 6374. [Google Scholar] [CrossRef]






| Loading | Aspect Ratio | 5 | 10 | 20 | |
|---|---|---|---|---|---|
| Compressing | Force(N) | Full model | 7.135 | 0.4257 | 0.02647 |
| Reduced-order model | 6.708 | 0.4204 | 0.02629 | ||
| Absolute error (N) | 0.427 | 0.0053 | 0.00018 | ||
| Relative error | 5.98% | 1.25% | 0.68% | ||
| Shearing | Force(N) | Full model | 27.801 | 1.697 | 0.1044 |
| Reduced-order model | 26.534 | 1.677 | 0.1051 | ||
| Absolute error (N) | 1.267 | 0.081 | 0.0007 | ||
| Relative error | 4.56% | 1.18% | 0.67% | ||
| Name | Cell Type | An Instance of Ei, Gij, and μij | Formulas of Ei, Gij, and μij |
|---|---|---|---|
| BCC | 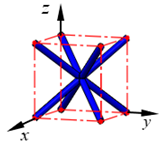 | ||
| BCCF |  | ||
| VC | 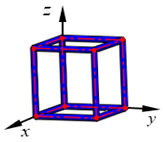 | ||
| FCC | 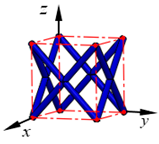 | ||
| FCCZ |  | ||
| VBCC |  | ||
| FBCC | 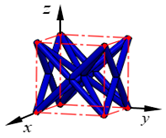 | ||
| FFC | 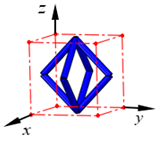 | ||
| VFC |  | ||
| OC |  | ||
| FC2R | 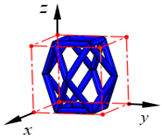 | ||
| TAC | 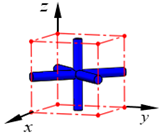 | ||
| TCC | 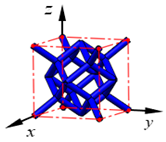 | ||
| RD |  | ||
| RC |  | ||
| FPT | 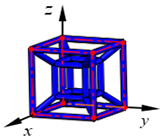 | ||
| ECC | 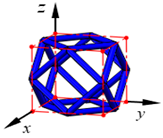 | ||
| BCCZ |  | ||
| BCCE | 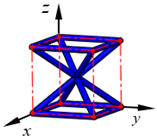 | ||
| FECC | 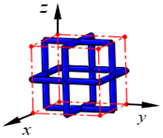 | ||
| AFCC | 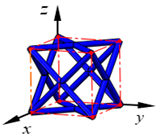 | ||
| THC | 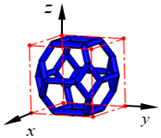 | ||
| TC | 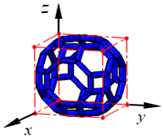 | ||
| BCCD | 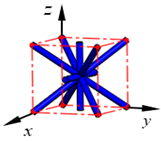 | ||
| BCCT | 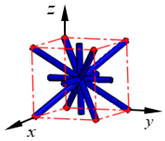 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, H.; Meng, J.; Liu, J.; Ao, X.; Lin, S.; Yang, Y. Evaluation of the Equivalent Mechanical Properties of Lattice Structures Based on the Finite Element Method. Materials 2022, 15, 2993. https://doi.org/10.3390/ma15092993
Xia H, Meng J, Liu J, Ao X, Lin S, Yang Y. Evaluation of the Equivalent Mechanical Properties of Lattice Structures Based on the Finite Element Method. Materials. 2022; 15(9):2993. https://doi.org/10.3390/ma15092993
Chicago/Turabian StyleXia, Huanxiong, Junfeng Meng, Jianhua Liu, Xiaohui Ao, Shengxiang Lin, and Ye Yang. 2022. "Evaluation of the Equivalent Mechanical Properties of Lattice Structures Based on the Finite Element Method" Materials 15, no. 9: 2993. https://doi.org/10.3390/ma15092993






