Template-Based Geometric Simulation of Flexible Frameworks
Abstract
:1. Introduction
2. Comparison to Conventional Simulation Methods
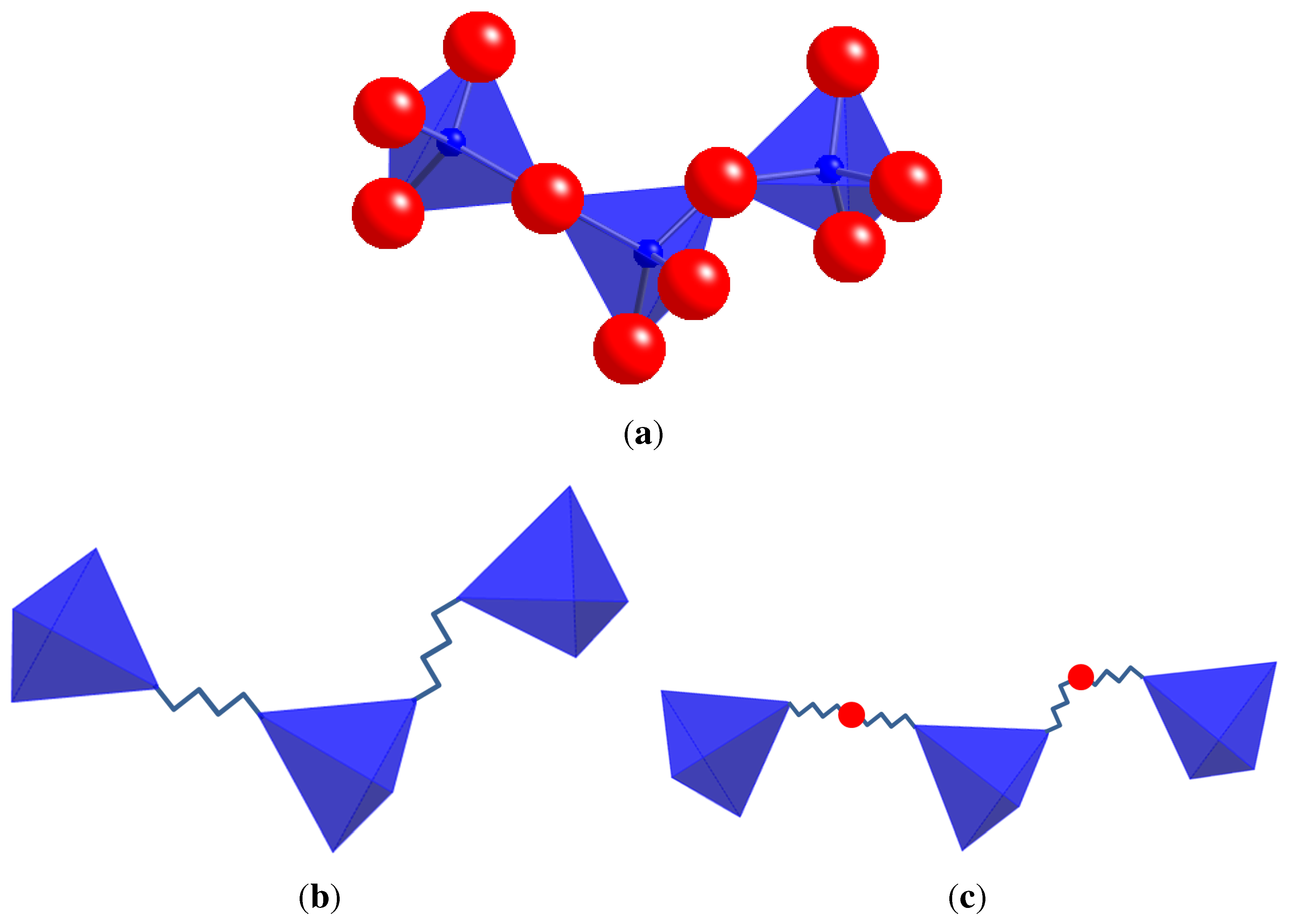
3. Templates for Geometric Analysis and Simulation
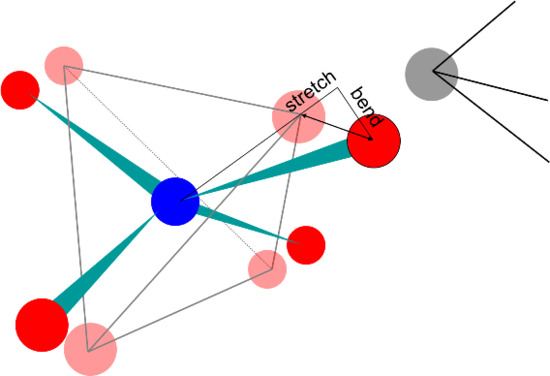
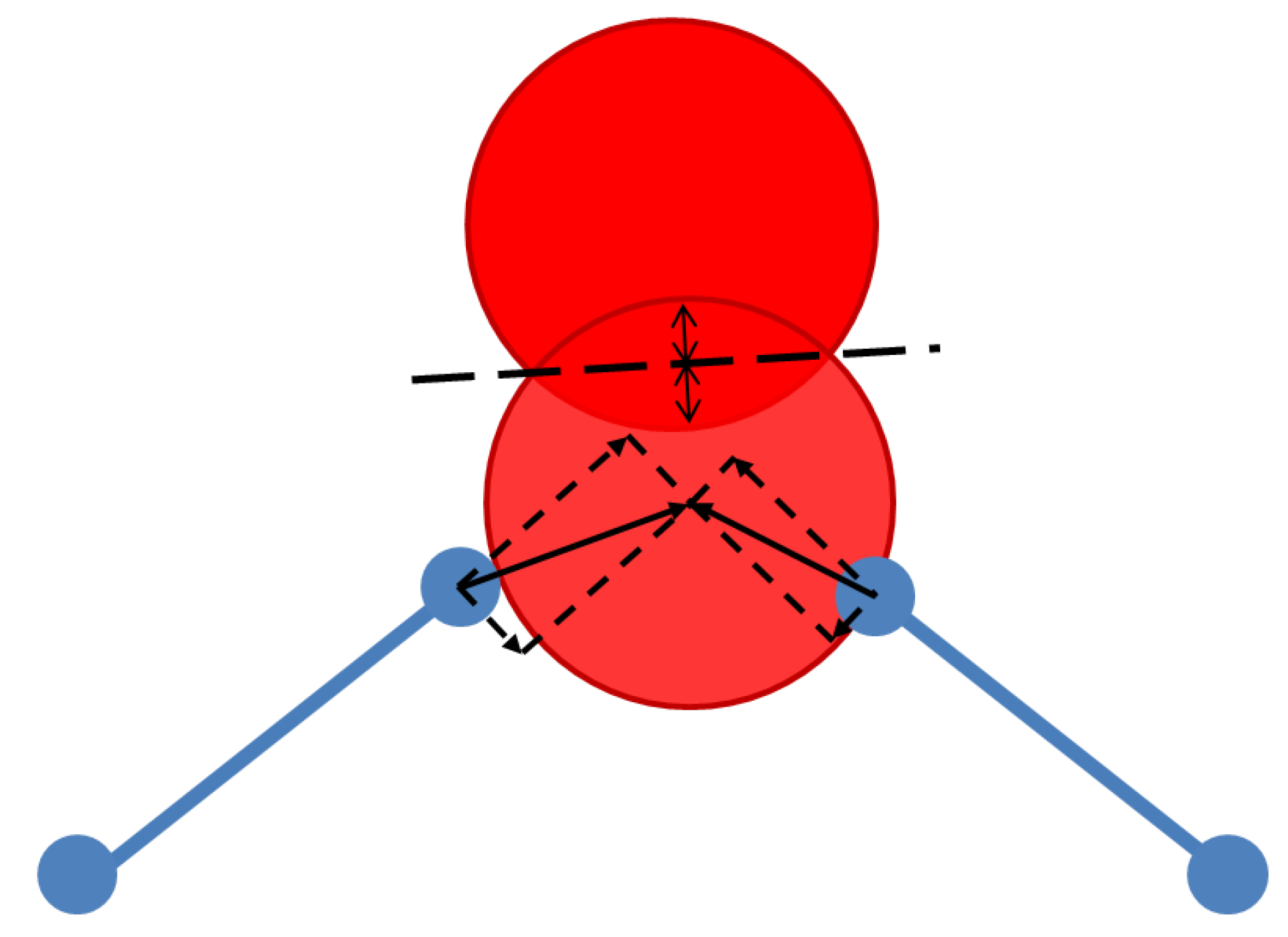
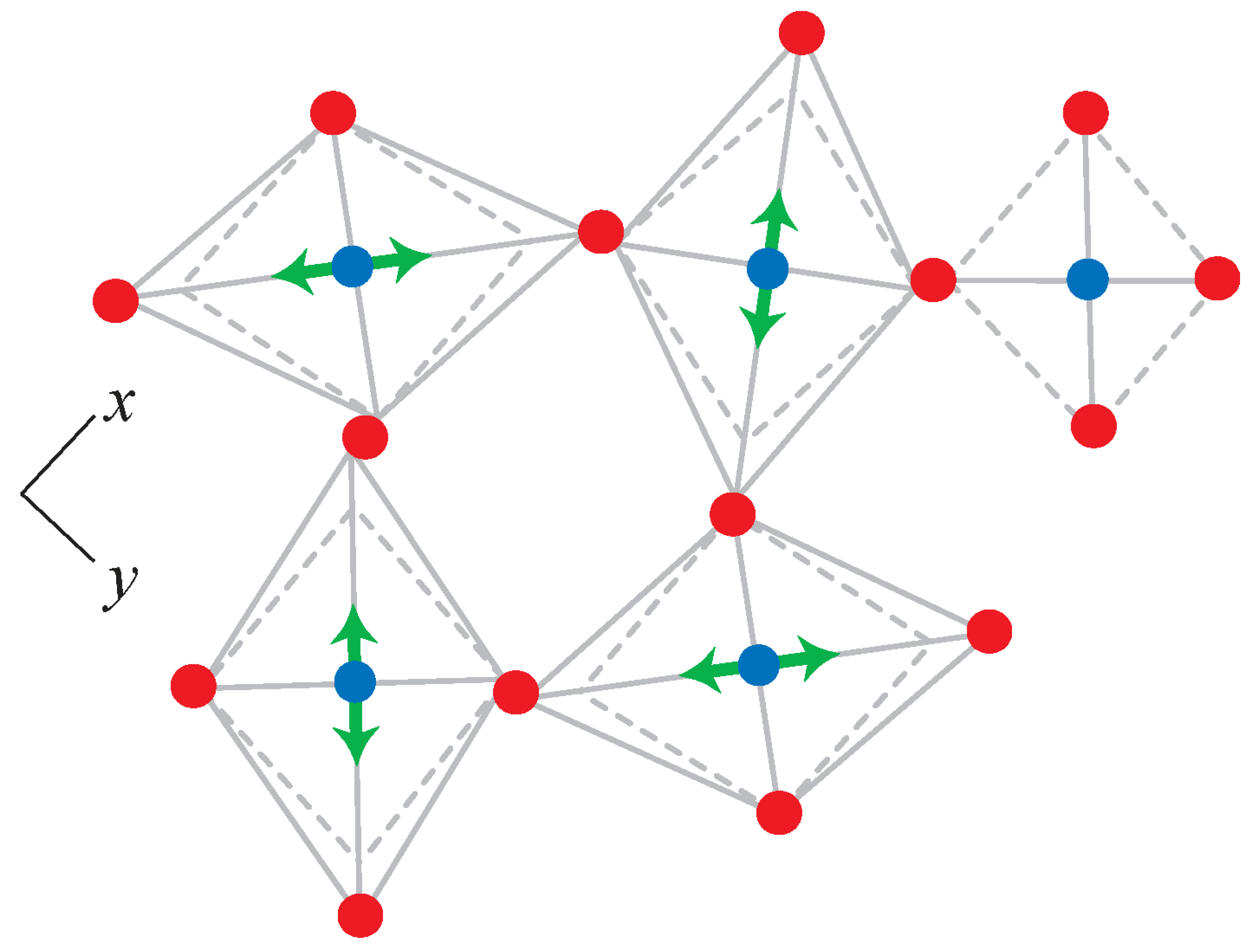
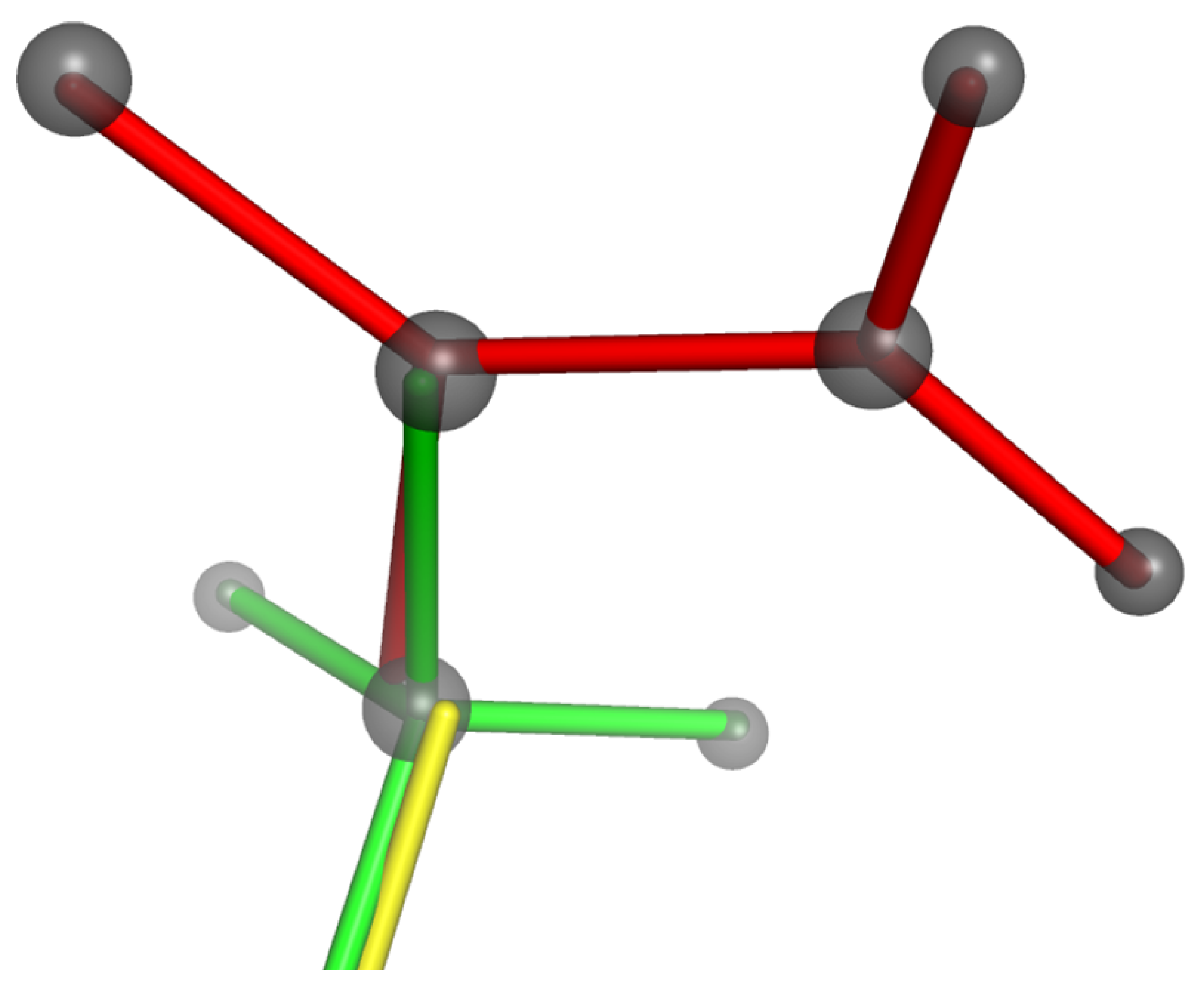
3.1. Polyhedral Alignment and Residual Mismatch
3.2. Force Models in Geometric Simulation
4. Applications of Geometric Analysis and Simulation
4.1. Dynamic Disorder in Frameworks
4.2. Framework Flexibility and Motion
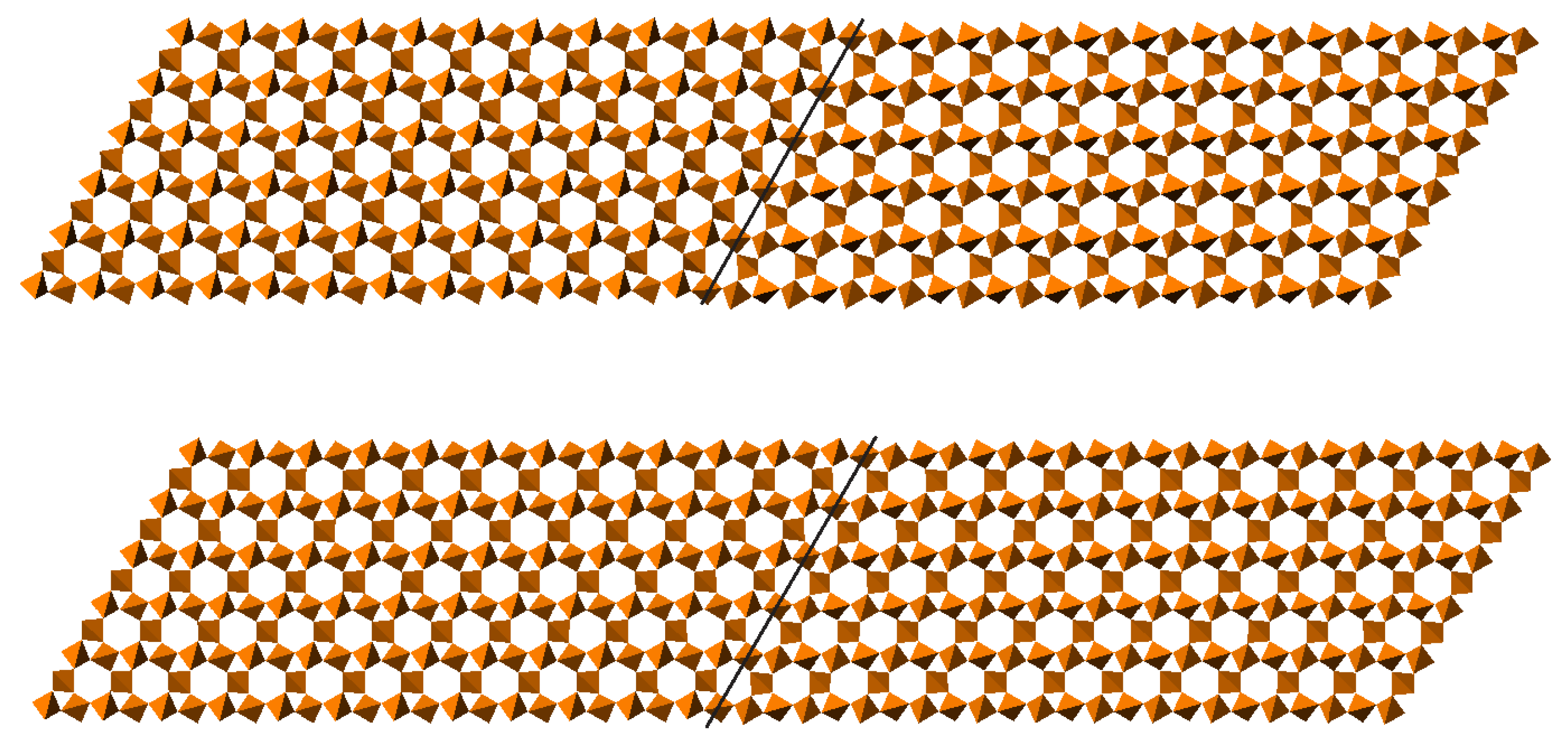
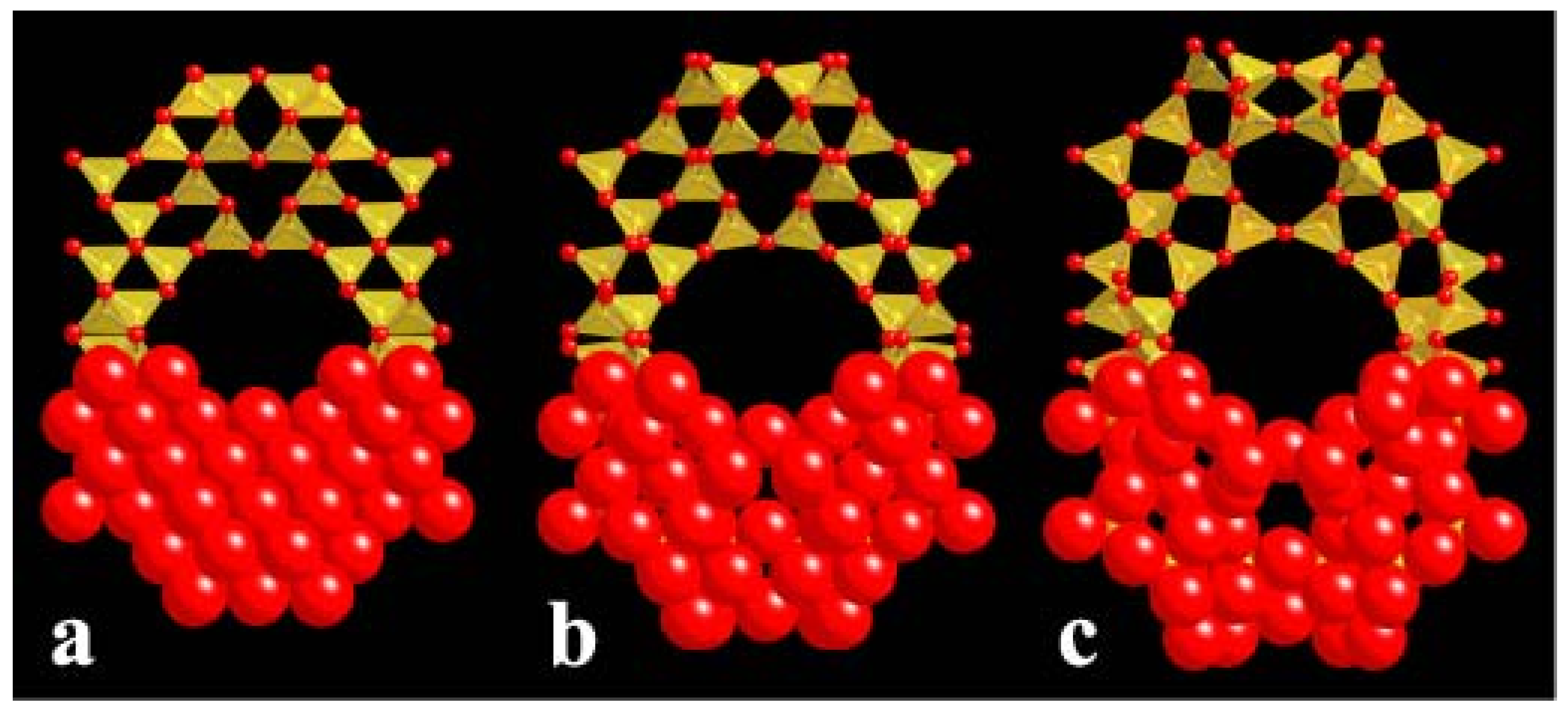
4.3. Compression Mechanisms in Zeolites
4.4. Generation of Hypothetical Zeolites
4.5. Application to Manganites: Modelling of Jahn–Teller Distortion
4.6. The Flexibility Window of Zeolites
4.7. Phase Transitions in Zeolites
4.8. Application to Proteins
5. Availability of Geometric Simulation Codes
Acknowledgements
References
- Wragg, D.S.; Morris, R.S.; Burton, A.W. Pure silica zeolite-type frameworks: A structural analysis. Chem. Mater. 2008, 20, 1561–1570. [Google Scholar] [CrossRef]
- Baur, W.H. Straight Si–O–Si bridging bonds do exist in silicates and silicon dioxide polymorphs. Acta Crystallogr. 1980, B36, 2198–2202. [Google Scholar] [CrossRef]
- Dove, M.T.; Heine, V.; Hammonds, K.D. Rigid unit modes in framework silicates. Mineral. Mag. 1995, 59, 629–639. [Google Scholar] [CrossRef]
- Dove, M.T.; Pryde, A.K.A.; Heine, V.; Hammonds, K.D. Exotic distributions of rigid unit modes in the reciprocal spaces of framework aluminosilicates. J. Phys. Condens. Matter 2007, 19, 275209. [Google Scholar] [CrossRef]
- Hammonds, K.D.; Dove, M.T.; Giddy, A.P.; Heine, V. CRUSH: A FORTRAN program for the analysis of the rigid unit mode spectrum of a framework structure. Am. Mineral. 1994, 79, 1207–1209. [Google Scholar]
- Giddy, A.P.; Dove, M.T.; Pawley, G.S.; Heine, V. The determination of rigid unit modes as potential soft modes for displacive phase transitions in framework crystal structures. Acta Crystallogr. 1993, A49, 697–703. [Google Scholar] [CrossRef]
- Wells, S.A.; Dove, M.T.; Tucker, M.G.; Trachenko, K. Real-space rigid-unit-mode analysis of dynamic disorder in quartz, cristobalite and amorphous silica. J. Phys. Condens. Matter 2002, 14, 4645. [Google Scholar] [CrossRef]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1995, 93, 629–637. [Google Scholar] [CrossRef]
- Bozin, E.S.; Sartbaeva, A.; Zheng, H.; Wells, S.A.; Mitchell, J.F.; Proffen, T.; Thorpe, M.F.; Billinge, S.J.L. Structure of CaMnO3 in the range 10K–550K from neutron time-of-flight total scattering. J. Phys. Chem. Solids 2008, 69, 2146–2150. [Google Scholar] [CrossRef]
- Wells, S.A.; Dove, M.T.; Tucker, M.G. Finding best-fit polyhedral rotations with geometric algebra. J. Phys. Condens. Matter 2002, 14, 4567–4584. [Google Scholar] [CrossRef]
- Sartbaeva, A.; Wells, S.A.; Redfern, S.A.T. Li+ ion motion in quartz and β-eucryptite studied by dielectric spectroscopy and atomistic simulations. J. Phys. Condens. Matter 2004, 16, 8173–8189. [Google Scholar] [CrossRef]
- Sartbaeva, A.; Wells, S.A.; Redfern, S.A.T.; Hinton, R.W.; Reed, S.J.B. Ionic diffusion in quartz studied by transport measurements, SIMS and atomistic simulations. J. Phys. Condens. Matter 2005, 17, 1099–1112. [Google Scholar] [CrossRef]
- Bornhauser, J.B.; Bougeard, D. Intensities of the vibrational spectra of siliceous zeolites by molecular dynamics calculations II—Raman spectra. J. Raman Spectrosc. 2001, 32, 279–285. [Google Scholar] [CrossRef]
- Baerlocher, C.; Hepp, A.; Meier, W.M. DLS-76, A FORTRAN Program for the Simulation of Crystal Structures by Geometric Refinement; Institut fur Kristallographie and Petrographie ETH: Zurich, Switzerland, 1978. [Google Scholar]
- Kapko, V.; Dawson, C.; Treacy, M.M.J.; Thorpe, M.F. Flexibility of ideal zeolite frameworks. Phys. Chem. Chem. Phys. 2010, 12, 8531–8541. [Google Scholar] [CrossRef] [PubMed]
- Kapko, V.; Dawson, C.; Rivin, I.; Treacy, M.M.J. Density of mechanisms within the flexibility window of zeolites. Phys. Rev. Lett. 2011, 107, 164304. [Google Scholar] [CrossRef] [PubMed]
- Dove, M.T.; Tucker, M.G.; Keen, D.A. Neutron total scattering method: Simultaneous determination of long-range and short-range order in disordered materials. Eur. J. Mineral. 2002, 14, 331–348. [Google Scholar] [CrossRef]
- Wells, S.A.; Dove, M.T.; Tucker, M.G. Reverse Monte Carlo with geometric analysis—RMC + GA. J. Appl. Crystallogr. 2004, 37, 536–544. [Google Scholar] [CrossRef]
- Keen, D.A.; Tucker, M.G.; Dove, M.T. Reverse Monte Carlo modelling of crystalline disorder. J. Phys. Condens. Matter 2005, 17, S15–S22. [Google Scholar] [CrossRef]
- Kimizuka, H.; Kaburaki, H.; Kogue, Y. Molecular-dynamics study of the high-temperature elasticity of quartz above the alpha-beta phase transition. Phys. Rev. B 2003, 167, 024105. [Google Scholar] [CrossRef]
- Goodwin, A.L.; Redfern, S.A.T.; Dove, M.T.; Keen, D.A.; Tucker, M.G. Ferroelectric nanoscale domains and the 905 K phase transition in SrSnO3: A neutron total-scattering study. Phys. Rev. B 2007, 76, 174114. [Google Scholar] [CrossRef]
- Hui, Q.; Tucker, M.G.; Dove, M.T.; Wells, S.A.; Keen, D.A. Total scattering and reverse Monte Carlo study of the 105 K displacive phase transition in strontium titanate. J. Phys. Condens. Matter 2005, 17, S111–S124. [Google Scholar] [CrossRef]
- Tucker, M.G.; Goodwin, A.L.; Dove, M.T.; Keen, D.A.; Wells, S.A.; Evans, J.S.O. Negative thermal expansion in ZrW2O8: Mechanisms, rigid unit modes, and neutron total scattering. Phys. Rev. Lett. 2005, 95, 255501. [Google Scholar] [CrossRef] [PubMed]
- Conterio, M.J.; Goodwin, A.L.; Tucker, M.G.; Keen, D.A.; Dove, M.T.; Peters, L.; Evans, S.O. Local structure in Ag3[Co(CN)6]: Colossal thermal expansion, rigid unit modes and argentophilic interactions. J. Phys. Condens. Matter 2008, 20, 255225. [Google Scholar] [CrossRef]
- Goodwin, A.L. The crystallography of flexibility: Local structure and dynamics in framework materials. Z. Krist. 2009, 30, 1–11. [Google Scholar] [CrossRef]
- Sartbaeva, A.; Redfern, S.A.T.; Lee, W.T. A neutron diffraction and Rietveld analysis of cooperative Li motion in beta-eucryptite. J. Phys. Condens. Matter 2004, 16, 5267–5278. [Google Scholar] [CrossRef]
- Wragg, D.S.; Akporiaye, D.; Fjellvag, H. Direct observation of catalyst behaviour under real working conditions with X-ray diffraction: Comparing SAPO-18 and SAPO-34 methanol to olefin catalysts. J. Catal. 2011, 279, 397–402. [Google Scholar] [CrossRef]
- Goodwin, A.L.; Wells, S.A.; Dove, M.T. Cation substitution and strain screening in framework structures: The role of rigid unit modes. Chem. Geol. 2006, 225, 213–221. [Google Scholar] [CrossRef]
- Gatta, G.D.; Wells, S.A. Rigid unit modes at high pressure: An explorative study of a fibrous zeolite-like framework with EDI topology. Phys. Chem. Miner. 2004, 31, 1–10. [Google Scholar] [CrossRef]
- Gatta, G.D.; Wells, S.A. Structural evolution of zeolite levyne under hydrostatic and non-hydrostatic pressure: Geometric modelling. Phys. Chem. Miner. 2006, 33, 1–10. [Google Scholar] [CrossRef]
- Zwijnenburg, M.A.; Simperler, A.; Wells, S.A.; Bell, R.G. Tetrahedral distortion and energetic packing penalty in “zeolite” frameworks: Linked phenomena? J. Phys. Chem. B 2005, 109, 14783–14785. [Google Scholar] [CrossRef] [PubMed]
- Treacy, M.M.J.; Randall, K.H.; Rao, S.; Perry, J.A.; Chadi, D.J. Enumeration of periodic tetrahedral frameworks. Z. Krist. 1997, 212, 768–791. [Google Scholar] [CrossRef]
- Treacy, M.M.J.; Rivin, I.; Balkovsky, E.; Randall, K.H.; Foster, M.D. Enumeration of periodic tetrahedral frameworks. II. Polynodal graphs. Microporous Microporous Mater. 2004, 74, 121–132. [Google Scholar] [CrossRef]
- Boisen, M.B.; Gibbs, G.V.; Bukowinski, M.S.T. Framework silica structures generated using simulated annealing with a potential energy function based on an H6Si2O7 molecule. Phys. Chem. Miner. 1994, 21, 269–284. [Google Scholar] [CrossRef]
- Wells, S.A.; Foster, M.D.; Treacy, M.M.J. A simple geometric structure optimizer for accelerated detection of infeasible zeolite graphs. Microporous Microporous Mater. 2007, 93, 151–157. [Google Scholar] [CrossRef]
- Sartbaeva, A.; Wells, S.A.; Thorpe, M.F.; Bozin, E.S.; Billinge, S.J.L. Quadrupolar ordering in LaMnO3 revealed from scattering data and geometric modelling. Phys. Rev. Lett. 2007, 99, 155503. [Google Scholar] [CrossRef] [PubMed]
- Sartbaeva, A.; Wells, S.A.; Thorpe, M.F.; Bozin, E.S.; Billinge, S.J.L. Geometric simulation of perovskite frameworks with Jahn-Teller distortions: Applications to the cubic manganites. Phys. Rev. Lett. 2006, 97, 065501. [Google Scholar] [CrossRef] [PubMed]
- Billinge, S.J.L. Nanoscale structural order from the atomic pair distribution function (PDF): There’s plenty of room in the middle. J. Solid State Chem. 2008, 181, 1695–1700. [Google Scholar] [CrossRef]
- Sartbaeva, A.; Wells, S.A.; Treacy, M.M.J.; Thorpe, M.F. The flexibility window in zeolites. Nat. Mater. 2006, 5, 962–965. [Google Scholar] [CrossRef] [PubMed]
- Rivin, I. Geometric simulations: A lesson from virtual zeolites. Nat. Mater. 2006, 5, 931–932. [Google Scholar] [CrossRef] [PubMed]
- Sartbaeva, A.; Gatta, G.D.; Wells, S.A. Flexibility window controls pressure-induced phase transition in analcime. Europhys. Lett. 2008, 83, 26002. [Google Scholar] [CrossRef]
- Gatta, G.D.; Sartbaeva, A.; Wells, S.A. Compression behaviour and flexibility window of the analcime-like feldspathoids: Experimental and theoretical findings. Eur. J. Mineral. 2009, 21, 571–580. [Google Scholar] [CrossRef]
- Wells, S.A.; Sartbaeva, A.; Gatta, G.D. Flexibility windows and phase transitions of ordered and disordered ANA framework zeolites. Europhys. Lett. 2011, 94, 56001. [Google Scholar] [CrossRef]
- Wells, S.A.; Menor, S.; Hespenheide, B.M.; Thorpe, M.F. Constrained geometric simulation of diffusive motion in proteins. Phys. Biol. 2005, 2, S127–S136. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, D.J.; Rader, A.J.; Kuhn, L.A.; Thorpe, M.F. Protein flexibility predictions using graph theory. Proteins Struct. Funct. Bioinfom. 2001, 44, 150–165. [Google Scholar] [CrossRef] [PubMed]
- Farrell, D.W.; Speranskiy, K.; Thorpe, M.F. Generating stereochemically acceptable protein pathways. Proteins Struct. Funct. Bioinfom. 2010, 78, 2908–2921. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.; Rippmann, F.; Barnickel, G.; Gohlke, H. A normal mode-based geometric simulation approach for exploring biologically relevant conformational transitions in proteins. J. Chem. Inform. Model. 2011, 51, 1604–1622. [Google Scholar] [CrossRef] [PubMed]
- Jimenez-Roldan, J.E.; Freedman, R.B.; Roemer, R.A.; Wells, S.A. Protein flexibility explored with normal modes and geometric simulation. Phys. Biol. 2012, 9, 016008. [Google Scholar] [CrossRef] [PubMed]

© 2012 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)
Share and Cite
Wells, S.A.; Sartbaeva, A. Template-Based Geometric Simulation of Flexible Frameworks. Materials 2012, 5, 415-431. https://doi.org/10.3390/ma5030415
Wells SA, Sartbaeva A. Template-Based Geometric Simulation of Flexible Frameworks. Materials. 2012; 5(3):415-431. https://doi.org/10.3390/ma5030415
Chicago/Turabian StyleWells, Stephen A., and Asel Sartbaeva. 2012. "Template-Based Geometric Simulation of Flexible Frameworks" Materials 5, no. 3: 415-431. https://doi.org/10.3390/ma5030415
APA StyleWells, S. A., & Sartbaeva, A. (2012). Template-Based Geometric Simulation of Flexible Frameworks. Materials, 5(3), 415-431. https://doi.org/10.3390/ma5030415