Formation of Degenerate Band Gaps in Layered Systems
Abstract
:1. Introduction
2. Formation of Degenerate Band Gaps
2.1. Formation of Degenerate Band Gaps Inside a Passing Band
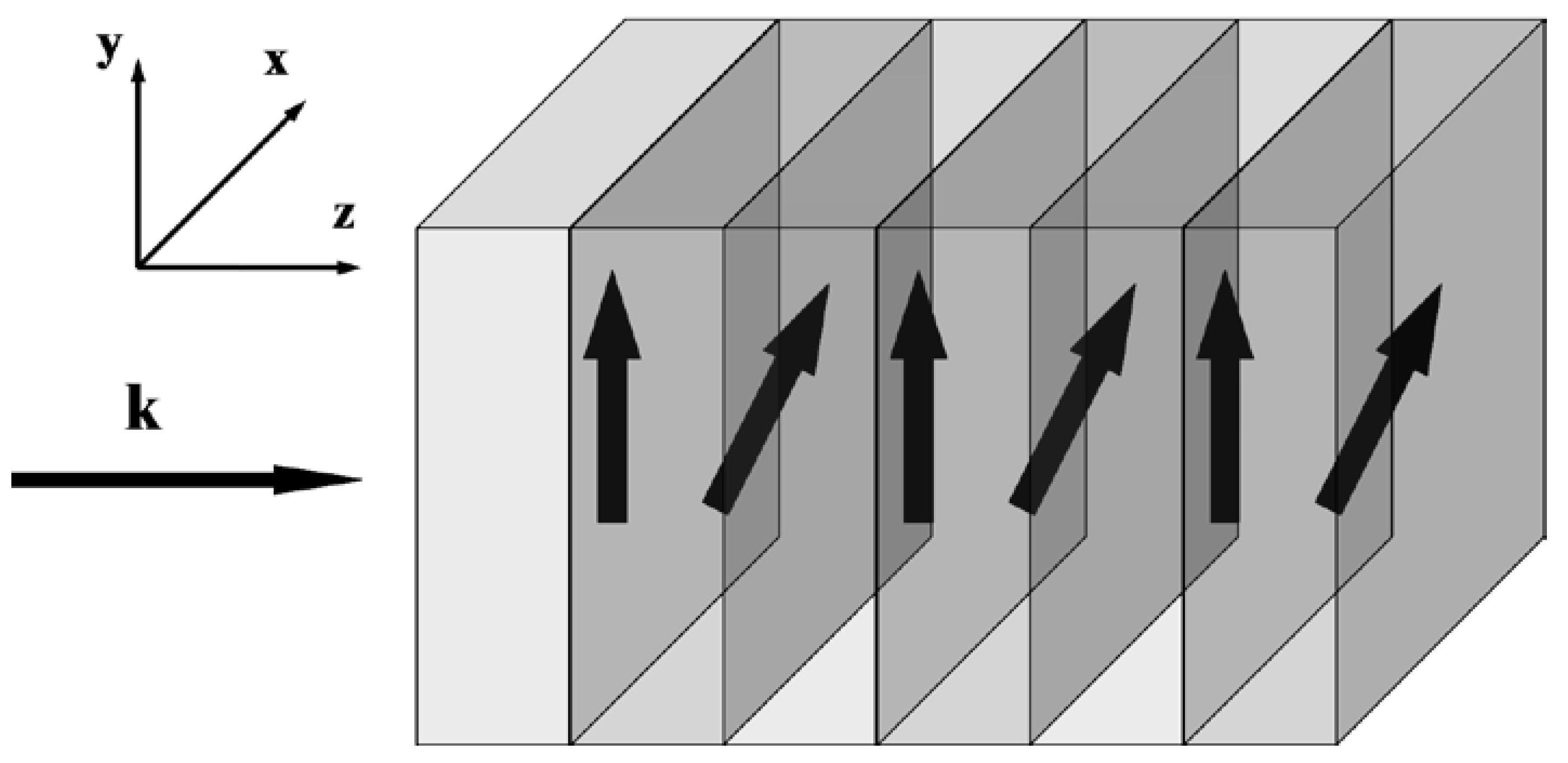
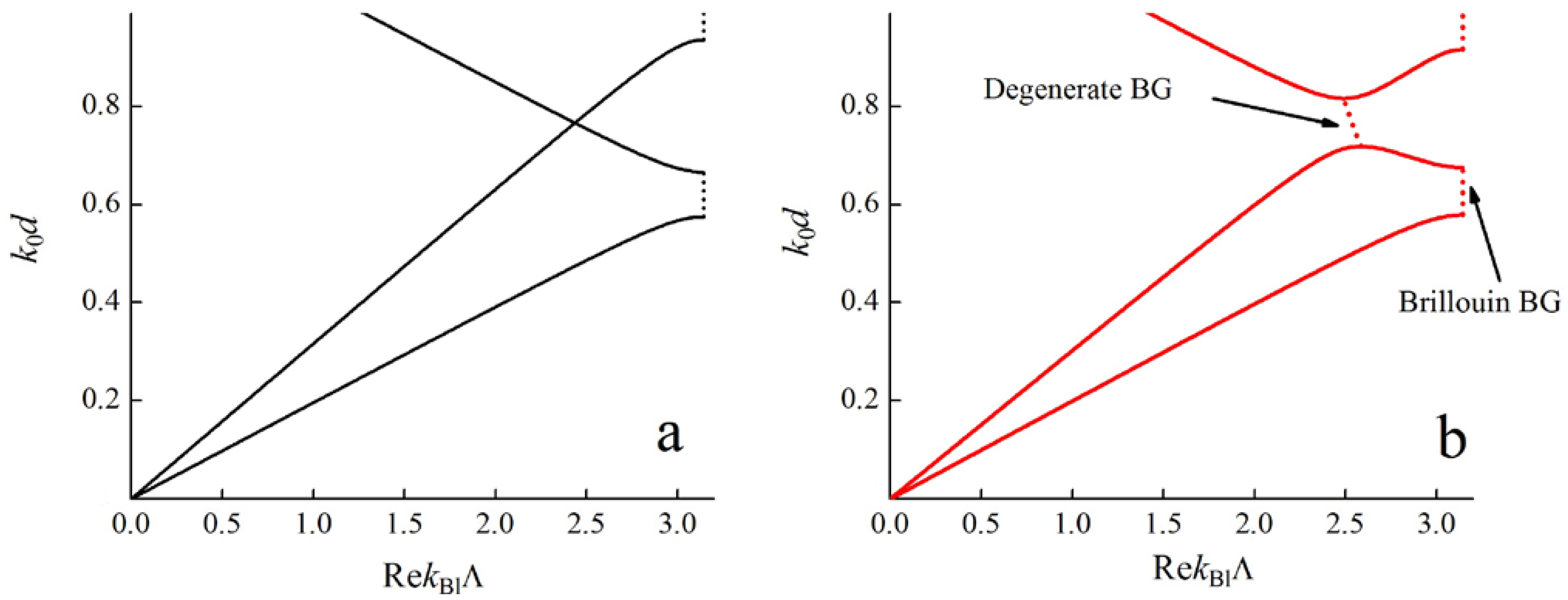
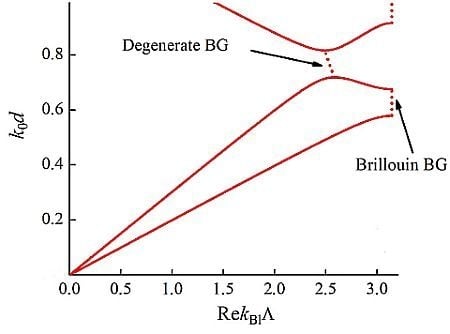
2.2. Formation of Degenerate Band Gaps Inside a Brillouin Band Gap
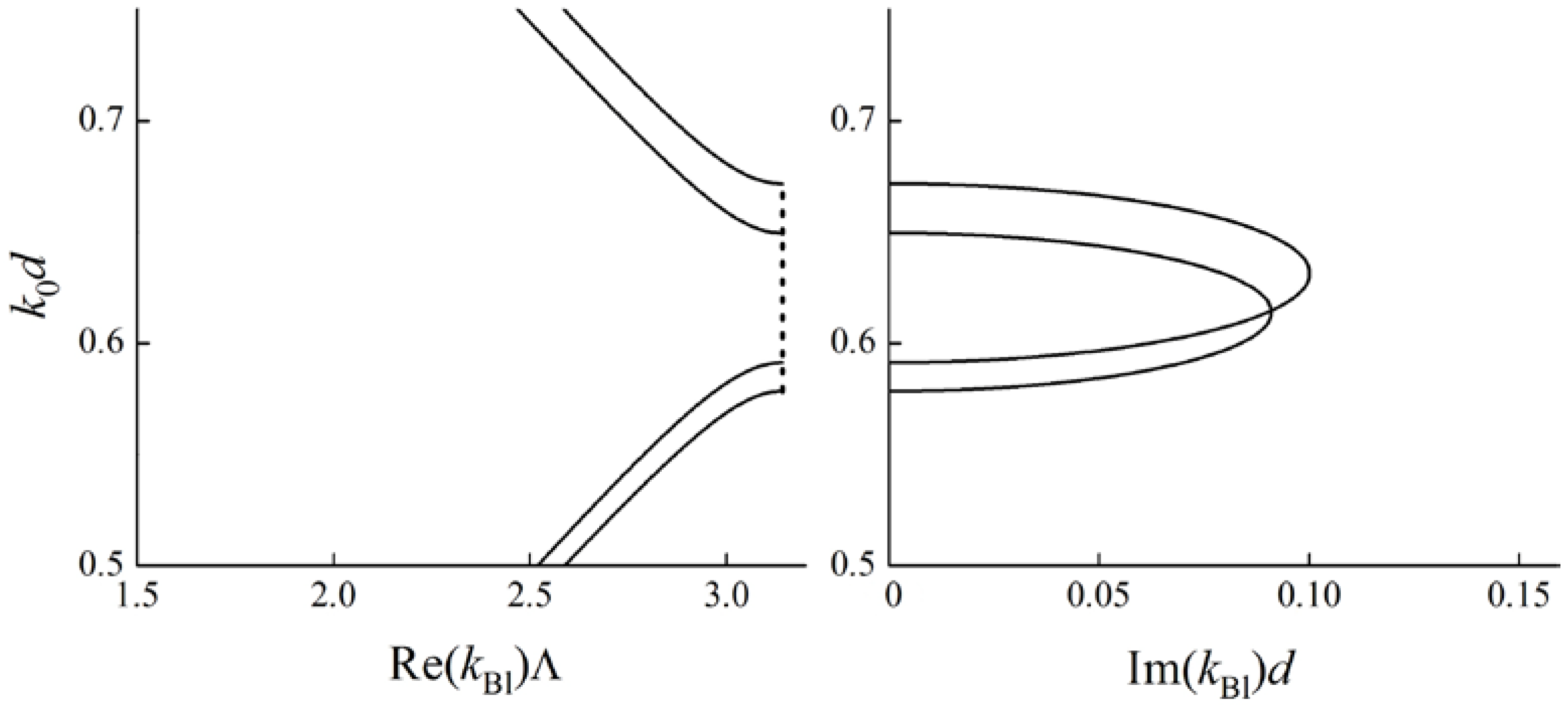
3. Properties of Degenerate Band Gaps
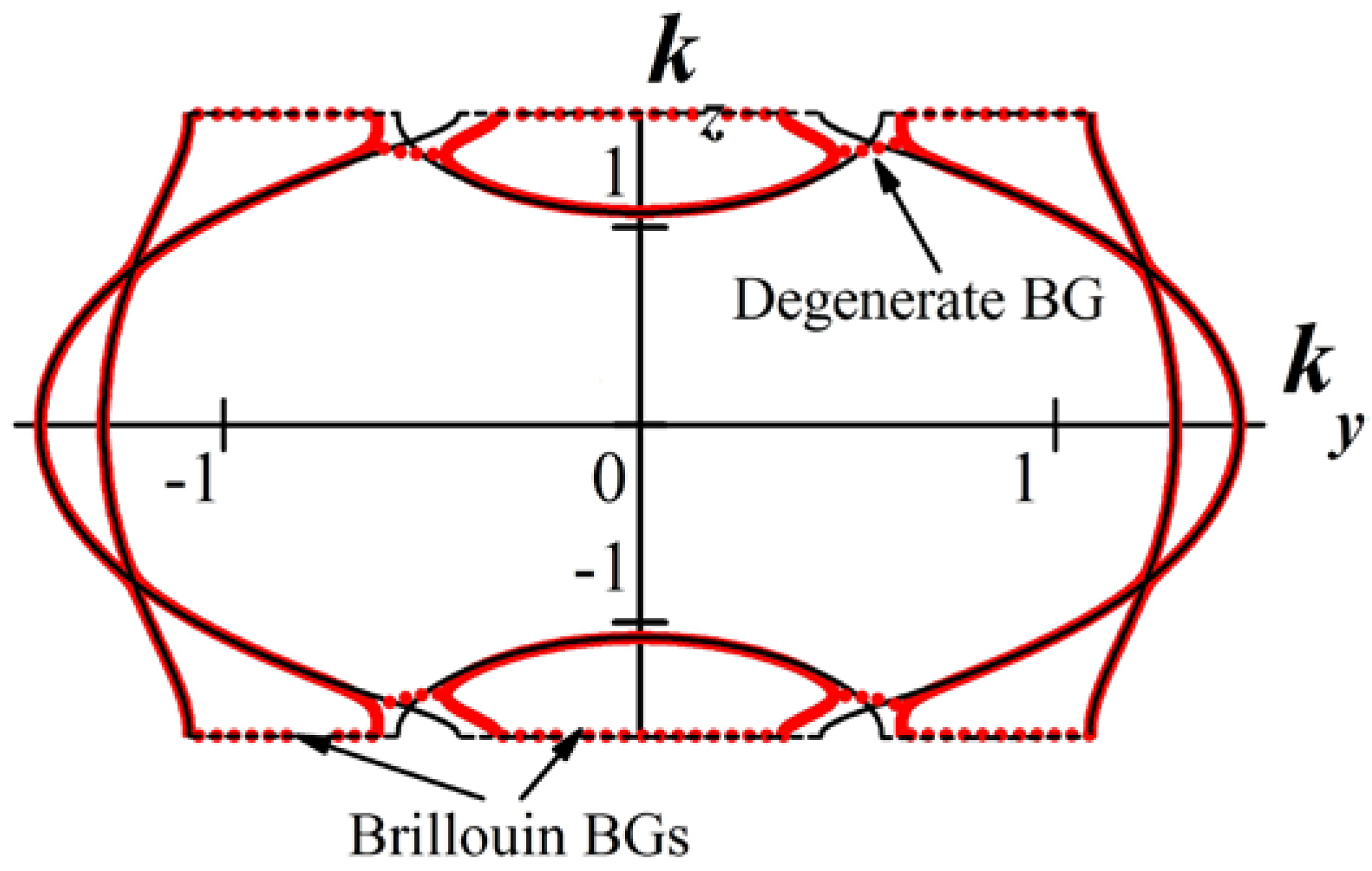
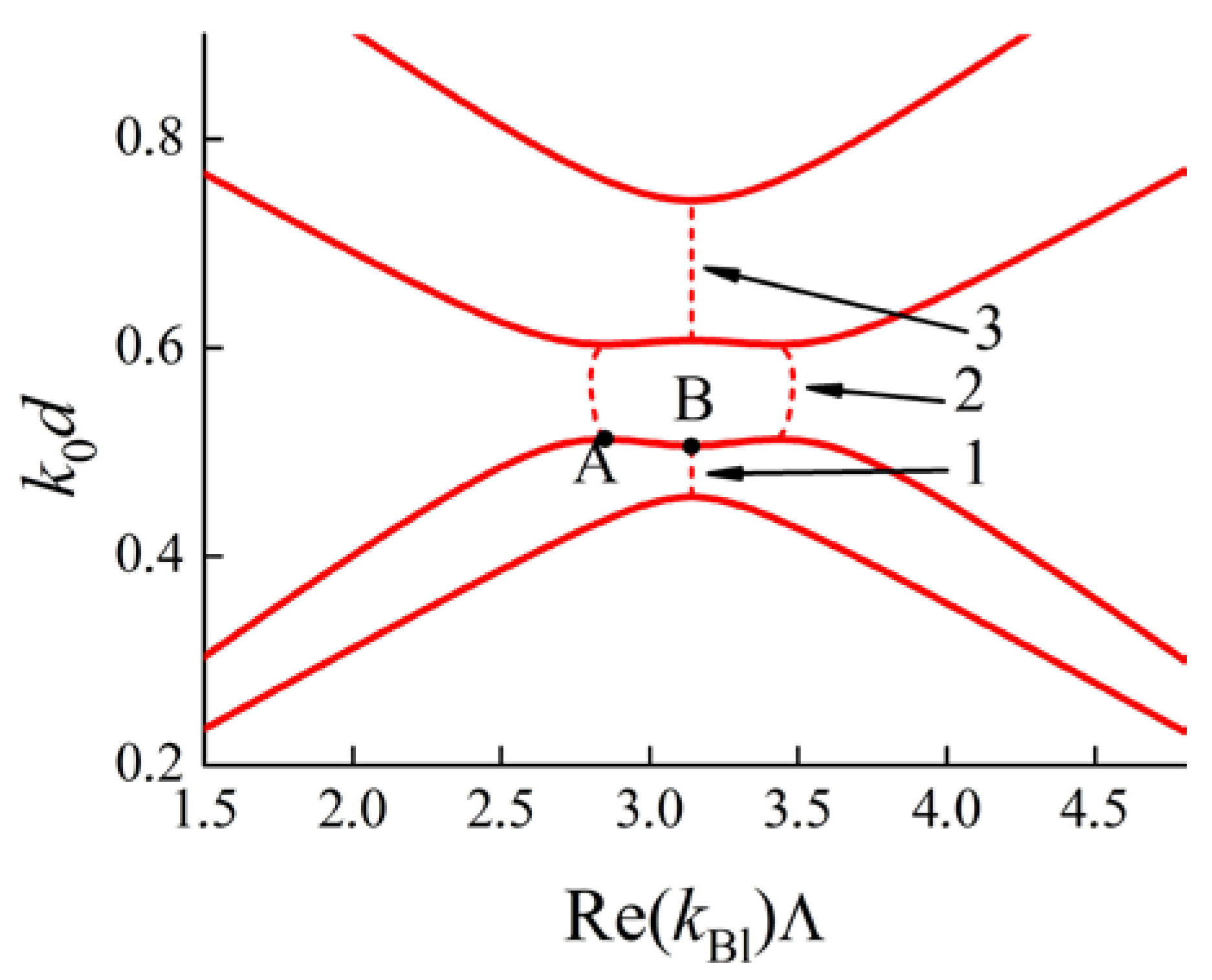
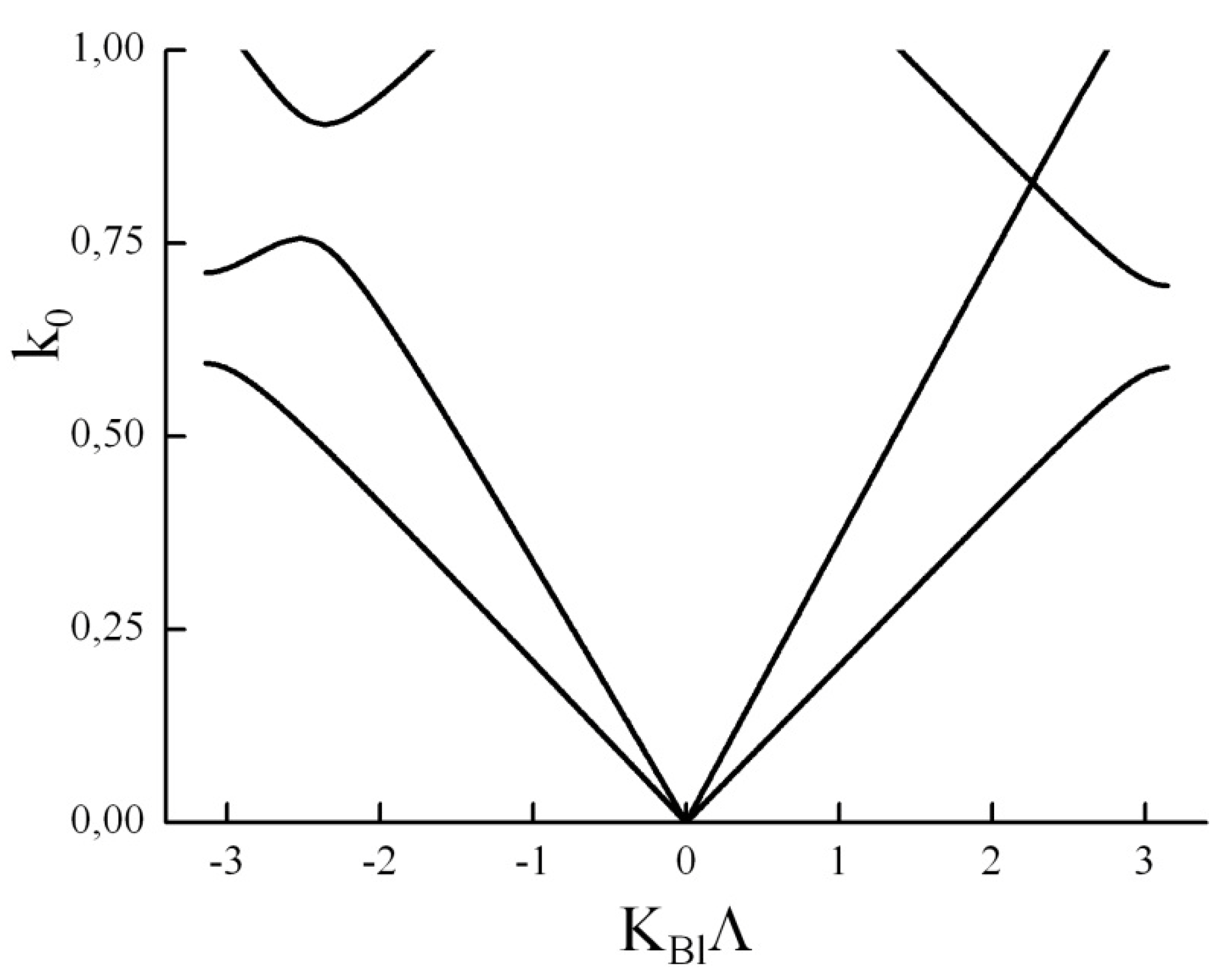
3.1. Linkage Between Brillouin and Degenerate Band Gaps. Formation of the So-Called “Degenerate Band Edge” and Frozen Mode
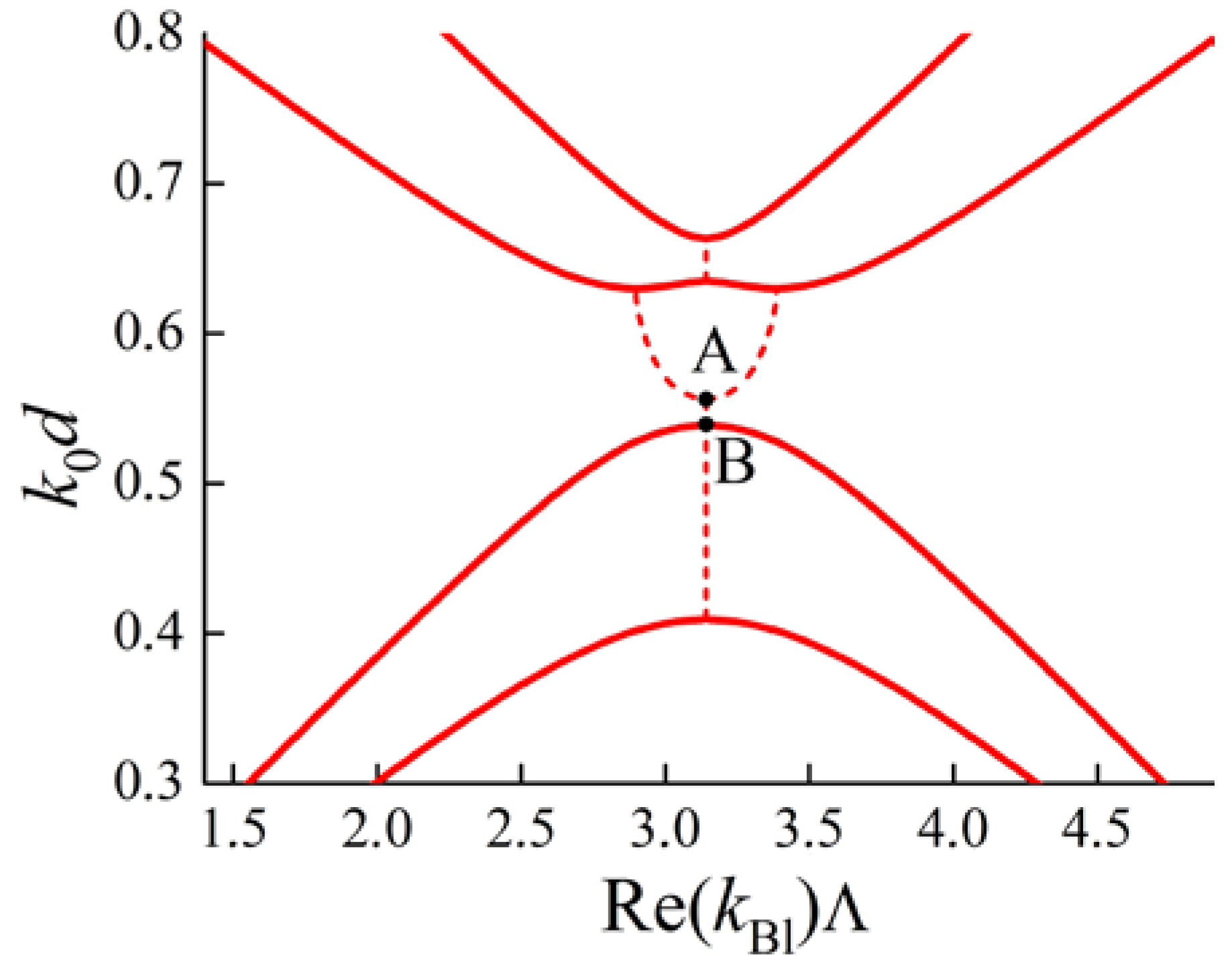
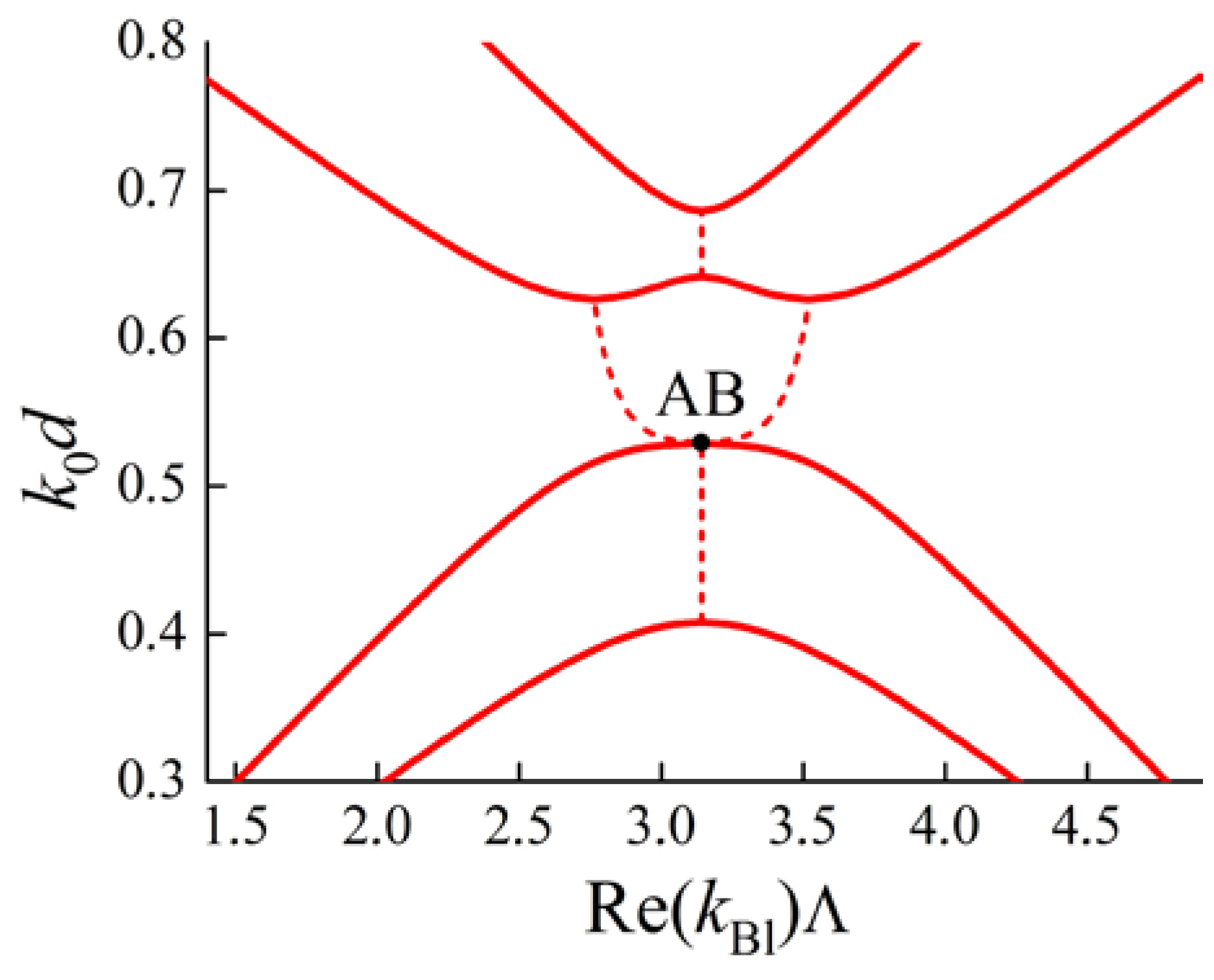

3.2. Linkage Between Anisotropic and Gyrotropic Degenerate Band Gaps
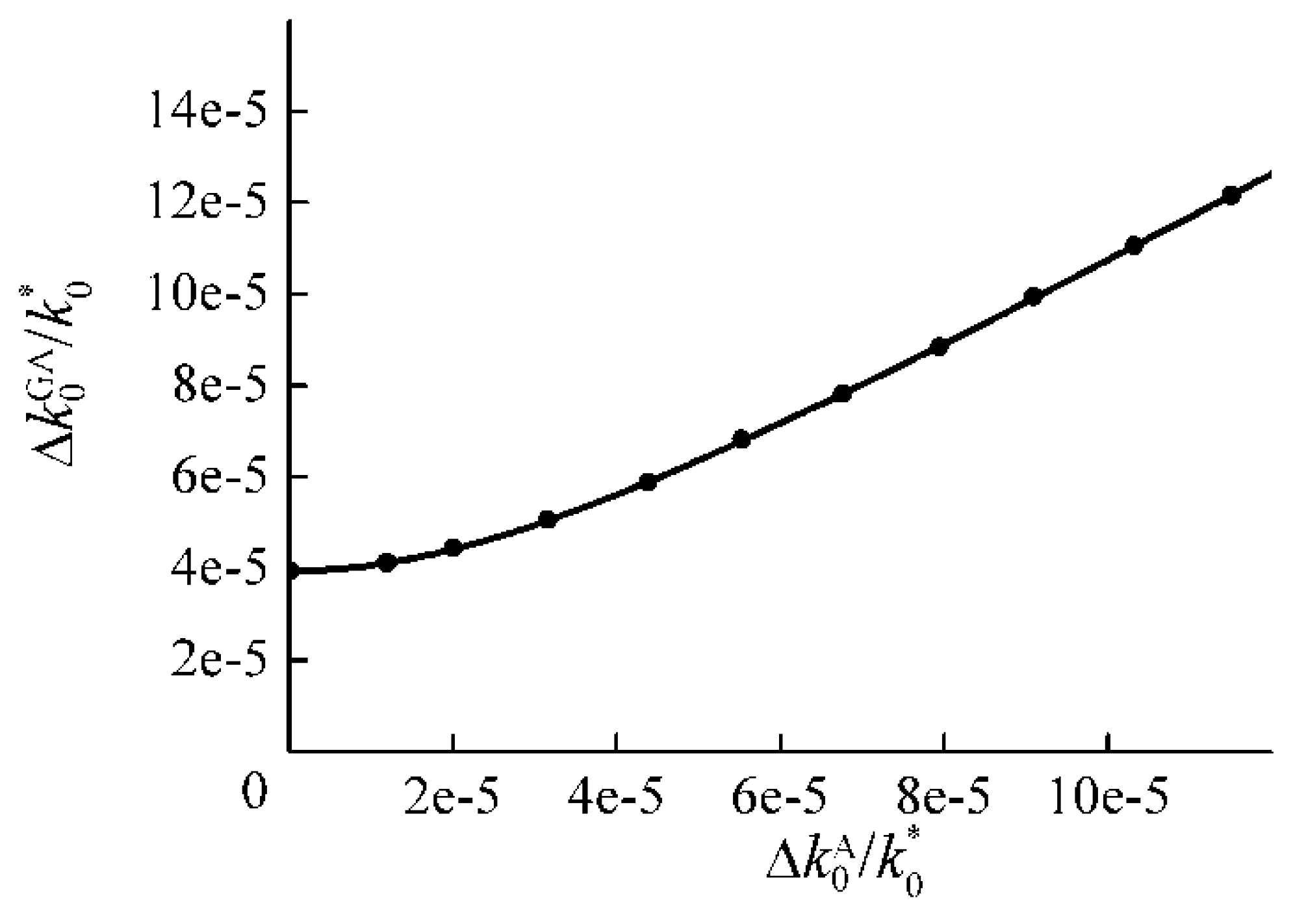
3.3. Absence of the Optical Borrmann Effect at the Boundary of a Degenerate Band Gap
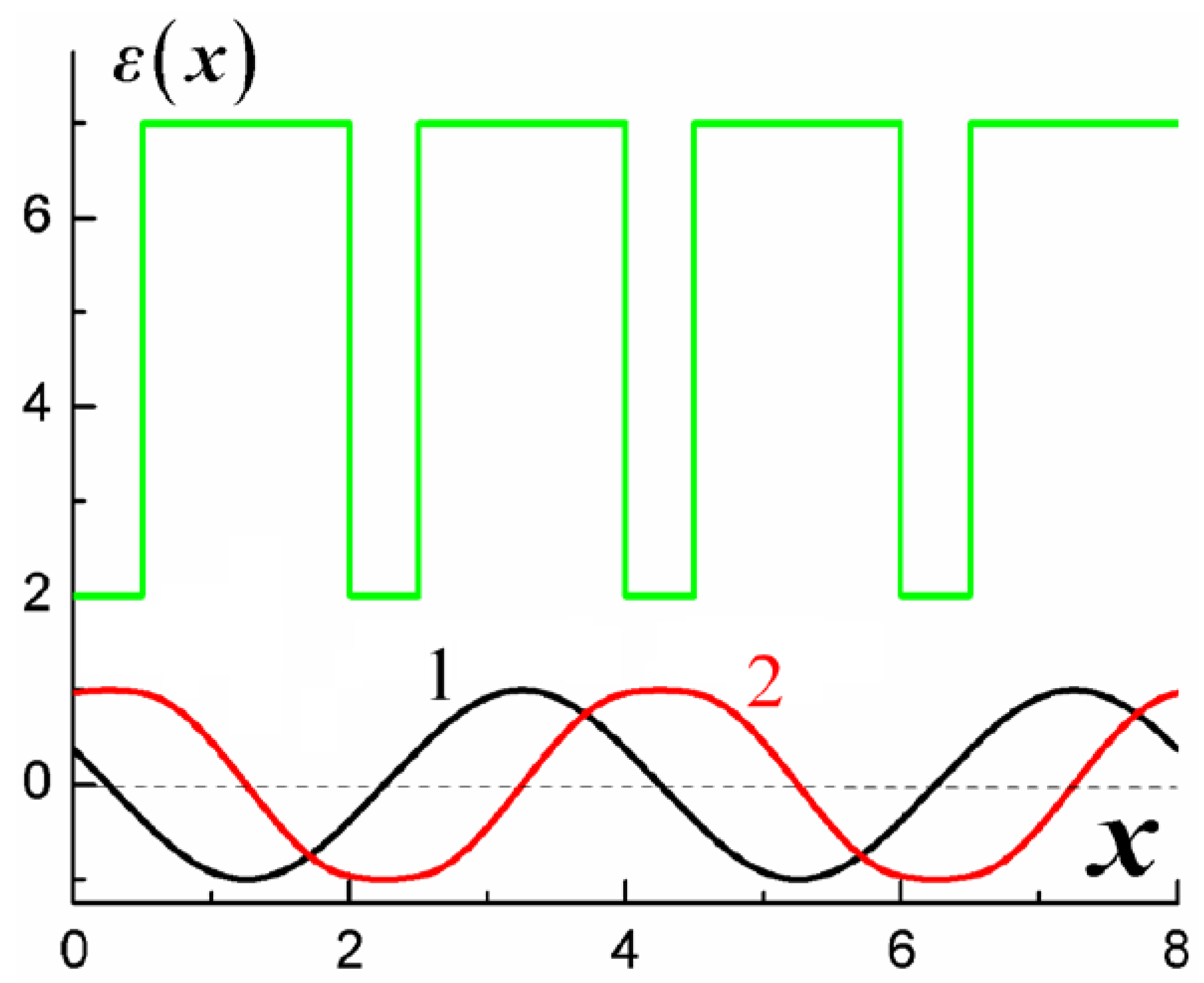


4. Formation of the Tamm States Based on Degenerate Band Gap

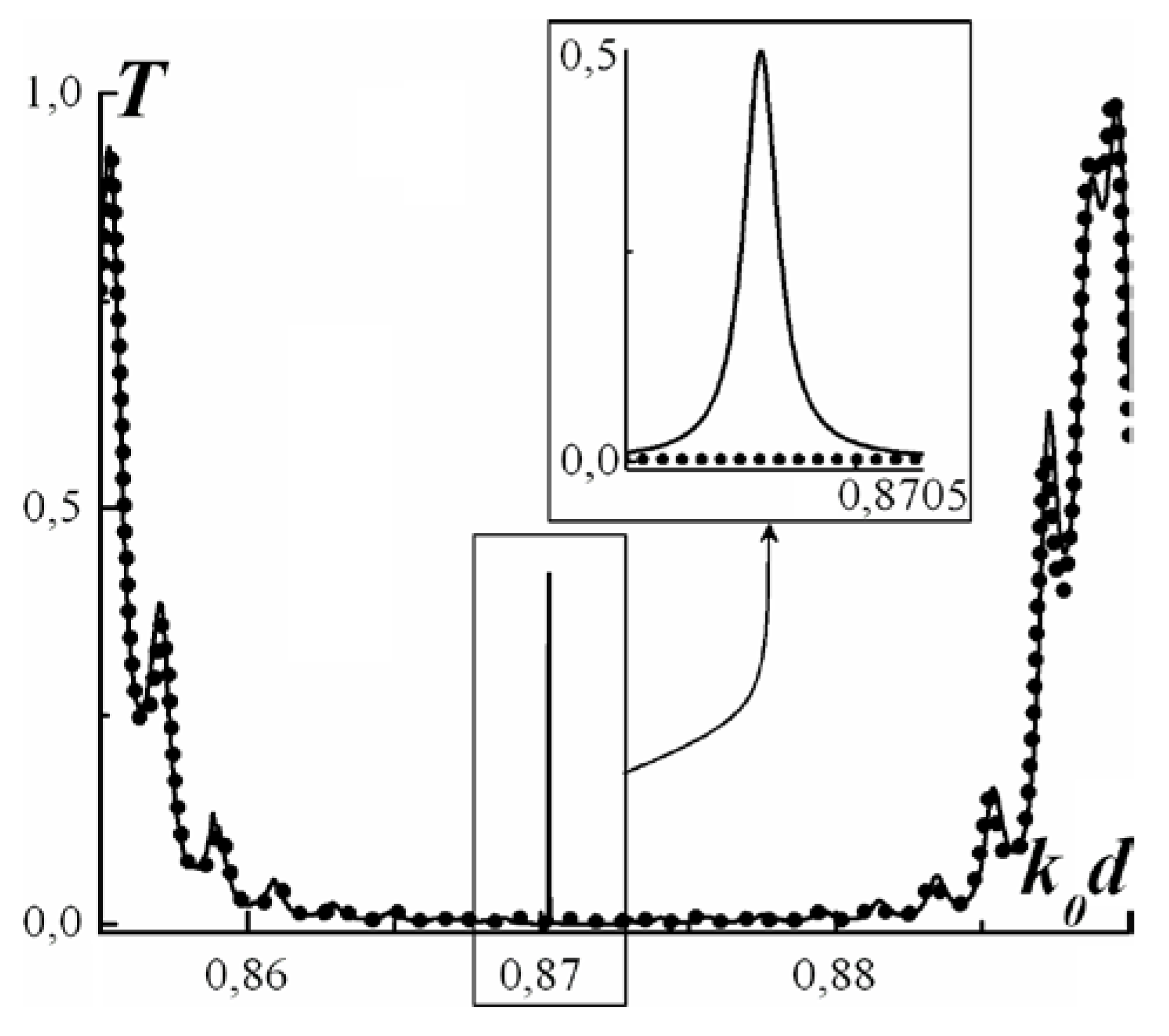
5. Anisotropy of Admittance
Acknowledgments
References
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [PubMed]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef] [PubMed]
- Sakoda, K. Optical Properties of Photonic Crystals; Springer-Verlag: Berlin, Germany, 2001. [Google Scholar]
- Sheng, P. Introduction to Wave Scattering, Localization and Mesoscopic Phenomena, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Vinogradov, A.P.; Dorofeenko, A.V.; Erokhin, S.G.; Inoue, M.; Lisyansky, A.A.; Merzlikin, A.M.; Granovsky, A.B. Surface state peculiarities in one-dimensional photonic crystal interfaces. Phys. Rev. B 2006, 74, 045128:1–045128:8. [Google Scholar] [CrossRef]
- Merzlikin, A.M.; Vinogradov, A.P.; Dorofeenko, A.V.; Inoue, M.; Levy, M.; Granovsky, A.B. Controllable tamm states in magnetophotonic crystal. Physica B 2007, 394, 277–280. [Google Scholar] [CrossRef]
- Namdar, A.; Shadrivov, I.V.; Kivshar, Y.S. Backward Tamm states in left-handed metamaterials. Appl. Phys. Lett. 2006, 89, 114104:1–114104:3. [Google Scholar] [CrossRef]
- Goto, T.; Dorofeenko, A.V.; Merzlikin, A.M.; Baryshev, A.V.; Vinogradov, A.P.; Inoue, M.; Lisyansky, A.A.; Granovsky, A.B. Optical tamm states in one-dimensional magnetophotonic structures. Phys. Rev. Lett. 2008, 101, 113902:1–113902:3. [Google Scholar] [CrossRef]
- Kavokin, A.; Shelykh, I.; Malpuech, G. Optical Tamm states for the fabrication of polariton lasers. Appl. Phys. Lett. 2005, 87, 261105:1–261105:3. [Google Scholar] [CrossRef]
- Kavokin, A.; Shelykh, I.; Malpuech, G. Lossless interface modes at the boundary between two periodic dielectric structures. Phys. Rev. B 2005, 72, 233102:1–233102:4. [Google Scholar] [CrossRef]
- Villa, F.; Gaspar-Armenta, J.A. Electromagnetic surface waves: Photonic crystal-photonic crystal interface. Opt. Commun. 2003, 223, 109–115. [Google Scholar] [CrossRef]
- Villa, F.; Gaspar-Armenta, J.A. Photonic crystal to photonic crystal surface modes: Narrow-bandpass filters. Opt. Express 2004, 12, 2338–2355. [Google Scholar] [CrossRef] [PubMed]
- Kaliteevski, M.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415:1–165415:5. [Google Scholar] [CrossRef]
- Brand, S.; Kaliteevski, M.A.; Abram, R.A. Optical Tamm states above the bulk plasma frequency at a Bragg stack/metal interface. Phys. Rev. B 2009, 79, 085416:1–085416:4. [Google Scholar] [CrossRef]
- Goto, T.; Baryshev, A.V.; Inoue, M.; Dorofeenko, A.V.; Merzlikin, A.M.; Vinogradov, A.P.; Lisyansky, A.A.; Granovsky, A.B. Tailoring surfaces of one-dimensional magnetophotonic crystals: Optical Tamm state and Faraday rotation. Phys. Rev. B 2009, 79, 125103:1–125103:5. [Google Scholar] [CrossRef]
- Merzlikin, A.M.; Vinogradov, A.P.; Lagarkov, A.N.; Levy, M.; Bergman, D.J.; Strelniker, Y.M. Peculiarities of Tamm states formed in degenerate photonic band gaps. Physica B 2010, 405, 2986–2989. [Google Scholar] [CrossRef]
- Yeh, P. Electromagnetic propagation in birefringent layered media. J. Opt. Soc. Am. 1979, 69, 742–756. [Google Scholar] [CrossRef]
- Shabtay, G.; Eidinger, E.; Zalevsky, Z.; Mendlovic, D.; Marom, E. Tunable birefringent filters—Optimal iterative design. Opt. Express 2002, 10, 1534–1541. [Google Scholar] [CrossRef] [PubMed]
- Zengerle, R. Light propagation in singly and doubly periodic planar waveguides. J. Mod. Optic. 1987, 34, 1589–1617. [Google Scholar] [CrossRef]
- Cojocaru, E. Forbidden gaps in periodic anisotropic layered media. Appl. Opt. 2000, 39, 4641–4648. [Google Scholar] [CrossRef] [PubMed]
- Merzlikin, A.M.; Vinogradov, A.P.; Inoue, M.; Khanikaev, A.B.; Granovsky, A.B. The Faraday effect in two-dimensional magneto-photonic crystals. J. Magn. Magn. Mater. 2006, 300, 108–111. [Google Scholar] [CrossRef]
- Levy, M.; Jalali, A.A. Band structure and Bloch states in birefringent one-dimensional magnetophotonic crystals: An analytical approach. J. Opt. Soc. Am. B 2007, 24, 1603–1609. [Google Scholar] [CrossRef]
- Jalali, A.A.; Levy, M. Local normal-mode coupling and energy band splitting in elliptically birefringent one-dimensional magnetophotonic crystals. J. Opt. Soc. Am. B 2008, 25, 119–125. [Google Scholar] [CrossRef]
- Da, H.-X.; Huang, Z.-G.; Li, Z.Y. Electrically controlled optical Tamm states in magnetophotonic crystal based on nematic liquid crystals. Opt. Lett. 2009, 34, 1693–1695. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Lakhtakia, A. Intra-Brillouin-zone bandgaps due to periodic misalignment in one-dimensional magnetophotonic crystals. Appl. Phys. Lett. 2008, 92, 011115:1–011115:3. [Google Scholar]
- Wang, F.; Lakhtakia, A. Magnetically controllable intra-Brillouin-zone band gaps in one-dimensional helicoidal magnetophotonic crystals. Phys. Rev. B 2009, 79, 193102:1–193102:4. [Google Scholar]
- Merzlikin, A.M.; Levy, M.; Jalali, A.A.; Vinogradov, A.P. Polarization degeneracy at Bragg reflectance in magnetized photonic crystals. Phys. Rev. B 2009, 79, 195103:1–195103:8. [Google Scholar] [CrossRef]
- Bertrand, P.; Hermann, C.; Lampel, G.; Peretti, J.; Safarov, V.I. General analytical treatment of optics in layered structures: Application to magneto-optics. Phys. Rev. B 2001, 64, 235421:1–235421:12. [Google Scholar] [CrossRef]
- Yariv, A.; Yeh, P. Optical Waves in Crystals; Wiley Interscience: Hoboken, NJ, USA, 2003. [Google Scholar]
- Šolc, I. A new kind of double refracting filter. Czech. J. Phys. 1954, 4, 65–66. [Google Scholar] [CrossRef]
- Greenwell, A.B.; Booruang, S.; Moharam, M.G. Multiple wavelength resonant grating at oblique incidence with broad angular acceptance. Opt. Express 2007, 15, 8626–8638. [Google Scholar] [CrossRef] [PubMed]
- Olivier, S.; Rattier, M.; Benisty, H.; Smith, C.J.M.; De La Rue, R.M.; Krauss, T.F.; Oesterle, U.; Houdré, R.; Weisbuch, C. Mini stopbands of a one-dimensional system: The channel waveguide in a two-dimensional photonic crystal. Phys. Rev. B 2001, 63, 113311:1–113311:6. [Google Scholar]
- Lupu, A.; Muhieddine, K.; Cassan, E.; Lourtioz, J.-M. Dual transmission band Bragg grating assisted asymmetric directional couplers. Opt. Express 2011, 19, 1246–1259. [Google Scholar] [CrossRef] [PubMed]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals. Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Johnson, S.G.; Joannopoulos, J.D. Photonic Crystals. The Road from Theory to Practice; Kluwer Academic Publishers: Boston, MA, USA, 2002. [Google Scholar]
- Figotin, A.; Vitebskiy, I. Frozen light in photonic crystals with degenerate band edge. Phys. Rev. E 2006, 74, 066613:1–066613:17. [Google Scholar] [CrossRef]
- Vinogradov, A.; Erokhin, S.; Granovsky, A.; Inoue, M. Investigation of the Faraday effect in multilayer one-dimensional structures. J. Commun. Technol. Electron. 2004, 49, 88–90. [Google Scholar]
- Vinogradov, A.; Erokhin, S.; Granovsky, A.; Inoue, M. The polar Kerr effect in multilayer systems (magnetophotonic crystals). J. Commun. Technol. Electron. 2004, 49, 682–685. [Google Scholar]
- Erokhin, S.; Vinogradov, A.; Granovsky, A.; Inoue, M. Field distribution of a light wave near a magnetic defect in one-dimensional photonic crystals. Phys. Solid State 2007, 49, 497–499. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Baryshev, A.B.; Lim, P.B.; Uchida, H.; Inoue, M.; Zhdanov, A.G.; Fedyanin, A.A.; Maydykovskiy, A.I.; Aktsipetrov, O.A. Nonlinear Verdet law in magnetophotonic crystals: Interrelation between Faraday and Borrmann effects. Phys. Rev. B 2008, 78, 193102:1–193102:4. [Google Scholar] [CrossRef]
- Figotin, A.; Vitebskiy, I. Absorption suppression in photonic crystals. Phys. Rev. B 2008, 77, 104421:1–104421:8. [Google Scholar] [CrossRef]
- Vinogradov, A.P.; Lozovik, Yu.E.; Merzlikin, A.M.; Dorofeenko, A.V.; Vitebskiy, I.; Figotin, A.; Granovsky, A.B.; Lisyansky, A.A. Inverse Borrmann effect in photonic crystals. Phys. Rev. B 2009, 80, 235106:1–235106:6. [Google Scholar] [CrossRef]
- Figotin, A.; Vitebskiy, I. Electromagnetic unidirectionality in magnetic photonic crystals. Phys. Rev. B 2003, 67, 165210:1–165210:20. [Google Scholar] [CrossRef]
- Ballato, J.; Ballato, A.; Figotin, A.; Vitebskiy, I. Frozen light in periodic stacks of anisotropic layers. Phys. Rev. E 2005, 71, 036612:1–036612:12. [Google Scholar] [CrossRef]
- Karalis, A.; Joannopoulos, J.D.; Soljacic, M. Plasmonic-dielectric systems for high-order dispersionless slow or stopped subwavelength light. Phys. Rev. Lett. 2009, 103, 043906:1–043906:4. [Google Scholar] [CrossRef]
- Slow Light: Science and Applications; Khurgin, J.B.; Tucker, R.S. (Eds.) Tailor and Francis: New York, NY, USA, 2009.
- Petrov, A.Yu.; Eich, M. Zero dispersion at small group velocities in photonic crystal waveguides. Appl. Phys. Lett. 2004, 85, 4866–4868. [Google Scholar] [CrossRef]
- Benisty, H. Dark modes, slow modes, and coupling in multimode systems. J. Opt. Soc. Am. B 2009, 26, 718–724. [Google Scholar] [CrossRef]
- Khayam, O.; Benisty, H. General recipe for flatbands in photonic crystal waveguides. Opt. Express 2009, 17, 14634–14646. [Google Scholar] [CrossRef] [PubMed]
- Benisty, H.; Khayam, O.; Cambournac, C. Emission control in broad periodic waveguides and critical coupling. Photon. Nanostruct. Fundam. Appl. 2010, 8, 210–217. [Google Scholar] [CrossRef]
- Benisty, H.; Piskunov, N.; Kashkarov, P.N.; Khayam, O. Crossing of manifolds leads to flat dispersion: Blazed Littrow waveguides. Phys. Rev. A 2011, 84, 063825:1–063825:5. [Google Scholar] [CrossRef]
- Ignatov, A.I.; Merzlikin, A.M.; Levy, M. Linkage between anisotropic and gyrotropic degenerate bandgaps. J. Opt. Soc. Amer. Opt. Physics 2011, 28, 1911–1915. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Pergamon Press: Oxford, UK, 1993. [Google Scholar]
- Lyubchanskii, I.L.; Dadoenkova, N.N.; Lyubchanskii, M.I.; Shapovalov, E.A.; Rasing, Th. Magnetic photonic crystals. J. Phys. D 2003, 36, R277–R287. [Google Scholar] [CrossRef]
- Figotin, A.; Vitebskiy, I. Nonreciprocal magnetic photonic crystals. Phys. Rev. E 2001, 63, 066609:1–066609:17. [Google Scholar] [CrossRef]
- Erokhin, S.G.; Lisyansky, A.A.; Merzlikin, A.M.; Vinogradov, A.P.; Granovsky, A.B. Photonic crystals built on contrast in attenuation. Phys. Rev. B 2008, 77, 233102:1–233102:3. [Google Scholar] [CrossRef]
- Velikhov, E.P.; Dykhne, A.M. Proceedings of the Sixth International Conference on Ionization Phenomenon in Gases, Paris, France, 8–13 July 1963; Hubert, P., Ed.; S.E.R.M.A.: Paris, France, 1963; p. 511.
- Bergman, D.J. The dielectric constant of a composite material—A problem in classical physics. Phys. Rep. 1978, 43, 377–407. [Google Scholar] [CrossRef]
- Tamm, I.E. On the possible bound states of electrons on a crystal surface. Phys. Z. Sowjetunion 1932, 1, 733–734. [Google Scholar]
Appendix
© 2012 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ignatov, A.I.; Merzlikin, A.M.; Levy, M.; Vinogradov, A.P. Formation of Degenerate Band Gaps in Layered Systems. Materials 2012, 5, 1055-1083. https://doi.org/10.3390/ma5061055
Ignatov AI, Merzlikin AM, Levy M, Vinogradov AP. Formation of Degenerate Band Gaps in Layered Systems. Materials. 2012; 5(6):1055-1083. https://doi.org/10.3390/ma5061055
Chicago/Turabian StyleIgnatov, Anton I., Alexander M. Merzlikin, Miguel Levy, and Alexey P. Vinogradov. 2012. "Formation of Degenerate Band Gaps in Layered Systems" Materials 5, no. 6: 1055-1083. https://doi.org/10.3390/ma5061055