Magnetic Properties of the Ferromagnetic Shape Memory Alloys Ni50+xMn27−xGa23 in Magnetic Fields
Abstract
: Thermal strain, permeability, and magnetization measurements of the ferromagnetic shape memory alloys Ni50+xMn27−xGa23 (x = 2.0, 2.5, 2.7) were performed. For x = 2.7, in which the martensite transition and the ferromagnetic transition occur at the same temperature, the martensite transition starting temperature TMs shift in magnetic fields around a zero magnetic field was estimated to be dTMs/dB = 1.1 ± 0.2 K/T, thus indicating that magnetic fields influences martensite transition. We discussed the itinerant electron magnetism of x = 2.0 and 2.5. As for x = 2.5, the M4 vs. B/M plot crosses the origin of the coordinate axis at the Curie temperature, and the plot indicates a good linear relation behavior around the Curie temperature. The result is in agreement with the theory by Takahashi, concerning itinerant electron ferromagnets.1. Introduction
Ferromagnetic shape memory alloys have been extensively studied as potential candidates for smart materials. Among these alloys, Ni2MnGa is the most familiar alloy [1]. It has a cubic L21 Heusler structure (space group ) with the lattice parameter a = 5.825 Å at room temperature, and it orders ferromagnetically at the Curie temperature TC ≈ 365 K [2,3]. Upon cooling from room temperature, a martensite transition occurs at the martensite transition temperature TM ≈ 200 K. Below TM, a superstructure forms because of lattice modulation [4,5]. For Ni-Mn-Ga Heusler alloys, the TM can vary from 200 to 330 K by nonstoichiometrically changing the concentration of composite elements.
Several studies on Ni-Mn-Ga alloys address the martensite transition and the correlation between magnetism and crystallographic structures [6–18]. Ma et al. [7] studied the crystallography of Ni50+xMn25Ga25−x alloys (2 ≤ x ≤ 11) by powder X-ray diffraction and optical microspectroscopy. In the martensite phase, typical microstructures were observed for x < 7. The martensite variants exhibit configurations typical of self-accommodation arrangements. The TEM image of Ni54Mn25Ga21 indicates that the typical width of a variant is about 1 μm.
Umetsu et al. [19] made a phase diagram of Ni50+xMn27−xGa23 alloys (−25 ≤ x ≤ 6). The martensite transition temperature TM and the ferromagnetic transition temperature (Curie temperature) TC cross over at around x = 2.5. The martensite transition temperature of Ni50+xMn27−xGa23 is higher than that of the stoichiometric composition. This property is very useful from the viewpoint of developing commercial applications.
The interaction between magnetism and crystallographic rearrangements was discussed in references [1,8,17,18]. Murray et al. [18] studied polycrystalline Ni-Mn-Ga alloys. The magnetization step at TM is also observed. This is a reflection of the magnetic anisotropy in the tetragonal martensite phase. In the martensite phase, a strong magnetic anisotropy exists. Under these circumstances, the magnetization that reflects the percentage of magnetic moments parallel to the magnetic field is smaller than that of the austenite phase, where the magnetic anisotropy is not strong in the weak magnetic field. Therefore, the magnetization step is observed at TM.
NMR experiments indicate Mn-Mn indirect exchange via the faults in Mn-Ga layers interchange, which are caused by excessive amounts of Ga [13]. This result indicates that the exchange interaction between Mn-Mn magnetic moments is sensitive to lattice transformation: during such a transformation, the magnetism changes from that of a soft magnet in the austenite phase to that of a hard magnet in the martensite phase; this is due to higher magnetic anisotropy. Dai et al. [20] reported this softening of the lattice; they did so by measuring the elastic constants of a Ni0.50Mn0.284Ga0.216 single crystal using the ultrasonic continuous-wave method. C11, C33, C66 and C44 modes were investigated; every mode indicated an abrupt softening around TM. This lattice softening appears to be affected by the abrupt expansion just above TM when cooling from the austenite phase.
Takahashi proposed a spin fluctuation theory of itinerant electron magnetism [21,22]. The induced magnetization M is written as the formula of
where is the spontaneous magnetization in the ground state; N0 is the molecular number; , where g is the g-factor and S is a spin; TA is the spin fluctuation parameter. Nishihara et al. [23] measured the magnetization of Ni and Ni2MnGa. Good linearity is observed in the M4 vs. H/M plot at the Curie temperature for Ni. This result indicates that the critical index δ (defined as ) is 5.0.
In this study, we focused on the physical effects of magnetic fields. By using polycrystalline samples, it was possible for us to provide information concerning the easy axis of magnetization in a martensite structure; we made temperature-dependent strain measurements under constant magnetic fields. In this paper, permeability, thermal strain, and magnetization measurements were performed for polycrystalline Ni50+xMn27−xGa23 (x = 2.5, 2.7) in magnetic fields (B). Thermal strain and magnetization results of Ni52Mn25Ga23 (x = 2.0) were used for discussing the magnetic field dependence of the martensite transition temperature and magnetization [24]. The results of thermal strain in a magnetic field and magnetic-field-induced strain yield information about the twin boundary motion in the fields. The experimental results were compared with those of other Ni-Mn-Ga single crystalline or polycrystalline alloys, and correlations between magnetism and martensite transition were found. Itinerant magnetism is also discussed, based upon the results of the magnetic field dependence of the magnetization and compared with the predictions of Takahashi’s theory [21,22].
The martensite transition temperature TM and reverse martensite phase transition TR are used when these are quoted from the references. To define these temperatures clearly, we used TM and TR as the martensite transition starting temperature TMs and the reverse martensite temperature finishing temperature TRf in our research results.
2. Experimental Procedures
The Ni50+xMn27−xGa23 (x = =2.5, 2.7) alloys were prepared by arc melting 99.99% pure Ni, 99.99% pure Mn, and 99.9999% pure Ga in an argon atmosphere. To obtain homogenized samples, the reaction products were sealed in double-evacuated silica tubes, and then annealed at 1123 K for 3 days and quenched in cold water. The obtained samples were polycrystalline. From X-ray powder diffraction, the monoclinic 6M phase martensite structure and the D022 tetragonal structure were mixed at 298 K. The size of the sample was 2.0 mm × 2.0 mm × 4.0 mm.
The measurements in this study were performed at atmospheric pressure (P = 0.10 MPa). Thermal strain measurements were performed using strain gauges (Kyowa Dengyo Co., Ltd., Chofu, Japan). The electrical resistivity of the strain gauges was measured by the four-probe method. The strain gauge was fixed parallel to the longitudinal axis of the sample.
Thermal strain measurements were performed using a 10 T helium-free cryo-cooled superconducting magnet at the High Field Laboratory for Superconducting Materials, Institute for Materials Research, Tohoku University. The magnetic field was applied along the sample’s longitudinal axis. The thermal strain is denoted by the reference strain at 360 K.
Magnetization measurements in a steady field at 5K and temperature dependence of the magnetization at 0.10 T were performed using a SQUID magnetometer installed at Ryukoku University. As for x = 2.7, the high temperature magnetization between 320 K and 370 K were performed using a home-made magnetometer within a weak AC fields (with the frequency f = 73 Hz and the maximum field Bmax = 0.0050 T, which has a compensating high homogeneity magnetic field. AC fields were applied along the sample’s longitudinal axis.), using an AC wave generator WF 1945B (NF Co., Ltd., Yokohama, Japan) and an audio amp PM17 (Marantz Co. Ltd., Kawasaki, Japan). The magnet was the same magnet with the thermal strain measurements. Pulsed magnetization measurements were performed using a Bitter-type water-cooled pulsed magnet (inner bore: 26 mm; total length: 200 mm) in a pulsed magnetic field at Ryukoku University. The magnetic field was applied along the sample’s longitudinal axis. The values of magnetization were corrected using the values of spontaneous magnetization for 99.99% pure Ni. The magnetic permeability measurements were performed in AC fields, which is as same as the AC magnetometer. Thermal experiments were carried out by means of DSC, using a rate of 10 K/min.
3. Results and Discussion
3.1. Magnetic Properties of Ni52.5Mn24.5Ga23 (x = 2.5)
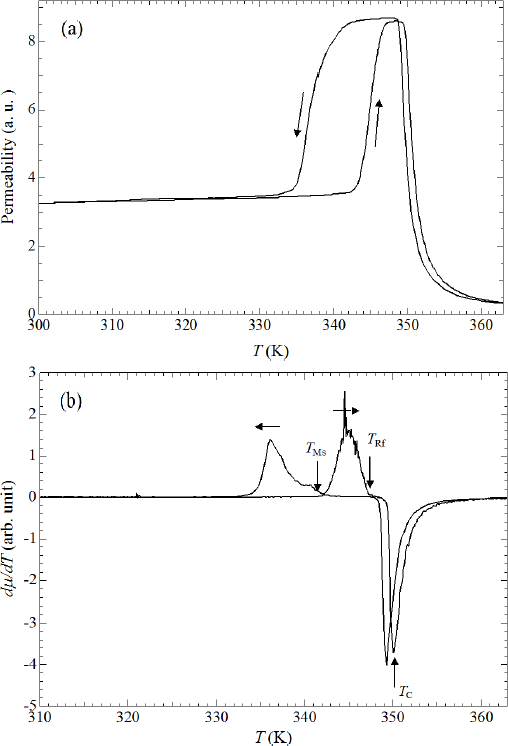
Figure 1a shows the temperature dependence of permeability. When heating from 300 K, permeability increases gradually. As shown in Figure 1a, permeability increases above 343 K and suddenly decreases around 350 K. When cooling from a high temperature, permeability shows a sudden increase at 355 K and decreases below 342 K. The sudden changes in permeability indicate that the ferrromagnetic transition occurs around 350 K. The temperature dependence of permeability for Ni52.5Mn24.5Ga23 is similar to that of Ni52Mn12.5Fe12.5Ga23’s, which shows a transition of a ferromagnetic–martensite (Ferro–M) phase to a ferromagnetic–austenite (Ferro–A) phase [25]. The step above 343 K (heating process) and below 342 K (cooling process) reflects stronger magnetic anisotropy in the tetragonal martensite phase, compared with that in the cubic austenite phase [8,18,24].
Polycrystalline Ni49.5Mn28.5Ga22, Ni50Mn28Ga22, and Ni52Mn12.5Fe12.5Ga23 alloys also indicate the magnetization (or permeability) step at TM [9,18,26] below the field of 10 mT. Figure 1b indicates the temperature dependence of the differential of permeability dμ/dT. The martensite transition starting temperature TMs and reverse martensite finishing temperature TRf, which correspond to the characteristic temperature of martensite transition for thermal strain shown in Figure 2, are indicated by arrows.
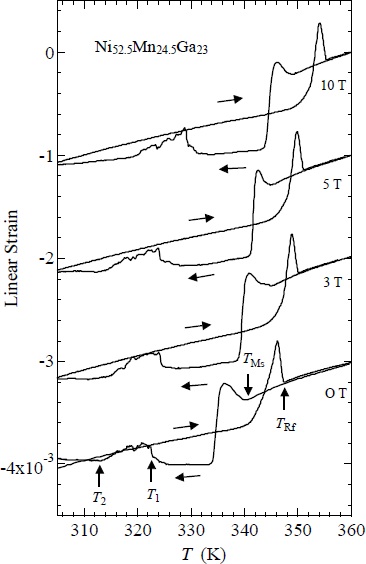
Figure 2 shows the linear thermal strain of Ni52.5Mn24.5Ga23. B means magnetic field and the unit is T (tesla). B is equal to μ0H, where μ0 is the absolute permeability of a vacuum; the unit of H is A/m. At zero magnetic fields, the memory strain was observed, as polycrystalline Ni53.6Mn27.1Ga19.3 [10]. When heating from 300 K, a slight strain was observed, first at zero magnetic fields. Above 342 K, a sharp strain is observed. The results of previous studies [6,7] suggest that this is because of the reverse martensite transition TRf = 347 K, which is denoted by an arrow. When cooling from 360 K, a sudden decrease is observed at 341 K. The martensite transition starting temperature TMs is 341 K, defined as the midpoint temperature of the transition. The permeability at the Ferro–M phase is very low compared with that of the Ferro–A phase. The results of permeability and linear strain measurements indicate that the region above TMs is a Ferro–A phase and that below TMs is a Ferro–M phase. The permeability measurement results indicate that the ferromagnetic transition from the paramagnetic–austenite (Para–A) phase to the Ferro–A phase occurs around TC = 350 K (see Figure 1a). At zero magnetic fields, and in magnetic fields, there is no visible anomaly around TC. When cooling from 360 K, the thermal strain also shows a peak at 336 K. This may be attributed to the intermingling of the L21 austenite lattices and the 6M martensite lattices at the martensite transition. A sequential phenomenon is observed in single crystalline Ni2.19Mn0.81Ga [20]. The thermal strain shows an anomaly around T1 = 323 K and T2 = 313 K. The reason of this anomaly is open question at the present time. The contraction at TMs under zero field is about 0.8 × 10−3 (0.08%). As for other Heusler alloys, Ni52Mn12.5Fe12.5Ga23 and Ni2Mn0.75Cu0.25Ga, the contraction occurs at the martensite temperature [26]. The strain at TM of polycrystalline Ni52Mn12.5Fe12.5Ga23 was estimated as 0.14% contraction. This value is larger than that of Ni52.5Mn24.5Ga23. After zero field measurements of the linear strain, measurements in magnetic fields from 3 T to 10 T were performed. The strains at TMs under the magnetic field were estimated as 0.08% contraction, which is the same as that at zero magnetic field (0.08%).
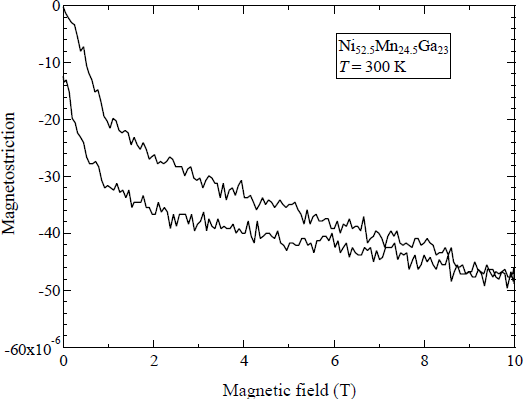
Figure 3 shows the magnetic-field-induced strain at 300 K (Ferro–M phase) in a static magnetic field. When increasing the magnetic field from zero field, a sudden contraction occurs up to 1 T. Above 1 T, a gradual contraction is observed. When decreasing the magnetic field from 10 T, a modicum of strain occurs. Below 1 T, a sudden strain is observed. The magnetic-field-induced strain at 10 T is −50 ppm or −0.005%.
The reasons that magnetic-field-induced strain is smaller than the strain at TM, in the linear strain measurements, were elucidated in references [18,24,27].
On heating from the martensite phase, an abrupt increase occurred in the field-induced strain around TM. They suggest that this is caused by lattice softening near TM. As for the thermal strain of Ni52.5Mn24.5Ga23, shown in Figure 2, peaks appear for both TMs and TRf in zero field and all values of the magnetic field. The peak at TRf, which is associated with heating, is larger than the one at TMs, which is associated with cooling. These peaks indicate that the lattice expands abruptly. The ultrasonic continuous-wave measurements by Dai et al. [20] indicated abrupt softening around TM. This lattice softening appears to be affected by the abrupt expansion just above TM or TR, when cooling or heating from or to the austenite phase, respectively.
Figure 4 shows the magnetic phase diagram of Ni52.5Mn24.5Ga23. With increasing field, TMs and TRf gradually increase. The shifts in TMs and TRf around zero magnetic field are estimated as dTMs/dB = 0.9 ± 0.2 K/T and dTRf/dB = 0.8 ± 0.2 K/T, which is larger than those of the Ni52Mn12.5Fe12.5Ga23 alloy’s (dTM/dB = 0.5 K/T) [26]. In Section 3.2, we will discuss the shifts in TMs and TRf under magnetic fields.
Figure 5a shows the magnetization curves of Ni52.5Mn24.5Ga23 at 5 K in a static magnetic field measured by a SQUID magnetometer. The unit of magnetization M is Am2/kg in the SI unit system or emu/g in the CGS unit system (both have identical numerical values). The saturation magnetization was 79.6 Am2/kg. The spontaneous magnetization was 77.7 Am2/kg (which was derived from the Arrott plot) as shown in Figure 5b. This spontaneous magnetization value is equal to a magnetic moment of 3.35 μB/f.u. This absolute value corresponds to 3.75 μB/Mn. The Mn magnetic moment of 3.75 μB is comparable to the magnetic moment of Mn on the B site, which is approximately 3.58 μB/Mn (as obtained from the powder neutron scattering experiments performed by Ahuja et al. [28]). Detailed expressions about the magnetic moments of Ni50+xMn27−xGa23 alloys (−25 ≤ x ≤ 6) were described by Umetsu et al. [19].
Figure 5c shows the temperature dependence of magnetization at 0.10 T. During the heating process, a decrease in magnetization occurred between 350 and 360 K, which corresponds to the magnetic transition, as shown in Figure 1a. Notably, this abrupt decrease in the M-T curve at TMs is different from that of usual ferromagnets. The assumed reason is that martensite transition occurs just below the Curie temperature TC for Ni52.5Mn24.5Ga23. For x =5, the M-T curve shows a gradual decrease at TMs during the heating process. At this composition, the magnetic transition occurs in the martensite phase.
Figure 6a shows the magnetization curves of Ni52.5Mn24.5Ga23 in a pulsed magnetic field up to 2.2 T. The M-B curves were measured from low temperatures. The hysteresis of the M-B curve is considerably small. The magnetocaloric effects in other magnetic materials were also reported; for example, Levitin et al. [29] reported for Gd3Ga5O12. They performed magnetization measurements at an initial temperature of 4.2 K, where the magnetic contribution to heat capacity is comparable to that of the lattice heat capacity. In our experiment, the temperature change of the sample due to the magnetocaloric effect is considered to be within 1 K. This is because these experiments were performed around room temperature, where the lattice heat capacity is much larger than the heating or cooling power of the magnetocaloric effect. Moreover, M-B curves in Figure 6a show rather small hysteresis, which indicates that the magnetizations have been measured under a static temperature condition.
The M-B curves show ferromagnetic behavior below 350 K. Clearly, the field dependence of magnetization at the Ferro–A phase above TRf = 347 K is different from that of the Ferro–M phase around TRf. At the Ferro–M phase, magnetization increases with magnetic fields. On the other hand, at the Ferro–A phase between 334 and 356 K, a sudden increase in magnetization occurs between 0 and 0.1 T.
Figure 6b shows the Arrott plot of Ni52.5Mn24.5Ga23. This plot was also used for estimating the spontaneous magnetization to discuss the dTM/dB by means of the Clausius-Clapeyron relation. The spontaneous magnetization in Ni52.5Mn24.5Ga23 at 338 K, just below TR is 39.1 Am2/kg, which was obtained by the Arrott plot in Figure 6b. When using this value as the MS, the magnetocrystalline anisotropy energy in the martensite phase of Ni52.5Mn24.5Ga23 is MSBS/2 = KU = 1.7 × 105 J/m3, which is on the same order as that in the martensite phase of Ni2MnGa. These magnetic properties were also shown for Ni51.9Mn23.2Ga24.9 [11], Ni49.5Mn25.4Ga25.1 [12], and Ni54Mn21Ga25 [13].
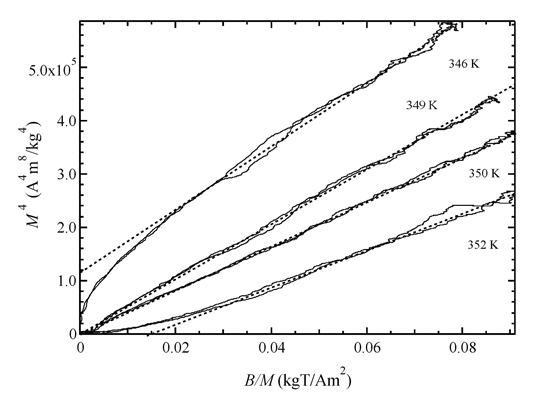
At large B/M values, the M2 vs. B/M plot seems to show a linear relation. However, around TC, the M2 vs. B/M plot strays out from a linear relation at low B/M values. Therefore, we made an attempt of other plot.
Figure 6c shows the M4 vs. B/M plots. The M4 vs. B/M plot indicates a good linear relation around the Curie temperature TC = 350 K. The critical index δ for Mδ vs. B is 5.0. The result is in agreement with the theory by Takahashi for weak itinerant electron ferromagnets [21,22].
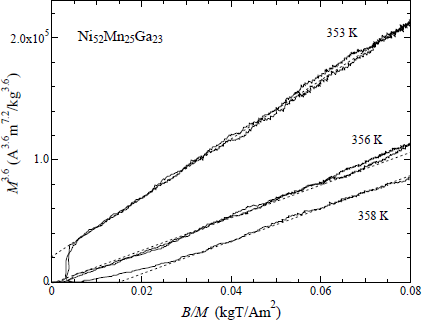
The M3.6 vs. B/M plot for Ni52Mn25Ga23 is shown in Figure 7. The magnetic properties were reported in our former research [24]. This plot indicates a good linear relation around the Curie temperature TC = 356 K. The critical index δ is 4.6. Nishihara et al. [23] investigated the magnetic field dependence of the magnetization of Ni2MnGa around TC = 363 K. The critical index δ is 4.77. As for Takahashi theory’s formula as shown in Equation (1), the critical index δ is 5.0. Therefore, we analyze of the characteristic temperature TA for Ni52.5Mn24.5Ga23.
From the magnetic moment 3.75 μB/Mn obtained from our magnetization measurement and the gradient of M4 vs. B/M in Figure 6c, we calculated the characteristic temperature TA as 1.06 × 104 K. This value is comparable to the value of Co2CrGa (1.0 × 104 K) [30] and Ni (1.76 × 104 K) [21]. These results reflect the nature of itinerant magnetism for Ni52.5Mn24.5Ga23.
3.2. Magnetic Properties of Ni52.7Mn24.3Ga23 (x = 2.7)
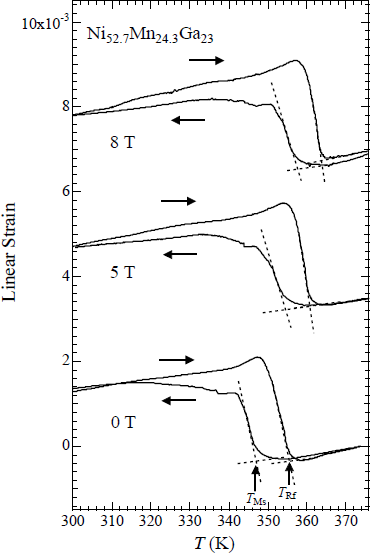
Ni52.7Mn24.3Ga23 is an alloy in which the martensite transition and ferromagnetic transition occurred at the same temperature [19]. Figure 8 shows the temperature dependence of the linear thermal strain of Ni52.7Mn24.3Ga23 in static magnetic fields, parallel to the longitudinal direction of the sample. With increasing field, TMs and TRf gradually increased. The shifts in TMs and TRf around zero magnetic field are estimated as dTMs/dB and dTRf/dB as 1.1 ± 0.2 K/T. Thermal strain results indicate that, with cooling from austenite phase, the elongation occurred at TMs. The same phenomenon was observed in the Ni2.19Mn0.81Ga and Ni2.20Mn0.80Ga polycrystalline samples. It should be noted that these alloys also show the martensitic and ferromagnetic transitions at the same temperature [31]. For the temperature dependence of the linear thermal strain of Ni52.7Mn24.3Ga23 perpendicular to the longitudinal direction, contraction occurred at TMs with cooling from austenite phase. As for the lattice parameters of Ni52.7Mn24.3Ga23, martensite phase c-axis parameter is 11% larger than austenite phase a-axis parameter, and, martensite phase a-axis parameter is 6% smaller than austenite phase a-axis parameter [19]. Therefore, it is conceivable that the difference of these linear strains parallel or perpendicular to the longitudinal direction of the sample is that the sample is oriented to some extent.
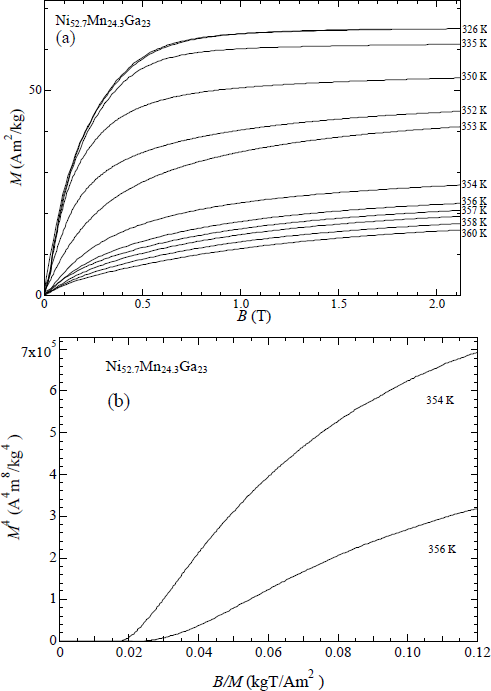
Figure 9a shows the magnetization process of Ni52.7Mn24.3Ga23. The experiments were performed in steady fields. This is because that this alloy shows the martensite transition and ferromagnetic transition at the same temperature. Then the latent heat is not small at TC. In order to avoid heating or cooling due to the ferromagnetic and martensite transition, we measured in steady fields and isothermal processes. The magnetization suddenly changes at TC = 356 K. The spontaneous magnetization change ∆M is 28 Am2/kg. The M4 vs. B/M plot is shown in Figure 9b. This plot did not indicate a linear relation around the Curie temperature. Takahashi’s theory can be applied to isotropic ferromagnet. Below x = 2.5, TC is higher than TM and a ferromagnetic transition occurs in the austenite phase. Between TM and TC, the magnetic property is isotropic ferromagnet. On the contrary, x = 2.7 transfers from the martensite ferromagnet to the austenite paramagnet. In the martensite phase, magnetic anisotropy is larger than that in the austenite phase. Therefore, it is supposed that Takahashi’s theory cannot be applied to x = 2.7.
3.3. The Magnetic Field Dependence of the Martensite Transition Temperature
Now we discuss about the field dependence of the martensite transition temperature.
The martensite transition temperature change (dT) induced by magnetic field change (dB) is approximately given by the Clausius-Clapeyron relation [8,32,33]:
where, ∆S and ∆M are the differences in entropy and magnetization between austenite and martensite phase. The entropy change ∆S was calculated by DSC result.
For Ni52Mn25Ga23, the entropy change ∆S due to the martensite transition is 20 J/kg·K. The magnetization change ∆M =11 Am2/kg, therefore ∆S/∆M = 1.8 T/K, and dTM/dB = 0.55 K/T. The experimental result of dTM/dB is 0.43 ± 0.1 K/T [24].
For Ni52.5Mn24.5Ga23, the entropy change ∆S is 22 J/kg·K. Magnetization change ∆M = 17 Am2/kg, therefore ∆S/∆M = 1.3 T/K, and dTM/dB = 0.77 K/T. The experimental result of dTM/dB is 0.9 ± 0.2 K/T (this work).
For Ni52.7Mn24.3Ga23, the entropy change ∆S is 26 J/kg·K. Magnetization change ∆M =34 Am2/kg, therefore ∆S/∆M =0.76 T/K, and dTM/dB = 1.3 K/T. The experimental result of dTM/dB is 1.1 ± 0.2 K/T (this work). The dTM/dB’s are approximately as same as that of the calculated values.
Khovailo et al. [34,35] discussed the correlation between the shifts in TM for Ni2+xMn1−xGa (0 ≤ x ≤ 0.19) using theoretical calculations according to Clausius-Clapeyron formalism. The experimental values of this shift for Ni2+xMn1−xGa (0 ≤ x ≤ 0.19) are in good agreement with the theoretical calculation results. In general, in a magnetic field, the Gibbs free energy is lowered by the Zeeman energy −∆MB, which enhances the motive force of the martensite phase transition. Thus the TM’s of the ferromagnetic Heusler alloys are considered to have shifted in accordance with magnetic fields because high magnetic fields are favorable for ferromagnetic martensite phases.
The relationship between magnetism and TM in magnetic fields is discussed for other Ni2MnGa-type Heusler alloys. Table 1 shows the spontaneous magnetizations and dTM/dB values of Ni2+xMn1−xGa, Ni52Mn12.5Fe12.5Ga23, Ni2Mn0.75Cu0.25Ga, Ni2MnGa0.88Cu0.12, and Ni52Mn25Ga23. As for Ni2+xMn1−xGa alloys, shifts in the TM of the magnetic fields were observed by magnetization measurements [2,34,36,37]. The TM and TC of Ni2MnGa (x = 0) are 200 and 360 K, respectively. The region above TM is the Ferro–A phase. A sample where x = 0 for Ni2+xMn1−xGa showed a phase transition from the Ferro–A to the Ferro–M phases at TM. A sample where x = 0.19 showed ferromagnetic transition and martensite transition at TM. When x = 0, the shift in TM was estimated as dTM/dB = 0.2 K/T [20] and where x = 0.19, dTM/dB = 0.8 K/T [37]. The shift in TM where x = 0.19 was higher than that for x = 0. The last four alloys in Table 1 show re-entrant magnetic transition. In these alloys, ferromagnetic transition occurs at the martensite transition. Below TM, the paramagnetic martensite phase (Para–M) appears. On the other hand, above TM, the austenite ferromagnetic phase (Ferro–A) appears. The ground states of these alloys are the ferromagnetic martensite phase at low temperature. Therefore, re-entrant magnetism appears. In a magnetic field, the ferromagnetic phase is more stable than the paramagnetic phase is. Therefore, TM decreases with increasing magnetic fields while the ferromagnetic phase area increases; the sign of dTM/dB is negative. In these alloys, the values of dTM/dB are large. This means that strong magneto-structural coupling was revealed through magnetic properties and phase transitions.
3.4. Magneto-Structural Coupling of Ni2MnGa-type Heusler Alloys
Finally, we comment on the x–T phase diagram of Ni2MnGa-type Heusler alloys. As for the x–T phase diagram of Ni50+xMn27−xGa23 alloys (−25 ≤ x ≤ 6), the TM increases with increasing x. In contrast, the TC decreases with decreasing x. Kataoka et al. [41] explained the phase diagram of Ni2Mn1−xCuxGa (0 ≤ x ≤ 0.40) alloys. They conceived of the Landau-type phenomenological free energy as a function of martensitic distortion and magnetization. Their analysis showed that the bi-quadratic coupling term of martensitic distortion and magnetization, together with a higher order term, play an important role in the interplay between the martensite and ferromagnetic phases. Their calculation was based on the phenomenological free energy, shown as:
where, Ftot is the total free energy; Fela, the free energy of the elastic strain eij; Fmag, the free energy of the magnetic system (including the magnetic exchange energy and the magnetocrystalline anisotropy energy) and Fmag−ela, the energy of the interaction between the distortion and the magnetization. The calculated x–T phase diagram of Ni2Mn1−xCuxGa agrees well with the phase diagram, which was obtained from the experimental results. In addition, using the martensitic distortion coefficient e3, they suggested that the bi-quadratic term, , in Fmag−ela, affects large magneto-structural coupling. ( , where, exx, eyy and ezz are strains along x, y, and z axis, respectively). Thus, strong magneto-structural coupling was shown to have an important role in the magnetic properties and phase transitions of ferromagnetic shape memory alloys. Large magnetocrystalline anisotropy influences magneto-elastic coupling Fmag−ela by means of the bi-quadratic term, . In Ni50−xCoxMn31.5Ga18.5 (0 ≤ x ≤ 9), magnetization M increases with the magnetic field between 338 K and 388 K [40]. The thermal hysteresis of the thermal strain also decreases at high magnetic fields. Other Heusler compounds, such as Ni50+xMn12.5Fe12.5Ga25−x, show an x-T phase diagram similar to that of Ni2Mn1−xCuxGa [26]. The magnetic field-induced strain in single crystals, or magnetostriction in polycrystals, of Ni2MnGa, Ni-Co-Mn-Ga, and Ni-Co-Mn-In alloys also suggest a strong magneto-structural coupling. The x–T phase diagram of Ni50+xMn27−xGa23 alloys (−25 ≤ x ≤ 6) also shows the same characters as that of Ni2Mn1−xCuxGa (0 ≤ x ≤ 0.40) alloys [19]. The x–T phase diagram of Ni50+xMn27−xGa23 indicates a strong magneto-structural coupling for Ni50+xMn27−xGa23 alloys.
To apply this theory to our present work, further theoretical consideration is needed to apply this theory for analyzing the relationship between the martensite variant structure and the magnetic field, which is reflected by the Zeeman term, and Jahn-Teller effect, which is applied to the ferrites and perovskite compounds [42,43].
4. Conclusions
Thermal strain, permeability, and magnetization measurements were performed on the Heusler alloys Ni52.5Mn24.5Ga23 (x = 2.5) and Ni52.7Mn24.3Ga23 (x = 2.7).
Thermal strain: When cooling from the austenite phase, a steep decrease in the thermal strain was obtained because of the martensite transition. TM and TR increased gradually with increasing magnetic fields. For x = 2.5, The shift in TM in the magnetic field was estimated as dTMs/dB = 0.9 ± 0.2 K/T. For x = 2.7, the shift in TM in the magnetic field was estimated as dTMs/dB = 1.1 ± 0.2 K/T.
The dTMs/dB values determined from the thermal strain results are approximately as same as the values calculated by the Clausius-Clapeyron relation.
For x = 2.5, at the Curie temperature, the M4 vs. B/M plot crossed the origin of the coordinate axis, and the M4 vs. B/M plot indicates a good linear relation around the Curie temperature TC = 350 K. The result is in agreement with the theory by Takahashi for weak itinerant electron ferromagnets. From the magnetic moment and the gradient of M4 vs. B/M, we calculated the spin fluctuation parameter TA as 1.06 × 104 K, which is comparable to the value of Ni (1.76 × 104 K).
Acknowledgments
The authors would like to express sincere thanks to Toetsu Shishido and Kazuo Obara of the Institute for Materials Research, Tohoku University for their help with the sample preparation. This study was supported by a Grant-in-Aid for Scientific Research (C) (Grant No. 21560693) from the Japan Society for the Promotion of Science (JSPS) of the Ministry of Education, Culture, Sports, Science and Technology, Japan.
This study was technically supported by the Center for Integrated Nanotechnology Support, Tohoku University, and the High Field Laboratory for Superconducting Materials, Institute for Materials Research, Tohoku University. One of the authors, Hiroyuki Nojiri, acknowledges support by GCOE-material integration.
Author Contributions
Takuo Sakon designed, directed, carried out the experiments and wrote the paper, Kohei Otsuka carried out the DSC measurements, Junpei Matsubayashi carried out the permeability and magnetization measurements by means of heliumu-free magnet, Yuushi Watanabe carried out the thermal expansion and magnetostriction measurements, Hironori Nishihara carried out the magnetization measurements by means of SQUID magnetometer, Kenta Sasaki carried out the thermal expansion and magnetostriction measurements, Satoshi Yamashita, Rie Y. Umetsu, and Takeshi Kanomata made and homogenized the samples. Hiroyuki Nojiri supported this experimental project at IMR, Tohoku University, Takeshi Kanomata also advised about the scientific meanings of this study and edited the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ullakko, K.; Huang, J.K.; Kantner, C.; O’Handley, R.C.; Kokorin, V.V. Large magnetic-field-induced strains in Ni2MnGa single crystals. Appl. Phys. Lett 1996, 69, 1966–1968. [Google Scholar]
- Webster, P.J.; Ziebeck, K.R.A.; Town, S.L.; Peak, M.S. Magnetic order and phase transformation in Ni2MnGa. Philos. Mag. B 1984, 49, 295–310. [Google Scholar]
- Brown, P.J.; Crangle, J.; Kanomata, T.; Matsumoto, M.; Neumann, K-.U.; Ouladdiaf, B.; Ziebeck, K.R.A. The crystal structure and phase transitions of the magnetic shape memory compound Ni2MnGa. J. Phys. Condens. Matter 2002, 14, 10159–10171. [Google Scholar]
- Pons, J.; Santamarta, R.; Chernenko, V.A.; Cesari, E. Long-Period martensitic structures of Ni-Mn-Ga alloys studied by high-resolution transmission electron microscopy. J. Appl. Phys 2005, 97, 083516:1–083516:7. [Google Scholar]
- Ranjan, R.; Banik, S.; Barman, S.R.; Kumar, U.; Mukhopadhyay, P.K.; Pandey, D. Powder X-ray diffraction study of the thermoelastic martensite transition in Ni2Mn1.05Ga0.95. Phys. Rev. B 2006, 74, 224443:1–224443:2. [Google Scholar]
- Jiang, C.; Feng, G.; Gong, S.; Xu, H. Effect of Ni excess on phase transformation temperatures of NiMnGa alloys. Mater. Sci. Eng. A 2003, 342, 231–235. [Google Scholar]
- Ma, Y.; Jiang, C.; Li, Y.; Xu, H.; Wang, C.; Liu, X. Study of Ni50+xMn25Ga25−x (x = 2–11) as high-temperature shape-memory alloys. Acta Mater 2007, 55, 1533–1541. [Google Scholar]
- Mañosa, L.; Moya, X.; Planes, A.; Krenke, T.; Acet, M.; Wassermann, E.F. Ni-Mn-based magnetic shape memory alloys: Magnetic properties and martensite transformation. Mater. Sci. Eng. A, 2008, 481–482, 49–56. [Google Scholar]
- Sánchez-Alarcos, V.; Pérez-Landazábal, J.I.; Gómez-Polo, C.; Recarte, V. Influence of the atomic order on the magnetic characteristics of a Ni-Mn-Ga ferromagnetic shape memory alloy. J. Magn. Magn. Mater 2008, 320, e160–e163. [Google Scholar]
- Rudajevová, A. Analysis of the thermal expansion characteristics of Ni53.6Mn27.1Ga19.3 alloy. J. Alloys Compd 2007, 430, 153–157. [Google Scholar]
- Zhu, F.Q.; Yang, F.Y.; Chien, C.L.; Ritchie, L.; Xiao, G.; Wu, G.H. Magnetic and thermal properties of Ni–Mn–Ga shape memory alloy with Martensite transition near room temperature. J. Magn. Magn. Mater 2005, 288, 79–83. [Google Scholar]
- Chernenko, V.A.; L’vov, V.A.; Khovailo, V.V.; Takagi, T.; Kanomata, T.; Suzuki, T.; Kainuma, R. Interdependence between the magnetic properties and lattice parameters of Ni-Mn-Ga martensite. J. Phys. Condens. Matter 2004, 16, 8345–8352. [Google Scholar]
- Golub, V.O.; Vovk, A.Y.; O’Connor, C.J.; Kotov, V.V.; Yakovenko, P.G.; Ullakko, K. Magnetic and structural properties of nonstoichiometric Ni2MnGa alloys with Ni and Ga excess. J. Appl. Phys 2003, 93, 8504–8506. [Google Scholar]
- Kim, J.; Inaba, F.; Fukuda, T.; Kakeshita, T. Effect of magnetic field on martensitic transformation temperature in Ni-Mn-Ga ferromagnetic shape memory alloys. Acta Mater 2006, 54, 493–499. [Google Scholar]
- González-Comas, A.; Obradó, E.; Mafiosa, L.; Planes, A.; Labarta, A. Magnetoelasticity in the Heusler Ni2MnGa alloy. J. Magn. Magn. Mater, 1999, 196–197, 637–638. [Google Scholar]
- Lanska, N.; Söderberg, O.; Sozinov, A.; Ge, Y.; Ullakko, K.; Lindroos, V.K. Composition and temperature dependence of the crystal structure of Ni-Mn-Ga alloys. J. Appl. Phys 2004, 95, 8074–8078. [Google Scholar]
- Likhachev, A.A.; Ullakko, K. Magnetic-field-controlled twin boundaries motion and giant magneto-mechanical effects in Ni-Mn-Ga shape memory alloy. Phys. Lett. A 2000, 275, 142–151. [Google Scholar]
- Murray, S.J.; Farinelli, M.; Kantner, C.; Huang, J.K.; Allen, S.M.; O’Handley, R.C. Field-induced strain under load in Ni-Mn-Ga magnetic shape memory materials. J. Appl. Phys 1998, 83, 7297–7299. [Google Scholar]
- Umetsu, R.Y.; Ando, H.; Yamashita, S.; Endo, K.; Nishihara, H.; Kainuma, R.; Kanomata, T.; Ziebeck, K.R.A. Phase diagram and magnetic moment of Ni50+xMn27−xGa23 ferromagnetic shape memory alloys. J. Alloys Compd 2013, 579, 521–528. [Google Scholar]
- Dai, L.; Cullen, J.; Wuttig, M. Intermartensitic transformation in a NiMnGa alloy. J. Appl. Phys 2004, 95, 6957–6959. [Google Scholar]
- Takahashi, Y. Quantum spin fluctuation theory of the magnetic equation of state of weak itinerant-electron ferromagnets. J. Phys. Condens. Matter 2001, 13, 6323–6358. [Google Scholar]
- Takahashi, Y. Spin Fluctuation Theory of Itinerant Electron Magnetism; Springer-Verlag: Berlin/Heiderberg, Germany, 2013. [Google Scholar]
- Nishihara, H.; Komiyama, K.; Oguro, I.; Kanomata, T.; Chernenko, V. Magnetization processes near the Curie temperatures of the itinerant ferromagnets, Ni2MnGa and pure nickel. J. Alloys. Compd 2007, 442, 191–193. [Google Scholar]
- Sakon, T.; Nagashio, H.; Sasaki, K.; Susuga, S.; Numakura, D.; Abe, M.; Endo, K.; Yamashita, S.; Nojiri, H.; Kanomata, T. Thermal strain and magnetization of the ferromagnetic shape memory alloy Ni52Mn25Ga23 in a magnetic field. J. Phys. Chem. Solids 2013, 74, 158–165. [Google Scholar]
- Kikuchi, D.; Kanomata, T.; Yamaguchi, Y.; Nishihara, H. Magnetic properties of ferromagnetic shape memory alloys Ni50+xMn12.5Fe12.5Ga25−x. J. Alloys Compd 2006, 426, 223–227. [Google Scholar]
- Sakon, T.; Nagashio, H.; Sasaki, K.; Susuga, S.; Endo, K.; Nojiri, H.; Kanomata, T. Thermal expansion and magnetization studies of novel ferromagnetic shape memory alloys Ni52Mn12.5Fe12.5Ga23 and Ni2Mn0.75Cu0.25Ga. Mater. Trans 2011, 52, 1142–1147. [Google Scholar]
- Okamoto, N.; Fukuda, T.; Kakeshita, T.; Takeuchi, T. Magnetocrystalline anisotropy constant and twinning stress in martensite phase of Ni-Mn-Ga. Mater. Sci. Eng. A, 2006, 438–440, 948–951. [Google Scholar]
- Ahuja, B.L.; Sharma, B.K.; Mathur, S.; Heda, N.L.; Itou, M.; Andrejczuk, A.; Sakurai, Y.; Chakrabarti, A.; Banik, S.; Awasthi, A.M.; et al. Magnetic Compton scattering study of Ni2+xMn1−x Ga ferromagnetic shape-memory alloys. Phys. Rev. B 2007, 75, 134403:1–134403:9. [Google Scholar]
- Levitin, R.Z.; Snegirev, V.V.; Kopylov, A.V.; Lagutin, A.S.; Gerber, A. Magnetic method of magnetocaloric effect determination in high pulsed magnetic fields. J. Magn. Magn. Mater 1997, 170, 223–227. [Google Scholar]
- Nishihara, H.; Furutani, Y.; Wada, T.; Kanomata, T.; Kobayashi, K.; Kainuma, R.; Ishida, K.; Yamauchi, T. Magnetization process near the curie temperature of a ferromagnetic heusler alloy Co2CrGa. J. Phys. Conf. Ser 2007, 200, 032053:1–032053:4. [Google Scholar]
- Vasil’ev, A.N.; Estrin, E.I.; Khovailo, V.V.; Bozhko, A.D.; Ischuk, R.A.; Matsumoto, M.; Takagi, T.; Tani, J. Dilatometric study of Ni2+xMn1−xGa under magnetic field. Int. Appl. Electromagn. Mech 2000, 12, 35–40. [Google Scholar]
- Banerjee, A.; Dash, S.; Lakhani, A.; Chaddah, P.; Chen, X.; Ramanujan, R.V. Relating field-induced shift in transition temperature to the kinetics of coexisting phases in magnetic shape memory alloys. Solid State Commun 2011, 151, 971–975. [Google Scholar]
- Kainuma, R.; Imano, Y.; Ito, W.; Sutou, Y.; Morino, H.; Okamoto, S.; Kitakami, O.; Oikawa, K.; Fujita, A.; Kanomata, T.; et al. Magnetic-field-induced shape recovery by reverse phase transformation. Nature 2006, 439, 957–960. [Google Scholar]
- Khovailo, V.V.; Novosad, V.; Takagi, T.; Filippov, D.A.; Levintin, R.Z.; Vasil’ev, A.N. Magnetic properties and magnetostructural phase transitions in Ni2+xMn1−x Ga shape memory alloys. Phys. Rev. B 2004, 70, 174413–174418. [Google Scholar]
- Khovailo, V.V.; Takagi, T.; Tani, T.J.; Levitin, R.Z.; Cherechukin, A.A.; Matsumoto, M.; Note, R. Magnetic properties of Ni2.18Mn0.82Ga Heusler alloys with a coupled magnetostructural transition. Phys. Rev. B 2002, 65, 092410–092413. [Google Scholar]
- Gonzàlez-Comas, A.; Obradó, E.; Maños, L.; Planes, A.; Chernenko, V.A.; Hattink, B.J.; Labarta, A. Premartensitic and martensitic phase transitions in ferromagnetic Ni2MnGa. Phys. Rev. B 1999, 60, 7085–7090. [Google Scholar]
- Filippov, D.A.; Khovailo, V.V.; Koledov, V.V.; Krasnoperov, E.P.; Levitin, R.Z.; Shavrov, V.G.; Takagi, T. The magnetic field influence on magnetostructural phase transition in Ni2.19Mn0.81Ga. J. Magn. Magn. Mater, 2003, 258–259, 507–509. [Google Scholar]
- Sakon, T.; Nagashio, H.; Sasaki, K.; Susuga, S.; Numakura, D.; Abe, M.; Endo, K.; Nojiri, H.; Kanomata, T. Thermal expansion and magnetization studies of the novel ferromagnetic shape memory alloy Ni2MnGa0.88Cu0.12 in a magnetic field. Phys. Scr 2011, 84, 045603:1–045603:6. [Google Scholar]
- Albertini, F.; Fabbrici, S.; Paoluzi, A.; Kamarad, J.; Arnold, Z.; Righi, L.; Solzi, M.; Porcari, G.; Pernechele, C.; Serrate, D.; et al. Reverse magnetostructural transitions by Co and In doping NiMnGa alloys: Structural, magnetic, and magnetoelastic properties. Mater. Sci. Forum 2011, 684, 151–163. [Google Scholar]
- Sakon, T.; Sasaki, K.; Numakura, D.; Abe, M.; Nojiri, H.; Adachi, Y.; Kanomata, T. Magnetic field-induced transition in Co-doped Ni41Co9Mn31.5Ga18.5 Heusler Alloy. Mater. Trans 2013, 54, 9–13. [Google Scholar]
- Kataoka, M.; Endo, K.; Kudo, N.; Kanomata, T.; Nishihara, H.; Shishido, T.; Umetsu, R.Y.; Nagasako, M.; Kainuma, R. Martensitic transformation, ferromagnetic transition, and their interplay in the shape memory alloys Ni2Mn1−x Cux Ga. Phys. Rev. B 2010, 82, 214423:1–214423:14. [Google Scholar]
- Kataoka, M.; Kanamori, J. A theory of the cooperative Jahn-Teller effect-crystal distortions in Cu1−x Nix Cr2O4 and Fe1−x Nix Cr2O. J. Phys. Soc. Jpn 1972, 32, 113–134. [Google Scholar]
- Gehring, G.A.; Gehring, K.A. Cooperative Jahn-Teller effects. Rep. Prog. Phys 1975, 38, 1–89. [Google Scholar]



| Sample | MM | MA | dTM/dB(K/T) | Remarks |
|---|---|---|---|---|
| Ni2MnGa | 90 Am2/kg at 180 K (*1) Ferro | 80 Am2/kg at 220 K (*1) Ferro | 0.20 (*2) 0.40 ± 0.25 (*3) | *1 [2]; *2 [36]; *3 [37] |
| Ni2.19Mn0.81Ga | 2.0 (a.u.) at 300 K Ferro | 0 (a.u.) at 350 K Para | 0.80 ± 0.5 | [34] |
| Ni52Mn12.5Fe12.5Ga23 | 63.1 Am2/kg at 250 K Ferro | 52.7 Am2/kg at 300 K Ferro | 0.5 | [26] |
| Ni2Mn0.75Cu0.25Ga | 42.4 Am2/kg at 300 K Ferro | 0 Am2/kg at 307 K Para | 1.2 | [26] |
| Ni2MnGa0.88Cu0.12 | 37.3 Am2/kg at 330 K Ferro | 0 Am2/kg at 340 K Para | 1.3 | [38] |
| Ni52Mn25Ga23 | 42 Am2/kg at 333 K Ferro | 34 Am2/kg at 335 K Ferro | 0.43 ± 0.1 | [24] |
| Ni52.5Mn24.5Ga23 | 39 Am2/kg at 338 K Ferro | 22 Am2/kg at 343 K Ferro | 0.9 ± 0.2 | this work |
| Ni52.7Mn24.3Ga23 | 34 Am2/kg at 352 K Ferro | 0 Am2/kg at 356 K Para | 1.1 ± 0.2 | this work |
| Ni45Co5Mn36.7In13.3 | 0 Am2/kg at 270 K Para | 70 Am2/kg at 320 K Ferro | −4.3 | [33] |
| Ni43Co7Mn31Ga19 | 20 Am2/kg at TCM ≤ T ≤ TM Para or weak Ferro | 59.2 Am2/kg at TM ≤ T ≤ TCA Ferro | −2.95 | [39] |
| Ni41Co9Mn32Ga18 | 4.0 Am2/kg at TCM ≤ T ≤ TM Para or weak Ferro | 53.3 Am2/kg at TM ≤ T ≤ TCA Ferro | −2.8 | [39] |
| Ni41Co9Mn31.5Ga18.5 | 12 Am2/kg at TCM ≤ T = 316 K ≤ TM Para or weak Ferro | 79 Am2/kg at TM ≤ T = 388 K ≤TCA Ferro | −4.2 | [40] |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sakon, T.; Otsuka, K.; Matsubayashi, J.; Watanabe, Y.; Nishihara, H.; Sasaki, K.; Yamashita, S.; Umetsu, R.Y.; Nojiri, H.; Kanomata, T. Magnetic Properties of the Ferromagnetic Shape Memory Alloys Ni50+xMn27−xGa23 in Magnetic Fields. Materials 2014, 7, 3715-3734. https://doi.org/10.3390/ma7053715
Sakon T, Otsuka K, Matsubayashi J, Watanabe Y, Nishihara H, Sasaki K, Yamashita S, Umetsu RY, Nojiri H, Kanomata T. Magnetic Properties of the Ferromagnetic Shape Memory Alloys Ni50+xMn27−xGa23 in Magnetic Fields. Materials. 2014; 7(5):3715-3734. https://doi.org/10.3390/ma7053715
Chicago/Turabian StyleSakon, Takuo, Kohei Otsuka, Junpei Matsubayashi, Yuushi Watanabe, Hironori Nishihara, Kenta Sasaki, Satoshi Yamashita, Rie Y. Umetsu, Hiroyuki Nojiri, and Takeshi Kanomata. 2014. "Magnetic Properties of the Ferromagnetic Shape Memory Alloys Ni50+xMn27−xGa23 in Magnetic Fields" Materials 7, no. 5: 3715-3734. https://doi.org/10.3390/ma7053715