Flexural Behavior of HPFRCC Members with Inhomogeneous Material Properties
Abstract
:1. Introduction
2. Experimental Study
2.1. Test Outline
2.2. Materials and Mix Design
| W/C | S/C | Unit Content (kg/m3) | 8 mm PVA Fiber | |||
|---|---|---|---|---|---|---|
| C | W | S | Fly Ash | |||
| 0.55 | 0.6 | 727 | 400 | 436 | 436 | 2% |
2.3. Compressive Behavior

2.4. Tensile Behavior


2.5. Flexural Behavior


3. Analysis Model for Cracking and Flexural Behavior of HPFRCC Beams
3.1. A Sequential Cracking Behavior Model

3.2. A Layered Section Analysis Method

3.3. Constitutive Models for the Materials
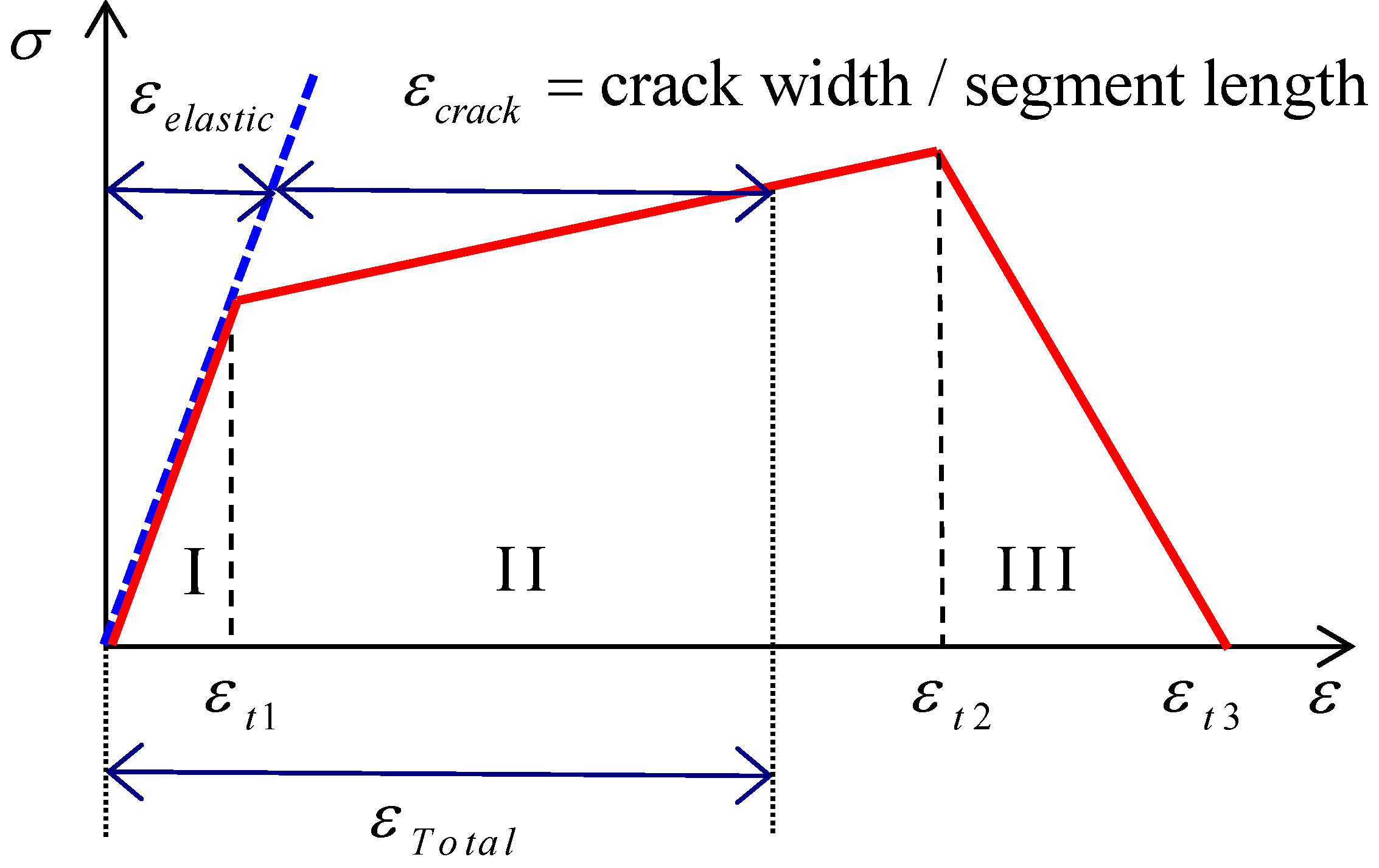
3.4. Determination of Segment Length
3.5. Calculation of Deflection


4. Analysis Results
4.1. Flexural Deformation Behavior


4.2. Monte Carlo Simulation of Flexural Behavior
| Classifications | Moment (kN·m) | Deflection (mm) | Crack Width (mm) | |
|---|---|---|---|---|
| Results with the homogeneity | 1.754 | 1.662 | 0.266 | |
| Monte Carlo simulation | Average | 1.661 | 1.284 | 0.203 |
| Standard Deviation | 0.046 | 0.164 | 0.010 | |
| Test results | Specimen 1 | 1.529 | 1.176 | 0.258 |
| Specimen 2 | 1.687 | 1.273 | 0.421 | |
| Specimen 3 | 1.635 | 1.337 | not available | |
| Average | 1.617 | 1.262 | 0.340 | |

5. Conclusions
- Compressive and tensile constitutive relations were proposed based on the experimental results. A bi-linear relation was assumed for the compression. Regarding the tensile behavior, the total strain was assumed to be a sum of the elastic and crack strains.
- In order to develop a realistic model that could account for sequential multiple cracking and localization behavior of the HPFRCC, the pure bending region was divided into several segments with random material properties. The properties of the segments are assigned based on the probabilistic distribution of the material parameters.
- A Monte Carlo simulation had been conducted in order to consider the uncertainty for the material properties of HPFRCC. Results of the Monte Carlo simulation showed that the test results are within the region of prediction with 99% certainty.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bentur, A.; Mindess, S. Fiber Reinforced Cementitious Composites; McGraw-Hill: New York, NY, USA, 1990. [Google Scholar]
- Balaguru, P.; Surendra, P. Fiber-Reinforced Cement Composites; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Naaman, A.E.; Reinhardt, H.W. High Performance Fiber Reinforced Cement Composites 4 (HPFRCC4); RILEM Proceedings PRO 30; RILEM Publications SARL: Bagneux, France, 2003. [Google Scholar]
- Naaman, A.E.; Reinhardt, H.W. High Performance Fiber Reinforced Cement Composites 2 (HPFRCC2); RILEM Proceedings 31; E&Fn Spon: London, UK, 1995. [Google Scholar]
- Fischer, G.; Li, V.C. International RILEM Workshop on High Performance Fiber Reinforced Cementitoius Composites (HPFRCC) in Structural Applications; RILEM Publications SARL: Bagneux, France, 2006. [Google Scholar]
- Lee, B.J.; Hyun, J.H.; Kim, Y.Y.; Shin, K.J. Chloride permeability of damaged high-performance fiber-reinforced cement composite by repeated compressive loads. Materials 2014, 7, 5802–5815. [Google Scholar]
- Maalej, M.; Li, V.C. Flexural/tensile-strength ratio in engineered cementitious composites. J. Mater. Civil Eng. 1994, 6, 513–528. [Google Scholar] [CrossRef]
- Tentative Guideline for Design and Construction of Engineering Cementitious Composites (ECC) (Draft); JSCE TC 334; Japan Society of Civil Engineers: Tokyo, Japan, 2005.
- Ostergaard, L.; Walter, R.; Olesen, J.F. Method for determination of tensile properties of engineered cementitious composites (ECC). In Proceedings of the 3rd International Conference on Construction Materials: Performance, Innovations and Structural Implications, Vancouver, BC, Canada, 22–24 August 2005.
- Zhang, J.; Stang, H. Applications of stress–crack width relationship in predicting the flexural behavior of fiber-reinforced concrete. Cement Concr. Res. 1998, 28, 439–452. [Google Scholar] [CrossRef]
- Matsumoto, T.; Li, V.C. Fatigue life analysis of fiber reinforced concrete with a fracture mechanics based model. Cement Concr. Compos. 1999, 21, 249–261. [Google Scholar] [CrossRef]
- Oh, B.H.; Park, D.G.; Kim, J.C.; Choi, Y.C. Experimental and theoretical investigation on the postcracking inelstic behavior of synthetic fiber reinforced concrete beams. Cement Concr. Res. 2005, 35, 384–392. [Google Scholar] [CrossRef]
- Szerszen, M.M.; Szwed, A.; Li, V.C. Flexural Response of Reinforced Beam with High Ductility Concrete Material; Woodhead Publisher: Warsaw, Poland, 2006; pp. 263–274. [Google Scholar]
- Caggiano, A.; Etse, G.; Martinelli, E. Zero-thickness interface model formulation for failure behavior of fiber-reinforced cementitious composites. Comput. Struct. 2012, 98, 23–32. [Google Scholar] [CrossRef]
- Caggiano, A.; Cremona, M.; Faella, C.; Lima, C.; Matrinelli, E. Fracture behavior of concrete beams reinforced with mixed long/short steel fibers. Constr. Build. Mater. 2012, 37, 832–840. [Google Scholar] [CrossRef]
- Olesen, J.F. Fictitious crack propagation in fiber-reinforced concrete beams. J. Eng. Mech. 2001, 127, 272–280. [Google Scholar] [CrossRef]
- Li, V.C.; Mishra, D.K.; Wu, H.C. Matrix design for pseudo-strain-hardening fibre reinforced cementitious composites. Mater. Struct. 1995, 28, 586–595. [Google Scholar] [CrossRef]
- Li, V.C.; Wang, S.; Wu, C. Tensile strain-hardening behavior of PVA-ECC. ACI Mater. J. 2001, 98, 483–492. [Google Scholar]
- Kim, Y.Y.; Kong, H.J.; Li, V.C. Design of engineered cementitious composite (ECC) suitable for wet-mix shotcreting. ACI Mater. J. 2003, 100, 511–518. [Google Scholar]
- Kim, Y.Y.; Kim, J.S.; Ha, G.J.; Kim, J.K. ECC produced with ground granulated blast furnace slag particles. In Proceedings of the 3rd International Conference on Construction Materials, Vancouver, BC, Canada, 22–24 August 2005.
- Park, R.; Paulay, T. Reinforced Concrete Structures; John Wiley and Sons: Hoboken, NJ, USA, 1975. [Google Scholar]
- Vecchio, F.J.; Collins, M.P. Predicting the response of reinforced concrete beams subjected to shear using modified compression field theory. ACI Struct. J. 1988, 85, 258–268. [Google Scholar]
- Bentz, E.C. Sectional Analysis of Reinforced Concrete Members. Ph.D. Thesis, Department of Civil Engineering, University of Toronto, Toronto, ON, Canada, 2000. [Google Scholar]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in Fortran 77; Combridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Hognestad, E.; Hanson, N.W.; McHenry, D. Concrete stress distribution in ultimate strength design. ACI J. Proc. 1955, 27, 455–479. [Google Scholar]
- Fanella, D.A.; Naaman, A. Stress–strain properties of fiber reinforced mortar in compression. ACI J. Proc. 1985, 82, 475–483. [Google Scholar]
- Barros, J.A.O.; Figueiras, J.A. Flexural behavior of steel fiber reinforced concrete: Testing and modelling. ASCE J. Mater. Civil Eng. 1999, 11, 331–339. [Google Scholar] [CrossRef]
- Qian, S.Z.; Li, V.C. Simplified inverse method for determining the tensile strain capacity of strain hardening cementitious composites. J. Adv. Concr. Technol. 2007, 5, 235–246. [Google Scholar] [CrossRef]
- Soranakom, C.; Mobasher, B. Moment–curvature response of strain softening and strain hardening cement based composites. Cement Concr. Compos. 2008, 30, 465–477. [Google Scholar] [CrossRef]
- Ulfkjaer, J.P.; Krenk, S.; Brincker, R. Analytical model for fictitious crack propagation in concrete beams. J. Eng. Mech. 1995, 121, 7–15. [Google Scholar] [CrossRef]
- Gere, J.M.; Timoshenko, S.P. Mechanics of Materials; PWS-KENT Publishing: Boston, MA, USA, 1990. [Google Scholar]
- Redon, C.; Li, V.C.; Wu, C.; Hoshiro, H.; Saito, T.; Ogawa, A. Measuring and modifying interface properties of PVA fibers in ECC matrix. J. Mater. Civil Eng. 2001, 13, 399–406. [Google Scholar] [CrossRef]
- Lee, S.-C.; Oh, J.-H.; Cho, J.-Y. Fiber orientation factor on a circular cross-section in concrete members. J. Korea Concr. Inst. 2014, 26, 307–313. [Google Scholar] [CrossRef]
- Lee, S.-C.; Oh, J.-H.; Cho, J.-Y. Fiber orientation factor on rectangular cross-section in concrete members. Int. J. Eng. Technol. 2015, 7, 470–473. [Google Scholar] [CrossRef]
- Ang, A.H.S.; Tang, W.H. Probability Concepts in Engineering Planning and Design; John Wiley and Sons: Hoboken, NJ, USA, 1975. [Google Scholar]
- Kanakubo, T. Tensile characteristics evaluation method for DFRCC. J. Adv. Concr. Technol. 2006, 4, 3–17. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, K.-J.; Jang, K.-H.; Choi, Y.-C.; Lee, S.-C. Flexural Behavior of HPFRCC Members with Inhomogeneous Material Properties. Materials 2015, 8, 1934-1950. https://doi.org/10.3390/ma8041934
Shin K-J, Jang K-H, Choi Y-C, Lee S-C. Flexural Behavior of HPFRCC Members with Inhomogeneous Material Properties. Materials. 2015; 8(4):1934-1950. https://doi.org/10.3390/ma8041934
Chicago/Turabian StyleShin, Kyung-Joon, Kyu-Hyeon Jang, Young-Cheol Choi, and Seong-Cheol Lee. 2015. "Flexural Behavior of HPFRCC Members with Inhomogeneous Material Properties" Materials 8, no. 4: 1934-1950. https://doi.org/10.3390/ma8041934
APA StyleShin, K.-J., Jang, K.-H., Choi, Y.-C., & Lee, S.-C. (2015). Flexural Behavior of HPFRCC Members with Inhomogeneous Material Properties. Materials, 8(4), 1934-1950. https://doi.org/10.3390/ma8041934






