Automatic Modulation Recognition Using Compressive Cyclic Features
Abstract
:1. Introduction
2. Statistical Characterization of Signal of Interest
3. CS-based AMR
3.1. CS-Based Cyclic Characteristic Analysis
3.2. Feature Selection
3.3. Feature Extraction
Support Vector Machine (SVM) Classifier
4. Simulation and Performance Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Su, W. Feature space analysis of modulation classification using very high-order statistics. Commun. Lett. 2013, 17, 1688–1691. [Google Scholar] [CrossRef]
- Swami, A.; Sadler, B.M. Hierarchical digital modulation classification using cumulants. Trans. Commun. 2000, 48, 416–429. [Google Scholar] [CrossRef]
- Dobre, O.A.; Bar-Ness, Y.; Su, W. Higher-order cyclic cumulants for high order modulation classification. Milit. Commun. Conf. 2003, 10, 112–117. [Google Scholar]
- Spooner, C.M. Classification of co-channel communication signals using cyclic cumulants. Signal. Syst. Comput. 2002, 8, 531–536. [Google Scholar]
- Spooner, C.M. On the utility of sixth-order cyclic cumulants for RF signal classification. Asilomar 2002, 8, 890–897. [Google Scholar]
- Dobre, O.A.; Rajan, S.; Inkol, R. Cyclostationarity-based robust algorithms for QAM signal identification. Commun. Lett. 2012, 16, 12–15. [Google Scholar] [CrossRef] [Green Version]
- Xie, L.; Wan, Q. Cyclic feature based modulation recognition using compressive sensing. Wirel. Commun. Lett. 2017, 6, 402–405. [Google Scholar] [CrossRef]
- Eric, L.; Chakravarthy, D.V.; Ratazzi, P.; Wu, Z.Q. Signal classification in fading channels using cyclic spectral analysis. Eurasip J. Wirel. Commun. Netw. 2009, 1, 3129–3142. [Google Scholar]
- Dobre, O.A.; Ali, A.; Yeheskel, B.-N.; Wei, S. Cyclostationarity-based modulation classification of linear digital modulations in flat fading channels. Wirel. Pers. Commun. Int. J. 2010, 1, 699–717. [Google Scholar] [CrossRef]
- Zhou, L.; Hong, M. Distributed automatic modulation classification based on cyclic feature via compressive sensing. Milit. Commun. Conf. 2013, 11, 40–45. [Google Scholar]
- Lim, C.; Wakin, M.B. Compressive temporal higher order cyclostationary statistics. IEEE Trans. Signal Process. 2015, 63, 2942–2956. [Google Scholar] [CrossRef]
- Spooner, C.M.; Gardner, W.A. The cumulant theory of cyclostationary time-series. II. Development and applications. IEEE Trans. Signal Process. 1994, 42, 3409–3429. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y.; Drori, I.; Starck, J.-L. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit. IEEE Trans. Inf. Theory 2012, 58, 1094–1121. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Dandawate, A.V.; Giannakis, G.B. Asymptotic theory of mixed time averages and kth-order cyclic-moment and cumulant statistics. IEEE Trans. Inf. Theory 1995, 41, 216–232. [Google Scholar] [CrossRef]
- Candesy, E.; Rombergy, J.; Tao, T. Robust uncertainty principles: Exact signal seconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar]
- Nakamura, E. Compressive samplers for RF environments. IEEE Commun. Mag. 2013, 51, 124–129. [Google Scholar] [CrossRef]
- Xie, L.J.; Qun, W. Blind symbol-rate estimation based on ompressive cyclic statistics. ICIC Express Lett. 2017, 11, 1199–1206. [Google Scholar]
- Davenport, M.A.; Wakin, M.B. Analysis of orthogonal matching pursuit using the restricted isometry property. IEEE Trans. Inf. Theory 2010, 56, 4395–4401. [Google Scholar] [CrossRef]
- Brereton, R.G.; Lloyd, G.R. Support vector machines for classification and regression. Analyst 2009, 135, 230–267. [Google Scholar] [CrossRef] [PubMed]
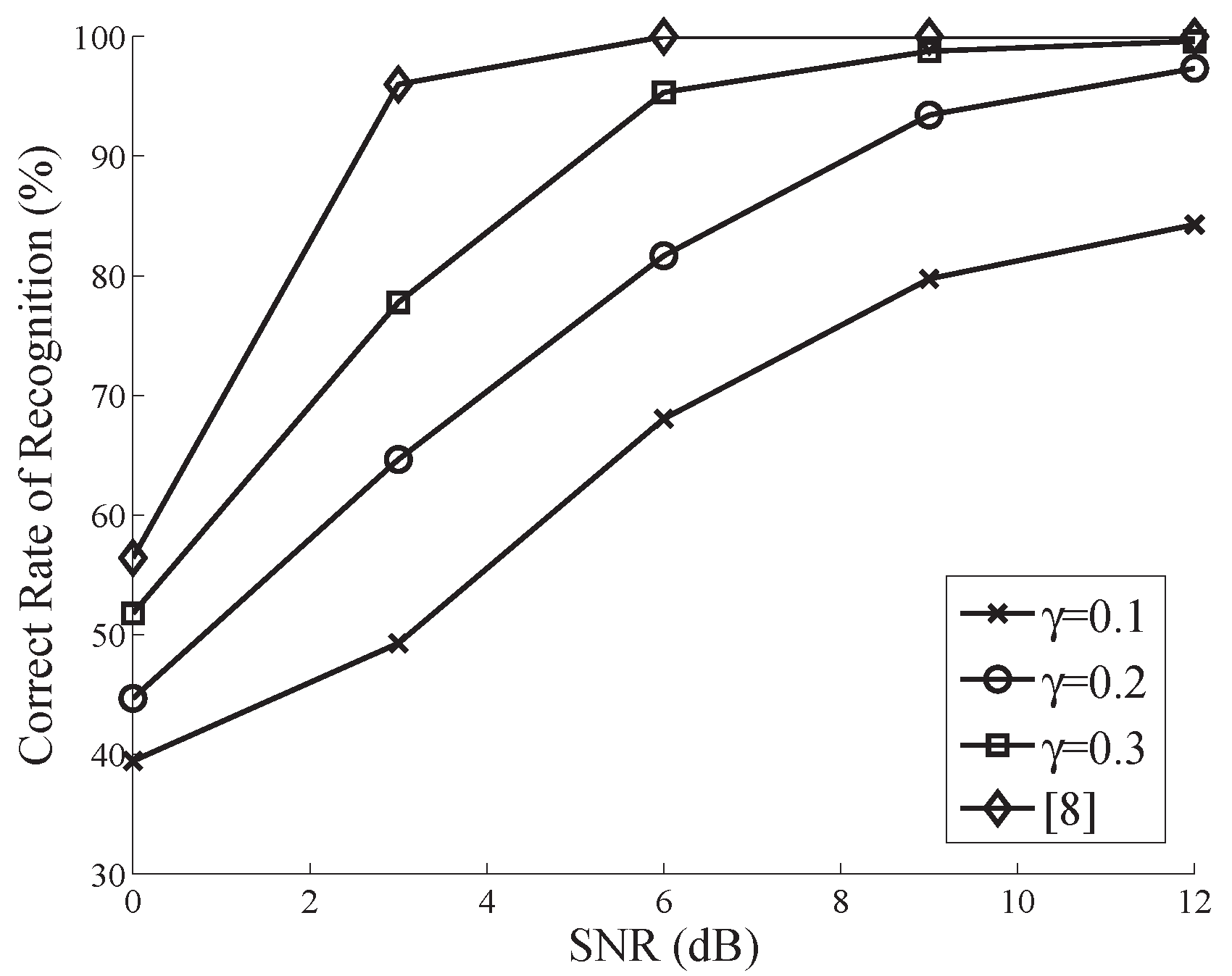
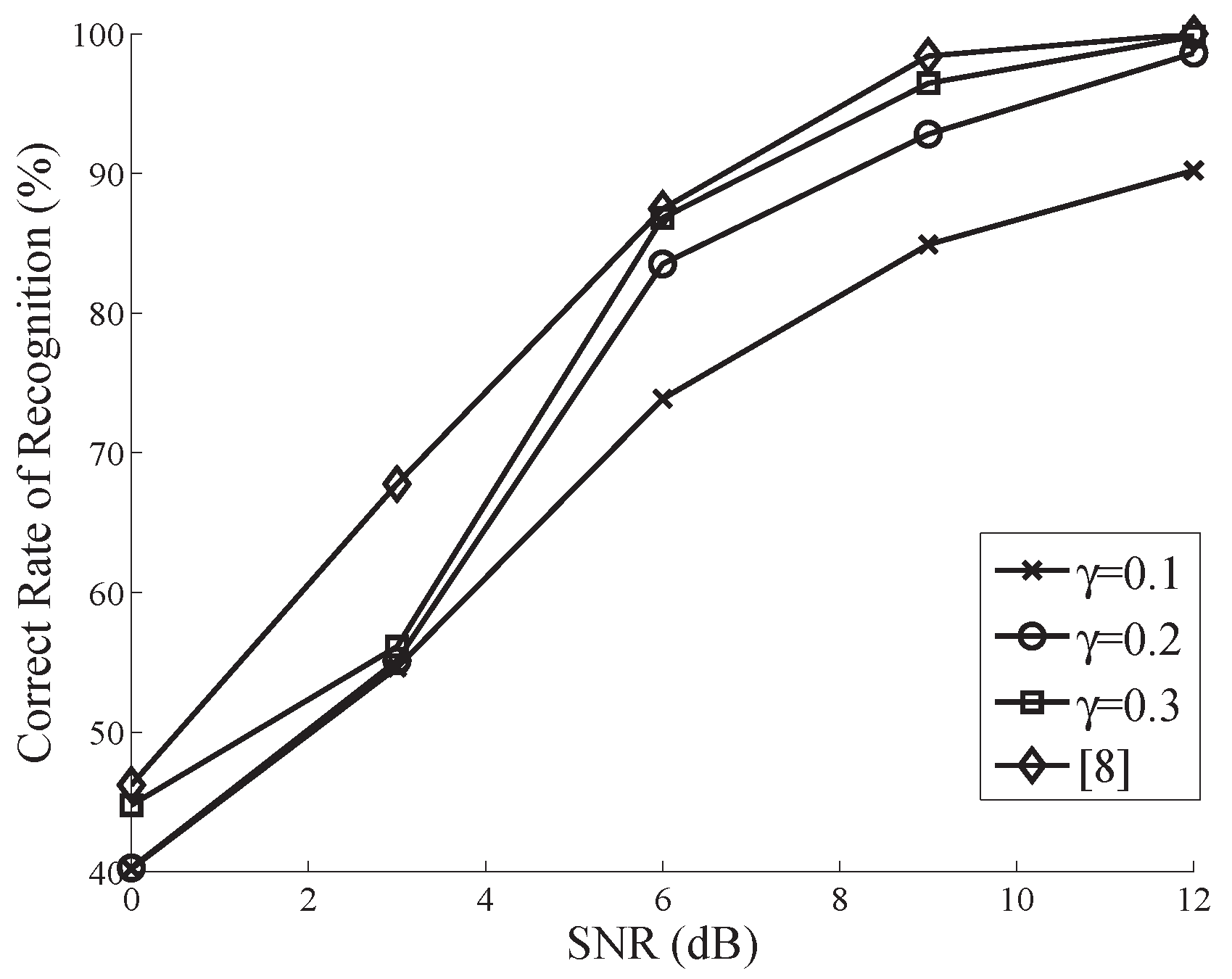
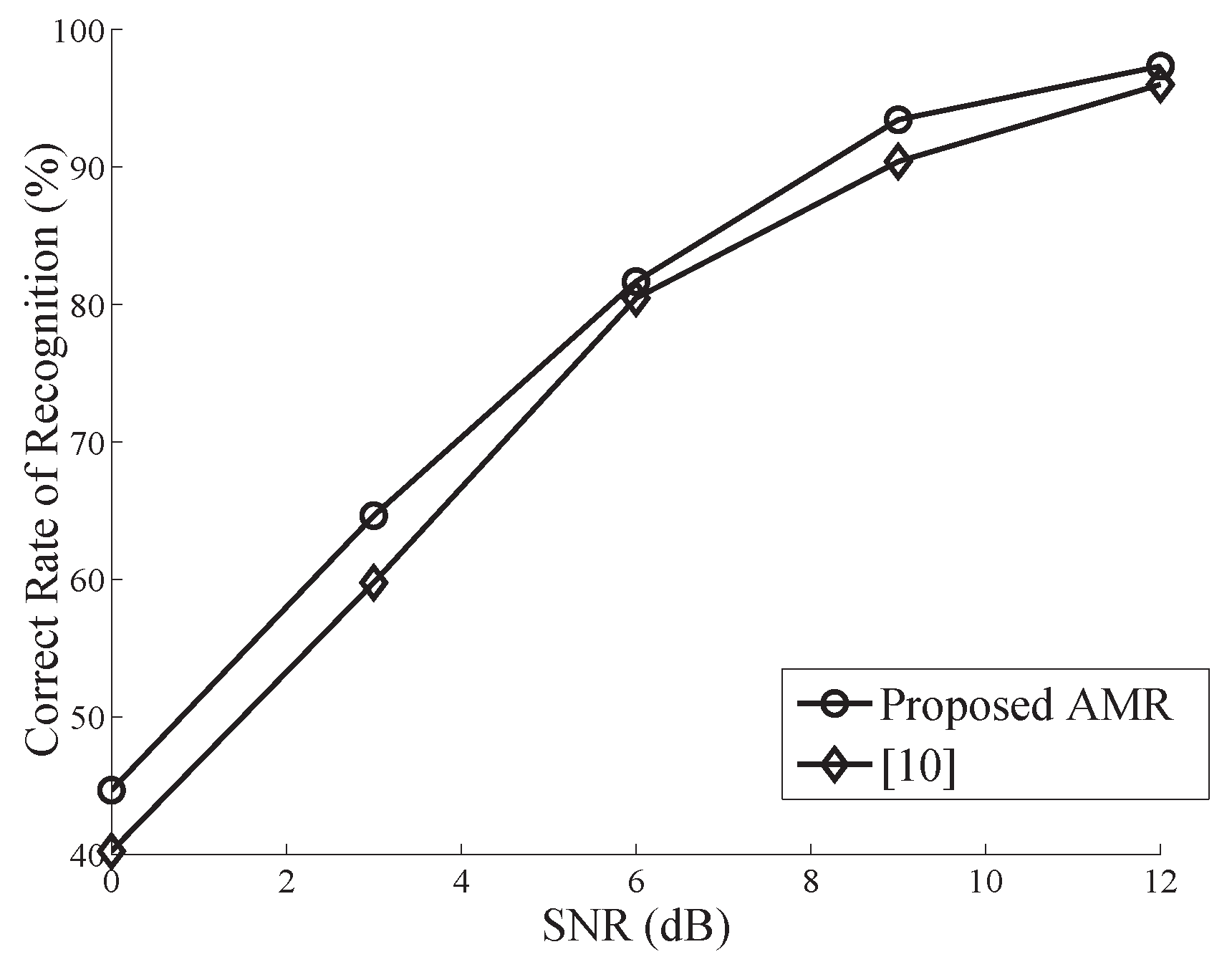

| 4QAM | 1 | 0 | −34 |
| 32QAM | −0.19 | 0 | −1.9926 |
| 16QAM | −0.68 | 0 | −13.9808 |
| 8ASK | −1.2381 | 7.1889 | −92.018 |
| 16PSK | 0 | 0 | 0 |
| Samples | 10,240 | 15,360 | 20,480 | |||
|---|---|---|---|---|---|---|
| Symbols | 4096 | 640 | 4096 | 960 | 4096 | 1280 |
| 0 dB | 39.4% | 38.4% | 44.7% | 40.9% | 51.8% | 44.4% |
| 3 dB | 52.8% | 49.2 % | 64.6% | 62.3% | 77.8% | 71.3% |
| 6 dB | 68.0% | 59.6% | 82.1 % | 81.7% | 95.3% | 90.2% |
| 9 dB | 79.7% | 78.4% | 93.4% | 92.7% | 98.8% | 97.2% |
| 12dB | 84.2% | 72.1% | 97.3% | 94.1% | 99.6% | 97.4% |
| Samples | 10,240 | 15,360 | 20,480 | |||
|---|---|---|---|---|---|---|
| Symbols | 4096 | 640 | 4096 | 960 | 4096 | 1280 |
| 0 dB | 40.2% | 37.8% | 42.9% | 40.3% | 46.2% | 40.9% |
| 3 dB | 57.7% | 55.1% | 68.6% | 56.1 % | 62.9% | 54.6% |
| 6 dB | 73.9% | 71.9% | 88.3% | 83.5% | 86.8% | 84.6% |
| 9 dB | 86.8% | 84.9% | 92.8% | 92.8% | 98.4% | 97.3% |
| 12dB | 90.2% | 88.7% | 98.6% | 96.0% | 99.8% | 98.8% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Wan, Q. Automatic Modulation Recognition Using Compressive Cyclic Features. Algorithms 2017, 10, 92. https://doi.org/10.3390/a10030092
Xie L, Wan Q. Automatic Modulation Recognition Using Compressive Cyclic Features. Algorithms. 2017; 10(3):92. https://doi.org/10.3390/a10030092
Chicago/Turabian StyleXie, Lijin, and Qun Wan. 2017. "Automatic Modulation Recognition Using Compressive Cyclic Features" Algorithms 10, no. 3: 92. https://doi.org/10.3390/a10030092





