GPU Adding-Doubling Algorithm for Analysis of Optical Spectral Images
Abstract
1. Introduction
2. Materials and Methods
2.1. Preliminaries of Adding Doubling (AD) Algorithm
2.1.1. Division of Incident and Reflected Light into Fluxes
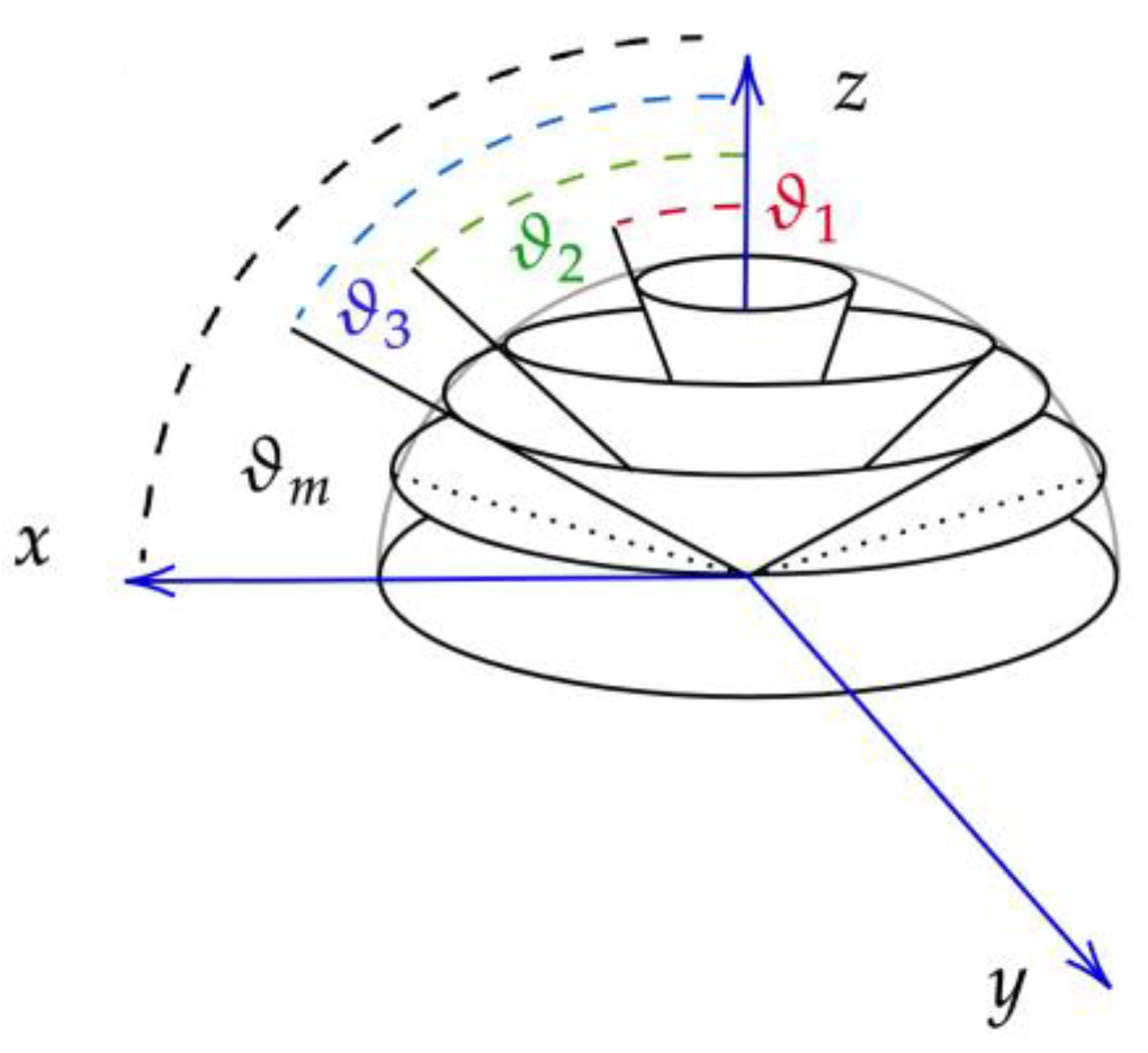
2.1.2. Approximating Reflected Flux Integral Using Quadrature
2.1.3. Calculating Scattering Phase Function
2.1.4. Initializing Starting Layer
2.1.5. Constructing the Entire Layer
2.1.6. Calculating Reflectance and Transmittance
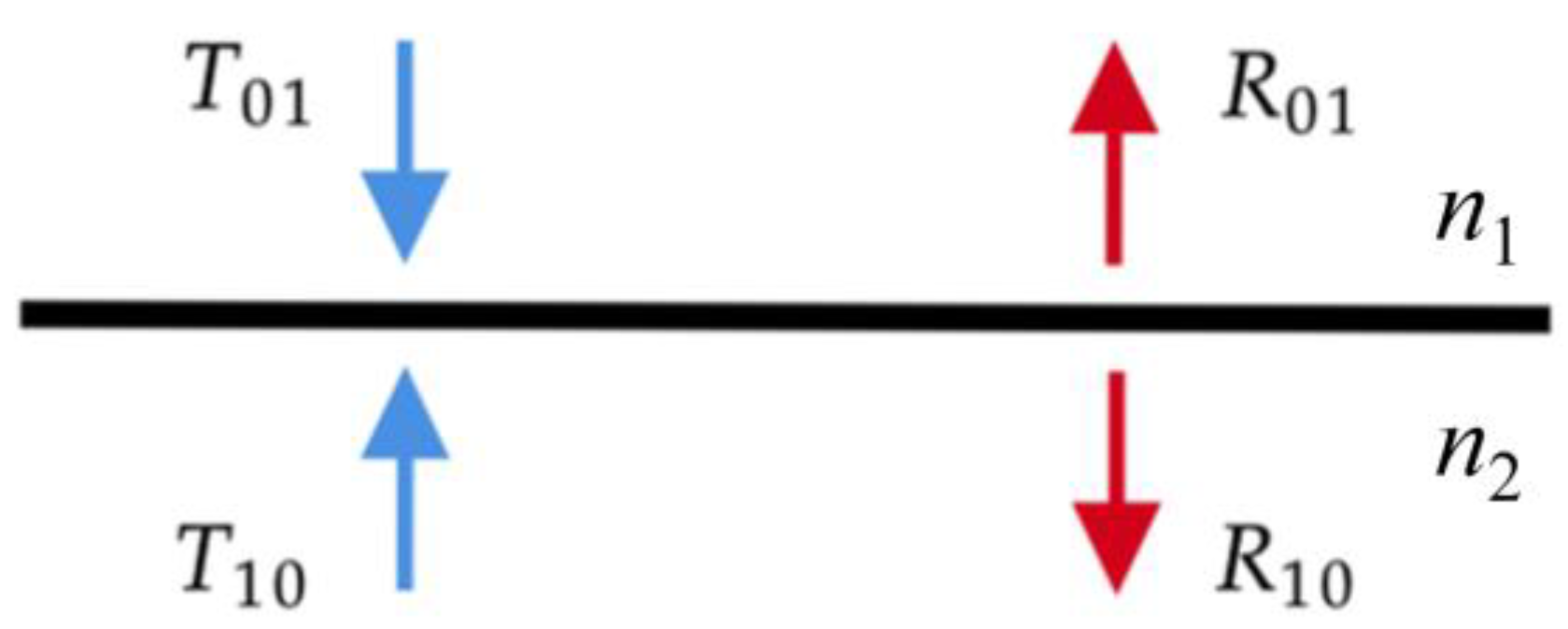
2.1.7. Adding Boundary Layers
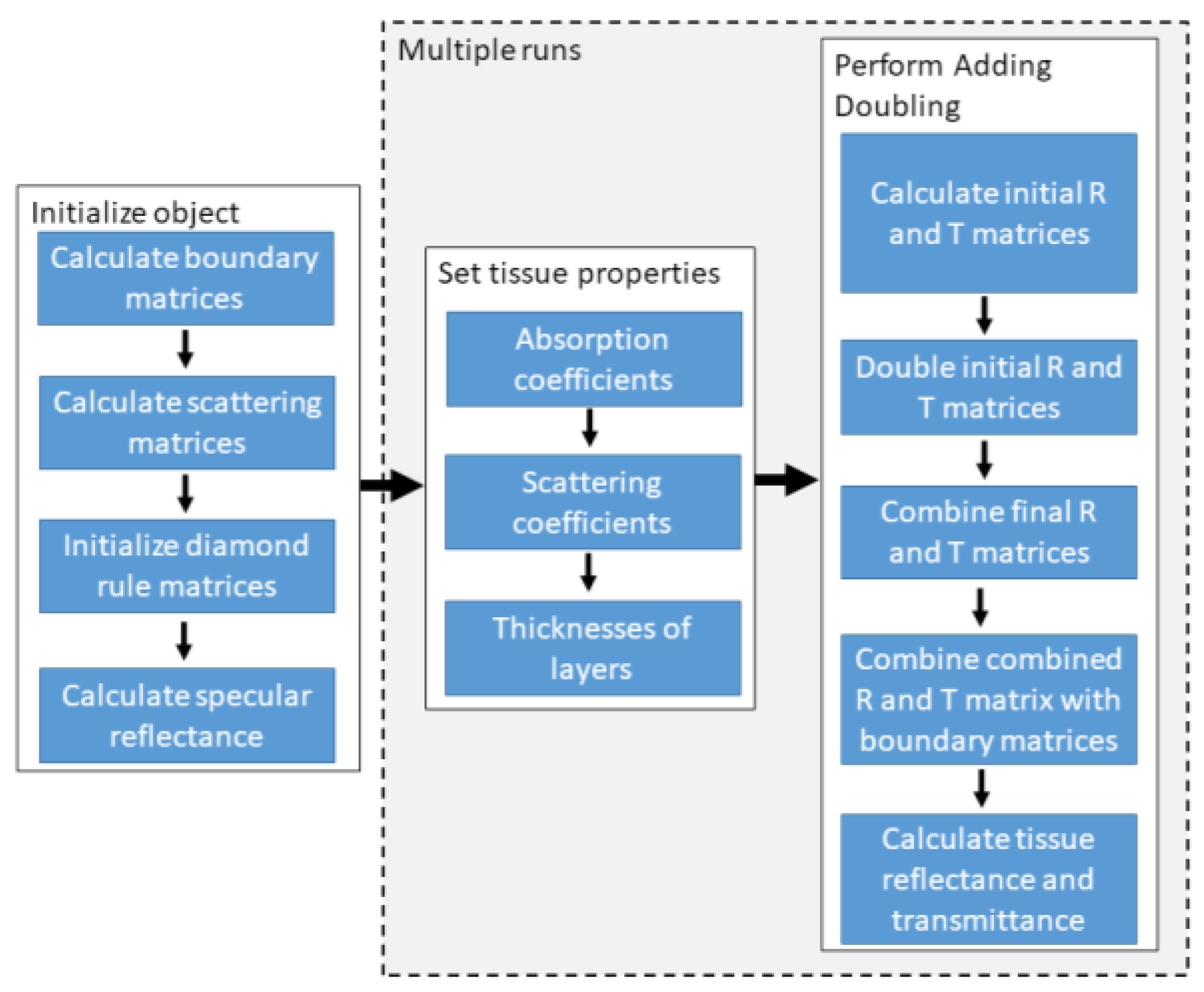
2.2. Implementation of the Adding-Doubling (AD) Algorithm
- 1.
- alpha—the Gegenbauer scattering phase function (SPF) exponent at the specified wavelengths lam for each sample. It is empty by default;
- 2.
- SPFtype—the type of SPF to be used. Currently implemented options are Henyey–Greenstein (HG) SPF and Gegenbauer (GB) SPF. To select HG SPF, the parameter value is 0, and to select GB SPF, the parameter value is 1. If GB SPF is selected, the alpha parameter must also be specified;
- 3.
- R0L—the reflectance of the bottom substrate, ranging between 0 and 1, if it is different from the upper environmental medium. This parameter is used in cases where a sample is placed on top of another thick substrate, such as a support plate. R0L is a matrix with Nl rows corresponding to lam and Ns columns corresponding to the number of samples;
- 4.
- nE—a column vector of environmental medium refraction indices with Nl values corresponding to lam. By default, the value is set to 1, representing air;
- 5.
- nS—a column vector of substrate refraction indices with Nl values corresponding to lam. By default, the value is set to 1.4.+;
- 6.
- m—the number of fluxes (even integer >= 2) used in the algorithm. The default value is 20, as it has been found to provide adequate accuracy for most combinations of optical parameters;
- 7.
- Nsam—the number of different spectra being calculated. By default, it is set to 1, meaning that only one set of different wavelengths is considered.
- -
- obj.Rn—2 diffuse reflectance;
- -
- obj.Tn—2 transmittance;
- -
- obj.Rsp—specular reflectance.
2.3. Single-Layer AD Model Simulations
2.4. Inverse Adding-Doubling (IAD) Solution
3. Results
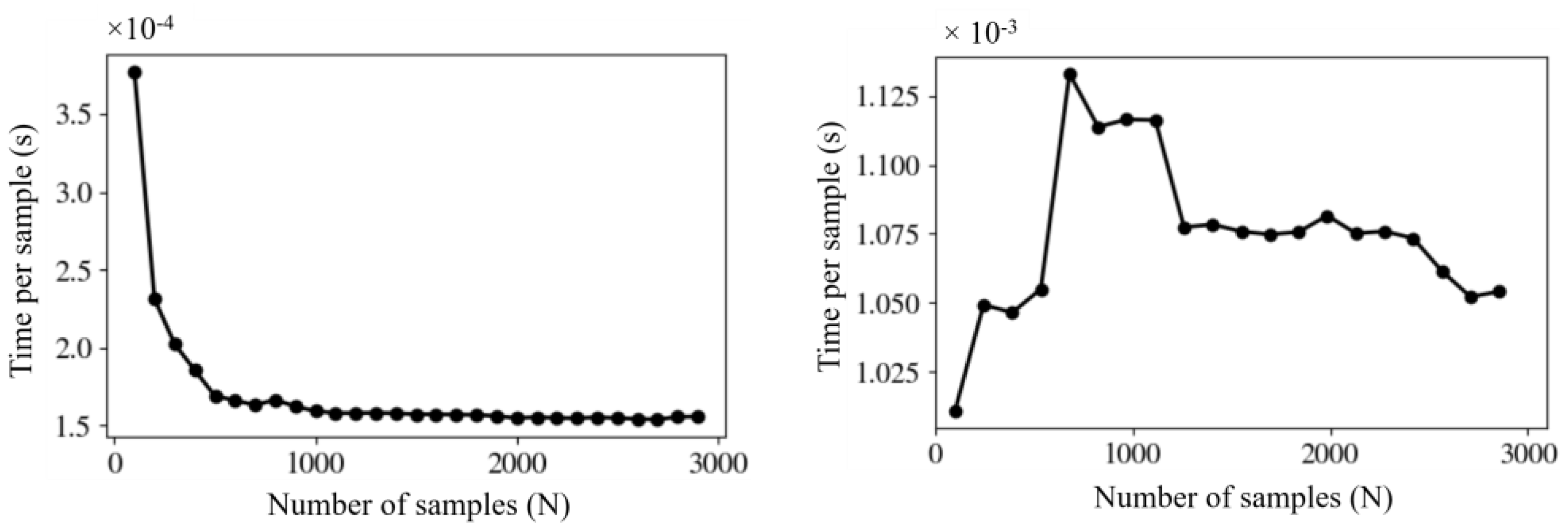
3.1. Comparison between the Performance of GPU-Accelerated AD and CPU AD Algorithms
3.2. Comparison between Single and Double Precision for Single-Layer AD Model Simulations
3.3. Single-Layer AD Model Simulations
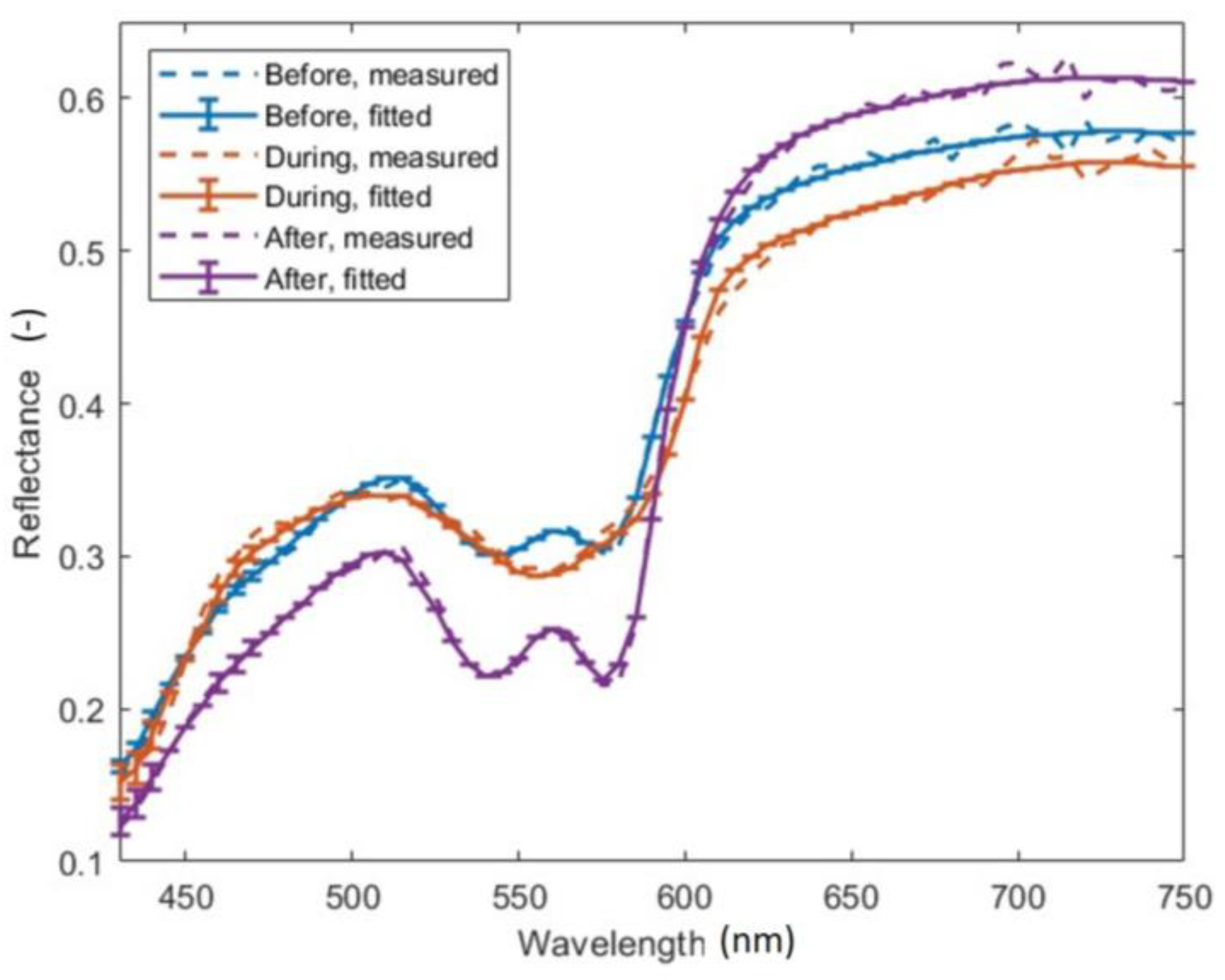
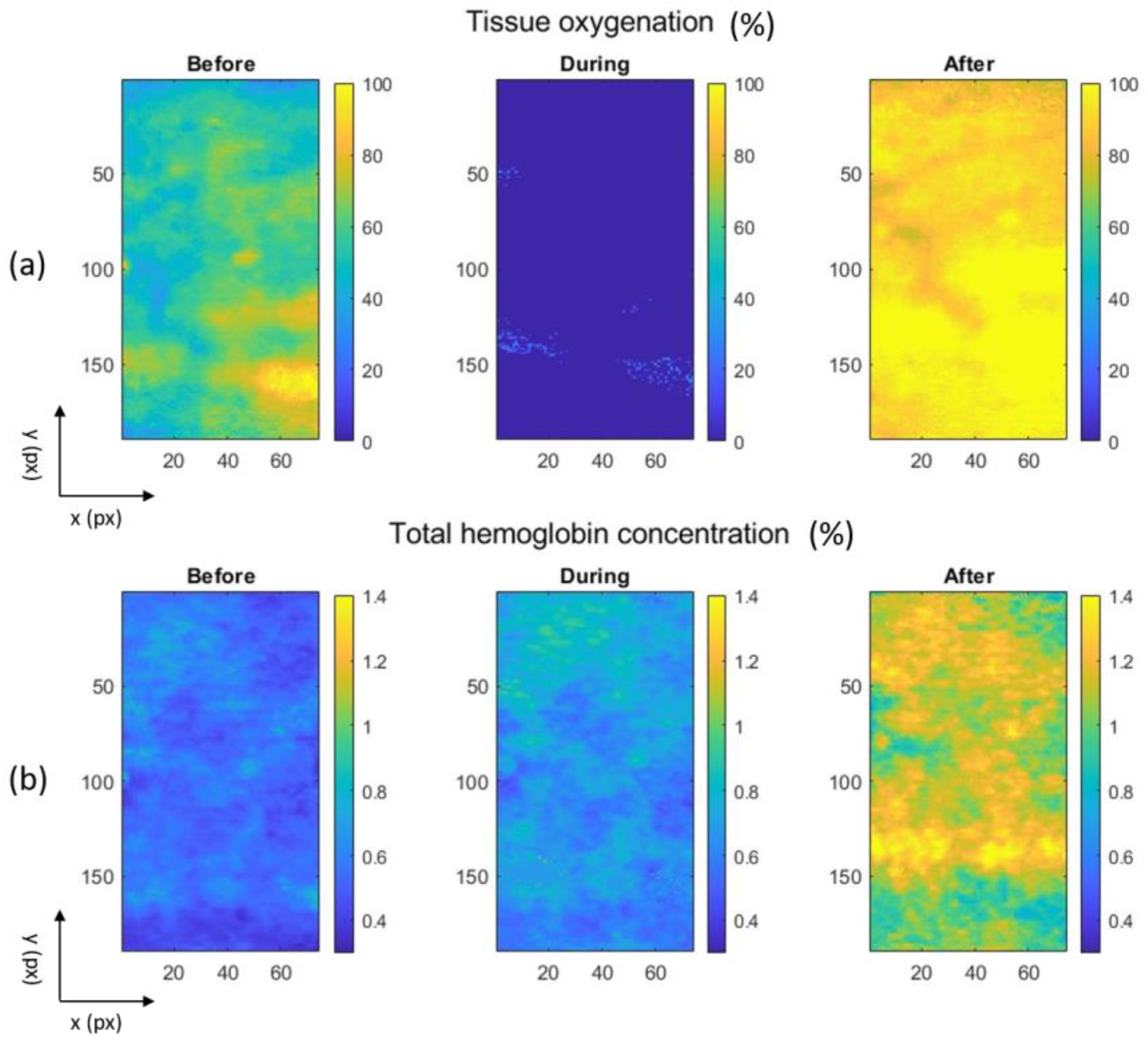
3.4. Inverse Adding-Doubling (IAD) Solution: Arterial Occlusion Test
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Optical Parameters of Epidermis and Dermis
Appendix A.1. Epidermis
Appendix A.2. Epidermis and Dermis
Appendix A.3. Dermis
Appendix A.4. Other Parameters
Appendix B. Levenberg–Marquardt Algorithm
Appendix B.1. Initialization
- lam—vector of wavelengths (Nl × 1);
- img—spectral image (Nx × Ny × Nl).
- Where Nl is the number of wavelengths, and Nx and Ny are the numbers of image pixels in x- and y-directions.
- dtype—the datatype used for the computation. It can be either ‘single’ for the single precision or ‘double’ for the double precision.
Appendix B.2. Algorithm Setup
- dp—fractional increment of parameters p for numerical derivatives (Npar × 1). Default: 0.005. Additional info:
- dp(j) > 0 central differences calculated;
- dp(j) < 0 one-sided ‘backwards’ differences calculated;
- dp(j) = 0 sets corresponding partials to zero, i.e., holds p(j) fixed;
- p_min—lower bounds for parameter values (Npar × 1). Default values depend on the tissue type;
- p_max—upper bounds for parameter values (Npar × 1). Default values depend on the tissue type;
- weight—weight matrices (Nl × Nl) or a scalar weight value; weight must be non-negative. For more information about weights, see [36]. Default value: 1;
- eps1—convergence in the gradient. Default value: 1 × 10−4;
- eps2—convergence in parameters. Default value: 1 × 10−4;
- eps3—convergence in χ2. Default value: 1 × 10−4;
- eps4—λlm update criterion. Default value: 1 × 10−3;
- MaxIter—maximum number of iterations. Default value: 200;
- L0—initial lambda value. Default value: 1 × 10−3;
- Lu—lambda increase multiplicator. Default value: 1.5;
- Ld—lambda decrease divisor. Default value: 5;
- Update_Type LM lambda update method. Parameter values: 1 = Levenberg–Marquardt lambda update (default), 2 = Quadratic update, 3 = Nielsen’s lambda update equations, 4 = geodesic acceleration;
- epsJtWJ—the minimum allowed value of the Levenberg-Marquardt damping term (Update_Type = 1). Default value: 1 × 10−3;
- dg—geodesic acceleration FD step. Default value: 0.1;
- galpha—geodesic acceleration acceptance criterion. Default value: 0.75;
- Broyden—Broyden’s rank 1 update for Jacobian, preventing the calculation of finite differences, 1 = use, 0 = do not use rank 1 approximation. Default value: 1;
- lambdaMax—maximum dumping parameter lambda. Default value: 10;
- muPenTer—penalty term for the nearest neighbor’s initial coefficient. Set to 0 if no term penalty is required. Default value: 1;
- Nsit—number of spectra fitted simultaneously. Default value: 10;
- Verbose—Display messages during execution. Parameter values: 0 = no messages, 1 = messages. Default value: 1
Appendix B.3. Running
Appendix B.4. Output
- pimgOut—fitted parameters (Nx × Ny × Npar);
- imgOut—fitted image (Nx × Ny × Nl);
- redX2—reduced χ2 (Nx × Ny × 1);
- sigma_p—asymptotic standard parameter errors (Nx × Ny × Npar);
- sigma_y—standard error of the fit (Nx × Ny × Nl);
- corr_p—parameter correlation matrix (Nx × Ny × Npar × Npar);
- R_sq—coefficient of multiple determination (Nx × Ny × 1);
- iterOut—matrix of iterations needed in each image point to stop fitting.
References
- Stokes, G.G., IV. On the intensity of the light reflected from or transmitted through a pile of plates. Proc. R. Soc. Lond. 1862, 11, 545–556. [Google Scholar] [CrossRef]
- van de Hulst, H.C.; Christoffel, H. A New Look at Multiple Scattering; NASA Institute for Space Studies: New York, NY, USA, 1962. [Google Scholar]
- Liu, Q.; Weng, F. Advanced Doubling–Adding Method for Radiative Transfer in Planetary Atmospheres. J. Atmos. Sci. 2006, 63, 3459–3465. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, P.; Kattawar, G.; Huang, H.-L.; Greenwald, T.; Li, J.; Baum, B.A.; Zhou, D.K.; Hu, Y. A fast infrared radiative transfer model based on the adding–doubling method for hyperspectral remote-sensing applications. J. Quant. Spectrosc. Radiat. Transf. 2007, 105, 243–263. [Google Scholar] [CrossRef]
- Mukai, S.; Sano, I.; Nakata, M. Improved Algorithms for Remote Sensing-Based Aerosol Retrieval during Extreme Biomass Burning Events. Atmosphere 2021, 12, 403. [Google Scholar] [CrossRef]
- Leyre, S.; Cappelle, J.; Durinck, G.; Abass, A.; Hofkens, J.; Deconinck, G.; Hanselaer, P. The use of the adding-doubling method for the optical optimization of planar luminescent down shifting layers for solar cells. Opt. Express 2014, 22, A765. [Google Scholar] [CrossRef] [PubMed]
- Pickering, J.W.; Prahl, S.A.; Van Wieringen, N.; Beek, J.F.; Sterenborg, H.J.C.M.; Van Gemert, M.J.C. Double-integrating-sphere system for measuring the optical properties of tissue. Appl. Opt. 1993, 32, 399. [Google Scholar] [CrossRef] [PubMed]
- Lemaillet, P.; Cooksey, C.C.; Hwang, J.; Wabnitz, H.; Grosenick, D.; Yang, L.; Allen, D.W. Correction of an adding-doubling inversion algorithm for the measurement of the optical parameters of turbid media. Biomed. Opt. Express 2018, 9, 55. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Gao, C.; Spurr, R. Scalar thermal radiation using the adding-doubling method. Opt. Express 2022, 30, 30075. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wu, Y. Monte-Carlo optical model coupled with Inverse Adding-Doubling for Building Integrated Photovoltaic smart window design and characterisation. Sol. Energy Mater. Sol. Cells 2021, 223, 110972. [Google Scholar] [CrossRef]
- Calvin, O.W.; Ganapol, B.D.; Borrelli, R.A. Introduction of the Adding and Doubling Method for Solving Bateman Equations for Nuclear Fuel Depletion. Nucl. Sci. Eng. 2023, 197, 558–588. [Google Scholar] [CrossRef]
- Prahl, S.A. The Adding-Doubling Method. In Optical-Thermal Response of Laser-Irradiated Tissue; Welch, A.J., Van Gemert, M.J.C., Eds.; Springer: Boston, MA, USA, 1995; pp. 101–129. [Google Scholar] [CrossRef]
- Prahl, S.A.; Van Gemert, M.J.C.; Welch, A.J. Determining the optical properties of turbid media by using the adding–doubling method. Appl. Opt. 1993, 32, 559. [Google Scholar] [CrossRef]
- Prahl, S.A. A Monte Carlo model of light propagation in tissue. In Proceedings of the Institutes for Advanced Optical Technologies, Berlin, Germany, 10 January 1989; Mueller, G.J., Sliney, D.H., Potter, R.F., Eds.; p. 1030509. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Kao, T.-C.; Chen, Y.-F.; Su, W.-W.; Shen, H.-J.; Sung, K.-B. Validation of an Inverse Fitting Method of Diffuse Reflectance Spectroscopy to Quantify Multi-Layered Skin Optical Properties. Photonics 2019, 6, 61. [Google Scholar] [CrossRef]
- Després, P.; Jia, X. A review of GPU-based medical image reconstruction. Phys. Medica 2017, 42, 76–92. [Google Scholar] [CrossRef] [PubMed]
- Kalaiselvi, T.; Sriramakrishnan, P.; Somasundaram, K. Survey of using GPU CUDA programming model in medical image analysis. Inform. Med. Unlocked 2017, 9, 133–144. [Google Scholar] [CrossRef]
- Smistad, E.; Falch, T.L.; Bozorgi, M.; Elster, A.C.; Lindseth, F. Medical image segmentation on GPUs—A comprehensive review. Med. Image Anal. 2015, 20, 1–18. [Google Scholar] [CrossRef]
- Alcaín, E.; Fernández, P.R.; Nieto, R.; Montemayor, A.S.; Vilas, J.; Galiana-Bordera, A.; Martinez-Girones, P.M.; Prieto-De-La-Lastra, C.; Rodriguez-Vila, B.; Bonet, M.; et al. Hardware Architectures for Real-Time Medical Imaging. Electronics 2021, 10, 3118. [Google Scholar] [CrossRef]
- Engler, H. Computation of Scattering Kernels in Radiative Transfer. arxiv 2015. [Google Scholar] [CrossRef][Green Version]
- Alerstam, E.; Svensson, T.; Andersson-Engels, S. Parallel computing with graphics processing units for high-speed Monte Carlo simulation of photon migration. J. Biomed. Opt. 2008, 13, 060504. [Google Scholar] [CrossRef]
- Stergar, J.; Hren, R.; Milanič, M. Design and Validation of a Custom-Made Laboratory Hyperspectral Imaging System for Biomedical Applications Using a Broadband LED Light Source. Sensors 2022, 22, 6274. [Google Scholar] [CrossRef]
- Rogelj, L.; Simončič, U.; Tomanič, T.; Jezeršek, M.; Pavlovčič, U.; Stergar, J.; Milanič, M. Effect of curvature correction on parameters extracted from hyperspectral images. J. Biomed. Opt. 2021, 26, 096003. [Google Scholar] [CrossRef]
- Rogelj, L.; Dolenec, R.; Tomšič, M.V.; Laistler, E.; Simončič, U.; Milanič, M.; Hren, R. Anatomically Accurate, High-Resolution Modeling of the Human Index Finger Using In Vivo Magnetic Resonance Imaging. Tomography 2022, 8, 2347–2359. [Google Scholar] [CrossRef] [PubMed]
- Rogelj, L.; Pavlovčič, U.; Stergar, J.; Jezeršek, M.; Simončič, U.; Milanič, M. Curvature and height corrections of hyperspectral images using built-in 3D laser profilometry. Appl. Opt. 2019, 58, 9002. [Google Scholar] [CrossRef]
- Verdel, N.; Marin, A.; Milanič, M.; Majaron, B. Physiological and structural characterization of human skin in vivo using combined photothermal radiometry and diffuse reflectance spectroscopy. Biomed. Opt. Express 2019, 10, 944. [Google Scholar] [CrossRef] [PubMed]
- Hren, R.; Sersa, G.; Simoncic, U.; Milanic, M. Imaging perfusion changes in oncological clinical applications by hyperspectral imaging: A literature review. Radiol. Oncol. 2022, 56, 420–429. [Google Scholar] [CrossRef] [PubMed]
- Hren, R.; Sersa, G.; Simoncic, U.; Milanic, M. Imaging microvascular changes in nonocular oncological clinical applications by optical coherence tomography angiography: A literature review. Radiol. Oncol. 2023, 57, 411–418. [Google Scholar] [CrossRef] [PubMed]
- Marin, A.; Hren, R.; Milanič, M. Pulsed Photothermal Radiometric Depth Profiling of Bruises by 532 nm and 1064 nm Lasers. Sensors 2023, 23, 2196. [Google Scholar] [CrossRef] [PubMed]
- Bjorgan, A.; Milanic, M.; Randeberg, L.L. Estimation of skin optical parameters for real-time hyperspectral imaging applications. J. Biomed. Opt. 2014, 19, 066003. [Google Scholar] [CrossRef] [PubMed]
- Tomanič, T.; Rogelj, L.; Milanič, M. Robustness of diffuse reflectance spectra analysis by inverse adding doubling algorithm. Biomed. Opt. Express 2022, 13, 921. [Google Scholar] [CrossRef]
- Klanecek, Z.; Hren, R.; Simončič, U.; Muc, B.T.; Lukač, M.; Milanič, M. Finite Element Method (FEM) Modeling of Laser-Tissue Interaction during Hair Removal. Appl. Sci. 2023, 13, 8553. [Google Scholar] [CrossRef]
- Young, A.R. Chromophores in human skin. Phys. Med. Biol. 1997, 42, 789–802. [Google Scholar] [CrossRef]
- Hren, R.; Stroink, G. Application of the surface harmonic expansions for modeling the human torso. IEEE Trans. Biomed. Eng. 1995, 42, 521–524. [Google Scholar] [CrossRef]
- Hren, R.; Zhang, X.; Stroink, G. Comparison between electrocardiographic and magnetocardiographic inverse solutions using the boundary element method. Med. Biol. Eng. Comput. 1996, 34, 110–114. [Google Scholar] [CrossRef] [PubMed]
- Gavin, H.P. The Levenberg-Marquardt Algorithm for Nonlinear Least Squares Curve-Fitting Problems. 27 November 2022. Available online: https://people.duke.edu/~hpgavin/ExperimentalSystems/lm.pdf (accessed on 3 February 2024).
- Du, Y.-C.; Stephanus, A. Levenberg-Marquardt Neural Network Algorithm for Degree of Arteriovenous Fistula Stenosis Classification Using a Dual Optical Photoplethysmography Sensor. Sensors 2018, 18, 2322. [Google Scholar] [CrossRef] [PubMed]
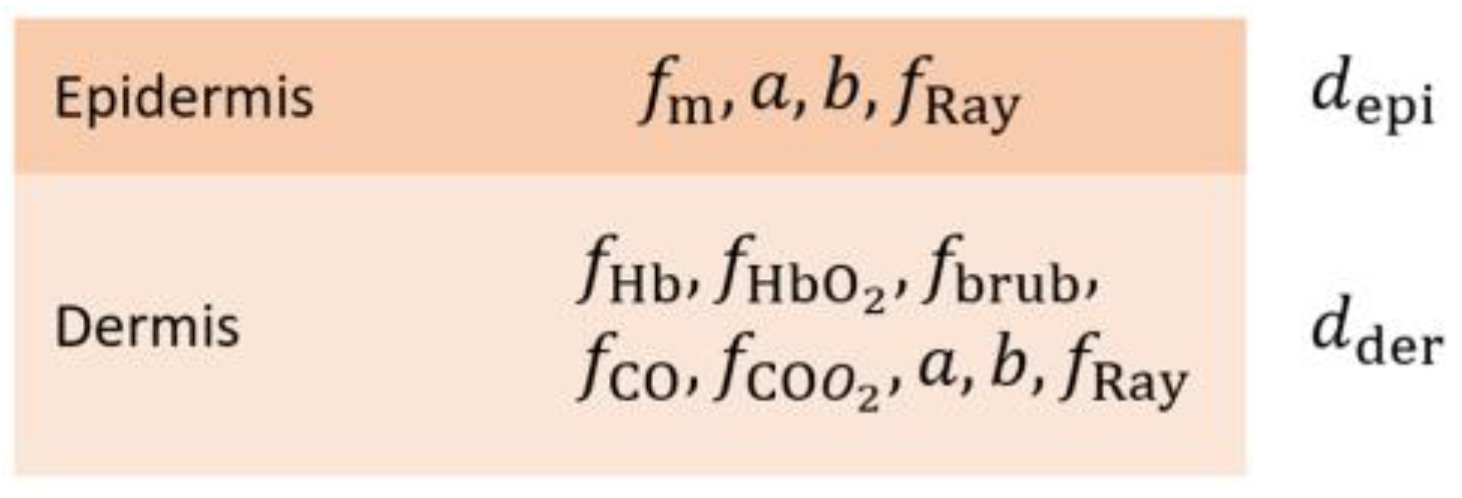
| Reflectance | Transmittance | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| μs | 25 | 50 | 100 | 150 | 25 | 50 | 100 | 150 | |
| μa | |||||||||
| 0.1 | 0.26 | 0.36 | 0.48 | 0.54 | 0.42 | 0.31 | 0.20 | 0.14 | |
| 0.5 | 0.09 | 0.15 | 0.24 | 0.31 | 0.18 | 0.11 | 0.05 | 0.03 | |
| 1.0 | 0.04 | 0.08 | 0.15 | 0.20 | 0.08 | 0.04 | 0.01 | 0.01 | |
| m = 8 | m = 12 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| μs | 25 | 50 | 100 | 150 | 25 | 50 | 100 | 150 | |
| μa | |||||||||
| 0.1 | 0.28 | 0.43 | 0.68 | 0.96 | 0.27 | 0.37 | 0.50 | 0.59 | |
| 0.5 | 0.07 | 0.13 | 0.25 | 0.34 | 0.08 | 0.15 | 0.24 | 0.31 | |
| 1.0 | 0.03 | 0.06 | 0.13 | 0.19 | 0.03 | 0.08 | 0.15 | 0.2 | |
| m = 16 | m = 20 | ||||||||
| μs | 25 | 50 | 100 | 150 | 25 | 50 | 100 | 150 | |
| μa | |||||||||
| 0.1 | 0.26 | 0.36 | 0.48 | 0.55 | 0.26 | 0.36 | 0.48 | 0.54 | |
| 0.5 | 0.09 | 0.15 | 0.24 | 0.31 | 0.09 | 0.15 | 0.24 | 0.31 | |
| 1.0 | 0.04 | 0.08 | 0.15 | 0.20 | 0.04 | 0.08 | 0.15 | 0.20 | |
| m = 8 | m = 12 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| μs | 25 | 50 | 100 | 150 | 25 | 50 | 100 | 150 | |
| μa | |||||||||
| 0.1 | 0.59 | 0.50 | 0.47 | 0.55 | 0.45 | 0.34 | 0.23 | 0.17 | |
| 0.5 | 0.28 | 0.17 | 0.10 | 0.07 | 0.20 | 0.11 | 0.05 | 0.03 | |
| 1.0 | 0.14 | 0.07 | 0.03 | 0.02 | 0.09 | 0.04 | 0.02 | 0.01 | |
| m = 16 | m = 20 | ||||||||
| μs | 25 | 50 | 100 | 150 | 25 | 50 | 100 | 150 | |
| μa | |||||||||
| 0.1 | 0.42 | 0.32 | 0.20 | 0.14 | 0.42 | 0.31 | 0.20 | 0.14 | |
| 0.5 | 0.18 | 0.11 | 0.05 | 0.03 | 0.18 | 0.11 | 0.05 | 0.03 | |
| 1.0 | 0.09 | 0.04 | 0.01 | 0.01 | 0.08 | 0.04 | 0.01 | 0.01 | |
| μs | 25 | 50 | 100 | 150 | |
|---|---|---|---|---|---|
| μa | |||||
| 0.1 | 1.5 | 1.7 | 3.1 | 7.3 | |
| 0.5 | 0.8 | 1.5 | 2.6 | 3.4 | |
| 1.0 | 0.8 | 1.3 | 2.0 | 2.6 | |
| Time per set (ms), N = 100 | μs | 25 | 50 | 100 | 150 | |
| μa | ||||||
| 0.1 | 1.1 | 1.1 | 1.2 | 1.2 | ||
| 0.5 | 1.1 | 1.1 | 1.2 | 1.2 | ||
| 1.0 | 1.1 | 1.1 | 1.2 | 1.2 | ||
| Time per set (ms), N = 1000 | μs | 25 | 50 | 100 | 150 | |
| μa | ||||||
| 0.1 | 0.30 | 0.31 | 0.33 | 0.34 | ||
| 0.5 | 0.29 | 0.31 | 0.32 | 0.34 | ||
| 1.0 | 0.30 | 0.31 | 0.31 | 0.34 | ||
| Time per set (ms), N = 3000 | μs | 25 | 50 | 100 | 150 | |
| μa | ||||||
| 0.1 | 0.24 | 0.25 | 0.27 | 0.29 | ||
| 0.5 | 0.24 | 0.25 | 0.27 | 0.29 | ||
| 1.0 | 0.23 | 0.25 | 0.27 | 0.29 | ||
| Time per set (ms), N = 100 | μs | 25 | 50 | 100 | 150 | |
| μa | ||||||
| 0.1 | 0.87 | 0.89 | 0.96 | 1.60 | ||
| 0.5 | 0.86 | 0.90 | 1.30 | 1.40 | ||
| 1.0 | 0.86 | 0.90 | 1.30 | 1.20 | ||
| Time per set (ms), N = 1000 | μs | 25 | 50 | 100 | 150 | |
| μa | ||||||
| 0.1 | 0.21 | 0.22 | 0.23 | 0.24 | ||
| 0.5 | 0.21 | 0.22 | 0.24 | 0.24 | ||
| 1.0 | 0.21 | 0.22 | 0.23 | 0.24 | ||
| Time per set (ms), N = 3000 | μs | 25 | 50 | 100 | 150 | |
| μa | ||||||
| 0.1 | 0.15 | 0.16 | 0.17 | 0.18 | ||
| 0.5 | 0.15 | 0.16 | 0.17 | 0.18 | ||
| 1.0 | 0.15 | 0.16 | 0.17 | 0.18 | ||
| μs | 25 | 50 | 100 | 150 | |
|---|---|---|---|---|---|
| μa | |||||
| 0.1 | 10,000 | 10,625 | 18,235 | 40,556 | |
| 0.5 | 5333 | 9375 | 15,294 | 18,889 | |
| 1.0 | 5333 | 8125 | 11,765 | 14,444 | |
| Before | During | After | |
|---|---|---|---|
| Tissue oxygenation (%) | 58.57 ± 10.83 | 0.24 ± 2.11 | 92.91 ± 6.02 |
| Total hemoglobin (%) | 0.54 ± 0.07 | 0.68 ± 0.09 | 1.11 ± 0.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milanic, M.; Hren, R. GPU Adding-Doubling Algorithm for Analysis of Optical Spectral Images. Algorithms 2024, 17, 74. https://doi.org/10.3390/a17020074
Milanic M, Hren R. GPU Adding-Doubling Algorithm for Analysis of Optical Spectral Images. Algorithms. 2024; 17(2):74. https://doi.org/10.3390/a17020074
Chicago/Turabian StyleMilanic, Matija, and Rok Hren. 2024. "GPU Adding-Doubling Algorithm for Analysis of Optical Spectral Images" Algorithms 17, no. 2: 74. https://doi.org/10.3390/a17020074
APA StyleMilanic, M., & Hren, R. (2024). GPU Adding-Doubling Algorithm for Analysis of Optical Spectral Images. Algorithms, 17(2), 74. https://doi.org/10.3390/a17020074







