Forecasting the Unit Cost of a Product with Some Linear Fuzzy Collaborative Forecasting Models
Abstract
:1. Introduction
- (1) How to integrate these forecasts?
- (2) How experts can refer to the forecasts of others to modify their own?
- (1) Some linear fuzzy regression models for the unit cost forecasting are proposed and compared.
- (2) Development of dedicated software to pass the forecast of each expert to other experts for their reference. In the meantime, the software can integrate different forecasts using the hybrid fuzzy intersection and back propagation network approach.
- (3) In reference to the forecasts of others, each expert subjectively modifies the parameters in the fuzzy linear regression method.
- (1) To enhance the accuracy of the unit cost forecast. In other words, the forecasts obtained must be very close to the actual values.
- (2) To improve the precision of the unit cost forecasting. Namely, a very small range containing the actual value can be estimated.
- (3) The application of an instance to compare the advantages and disadvantages of different linear fuzzy collaborative forecasting models.
2. Related Work
- (1) The unit cost forecasted by the existing methods may be lower than the actual value, resulting in over-estimated profits if the financial plan is based on the forecasts.
- (2) For precision in the unit cost forecasting, the narrowest scope containing the actual value is required; however, this has rarely been discussed.
- (3) The peak and average unit costs are forecasted separately, which is problematic because it is possible that the forecast becomes invalid in the sense that the average value may be higher than the peak value [10].
- (4) The existing fuzzy linear regression-back propagation network methods selected particular fuzzy linear regression methods, but did not explain the reasons or compared with other fuzzy linear regression methods.
3. Methodology
- (1) b: learning constant.
- (2)
: normalized unit cost at period t.
- (3) ct: actual unit cost at period t.
- (4)
: fuzzy unit cost forecast at period t.
if it is represented with a triangular fuzzy number .
- (5) C: unit wafer cost.
- (6) G: gross die.
- (7) r(t): homoscedastical, serially non-correlated error term.
- (8) t: period.
- (9) T: current period.
- (10) Yt: yield at period t.
- (11) Y0: asymptotic/final yield.
3.1. Fuzzy Linear Regression Methods for Forecasting the Unit Cost

























































 ; d is the desired range of every fuzzy forecast;
; d is the desired range of every fuzzy forecast;  ; m represents the relative importance of the outliers in fitting the fuzzy linear regression equation;
; m represents the relative importance of the outliers in fitting the fuzzy linear regression equation;  . When m = 1, the relative importance of the outliers is the highest and is equal to that of the non-outliers. o should be set within [0 1] if the variation in the variable is less than 1. Otherwise, it should be greater than 1. The two nonlinear programming models are indicated with CL1(o, s) and CL2(o, d, m), respectively.
. When m = 1, the relative importance of the outliers is the highest and is equal to that of the non-outliers. o should be set within [0 1] if the variation in the variable is less than 1. Otherwise, it should be greater than 1. The two nonlinear programming models are indicated with CL1(o, s) and CL2(o, d, m), respectively.3.2. Aggregation of Fuzzy Forecasts in Fuzzy Collaborative Forecasting

 indicates the result of obtaining the fuzzy intersection of the fuzzy forecasts by L experts. If these fuzzy forecasts are approximated with triangular fuzzy numbers, then the fuzzy intersection is a polygon-shaped fuzzy number (see Figure 1).
indicates the result of obtaining the fuzzy intersection of the fuzzy forecasts by L experts. If these fuzzy forecasts are approximated with triangular fuzzy numbers, then the fuzzy intersection is a polygon-shaped fuzzy number (see Figure 1).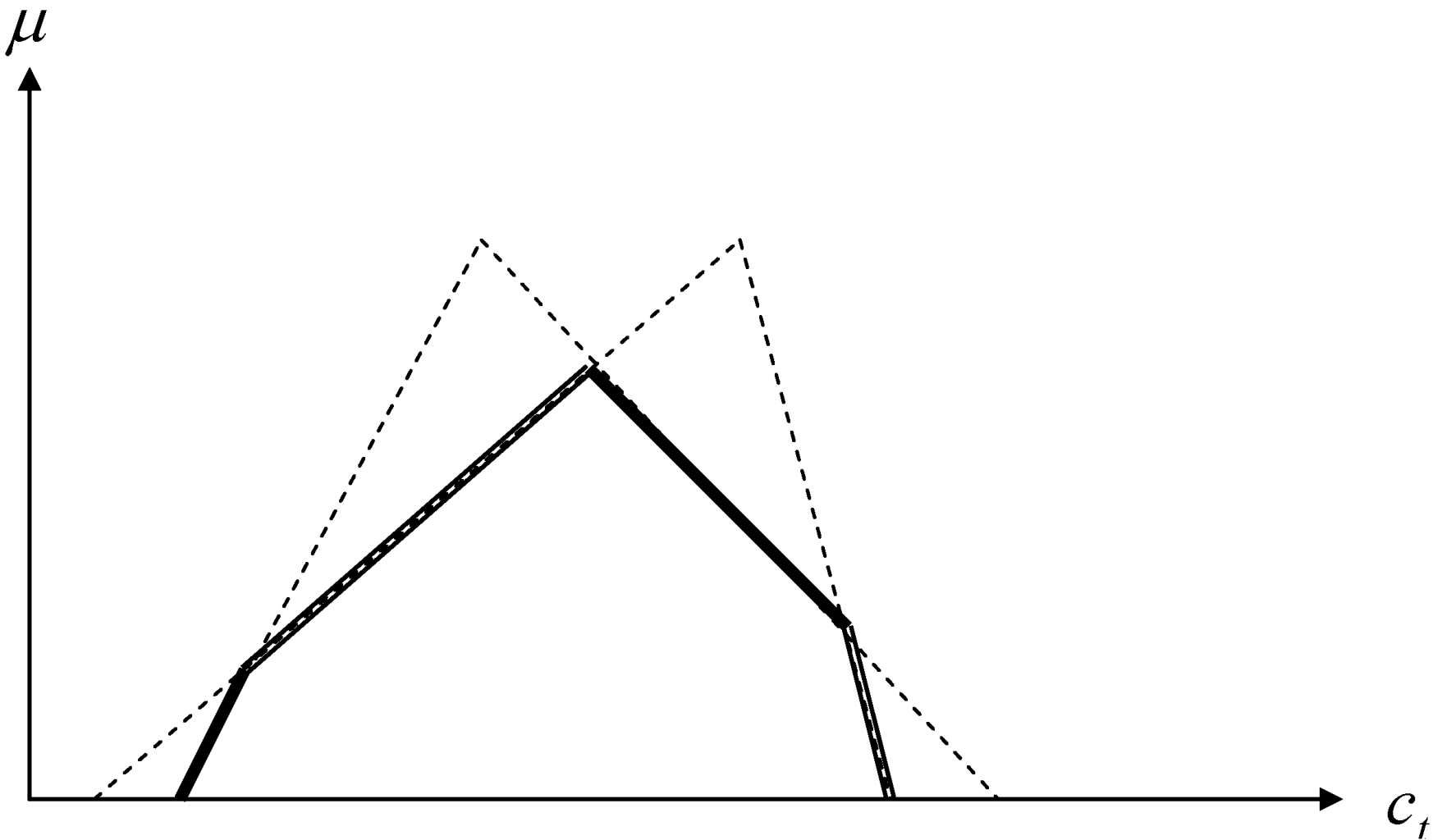
- (1) Inputs: 2m parameters corresponding to the m corners of the polygon-shaped fuzzy number and the membership function values of these corners. The reason is that simple–aggregation results in a convex domain and each point in it can be expressed with the combination of corners. The fuzzy intersection of L fuzzy forecasts will have at most 2·(2L + 2) corners. All input parameters have to be normalized into a range narrower than [0 1] before they are fed into the network.
- (2) Single hidden layer: Generally one or two hidden layers are more beneficial for the convergence property of the back propagation network.
- (3) The number of neurons in the hidden layer is chosen from 1~4m according to a preliminary analysis, considering both effectiveness (forecasting accuracy) and efficiency (execution time).
- (4) Output: the crisp forecast.
- (5) Network learning rule: Delta rule.
- (6) Network learning algorithms: There are many advanced algorithms for training a back propagation network, e.g. the Fletcher–Reeves algorithm, the Broydon–Fletcher–Goldfarb–Shanno algorithm, the Levenberg–Marquardt algorithm, and the Bayesian regularization method [34]. In this study, the Levenberg-Marquardt algorithm is applied.
- (7) Number of epochs per replication: 10,000.
- (8) Activation function: Log-sigmoid function.
- (9) Number of initial conditions/replications: Because the performance of a back propagation network is sensitive to the initial condition, the training process will be repeated many times with different initial conditions that are randomly generated. Among the results, the best one is chosen for the subsequent analyses.



3.3. Performance Evaluation in Fuzzy Collaborative Forecasting
 . The precision and accuracy of F(p) are indicated with Prec(F(p)) and Accur(F(p)), respectively. Some of the common functions for Prec(F(p)) and Accur(F(p)) are described below:
. The precision and accuracy of F(p) are indicated with Prec(F(p)) and Accur(F(p)), respectively. Some of the common functions for Prec(F(p)) and Accur(F(p)) are described below:


 is the actual value at period t.
is the actual value at period t.





3.4. Some Fuzzy Collaborative Forecasting Models for the Unit Cost Forecasting
| t | ct (US$) |
|---|---|
| 1 | 2.57 |
| 2 | 1.61 |
| 3 | 1.76 |
| 4 | 1.28 |
| 5 | 1.53 |
| 6 | 1.19 |
| 7 | 1.32 |
| 8 | 1.32 |
| 9 | 1.61 |
| 10 | 1.32 |
- PrecAR(WT(0.3)) = 0.56
- PrecAR(WT(0.6)) = 1.14
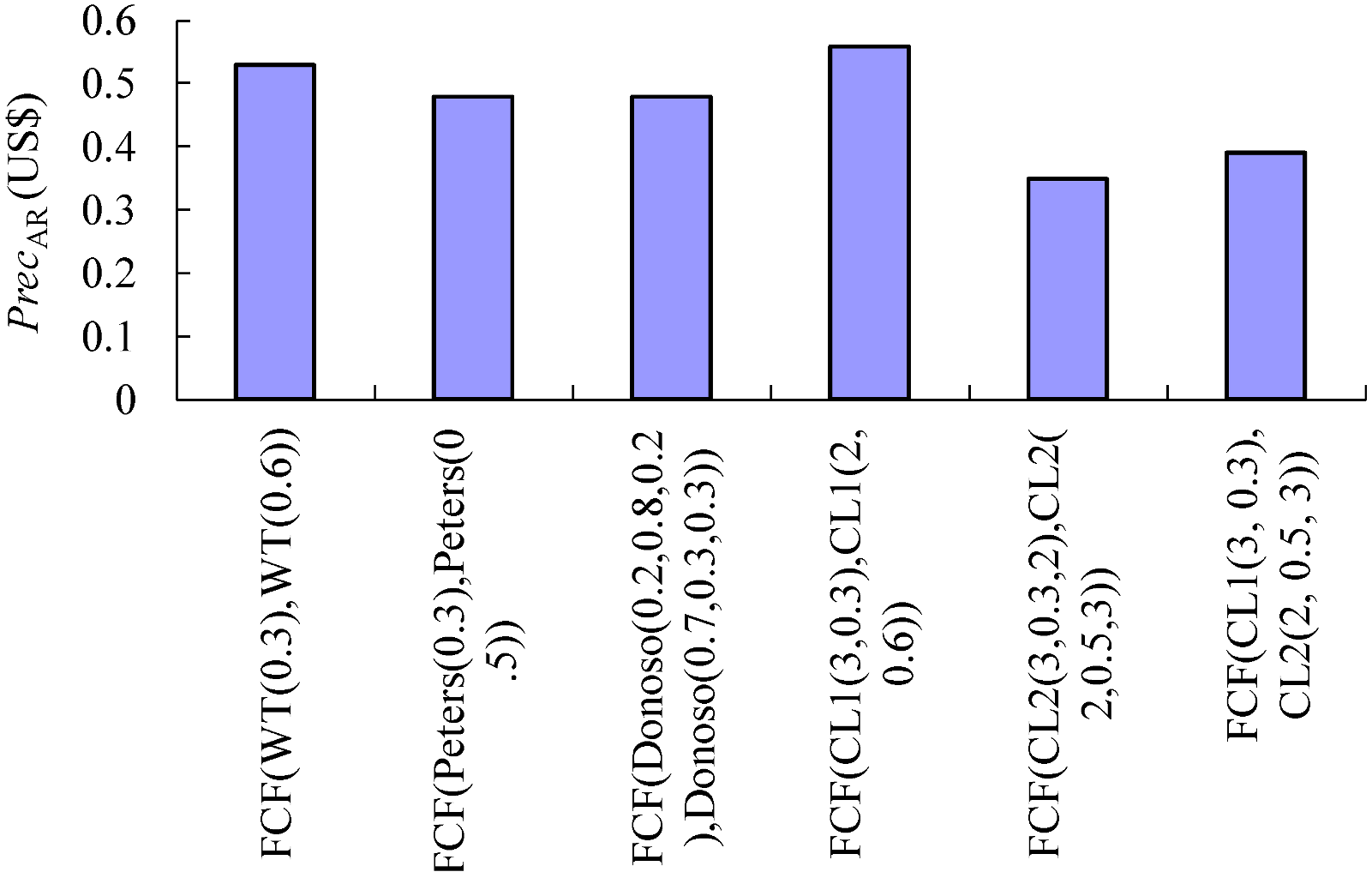
- PrecAR(FCF(WT(0.3), WT(0.6))) = 0.53
- QoCpMPI,AR(FCF(WT(0.3), WT(0.6))) = max((1.14 − 0.53)/1.14, (0.56 − 0.53)/0.56) = 54%.
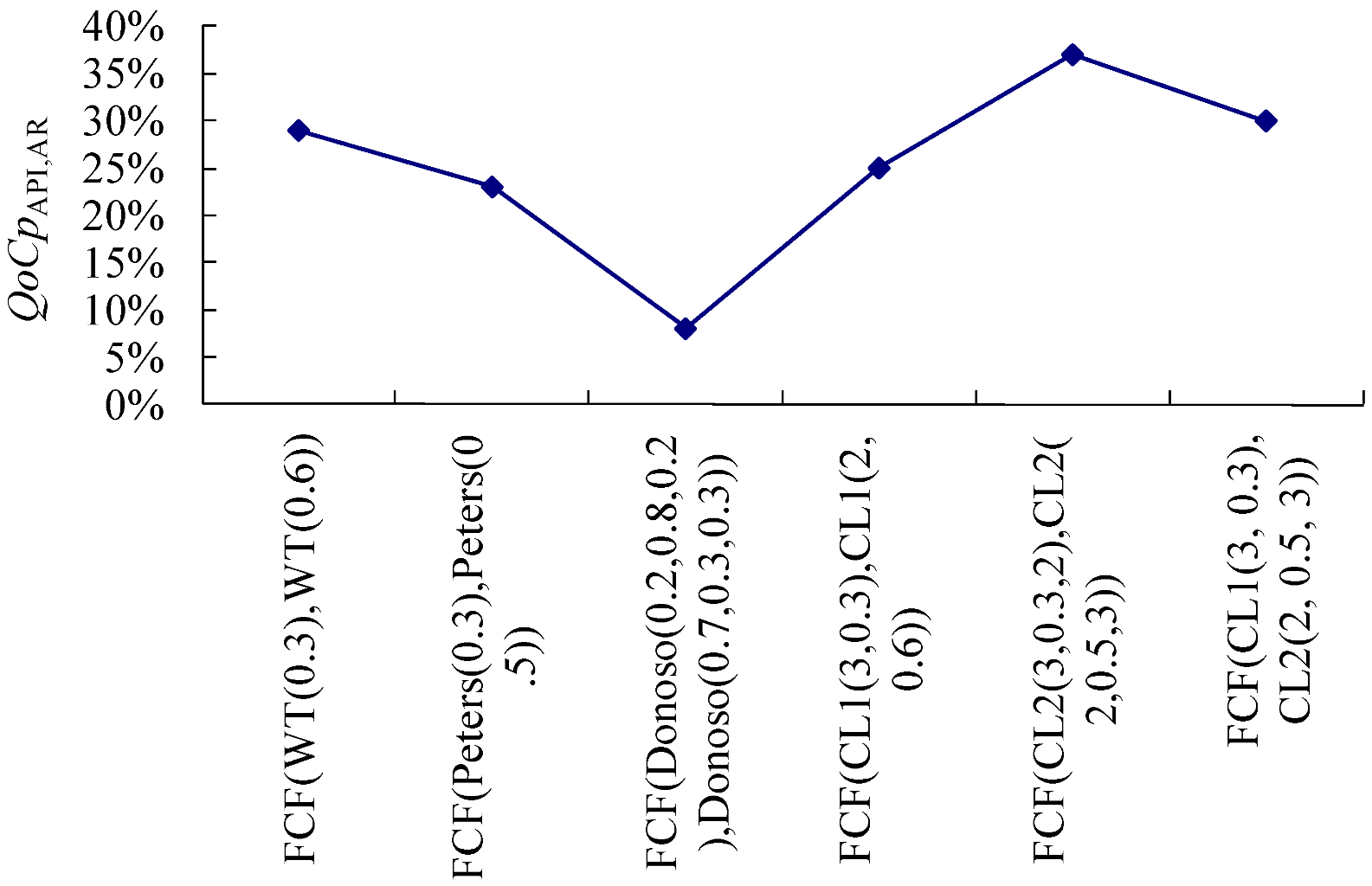
- QoCpAPI,AR(FCF(WT(0.3), WT(0.6))) = ((1.14 − 0.53)/1.14 + (0.56 − 0.53)/0.56)/2 = 29%.
- AccuMAE(WT(0.3)) = 0.16
- AccuMAE(WT(0.6)) = 0.24
- AccuMAPE(WT(0.3)) = 10%
- AccuMAPE(WT(0.6)) = 15%
- AccuRMSE(WT(0.3)) = 0.19
- AccuRMSE(WT(0.6)) = 0.31
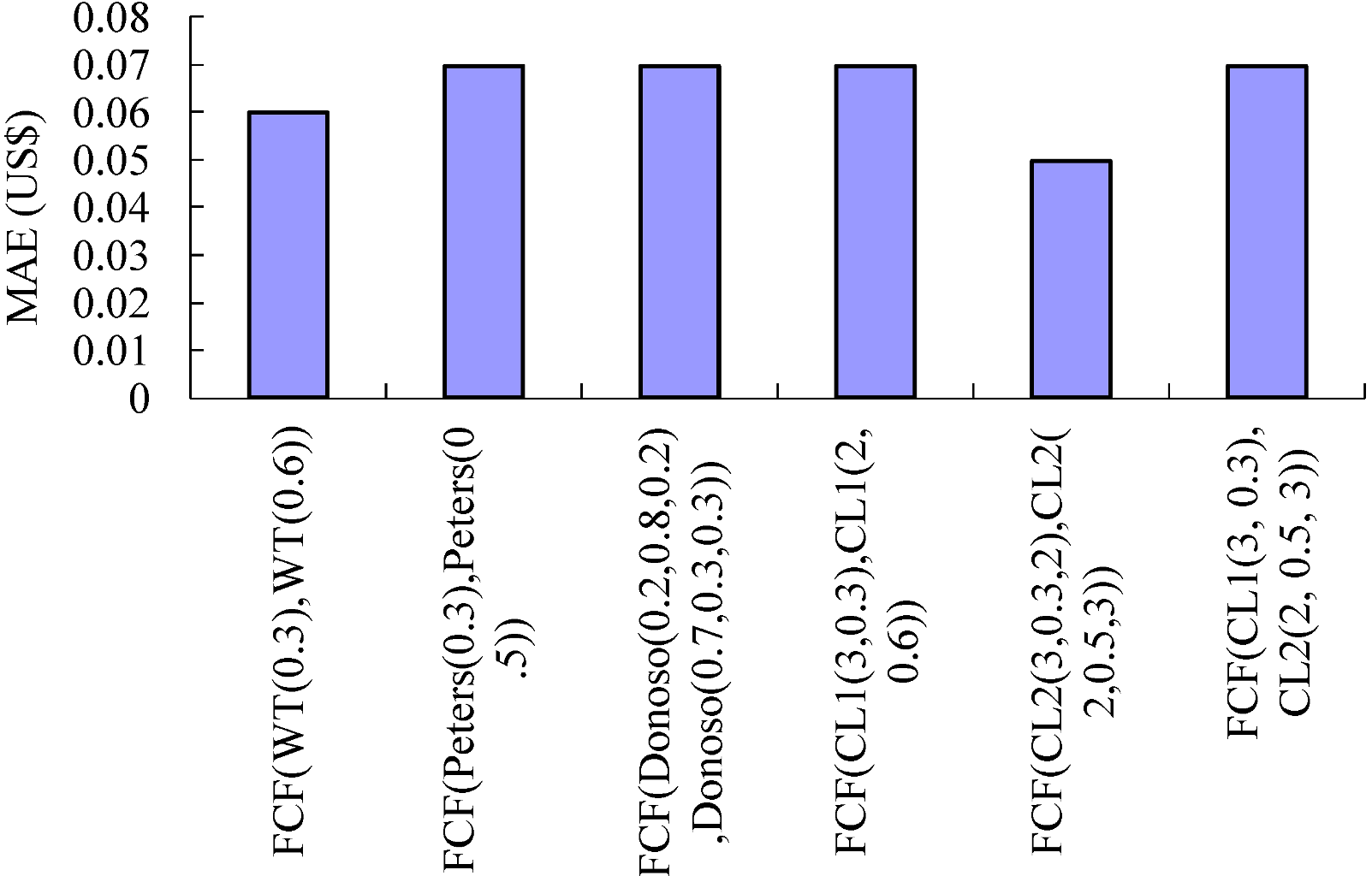
- AccuMAE(FCF(WT(0.3), WT(0.6))) = 0.06
- AccuMAPE(FCF(WT(0.3), WT(0.6))) = 4%
- AccuRMSE(FCF(WT(0.3), WT(0.6))) = 0.10
- QoCaMPI,MAE(FCF(WT(0.3), WT(0.6))) = max((0.16 − 0.07)/0.16, (0.24 − 0.07)/0.24) = 71%.
- QoCaAPI,MAE(FCF(WT(0.3), WT(0.6))) = ((0.16 − 0.07)/0.16 + (0.24 − 0.07)/0.24)/2 = 64%.
- QoCaMPI,MAPE(FCF(WT(0.3), WT(0.6))) = max((10% − 5%)/10%, (15% − 5%)/15%) = 67%.
- QoCaAPI,MAPE(FCF(WT(0.3), WT(0.6))) = ((10% − 5%)/10% + (15% − 5%)/15%)/2 = 58%.
- QoCaMPI,RMSE(FCF(WT(0.3), WT(0.6))) = max((0.19 − 0.15)/0.19, (0.31 − 0.15)/0.31) = 52%.
- QoCaAPI,RMSE(FCF(WT(0.3), WT(0.6))) = ((0.19 − 0.15)/0.19 + (0.31 − 0.15)/0.31)/2 = 36%.
- PrecAR(Peters(0.3)) = 0.48
- PrecAR(Peters(0.5)) = 0.68
- AccuMAE(Peters(0.3)) = 0.16
- AccuMAE(Peters(0.5)) = 0.20
- AccuMAPE(Peters(0.3)) = 10%
- AccuMAPE(Peters(0.5)) = 12%
- AccuRMSE(Peters(0.3)) = 0.19
- AccuRMSE(Peters(0.5)) = 0.25
- PrecAR(FCF(Peters(0.3), Peters(0.5))) = 0.48
- AccuMAE(FCF(Peters(0.3), Peters(0.5))) = 0.07
- AccuMAPE(FCF(Peters(0.3), Peters(0.5))) = 6%
- AccuRMSE(FCF(Peters(0.3), Peters(0.5))) = 0.13
- QoCpMPI,AR(FCF(Peters(0.3), Peters(0.5))) = 29%.
- QoCpAPI,AR(FCF(Peters(0.3), Peters(0.5))) = 15%.
- QoCaMPI,MAE(FCF(Peters(0.3), Peters(0.5))) = 65%.
- QoCaAPI,MAE(FCF(Peters(0.3), Peters(0.5))) = 61%.
- QoCaMPI,MAPE(FCF(Peters(0.3), Peters(0.5))) = 50%.
- QoCaAPI,MAPE(FCF(Peters(0.3), Peters(0.5))) = 45%.
- QoCaMPI,RMSE(FCF(Peters(0.3), Peters(0.5))) = 48%.
- QoCaAPI,RMSE(FCF(Peters(0.3), Peters(0.5))) = 40%.
- (k11, k21, s1) = (0.2, 0.8, 0.2)
- (k12, k22, s2) = (0.7, 0.3, 0.3)
- PrecAR(Donoso(0.2, 0.8, 0.2)) = 0.48
- PrecAR(Donoso(0.7, 0.3, 0.3)) = 0.57
- AccuMAE(Donoso(0.2, 0.8, 0.2)) = 0.15
- AccuMAE(Donoso(0.7, 0.3, 0.3)) = 0.14
- AccuMAPE(Donoso(0.2, 0.8, 0.2)) = 9%
- AccuMAPE(Donoso(0.7, 0.3, 0.3)) = 9%
- AccuRMSE(Donoso(0.2, 0.8, 0.2)) = 0.17
- AccuRMSE(Donoso(0.7, 0.3, 0.3)) = 0.18
- PrecAR(FCF(Donoso(0.2, 0.8, 0.2), Donoso(0.7, 0.3, 0.3))) = 0.48
- AccuMAE(FCF(Donoso(0.2, 0.8, 0.2), Donoso(0.7, 0.3, 0.3))) = 0.07
- AccuMAPE(FCF(Donoso(0.2, 0.8, 0.2), Donoso(0.7, 0.3, 0.3))) = 5%
- AccuRMSE(FCF(Donoso(0.2, 0.8, 0.2), Donoso(0.7, 0.3, 0.3))) = 0.10
- QoCpMPI,AR(FCF(Donoso(0.2, 0.8, 0.2), Donoso(0.7, 0.3, 0.3)))) = 16%.
- QoCpAPI,AR(FCF(Donoso(0.2, 0.8, 0.2), Donoso(0.7, 0.3, 0.3)))) = 8%.
- QoCaMPI,MAE(FCF(Donoso(0.2, 0.8, 0.2), Donoso(0.7, 0.3, 0.3)))) = 53%.
- QoCaAPI,MAE(FCF(Donoso(0.2, 0.8, 0.2), Donoso(0.7, 0.3, 0.3)))) = 52%.
- QoCaMPI,MAPE(FCF(Donoso(0.2, 0.8, 0.2), Donoso(0.7, 0.3, 0.3)))) = 44%.
- QoCaAPI,MAPE(FCF(Donoso(0.2, 0.8, 0.2), Donoso(0.7, 0.3, 0.3)))) = 44%.
- QoCaMPI,RMSE(FCF(Donoso(0.2, 0.8, 0.2), Donoso(0.7, 0.3, 0.3)))) = 44%.
- QoCaAPI,RMSE(FCF(Donoso(0.2, 0.8, 0.2), Donoso(0.7, 0.3, 0.3)))) = 43%.
- (o1, s1) = (3, 0.3)
- (o2, s2) = (2, 0.6)
- PrecAR(CL1(3, 0.3)) = 0.56
- PrecAR(CL1(2, 0.6)) = 1.12
- AccuMAE(CL1(3, 0.3)) = 0.16
- AccuMAE(CL1(2, 0.6)) = 0.23
- AccuMAPE(CL1(3, 0.3)) = 10%
- AccuMAPE(CL1(2, 0.6))) = 14%
- AccuRMSE(CL1(3, 0.3)) = 0.19
- AccuRMSE(CL1(2, 0.6)) = 0.30
| PrecAR | AccuMAE | AccuMAPE | AccuRMSE | |
|---|---|---|---|---|
| WT(0.3) | 0.56 | 0.16 | 0.1 | 0.19 |
| CL1(3, 0.3) | 0.56 | 0.16 | 0.1 | 0.19 |
| WT(0.6) | 1.14 | 0.24 | 0.15 | 0.31 |
| CL1(2, 0.6) | 1.12 | 0.23 | 0.14 | 0.3 |
- QoCpMPI,AR(FCF(CL1(3, 0.3), CL1(2, 0.6))) = 50%.
- QoCpAPI,AR(FCF(CL1(3, 0.3), CL1(2, 0.6))) = 25%.
- QoCaMPI,MAE(FCF(CL1(3, 0.3), CL1(2, 0.6))) = 71%.
- QoCaAPI,MAE(FCF(CL1(3, 0.3), CL1(2, 0.6))) = 65%.
- QoCaMPI,MAPE(FCF(CL1(3, 0.3), CL1(2, 0.6))) = 67%.
- QoCaAPI,MAPE(FCF(CL1(3, 0.3), CL1(2, 0.6))) = 60%.
- QoCaMPI,RMSE(FCF(CL1(3, 0.3), CL1(2, 0.6))) = 66%.
- QoCaAPI,RMSE(FCF(CL1(3, 0.3), CL1(2, 0.6))) = 57%.
| FCF(WT(0.3), WT(0.6)) | FCF(CL1(3, 0.3), CL1(2, 0.6)) | |
|---|---|---|
| QoCpMPI,AR | 54% | 50% |
| QoCpAPI,AR | 29% | 25% |
| QoCaMPI,MAE | 71% | 71% |
| QoCaAPI,MAE | 64% | 65% |
| QoCaMPI,MAPE | 67% | 67% |
| QoCaAPI,MAPE | 58% | 60% |
| QoCaMPI,RMSE | 52% | 66% |
| QoCaAPI,RMSE | 36% | 57% |
- (o1, d1, m1) = (3, 0.3, 2)
- (o2, d2, m2) = (2, 0.5, 3)
- PrecAR(CL2(3, 0.3, 2)) = 0.48
- PrecAR(CL2(2, 0.5, 3)) = 0.66
- AccuMAE(CL2(3, 0.3, 2)) = 0.16
- AccuMAE(CL2(2, 0.5, 3)) = 0.16
- AccuMAPE(CL2(3, 0.3, 2)) = 10%
- AccuMAPE(CL2(2, 0.5, 3))) = 10%
- AccuRMSE(CL2(3, 0.3, 2)) = 0.19
- AccuRMSE(CL2(2, 0.5, 3)) = 0.20
- PrecAR(FCF(CL2(3, 0.3, 2), CL2(2, 0.5, 3))) = 0.35
- AccuMAE(FCF(CL2(3, 0.3, 2), CL2(2, 0.5, 3))) = 0.05
- AccuMAPE(FCF(CL2(3, 0.3, 2), CL2(2, 0.5, 3))) = 4%
- AccuRMSE(FCF(CL2(3, 0.3, 2), CL2(2, 0.5, 3))) = 0.09
- QoCpMPI,AR(FCF(CL2(3, 0.3, 2), CL2(2, 0.5, 3))) = 46%.
- QoCpAPI,AR(FCF(CL2(3, 0.3, 2), CL2(2, 0.5, 3))) = 37%.
- QoCaMPI,MAE(FCF(CL2(3, 0.3, 2), CL2(2, 0.5, 3))) = 69%.
- QoCaAPI,MAE(FCF(CL2(3, 0.3, 2), CL2(2, 0.5, 3))) = 68%.
- QoCaMPI,MAPE(FCF(CL2(3, 0.3, 2), CL2(2, 0.5, 3))) = 63%.
- QoCaAPI,MAPE(FCF(CL2(3, 0.3, 2), CL2(2, 0.5, 3))) = 63%.
- QoCaMPI,RMSE(FCF(CL2(3, 0.3, 2), CL2(2, 0.5, 3))) = 54%.
- QoCaAPI,RMSE(FCF(CL2(3, 0.3, 2), CL2(2, 0.5, 3))) = 53%.
- (o1, s1) = (3, 0.3)
- (o2, d2, m2) = (2, 0.5, 3)
- PrecAR(FCF(CL1(3, 0.3), CL2(2, 0.5, 3))) = 0.39
- AccuMAE(FCF(CL1(3, 0.3), CL2(2, 0.5, 3))) = 0.07
- AccuMAPE(FCF(CL1(3, 0.3), CL2(2, 0.5, 3))) = 5%
- AccuRMSE(FCF(CL1(3, 0.3), CL2(2, 0.5, 3))) = 0.11
- QoCpMPI,AR(FCF(CL1(3, 0.3), CL2(2, 0.5, 3))) = 41%.
- QoCpAPI,AR(FCF(CL1(3, 0.3), CL2(2, 0.5, 3))) = 30%.
- QoCaMPI,MAE(FCF(CL1(3, 0.3), CL2(2, 0.5, 3))) = 59%.
- QoCaAPI,MAE(FCF(CL1(3, 0.3), CL2(2, 0.5, 3))) = 59%.
- QoCaMPI,MAPE(FCF(CL1(3, 0.3), CL2(2, 0.5, 3))) = 52%.
- QoCaAPI,MAPE(FCF(CL1(3, 0.3), CL2(2, 0.5, 3))) = 52%.
- QoCaMPI,RMSE(FCF(CL1(3, 0.3), CL2(2, 0.5, 3))) = 46%.
- QoCaAPI,RMSE(FCF(CL1(3, 0.3), CL2(2, 0.5, 3))) = 45%.
3.5. Comparison of the Performances of the Fuzzy Collaborative Forecasting Models
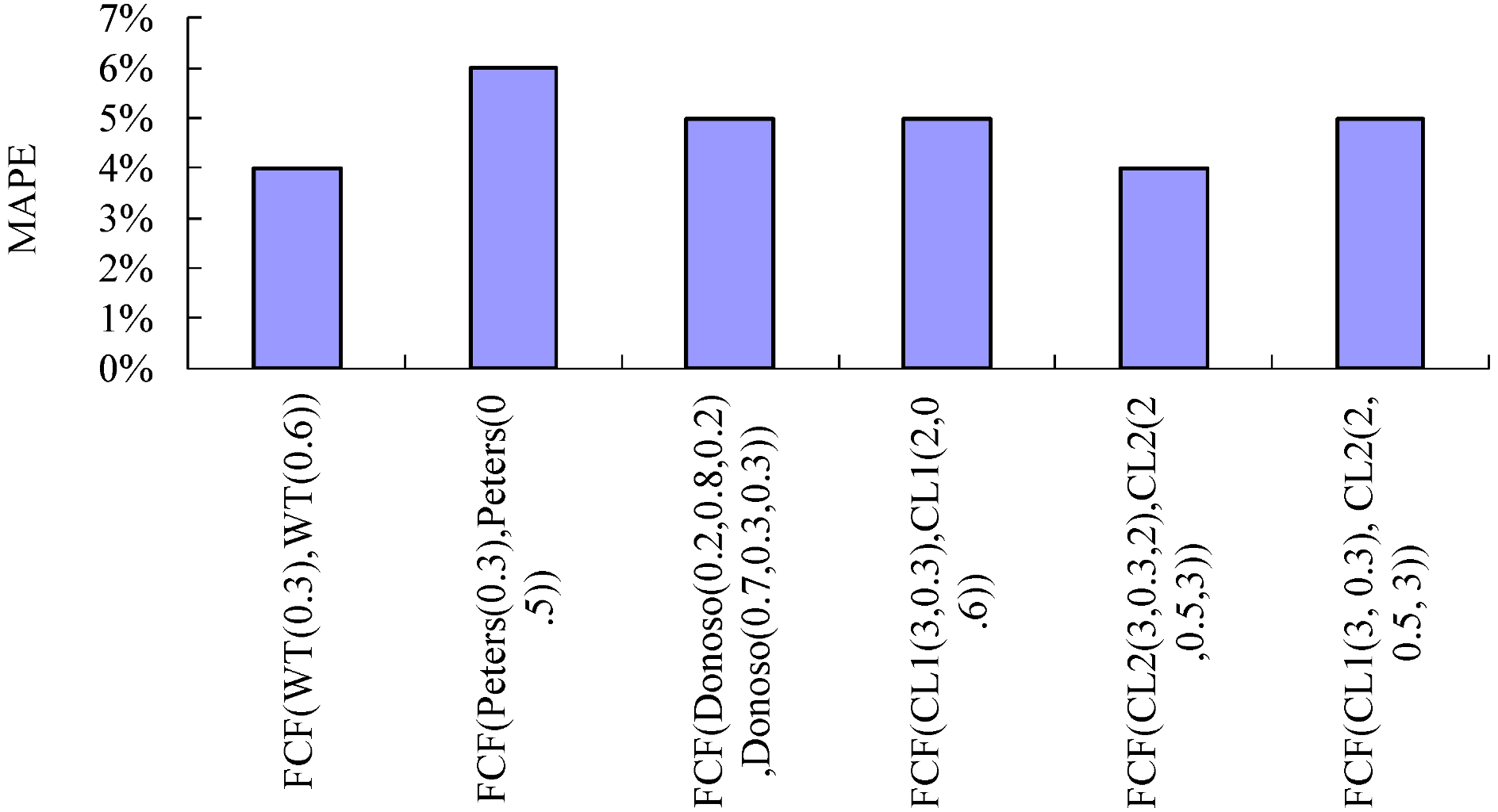
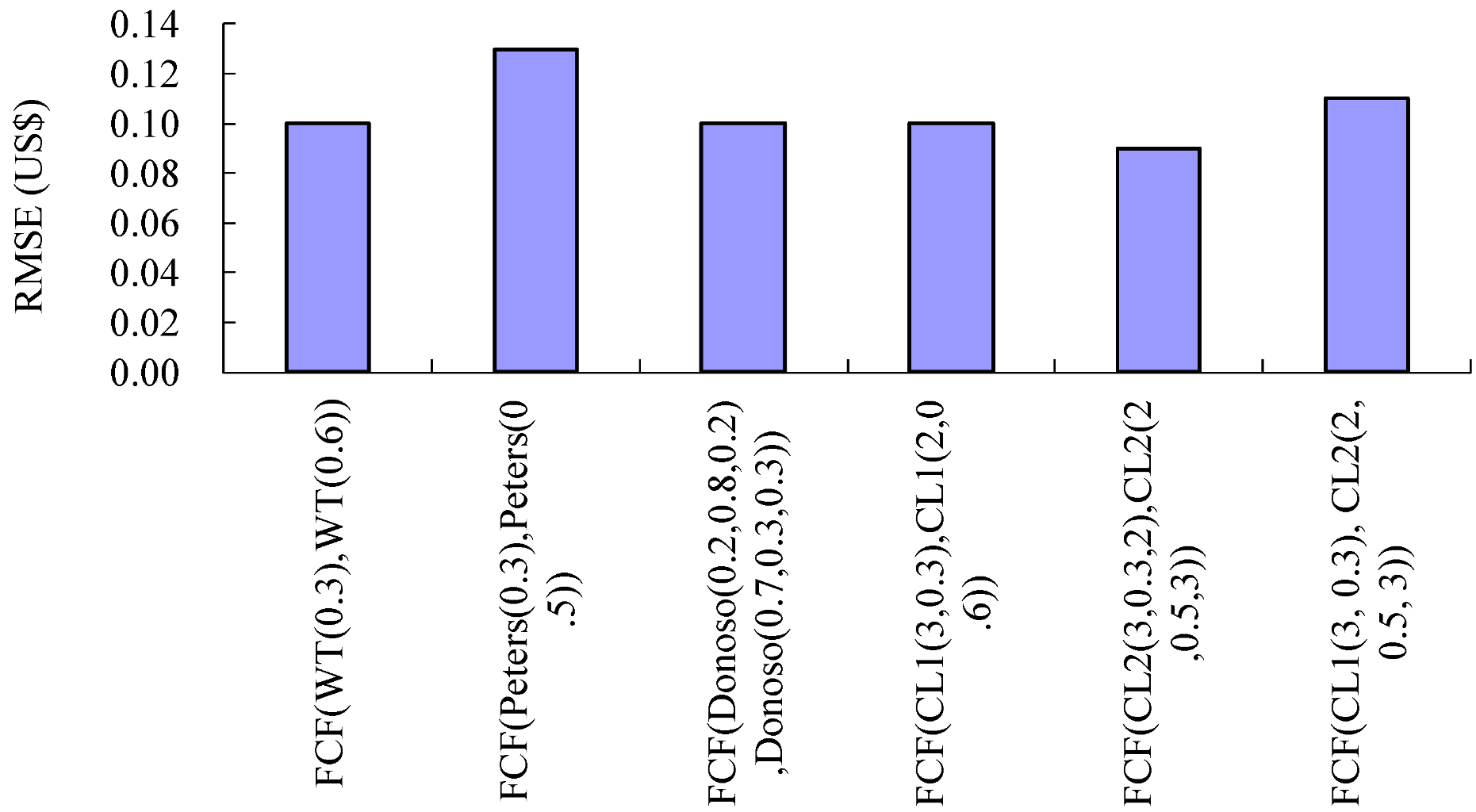
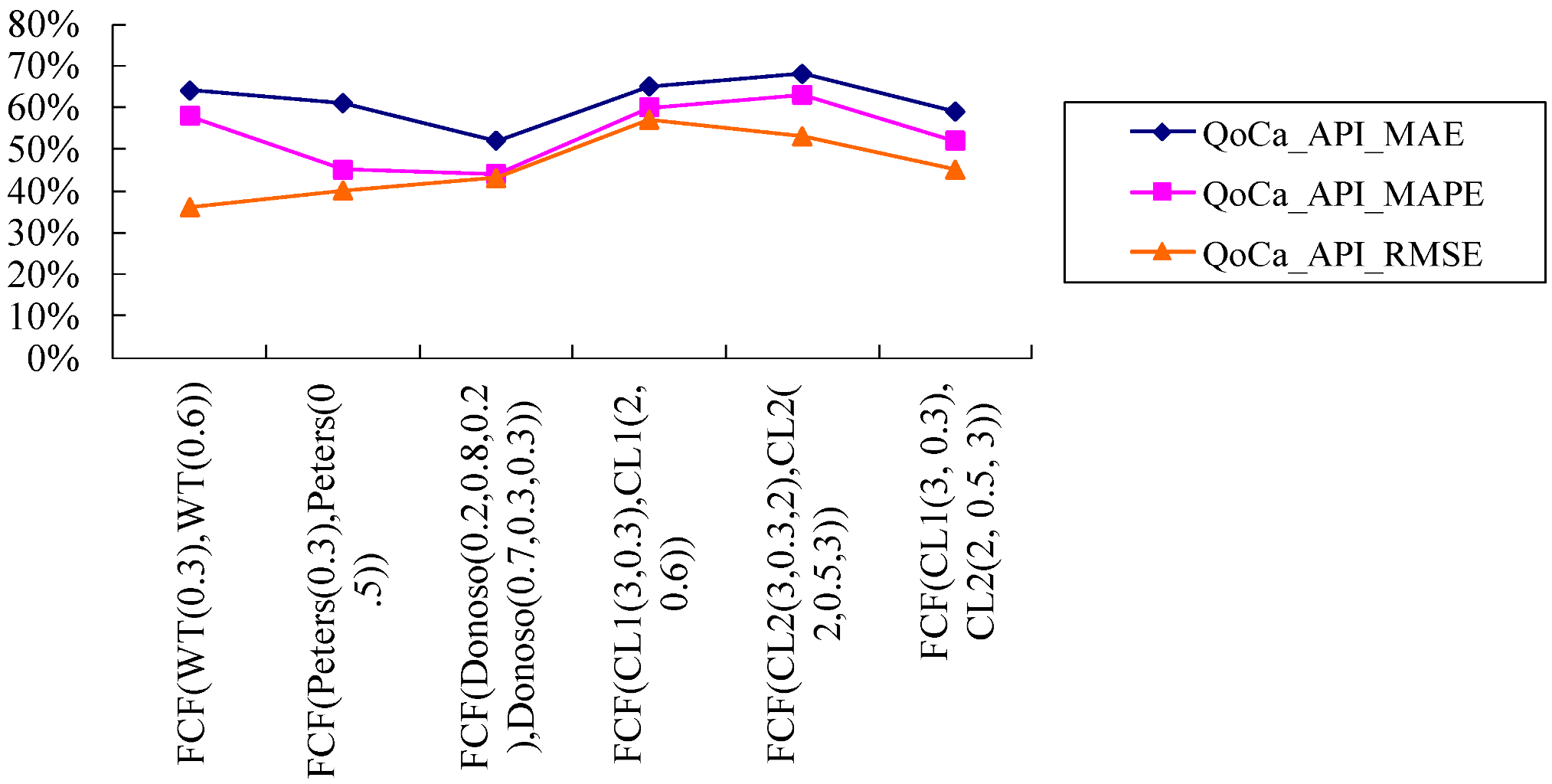
4. Conclusions
- (1) The effectiveness of the unit cost forecasting was greatly improved through the collaboration of the experts, especially when using FCF(CL2(o1, d1, m1), CL2(o2, d2, m2)).
- (2) With respect to the quality of collaboration on the forecasting precision, only one performance measure is proposed and the proposed performance measure can effectively compare the differences among the models.
- (3) With respect to the forecasting accuracy on the forecasting accuracy among the performance measures, the one that considers MAPE can effectively compare the differences among the models.
- (1) Six fuzzy collaborative forecasting models for the unit cost forecasting are investigated. From this, the most effective one can be identified.
- (2) More performance measures on the quality of collaboration have been proposed.
Acknowledgements
References
- Chen, T. A fuzzy-neural knowledge-based system for job completion time prediction and internal due date assignment in a wafer fabrication plant. Int. J. Sys. Sci. 2009, 40, 889–902. [Google Scholar]
- Chen, T. A hybrid fuzzy and neural approach with virtual experts and partial consensus for DRAM price forecasting. Int. J. Innov. Comput. Inf. Control 2012, 8, 583–598. [Google Scholar]
- Chen, T. An online collaborative semiconductor yield forecasting system. Expert Sys. Appl. 2009, 36, 5830–5843. [Google Scholar] [CrossRef]
- Chen, T. An application of fuzzy collaborative intelligence to unit cost forecasting with partial data access by security consideration. Int. J. Technol. Intel. Plan. 2011, 7, 201–214. [Google Scholar] [CrossRef]
- Chen, T. Applying a fuzzy and neural approach for forecasting the foreign exchange rate. Int. J. Fuzzy Sys. Appl. 2011, 1, 36–48. [Google Scholar] [CrossRef]
- Chen, T. Applying the hybrid fuzzy c means-back propagation network approach to forecast the effective cost per die of a semiconductor product. Comput. Ind. Eng. 2011, 61, 752–759. [Google Scholar] [CrossRef]
- Chen, T. Some linear fuzzy collaborative forecasting models for semiconductor unit cost forecasting. Int. J. of Fuzzy Sys. Appl. 2012, in press. [Google Scholar]
- Chen, T.; Lin, Y.C. A fuzzy-neural system incorporating unequally important expert opinions for semiconductor yield forecasting. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2008, 16, 35–58. [Google Scholar] [CrossRef]
- Chen, T.; Lin, C.W.; Wang, Y.C. A fuzzy collaborative forecasting approach for WIP level estimation in a wafer fabrication factory. Appl. Math. Inf. Sci. 2012, in press. [Google Scholar]
- Chen, T.; Wang, Y.C. A fuzzy-neural approach for global CO2 concentration forecasting. Intel. Data Anal. 2011, 15, 763–777. [Google Scholar]
- Chen, T.; Wang, Y.C. A hybrid fuzzy and neural approach for forecasting the book-to-bill ratio in the semiconductor manufacturing industry. Int. J. Adv. Manuf. Technol. 2011, 54, 377–389. [Google Scholar] [CrossRef]
- Pedrycz, W. Collaborative architectures of fuzzy modeling. Lect. Notes Comput. Sci. 2008, 5050, 117–139. [Google Scholar]
- Pedrycz, W. Collaborative fuzzy clustering. Pattern Recognit. Lett. 2002, 23, 1675–1686. [Google Scholar]
- Pedrycz, W.; Rai, P. A multifaceted perspective at data analysis: A study in collaborative intelligent agents. IEEE Trans. Syst., Man. Cybern., Part B: Cybern. 2008, 38, 1062–1072. [Google Scholar] [CrossRef]
- Carnes, R. Long-term cost of ownership: beyond purchase price. In Proceedings of 1991 IEEE/SEMI International Semiconductor Science Symposium, Burlingame, CA, USA, 20-22 May 1991; pp. 39–43.
- Wood, S.C. Cost and cycle time performance of fabs based on integrated single-wafer processing. IEEE Trans. Semi. Manuf. 1997, 10, 98–111. [Google Scholar] [CrossRef]
- Pfitzner, L.; Benesch, N.; Öchsner, R.; Schmidt, C.; Schneider, C.; Tschaftary, T.; Trunk, R.; Dudenhausen, H.M. Cost reduction strategies for wafer expenditure. Microelectr. Eng. 2001, 56, 61–71. [Google Scholar] [CrossRef]
- Shai, O.; Reich, Y. Infused design I. Theory. Res. Eng. Design Res. 2004, 15, 93–107. [Google Scholar]
- Shai, O.; Reich, Y. Infused design II. Practice. Res. Eng. Design Res. 2004, 15, 108–121. [Google Scholar]
- Büyüközkan, G.; Vardaloglu, Z. Analyzing of Collaborative Planning, Forecasting and Replenishment Approachusing Fuzzy Cognitive Map. In Proceeding of 2009 International Conference on Computers and Industrial Engineering, University of Technology of Troyes, France, 6–8 July 2009; pp. 1751–1756.
- Büyüközkan, G.; Feyzioglu, O.; Vardaloglu, Z. Analyzing CPFR supporting factors with fuzzy cognitive map approach. World Academy Sci. Eng. Technol. 2009, 31, 412–417. [Google Scholar]
- Poler, R.; Hernandez, J.E.; Mula, J.; Lario, F.C. Collaborative forecasting in networked manufacturing enterprises. J. Manuf. Technol. Manag. 2008, 19, 514–528. [Google Scholar] [CrossRef]
- Ostrosi, E.; Haxhiaj, L.; Fukuda, S. Fuzzy modelling of consensus during design conflict resolution. Res. Eng. Design 2012, 23(1), 53–70. [Google Scholar]
- Cheikhrouhou, N.; Marmier, F.; Ayadi, O.; Wieser, P. A collaborative demand forecasting process with event-based fuzzy judgements. Comput. Ind. Eng. 2011, 61, 409–421. [Google Scholar] [CrossRef]
- Gruber, H. Learning and Strategic Product Innovation: Theory and Evidence for the Semiconductor Industry; Elsevier: Amsterdam, the Netherlands, 1994. [Google Scholar]
- Chen, T. A fuzzy back propagation network for output time prediction in a wafer fab. Appl. Soft Comput. 2003, 2, 211–222. [Google Scholar] [CrossRef]
- Chen, T. A hybrid fuzzy and neural approach for evaluating the cost competitiveness of a semiconductor product. Int. J. Technol. Intel. Plan. 2010, 6, 373–386. [Google Scholar] [CrossRef]
- Chen, T. A SOM-FBPN-ensemble approach with error feedback to adjust classification for wafer-lot completion time prediction. Int. J. Adv. Manuf. Technol. 2008, 37, 782–792. [Google Scholar] [CrossRef]
- Chen, T.; Wang, M.J.J. A fuzzy set approach for yield learning modeling in wafer manufacturing. IEEE Trans. Semicond. Manuf. 1999, 12, 252–258. [Google Scholar] [CrossRef]
- Tanaka, H.; Watada, J. Possibilistic linear systems and their application to the linear regression model. Fuzzy Sets Syst. 1988, 272, 275–289. [Google Scholar] [CrossRef]
- Peters, G. Fuzzy linear regression with fuzzy intervals. Fuzzy Sets Syst. 1994, 63, 45–55. [Google Scholar] [CrossRef]
- Donoso, S.; Marin, N.; Vila, M.A. Quadratic programming models for fuzzy regression. In Proceedings of International Conference on Mathematical and Statistical Modeling in Honor of Enrique Castillo, Ciudad Real, Spain, 28–30 June 2006.
- Liu, X. Parameterized defuzzification with maximum entropy weighting function—another view of the weighting function expectation method. Math. Com. Mod. 2007, 45, 177–188. [Google Scholar] [CrossRef]
- Eraslan, E. The estimation of product standard time by artificial neural networks in the molding industry. Math. Probl. Eng. 2009. article ID 527452. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, T. Forecasting the Unit Cost of a Product with Some Linear Fuzzy Collaborative Forecasting Models. Algorithms 2012, 5, 449-468. https://doi.org/10.3390/a5040449
Chen T. Forecasting the Unit Cost of a Product with Some Linear Fuzzy Collaborative Forecasting Models. Algorithms. 2012; 5(4):449-468. https://doi.org/10.3390/a5040449
Chicago/Turabian StyleChen, Toly. 2012. "Forecasting the Unit Cost of a Product with Some Linear Fuzzy Collaborative Forecasting Models" Algorithms 5, no. 4: 449-468. https://doi.org/10.3390/a5040449







