An Overview on the Applications of Matrix Theory in Wireless Communications and Signal Processing
Abstract
:1. Introduction
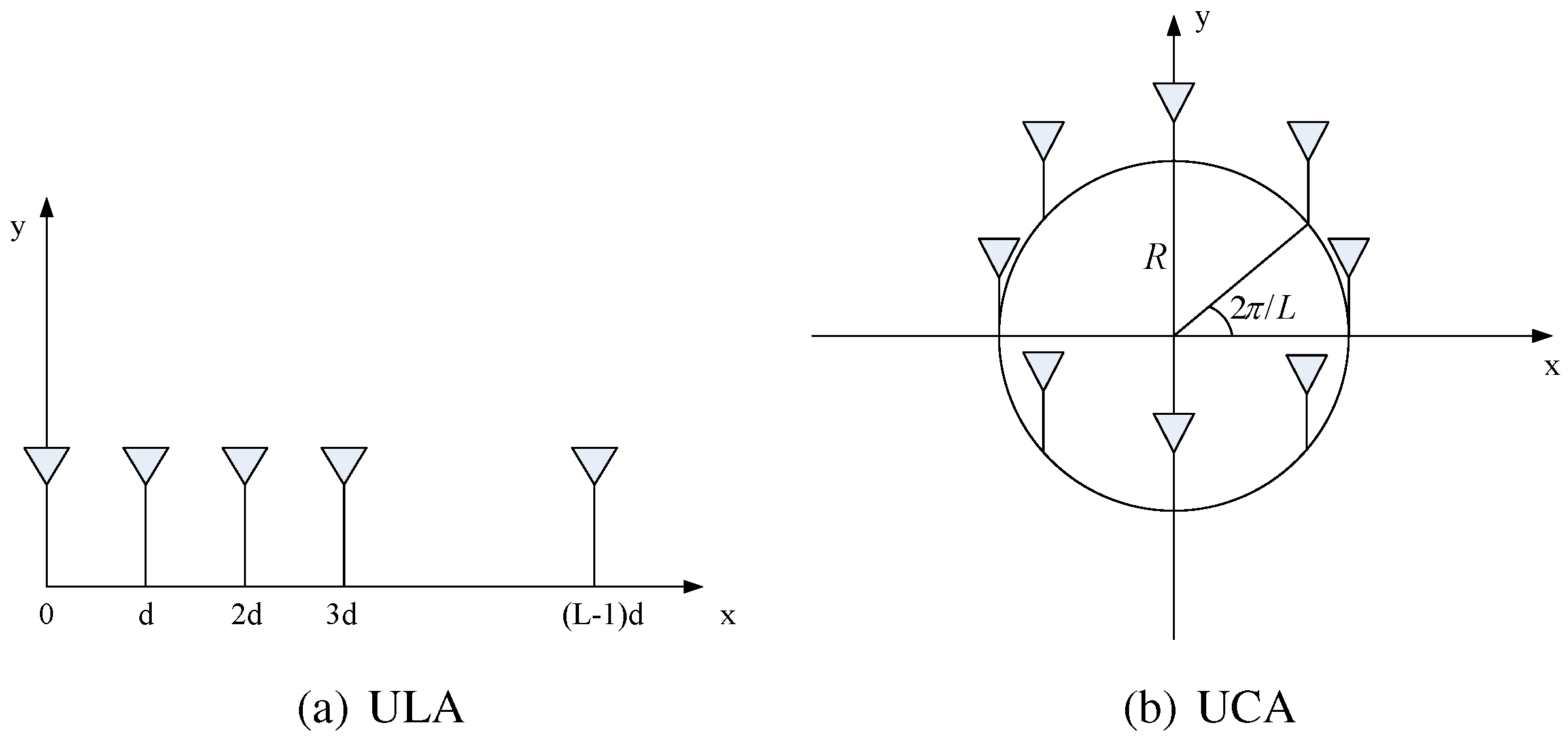
2. Matrix Theory in Modern Wireless Communication Systems
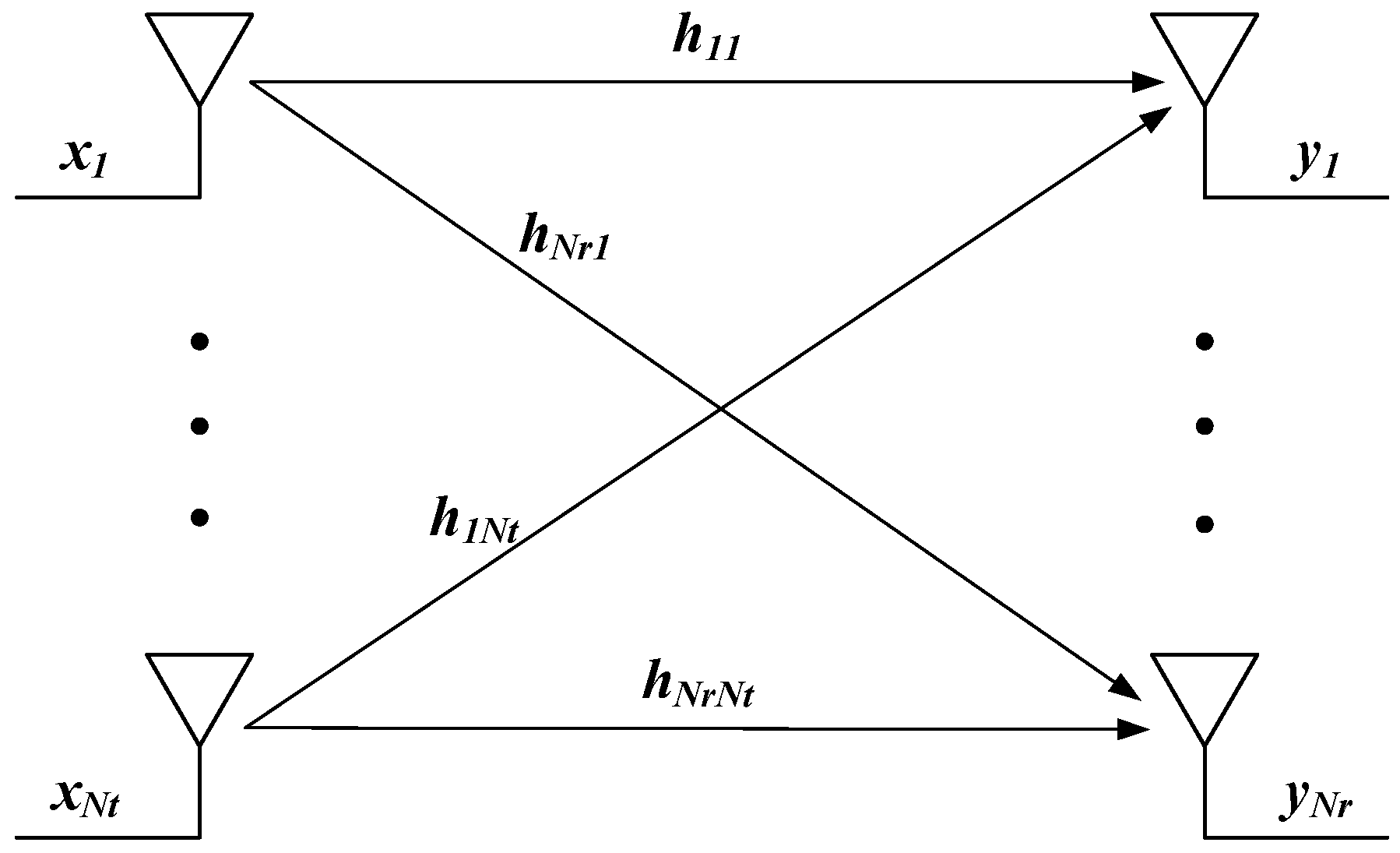
2.1. SVD for Modeling MIMO Channels
2.2. Matrix Representation of OFDM
Matrix Analysis of OFDM
3. Matrix Applications in Signal Estimation Theory
3.1. Cholesky Decomposition for Whitening the Noise
3.2. SVD for Least-Squares Based Estimation
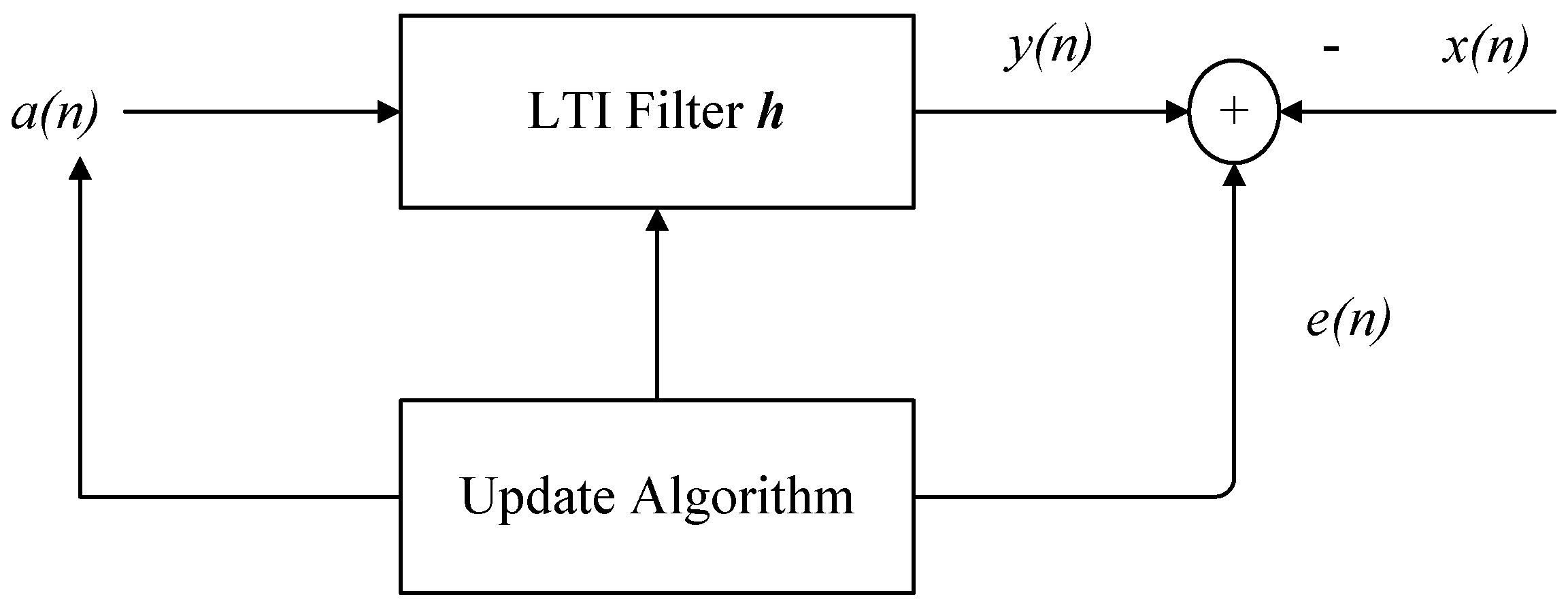
3.3. Matrix Inverse Lemma for Derivation of the Recursive Least-Squares Filter
- (1)
- Choose a large positive number α, and initialize and .
- (2)
- For , sequentially update
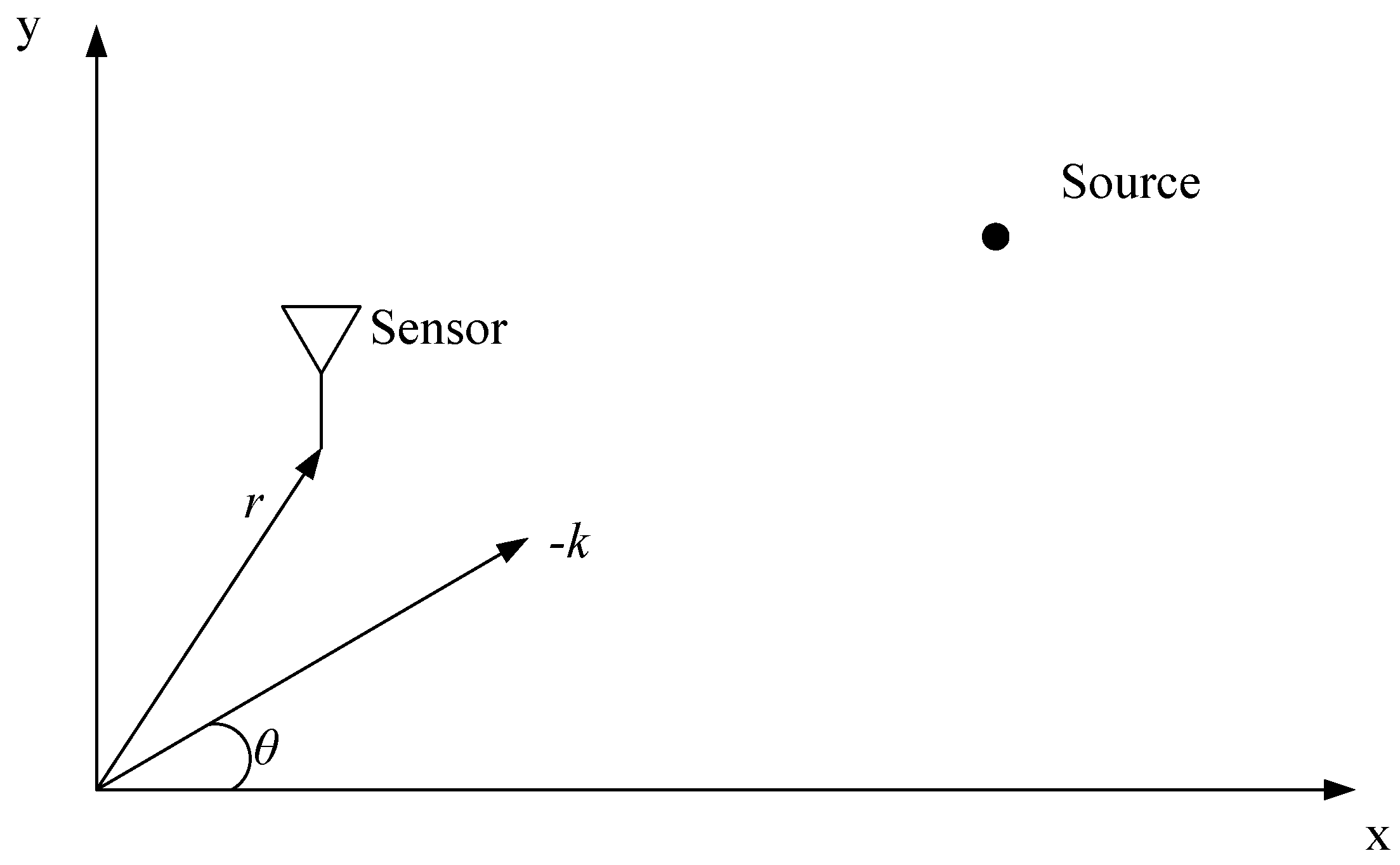
3.4. Matrix Theory in Sensor Array Signal Processing
3.5. Random Matrix Theory in Signal Estimation and Detection
4. Matrices in Image Processing
4.1. Block Transform Coding
4.2. Wavelet Representation
5. Compressive Sensing
5.1. Good Sensing Matrices
5.2. Compressive Signal Reconstruction
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Introduction to LTE-Advanced: Application Note. Agilent Technol. 2011. Available online: http://cp.literature.agilent.com/litweb/pdf/5990-6706EN.pdf (accessed on 6 January 2016).
- Telatar, E. Capacity of multi-antenna Gaussian channels. Eur. Trans. Telecommun. 1999, 10, 585–596. [Google Scholar] [CrossRef]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Foschini, G.J. Layered space-time architecture for wireless communication in fading environments when using multi-element antennas. Bell Labs Tech. J. 1996, 1, 41–59. [Google Scholar] [CrossRef]
- Foschini, G.J.; Gans, M.J. On limits of wireless communications in fading environment when using multiple antennas. Wirel. Pers. Commun. 1998, 6, 311–335. [Google Scholar] [CrossRef]
- Goldsmith, A.; Jafar, S.A.; Jindal, N.; Vishwanath, S. Capacity limits of MIMO channels. IEEE J. Sel. Areas Commun. 2003, 21, 684–702. [Google Scholar] [CrossRef]
- Wang, X.; Serpedin, E.; Qaraqe, K. A variational approach for assessing the capacity of a memoryless nonlinear MIMO channel. IEEE Commun. Lett. 2014, 18, 1315–1318. [Google Scholar] [CrossRef]
- Gray, R.M. Toeplitz and Circulant Matrices: A Review; Now Publishers Inc.: Norwell, MA, USA, 2006. [Google Scholar]
- Bolcskei, H.; Zurich, E. MIMO-OFDM wireless systems: Basics, perspectives, and challenges. IEEE Trans. Wirel. Commun. 2006, 13, 31–37. [Google Scholar]
- Golub, G.H.; VanLoan, C.F. Matrix Computations; The Johns Hopkins University Press: Baltimore, MA, USA, 1996. [Google Scholar]
- Kay, S. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Reilly, J.P. Matrix Computations in Signal Processing: Lecture Notes; Electrical and Computer Engineering Department, McMaster University: Hamilton, ON, Canada, 24 September 2006. [Google Scholar]
- Haykin, S. Array Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1985. [Google Scholar]
- Paleologu, C.; Ciochina, S.; Enescu, A. A family of recursive least-squares adaptive algorithms suitable for fixed-point implementation. Int. J. Adv. Telecommun. 2009, 2, 88–97. [Google Scholar]
- Liavas, A.; Regalia, P. On the numerical stability and accuracy of the conventional recursive least squares algorithm. IEEE Trans. Signal Process. 1999, 47, 88–96. [Google Scholar] [CrossRef]
- Ljung, S.; Ljung, L. Error propagation properties of recursive least-squares adaptation algorithms. Automatica 1985, 21, 157–167. [Google Scholar] [CrossRef]
- Verhaegen, M. Round-off error propagation in four generally-applicable, recursive, least-squares estimation schemes. Automatica 1989, 25, 437–444. [Google Scholar] [CrossRef]
- Bhotto, Z.; Antoniou, A. New improved recursive least-squares adaptive-filtering algorithms. IEEE Trans. Circuits Syst. I Reg. Pap. 2013, 60, 1548–1558. [Google Scholar] [CrossRef]
- Leung, S.; So, C. Gradient-based variable forgetting factor RLS algorithm in time-varying environments. IEEE Trans. Signal Process. 2005, 53, 3141–3150. [Google Scholar] [CrossRef]
- Paleologu, C.; Benesty, J.; Ciochina, S. A robust variable forgetting factor recursive least-squares algorithm for system identification. IEEE Signal Process. Lett. 2008, 15, 597–600. [Google Scholar] [CrossRef]
- Ardalan, S. Floating-point roundoff error analysis of the exponentially windowed RLS algorithm for time-varying systems. IEEE Trans. Circuits Syst. 1986, 33, 1192–1208. [Google Scholar] [CrossRef]
- Bottomley, G.; Alexander, S. A novel approach for stabilizing recursive least squares filters. IEEE Signal Process. Lett. 1991, 39, 1770–1779. [Google Scholar] [CrossRef]
- Chansakar, M.; Desai, U. A robust recursive least squares algorithm. IEEE Signal Process. Lett. 1997, 45, 1726–1735. [Google Scholar] [CrossRef]
- Haykin, S. Adpative Filtering Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Krim, H.; Viberg, M. Two decades of array signal processing research. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Stoica, P.; Moses, R.L. Introduction to Spectral Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Wigner, E. Characteristic vectors of bordered matrices with infinite dimensions. Ann. Math. 1955, 62, 548–564. [Google Scholar] [CrossRef]
- Marcenko, V.A.; Pastur, L.A. Distributions of eigenvalues for some sets of random matrices. Math. USSR-Sbornik 1967, 1, 457–483. [Google Scholar] [CrossRef]
- Couillet, R.; Debbah, M. Signal processing in large systems: A new paradigm. IEEE Signal Process. Mag. 2003, 30, 24–39. [Google Scholar] [CrossRef]
- Couillet, R.; Debbah, M.; Siverstein, J.W. A deterministic equivalent for the analysis of correlated MIMO multiple access channels. IEEE Trans. Inf. Theory 2011, 57, 3493–3514. [Google Scholar] [CrossRef]
- Dupuy, F.; Loubaton, P. On the capacity achieving covariance matrix for frequency selective MIMO channels using the asymptotic approach. IEEE Trans. Inf. Theory 2011, 57, 5737–5753. [Google Scholar] [CrossRef] [Green Version]
- Couillet, R.; Debbah, M. Random Matrix Methods for Wireless Communications; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Tulino, M.A.; Verdu, S. Random Matrix Theory and Wireless Communications; Now Publishers: Norwell, MA, USA, 2004. [Google Scholar]
- Girko, V.L. Theory of Random Determinants; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Baraniuk, R.G. Compressive Sensing. IEEE Signal Process. Mag. 2007, 24, 119–121. [Google Scholar] [CrossRef]
- Dandes, E.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar]
- Dandes, E.; Romberg, J. Quantitative robust uncertainty principles and optimally sparse decompositions. Found. Comput. Math. 2006, 6, 227–254. [Google Scholar]
- Candes, E.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar] [CrossRef]
- Candes, E.; Tao, T. Near optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. Theory 2006, 51, 5406–5425. [Google Scholar] [CrossRef]
- Donoho, D.L. For most large underdetermined systems of equations, the minimal l1-norm near-solution approximates the sparsest near-solution. Commun. Pure Appl. Math. 2004, 59, 797–829. [Google Scholar] [CrossRef]
- Baraniuk, R.G.; Davenport, M.A.; DeVore, R.A.; Wakin, M.B. A simple proof of the restricted isometry property for random matrices. Constr. Approx. 2008, 28, 253–263. [Google Scholar] [CrossRef]
- Natarajan, B.K. Sparse approximate solutions to linear systems. SIAM J. Comput. 1995, 24, 227–234. [Google Scholar] [CrossRef]
- Holtz, H.V. Compressive sensing: A paradigm shift in signal processing. 2008; arXiv:0812.3137. [Google Scholar]
- Donoho, D.L.; Huo, X. Uncertainty principles and ideal atomic decomposition. IEEE Trans. Inf. Theory 2001, 47, 2845–2862. [Google Scholar] [CrossRef]
- Wang, X.; Alshawaqfe, M.; Dang, X.; Wajid, B.; Noor, A.; Qaraqe, M.; Serpedin, E. An overview of NCA-based algorithms for transcriptional regulatory network inference. Microarrays 2015, 4, 596–617. [Google Scholar] [CrossRef] [PubMed]
- Noor, A.; Serpedin, E.; Nounou, M.; Nounou, H. An overview of the statistical methods for inferring gene regulatory networks and protein-protein interaction networks. Adv. Bioinform. 2013, 2013, 953814. [Google Scholar] [CrossRef] [PubMed]
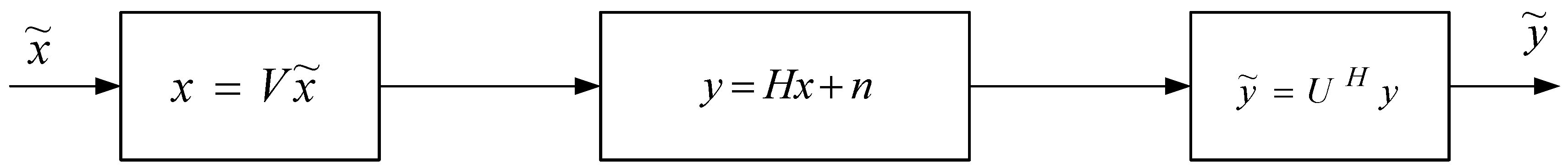



© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Serpedin, E. An Overview on the Applications of Matrix Theory in Wireless Communications and Signal Processing. Algorithms 2016, 9, 68. https://doi.org/10.3390/a9040068
Wang X, Serpedin E. An Overview on the Applications of Matrix Theory in Wireless Communications and Signal Processing. Algorithms. 2016; 9(4):68. https://doi.org/10.3390/a9040068
Chicago/Turabian StyleWang, Xu, and Erchin Serpedin. 2016. "An Overview on the Applications of Matrix Theory in Wireless Communications and Signal Processing" Algorithms 9, no. 4: 68. https://doi.org/10.3390/a9040068




