Forest Aboveground Biomass Estimation in Subtropical Mountain Areas Based on Improved Water Cloud Model and PolSAR Decomposition Using L-Band PolSAR Data
Abstract
:1. Introduction
2. Study Site and Dataset
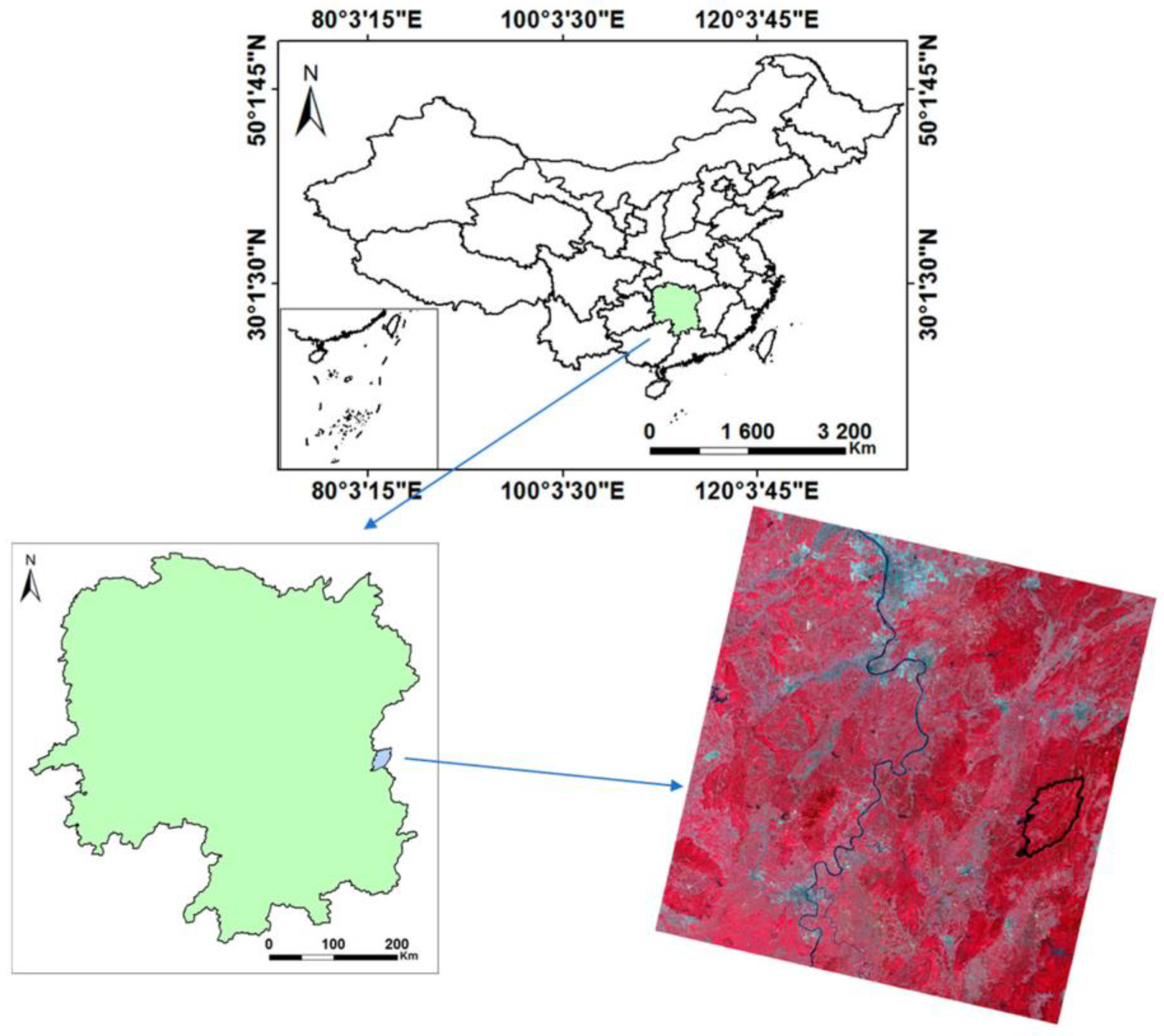
2.1. Study Site
2.2. Ground Data
2.3. SAR Data and Ancillary Data
3. Method
3.1. Polarimetric SAR Terrain Correction
3.2. AGB Estimation Model
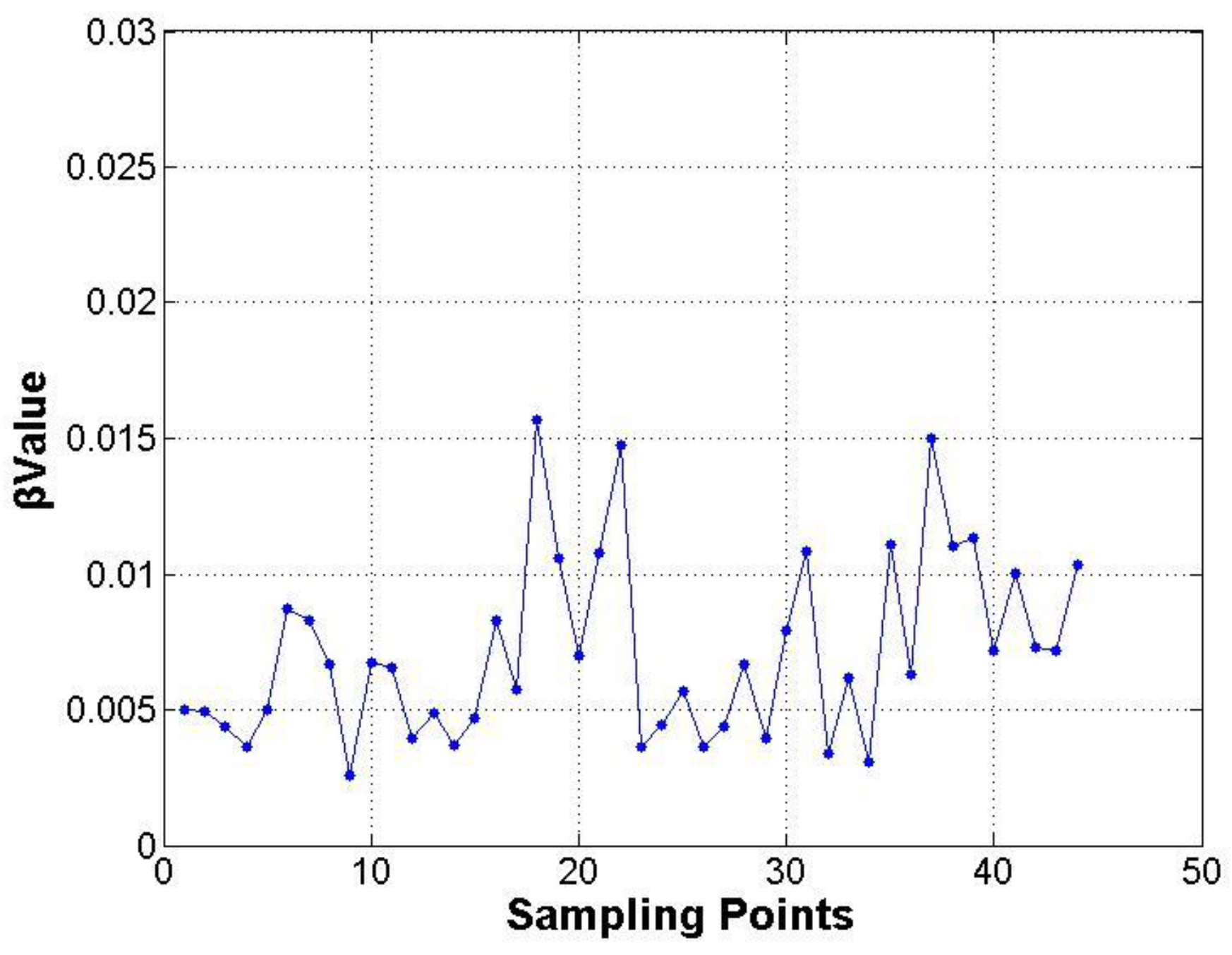
3.3. Model Inversion
3.4. Model Accuracy Evaluation
4. Results and Analysis
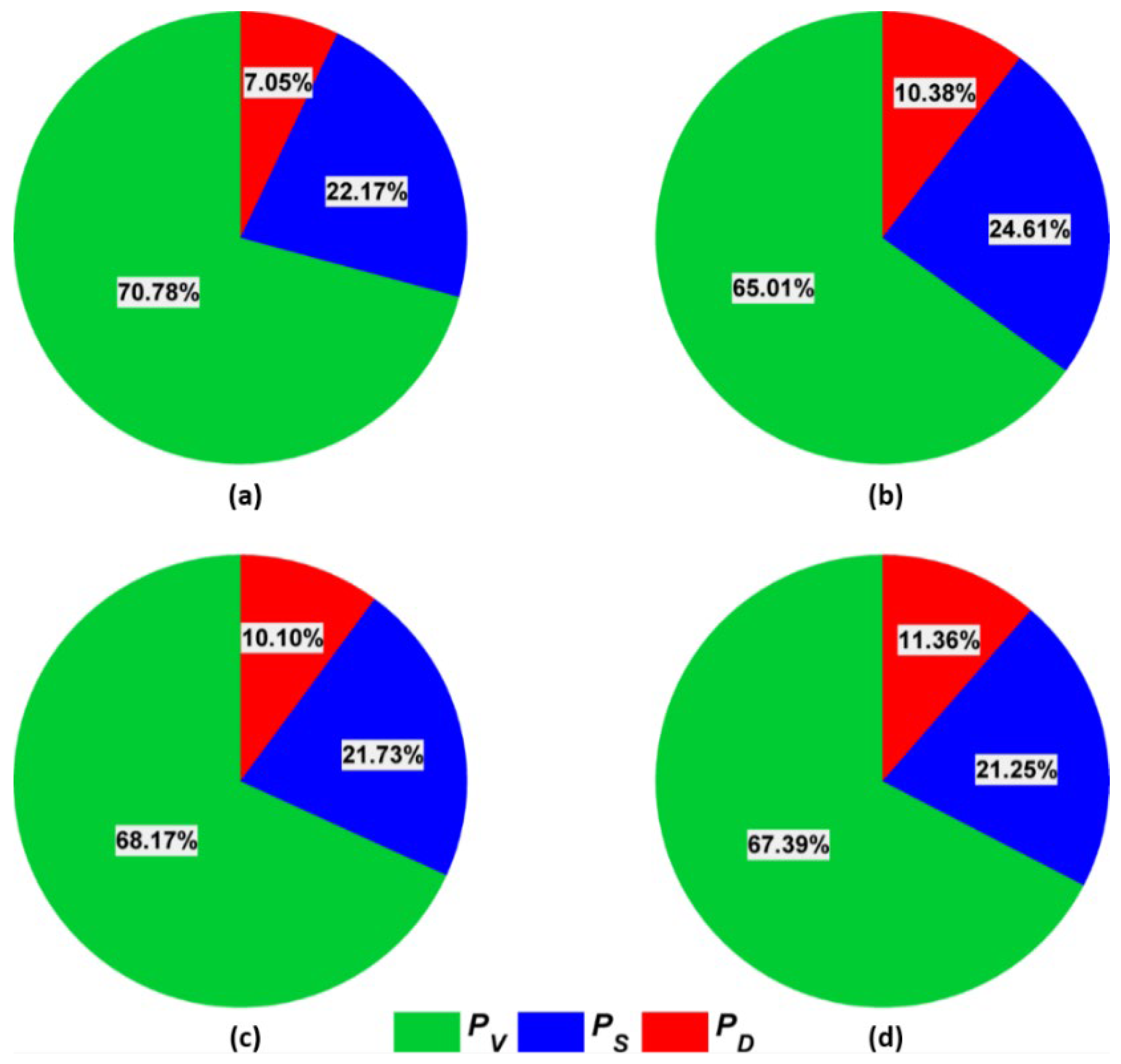
4.1. Effect of Terrain Correction on Scattering Mechanism
4.2. Forest AGB Estimation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Toan, T.L.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Ulander, L. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Houghton, R.A.; Hall, F.; Goetz, S.J. Importance of biomass in the global carbon cycle. J. Geophys. Res. 2009, 114, G00E03. [Google Scholar] [CrossRef]
- Chang, Q.; Zwieback, S.; Devries, B.; Berg, A. Application of L-band SAR for mapping tundra shrub biomass, leaf area index, and rainfall interception. Remote Sens. Environ. 2022, 268, 112747. [Google Scholar] [CrossRef]
- Huy, B.; Truong, N.Q.; Khiem, N.Q.; Poudel, K.P.; Temesgen, H. Deep learning models for improved reliability of tree aboveground biomass prediction in the tropical evergreen broadleaf forests. For. Ecol. Manag. 2022, 508, 120031. [Google Scholar] [CrossRef]
- Puliti, S.; Hauglin, M.; Breidenbach, J.; Montesano, P.M.; Astrup, R. Modeling above-ground biomass stock over Norway using national forest inventory data with ArcticDEM and Sentinel-2 data. Remote Sens. Environ. 2020, 236, 111501. [Google Scholar] [CrossRef]
- Chopping, M.; Wang, Z.; Schaaf, C.; Bull, M.A.; Duchesne, R.R. Forest aboveground biomass in the southwestern United States from a MISR multi-angle index, 2000–2015. Remote Sens. Env. 2022, 275, 112964. [Google Scholar] [CrossRef]
- Chen, C.; Ma, Y.; Ren, G.B.; Wang, J.B. Aboveground biomass of salt-marsh vegetation in coastal wetlands: Sample expansion of in situ hyperspectral and sentinel-2 data using a generative adversarial network. Remote Sens. Environ. 2022, 270, 112885. [Google Scholar] [CrossRef]
- Liao, Z.M.; Dijk, A.I.J.M.V.; He, B.B.; Larraondo, P.R.; Scarth, P.F. Woody vegetation cover, height and biomass at 25-m resolution across Australia derived from multiple site, airborne and satellite observations. Int. J. Appl. Earth Obs. 2020, 93, 102209. [Google Scholar] [CrossRef]
- Fang, P.; Yan, N.N.; Wei, P.P.; Zhao, Y.F.; Zhang, X.W. Aboveground Biomass Mapping of Crops Supported by Improved CASA Model and Sentinel-2 Multispectral Imagery. Remote Sens. 2021, 13, 2755. [Google Scholar] [CrossRef]
- Beyene, S.M.; Hussin, Y.A.; Kloosterman, H.E.; Ismail, M.H. Forest Inventory and Aboveground Biomass Estimation with Terrestrial LiDAR in the Tropical Forest of Malaysia. Can. J. Remote Sens. 2020, 46, 130–145. [Google Scholar] [CrossRef]
- Musthafa, M.; Singh, G. Forest above-ground woody biomass estimation using multi-temporal space-borne LiDAR data in a managed forest at Haldwani, India. Adv. Space Res. 2022, 69, 3245–3257. [Google Scholar] [CrossRef]
- Xu, D.D.; Wang, H.B.; Xu, W.X.; Luan, Z.Q.; Xu, X. LiDAR Applications to Estimate Forest Biomass at Individual Tree Scale: Opportunities, Challenges and Future Perspectives. Forests 2021, 12, 550. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.; Neuenschwander, A.; Zhou, T.; Srinivasan, S.; Harbeck, K. Estimating aboveground biomass and forest canopy cover with simulated ICESat-2 data. Remote Sens. Environ. 2019, 224, 1–11. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.C.; Malambo, L. Using ICESat-2 to estimate and map forest above ground biomass: A First Example. Remote Sens. 2020, 12, 1824. [Google Scholar] [CrossRef]
- Englhart, S.; Keuck, V.; Siegert, F. Aboveground biomass retrieval in tropical forests-The potential of combined X- and L- band SAR data use. Remote Sens. Environ. 2011, 115, 1260–1271. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Quegan, S.; Le Toan, T.; Dinh, H.T.M.; Saatchi, S.S.; Carvalhais, N.; Reichstein, M.; Scipal, K. Coverage of high biomass forests by the ESA BIOMASS mission under defense restrictions. Remote Sens. Environ. 2017, 196, 154–162. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O. Research Pathways of Forest Above-Ground Biomass Estimation Based on SAR Backscatter and Interferometric SAR Observations. Remote Sens. 2018, 10, 608. [Google Scholar] [CrossRef]
- Cartus, O.; Santoro, M.; Wegmueller, U.; Rommen, B. Benchmarking the retrieval of biomass in boreal forests using P-band SAR backscatter with multi-temporal C-and L-band observations. Remote Sens. 2019, 11, 1695. [Google Scholar] [CrossRef]
- Pardini, M.; Cazcarra-Bes, V.; Papathanassiou, K.P. TomoSAR Mapping of 3D Forest Structure: Contributions of L-Band Configurations. Remote Sens. 2021, 13, 2255. [Google Scholar] [CrossRef]
- Fu, B.; Xie, S.; He, H.; Zuo, P.; Sun, J.; Liu, L.; Huang, L.; Fan, D.; Gao, E. Synergy of multi-temporal polarimetric SAR and optical image satellite for mapping of marsh vegetation using object-based random forest algorithm. Ecol. Indic. 2021, 131, 108173. [Google Scholar] [CrossRef]
- Lucas, R.; Armston, J.; Fairfax, R.; Fensham, R.; Accad, A.; Carreiras, J.; Kelley, J.; Bunting, P.; Clewley, D.; Bray, S.; et al. An Evaluation of the ALOS PALSAR L-Band Backscatter—Above Ground Biomass Relationship Queensland, Australia: Impacts of Surface Moisture Condition and Vegetation Structure. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sen. 2010, 3, 576–593. [Google Scholar] [CrossRef]
- Zhang, H.B.; Zhu, J.J.; Wang, C.C.; Lin, H.; Liu, Z.W. Forest Growing Stock Volume Estimation in Subtropical Mountain Areas Using PALSAR-2 L-Band PolSAR Data. Forests 2019, 10, 276. [Google Scholar] [CrossRef]
- Mermoz, S.; Le Toan, T.; Villard, L.; Réjou-Méchain, M.; Seifert-Granzin, J. Biomass assessment in the Cameroon savanna using ALOS PALSAR data. Remote Sens. Environ. 2014, 155, 109–119. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Vasconcelos, M.J.; Lucas, R.M. Understanding the relationship between aboveground biomass and ALOS PALSAR data in the forests of GuineaBissau (West Africa). Remote Sens. Environ. 2012, 121, 426–442. [Google Scholar] [CrossRef]
- Michelakis, D.; Stuart, N.; Brolly, M.; Woodhouse, I.H.; Lopez, G.; Linares, V. Estimation of woody biomass of pine savanna woodlands from ALOS PALSAR images. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 244–254. [Google Scholar] [CrossRef]
- Schlund, M.; Scipal, K.; Quegan, S. Assessment of a Power Law Relationship between P-Band SAR Backscatter and Aboveground Biomass and Its Implications for BIOMASS Mission Performance. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 3538–3547. [Google Scholar] [CrossRef]
- Peregon, A.; Yamagata, Y. The use of ALOS/PALSAR backscatter to estimate above-ground forest biomass: A case study in Western Siberia. Remote Sens. Environ. 2013, 137, 139–146. [Google Scholar] [CrossRef]
- Hame, T.; Ahola, H.; Antropov, O.; Rauste, Y. Stand-Level Stem Volume of Boreal Forests from Spaceborne SAR Imagery at L-Band. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 35–44. [Google Scholar]
- Long, J.P.; Lin, H.; Wang, G.X.; Sun, H.; Yan, E.P. Mapping growing stem volume of Chinese Fir Plantation using a saturation-based multivariate method and quad-polarimetric SAR images. Remote Sens. 2019, 11, 1872. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Fransson, J.E.S. Integration of allometric equations in the water cloud model towards an improved retrieval of forest stem volume with L-band SAR data in Sweden. Remote Sens. Environ. 2021, 253, 112235. [Google Scholar] [CrossRef]
- Lu, D.S.; Chen, Q.; Wang, G.X.; Liu, L.J.; Li, G.Y.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Santoro, M.; Beaudoin, A.; Beer, C.; Fransson, J.E.S.; Hall, R.J.; Pathe, C.; Schmullius, C.; Schepaschenko, D.; Shvidenko, A. Forest growing stock volume of the northern hemisphere: Spatially explicit estimates for 2010 derived from Envisat ASAR. Remote Sens. Env. 2015, 168, 316–334. [Google Scholar] [CrossRef]
- Cartus, O.; Santoro, M.; Kellndorfer, J. Mapping forest aboveground biomass in the Northeastern United States with ALOS PALSAR dual-polarization L-band. Remote Sens. Environ. 2012, 124, 446–478. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Fransson, J.E.S.; Wegmüller, U. Complementarity of X-, C-, and L-band SAR Backscatter Observations to Retrieve Forest Stem Volume in Boreal Forest. Remote Sens. 2019, 11, 1563. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Le Toan, T.; Beaudoin, A.; Christensen, N. Dependence of radar backscatter on coniferous forest biomass. IEEE Trans. Geosci. Remote Sens. 1992, 30, 412–415. [Google Scholar] [CrossRef]
- Pulliainen, J.T.; Kurvonen, L.; Hallikainen, M.T. Multitemporal behavior of L- and C-band SAR observations of boreal forests. IEEE Trans. Geosci. Remote Sens. 1999, 37, 927–937. [Google Scholar] [CrossRef]
- Ningthoujam, R.K.; Balzter, H.; Tansey, K.; Feldpausch, T.R.; Mitchard, E.T.A.; Wani, A.A.; Joshi, P.K. Relationships of S-band radar backscatter and forest aboveground biomass in different forest types. Remote Sens. 2017, 9, 1116. [Google Scholar] [CrossRef]
- Santoro, M.; Beer, C.; Cartus, O.; Schmullius, C.; Shvidenko, A.; McCallum, I.; Wegmüller, U.; Wiesmann, A. Retrieval of growing stock volume in boreal forest using hyper-temporal series of Envisat ASAR ScanSAR backscatter measurements. Remote Sens. Environ. 2011, 115, 490–507. [Google Scholar] [CrossRef]
- Bouvet, A.; Mermoz, S.; Le Toan, T.; Villard, L.; Mathieu, R.; Naidoo, L.; Asner, G.P. An above-ground biomass map of African savannahs and woodlands at 25 m resolution derived from ALOS PALSAR. Remote Sens. Environ. 2018, 206, 156–173. [Google Scholar] [CrossRef]
- Bharadwaj, P.S.; Kumar, S.; Kushwaha, S.; Bijker, W. Polarimetric scattering model for estimation of above ground biomass of multilayer vegetation using ALOS-PALSAR quad-pol data. Phys. Chem. Earth 2015, 83, 187–195. [Google Scholar] [CrossRef]
- Kumar, S.; Garg, R.D.; Govil, H.; Kushwaha, S. PolSAR-Decomposition-Based Extended Water Cloud Modeling for Forest Aboveground Biomass Estimation. Remote Sens. 2019, 11, 2287. [Google Scholar] [CrossRef]
- Deng, S.Q.; Katoh, M.; Guan, Q.W.; Yin, N.; Li, M.Y. Estimating forest aboveground biomass by combining ALOSPALSAR and Word View-2 data: A case study at purple mountain national park, Nanjing, China. Remote Sens. 2014, 6, 7878–7910. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Zhang, J.G.; Duan, A.G. Compatibility of Stand Volume Model for Chinese Fir Based on Tree-Level Stand-Level. Sci. Silvae Sin. 2014, 50, 83–87. [Google Scholar]
- Ghasemi, N.; Tolpekin, V.; Stein, A. Assessment of Forest Above-ground Biomass Estimation from PolInSAR in The Presence of Temporal Decorrelation. Remote Sens. 2018, 10, 815–837. [Google Scholar] [CrossRef]
- Pereira, L.O.; Furtado, L.F.A.; Novo, E.M.L.M.; Sant’Anna, S.J.S.; Liesenberg, V.; Silva, T.S.F. Multifrequency and full-polarimetric SAR assessment for estimating above ground biomass and leaf area index in the Amazon Várzea wetlands. Remote Sens. 2018, 10, 1355. [Google Scholar] [CrossRef]
- Lee, J.S.; Schuler, D.L.; Ainsworth, T.L. Polarimetric SAR data compensation for terrain azimuth slope variation. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2153–2163. [Google Scholar]
- Zhao, L.; Chen, E.X.; Li, Z.Y.; Zhang, W.F.; Gu, X.Z. Three-Step Semi-Empirical Radiometric Terrain Correction Approach for PolSAR Data Applied to Forested Areas. Remote Sens. 2017, 9, 269. [Google Scholar] [CrossRef]
- Small, D. Flattening gamma: Radiometric terrain correction for SAR imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3081–3093. [Google Scholar] [CrossRef]
- Castel, T.; Beaudoin, A.; Stach, N.; Stussi, N.; Le Toan, T.; Durand, P. Sensitivity of space-borne SAR data to forest parameters over sloping terrain. Theory and experiment. Int. J. Remote Sens. 2001, 22, 2351–2376. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Volume Scattering and Emission Theory. In Microwave Remote Sensing Active and Passive; Artech House: Norwood, MA, USA, 1982; Volume III. [Google Scholar]
- Askne, J.I.H.; Dammert, P.B.G.; Ulander, L.M.H. C-band repeat-pass interferometric SAR observations of the forest. IEEE Trans. Geosci. Remote Sens. 1997, 35, 25–35. [Google Scholar] [CrossRef]
- Freeman, A. Fitting a tow-component scattering model to polarimetric SAR data from forests. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Xie, Q.H.; Berman, J.D.B.; Lopez-sanchez, J.M.; Zhu, J.J.; Wang, C.C. Quantitative analysis of polarimetric model-based decomposition methods. Remote Sens. 2016, 8, 977. [Google Scholar] [CrossRef]
- Su, Y.J.; Guo, Q.H.; Xue, B.L.; Hu, T.Y.; Alvarez, O.; Tao, S.L.; Fang, J.Y. Spatial distribution of forest aboveground biomass in China: Estimation through combination of spaceborne lidar, optical imagery, and forest inventory data. Remote Sens. Environ. 2016, 173, 187–199. [Google Scholar] [CrossRef]
- Huang, X.; Ziniti, B.; Torbick, N.; Ducey, M.J. Assessment of forest above ground biomass estimation using multi-temporal C-band Sentinel-1 and Polarimetric L-band PALSAR-2 data. Remote Sens. 2018, 10, 1424. [Google Scholar] [CrossRef]
- Santoro, M.; Wegmüller, U.; Askne, J. Forest stem volume estimation using C-band interferometric SAR coherence data of the ERS-1 mission 3-days repeat-interval phase. Remote Sens. Environ. 2018, 216, 684–696. [Google Scholar] [CrossRef]
- Ranson, K.J.; Sun, G.; Weishampel, J.F.; Knox, R.G. Forest biomass from combined ecosystem and radar backscatter modeling. Remote Sens. Environ. 1997, 59, 118–133. [Google Scholar] [CrossRef]
- Kumar, S.; Pandey, U.; Kushwaha, S.P.; Chatterjee, R.S.; Bijker, W. Aboveground biomass estimation of tropical forest from Envisat advanced synthetic aperture radar data using modeling approach. J. Appl. Remote Sens. 2012, 6, 063588. [Google Scholar] [CrossRef]
- Souyris, J.C.; Imbo, P.; Fjortoft, R.; Mingot, S.; Lee, J.S. Compact polarimetry based on symmetry properties of geophysical media: The π/4 mode. IEEE Trans. Geosci. Remote Sens. 2005, 43, 634–646. [Google Scholar] [CrossRef]




| Parameter | Range | Mean |
|---|---|---|
| DBH (cm) | 4.06 to 30.10 | 17.84 |
| Height (m) | 4.60 to 20.20 | 13.24 |
| Number of stems | 30 to 350 | 96 |
| AGB (t/ha) | 2.46 to 155.52 | 71.67 |
| Channel | Woodland | Shrubbery | Spare Woodland | Other Forest |
|---|---|---|---|---|
| HH | 1.24 | 1.23 | 1.52 | 1.42 |
| HV | 0.82 | 0.74 | 0.82 | 0.63 |
| VV | 1.09 | 1.20 | 1.39 | 1.29 |
| Types | K11 | K12 | K13 | K21 | K22 | K23 | K31 | K32 | K33 |
|---|---|---|---|---|---|---|---|---|---|
| Woodland | 1.24 | 2.06 | 2.35 | 2.26 | 0.82 | 1.91 | 2.35 | 1.91 | 1.09 |
| Shrubbery | 1.23 | 1.97 | 2.43 | 1.97 | 0.74 | 1.94 | 2.43 | 1.94 | 1.20 |
| Spare woodland | 1.52 | 2.34 | 2.91 | 2.34 | 0.82 | 2.21 | 2.91 | 2.21 | 1.39 |
| Other forest | 1.42 | 2.05 | 2.71 | 2.05 | 0.63 | 1.92 | 2.71 | 1.92 | 1.29 |
| HH | HV | VV | |
|---|---|---|---|
| Forest AGB | 0.395 | 0.550 | 0.439 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wang, C.; Zhu, J.; Fu, H.; Han, W.; Xie, H. Forest Aboveground Biomass Estimation in Subtropical Mountain Areas Based on Improved Water Cloud Model and PolSAR Decomposition Using L-Band PolSAR Data. Forests 2023, 14, 2303. https://doi.org/10.3390/f14122303
Zhang H, Wang C, Zhu J, Fu H, Han W, Xie H. Forest Aboveground Biomass Estimation in Subtropical Mountain Areas Based on Improved Water Cloud Model and PolSAR Decomposition Using L-Band PolSAR Data. Forests. 2023; 14(12):2303. https://doi.org/10.3390/f14122303
Chicago/Turabian StyleZhang, Haibo, Changcheng Wang, Jianjun Zhu, Haiqiang Fu, Wentao Han, and Hongqun Xie. 2023. "Forest Aboveground Biomass Estimation in Subtropical Mountain Areas Based on Improved Water Cloud Model and PolSAR Decomposition Using L-Band PolSAR Data" Forests 14, no. 12: 2303. https://doi.org/10.3390/f14122303
APA StyleZhang, H., Wang, C., Zhu, J., Fu, H., Han, W., & Xie, H. (2023). Forest Aboveground Biomass Estimation in Subtropical Mountain Areas Based on Improved Water Cloud Model and PolSAR Decomposition Using L-Band PolSAR Data. Forests, 14(12), 2303. https://doi.org/10.3390/f14122303







