Elastoplastic Analysis of Timber Connections with Dowel-Type Fasteners at Ambient and High Temperatures
Abstract
:1. Introduction
2. Materials and Methods
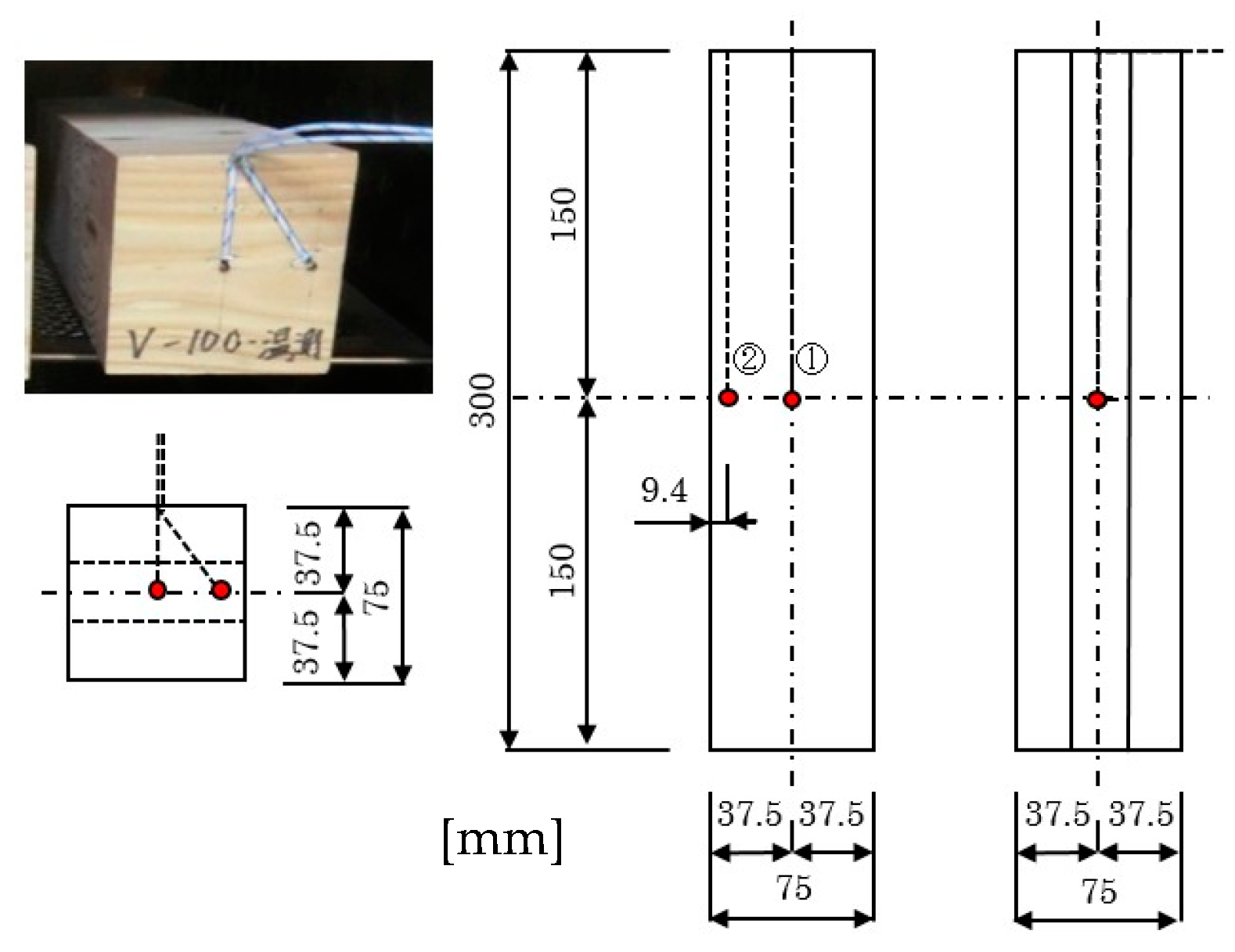
2.1. Compression Tests
2.1.1. Materials and Methods of Compression Tests
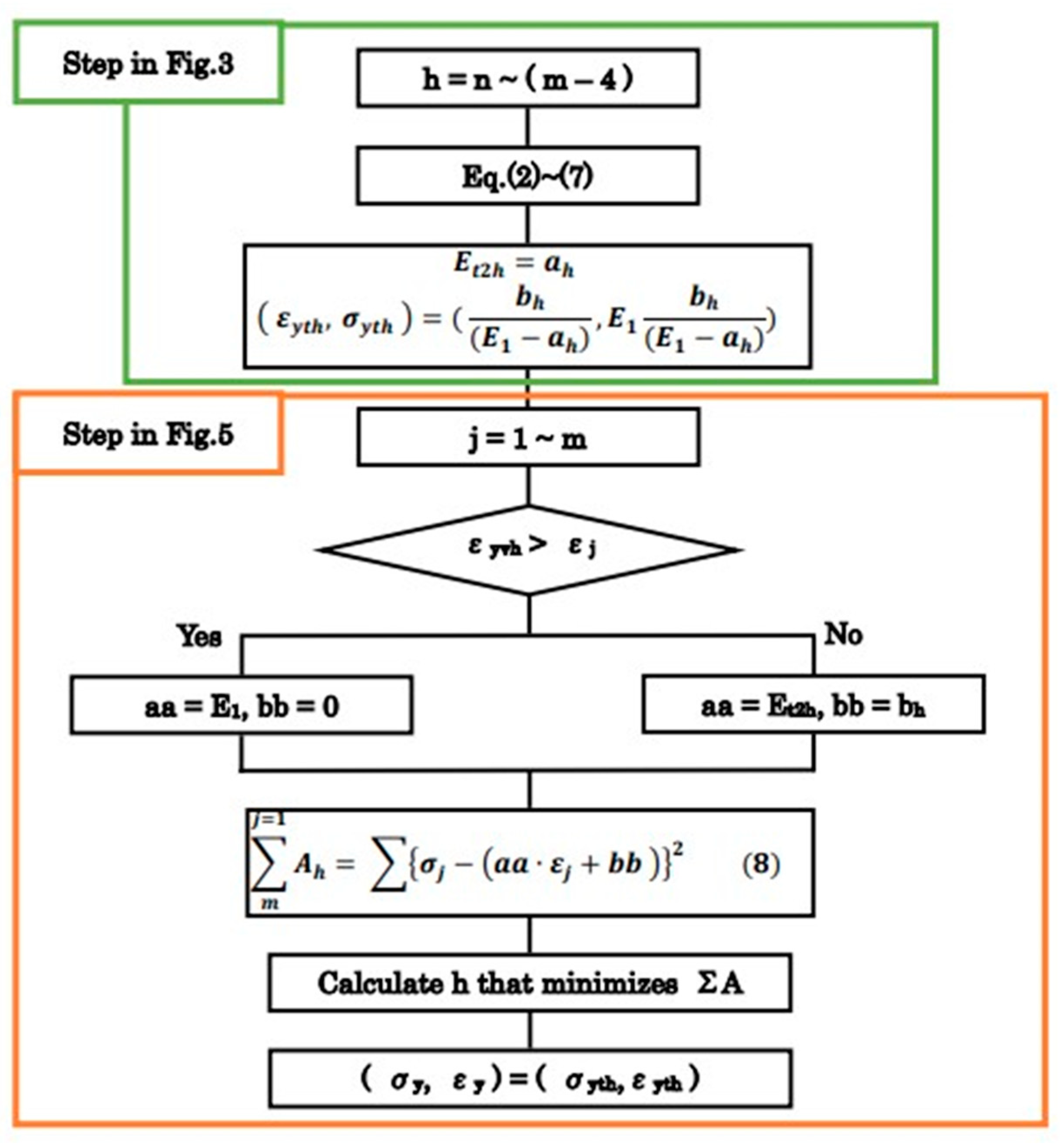
2.1.2. Bilinearization of Stress–Strain Relationship from the Test Results
- σmax0.5: 50 % stress of the maximum stress;
- σmax0.1: 10 % stress of the maximum stress;
- εn: strain at σmax0.5
- εi: strain at σmax0.1.
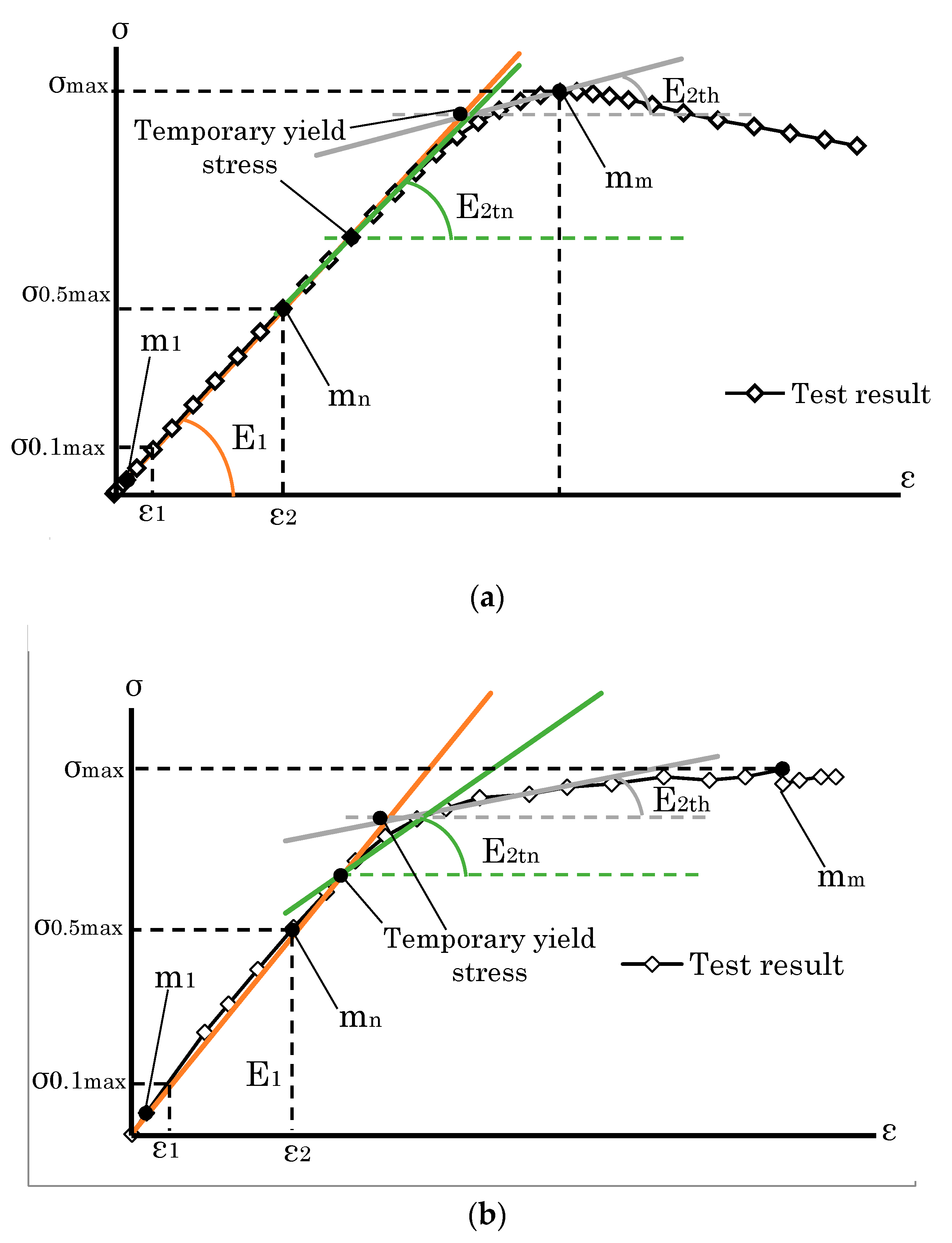
- σj: Stress from the test result at point j;
- εj: Strain from the test result at point j;
- aa is E1 when εj is less than εyth and Et2h when εj is greater than εyth;
- bb is 0 when εj is less than εyth and bh when εj is greater than εyth.
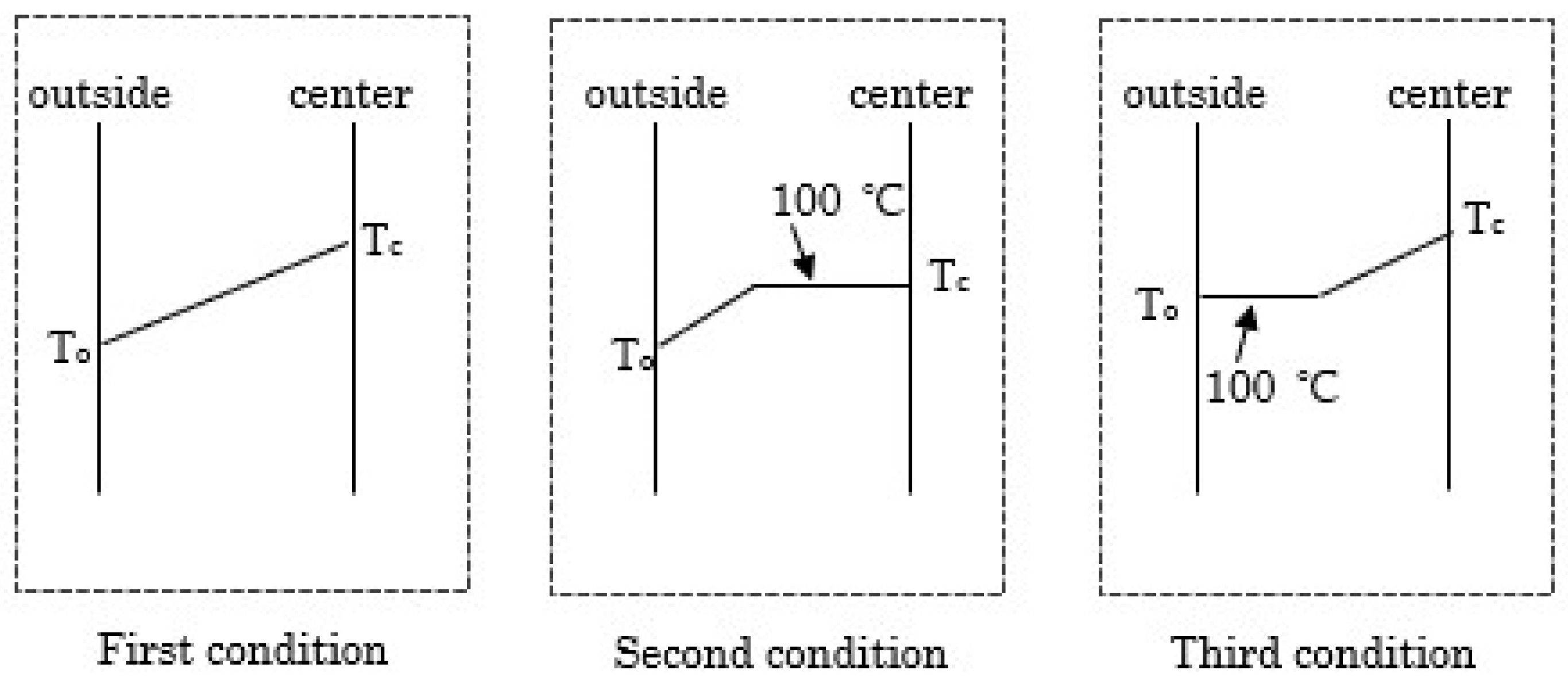
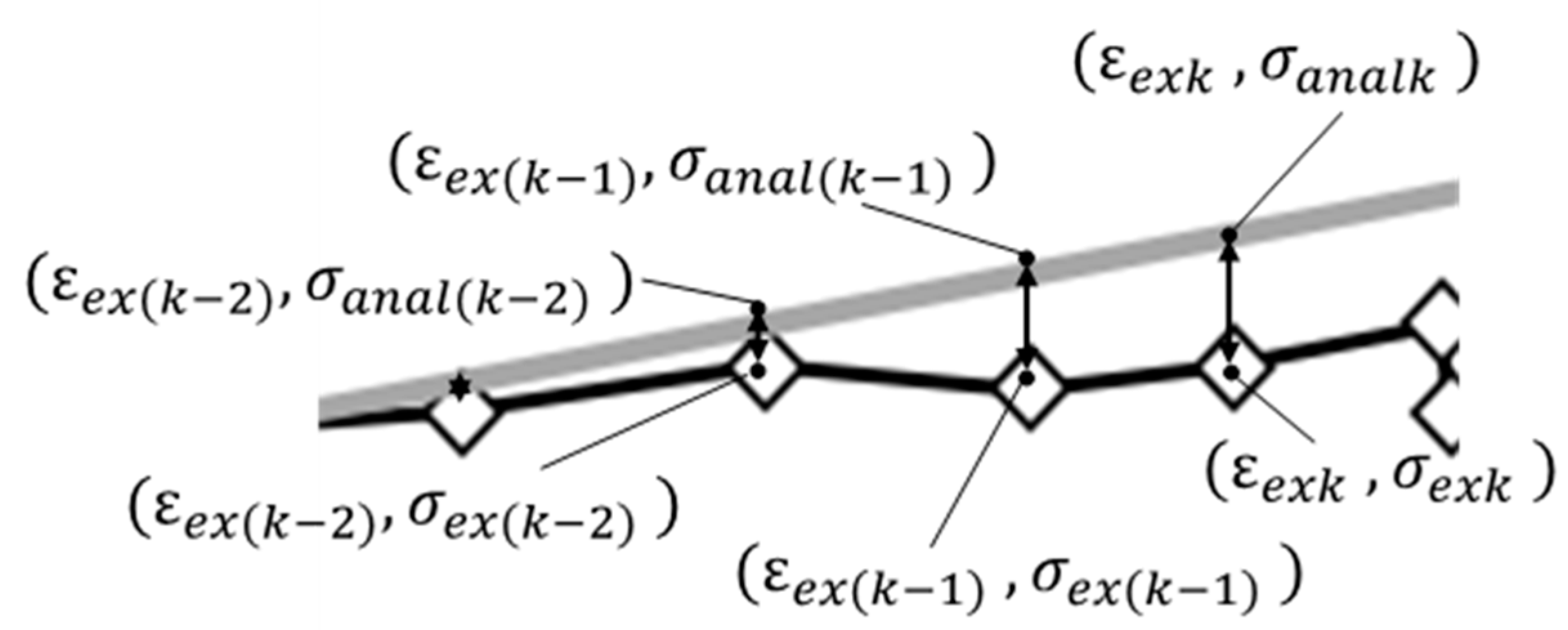
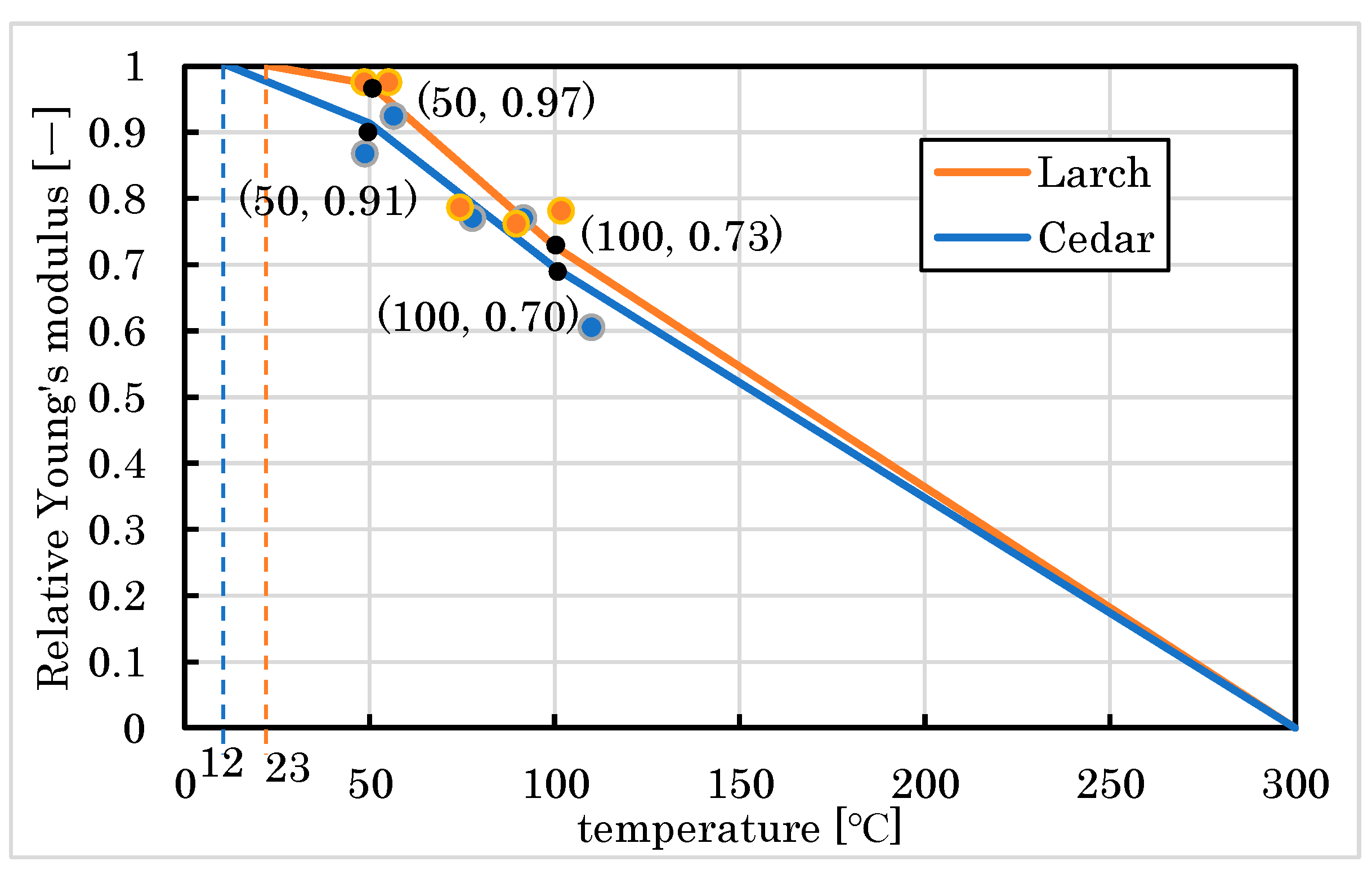
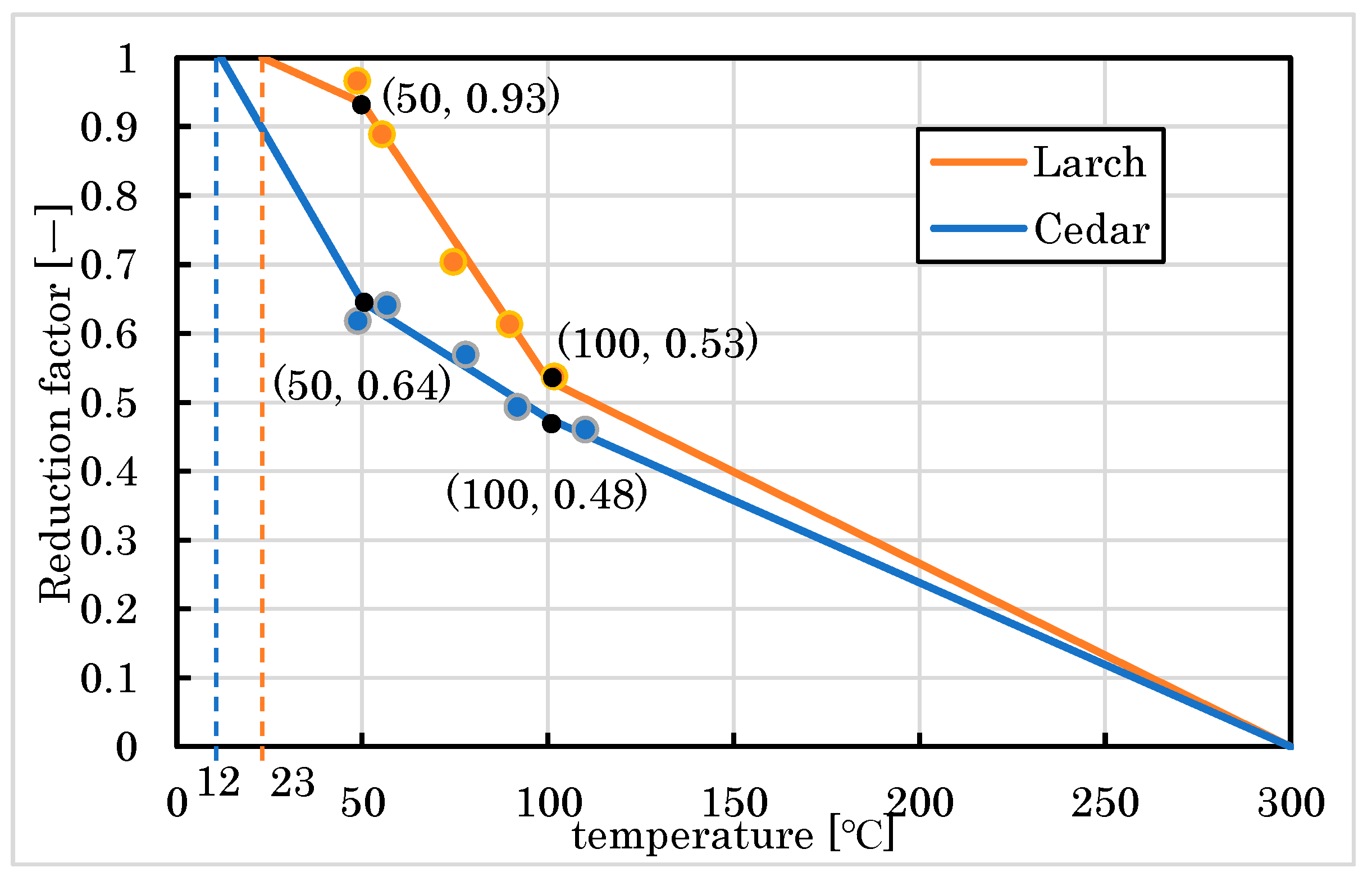
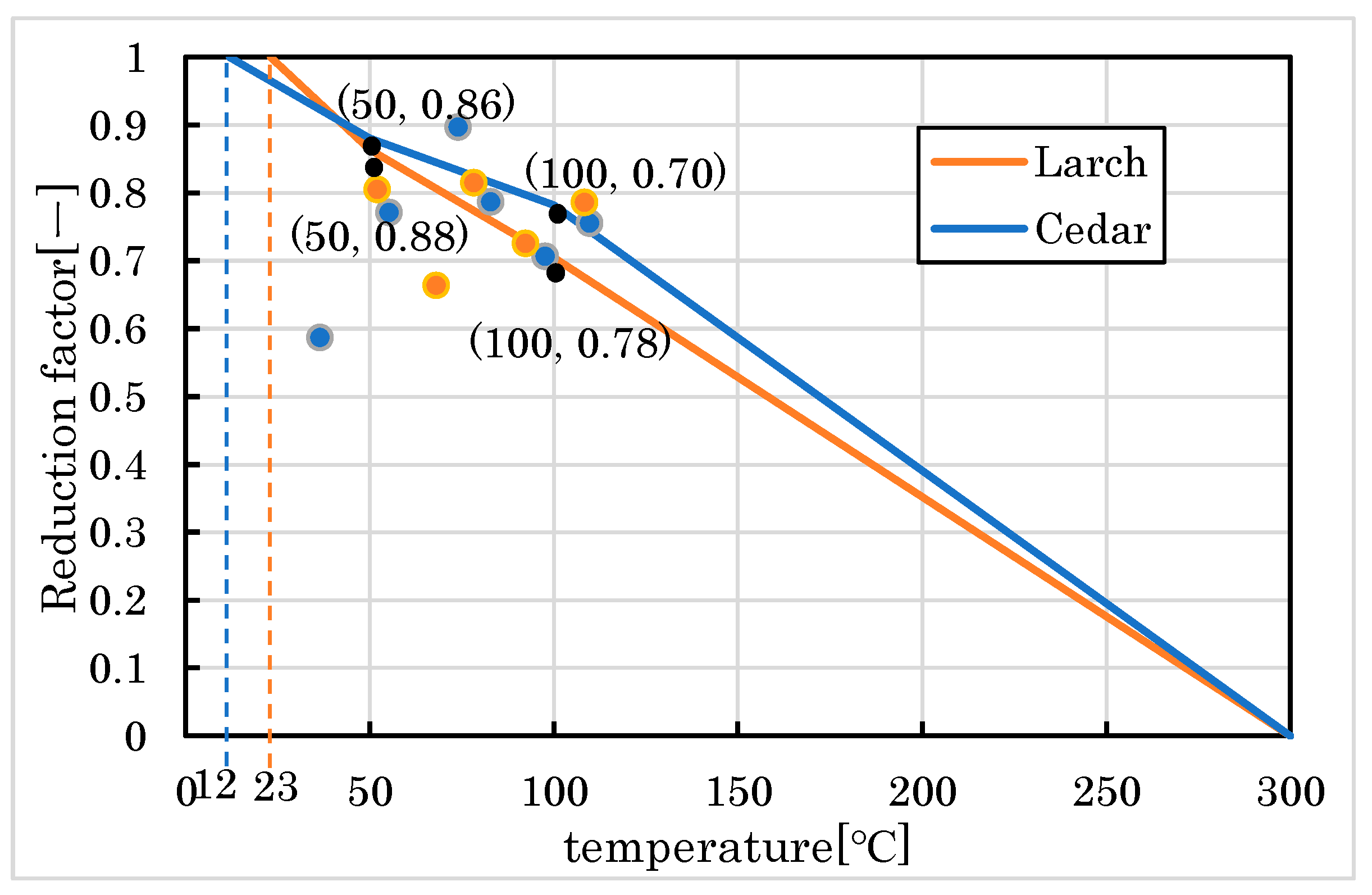
2.1.3. Material Properties at High Temperature Used in FE Analysis
- T1,T2,Tn: temperature;
- y1,y2,yn: Young’s modulus or yield strength.
2.1.4. Finite Element Modeling
- Ex, Ey, Ez: Young’s modulus;
- νxy,νyx, νyz, νzy, νzx, νxz: Poison’s ratios.
- Gxy, Gyz, Gzx: share modulus.

| Cedar | Larch | ||
|---|---|---|---|
| Young’s modulus (N/mm2) | EL | 7676.96 | 10,263.70 |
| ER | 413.25 | 298.86 | |
| ET | 413.25 | 298.86 | |
| Poison’s ratios (–) | νLR | 0.40 | 0.48 |
| νRT | 0.90 | 0.93 | |
| νTL | 0.032 | 0.015 | |
| Shear modulus (N/mm2) | GLR | 384.29 | 286.51 |
| GRT | 142.50 | 102.00 | |
| GTL | 380.58 | 286.23 | |
| Yield stress (N/mm2) | σyL | 32.20 | 29.73 |
| σyR | 2.03 | 2.67 | |
| σyT | 2.03 | 2.67 | |
2.2. Embedment Tests
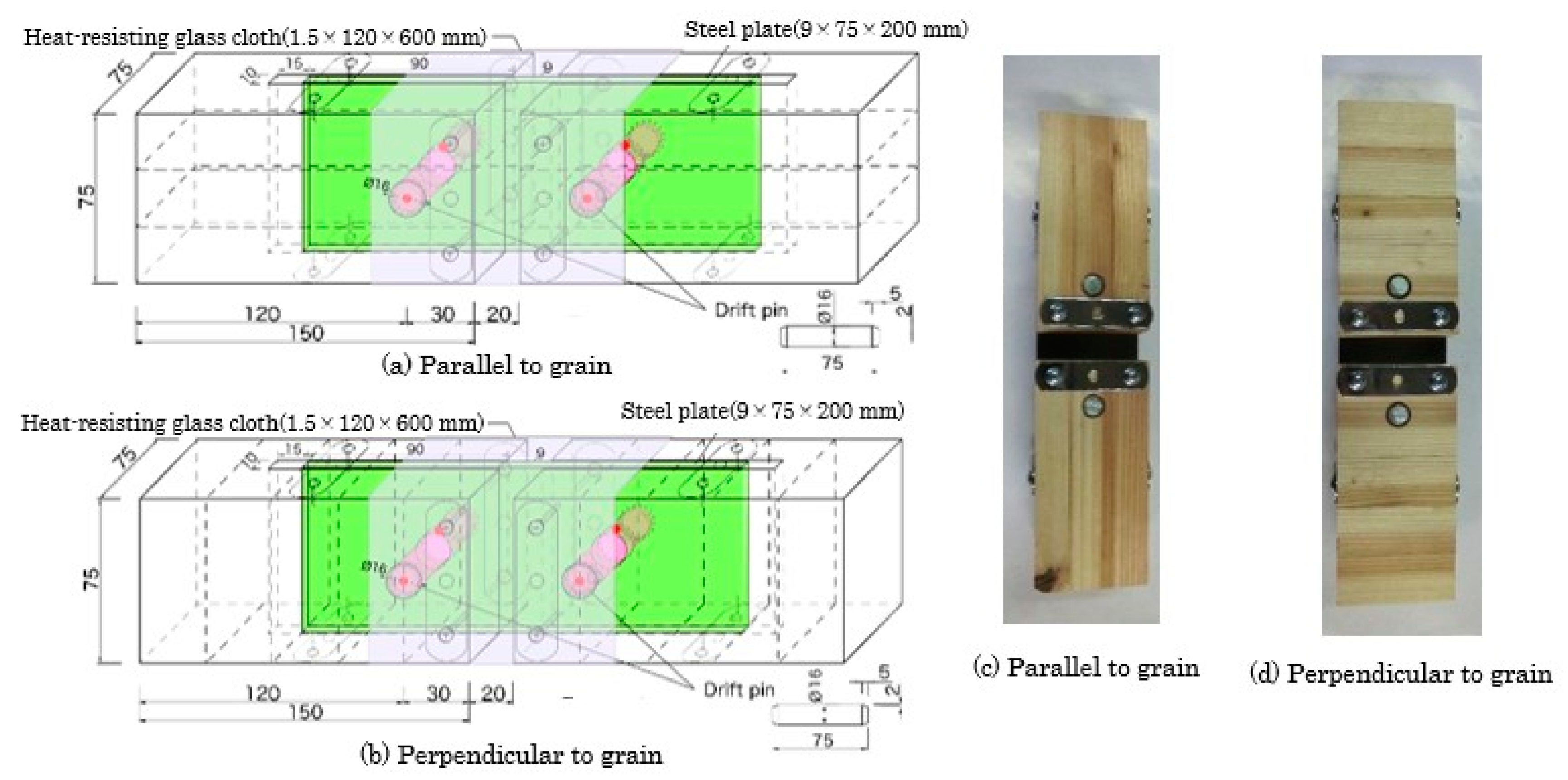
2.2.1. Overview of Embedment Tests
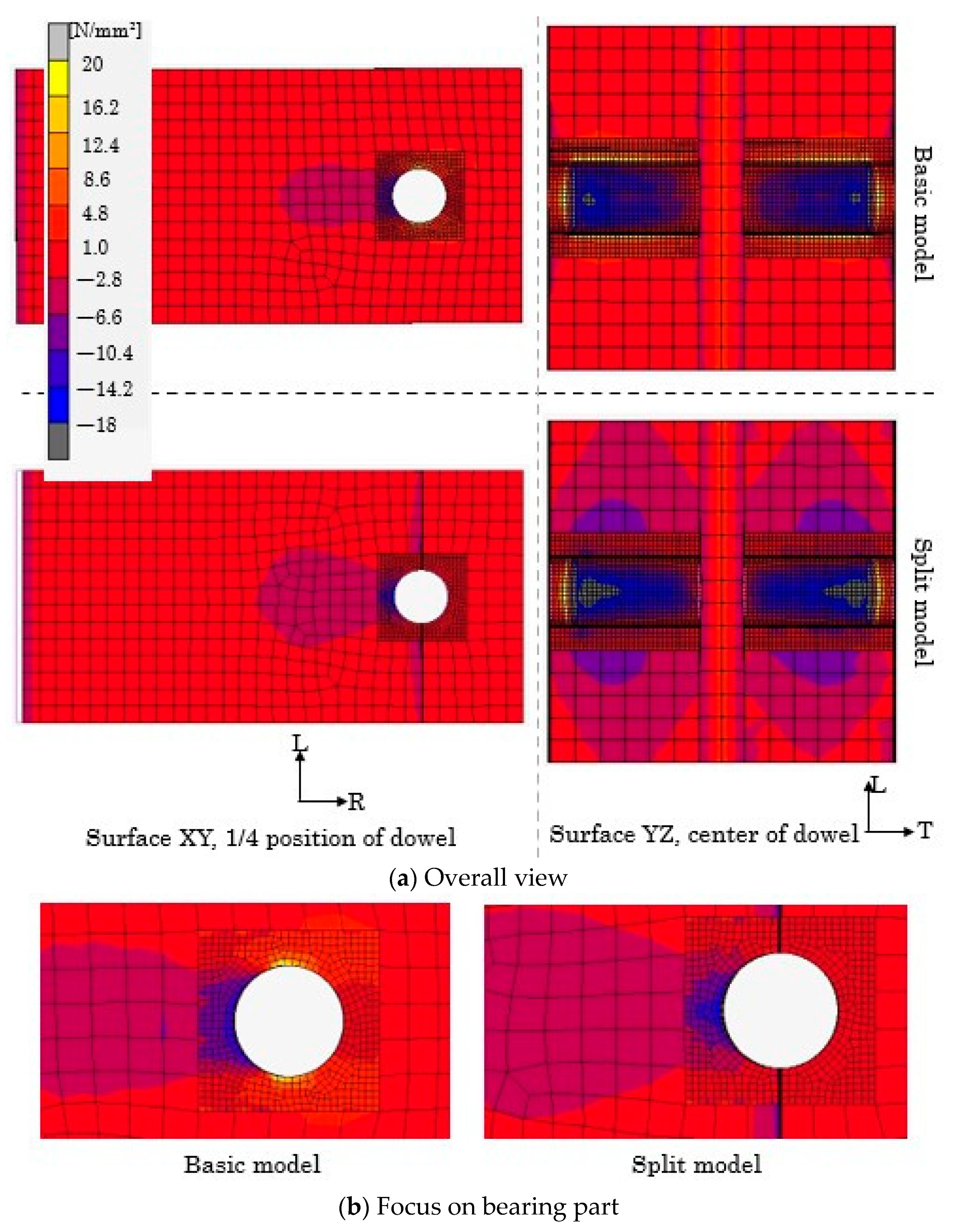
2.2.2. Finite Element Modeling
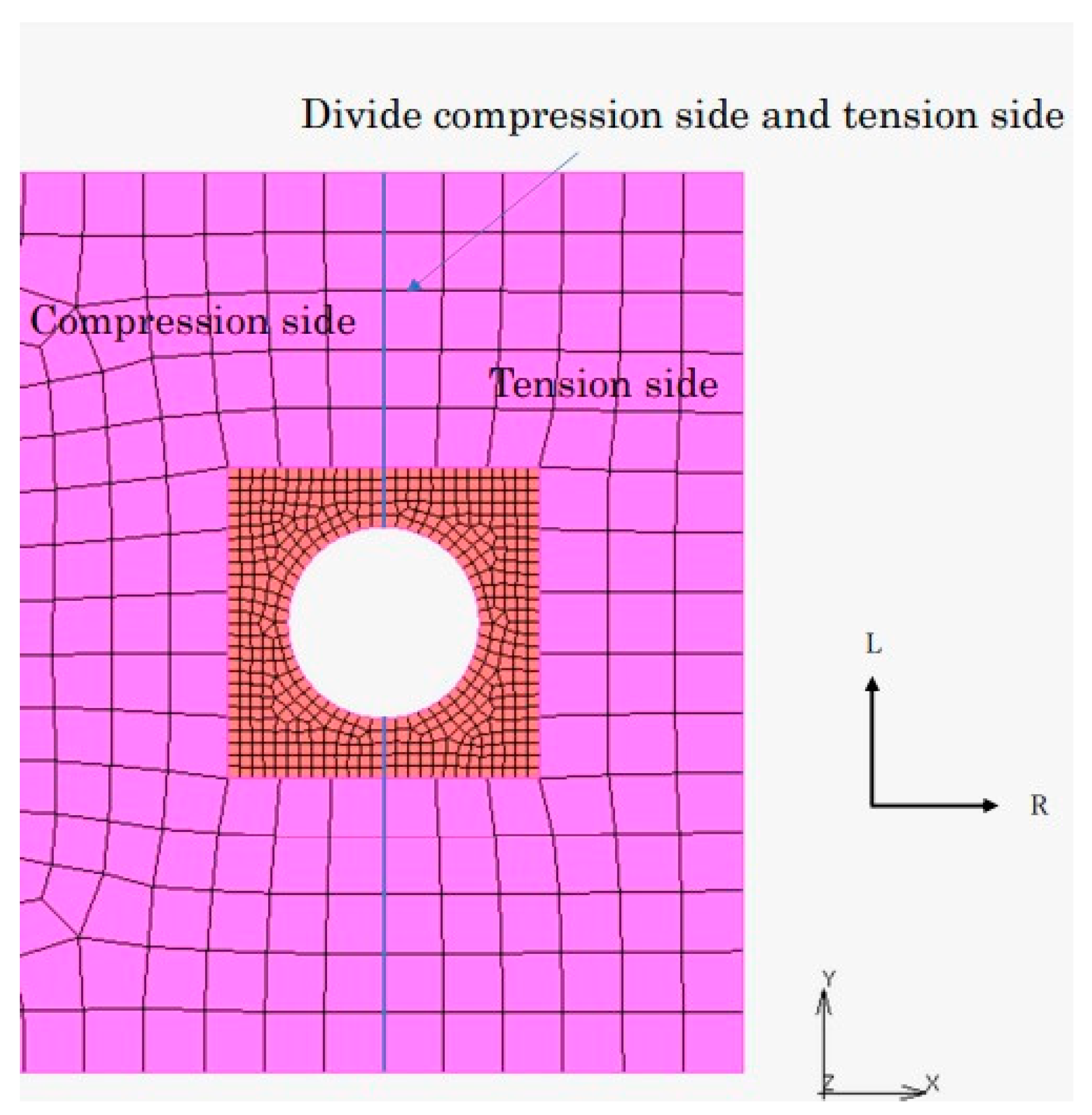
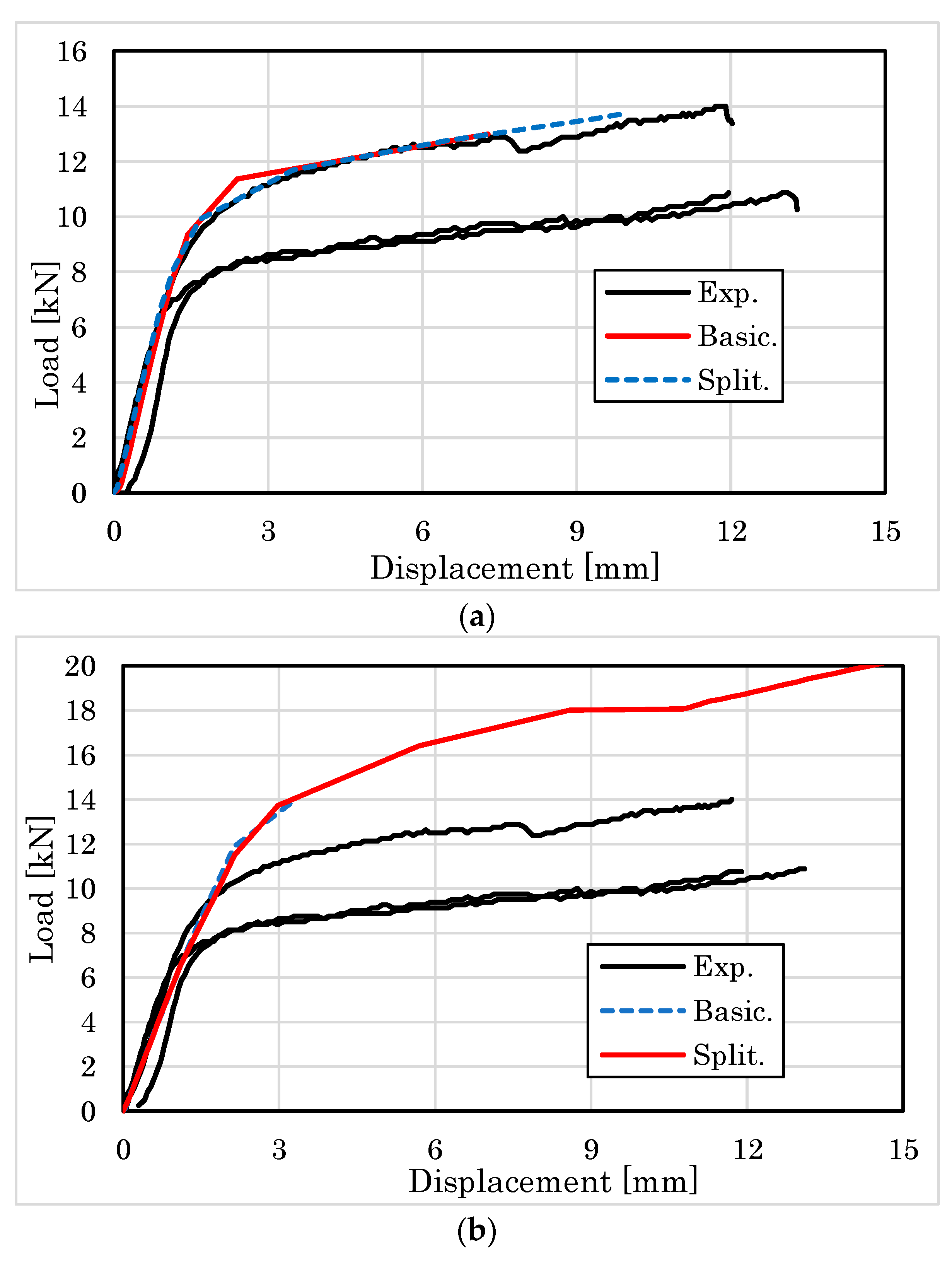
Basic Model (for Specimens Loaded Perpendicular and Parallel to the Grain)
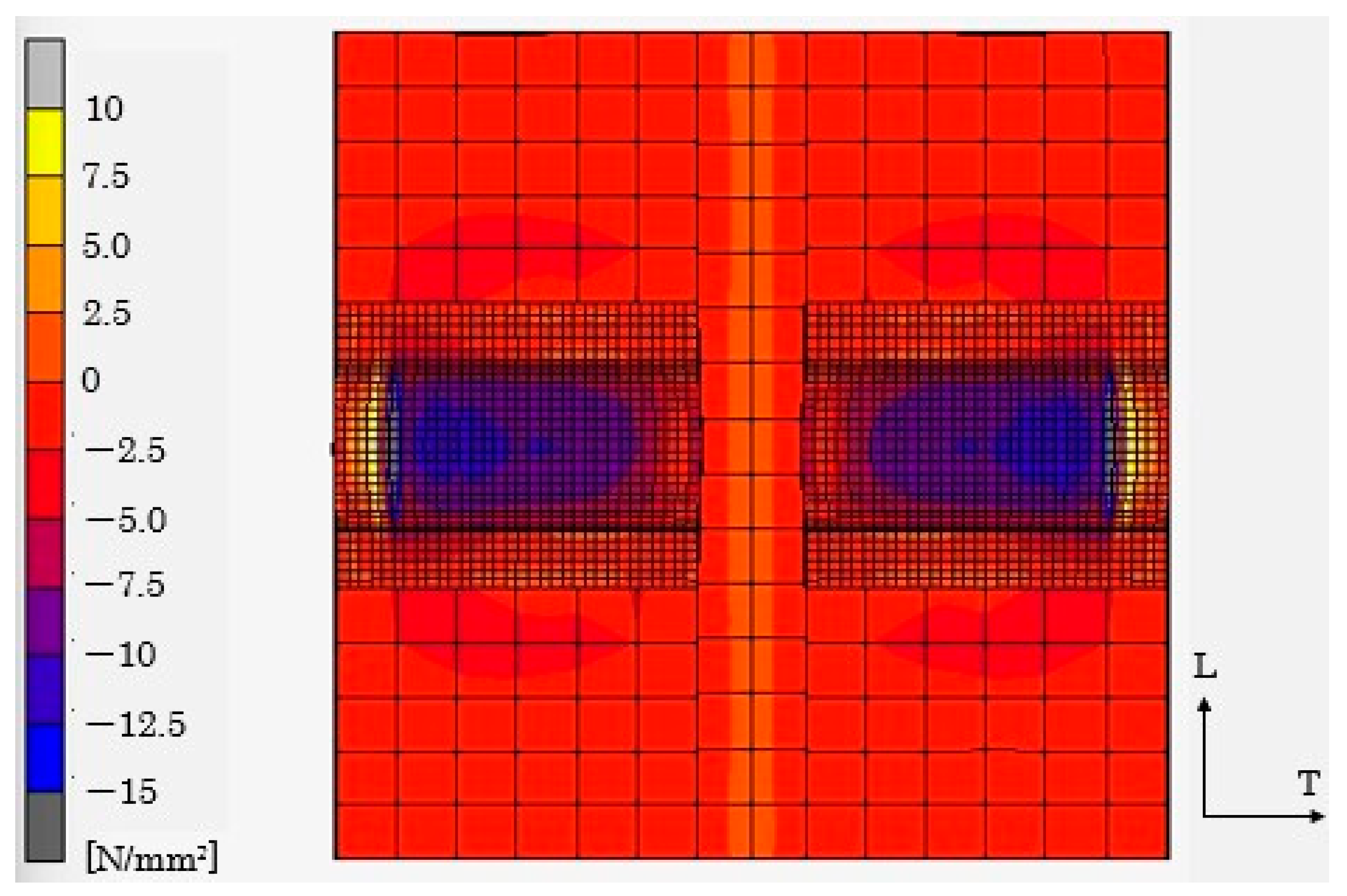
Split Model (for Specimens Loaded Perpendicular to the Grain)
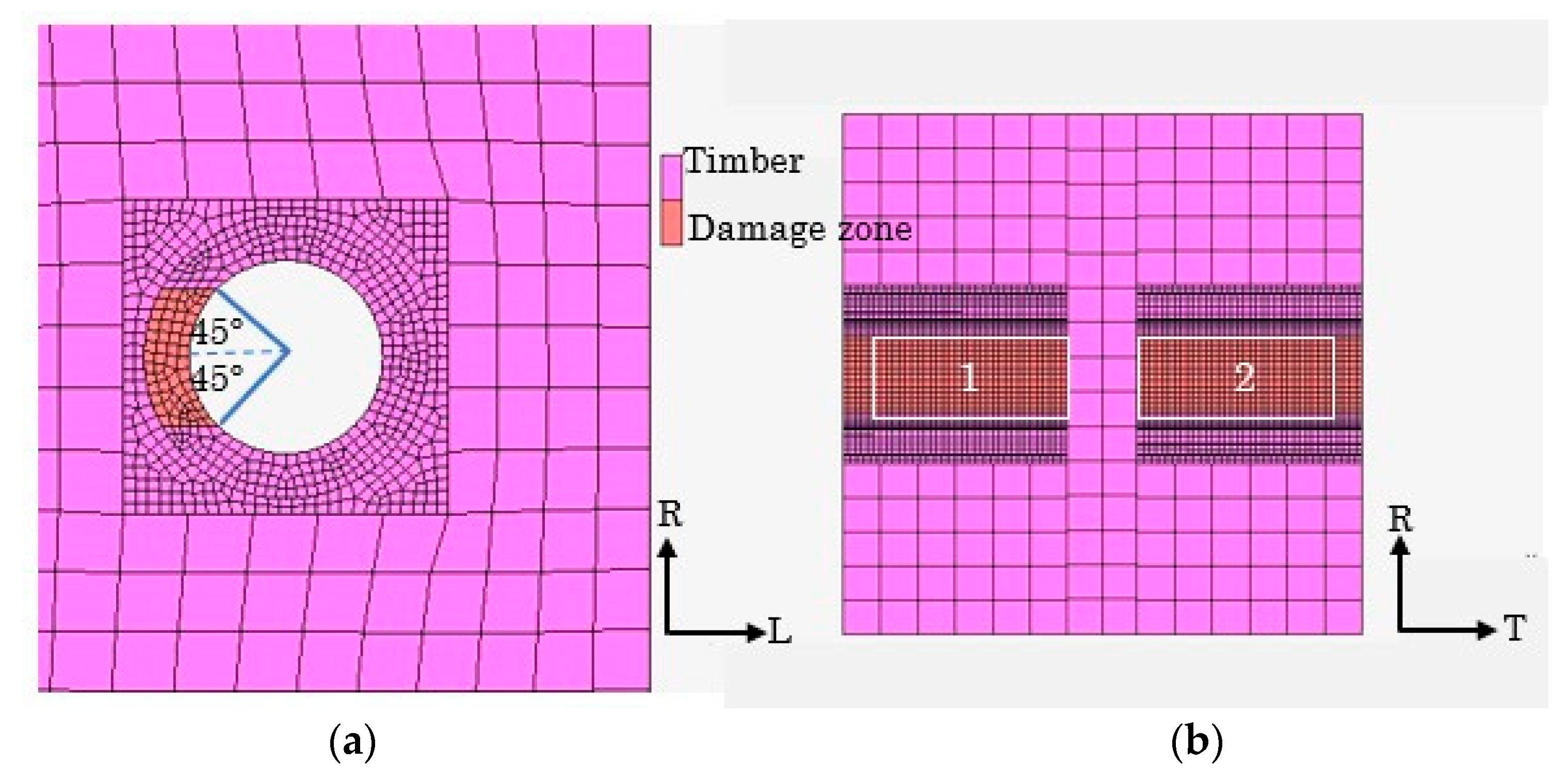
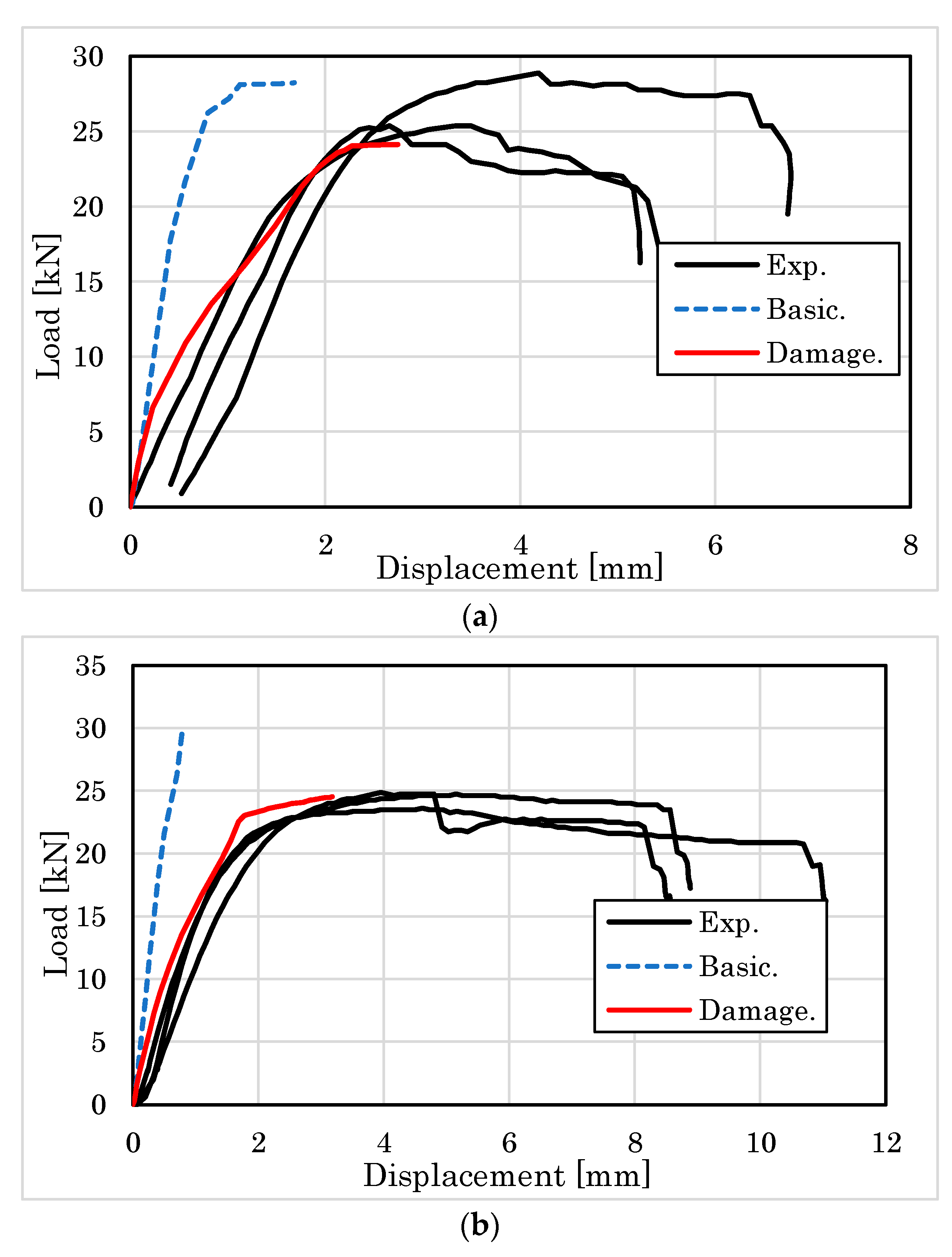
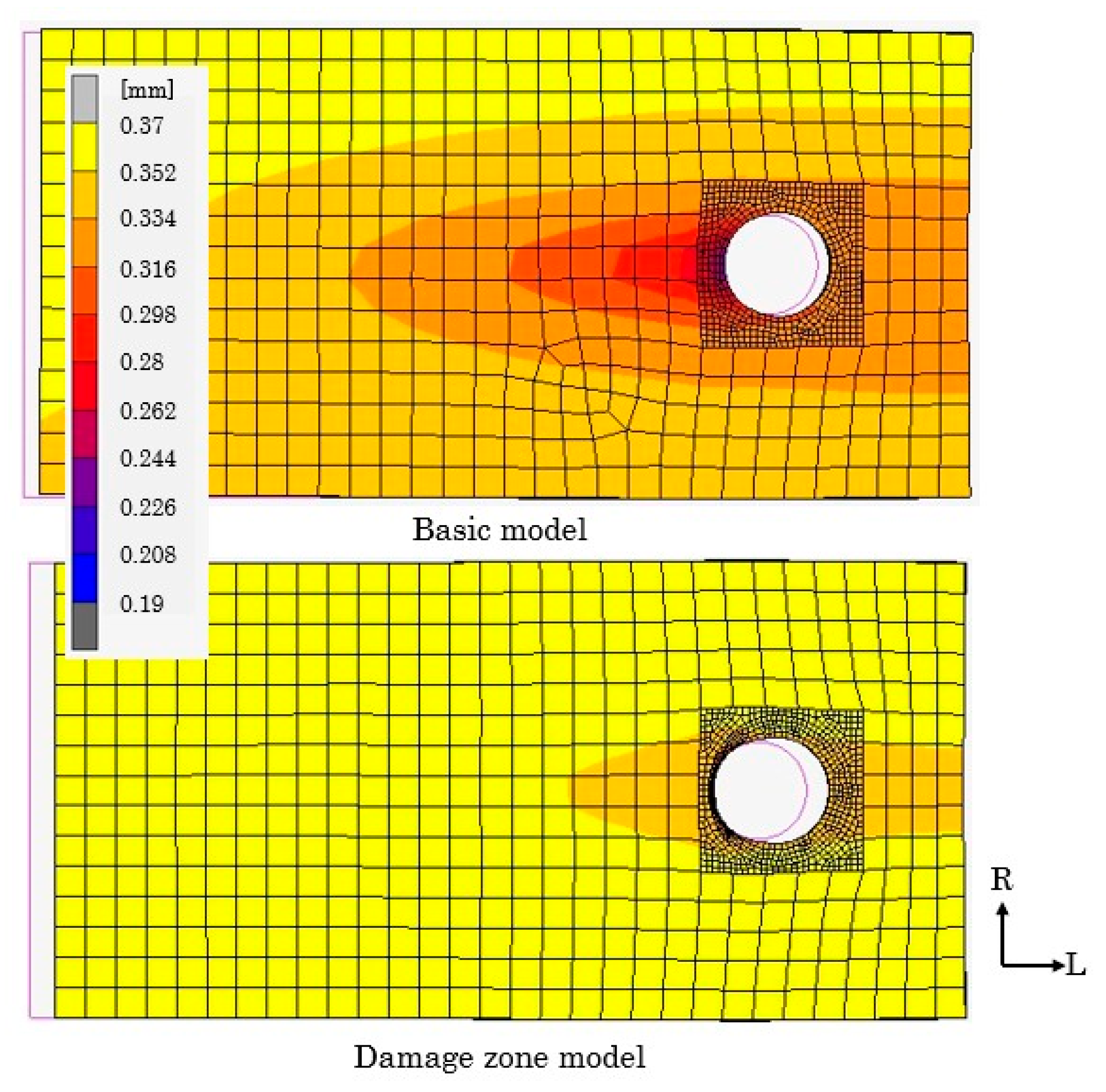
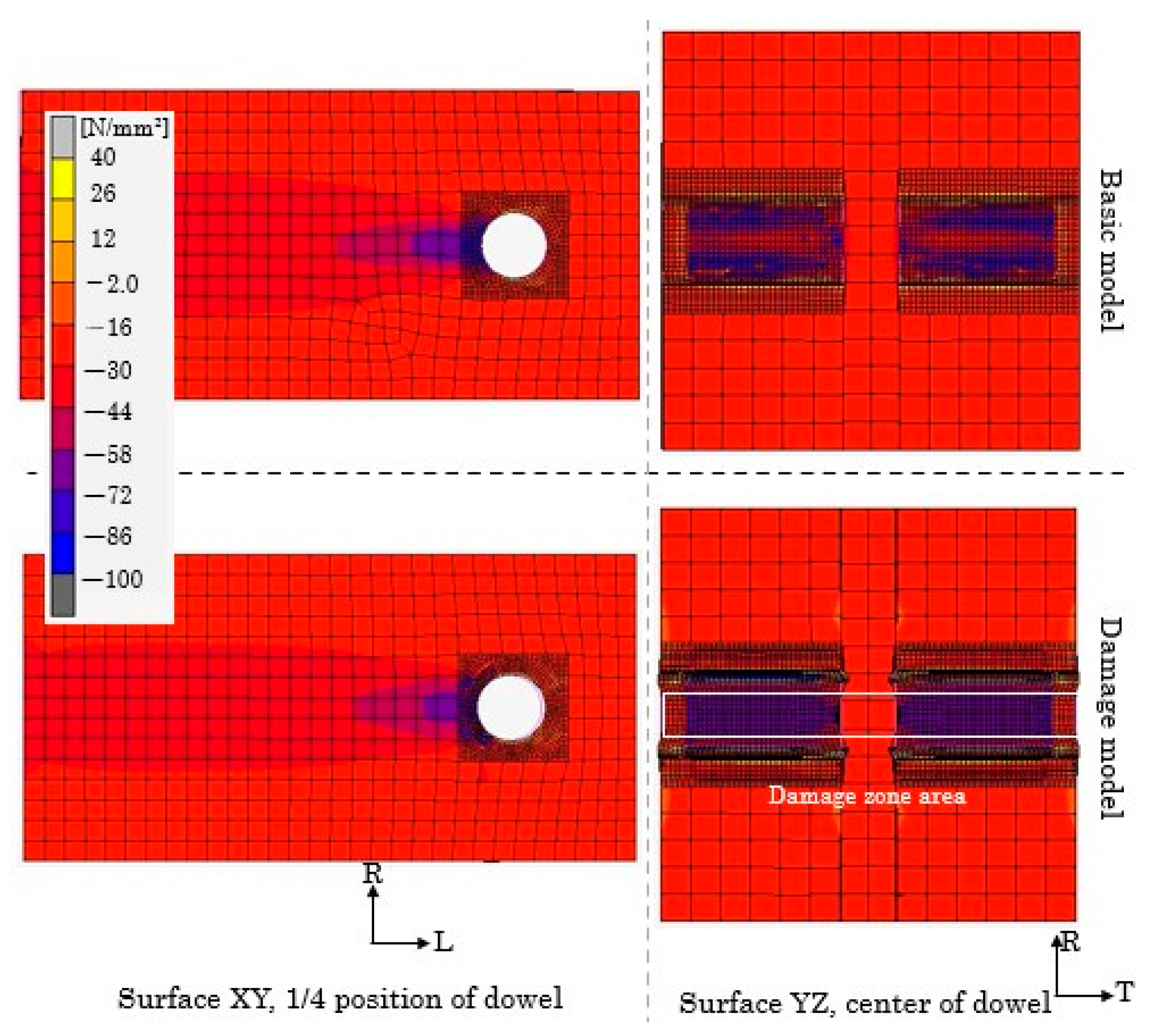
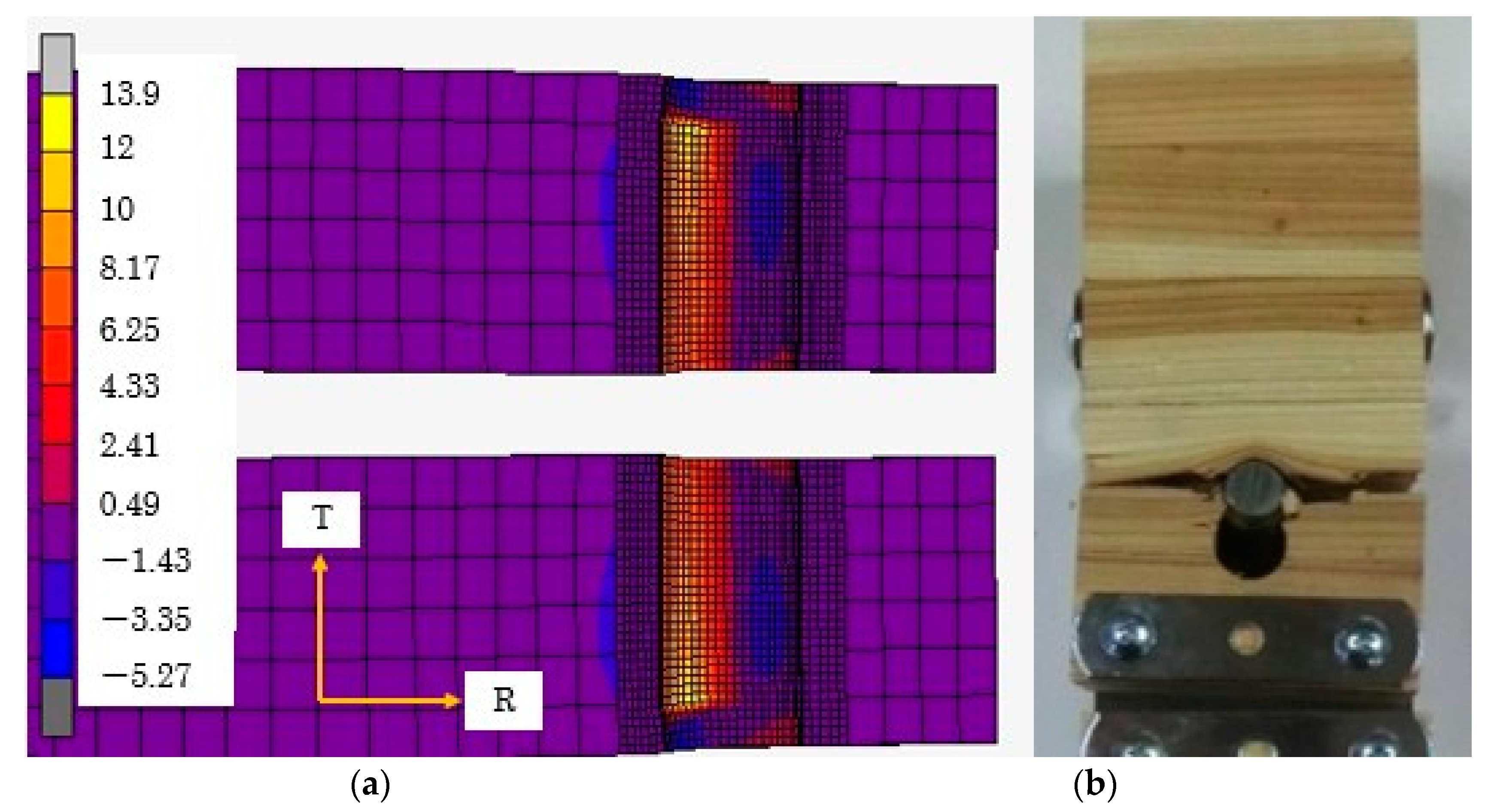
Damage Zone Model (for Specimens Loaded Parallel to the Grain)
- x: length of the damage zone;
- A’: horizontal projected area of the contacted area;
- k: coefficient according to the processing method;
- xs: length of the damage zone of the reference specimen.
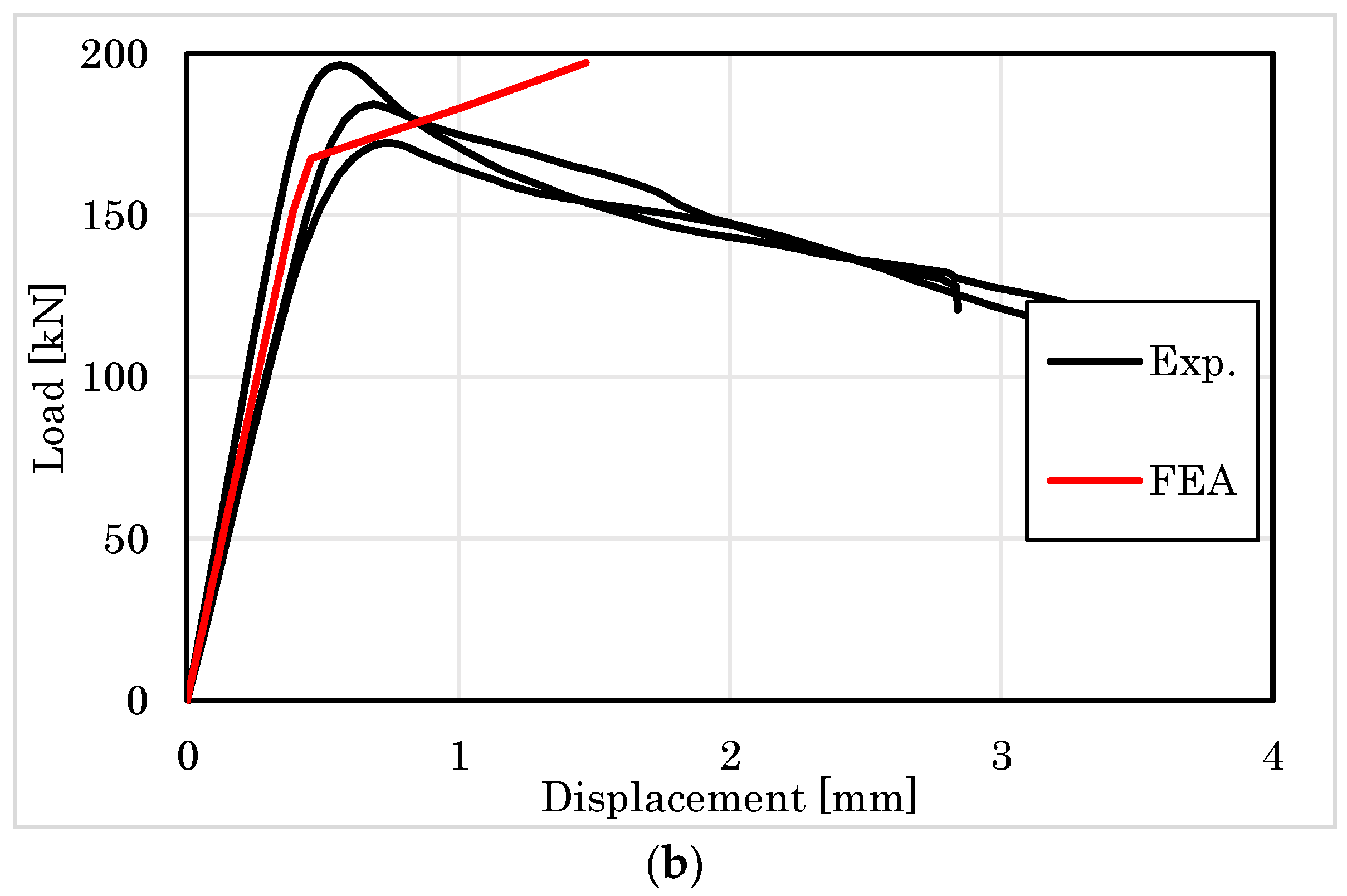
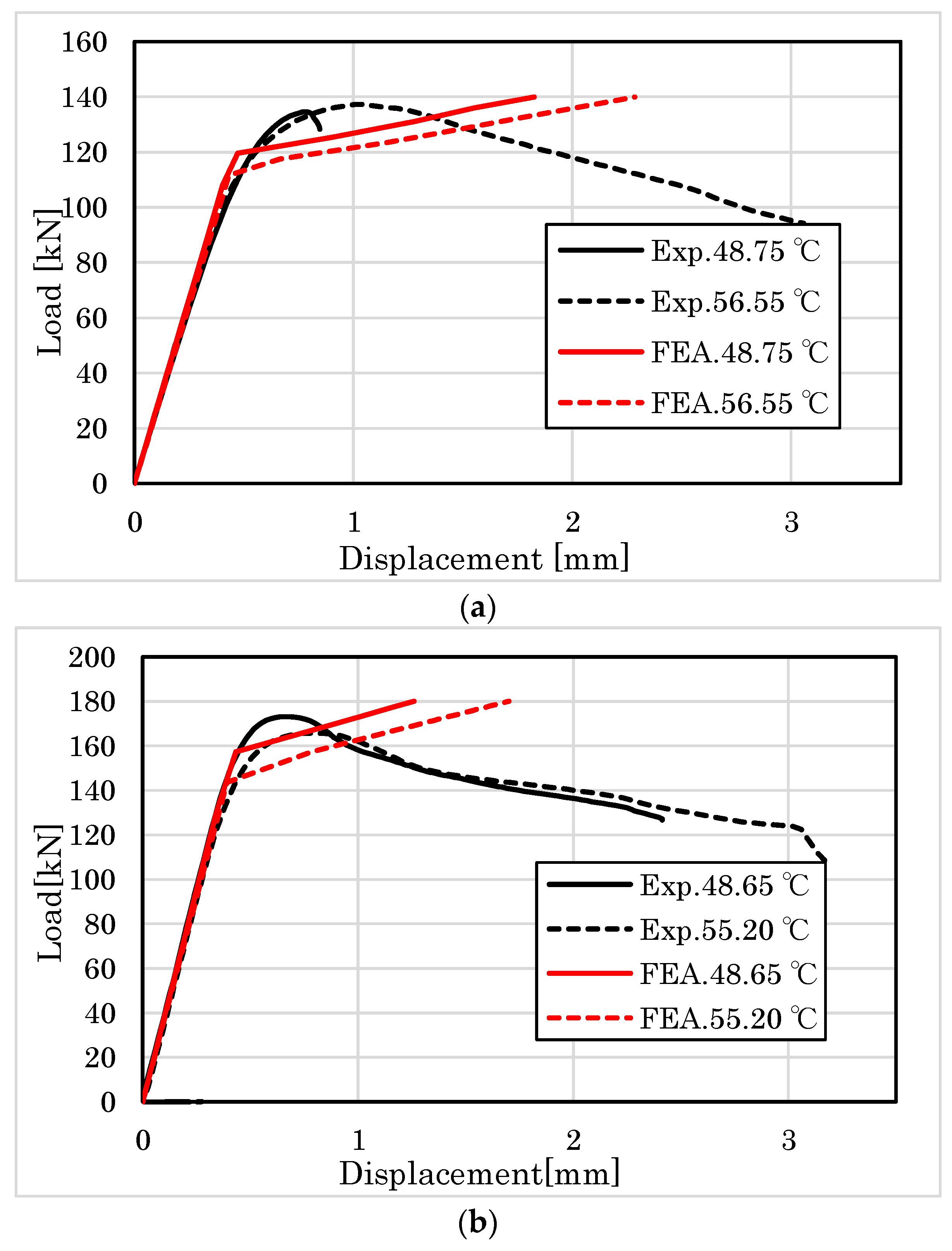
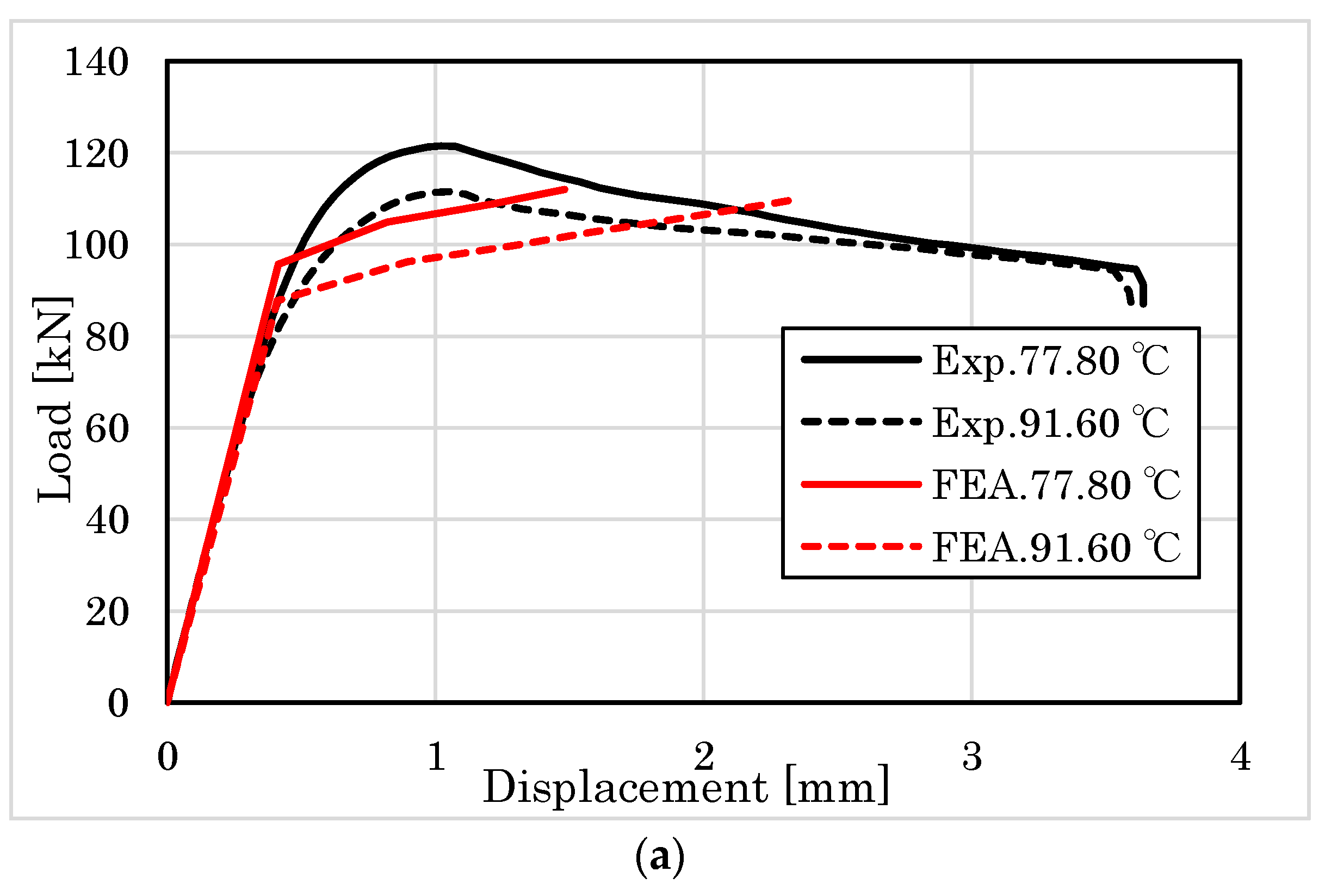
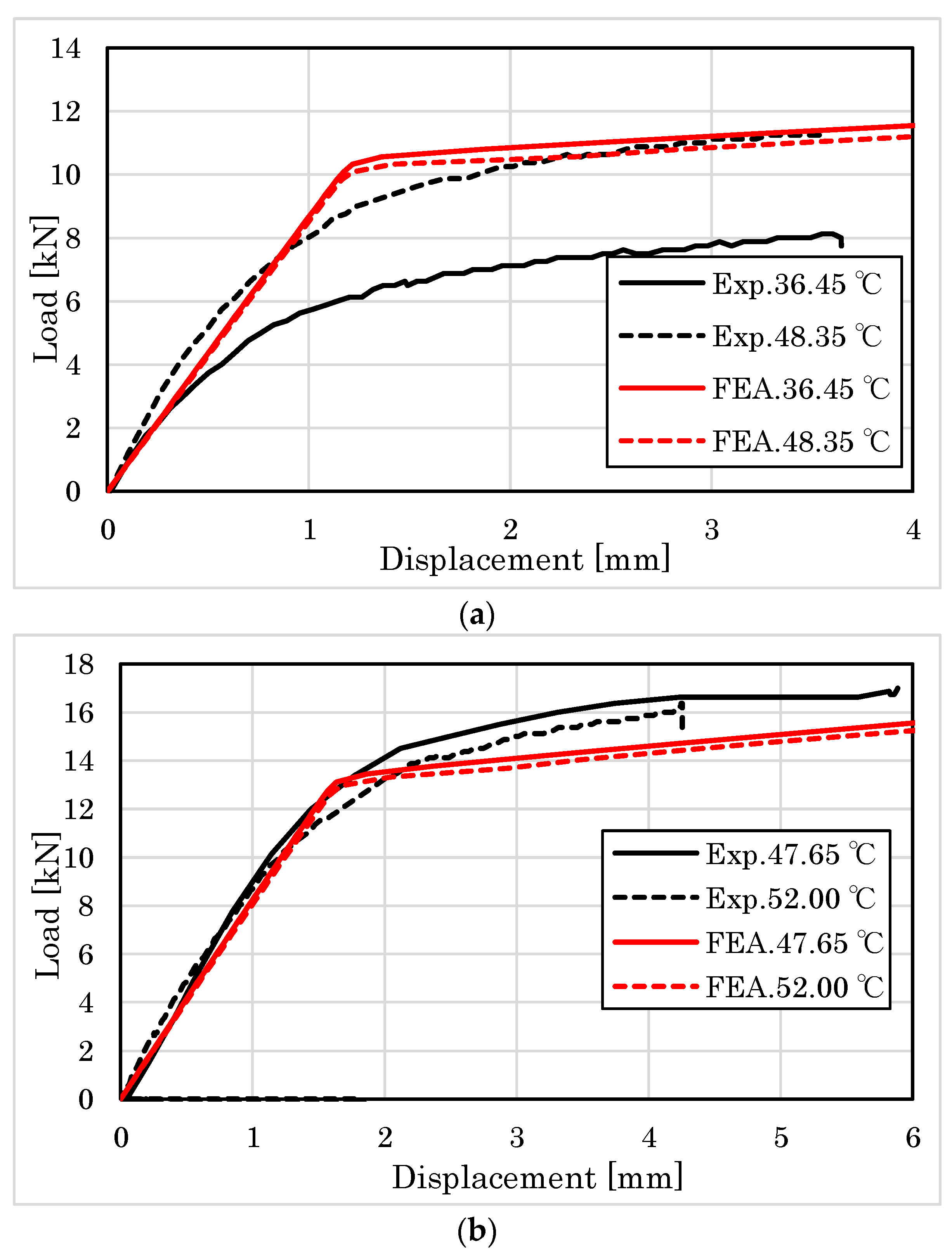
3. Results
3.1. Compression Results
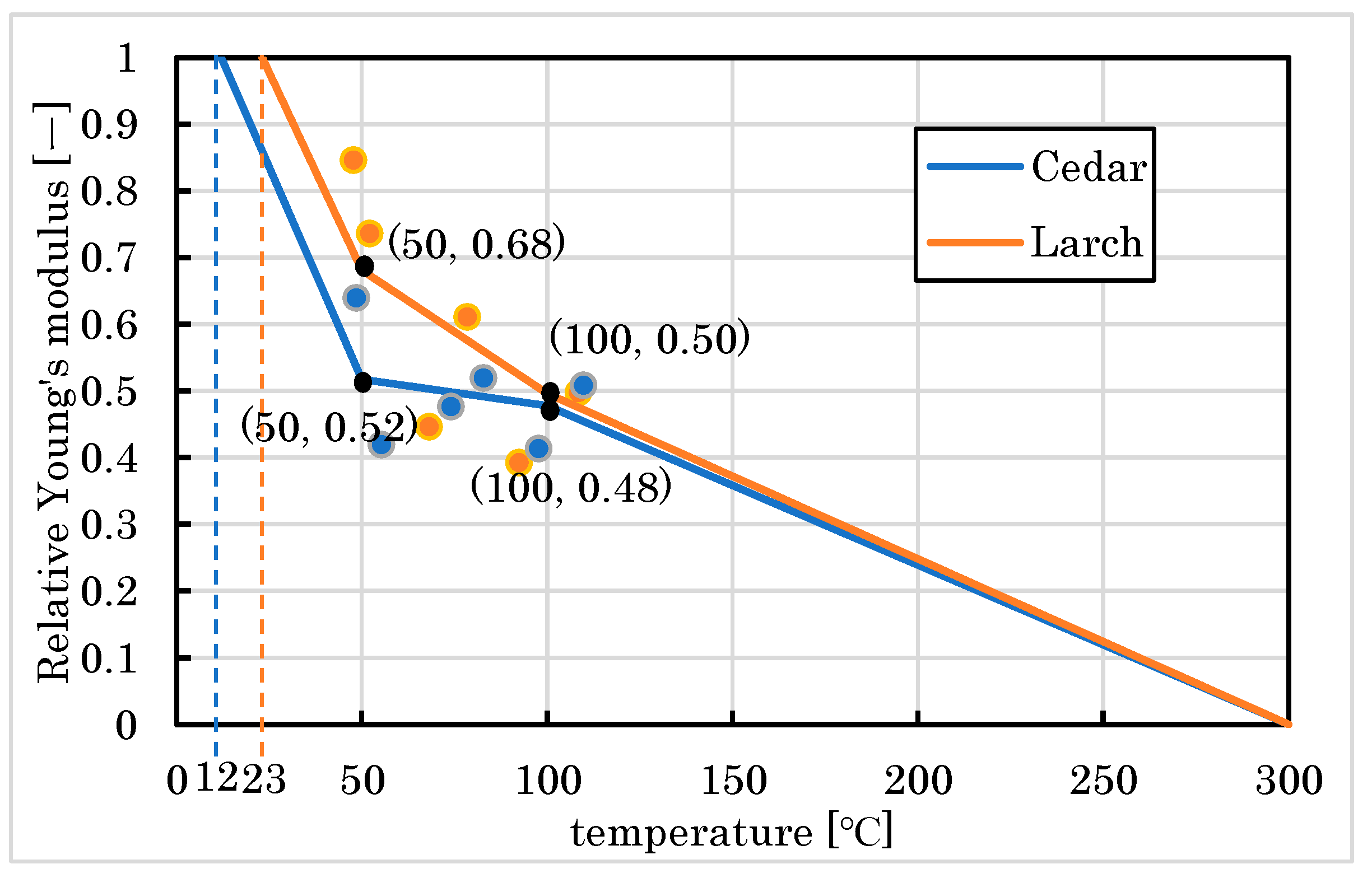
3.2. Embedment Results
4. Discussion
4.1. Compression Behavior
4.2. Embedment Behavior
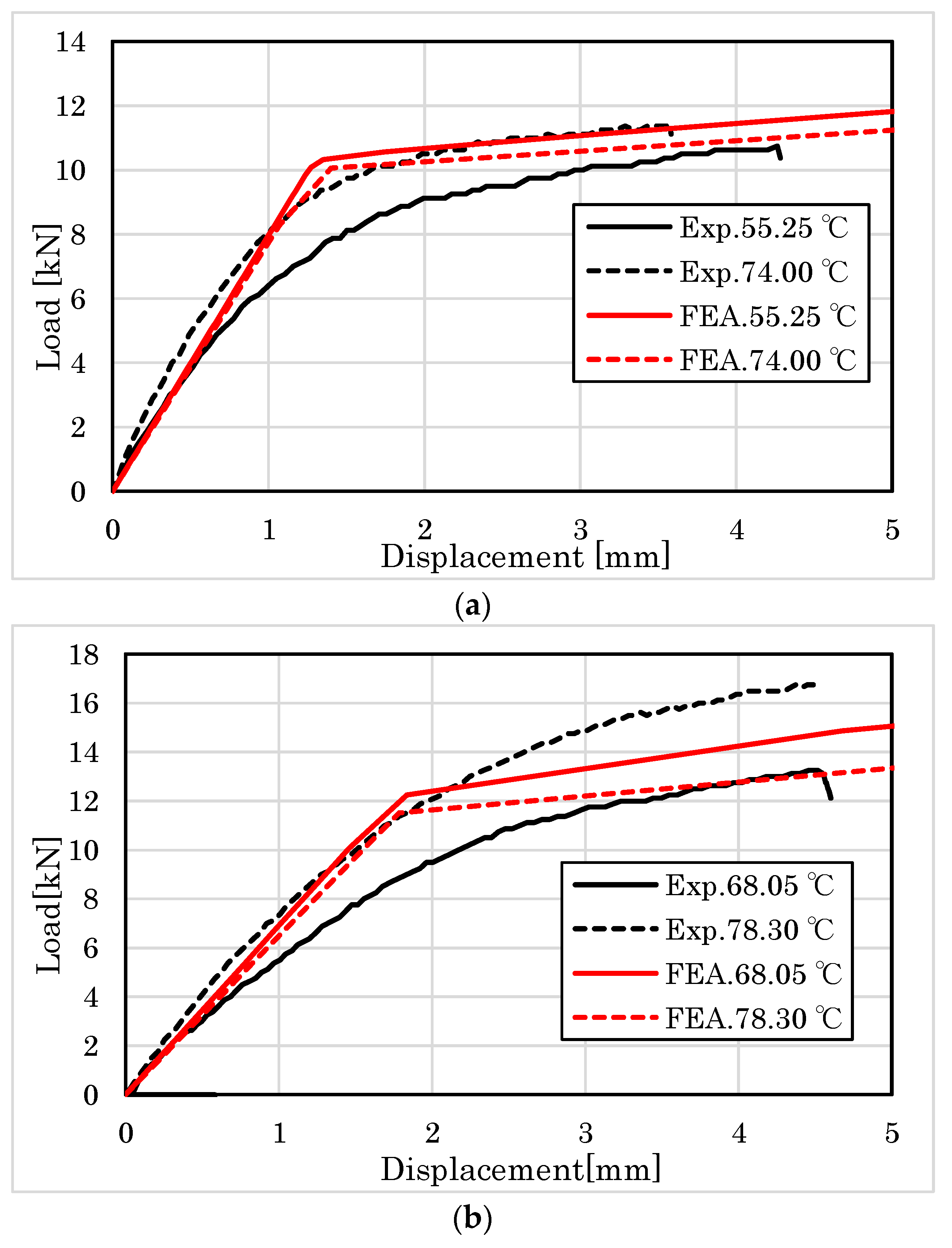
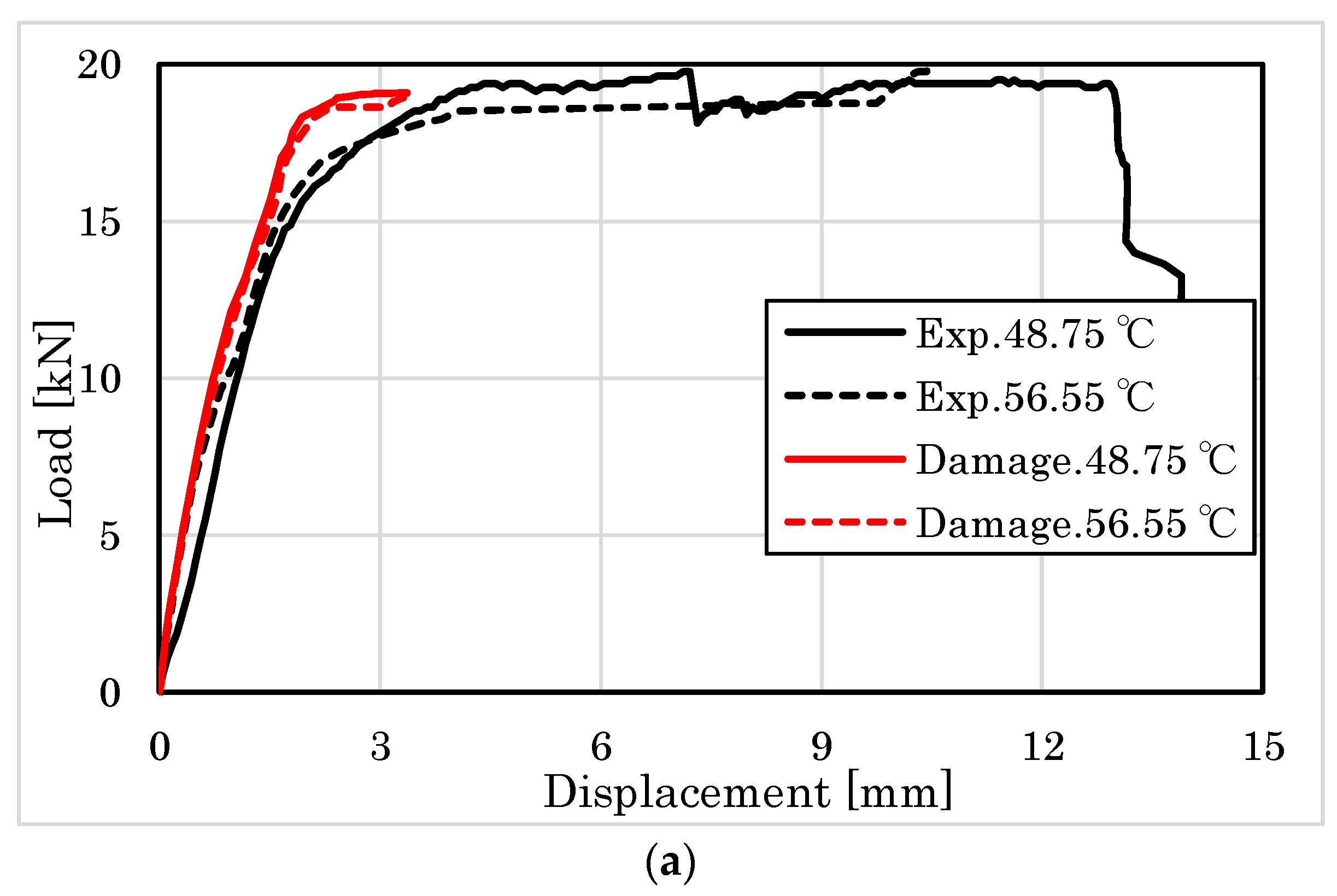
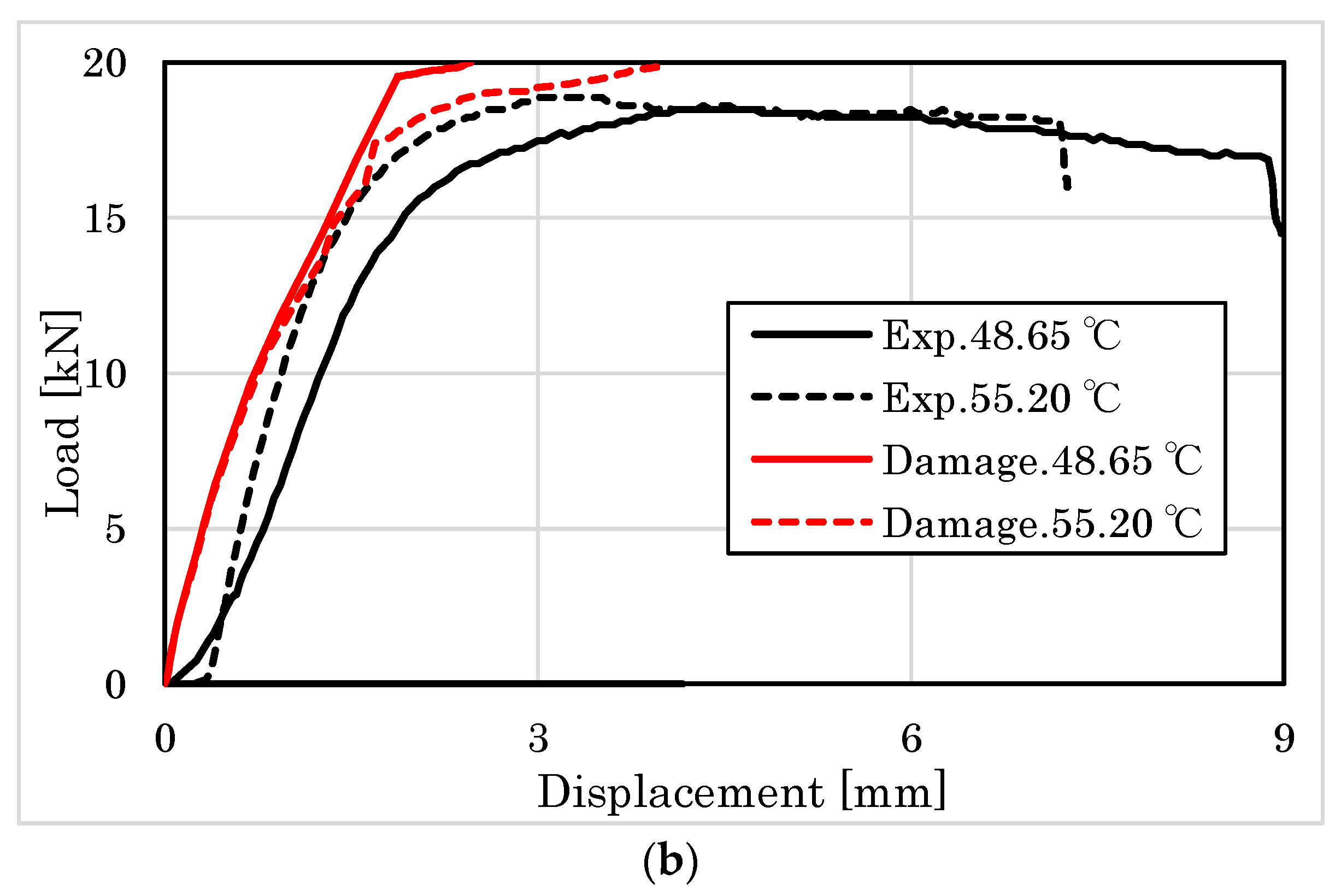
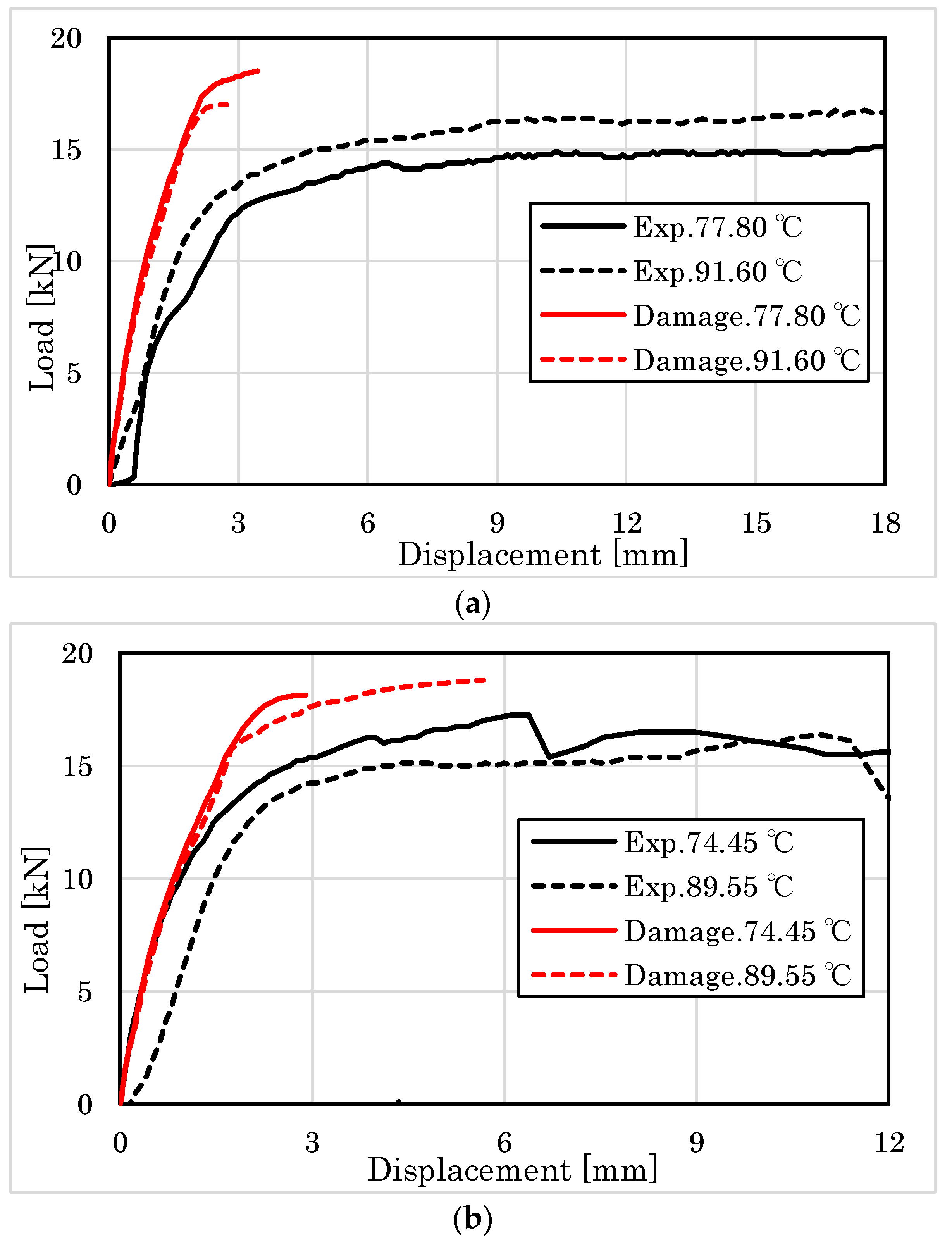
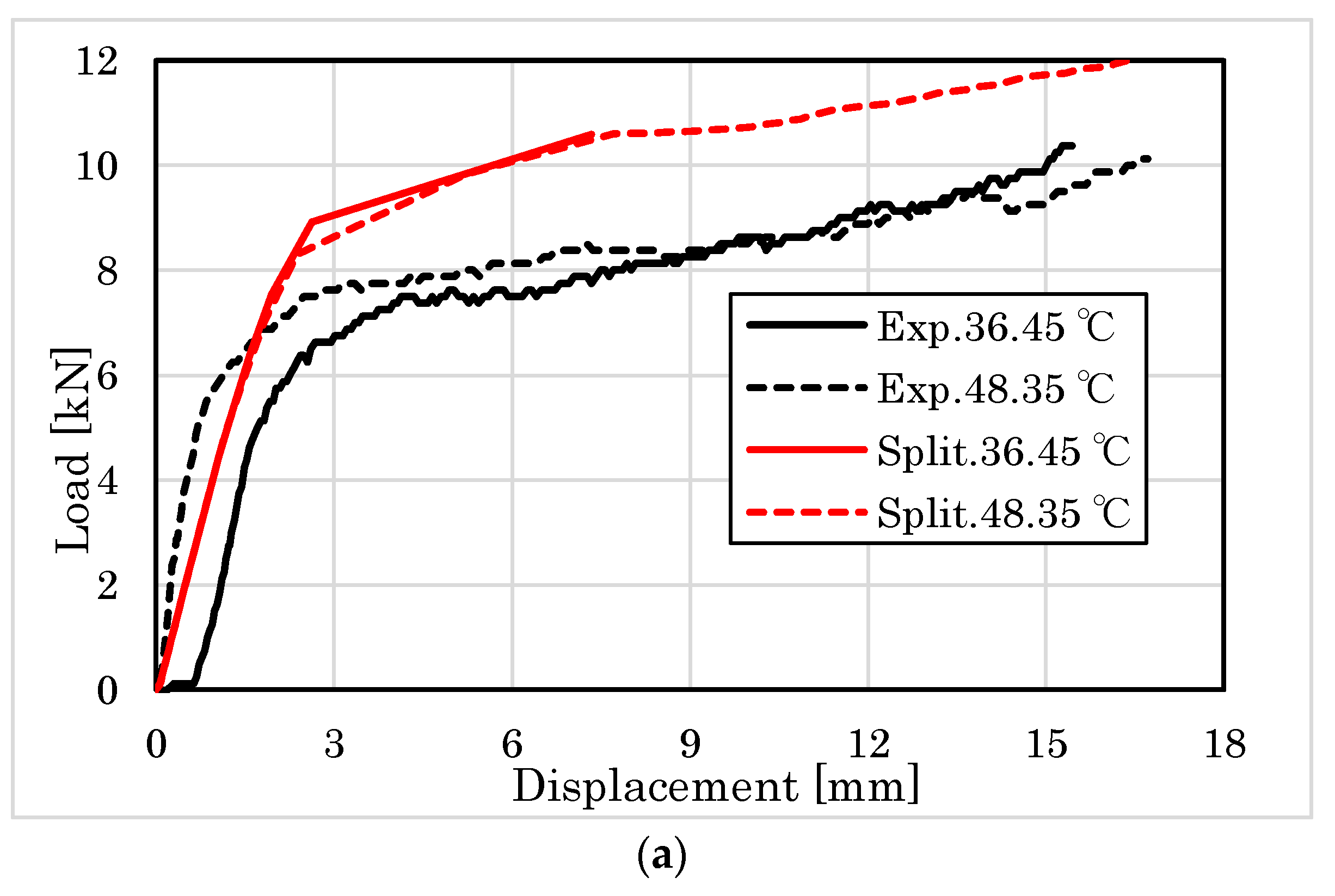
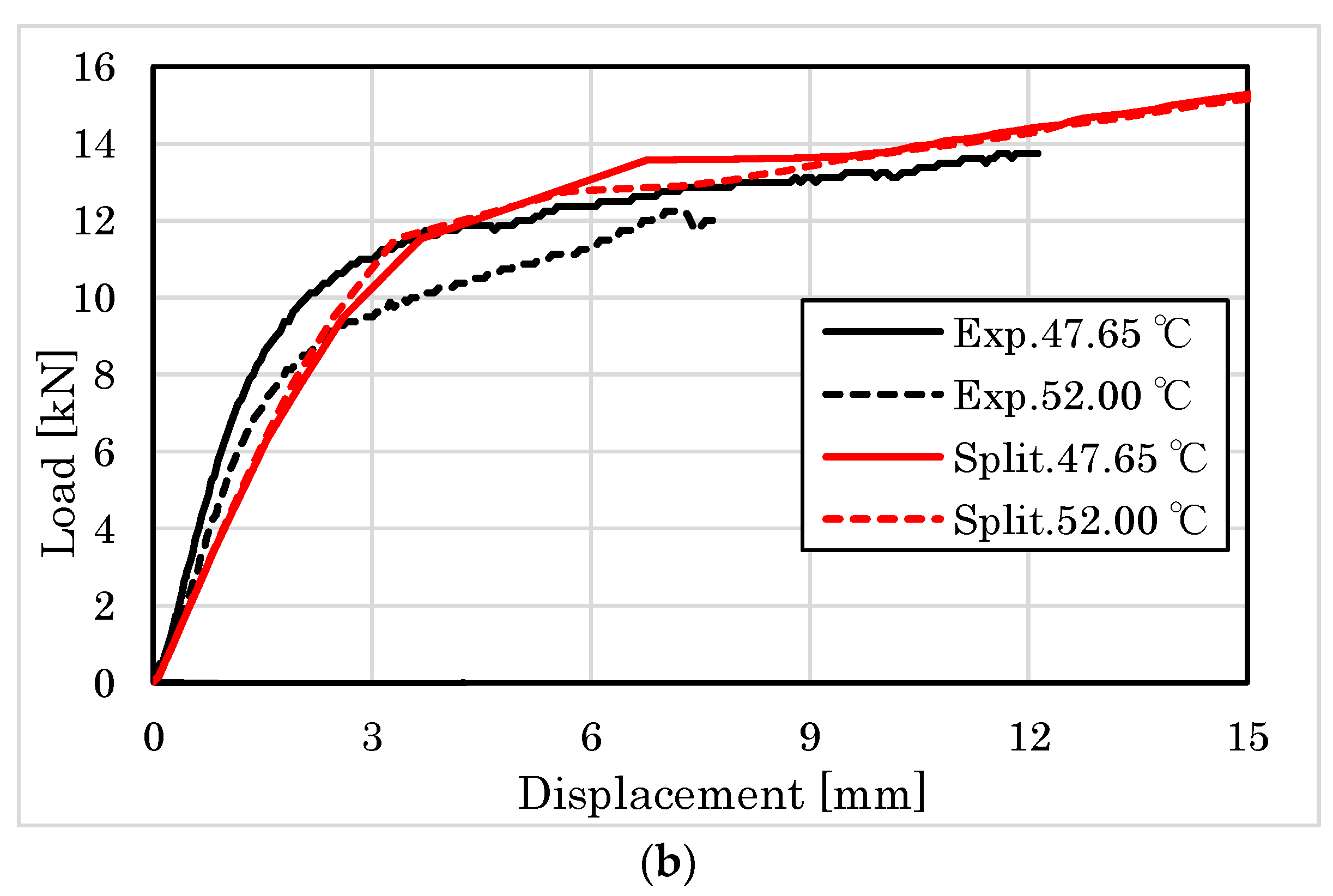
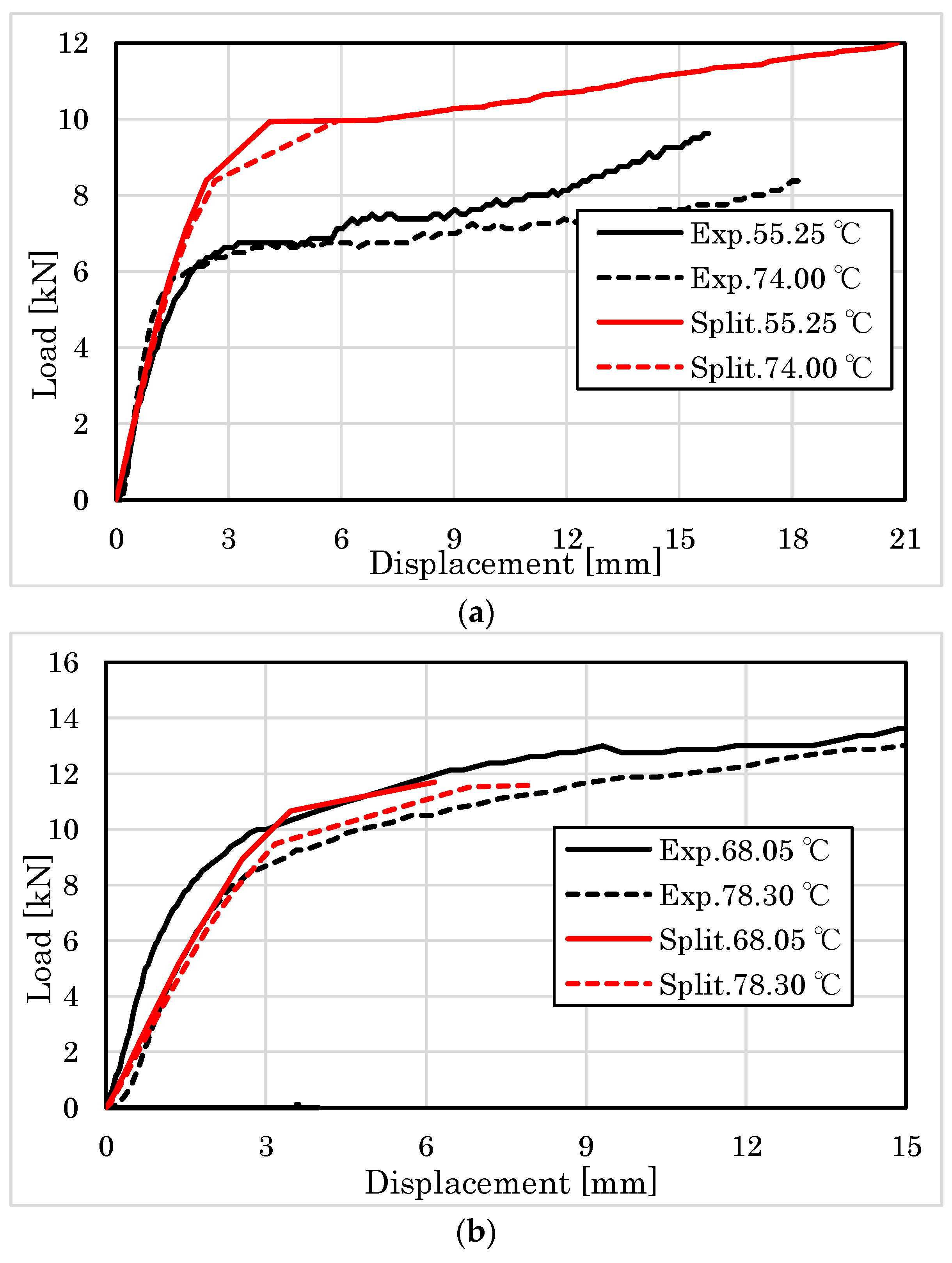
4.2.1. Embedment Behavior of Parallel to the Grain
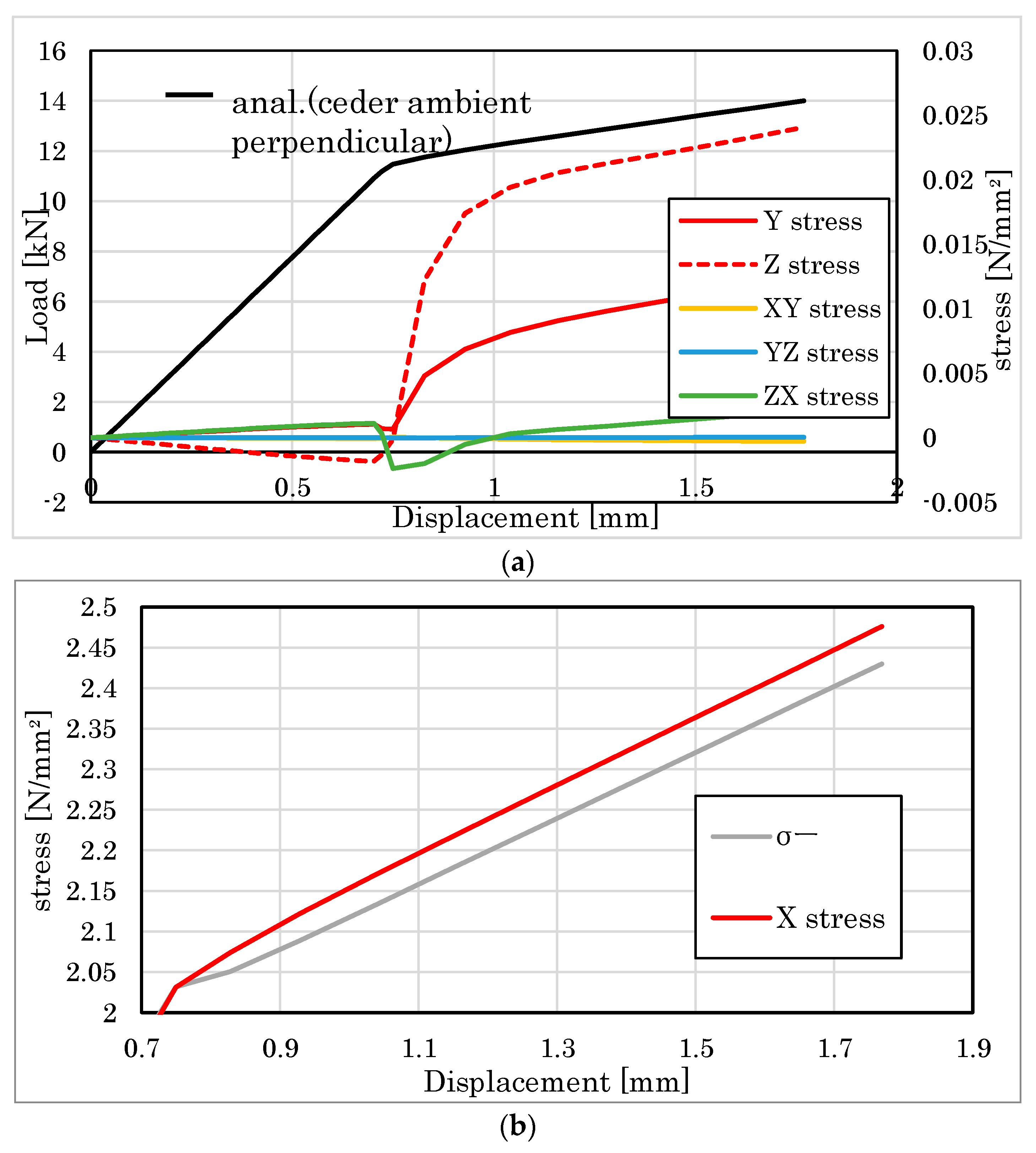
4.2.2. Embedment Behavior Perpendicular to the Grain
5. Conclusions
5.1. FE Analysis of Compression Tests
5.2. FE Analysis of Embedment Tests
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, C.; Guo, H.; Jung, K.; Harris, R.; Chang, W. Using self-tapping screw to reinforce dowel-type connection in a timber portal frame. Eng. Struct. 2019, 178, 656–664. [Google Scholar] [CrossRef]
- Schneid, E.; de Moraes, P.D. Grain angle and temperature effect on embedding strength. Constr. Build Mater. 2017, 150, 442–449. [Google Scholar] [CrossRef]
- Yurrita, M.; Cabrero, J.M. New criteria for the determination of the parallel-to-grain embedment strength of wood. Constr. Build Mater. 2018, 173, 238–250. [Google Scholar] [CrossRef]
- Van Blokland, J.; Florisson, S.; Schweigler, M.; Ekevid, T.; Bader, T.K.; Adamopoulos, S. Embedment properties of thermally modified spruce timber with dowel-type fasteners. Constr. Build Mater. 2021, 313, 125517. [Google Scholar] [CrossRef]
- Totsuka, M.; Hayakawa, J.; Aoki, K.; Inayama, M. Evaluation of stiffness parallel to grain of wood based on strongest link model. J. Struct. Constr. Eng. 2022, 87, 770–779. [Google Scholar] [CrossRef]
- Johansen, K.W. Theory of timber connections. Int. Assoc. Bridge Struct. Eng. 1949, 9, 249–262. [Google Scholar]
- EN 1995-7-2 Eurocode5: Design of Timber Structures; European Union: Bruxelles, Belgium, 1995; p. 51.
- Kawarabayashi, F.; Kikuchi, T.; Yotumoto, N.; Totsuka, M.; Hirashima, T.; Nakayama, Y. Load-Bearing Fire Tests of Structural Glulam Timber Frame of Larch with Dowel Connections Part 1: Outlines of the tests and Results of Ambient tests. In Proceeding of Architectural Research Meetings; Kanto Chapter; Architectural Institute of Japan: Tokyo, Japan, 2022; p. 3. [Google Scholar]
- Oudjene, M.; Khelifa, M. Elasto-plastic constitutive law for wood behavior under compressive loadings. Constr. Build Mater. 2009, 23, 3359–3366. [Google Scholar] [CrossRef]
- Xu, B.H.; Bouchair, A.; Taazount, M.; Vega, E.J. Numerical and experimental analyses if multiple-dowel steel-to-timber joints in tension perpendicular to grain. Eng. Struct. 2009, 31, 2357–2367. [Google Scholar] [CrossRef]
- Audebert, M.; Dhima, D.; Bouchaïr, A.; Frangi, A. Review of experimental data for timber connections with dowel-type fasteners under standard fire exposure. Fire Safe. J. 2019, 107, 217–234. [Google Scholar] [CrossRef]
- Peng, L.; Hadjisophocleous, G.; Mehaffey, J.; Mohammad, M. Fire resistance performance of unprotected wood–wood–wood and wood–steel–wood connections: A literature review and new data correlations. Fire Saf. J. 2010, 45, 392–399. [Google Scholar] [CrossRef]
- Kawarabayashi, F.; Kikuchi, T.; Totsuka, M.; Hirashima, T. Embedding behaviors of a doweled connection in structural glulam timbers at high temperature. J. Struct. Constr. Eng. 2022, 87, 498–509. [Google Scholar] [CrossRef]
- Kikuchi, T.; Yotsumoto, J.; Kawarabayashi, F.; Ishida, Y.; Totsuka, M.; Hirashima, T. Experimental study on fire performance of glulam timber frames (part 1)—Temperature and charring behavior of the beam-column connections exposed to standard fire heating for more than 1 hour. J. Struct. Constr. Eng. 2022. In press. [Google Scholar] [CrossRef]
- Cachim, P.B.; Franssen, J.M. Numerical modelling of timber connections under fire loading using a component model. Fire Saf. J. 2009, 44, 840–853. [Google Scholar] [CrossRef]
- Nakayama, Y.; Kikuchi, T.; Totsuka, M.; Hirashima, T. Numerical model for non-linear M-θ relationships of dowel-type timber connections exposed to fire. In Proceedings of the 12th International Conference on Structures in Fire, Hong Kong, China, 30 November–2 December 2022; pp. 1064–1075. [Google Scholar]
- Audebert, M.; Dhima, D.; Taazount, M.; Bouchaïr, A. Experimental and numerical analysis of timber connections in tension perpendicular to grain in fire. Fire Saf. J. 2014, 63, 125–137. [Google Scholar] [CrossRef]
- Khelifa, M.; Khennane, A.; Ganaoui, M.E.I.; Rogaume, Y. Analysis of the behavior of multiple dowel timber connections in fire. Fire Saf. J. 2014, 68, 119–128. [Google Scholar] [CrossRef]
- Sawata, K.; Yasumura, M. Determination of embedding strength of wood for dowel-type fasteners. J. Wood Sci. 2002, 48, 138–146. [Google Scholar] [CrossRef]
- Inayama, M. Mokuzainomerikomirirontosonoouyou-jinseinikitaishitamokushituramensetugoubunotaishinnsekkeihounikannsurukenkyuu. Ph.D. Thesis, The University of Tokyo, Tokyo, Japan, 1991. [Google Scholar]
- MSC.MARC User’s Manual. Vol. A: Theory and User Information; MSC Software Corporation: Stockholm, Sweden, 2017.
- Wood Industry Handbook–Part 2 Wood Properties 174, 3rd ed.; Maruzen Co.: Ichikawa, Japan, 1982.
- Hirosue, M.; Nakagome, T.; Fujioka, T.; Kanbe, W.; Kamakura, M. An analytical study for mode 1 fracture toughness of woods with FEM considered orthotropic anisotropy Part 3 analysis result. In Summary of Technical Papers of the Annual Meeting; Architectural Institute of Japan: Tokyo, Japan, 2011; pp. 217–218. [Google Scholar]
- Shibuya, T.; Takino, A.; Miyamoto, Y. Study on wood material model including orthotropy in 3D finite element analysis. In Summary of Academic Papers DVD; Architectural Institute of Japan: Tokyo, Japan, 2012; pp. 679–680. [Google Scholar]
- Japanese Industrial Standard G 3101; Rolled Steels for General Structure. Japanese Standards Association: Tokyo, Japan, 2020.
- Zink, A.G.; Davidson, R.W.; Hanna, R.B. Strain measurement in wood using a digital image correlation technique. Wood Fiber Sci. 1995, 27, 346–359. [Google Scholar]
- Xavier, J.; de Jesus, A.M.P.; Morais, J.J.L.; Pinto, J.M.T. Stereovision measurements on evaluating the modulus of elasticity of wood by compression tests parallel to the grain. Constr. Build Mater. 2011, 26, 207–215. [Google Scholar] [CrossRef]
- Martin, B.; Jan, T.; Václav, S.; Jaromír, M.; Peter, R. Standard and non-standard deformation behavior of European beech and Norway spruce during compression. Holzforschung 2015, 69, 1107–1116. [Google Scholar] [CrossRef]
- Totsuka, M.; Jockwer, R.; Aoki, K.; Inayama, M. Experimental study on partial compression parallel to grain of solid timber. J. Wood. Sci. 2021, 67, 39. [Google Scholar] [CrossRef]
- Totsuka, M.; Jockwer, R.; Kawahara, H.; Aoki, K.; Inayama, M. Experimental study of compressive properties parallel to grain of glulam. J. Wood Sci. 2022, 68, 33. [Google Scholar] [CrossRef]





| Load Direction | Thermal Condition | Total | |||||
|---|---|---|---|---|---|---|---|
| Parallel to grain and perpendicular to grain | Ambient Temp. | 3 | 3 | ||||
| Constant temperatures (°C) | Heating time (hour) | ||||||
| 0.5 | 1 | 1.5 | 2 | 4 | |||
| 60 | - | 1 | - | 1 | 1 | 3 | |
| 100 | - | 1 | - | 1 | 1 | 3 | |
| 150 | - | 1 | - | 1 | 1 | 3 | |
| 200 | - | 1 | - | 1 | - | 2 | |
| (a) Cedar | |||||
| Cedar | Constant Temperature (°C) | Heating Time (hour) | Temperature Measurement | ||
| ① | ② | Average | |||
| Parallel to grain | 60 | 1 | 44.1 | 53.4 | 48.75 |
| 2 | 54.8 | 58.3 | 56.55 | ||
| 100 | 1 | 69.7 | 85.9 | 77.8 | |
| 2 | 88.2 | 95 | 91.6 | ||
| 150 | 1 | 97.6 | 122.4 | 110 | |
| 2 | 112.3 | 136.1 | 124.2 | ||
| 200 | 1 | 105.3 | 163.8 | 134.55 | |
| 2 | 151.2 | 193.2 | 172.2 | ||
| Perpendicular to grain | 60 | 1 | 32.1 | 40.8 | 36.45 |
| 2 | 46.3 | 50.4 | 48.35 | ||
| 100 | 1 | 45.4 | 65.1 | 55.25 | |
| 2 | 68.4 | 79.6 | 74 | ||
| 150 | 1 | 71.5 | 94 | 82.75 | |
| 2 | 94.6 | 124.7 | 109.65 | ||
| 200 | 1 | 80.3 | 114.8 | 97.55 | |
| 2 | 125.7 | 175.3 | 150.5 | ||
| (b) Larch | |||||
| Larch | Constant temperature (°C) | Heating time (hour) | Temperature Measurement | ||
| ① | ② | average | |||
| Parallel to grain | 60 | 1 | 45.5 | 51.8 | 48.65 |
| 2 | 53.9 | 56.5 | 55.2 | ||
| 100 | 1 | 67 | 81.9 | 74.45 | |
| 2 | 86 | 93.1 | 89.55 | ||
| 150 | 1 | 92.5 | 110.9 | 101.7 | |
| 2 | 110.1 | 123.5 | 116.8 | ||
| 200 | 1 | 112.5 | 149.7 | 131.1 | |
| 2 | 131.9 | 169.5 | 150.7 | ||
| Perpendicular to grain | 60 | 1 | 45.7 | 49.6 | 47.65 |
| 2 | 49.9 | 54.1 | 52 | ||
| 100 | 1 | 64.4 | 71.7 | 68.05 | |
| 2 | 73.1 | 83.5 | 78.3 | ||
| 150 | 1 | 82 | 102.6 | 92.3 | |
| 2 | 97.5 | 119.1 | 108.3 | ||
| 200 | 1 | 100 | 130.6 | 115.3 | |
| 2 | 144.2 | 164.5 | 154.35 | ||
| (a) Cedar | ||||
| Cedar | Constant Temperature (°C) | Heating Time (hour) | Young’s Modulus(N/mm2) | Yield Stress (N/mm2) |
| Parallel to grain | ambient | 7676.96 | 32.20 | |
| 60 | 1 | 6664.23 | 20.10 | |
| 2 | 7104.02 | 20.84 | ||
| 100 | 1 | 5913.00 | 18.51 | |
| 2 | 5914.02 | 16.04 | ||
| 150 | 1 | 4647.45 | 14.97 | |
| 2 | 4952.51 | 16.52 | ||
| 200 | 1 | 4165.56 | 14.22 | |
| 2 | 5062.71 | 16.69 | ||
| Perpendicular to grain | ambient | 413.25 | 2.03 | |
| 60 | 1 | 178.92 | 1.11 | |
| 2 | 264.19 | 2.11 | ||
| 100 | 1 | 173.57 | 1.46 | |
| 2 | 197.05 | 1.70 | ||
| 150 | 1 | 214.54 | 1.49 | |
| 2 | 210.17 | 1.43 | ||
| 200 | 1 | 170.94 | 1.34 | |
| 2 | 229.76 | 1.34 | ||
| (b) Larch | ||||
| Larch | Constant temperature (°C) | Heating time (hour) | Young’s modulus (N/mm2) | Yield stress (N/mm2) |
| Parallel to grain | ambient | 10,263.67 | 29.36 | |
| 60 | 1 | 10,013.69 | 28.38 | |
| 2 | 10,013.05 | 26.10 | ||
| 100 | 1 | 8077.27 | 20.67 | |
| 2 | 7822.52 | 18.00 | ||
| 150 | 1 | 8022.64 | 15.78 | |
| 2 | 6884.81 | 15.85 | ||
| 200 | 1 | 5968.15 | 21.39 | |
| 2 | 7487.83 | 22.87 | ||
| Perpendicular to grain | ambient | 298.86 | 2.67 | |
| 60 | 1 | 252.93 | 2.69 | |
| 2 | 220.10 | 2.15 | ||
| 100 | 1 | 133.42 | 1.77 | |
| 2 | 182.58 | 2.17 | ||
| 150 | 1 | 117.50 | 1.93 | |
| 2 | 148.65 | 2.10 | ||
| 200 | 1 | 106.60 | 1.90 | |
| 2 | 169.21 | 1.78 | ||
| Joining Hardware | Steel Plate | Drift Pin |
|---|---|---|
| JIS G 3101 | SS400 | SS400 |
| Specimen size (mm) | 9.0 × 75 × 200 | φ16 × 75 |
| Yield point (N/mm2) | 336 | 296 |
| Tensile strength (N/mm2) | 454 | 470 |
| Cedar | Larch | ||
|---|---|---|---|
| Young’s modulus (N/mm2) | EL | 138.19 | 181.02 |
| ER | 413.25 | 298.86 | |
| ET | 413.25 | 298.86 | |
| Poison’s ratios (–) | νLR | 0.0073 | 0.0136 |
| νRT | 0.90 | 0.93 | |
| νTL | 0.032 | 0.015 | |
| Share modulus (N/mm2) | GLR | 103.00 | 113.22 |
| GRT | 142.50 | 102.00 | |
| GTL | 102.74 | 113.52 | |
| Yield stress (N/mm2) | σyL | 32.20 | 29.73 |
| σyR | 2.03 | 2.67 | |
| σyT | 2.03 | 2.67 | |
| Damage Zone length (mm) | 3.7 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawai, Y.; Totsuka, M.; Hirashima, T. Elastoplastic Analysis of Timber Connections with Dowel-Type Fasteners at Ambient and High Temperatures. Forests 2023, 14, 373. https://doi.org/10.3390/f14020373
Kawai Y, Totsuka M, Hirashima T. Elastoplastic Analysis of Timber Connections with Dowel-Type Fasteners at Ambient and High Temperatures. Forests. 2023; 14(2):373. https://doi.org/10.3390/f14020373
Chicago/Turabian StyleKawai, Yuga, Marina Totsuka, and Takeo Hirashima. 2023. "Elastoplastic Analysis of Timber Connections with Dowel-Type Fasteners at Ambient and High Temperatures" Forests 14, no. 2: 373. https://doi.org/10.3390/f14020373





