1. Introduction
Estimation of carbon stock in forests is usually obtained from the measurement of above-ground biomass [
1]. The destructive method is still considered as the most accurate method for biomass estimation via cutting down trees and weighting their parts [
2]. Larger-scale biomass estimation is carried out by relating detailed measurements obtained from the destructive approach with the more easily derived biophysical properties of trees such as diameter at breast height (DBH), tree height, and crown size via biometric measurements. The relationship is explained by a specific function called an allometric equation. The Malaysian rainforest is well known for its tree species diversity and until now, there is still a limited number of allometric equations available. Therefore, efforts are still required in developing species-specific allometric equations that at least account for dominant tree species in Malaysia. Until now, the most cited allometric equations for biomass estimation in South East Asia were only obtained from certain studies that cover certain tree species in specific areas [
1,
3]. Remote sensing offers effective solutions for biomass estimation at various scales. Terrestrial sensors have been used for a large-scale biomass estimation, and the upscaling process of such measurements over larger area is usually done using airborne and spaceborne remote sensing data. Previous studies have shown that remote sensing data can be used to estimate aboveground biomass by relating individual tree properties (e.g., tree height, DBH, crown size and etc.) and optical properties of reflection collected over forested areas [
1,
4,
5,
6,
7,
8].
Unlike image-based remotely sensed data, light detection and ranging (LiDAR) provides detailed information on forest structure with good laser penetration under various forest canopy conditions. LiDAR can be operated from three different platforms, namely the ground (terrestrial), airborne and satellite platforms. These LiDAR operating platforms provide different scales and details of three-dimensional measurements of forest structure and canopy that are useful for forest inventory parameter estimation [
8]. Terrestrial LiDAR can be classified based on the measuring techniques, i.e., pulse ranging or time-of-flight (TOF) and the phase difference technique [
9]. The latter is capable of producing range measurements at a very high rate with a high degree of accuracy but only operates over short distances. The TOF method allows range measurements of longer distances (i.e., hundreds of meters) with a much reduced measurement rate and lower accuracy compared to the phase difference method. Terrestrial laser scanning (TLS), a ground-based LiDAR system has been utilized in many applications, e.g., building reconstruction, virtual reality of the earth’s surface, architecture, civil engineering, archeology, plant design, automation systems and forestry. In forestry, TLS can provide detailed measurements of individuals and group of trees. At the plot level, TLS can be used to estimate several useful tree parameters, for example, the number of trees and their position, tree height, DBH, tree volume and so on [
2,
10].
TLS has the potential to provide accurate positions of trees and their structure, including how the foliage and stems are arranged [
11,
12]. The TLS system can also allow three-dimensional modelling and geometrical characterization of trees that could replace the manual practice of conventional forest surveys [
13]. Many studies have successfully derived detailed individual tree measurements using terrestrial LiDAR, such as branch and trunk diameter at different distance intervals, tree height, tree volume, individual tree biomass [
2,
11,
13,
14,
15] and crown volume [
16]. However, only a few studies have focused on individual total tree above ground biomass (TAGB) estimation using tree geometry reconstruction and measurement using dense point clouds of TLS. A previous study used TLS for individual tree biomass estimation of Scots pine and Norway spruce [
2]. TAGB is composed of the biomass of living branches, dead branches, bark and stem. New models for above ground biomass (AGB) were introduced and compared with the existing models that were normally based on DBH, height, and species. The results showed that the newly developed model that included several new independent variables, i.e., stem curve and crown size derived from TLS, improved the estimation accuracies, especially for branch biomass. Some of the tested variables of crown geometry of the newly developed models were suitable to improve current allometric equations for TAGB estimation. The study focused only on a single tree and tree measurements from point clouds without geometric reconstruction of the tree.
Another study estimated residual biomass from individual tree architecture in an urban forest using TLS and ground measurements [
13]. The biomass of the trimmed tree crown was measured in the field and compared to the value obtained by modelling the point clouds of TLS. The tree crown was reconstructed, and its volume was measured using convex-hull, triangulation and voxel modelling of point clouds. The results showed good potential of TLS measurements for biomass estimation of pruned crowns. There is a method to calculate individual tree wood volume using TLS [
17]. The point clouds were used to reconstruct the geometry of the entire woody parts of a tree by generating different resolutions of voxels in the point clouds. The total volume was calculated by the total volume of the voxels. A previous study applied sectional volumes based on measured diameter at several heights using cylinder fitting and estimated biomass by multiplying the volume estimated with wood specific density [
18]. However, this study did not include information for the crown structure when crown biomass was based on the assumption that crown biomass accounts for 20% of total aboveground biomass. There was also a study that aimed to estimate tree branch biomass using TLS with different scanning resolutions [
19]. The complexity of tree branches was simulated using logging residuals, and the scanning was done at different scanning distances. The results showed that biomass estimation was not affected by scanning distances, and the method successfully estimated the biomass with an accuracy of 95%.
In another study, a single-scan experimental echidna validation instrument (EVI) was used to estimate the biomass of conifer and broadleaves trees; a high correlation with field-measured biomass was achieved (
r2 = 0.85). This study used horizontal slices for diameter at breast height measurements and employed allometric models for EVI biomass estimation. A multi-scan approach provides more detailed datasets that can be used in tree reconstruction to measure wood and leaf volume directly from the point clouds, providing a more geometrical-based biomass estimation rather than depending on allometric equations. Several studies have been devoted to biomass estimation of shrubs. There was a study that utilized TLS for shrub biomass estimations using volumetric surface differencing and voxel counting [
20]. Both methods produced strong relationships between harvested and estimated biomass. Point clouds obtained from airborne LiDAR and TLS were combined to estimate the biomass of sagebrush based on regression models between voxel-volume, TIN-volume, convex hull-volume, airborne LiDAR-derived percent vegetation cover (PVC) and harvested biomass [
21]. The results showed the voxel-volume approach produced better results for individual shrub biomass estimation. The PVC method showed a good correlation with the field-measured shrub biomass at the plot scale. In another study, the aboveground biomass of sagebrush was estimated using regression models between shrub volume estimated using voxel, convex hull and harvested biomass [
22]. The biomass estimate obtained using the convex-hull volume outperformed the voxel approach. The methods used for shrub volume estimation could be used for tree crown biomass estimation in forest areas.
Tropical rainforests are known for their dense forest cover and understorey vegetation. This condition would limit the visibility of the TLS, which might cause imperfect distribution of point clouds over individual trees. This can complicate detailed tree measurements and the biomass estimation process that relies on the generated point clouds. Besides the destructive method, previous recommended laser-based methods have shown that useful allometric equations for individual tree biomass estimation can be developed and extended using the non-destructive approach. However, most of the previous studies were conducted using residuals, individual tree and area covered by low and sparse shrubs, which has different challenges compared to work carried out in tropical rain forests, especially in The Royal Belum forest reserve, one of the oldest rainforests in the world. This study aims to estimate individual tree biomass of various species of trees in a tropical rain forest in Malaysia using point clouds generated from TLS. With additional information from individual tree measurements, several species-specific allometric equations for above ground biomass estimation have been produced in this study.
2. Materials and Methods
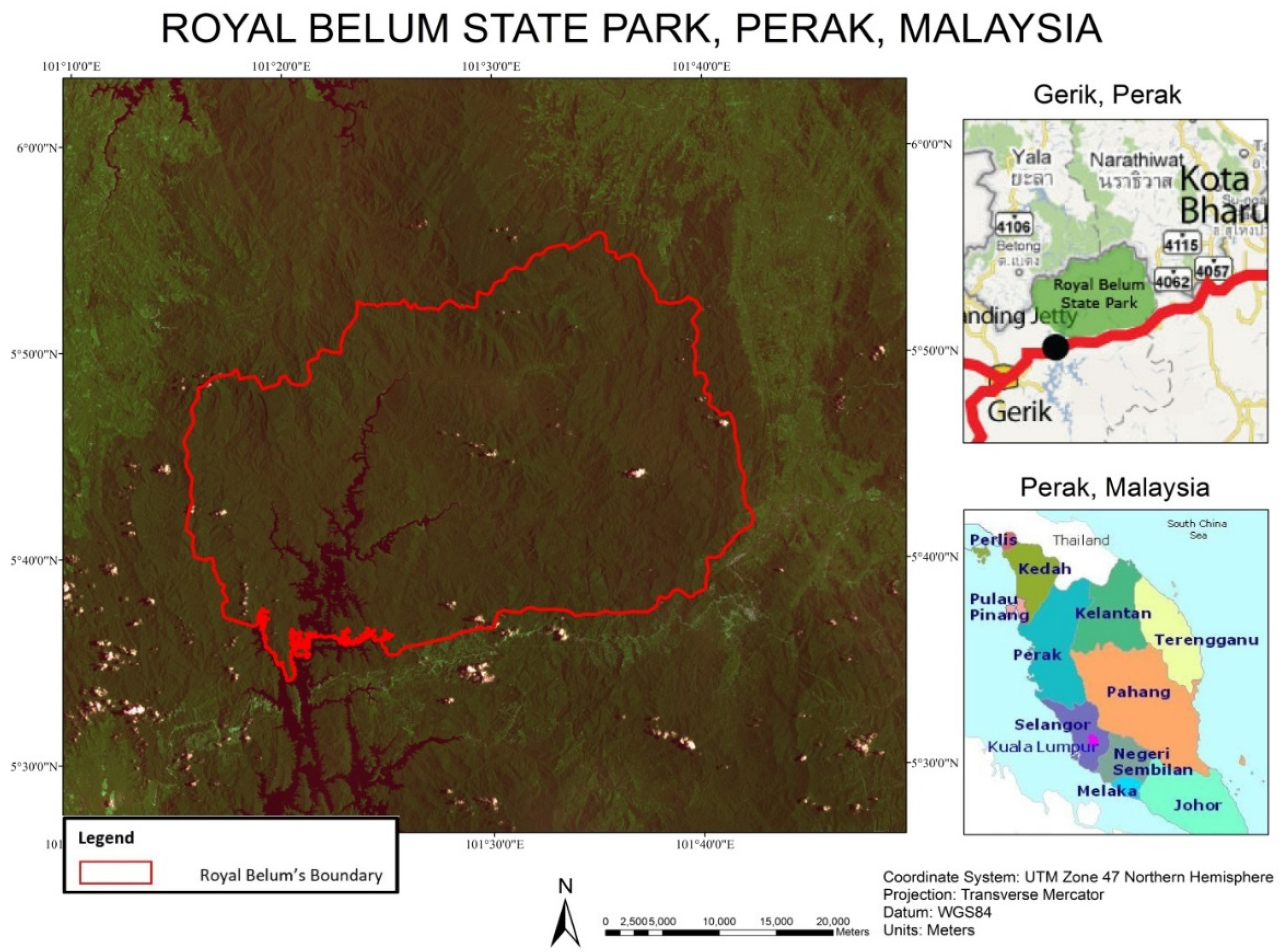
The Royal Belum forest reserve consists of 300,000 hectares of tropical rainforest, believed to exist for over 130 million years. The forest reserve is located in Gerik, Perak state of Peninsular Malaysia (
Figure 1). The forest is covered by dense dipterocarp forest and is home to at least 14 threatened tree species [
23]. Furthermore, it is also known to be an area rich in endangered animals such as Malayan Tigers, Asian Elephants and Sumatran Rhinoceroses. The area remains warm and humid throughout the year; the temperature ranges from 23 °C to 32 °C, with 2205 mm average rainfall, and the highest altitude of the study area is 1533 m.
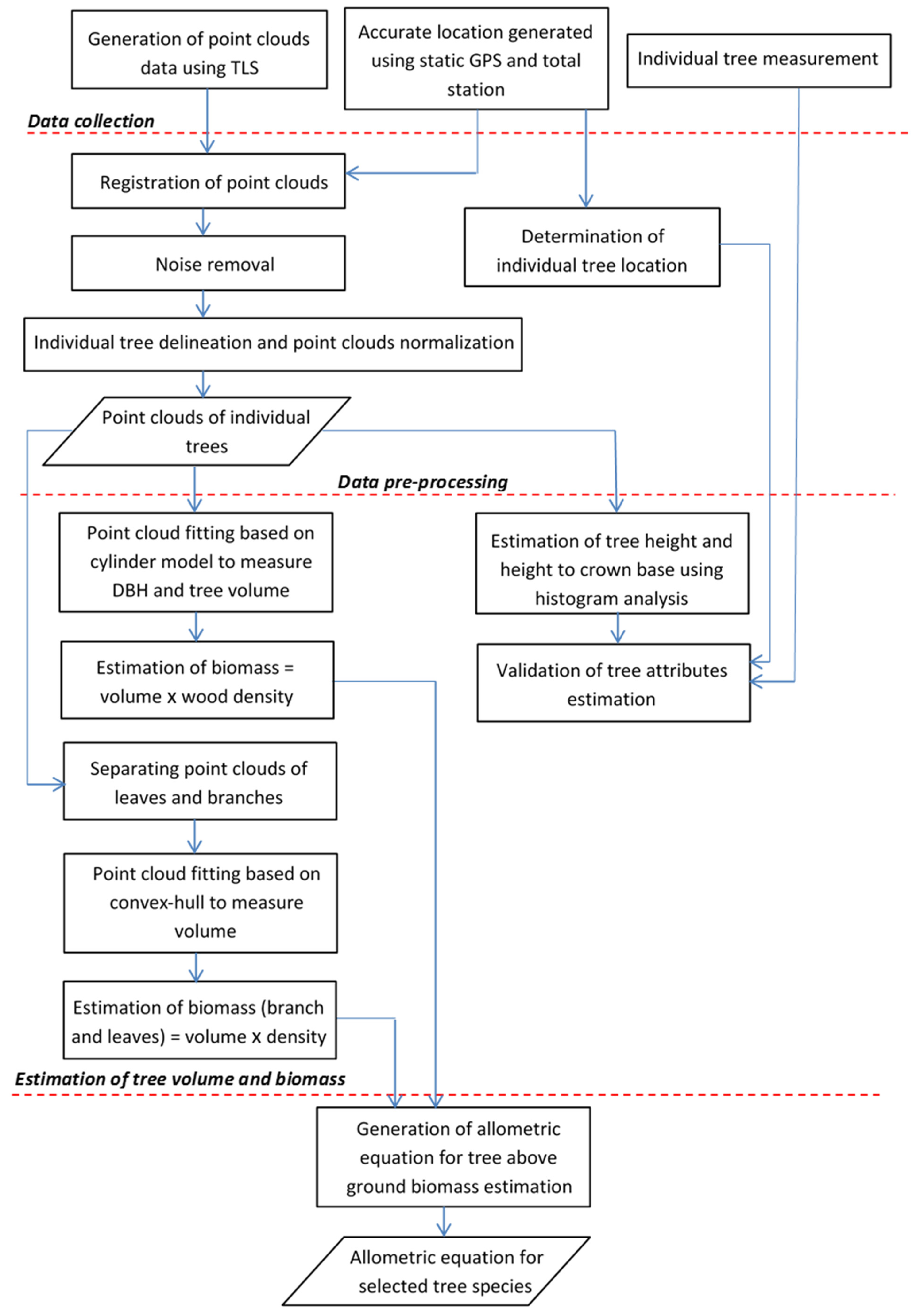
In general, the methodology used to obtain tree biometric parameters and estimate the total above ground biomass (TAGB) in the Royal Belum reserve forest can be divided into four major steps, namely, data collection, data pre-processing, estimation of tree volume and biomass, and development of allometric equations for selected tree species (see
Figure 2). The first stage focused on the generation of point cloud data and individual tree measurements of forest plots. The data were used for geometric reconstruction of individual trees and validation of estimated tree properties, i.e., tree location, DBH, tree height, and height to crown base. In the data pre-processing stage, the raw point clouds were registered using accurate locations given by global positioning system (GPS) and the total station method. A similar approach of location determination was used for individual tree location. In the third stage, different parts of individual tree volumes and biomass were estimated. This non-destructive approach of biomass estimation requires wood and leaf density to be estimated for different tree species. Finally, a new set of allometric equations was generated based on tree DBH, height, crown size, and height to crown base. The estimated tree AGB was compared with the value estimated using different allometric equations that have been developed for tropical forests. A more detailed description of each of the steps is provided in the following sub sections.
2.1. Individual Tree Inventory: A Conventional Approach
The individual tree measurements were completed for 36 plots, which were randomly selected over the study area. Each plot has a circular shape with a diameter of approximately 30 m. During the inventory process, trees with 10-cm DBH were labelled with unique signage (see
Figure 3), and tree attributes such as tree height, DBH, tree species, height to crown base, and location were recorded. Tree height was measured using a clinometer and laser-aided hypsometer. Tree DBH was measured using a diameter measuring tape, and the tree position was recorded by using a combination of static GPS and reflectorless total station. The static measurement of GPS was carried out in an open space usually located at the edge of the forest area. The accurate local coordinates were transferred to the specific forest plot and individual trees using reflectorless total station.
2.2. Generation of Point Clouds in Sample Plots
Manual tree biometric measurements were accompanied by a semi-automatic laser-based approach, which allows detailed measurements of individual trees. The semi-automatic measurement approach was carried out on point clouds generated using VZ-400 Riegl TLS (Riegl, Austria) (see
Figure 4). During the fieldwork, we scanned all 36 forest plots with the TLS that includes various sizes of dominant trees and understorey vegetation. Sample plots with relatively dense understorey vegetation were cleared to facilitate the scanning process. Each plot was scanned with 4 positions, which covered the centre and 3 edge locations of the forest plot with a distance approximately 14.6 m from the centre. Each scanning position was selected based on the location of trees and the condition of the terrain. The TLS should be placed on firm and relatively flat stable ground to ensure a consistent measurement process. The coordinate of each scanning position was determined using a total station and static Global Positioning System (GPS). The static measurement of GPS was carried out in an open space usually located at the edge of the forest area. These accurate positioning data were transferred to a specific forest plot by using reflectorless total station (TS).
Generation of point clouds of trees in the forest area using TLS requires multiple scanning processes with careful selection of scanning positions. This is very important to ensure that the scanning process will be able to produce dense point clouds for individual trees. Each point cloud set produced by separate scanning processes was combined and registered using common tie points located in the selected points in each sample plot. Tie points created using a cylindrical shape reflector were located randomly in each forest plot and could be seen by all scanning positions. The point clouds were transferred to the local ground coordinate system by using the real coordinate measurements produced by TS and GPS.
Furthermore, for individual tree identification and extraction, each tree was marked with reference signage with a unique number. The unique signage is required to assist the matching process of trees as identified from the point clouds and field observations. The purpose of the tree matching process is to extract individual trees from the point clouds and to compare the estimated forest attributes with the field measurements. This signage can also be used as additional tie points for the point cloud registration process. For accurate and dense point cloud generation, the scanning mode was set to discrete with full-waveform approaches. The discrete scanning approach was accompanied by red, green and blue (RGB) data that give colour to individual points. The discrete mode of scanning requires longer operation compared to full-waveform mode as it generates detailed waveforms of signals reflected by different parts of the forest.
2.3. Semi-Automatic Approach for Individual Tree Measurement
2.3.1. Pre-Processing of Point Cloud Data
The pre-processing stage involved preparation of the raw point cloud data for further processing such as aligning all scanning positions together and removing unnecessary point clouds. For the purpose of point cloud registration, tie points were used as a reference to merge the point clouds obtained from all scanning positions into one projected coordinate system. The process is known as point cloud registration. The first scan was registered as a reference, and the subsequent scans were registered relative to the first scan. The minimum number of tie points required to register two scanning positions is three, and these tie points were set up at several locations at a height approximately 1.5 m above ground. In the case of dense tropical rainforests (such as the case of this study), additional control points were located with large size reflective cylinders to facilitate the registration process.
After registration, noise or unnecessary point clouds originating from neighboring trees, understory trees and the ground surface were removed so that further processing focused on a single tree. The noise was removed manually by a careful inspection of every single tree marked in the field based on the trees and the signs that could be seen in the point clouds. The cleaned point clouds were then separated into individual trees for tree attribute estimation. Further cleaning processes for leaf and small branches were required to separate the trunk and branches prior to diameter estimation at different height intervals. The filtered point clouds of individual trees were then normalized by subtracting the base elevation of the tree from the elevation values of point clouds belonging to a particular tree. This process transforms the elevation value of point clouds to height information.
2.3.2. Estimation of Individual Tree Attributes
Estimation of individual tree attributes was divided into: (1) tree location; (2) height to crown base; (3) DBH; (4) tree trunk volume (5) branch volume; (6) leaf volume; and (7) tree height. Tree height and height to crown base were estimated using histogram analysis of the point cloud height values. The branch and leaf volumes were estimated based on the convex-hull volume pertaining to the point clouds. Estimations of DBH and tree trunk volume were based on the cylindrical models fitted to point clouds.
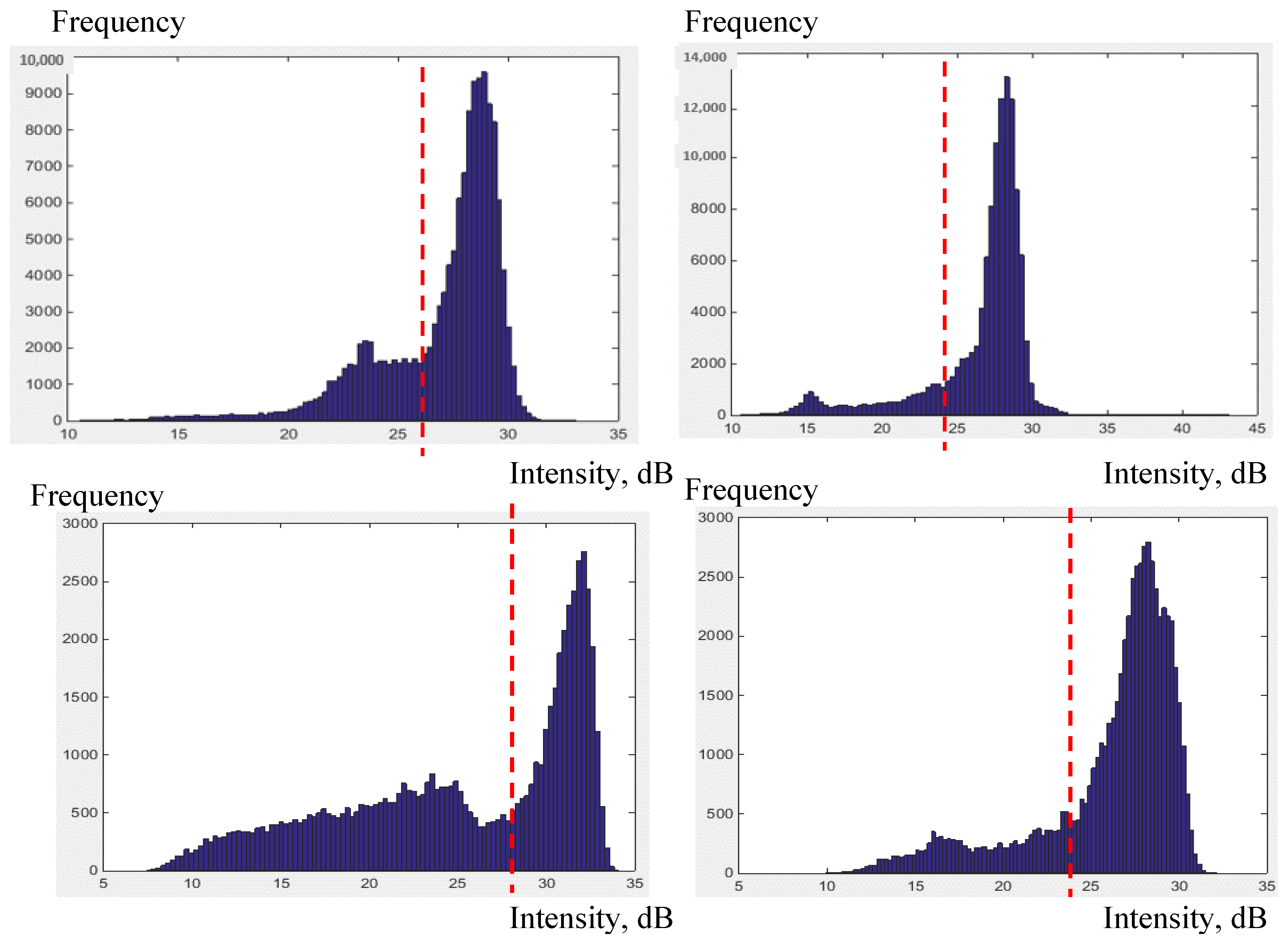
Prior to the tree attribute estimation process, the point clouds of a single tree were divided into branches, leaves and the tree trunk. The intensity values of point clouds were used to separate tree branches from leaves. The process relies on the assumption that the recorded near infrared intensity of leaves would have higher value compared to tree branches. The histogram of intensity values of the tree crown was used to manually define a suitable threshold value for this purpose (
Figure 5). The point clouds with an intensity value above the threshold were classified into leaves, and the rest were assigned to branches. Each tree has a different shape of the intensity histogram, requiring different values of the threshold to separate leaves and branches. This might be due to the reflectivity from various scanning distances between trees, the scanner and variation in the infrared reflectivity from the leaves.
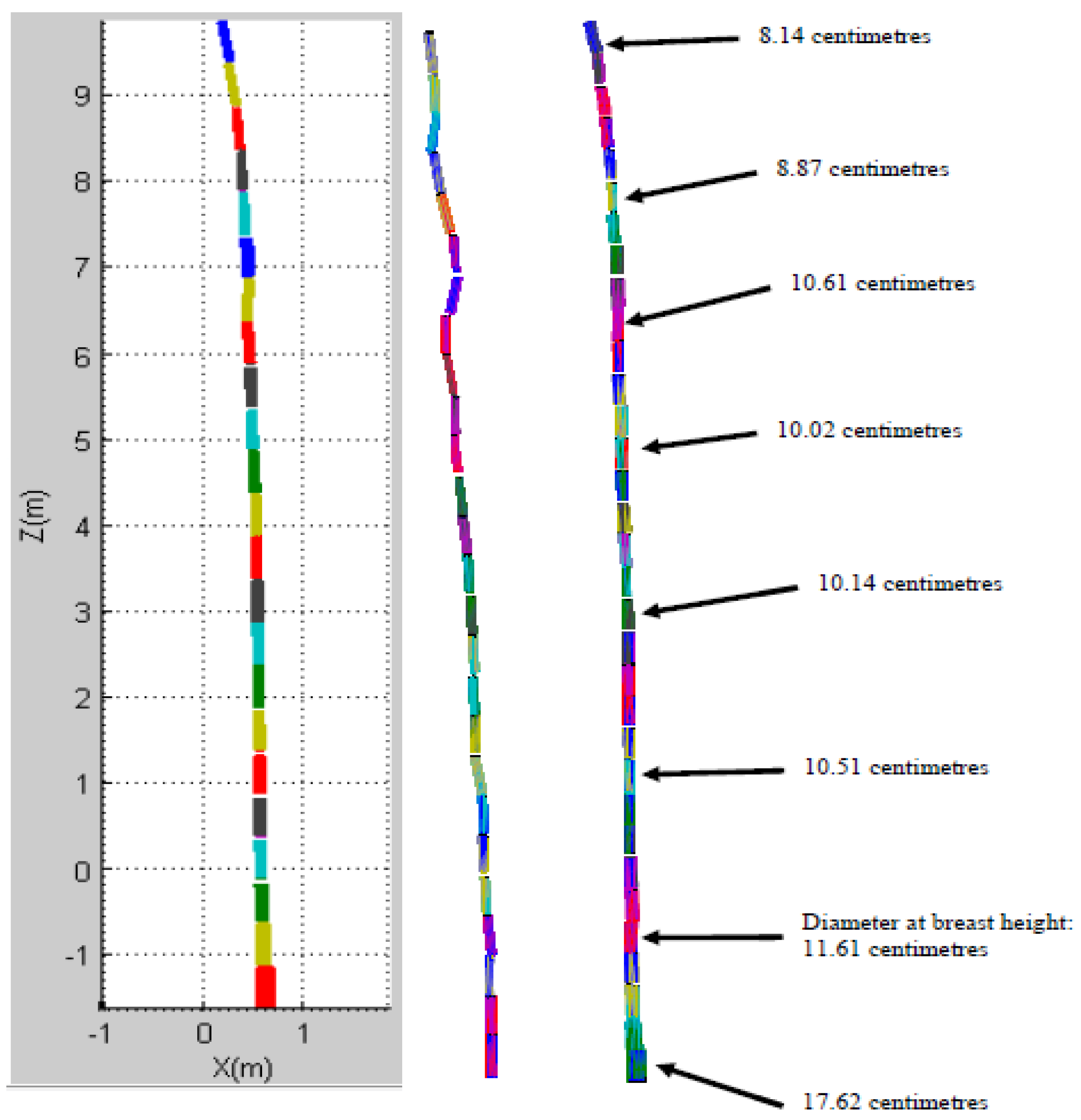
The fitting process of point clouds that belong to the tree trunk was done using a cylinder model at different height intervals. The fitting process requires two input parameters, namely a distance interval and axis (X, Y or Z), where the point clouds will be partitioned. Tree trunk diameter and total trunk volume were estimated based on the cylinder diameter at a selected height and the total volume of the fitted cylinder models, respectively. Methods for tree height and crown base height estimation were adopted from a previous study [
24]. The method employs a Gaussian model fitted to the histogram of elevation that marks the height boundary of tree height and crown base height.
Figure 6 shows an example of a histogram constructed based on point clouds obtained for a single tree. The histogram was fitted with multiple Gaussian functions, in which the crown base height is marked by two Gaussian curves of the tree crown and ground surface. The initial boundary for crown base height was determined by subtracting three standard deviations from the mean value of the lowest Gaussian function from the tree crown. The end point that marked the ground surface was determined by adding three standard deviations to the mean value of the Gaussian function of the ground surface. Finally, the crown base height was calculated by subtracting the value of the end boundary from the start boundary. Tree height was calculated based on the highest Gaussian function of the tree crown. The height was determined by adding three standard deviations to the mean value of the Gaussian function.
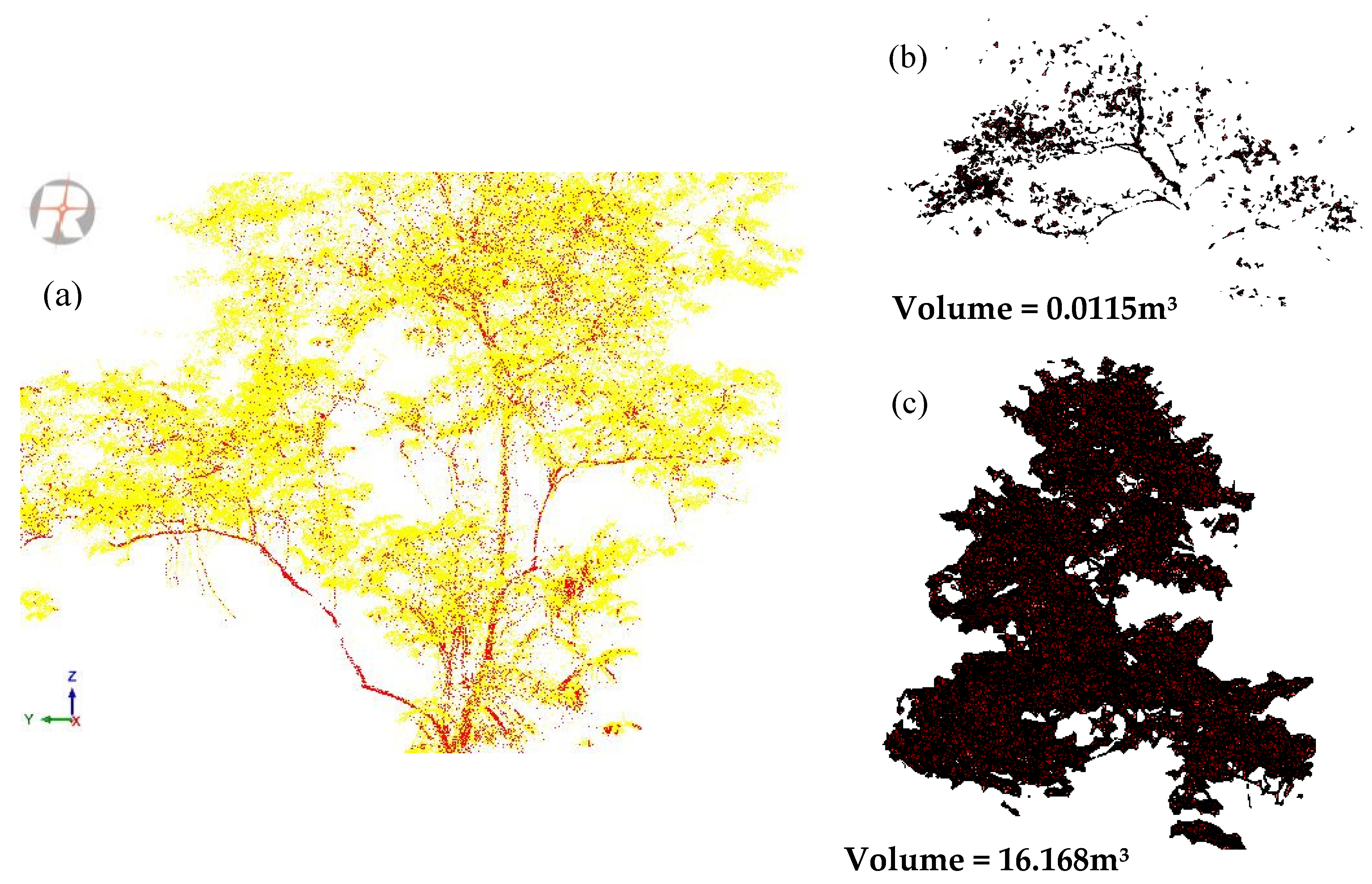
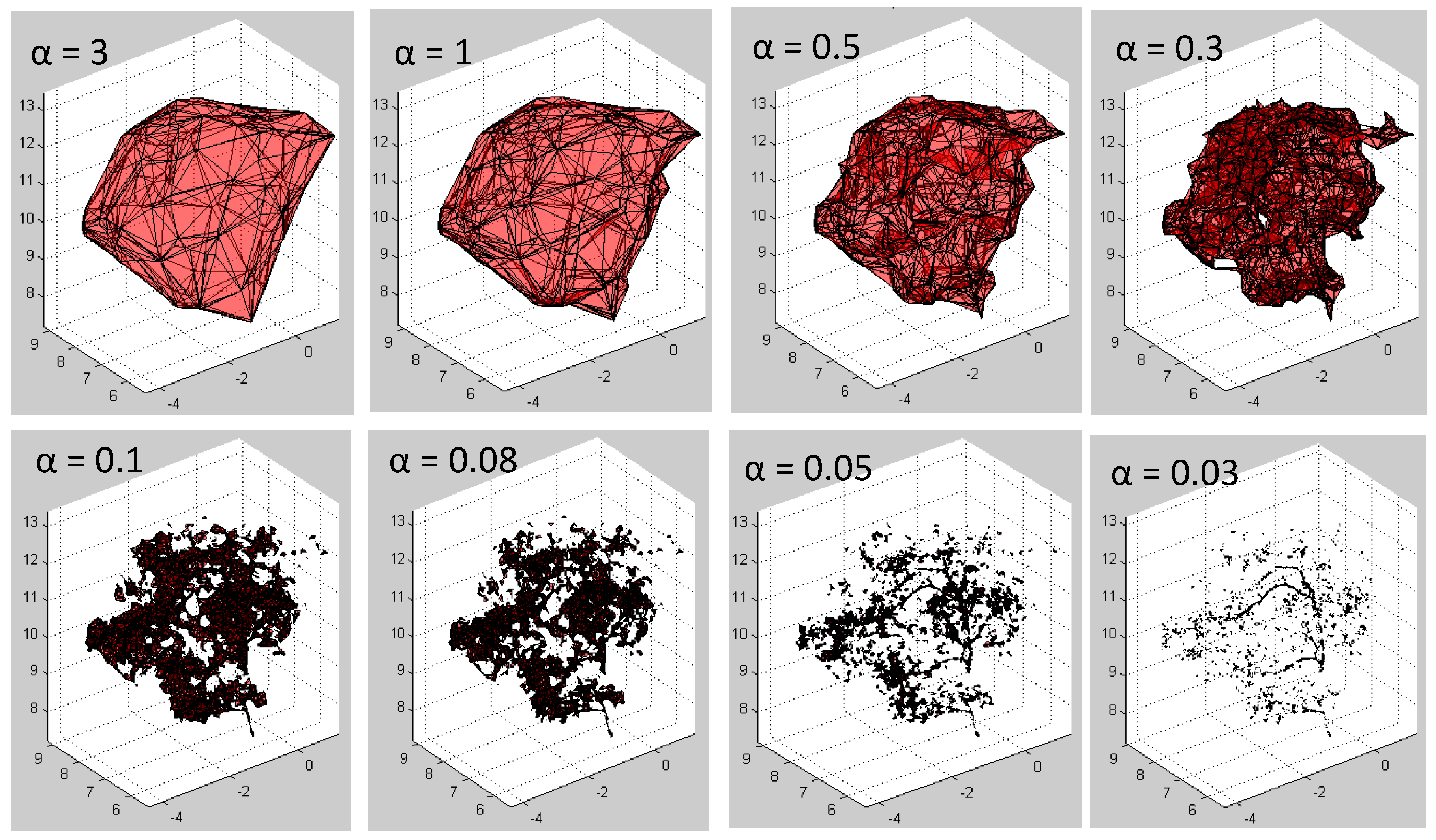
Branch and leaf volumes were estimated using a convex hull algorithm, which constructs the three-dimensional boundary of a closed convex surface based on Delaunay Triangulations of the outer points. The convex hull algorithm was applied to points belonging to branches and leaves. The tree branches and leaf volumes were estimated from the volume of the closed triangulated surface.
2.4. Individual Tree Biomass Estimation Using a Reconstructed Tree Model
Estimation of above ground biomass for individual trees is divided into tree stem, branches and leaves. The total volume for tree stem was estimated based on the volume of the tree stem estimated as the total volume of fitted cylindrical models over point clouds of TLS data (Equation (1)). The above ground biomass for tree stem
was then estimated by multiplying the total volume with the wood density
[
24] of a specific tree species. Biomasses of tree branches
and leaves
were estimated by multiplying the total branch volume
with wood density
and
leaf density
[
21,
22,
23] of a specific tree species (Equations (2) and (3)). The total above ground biomass
of a single tree is defined as in Equation (4).
Secondary level allometric equations were generated based on the regression analyses between estimated biomass values and tree biometric parameters obtained from TLS data. Wood density was chosen based on different tree species (see
Table 1), while leaf density was taken as the mean value of 0.41 g·cm
−3 [
25,
26]. The biomass of these individual components was assessed with values calculated using allometric equations developed by [
27]. These allometric equations (Equations (5) to (8)) were developed based on data collected in the Pasoh reserve forest in Malaysia.
2.5. Individual Tree Biomass Estimation Using Field-Collected Tree Attributes
Biomass estimation from field-collected tree attributes is required to validate the estimation using TLS data. Activities in and disturbances to the ecosystem are not allowed in Royal Belum State Park, which limits this study to develop primary allometric equations, which require destructive methods. Therefore, existing allometric equations [
27] were used to validate the estimation of the weight of stems, branches, leaves, and TAGB from TLS data. Equations (5) to (9) show the allometric equation introduced by [
27], and the input parameters were obtained from the field measurements.
where
Ws is the weight of the stem (kg),
Wb is the weight of branches (kg),
Wl is the weight of leaves (kg),
dbh is the diameter at breast height (cm),
h is the tree height (m) and
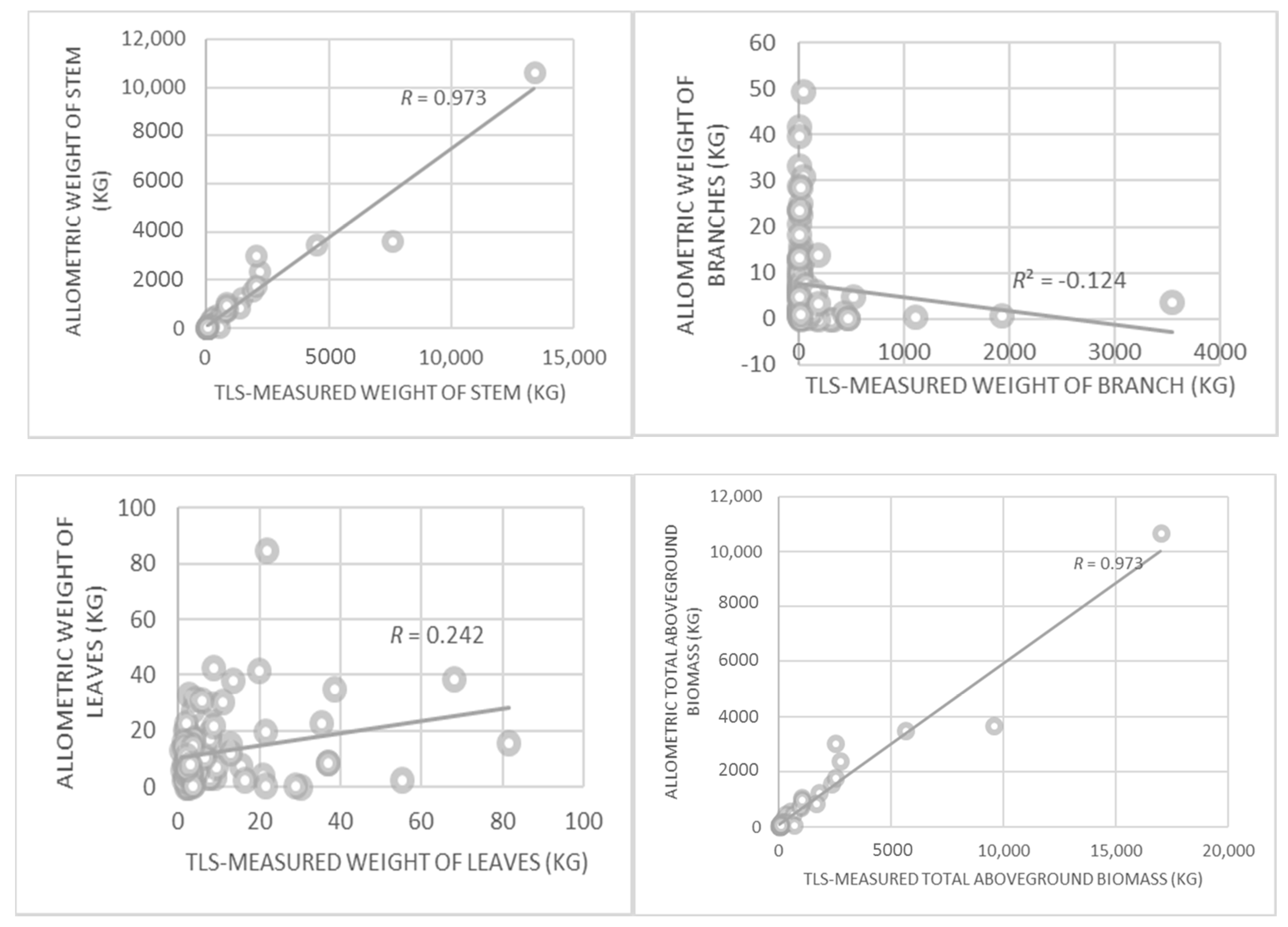
TAGB is the total above-ground biomass (kg). The allometric equations were developed based on tree information collected in the Pasoh reserve forest in Malaysia. In the study, the ABG was calculated based on a destructive method over 2 different samplings conducted in February-March 1971 and March-April 1973, with 73 and 83 trees, respectively. The differences between the estimated and the harvested dry weight of stems, branches, and leaves without lianas were 3266 kg, 1736 kg, and 71 kg, respectively. With lianas, the differences between the harvested and estimated dry weight of stems with branches and leaves without lianas were 6289 kg and 26 kg, respectively. The allometric equations allow AGB estimations for different tree parts, i.e., stem, branch and leaf.
4. Conclusions
Terrestrial laser scanner (TLS) allows high-density point clouds to be collected for different types of objects including trees. The scanning process in a dense natural forest area is very challenging due to dense understorey vegetation, uneven tree distribution and growth, which causes occlusion of TLS observations and uneven densities of point clouds for each tree. Moreover, an intensive cleaning process should be done for points reflected by vegetation that grows near observed trees. The point clouds of branches and leaves are consistently affected by this occlusion effect, which significantly decreases the point density obtained. In this study, we used multi-station scanning techniques at a specified distance from the scanning centre, which allows better distribution of point clouds over trees in a plot. The combination of a simple, single-tree stem reconstruction and wood density can be used to estimate stem biomass comparable to the results that are usually obtained through existing allometric equations. However, serious errors were discovered for branch and leaf biomass estimations, mainly due to limited numbers of point clouds in the upper part of the forest. The results show that the serious error in leaf and branch biomass disappeared after combination with stem biomass. We have highlighted several limitations and issues related to branch and leaf biomass estimation, which requires further improvements in data acquisition and the processing step as recommended in this study.
It has been shown that better estimation of stem biomass requires detailed TLS observations and models for volume calculation. The TLS-based biomass estimation method introduced in this study can be used for the generation of general allometric equations and species-specific allometric equations. However, to strengthen the quality of the allometric equations, they should be calibrated and validated by means of destructive biomass methods in another area. Stem weight estimated from a combination of all tree species had RMSE and MAE values higher than 500 kg, which are close to the average total aboveground biomass of a single tree in Royal Belum. DBH, stem volume and tree height consistently produced good biomass estimation results for all tree species. This study also suggests that the laser-based biomass estimation method produced better results when the estimation process was done separately for each tree species. However, the findings also suggest that the upscaling process of biomass using airborne LiDAR data might have to take into account information about tree species.