Abstract
The canopy shading model is widely used in agroforestry systems. However, the canopy shading model cannot be verified by the measured shading distribution of an apple tree due to the uneven ground and adjacent apple trees. This paper measures the spatial‒temporal distribution of the shading of apple trees based on the similarity principle of parallel solar light combined with 3D printing technology to improve the canopy shading model. The following results are drawn: (1) The current widely used canopy shading model does not consider the effect of the canopy penumbra, resulting in poor simulation accuracy in the shading distribution compared to the actual measurement; (2) The effect of canopy penumbra causes the deflection of sunlight. Hence, the paper presents the deflection equation of sunlight with statistically defined parameters derived using measured data of the shading distribution. The deflection equation of sunlight is added to the improved canopy shading model. The improved model can accurately simulate the shading distribution of an apple tree, and the simulation accuracy exceeds 94.12% when compared with the shading distribution of an apple tree; (3) The improved canopy shading model is applied to simulate the spatial‒temporal distribution of the shading of apple trees in a conventional arrangement (4 m × 5 m), and the simulation accuracy exceeds 89%. Thus, the improved canopy shading model can be applied to simulate the spatial‒temporal distribution of shading of apple trees.
1. Introduction
The agroforestry system provides new thoughts and ideas for agriculturally sustainable development [1,2]. Agroforestry is considered an efficient practice to solve the competition between agriculture and forestry, as well as the contradiction between humans and land. Furthermore, agroforestry is an efficient approach and technical method to assist soil and water conservation, ecological restoration and reconstruction [3,4,5,6]. Consequently, it has been widely promoted and applied in the Loess Plateau of China.
The agroforestry system changes a single planting structure through a horizontal and stereo arrangement in space and a combination of temporal sequences among species [7]. The planting practice presents a new interaction with the distribution and utilization of light, water and nutrients between different species. This relationship is not only competitive but also complementary [8]. Therefore, taking full advantage of trees and crops, minimizing competition among species, and maximizing the use of available resources are key to deciding structural arrangements in agroforestry systems [9,10]. Additionally, it is a major constraint that affects ecological, economic, and social benefits [11,12]. Thus, the interspecific relationships and regulation of agroforestry systems play an important role in the theoretical research and production practice of agroforestry systems.
Studies showed that the interspecific relationship of the agroforestry system mainly includes competition, complementarity and allelopathy among species [13]. In some related studies, the results indicated that the key to coordinating the interspecific relationship is to reduce the interspecific competition for water and nutrients [14,15,16]. However, other studies reported that light competition is the main reason for the reduction in intercrops [17,18,19,20]. The intensity and distribution of solar radiation would be changed under forest in agroforestry systems due to the complex community structure [21]. This causes high spatial‒temporal heterogeneity at different altitudes, horizontal positions and times. The heterogeneity directly affects the ecological processes and productivity levels of intercrops [22].
Light is an inevitable condition for photosynthesis, and affects photosynthesis and photosynthetic rate: 90–95% of the biological yield of vegetables comes from photosynthesis [23]. However, the canopy shading reduces the net photosynthetic rate of the leaves, as well as the initial light energy conversion rate of PSII, so that the photosynthesis of vegetable is affected [24]. Studies have shown that leaves become thinner, leaf area becomes larger, and stem height increases in shading conditions in order to improve the ability to absorb and capture light [25,26]. At the same time, the leaves absorb more light, which causes the chlorophyll a/chlorophyll b to decrease and the pore density to decrease. Excessive shading can cause etiolation of vegetables [27,28]. Under the condition of insufficient light, the central bud of the vegetables will have blind buds and crack buds. Shading reduces the accumulation of assimilation and reduces the fruit ripening rate. When the light intensity of the shade falls below the light compensation point, the energy supply of the carbohydrate is reduced, resulting in a decrease in the number of young fruit cells and fruit size [24]. Light has a positive effect on the distribution and utilization of photosynthetic products. The distribution and utilization of the product is affected under shading condition, resulting in changes in mineral nutrients in the vegetables. Nevertheless, some studies suggest that moderate shading has a positive effect on some plants [23]. Consequently, scholars gradually realized the significance of studying the light environment in agroforestry systems [29]. The studies of the light environment include spatial‒temporal distribution of shading and solar radiation in agroforestry systems. The studies showed that the light interception of a tree directly affects the luminous intensity and shading time below trees [30]. The shadow of forests has been simulated by the canopy shading model [31,32], NDVI (normalized differential vegetation index) [33], and solar radiation transmission model [17,34,35] combined with the geometric structure of the canopy and the equation of the apparent motion of sunlight. So, the shape and area of the canopy shadow, luminousness and solar radiation intensity below trees can be determined. The shade distribution of forests obtained by NDVI is limited in analyzing the continuous shade changes of forests, adjacent interference and ecological environment simulation of the agroforestry complex system. The canopy shading model can simulate the spatial‒temporal distribution of the shading of trees, so as to clarify the shading area of the trees and the degree of shade. It is very important to explore the spatial‒temporal distribution of the light environment under forests in agroforestry systems to enhance the production of intercrops and provide the optimum arrangement of intercrops. Additionally, increased production and optimized arrangement can promote sustainable development in land use.
The canopy shading model still has some problems. The accuracy of the canopy shading model cannot be verified because of the poor flatness on the ground and because the neighboring tree interference cannot be measured, making the shading model less accurate. In this study, 3D printing technology was used to obtain the 3D tree model. The temporal‒spatial distribution of tree shading during the day was measured using a 3D tree model. Through comparative analysis of the measured shading distribution and simulated shading distribution by the canopy shading model, the canopy shading model is modified to improve the simulation accuracy. This paper will provide a basis for the study of the spatial‒temporal distribution characteristics of forestry shading. It is clear that the spatial distribution of shading time can be accepted in intercrop areas.
2. Materials and Methods
2.1. Study Area
The study area is located in Ji County southwest (36°20′20″ E, 110°45′47″ N) of Lin Feng City, Shanxi Province, China. The geomorphic types are mainly divided into loess hill, residual gully and bedrock landforms, and the topography is varied and fluctuant. The weather of Ji County belongs to the monsoon climate of medium latitudes. The mean annual temperature ranges from 9.3 °C to 11.3 °C. The mean annual precipitation is approximately 532.8 mm. Heavy rainfall mainly falls from June to October. The region has abundant light supply, and the annual sunshine duration reaches 2538 h.
The region has been performing ecological engineering based on Replacing Agriculture with Forestation since 1999, when slope farmlands were shifted to woodland and grassland. Economical forest, such as apple (Malus pumila) and pear (Pyrus spp.), was widely planted in Ji County.
2.2. Materials and Experimental Design
To study the shade range of a six-year-old apple tree, 3D printing technology was used. Based on the similarity principle of parallel sun rays, a 3D model of an apple tree reducing the average size of the apple tree by 50 times was constructed by the software of Rhinoceros version 5.0 (Robert McNeel company, Seattle, WA, USA). The 3D model was printed by the equipment of UnionTech SPSS version 600 (the company of WeNext factory, Shenzhen, China). The 3D model was used to study the tree shade distribution and improve the canopy shading model for apple trees. Based on the improved canopy shading model for apple trees, the shading distribution of apple trees under conventional arrangements was studied.
2.2.1. The Construction of the Model of an Apple Tree
2.2.2. Shade Distribution
The shading distribution of a six-year-old apple tree was estimated using the 3D model manufactured by 3D printing. The shading distribution was performed by shadowing the 3D model irradiated by the sun’s rays. The 3D models were fixed in three grid papers. The shading distribution of the shadow of the 3D model was described and recorded at 1-h intervals during the daytime (8:00–17:00). These treatments were measured on three sunny days in July 2017.
2.2.3. The Improvement of the Canopy Shading Model for the Apple Tree
For improving the canopy shading model, the shading distribution obtained via the canopy shading model was compared with the measured shading range. The formula of the sun’s apparent motion was applied to calculate the canopy shading model. Later in the section, we present the formula of the canopy shading model and the sun’s apparent motion.
The canopy shading model described here is based on studies by Shu-ren Li (1994) and Talbot et al. (2011). The canopy shading model assumes the sun’s rays to be parallel, and the direction of the sun’s rays penetrating the crown is uniform. The point Q (x, y, z) acts as an arbitrary point from the tree. Q′ (x1, y1) is the shading point of Q (Figure A2). The shading point can be described as follows:
where x1 is the value of the X-axis for shading point Q′, y1 is the value of the Y-axis for shading point Q′, x is the value of the X-axis for tree arbitrary point Q, y is the value of the Y-axis for tree arbitrary point Q′, z is the value of the Z-axis for tree arbitrary point Q′, h is the solar altitude angle, and A is the solar azimuth angle.
To determine shading point Q′, the solar altitude angle (h) and azimuth angle (A) need to be evaluated by the formula for the sun’s apparent motion. The sun’s apparent motion is based on the fact that the sun moves around the earth. The formula can be described as follows (Purple Mountain Observatory):
where h is the solar altitude angle, and A is the solar azimuth angle. The range of the solar azimuth angle is from −180° to 180 h°, where the direction of South is 0°, the clockwise direction is positive (+), and the counter-clockwise direction is negative (−). The solar altitude angle (h) and azimuth angle (A) change over time during a year. ψ is the geographic latitude in the study area, δ is solar declination, and ω is the solar hour angle.
Solar declination (δ) is an angle formed between incident sunlight and the equator. The angle has persistent invariability between the earth’s rotational axis and the surface of the earth’s orbit. The range of periodical annual change is from 23°26′ N to 23°26′ S. The mean daily motion of solar declination is only 0.13°. δ is assumed to be constant across a day. Solar declination at a certain time is given by the following:
where δ is solar declination, δ is positive (+) north of the equator, and δ is negative (−) south of the equator. α is the radian at a certain time, and dn is days from 1 January to a certain time.
The hour angle (ω) is the angle between the celestial meridian and the celestial red meridian. The formula for calculating the hour angle is given by the following:
with
where ω is the solar hour angle, Ts is apparent solar time, t is Beijing time, and ψ is the geographic latitude of the study sample.
2.2.4. Shading Distribution of Apple Trees under the Conventional Arrangement
The shading distribution of apple trees was estimated using the 3D model. The shading distribution was performed by shadowing the 3D model irradiated by the sun’s rays. 3D models were fixed on grid paper according to the plant spacing configuration (4 m × 5 m) and reduced by 50 times (80 mm × 100 mm) (Figure A3). The shading distribution of the shadow of the 3D model was described and recorded at 1 h intervals during the daytime (8:00–17:00). These treatments were measured on three sunny days in July 2017.
3. Results
3.1. Simulation Accuracy of the Canopy Shading Model
The shading range obtained via measurement was compared that obtained via simulation using the canopy shading model (Figure A4). Figure A4 shows that the simulated shading distribution of apple trees is obviously different from the measured range. The simulated shading distribution is expanded and migrated to the southwest. On one day (8:00–17:00), there are large errors at 8:00, 9:00, 16:00 and 17:00. The coincidence degree between the simulated shading and measured shading distribution was 72.63%, 80.02%, 78.76% and 84.00%, respectively. In the 9:00–15:00 range, the error of the shading range is small, and the coincidence degree is higher than 90.12% (Table A2). In space, simulated shading moved south to the maximum offset of 0.37 m and shifted westward to 0.35 m.
According to the factors analysis caused the shading of tree, the main reason is that the canopy shading model does not consider the effect of the canopy penumbra [35,36]. The sunlight touching the canopy of the apple tree exhibits deflection. Thus, the shadow boundary is changed by the influence of the angle of deflection of sunlight. The deflection of sunlight changes the solar altitude (h) and the solar azimuth (A). The solar altitude angle appears to be slightly enlarged, resulting in a reduction in the shaded area of an apple tree. With the time approaching 12:00, the solar altitude angle increases, and the shadow deformation of the apple tree decreases. Therefore, the closer the time is to 12:00 on a day, the higher the coincidence degree of the shaded area becomes. At the same time, the solar azimuth also appears to be slightly enlarged when the sunlight is deflected, causing a change in the shading distribution of the apple tree. Compared to the shading range simulated by the canopy shading model, the measured shading range moves from east to west.
3.2. The Improvement of the Canopy Shading Model for Apple Trees
The solar azimuth and altitude angle were changed when sunlight touched the canopy due to the effect of the canopy penumbra. The angle change caused by the effect of the canopy penumbra is unknown. It is necessary to improve the shading simulation model based on the measured data. We define the angle of deflection of sunlight when contact with the canopy as the modified solar azimuth (A1) and modified solar altitude (h1). The parameters (A1, h1) were introduced to improve the canopy shading model. The modified solar azimuth (A1) and modified solar altitude (h1) are given by the following:
where the position point (x, y, z) of the 3D apple tree model and the position point corresponding to the coordinate point (x’, y’) of the measured shading range were extracted at the corresponding time. A1 is the modified solar azimuth, and h1 is the modified solar altitude.
The modified solar azimuth (A1) and the solar azimuth (A), as well as the modified solar altitude angle (h1) and the solar altitude angle (h), are fitted (Figure A5). The deflection equation of sunlight is as follows:
(1) Modified solar azimuth (A1) and solar azimuth (A)
where A1 is the modified solar azimuth angle, A is the solar azimuth angle, and the range of the solar azimuth angle is from −180° to +180°, where the direction of south is 0°, the clockwise direction is positive (+), and the counter-clockwise direction is negative (−). Across a day, the negative values are before 12:00, and the positive values are after 12:00; 12:00 is the central symmetry axis. The solar azimuth angles from 8:00 to 12:00 and 12:00–17:00 are equal, but the signs are opposite.
When A < 0 (before 12:00 in a day), as the solar azimuth increases, the modified solar azimuth gradually changes from steep to slow. When A > 0 (after 12:00 in a day), as the solar azimuth increases, the modified solar azimuth gradually changes from slow to steep. A = 0° (Beijing time 12:00) is the turning point.
(2) Modified solar altitude angle (h1) and solar altitude angle (h):
where h1 is the modified solar altitude angle, h is the solar altitude angle, and the range of the solar altitude angle is from 0 to 90°. On one day, 12:00 is the central symmetry axis, and the solar altitude angles from 8:00 to 12:00 and 12:00–17:00 are equal.
According to the introduced deflection equation of sunlight (11) and (12), the improved canopy shading model is given by the following:
where the point Q (x, y, z) is an arbitrary point from the 3D model apple tree. Q′ (x1, y1) is the shading point of Q, h1 is the modified solar altitude angle, A1 is the modified solar azimuth angle, and the simulated shading point (Q′) was calculated by Equations (13) and (14) at one-hour intervals across a day (8:00–17:00). Shading points were connected to draw the simulated shading range over time (one-hour intervals) in a day.
The spatial‒temporal distribution of the shading range obtained via measurement was compared with that obtained via simulation using the improved canopy shading model (Figure A6). According to Figure A6, the improved canopy shading model can accurately simulate the shading range of an apple tree. The simulation accuracy exceeds 94.12%. On one day (8:00–17:00), the coincidence degree of the shaded area is shown in Table A2. Consequently, the improved canopy shading model can accurately simulate the shading range of apple trees.
3.3. Applicability Analysis of the Improved Canopy Shading Model
To verify the applicability of the improved canopy shading model, we selected the conventional plant spacing arrangement (plant spacing 4 m × 5 m) to test the spatial‒temporal distribution of apple tree shading.
In the conventional plant spacing arrangement, the measured shading range of apple trees is affected by adjacent apple trees. According to Figure A7a, the shading of an apple tree in a row is superimposed on the other trees at the 8:00 and 17:00 time periods. The shading is not superimposed on the row in the remaining periods. The maximum distance of shade from the north of the apple tree is approximately 2.1 m, and the maximum distance of shade from the south is approximately 1.7 m. There is no overlapping effect on the shading of the apple tree between rows. Over time, some areas are continuously shaded by the neighboring apple trees in a row (Figure A7b). The duration of shading is 4–7 h. The duration of shading is shortened as the distance from the apple trees increases.
The improved canopy shading model was used to simulate the spatial‒temporal shading distribution of apple trees in conventional arrangements. The simulated shading distribution was compared to the measured shading distribution (Figure A8). The coincidence degree between simulated shading and measured shading was 89.00%. Compared with the coincidence degree of a single apple tree, the coincidence degree is decreased. The reasons for the decrease may be that multiple apple trees affect each other and that there is an error in the actual measurement. Although the coincidence degree is decreased, the simulation effect can still better simulate the distribution of the shading distribution of apple trees in the conventional arrangement. This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation as well as the experimental conclusions that can be drawn.
4. Discussion
Defining the shading distribution of apple trees is the basis for designing and optimizing spatial arrangement of apple intercropping system [22,27]. The canopy shading model is widely used to simulate shading distribution of forests [31,32]. The challenge is that the canopy shading model cannot be verified by measured shading, making the shading model less accurate. To track the problem, this paper introduces 3D printing technology to obtain a 3D apple tree to measure the spatial‒temporal distribution characteristics of apple tree shading and improve the canopy shading model using measured data. Experiments results revealed the improved canopy shading model generated higher accuracy than the canopy shading model, and the improved model can be applied to simulate the spatial‒temporal distribution of shading of apple trees. Based on the results in this study, relevant issues are discussed in the following.
By comparing the shading distribution obtained via measurement and obtained via simulation using the canopy shading model, the canopy shading model has a larger simulation error. The factors that caused the shading of tree were carefully analyzed. The results showed that the canopy shading model did not consider the effect of canopy penumbra [36,37]. The improved canopy shading model introduces the deflection equation caused by the effect of canopy penumbra, so that significantly improved simulation accuracy. The improved canopy shading model is compared to other methods (NDVI, the canopy shading model, crown shadow, etc.). The improved model can accurately simulate shading distribution and analyze the continuous shade changes of forests, adjacent interference as well as ecological environment simulation of the agroforestry complex system.
The paper introduces 3D printing technology as a new study method into shading measurement of apple tree. However, the 3D apple tree has a smooth border, so the shading distribution does not reflect the influence of rough foliage on light. In addition, this paper only studies the spatial‒temporal distribution of the shading of apple trees. From the overall consideration of the light environment system, we should study the intensity of solar radiation combined with shading distribution under the forest in future research to design and optimize the spatial arrangement of the agroforestry intercropping system in the future.
Shading treatment reduces the PAR (photosynthetically active radiation) for intercrops and changes the microclimate under the canopy, resulting in decreased photosynthesis and transpiration rates. However, the intercrops can adapt to the low light intensity with changes in chlorophyll and the intercellular CO2 concentration [24,25,26]. The physiological characteristics and productivity of intercrops impacted by the changed microclimate need further investigation [38]. Those results showed that the light interception of trees decreased, and the photosynthetic efficiency of intercrops increased. The biomass and yield of crops increased gradually with increasing distance from tree lines [39]. The effect range of intercrops was also significantly different due to trees being in different growth seasons and different rows [40]. This is consistent with the spatial‒temporal distribution of shading of apple trees simulated by the improved shading model. This is necessary for the analysis of shading distribution to use the improved shading model. Tree spacing arrangements should be determined according to the analysis of shading distribution. The planting region of intercrops should be chosen by shading time in order to avoid low economic efficiency.
5. Conclusions
In this study, an improvement in the canopy shading model is proposed to make the simulation of the shading distribution more accurate. The improved canopy shading model overcomes the shortcoming of the canopy shading model in which the effect of the canopy penumbra was not considered. The deflection equation of sunlight is introduced in the improved canopy shading model because of the effect of the canopy penumbra. The deflection equation is statistically put forward using measured data of the shading distribution. Applying the new model to the shading distribution from a single apple tree indicates that the improved canopy shading model provides more reliable shading distribution simulations of apple trees. Additionally, the accuracy provided by the improved canopy shading model is increased more than that of the canopy shading model.
The shading distribution of apple trees in conventional arrangements was estimated using the improved canopy shading model. The results showed good agreement between the simulated shading from the improved canopy shading model and the measured shading, which indicates that the improved canopy shading model can effectively and reliably simulate the shading distribution of apple trees.
Author Contributions
J.W. and H.B. conceived and designed the experiments; J.W., Y.S., H.D. and R.P. performed the experiments; J.W. analyzed the data; J.W. wrote the paper; J.W., H.B. and Y.S. revised the paper.
Funding
This work was financially supported by the National Natural Science Foundation of China (No. 31470638), the National Key Technology R & D Program of the Ministry of Science and Technology of China (No. 2015BAD07B0502), the National Key R & D Program of China (No. 2016YFC0501704) and the Beijing Municipal Education Commission (CEFF-PXM2018_014207_000024).
Acknowledgments
The authors are grateful for the support received from the Ji County Forest Ecosystem Research Station. Many thanks are given to the anonymous reviewers and the editors for their helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Figure A1.
The three-dimensional (3D) model.

Figure A2.
Shading point of a forest at any point under sunlight.

Figure A3.
Point design figure of the 3D model of the plant spacing arrangement.

Figure A4.
Comparison of shade changes for an apple tree measured and simulated by the model over time across a day.

Figure A5.
Fitting figure: (a) Fitting figure for the modified solar altitude; (b) fitting figure of the modified solar azimuth.

Figure A6.
Comparison of shade changes for apple trees measured and simulated by a modified model over time across a day.

Figure A7.
(a) Temporal‒spatial distribution of apple tree shading in the conventional plant spacing arrangement based on the measured shading range of apple trees; (b) the time distribution of apple tree shading in the conventional plant spacing arrangement based on the measured shading range of apple trees.
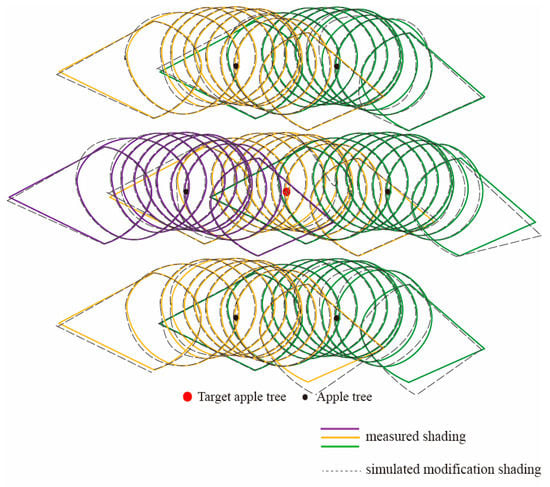
Figure A8.
Comparison of the shade distribution for apple trees measured and simulated by the modified model.

Table A1.
Characteristics of six-year-old apple trees in the study area in July 2016 (mean value).
Table A1.
Characteristics of six-year-old apple trees in the study area in July 2016 (mean value).
| Measurement | Apple Tree | 3D Model (1/50) | |
|---|---|---|---|
| Crown breadth | North and south (NS)/m | 4.192 | 0.084 |
| East and west (EW)/m | 4.001 | 0.080 | |
| Tree height (H)/m | 3.486 | 0.070 | |
| Height of tree trunk (h)/m | 0.752 | 0.015 | |
| Height under Crown breadth (A)/m | 0.883 | 0.018 | |

Table A2.
The coincidence degree between measured and simulated shade area/%.
Table A2.
The coincidence degree between measured and simulated shade area/%.
| Time | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 | 16:00 | 17:00 |
|---|---|---|---|---|---|---|---|---|---|---|
| Before improved | 72.63 | 80.02 | 89.90 | 91.24 | 94.02 | 92.14 | 88.51 | 86.12 | 78.76 | 84.00 |
| After improved | 94.12 | 95.17 | 95.32 | 96.22 | 97.00 | 97.13 | 95.56 | 96.41 | 95.31 | 95.01 |
References
- Mbow, C.; Van Noordwijk, M.; Luedeling, E.; Neufeldt, H.; Minang, P.A.; Kowero, G. Agroforestry solutions to address food security and climate change challenges in Africa. Curr. Opin. Environ. Sustain. 2014, 6, 61–67. [Google Scholar] [CrossRef]
- Cao, F.L.; Kimmins, J.P.; Wang, J.R. Competitive interactions in Ginkgo and crop species mixed agroforestry systems in Jiangsu, China. Agrofor. Syst. 2012, 84, 401–415. [Google Scholar] [CrossRef]
- Santiago-Freijanes, J.J.; Pisanelli, A.; Rois-Díaz, M.; Aldrey-Vázquez, J.A.; Rigueiro-Rodríguez, A.; Pantera, A.; Vityi, A.; Lojka, B.; Ferreiro-Domínguez, N.; Mosquera-Losada, M.R. Agroforestry development in Europe: Policy issues. Land Use Policy 2018, 76, 144–156. [Google Scholar] [CrossRef]
- Benjamin, E.O.; Ola, O.; Buchenrieder, G. Does an agroforestry scheme with payment for ecosystem services (PES) economically empower women in sub-Saharan Africa? Ecosyst. Serv. 2018, 31, 1–11. [Google Scholar] [CrossRef]
- Escribano, M.; Diaz-Caro, C.; Mesias, F.J. A participative approach to develop sustainability indicators for dehesa agroforestry farms. Sci. Total Environ. 2018, 640–641, 89–97. [Google Scholar] [CrossRef] [PubMed]
- Torralba, M.; Fagerholm, N.; Burgess, P.J.; Moreno, G.; Plieninger, T. Do European agroforestry systems enhance biodiversity and ecosystem services? A meta-analysis. Agric. Ecosyst. Environ. 2016, 230, 150–161. [Google Scholar] [CrossRef]
- Calfapietra, C.; Gielen, B.; Karnosky, D.; Ceulemans, R.; Scarascia Mugnozza, G. Response and potential of agroforestry crops under global change. Environ. Pollut. 2010, 158, 1095–1104. [Google Scholar] [CrossRef] [PubMed]
- Nassab, A.D.M.; Amon, T.; Kaul, H.P. Competition and yield in intercrops of maize and sunflower for biogas. Ind. Crops Prod. 2011, 34, 1203–1211. [Google Scholar] [CrossRef]
- Sun, Y.; Bi, H.; Xu, H.; Duan, H.; Peng, R.; Wang, J. Below-Ground Interspecific Competition of Appl (Malus pumila M.)–Soybean (Glycine max L. Merr.) Intercropping Systems Based on Niche Overlap on the Loess Plateau of China. Sustainability 2018, 10, 3022. [Google Scholar] [CrossRef]
- Gyau, A.; Franzel, S.; Chiatoh, M.; Nimino, G.; Owusu, K. Collective action to improve market access for smallholder producers of agroforestry products: Key lessons learned with insights from Cameroon’s experience. Curr. Opin. Environ. Sustain. 2014, 6, 68–72. [Google Scholar] [CrossRef]
- Klimek-Kopyra, A.; Zajac, T.; Rebilas, K. A mathematical model for the evaluation of cooperation and competition effects in intercrops. Eur. J. Agron. 2013, 51, 9–17. [Google Scholar] [CrossRef]
- Foster, K.; Neufeldt, H. Biocarbon projects in agroforestry: Lessons from the past for future development. Curr. Opin. Environ. Sustain. 2014, 6, 148–154. [Google Scholar] [CrossRef]
- Fagerholm, N.; Torralba, M.; Burgess, P.J.; Plieninger, T. A systematic map of ecosystem services assessments around European agroforestry. Ecol. Indic. 2016, 62, 47–65. [Google Scholar] [CrossRef]
- Cai, C.F.; Wang, F.; Ding, S.W.; Huang, L.; Hua, S.Z. Nutrients Competition and Its Action Mechanism Between Component Parts in Inter-cropping Systems and Agroforestry. Res. Soil Water Conserv. 2000, 7, 219–222. [Google Scholar] [CrossRef]
- Jia, G.M.; Zhang, P.D.; Wang, G.; Cao, J.; Han, J.C.; Huang, Y.P. Relationship Between Microbial Community and Soil Properties During Natural Succession of Abandoned Agricultural Land. Pedosphere 2010, 20, 352–360. [Google Scholar] [CrossRef]
- Ren, Y.Y.; Liu, J.J.; Wang, Z.L.; Zhang, S.Q. Planting density and sowing proportions of maize–soybean intercrops affected competitive interactions and water-use efficiencies on the Loess Plateau, China. Eur. J. Agron. 2016, 72, 70–79. [Google Scholar] [CrossRef]
- Charbonnier, F.; le Maire, G.; Dreyer, E.; Casanoves, F.; Christina, M.; Dauzat, J.; Eitel, J.U.H.; Vaast, P.; Vierling, L.A.; Roupsard, O. Competition for light in heterogeneous canopies: Application of MAESTRA to a coffee (Coffea arabica L.) agroforestry system. Agric. For. Meteorol. 2013, 181, 152–169. [Google Scholar] [CrossRef]
- Zhang, D.S.; Du, G.J.; Sun, Z.X.; Bai, W.; Wang, Q.; Feng, L.S.; Zheng, J.M.; Zhang, Z.; Liu, Y.; Yang, S.; et al. Agroforestry enables high efficiency of light capture, photosynthesis and dry matter production in a semi-arid climate. Eur. J. Agron. 2018, 94, 1–11. [Google Scholar] [CrossRef]
- Zhang, L.; van der Werf, W.; Bastiaans, L.; Zhang, S.; Li, B.; Spiertz, J.H.J. Light interception and utilization in relay intercrops of wheat and cotton. Field Crops Res. 2008, 107, 29–42. [Google Scholar] [CrossRef]
- Wang, Z.K.; Zhao, X.N.; Wu, P.T.; Gao, Y.; Yang, Q.; Shen, Y.Y. Border row effects on light interception in wheat/maize strip intercropping systems. Field Crops Res. 2017, 214, 1–13. [Google Scholar] [CrossRef]
- Zhao, W.G.; Qualls, R.J.; Berliner, P.R. Modeling of the short wave radiation distribution in an agroforestry system. Agric. For. Meteorol. 2003, 118, 185–206. [Google Scholar] [CrossRef]
- Zamora, D.S.; Jose, S.; Nair, P.K.R.; Ramsey, C.L. Interspecific competition in a pecan–cotton alleycropping system in the southern United States: Production physiology. Can. J. Bot. 2006, 84, 1686–1694. [Google Scholar] [CrossRef]
- Ramanna, L.; Rawat, I.; Bux, F. Light enhancement strategies improve microalgal biomass productivity. Renew. Sustain. Energy Rev. 2017, 80, 765–773. [Google Scholar] [CrossRef]
- Zivcak, M.; Brestic, M.; Kalaji, H.M. Photosynthetic responses of sun and shade grown barley leaves to high light: Is the lower PSII connectivity in shade leaves associated with protection against excess of light? Photosynth. Res. 2014, 119, 339–354. [Google Scholar] [CrossRef] [PubMed]
- De Casas, R.R.; Vargas, P.; Pérez-Corona, E.; Manrique, E.; García-Verdugo, C.; Balaguer, L. Sun and shade leaves of Olea europaea respond differently to plant size, light availability and genetic variation. Funct. Ecol. 2011, 25, 802–812. [Google Scholar] [CrossRef]
- Givinish, T.J. Adaptation to Sun and Shade: A Whole-plant perspective. Aust. J. Plant Physiol. 1988, 15, 63–92. [Google Scholar] [CrossRef]
- Terashima, I.; Hanba, Y.T.; Tazoe, Y.; Vyas, P.; Yano, S. Irradiance and phenotype: Comparative eco-development of sun and shade leaves in relation to photosynthetic CO2 diffusion. J. Exp. Bot. 2005, 57, 343–354. [Google Scholar] [CrossRef] [PubMed]
- Wobbe, L.; Bassi, R.; Kruse, O. Multi-level light capture control in plants and greenalgae. Trends Plant Sci. 2016, 21, 55–68. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.B.; Xu, H.S.; Bi, H.X.; Xi, W.M.; Bao, B.; Wang, X.Y.; Bi, C.; Chang, Y.F. Intercropping competition between apple trees and crops in agroforestry systems on the Loess Plateau of China. PLoS ONE 2013, 8, e70739. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, T.P.; Brook, R.M.; Wagstaff, P.; Sinclair, F.L. Effects of light environment on maize in hillside agroforestry systems of Nepal. Food Secur. 2012, 4, 103–114. [Google Scholar] [CrossRef]
- Annandale, J.G.; Jovanovic, N.Z.; Campbell, G.S.; Du Sautoy, N.; Lobit, P. Two-dimensional solar radiation interception model for hedgerow fruit trees. Agric. For. Meteorol. 2004, 121, 207–225. [Google Scholar] [CrossRef]
- Bellow, J.G.; Nair, P.K.R. Comparing common methods for assessing understory light availability in shaded-perennial agroforestry systems. Agric. For. Meteorol. 2003, 114, 197–221. [Google Scholar] [CrossRef]
- Alam, B.; Singh, R.; Uthappa, A.R.; Chaturvedi, M.; Singh, A.K.; Newaj, R.; Handa, A.K.; Chaturvedi, O.P. Different genotypes of Dalbergia sissoo trees modified microclimate dynamics differently on understory crop cowpea (Vigna unguiculata) as assessed through ecophysiological and spectral traits in agroforestry system. Agric. For. Meteorol. 2018, 249, 138–148. [Google Scholar] [CrossRef]
- Bertomeu, M. Growth and yield of maize and timber trees in smallholder agroforestry systems in Claveria, northern Mindanao, Philippines. Agrofor. Syst. 2011, 84, 73–87. [Google Scholar] [CrossRef]
- Keesman, K.J.; Graves, A.; van der Werf, W.; Burgess, P.J.; Palma, J.; Dupraz, C.; van Keulen, H. A system identification approach for developing and parameterising an agroforestry system model under constrained availability of data. Environ. Model. Softw. 2011, 26, 1540–1553. [Google Scholar] [CrossRef]
- Denholm, J.V. The influence of penumbra on canopy photosynthesis II. canopy of horizontal circulr leaves. Agric. Meteorol. 1981, 25. [Google Scholar] [CrossRef]
- Salazar, T.J.H. Calculation of the shadow-penumbra relation and its application on efficient architectural design. Sol. Energy 2014, 110, 139–150. [Google Scholar] [CrossRef]
- Li, S.R.; Yong, Z. Study on the shading mathmatic model of tree crown. Acta Agric. Univ. Henanensis 1994, 28, 361–366. [Google Scholar] [CrossRef]
- Talbot, G.; Dupraz, C. Simple models for light competition within agroforestry discontinuous tree stands: Are leaf clumpiness and light interception by woody parts relevant factors? Agrofor. Syst. 2011, 84, 101–116. [Google Scholar] [CrossRef]
- Adelinea, K.R.M.; Briotteta, X.; Ceamanosa, X.; Dartigalonguea, T.; Gastellu-Etchegorryc, J.P. ICARE-VEG: A 3D physics-based atmospheric correction method for treeshadows in urban areas. ISPRS J. Photogramm. Remote Sens. 2018, 142, 311–327. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).