Optimal Coordination Strategy of Regional Vertical Emission Abatement Collaboration in a Low-Carbon Environment
Abstract
:1. Introduction
2. Materials and Methods
3. Collaborative Centralized Scenario
4. Decentralized Scenarios
4.1. Non-Cost-Sharing Decentralized Scenario
4.2. Cost-Sharing Decentralized Scenario
5. Comparison and Analysis
6. Numerical Example
6.1. Case Description
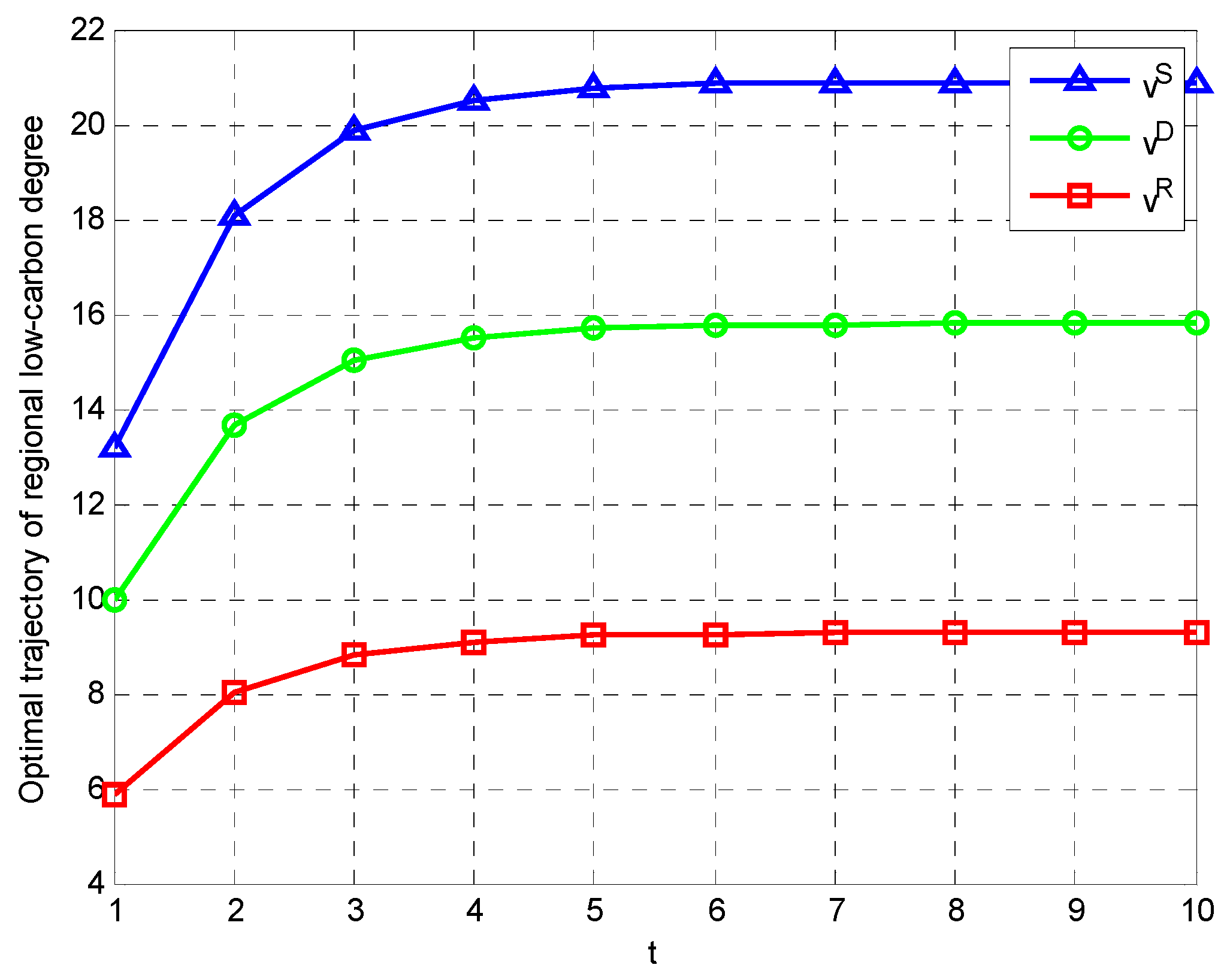
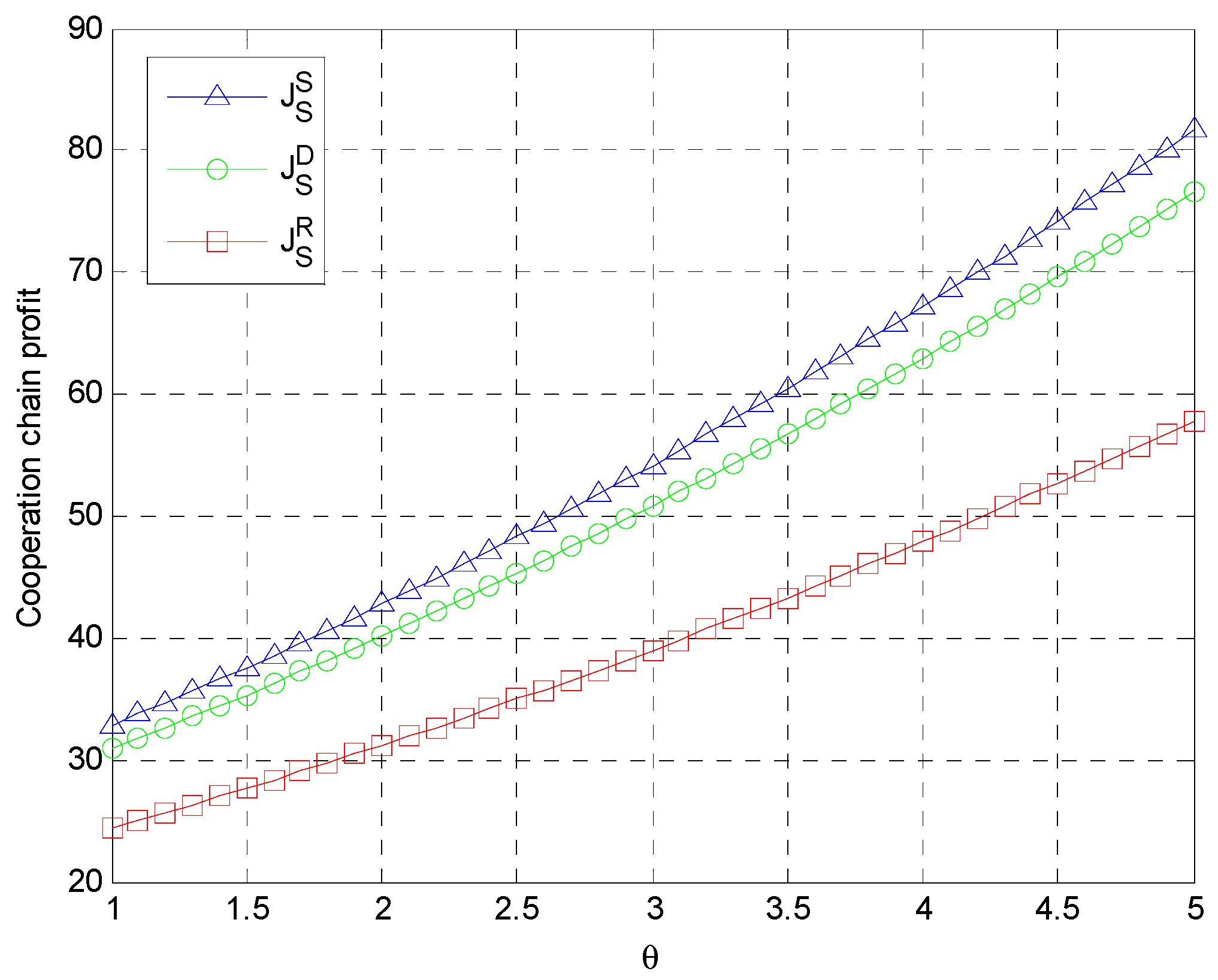
6.2. Numerical Simulation
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Meng, F.Y.; Su, B.; Thomson, E.; Zhou, D.Q.; Zhou, P. Measuring China’s regional energy and carbon emission efficiency with DEA models: A survey. Appl. Energy 2016, 183, 1–21. [Google Scholar] [CrossRef]
- Global Carbon Atlas. 2017. Available online: http://www.globalcarbonatlas.org/en/CO2-emissions (accessed on 25 January 2018).
- United Nations Framework Convention on Climate Change (UNFCCC). Intended National Determined Contributions (INDC) Submissions, 2015. Available online: http://www4.unfccc.int/Submissions/INDC/Submission%20Pages/submissions.aspx (accessed on 25 January 2018).
- Mi, Z.F.; Meng, J.; Guan, D.B.; Shan, Y.L.; Song, M.L.; Wei, Y.M.; Liu, Z.; Hubacek, K. Chinese CO2 emission flows have reversed since the global financial crisis. Nat. Commun. 2017, 8, 1712. [Google Scholar] [CrossRef] [PubMed]
- Mi, Z.F.; Meng, J.; Guan, D.B.; Shan, Y.L.; Liu, Z.; Wang, Y.T.; Feng, K.S.; Wei, Y.M. Pattern changes in determinants of Chinese emissions. Environ. Res. Lett. 2017, 12, 1–10. [Google Scholar] [CrossRef]
- Lin, B.Q.; Xin, Y.; Liu, X.Y. The strategic adjustment of China’s energy use structure in the context of energy-saving and carbon emission-reducing initiatives. Soc. Sci. China 2010, 1, 58–71. [Google Scholar]
- China Environmental State Bulletin. 2016. Available online: http://www.zhb.gov.cn/hjzl/zghjzkgb/lnzghjzkgb/201706/P020170605833655914077.pdf (accessed on 25 January 2018).
- Liu, H.; Zhang, Y.L.; Bi, J. Scenario analysis of China’s low-carbon development at local level-the case of Jiangsu Province, China. Popul. Resour. Environ. 2011, 4, 10–18. [Google Scholar]
- Zhao, L.M.; Chen, Z.J.; Liu, J.Y. Low-carbon cooperative strategy between government and enterprise based on differential games. Syst. Eng. 2016, 1, 84–90. [Google Scholar]
- Li, Z.; Zhang, M. A political economics analysis on China’s regional low-carbon competitiveness: Theory and empirical test. J. Financ. Econ. 2016, 42, 33–144. [Google Scholar]
- Tu, J.M.; Li, X.Y.; Guo, Z.C. Conception of enterprise carbon budget embedded in comprehensive budget system under low-carbon economy. China Ind. Econ. 2014, 3, 147–160. [Google Scholar]
- Montgomery, W.D. Markets in licenses and efficient pollution control programs. J. Econ. Theory 1972, 3, 395–418. [Google Scholar] [CrossRef]
- Zhang, L.M.; Yang, W.; Yuan, Y.; Zhou, R. An integrated carbon policy-based interactive strategy for carbon reduction and economic development in a construction material supply chain. Sustainability 2017, 9, 2107. [Google Scholar] [CrossRef]
- Zeng, S.H.; Nan, X.; Liu, C.; Chen, J.Y. The response of the Beijing carbon emissions allowance price (BJC) to macroeconomic and energy price indices. Energy Policy 2017, 106, 111–121. [Google Scholar] [CrossRef]
- Abildtrup, J.; Jensen, F.; Dubgaard, A. Does the Coase theorem hold in real markets? An application to the negotiations between waterworks and farmers in Denmark. J. Environ. Manag. 2012, 93, 169–176. [Google Scholar] [CrossRef] [PubMed]
- Chew, I.M.L.; Tan, R.R.; Foo, D.C.Y.; Chui, A.S.F. Game theory approach to the analysis of inter-plant water integration in an eco-industrial park. J. Clean. Prod. 2009, 17, 1611–1619. [Google Scholar] [CrossRef]
- Liao, Z.L.; Zhu, X.L.; Shi, J.R. Case study on initial allocation of Shanghai carbon emission trading based on Shapley value. J. Clean. Prod. 2015, 103, 338–344. [Google Scholar] [CrossRef]
- Yi, H.T.; Feiock, R.C.; Berry, F.S. Overcoming collective action barriers to energy sustainability: A longitudinal study of climate protection accord adoption by local governments. Renew. Sustain. Energy Rev. 2017, 79, 339–346. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Jin, X.C.; Yang, Q.X.; Zhang, Y. An empirical study on the institutional factors of energy conservation and emissions reduction: Evidence from listed companies in China. Energy Policy 2013, 57, 36–42. [Google Scholar] [CrossRef]
- Zeng, S.H.; Liu, Y.C.; Liu, C.; Nan, X. A review of renewable energy investment in the BRICS countries: history, models, problems and solutions. Renew. Sustain. Energy Rev. 2017, 74, 860–872. [Google Scholar] [CrossRef]
- Wu, J.; Chang, I.S.; Yilihamu, Q.; Zhou, Y. Study on the practice of public participation in environmental impact assessment by environmental non-governmental organizations in China. Renew. Sustain. Energy Rev. 2017, 74, 186–200. [Google Scholar] [CrossRef]
- Li, Q.W.; Long, R.Y.; Chen, H. Empirical study of the willingness of consumers to purchase low-carbon products by considering carbon labels: A case study. J. Clean. Prod. 2017, 161, 1237–1250. [Google Scholar] [CrossRef]
- Wirl, F. Social interactions within a dynamic competitive economy. J. Optim. Theory Appl. 2007, 133, 385–400. [Google Scholar] [CrossRef]
- Song, B.D.; Ko, Y.D. Effect of inspection policies and residual value of collected used products: A mathematical model and genetic algorithm for a closed-loop green manufacturing system. Sustainability 2017, 9, 1589. [Google Scholar] [CrossRef]
- Su, B.; Thomson, E. China’s carbon emissions embodied in (normal and processing) exports and their driving forces, 2006–2012. Energy Econ. 2016, 59, 414–422. [Google Scholar] [CrossRef]
- Yin, J.H.; Zheng, M.Z.; Chen, J. The effects of environmental regulation and technical progress on CO2 Kuznets curve: An evidence from China. Energy Policy 2015, 77, 97–108. [Google Scholar] [CrossRef]
- Su, B.; Ang, B.W. Multiplicative structural decomposition analysis of aggregate embodied energy and emission intensities. Energy Econ. 2017, 65, 137–147. [Google Scholar] [CrossRef]
- Xia, X.H.; Hu, Y.; Chen, G.Q.; Alsaedi, A.; Hayat, T.; Wu, X.D. Vertical specialization, global trade and energy consumption for an urban economy: A value added export perspective for Beijing. Ecol. Model. 2015, 318, 49–58. [Google Scholar] [CrossRef]
- Li, C.S.; Fan, Y.; Zhu, L. The study of carbon dioxide emission intensity abatement mechanism of iron and steel industry based on two-stage game model. Chin. J. Manag. Sci. 2012, 2, 93–101. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, D.Z.; Zhu, X.G. A game model for government and enterprise behavior based on a carbon tax. Resour. Sci. 2013, 1, 125–131. [Google Scholar]
- Decanio, S.J.; Fremstad, A. Game theory and climate diplomacy. Ecol. Econ. 2013, 85, 177–187. [Google Scholar] [CrossRef]
- Zhang, G.X.; Zhang, X.T.; Cheng, S.J.; Chai, G.R.; Wang, L.L. Signaling game model of government and enterprise based on the subsidy policy for energy saving and emission reduction. Chin. J. Manag. Sci. 2013, 21, 129–136. [Google Scholar]
- Zhao, R.; Zhou, X.; Han, J.J.; Liu, C.L. For the sustainable performance of the carbon reduction labeling policies under an evolutionary game simulation. Technol. Forecast. Soc. Chang. 2016, 112, 262–274. [Google Scholar] [CrossRef]
- Jørgensen, S.; Zaccour, G. Time consistent side payments in a dynamic game of downstream pollution. J. Econ. Dyn. Control. 2001, 25, 1973–1987. [Google Scholar] [CrossRef]
- Huang, Z.S.; Nie, J.J.; Tsai, S.B. Dynamic collection strategy and coordination of a remanufacturing closed-loop supply chain under uncertainty. Sustainability 2016, 9, 683. [Google Scholar] [CrossRef]
- Yeung, D.W.K.; Petrosyan, L.A. Subgame consistent solutions of a cooperative stochastic differential game with nontransferable payoffs. J. Optim. Theory Appl. 2005, 124, 701–724. [Google Scholar] [CrossRef]
- Guo, D.X.; Wu, Y.Y.; Xu, Q.Y. Analysis of supply chain under different subsidy policies of the government. Susainability 2016, 8, 1290. [Google Scholar] [CrossRef]
- Jørgensen, S.; Zaccour, G. A survey of game-theoretic models of cooperative advertising. Eur. J. Oper. Res. 2014, 237, 1–14. [Google Scholar] [CrossRef]
- Yeung, D.W.K.; Petrosyan, L.A. Subgame consistent cooperative solution for NTU dynamic games via variable weights. Automatica 2015, 59, 84–89. [Google Scholar] [CrossRef]
- Benchekroun, H.; Martín-Herrán, G. The impact of foresight in a tansboundary pollution game. Eur. J. Oper. Res. 2016, 251, 300–309. [Google Scholar] [CrossRef]
- Bertinelli, L.; Camacho, C.; Zou, B.T. Carbon capture and storage and transboundary pollution: A differential game approach. Eur. J. Oper. Res. 2014, 237, 721–728. [Google Scholar] [CrossRef]
- Wang, Z.H.; Yang, L. Delinking indicators on regional industry development and carbon emissions: Beijing-Tianjin-Hebei economic band case. Ecol. Indic. 2015, 45, 41–48. [Google Scholar] [CrossRef]
- Jørgensen, S.; Taboubi, S.; Zaccour, G. Retail promotions with negative brand image effects: Is cooperation possible? Eur. J. Oper. Res. 2003, 150, 395–405. [Google Scholar] [CrossRef]
- Breton, M.; Sokri, A.; Zaccour, G. Incentive equilibrium in an overlapping-generations environmental game. Eur. J. Oper. Res. 2008, 185, 687–699. [Google Scholar] [CrossRef]
- Chen, Q.X.; Kang, C.Q.; Ming, H.; Wang, Z.Y.; Xia, Q.; Xu, G.X. Assessing the low-carbon effects of inter-regional energy delivery in China’s electricity sector. Renew. Sustain. Energy Rev. 2014, 32, 671–683. [Google Scholar] [CrossRef]
- Zaccour, G. On the coordination of dynamic marketing channels and two-part tariffs. Automatica 2008, 44, 1233–1239. [Google Scholar] [CrossRef]
- Dockner, E.J.; Van Long, N. International pollution control: Cooperative versus noncooperative strategies. J. Environ. Econ. Manag. 1993, 25, 13–29. [Google Scholar] [CrossRef]
- Yu, W.; Han, R.Z. Coordinating a two-echelon supply chain under carbon tax. Sustainability 2017, 12, 2360. [Google Scholar] [CrossRef]
- Qin, F.F.; Zhang, X.N. Designing an optimal subsidy scheme to reduce emissions for a competitive urban transport market. Sustainability 2015, 7, 11933–11948. [Google Scholar] [CrossRef]
- Wei, C.; Ni, J.L.; Du, L.M. Regional allocation of carbon dioxide abatement in China. China Econ. Rev. 2012, 23, 552–565. [Google Scholar] [CrossRef]
- Chen, J.X.; Chen, J. Supply chain carbon footprinting and responsibility allocation under emission regulations. J. Environ. Manag. 2017, 188, 255–267. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Zhang, Q.; Ji, J. Pricing and carbon emission reduction decisions in supply chains with vertical and horizontal cooperation. Int. J. Prod. Econ. 2017, 191, 286–297. [Google Scholar] [CrossRef]
- Eyland, T.; Zaccour, G. Carbon tariffs and cooperative outcomes. Energy Policy 2014, 65, 718–728. [Google Scholar] [CrossRef]
- Wei, Y.M.; Mi, Z.F.; H, Z.M. Climate policy modeling: An online SCI-E and SSCI based literature review. Omega 2015, 57, 70–84. [Google Scholar] [CrossRef]
- Air Pollution Prevention and Control Action Plan. 2013. Available online: http://www.gov.cn/zhengce/content/2013-09/13/content_4561.htm (accessed on 27 January 2018).
- Beijing-Tianjin-Hebei Reinforcement Measures for Air Pollution Control (2016–2017). 2016. Available online: http://www.envsc.net/file/201609301225182778.pdf (accessed on 27 January 2018).
- Law of the People’s Republic of China on Prevention and Control of Atmospheric Pollution. 2016. Available online: http://www.zhb.gov.cn/gzfw_13107/zcfg/fl/201605/t20160522_343394.shtml (accessed on 27 January 2018).
- Tianjin Environmental Statement. 2016. Available online: http://www.tjhb.gov.cn/root16/mechanism/standard_monitoring_of_the_Department_of_science_andtechnology/201706/P020170605593040876560.pdf (accessed on 27 January 2018).
- Ambient Air Quality Standards. 2012. Available online: http://kjs.mep.gov.cn/hjbhbz/bzwb/dqhjbh/dqhjzlbz/201203/W020120410330232398521.pdf (accessed on 28 January 2018).
- Jørgensen, S.; Martín-Herrán, G.; Zaccour, G. Dynamic games in the economics and management of pollution. Environ. Model. Assess. 2010, 15, 433–467. [Google Scholar] [CrossRef]




| Parameter | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Basic values | 8.16/4.58 | 3.27/6.53 | 2.75/2.75 | 9.27/15.8 | 20.90 | 39.00/50.83 | 21.67/32.50 | ||||||
| α = (1.00→3.00) | + | + | + | + | × | × | + | + | + | + | + | + | + |
| β = (0.50→1.50) | + | + | × | × | + | + | + | + | + | + | + | + | + |
| φ = (0.50→1.50) | − | − | − | − | − | − | − | − | − | − | − | − | − |
| ϕ = (2.50→7.50) | × | × | × | × | × | × | × | × | × | + | + | + | + |
| δ = (2.50→7.50) | + | + | + | + | × | × | + | + | + | + | + | + | + |
| τ = (1.50→4.50) | + | + | × | × | + | + | + | + | + | + | + | + | + |
| θ = (1.50→4.50) | + | + | + | + | + | + | + | + | + | + | + | + | + |
| ρ = (0.15→0.45) | − | − | − | − | − | − | − | − | − | − | − | − | − |
| μG = (0.50→1.50) | − | − | − | − | × | × | − | − | − | − | − | − | − |
| μM = (0.50→1.50) | × | × | × | × | − | − | − | − | − | − | − | − | − |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, D.; Jiang, K.; Li, Z. Optimal Coordination Strategy of Regional Vertical Emission Abatement Collaboration in a Low-Carbon Environment. Sustainability 2018, 10, 571. https://doi.org/10.3390/su10020571
You D, Jiang K, Li Z. Optimal Coordination Strategy of Regional Vertical Emission Abatement Collaboration in a Low-Carbon Environment. Sustainability. 2018; 10(2):571. https://doi.org/10.3390/su10020571
Chicago/Turabian StyleYou, Daming, Ke Jiang, and Zhendong Li. 2018. "Optimal Coordination Strategy of Regional Vertical Emission Abatement Collaboration in a Low-Carbon Environment" Sustainability 10, no. 2: 571. https://doi.org/10.3390/su10020571
APA StyleYou, D., Jiang, K., & Li, Z. (2018). Optimal Coordination Strategy of Regional Vertical Emission Abatement Collaboration in a Low-Carbon Environment. Sustainability, 10(2), 571. https://doi.org/10.3390/su10020571





