Investigating the Potential of Using POI and Nighttime Light Data to Map Urban Road Safety at the Micro-Level: A Case in Shanghai, China
Abstract
:1. Introduction
2. Study Area and Data
3. Methods
3.1. Network Kernel Density Estimation
3.2. Variable Collinearity Analysis
3.3. Random Forest Regression Algorithm
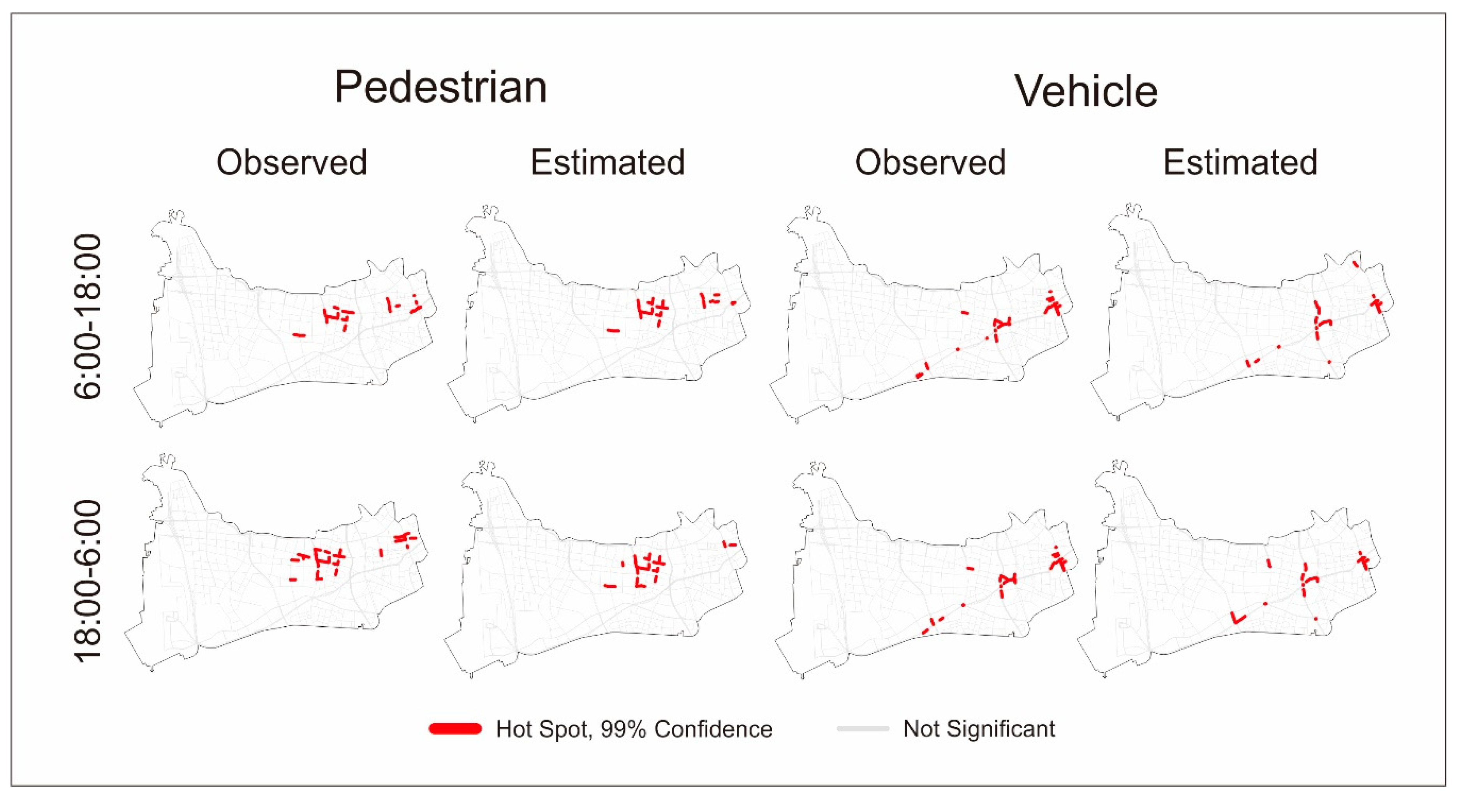
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Global Status Report on Road Safety 2018; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Elvik, R. Laws of accident causation. Accid. Anal. Prev. 2006, 38, 742–747. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Quddus, M.A.; Ison, S.G. The effect of traffic and road characteristics on road safety: A review and future research direction. Saf. Sci. 2013, 57, 264–275. [Google Scholar] [CrossRef]
- Lee, C.; Hellinga, B.; Saccomanno, F. Real-Time Crash Prediction Model for Application to Crash Prevention in Freeway Traffic. Transp. Res. Rec. J. Transp. Res. Board 2007, 1840, 67–77. [Google Scholar] [CrossRef]
- Bao, J.; Liu, P.; Ukkusuri, S.V. A spatiotemporal deep learning approach for citywide short-term crash risk prediction with multi-source data. Accid. Anal. Prev. 2019, 122, 239–254. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.M.; Abdel-Aty, M.A. The viability of using automatic vehicle identification data for real-time crash prediction. IEEE Trans. Intell. Transp. Syst. 2012, 13, 459–468. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Abdel-Aty, M.; Yu, R. Bayesian Updating Approach for Real-Time Safety Evaluation with Automatic Vehicle Identification Data. Transp. Res. Rec. J. Transp. Res. Board 2013, 2280, 60–67. [Google Scholar] [CrossRef]
- Basso, F.; Basso, L.J.; Bravo, F.; Pezoa, R. Real-time crash prediction in an urban expressway using disaggregated data. Transp. Res. Part C Emerg. Technol. 2018, 86, 202–219. [Google Scholar] [CrossRef]
- Shirazinejad, R.S.; Dissanayake, S.; Al-Bayati, A.J.; York, D.D. Evaluating the safety impacts of increased speed limits on freeways in kansas using before-and-after study approach. Sustainability 2018, 11, 119. [Google Scholar] [CrossRef]
- Chang, L.Y.; Chen, W.C. Data mining of tree-based models to analyze freeway accident frequency. J. Saf. Res. 2005, 36, 365–375. [Google Scholar] [CrossRef]
- Bao, J.; Liu, P.; Qin, X.; Zhou, H. Understanding the effects of trip patterns on spatially aggregated crashes with large-scale taxi GPS data. Accid. Anal. Prev. 2018, 120, 281–294. [Google Scholar] [CrossRef]
- Qin, X.; Ivan, J.N.; Ravishanker, N. Selecting exposure measures in crash rate prediction for two-lane highway segments. Accid. Anal. Prev. 2004, 36, 183–191. [Google Scholar] [CrossRef]
- Hou, Q.; Tarko, A.P.; Meng, X. Investigating factors of crash frequency with random effects and random parameters models: New insights from Chinese freeway study. Accid. Anal. Prev. 2020, 120, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Wier, M.; Weintraub, J.; Humphreys, E.H.; Seto, E.; Bhatia, R. An area-level model of vehicle-pedestrian injury collisions with implications for land use and transportation planning. Accid. Anal. Prev. 2009, 41, 137–145. [Google Scholar] [CrossRef] [PubMed]
- Graham, D.J.; Glaister, S. Spatial variation in road pedestrian casualties: The role of urban scale, density and land-use mix. Urban Stud. 2003, 40, 1591–1607. [Google Scholar] [CrossRef]
- Tulu, G.S.; Washington, S.; Haque, M.M.; King, M.J. Investigation of pedestrian crashes on two-way two-lane rural roads in Ethiopia. Accid. Anal. Prev. 2015, 78, 118–126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- LaScala, E.A.; Gerber, D.; Gruenewald, P.J. Demographic and environmental correlates of pedestrian injury collisions: A spatial analysis. Accid. Anal. Prev. 2000, 32, 651–658. [Google Scholar] [CrossRef]
- Yao, S.; Loo, B.P.Y.; Lam, W.W.Y. Measures of activity-based pedestrian exposure to the risk of vehicle-pedestrian collisions: Space-time path vs. potential path tree methods. Accid. Anal. Prev. 2015, 75, 320–332. [Google Scholar] [CrossRef]
- Shirazinejad, R.S.; Al-Bayati, A.J. Impact of advertising signs on freeway crashes within a certain distance in Michigan. In Proceedings of the Construction Research Congress 2018: Safety and Disaster Management-Selected Papers from the Construction Research Congress 2018, New Orleans, LA, USA, 2–4 April 2018; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 698–705. [Google Scholar]
- Alkahtani, K.F.; Abdel-Aty, M.; Lee, J. A zonal level safety investigation of pedestrian crashes in Riyadh, Saudi Arabia. Int. J. Sustain. Transp. 2019, 13, 255–267. [Google Scholar] [CrossRef]
- Loukaitou-Sideris, A.; Liggett, R.; Sung, H.-G. Death on the crosswalk—A study of pedestrian-automobile collisions in Los Angeles. J. Plan. Educ. Res. 2007, 26, 338–351. [Google Scholar] [CrossRef]
- Rifaat, S.M.; Tay, R.; Raihan, S.M.; Fahim, A.; Touhidduzzaman, S.M. Vehicle-Pedestrian crashes at Intersections in Dhaka city. Open Transp. J. 2017, 11. [Google Scholar] [CrossRef]
- Yao, S.; Wang, J.; Fang, L.; Wu, J. Identification of vehicle-pedestrian collision hotspots at the micro-level using network kernel density estimation and random forests: A case study in Shanghai, China. Sustainability 2018, 10, 4762. [Google Scholar] [CrossRef]
- Jia, R.; Khadka, A.; Kim, I. Traffic crash analysis with point-of-interest spatial clustering. Accid. Anal. Prev. 2018, 121, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Seto, K.C. Mapping urbanization dynamics at regional and global scales using multi-temporal DMSP/OLS nighttime light data. Remote Sens. Environ. 2011, 115, 2320–2329. [Google Scholar] [CrossRef]
- Ma, Q.; He, C.; Wu, J.; Liu, Z.; Zhang, Q.; Sun, Z. Quantifying spatiotemporal patterns of urban impervious surfaces in China: An improved assessment using nighttime light data. Landsc. Urban Plan. 2014, 130, 36–49. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Yao, S.; Wu, Q.; Chen, Z.; Wu, J. A surface network based method for studying urban hierarchies by night time light remote sensing data. Int. J. Geogr. Inf. Sci. 2019, 33, 1377–1398. [Google Scholar] [CrossRef]
- Propastin, P.; Kappas, M. Assessing Satellite-Observed Nighttime Lights for Monitoring Socioeconomic Parameters in the Republic of Kazakhstan. GISci. Remote Sens. 2012, 49, 538–557. [Google Scholar] [CrossRef]
- Ma, T.; Zhou, C.; Pei, T.; Haynie, S.; Fan, J. Responses of Suomi-NPP VIIRS-derived nighttime lights to socioeconomic activity in Chinas cities. Remote Sens. Lett. 2014, 5, 165–174. [Google Scholar] [CrossRef]
- Yu, B.; Shi, K.; Hu, Y.; Huang, C.; Chen, Z.; Wu, J. Poverty Evaluation Using NPP-VIIRS Nighttime Light Composite Data at the County Level in China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1217–1229. [Google Scholar] [CrossRef]
- Zhao, X.; Yu, B.; Liu, Y.; Chen, Z.; Li, Q.; Wang, C.; Wu, J. Estimation of Poverty Using Random Forest Regression with Multi-Source Data: A Case Study in Bangladesh. Remote Sens. 2019, 11, 375. [Google Scholar] [CrossRef]
- Shanghai Municipal People’s Government. Available online: http://www.shanghai.gov.cn (accessed on 29 August 2019).
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD). Code for Design of Urban Road Engineering; MOHURD: Beijing, China, 2016.
- Letu, H.; Hara, M.; Tana, G.; Nishio, F. A saturated light correction method for DMSP/OLS nighttime satellite imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 389–396. [Google Scholar] [CrossRef]
- Schueler, C.F.; Lee, T.F.; Miller, S.D. VIIRS constant spatial-resolution advantages. Int. J. Remote Sens. 2013, 34, 5761–5777. [Google Scholar] [CrossRef]
- Shi, K.; Huang, C.; Yu, B.; Yin, B.; Huang, Y.; Wu, J. Evaluation of NPP-VIIRS night-time light composite data for extracting built-up urban areas. Remote Sens. Lett. 2014, 5, 358–366. [Google Scholar] [CrossRef]
- Ou, J.; Liu, X.; Li, X.; Li, M.; Li, W. Evaluation of NPP-VIIRS nighttime light data for mapping global fossil fuel combustion CO2 emissions: A comparison with DMSP-OLS nighttime light data. PLoS ONE 2015, 10, e0138310. [Google Scholar] [CrossRef] [PubMed]
- Version 1 VIIRS Day/Night Band Nighttime Lights. Available online: https://ngdc.noaa.gov/eog/viirs/%0 Adownload_dnb_composites.html (accessed on 5 November 2018).
- Xie, Z.; Yan, J. Kernel Density Estimation of traffic accidents in a network space. Comput. Environ. Urban Syst. 2008, 32, 396–406. [Google Scholar] [CrossRef] [Green Version]
- Gibin, M.; Longley, P.; Atkinson, P. Kernel density estimation and percent volume contours in general practice catchment area analysis in urban areas. In Proceedings of the GIScience Research UK Conference (GISRUK), Maynooth, UK, 11–13 April 2007. [Google Scholar]
- Okabe, A.; Satoh, T.; Sugihara, K. A kernel density estimation method for networks, its computational method and a GIS-based tool. Int. J. Geogr. Inf. Sci. 2009, 23, 7–32. [Google Scholar] [CrossRef]
- Xie, Z.; Yan, J. Detecting traffic accident clusters with network kernel density estimation and local spatial statistics: An integrated approach. J. Transp. Geogr. 2013, 31, 64–71. [Google Scholar] [CrossRef]
- Sawalha, Z.; Sayed, T. Traffic accident modeling: Some statistical issues. Can. J. Civ. Eng. 2006, 33, 1115–1124. [Google Scholar] [CrossRef]
- Colinearity in Random Forests-Does It Matter? Available online: http://www.innocentheroine.com/2017./08/colinearity-in-random-forests-does-it.html (accessed on 29 August 2019).
- Wichers, C.R. The Detection of Multicollinearity: A Comment. Rev. Econ. Stat. 1975, 57, 366–368. [Google Scholar] [CrossRef]
- Belsley, D.A. A Guide to using the collinearity diagnostics. Comput. Sci. Econ. Manag. 1991, 4, 33–50. [Google Scholar]
- Næs, T.; Mevik, B.H. Understanding the collinearity problem in regression and discriminant analysis. J. Chemom. 2001, 15, 413–426. [Google Scholar] [CrossRef]
- Mason, C.H.; Perreault, W.D. Collinearity, Power, and Interpretation of Multiple Regression Analysis. J. Mark. Res. 2006, 28, 268. [Google Scholar] [CrossRef]
- Miles, J. Tolerance and Variance Inflation Factor. Wiley StatsRef Stat. Ref. Online 2014, 4, 2055–2056. [Google Scholar]
- Zainodin, H.J.; Yap, S.J. Overcoming multicollinearity in multiple regression using correlation coefficient. AIP Conf. Proc. 2013, 1557, 416–419. [Google Scholar]
- Bollinger, G.; Belsley, D.A.; Kuh, E.; Welsch, R.E. Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. J. Mark. Res. 1981, 18, 392. [Google Scholar] [CrossRef]
- O’Brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Grömping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random forests. In Ensemble Machine Learning Methods Applications; Springer: New York, NY, USA, 2012; pp. 157–175. [Google Scholar]
- Leo, B. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [Green Version]
- Wolpert, D.H. An Efficient Method to Estimate Bagging’s Generalization Error. Mach. Learn. 1997, 35, 41–55. [Google Scholar] [CrossRef]
- Kim, Y.; Jeong, S.; Kimy, D. Classification and Regression Trees Classification and Regression Trees, 1984. IEICE Trans. Commun. 2008, 91, 3544–3551. [Google Scholar] [CrossRef]
- Scikit-Learn. Available online: https://scikit-learn.org/stable/ (accessed on 29 August 2019).
- Lerman, P.M. Fitting Segmented Regression Models by Grid Search. Appl. Stat. 1980, 29, 77. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: Experiences from the scikit-learn project. arXiv 2013, arXiv:1309.0238. [Google Scholar]
- Kühnlein, M.; Appelhans, T.; Thies, B.; Nauss, T. Improving the accuracy of rainfall rates from optical satellite sensors with machine learning-A random forests-based approach applied to MSG SEVIRI. Remote Sens. Environ. 2014, 141, 129–143. [Google Scholar] [CrossRef]
- Ord, J.K.; Getis, A. The Analysis of Spatial Association. Geogr. Anal. 1992, 24, 189–206. [Google Scholar]





| Road Type | Design Standard | Function | ||
|---|---|---|---|---|
| Width (m) | No. of Lanes | Design Speed (km/h) | ||
| Expressway | ≥40 | ≥4 (one-way) | 60–100 | Territory-wide transportation |
| Arterial road | 30–40 | - | 40–60 | Transportation between districts |
| Secondary trunk road | 25–40 | - | 30–50 | Connecting arterial roads to districts |
| Branch road | 12–25 | - | 20–40 | Connecting secondary trunk roads to communities |
| Road Type | Total Length/m (%) | No. of Vehicle–Pedestrian Collisions (%) | No. of Vehicle–Vehicle Collisions (%) |
|---|---|---|---|
| Expressway | 71,361.66 (19.6%) | 5 (0.2%) | 519 (0.7%) |
| Arterial road | 91,691.49 (25.1%) | 672 (27.1%) | 26,784 (38.4%) |
| Secondary trunk road | 40,343.97 (11.1%) | 456 (18.4%) | 11,268 (16.2%) |
| Branch road | 161,605.70 (44.3%) | 1351 (54.4%) | 31,098 (44.6%) |
| All | 365,002.80 (100%) | 2484 (100%) | 69,669 (100%) |
| Variable Name | Description | Data Source |
|---|---|---|
| NTL | NTL value of each road segment (nanoWatts/cm2/sr) | NPP-VIIRS NTL |
| NoBank | Number of banking service facilities within 500 m of each segment | Baidu POI |
| NoCom | Number of commercial buildings within 500 m of each segment | |
| NoRet | Number of retail shops within 500 m of each segment | |
| NoMed | Number of medical services within 500 m of each segment | |
| NoEdu | Number of educational institutions within 500 m of each segment | |
| NoBus | Number of bus stops within 500 m of each segment |
| Parameter Name | Description 1 | Best Value |
|---|---|---|
| n_estimators | The number of trees in RFR. | 600 |
| max_features | The largest number of features to consider when branching. | 2 |
| max_depth | The maximum depth of a single tree. | 25 |
| min_samples_split | The minimum number of samples required to split an internal node. | 6 |
| min_samples_leaf | The minimum number of samples required to be at a leaf node. | 1 |
| Variables | Tolerance | VIF |
|---|---|---|
| NTL | 0.767 | 1.304 |
| NoBank | 0.396 | 2.524 |
| NoCom | −0.591 | 1.692 |
| NoRet | 0.249 | 4.017 |
| NoMed | 0.604 | 1.655 |
| NoEdu | 0.422 | 2.371 |
| NoBus | 0.619 | 1.615 |
| Collision Type | Road Type | Data | OOB Scores in Each Period | |
|---|---|---|---|---|
| 6:00–18:00 | 18:00–6:00 | |||
| Vehicle–Pedestrian | Arterial | POI | 0.80 | 0.75 |
| POI + NTL | 0.84 (+5%) | 0.79 (+5%) | ||
| Secondary trunk | POI | 0.84 | 0.74 | |
| POI + NTL | 0.84 (+0%) | 0.78 (+5%) | ||
| Branch | POI | 0.75 | 0.70 | |
| POI + NTL | 0.80 (+6%) | 0.74 (+6%) | ||
| Expressway | POI | −0.18 | 0.07 | |
| POI + NTL | 0.18 (200%) | 0.12 (+58%) | ||
| Vehicle–Vehicle | Arterial | POI | 0.70 | 0.69 |
| POI + NTL | 0.77 (+10%) | 0.75 (+10%) | ||
| Secondary trunk | POI | 0.80 | 0.79 | |
| POI + NTL | 0.83 (+4%) | 0.82 (+4%) | ||
| Branch | POI | 0.52 | 0.54 | |
| POI + NTL | 0.60 (+16%) | 0.62 (+16%) | ||
| Expressway | POI | 0.06 | 0.07 | |
| POI + NTL | 0.12 (+100%) | 0.12 (+84%) | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N.; Liu, Y.; Wang, J.; Qian, X.; Zhao, X.; Wu, J.; Wu, B.; Yao, S.; Fang, L. Investigating the Potential of Using POI and Nighttime Light Data to Map Urban Road Safety at the Micro-Level: A Case in Shanghai, China. Sustainability 2019, 11, 4739. https://doi.org/10.3390/su11174739
Wang N, Liu Y, Wang J, Qian X, Zhao X, Wu J, Wu B, Yao S, Fang L. Investigating the Potential of Using POI and Nighttime Light Data to Map Urban Road Safety at the Micro-Level: A Case in Shanghai, China. Sustainability. 2019; 11(17):4739. https://doi.org/10.3390/su11174739
Chicago/Turabian StyleWang, Ningcheng, Yufan Liu, Jinzi Wang, Xingjian Qian, Xizhi Zhao, Jianping Wu, Bin Wu, Shenjun Yao, and Lei Fang. 2019. "Investigating the Potential of Using POI and Nighttime Light Data to Map Urban Road Safety at the Micro-Level: A Case in Shanghai, China" Sustainability 11, no. 17: 4739. https://doi.org/10.3390/su11174739





