Economic Dispatch Optimization of Multi-Water Resources: A Case Study of an Island in South Korea
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Existing Water Supply System and Possible Risks to the System
2.3. Data Source and Collection
2.4. Methodology
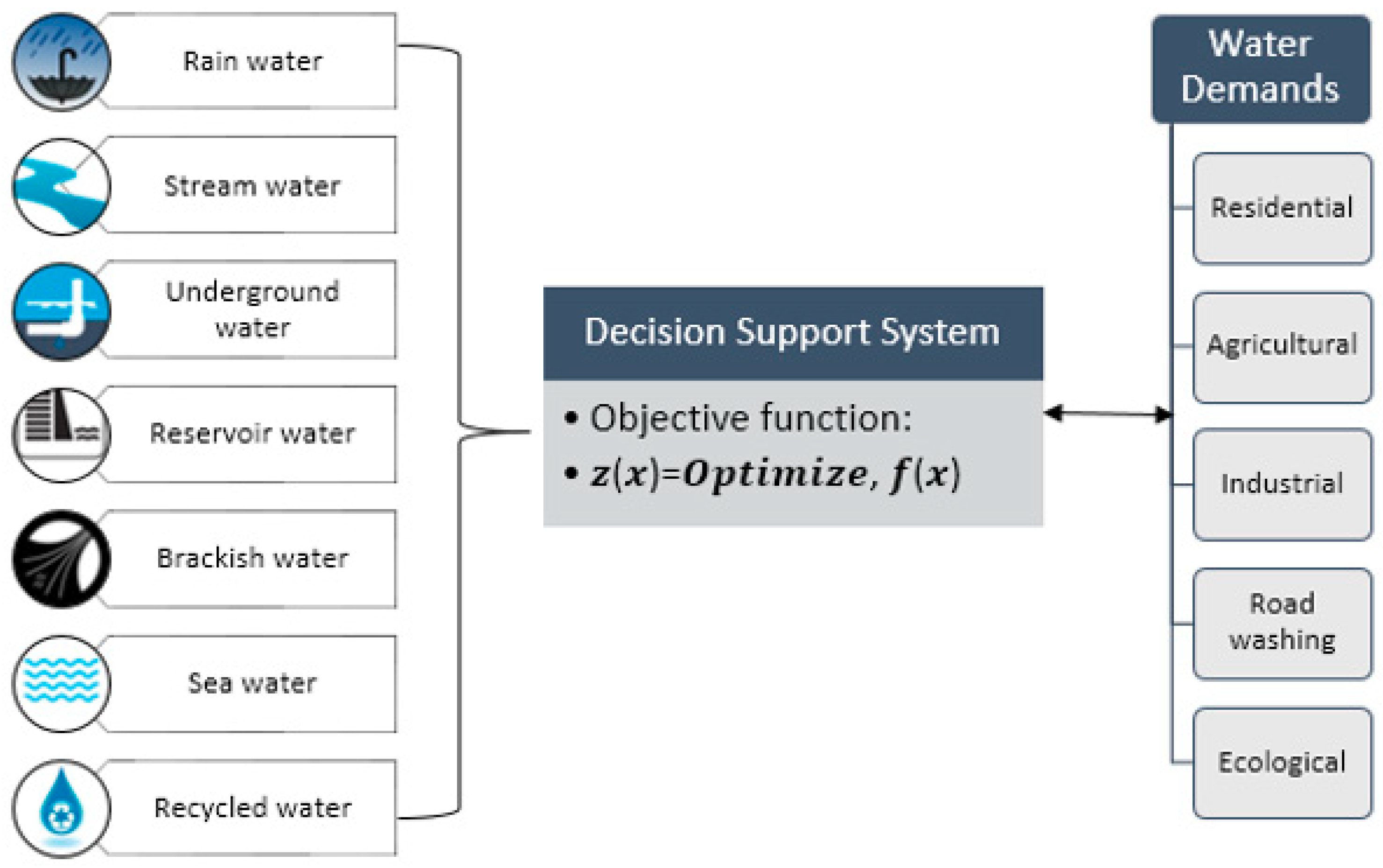
2.4.1. Optimization Problem Formulation
2.4.2. Objective Functions
- Xij = supplied water volume from the water source i to the user j;
- i = water source type, i = 1, 2, 3, 4, 5, 6, and 7;
- j = water user or demand type, j = 1, 2, 3, 4, and 5;
- ∝ij = cost function of water supply from source i to user j. The cost function ∝ij is dependent on capital cost, operation and maintenance (O&M) cost, and environmental cost.
2.4.3. Water Withdrawal Constraints/Conditions
Constraints Related to Water Volume
- The volume of water withdrawn must be less than or equal to the maximum capacity of the supply available from the sources considered (Si):where, Si = 20, 43.78, 18.7, 0.76, 55.18, 50, and 121, are the maximum supply capacity of water sources: rain water, stream water, underground water, reservoir water, brackish water, sea water, and recycled water, respectively. Unit of Si = 103 m3/day.
- The volume of water withdrawn from each water source, which undergoes treatment, must be less than or equal to the maximum capacity (Qi) of the respective water treatment plant (WTP):where, Qi = 20, 45, 20, 1, 60, and 50 are the maximum treatment capacity of WTPs for rain water, stream water, underground water, reservoir water, brackish water, and sea water, respectively. Unit of Qi = 103 m3/day.
- Reclaimed (Grey) water must not be considered for domestic/residential use:
- Decision variables involved in the optimization calculation must be greater than or equal to zero (non-negativity constraint of decision variables):
Constraints Related to Water Quality in Total Dissolved Solids (TDS; unit = ppm)
- For the case of waste water/grey water:
- If TDS < 2000, supply to the agricultural purpose without any treatment.
- If TDS > 2000, blend with available rain/stream/underground/reservoir water until TDS value falls below 2000 ppm and supply it to agricultural purpose.
- If 2000 < TDS < 10,000, use the BWRO process for purification of water, and for more than TDS > 10,000, use the SWRO process.
2.5. Water Withdrawal Rules
2.6. Water Withdrawal Scenarios
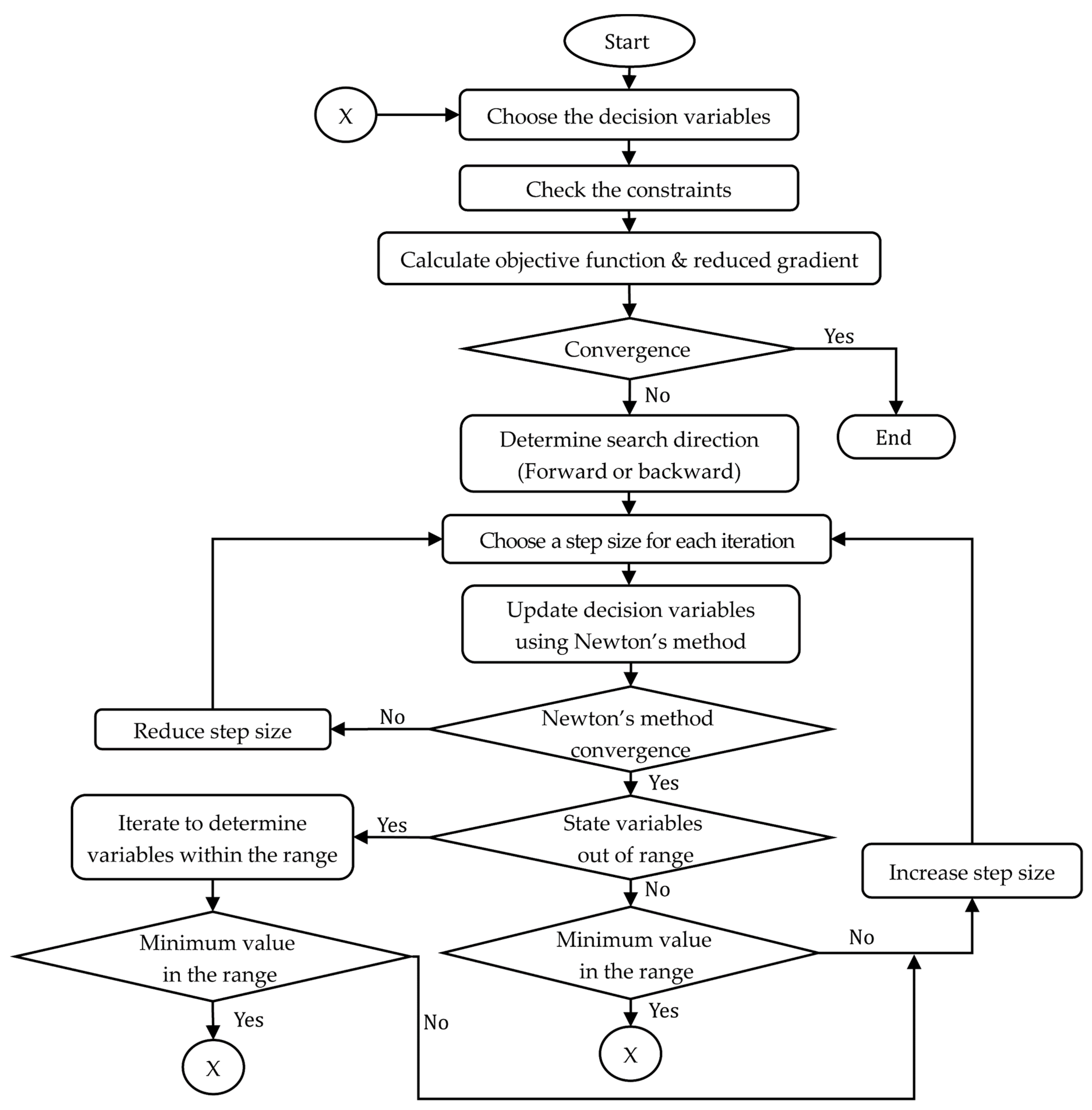
2.7. Generalized Reduced Gradient Algorithm
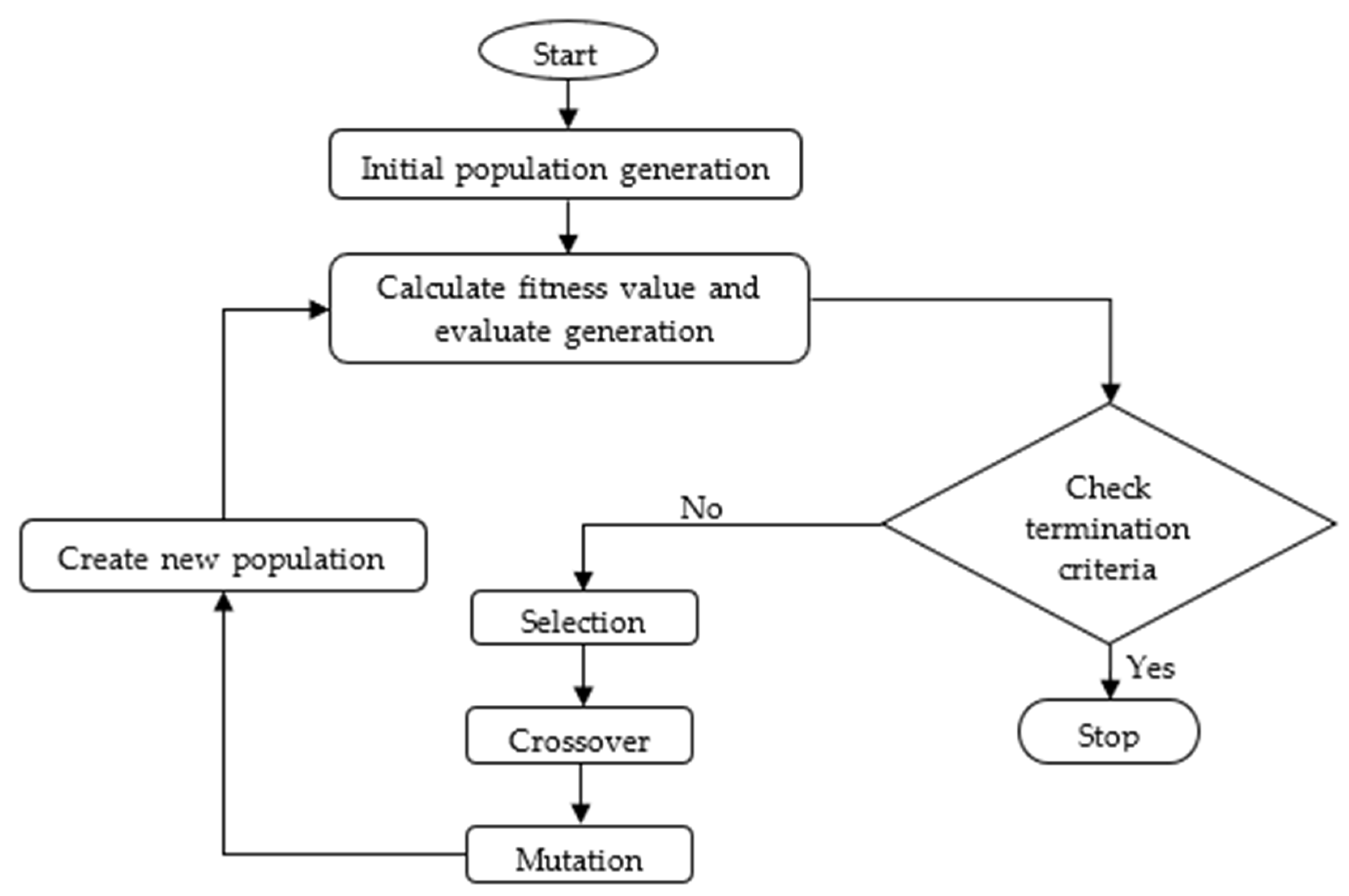
2.8. Genetic Algorithm
2.9. Self-Reliance of the Island Using Locally Available Multiple Water Sources
3. Results and Discussion
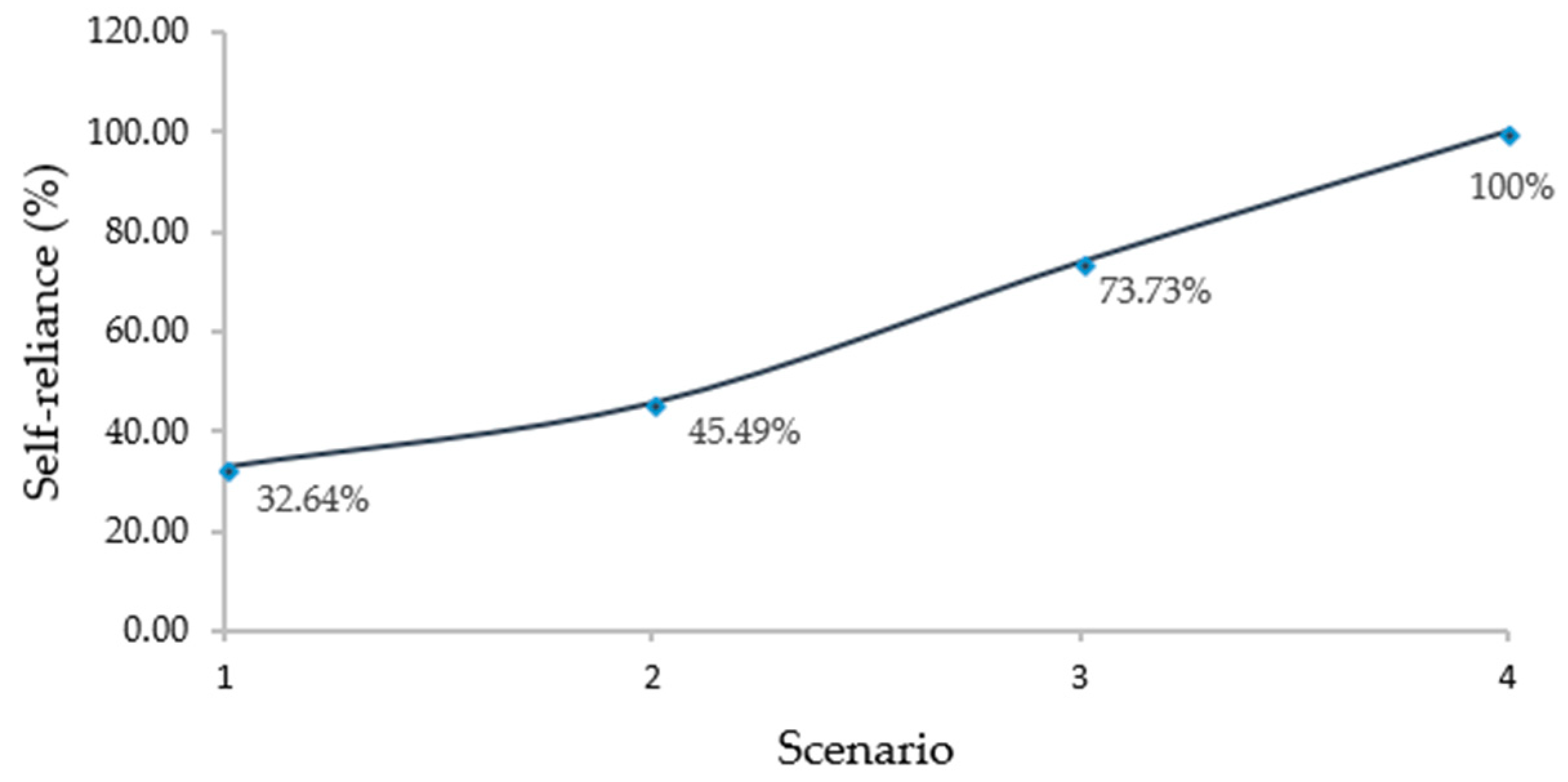
3.1. Self-Reliance (%) from Locally Available Multi-Water Sources in Different Scenarios
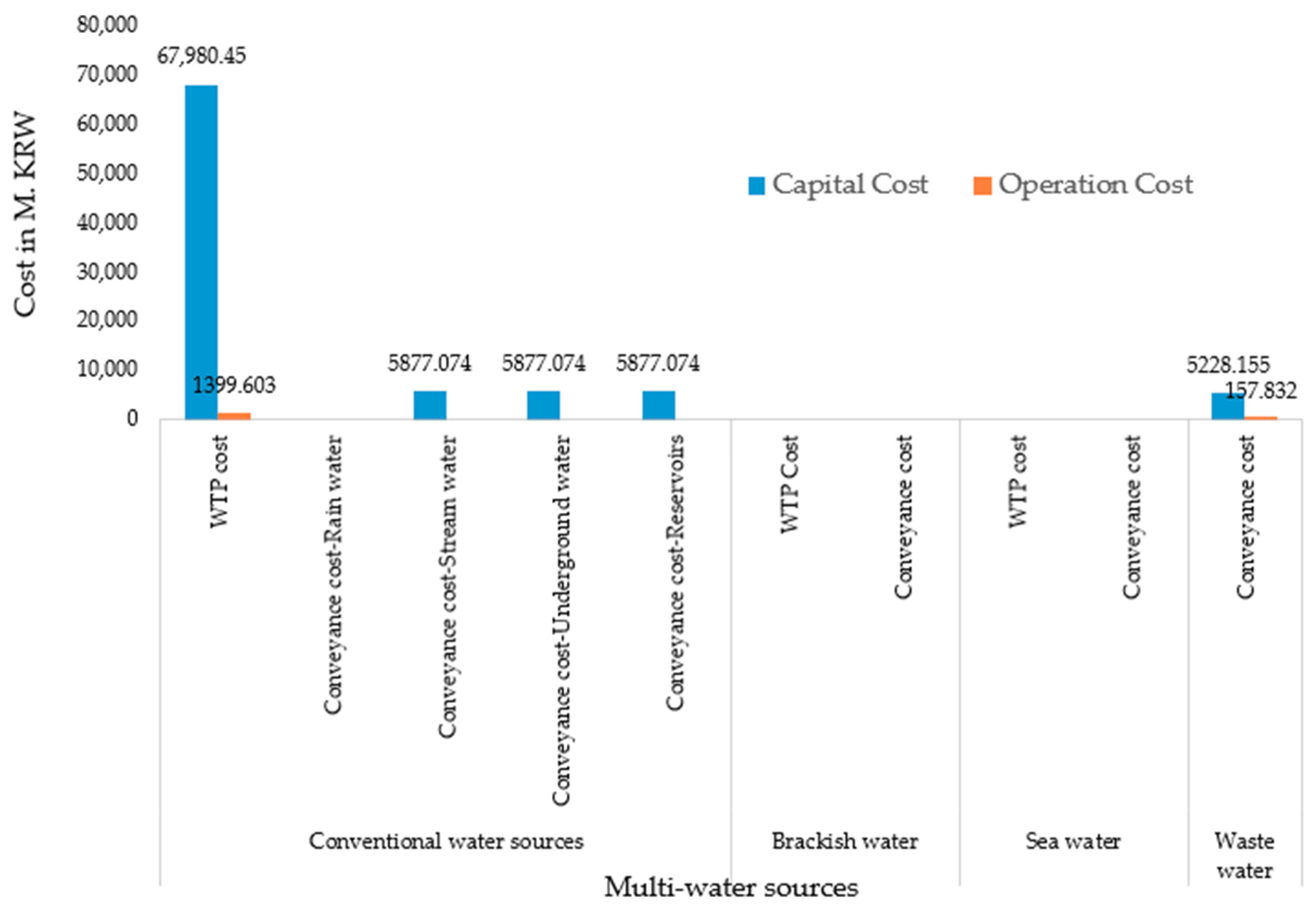
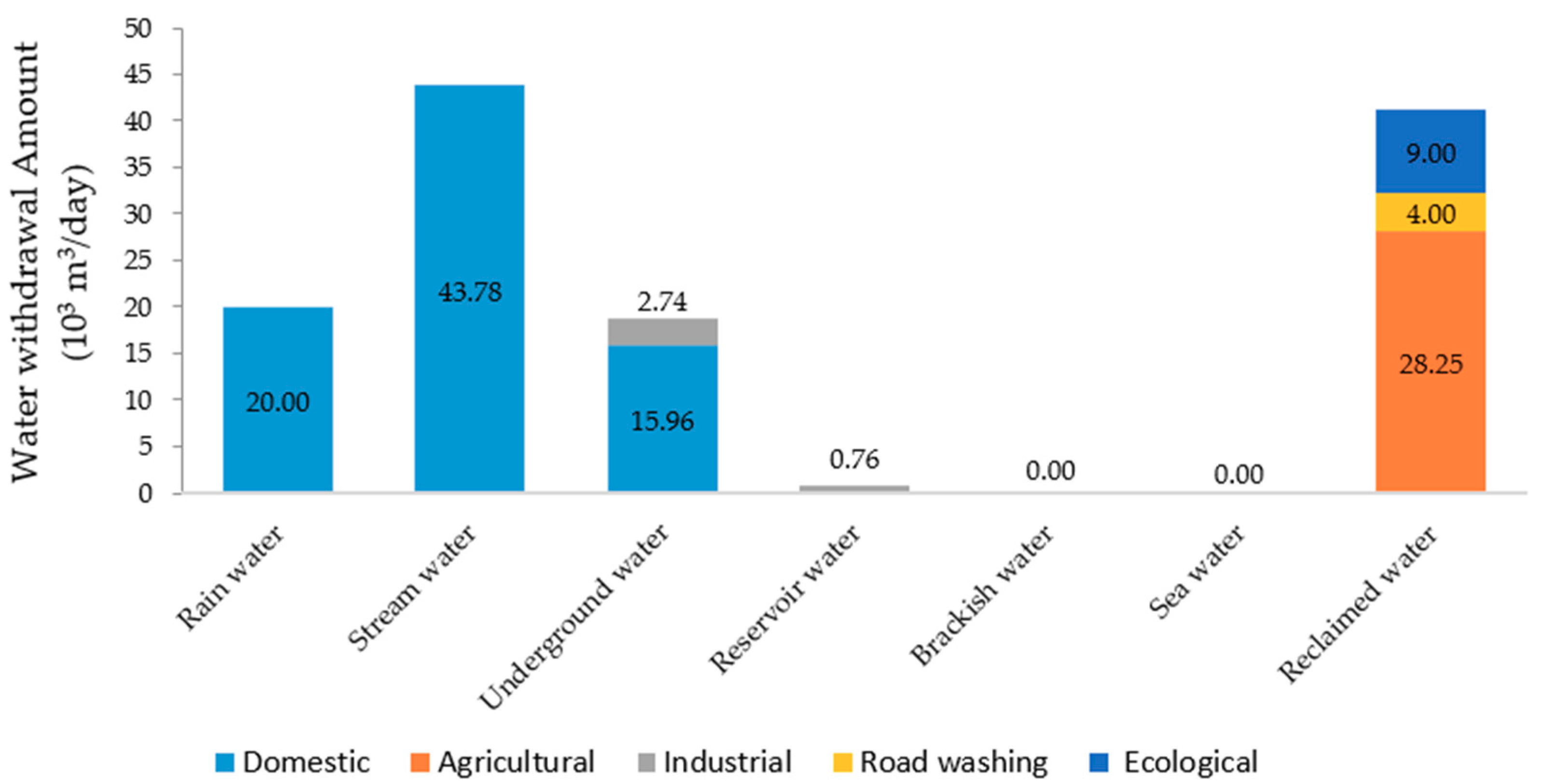
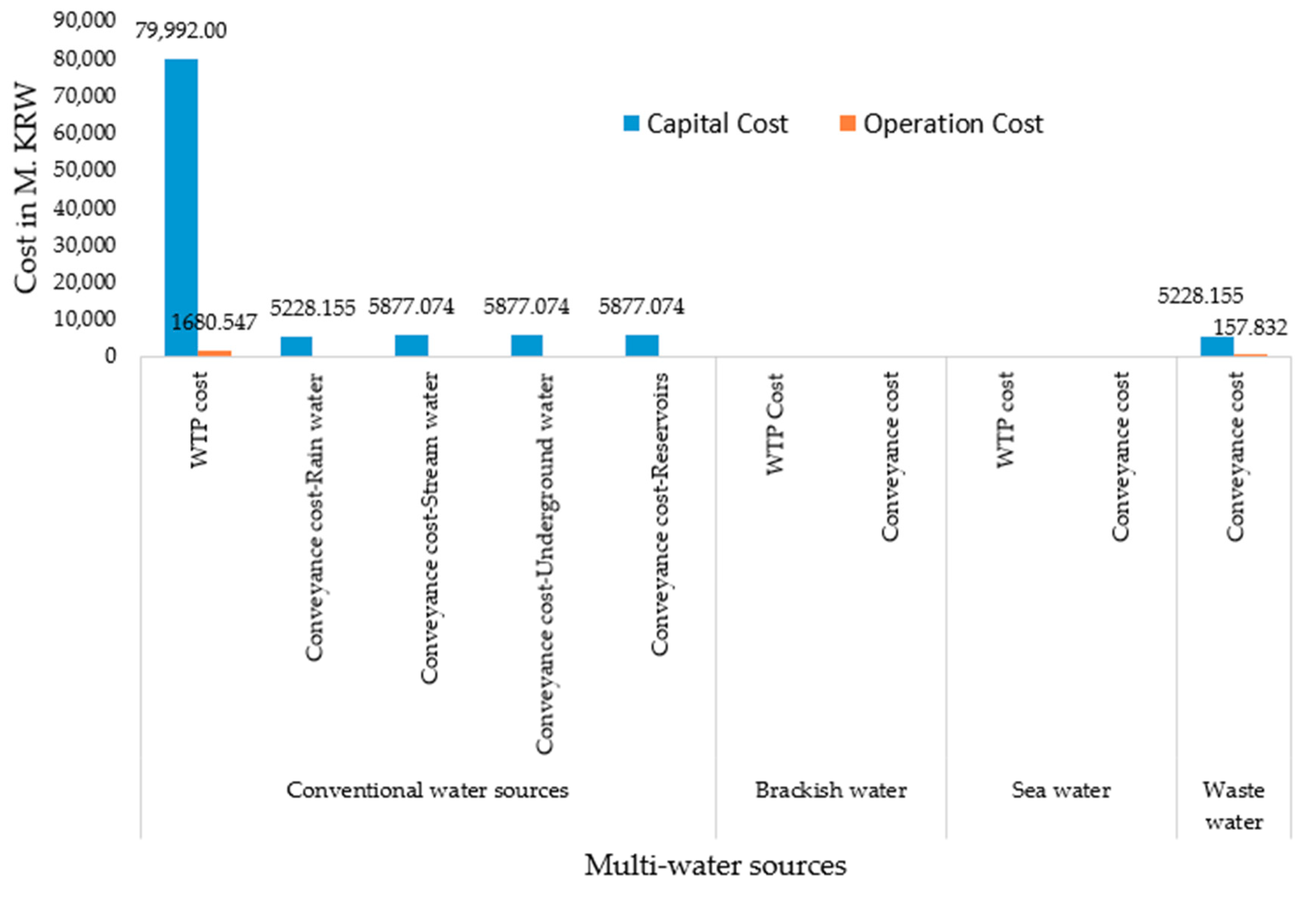
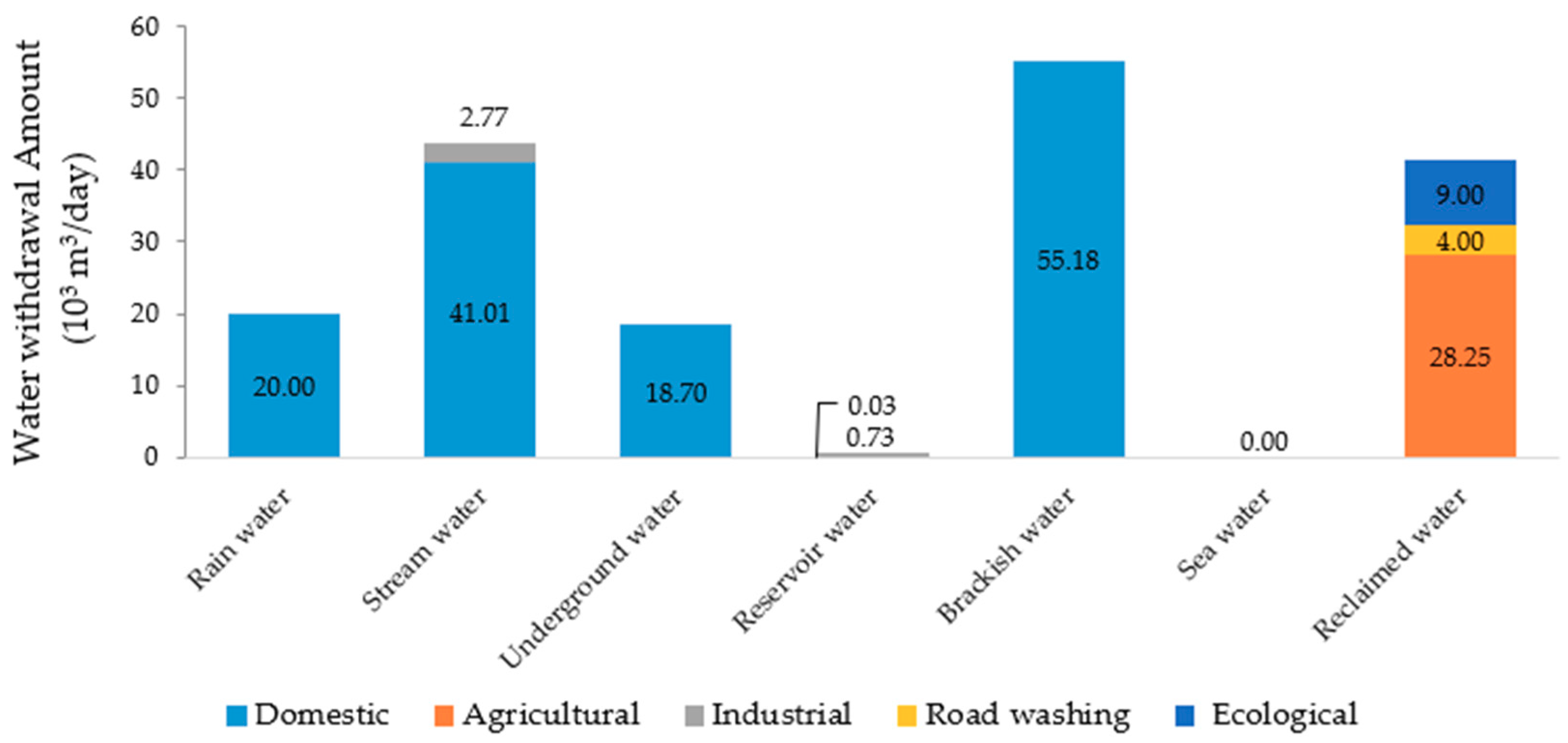
3.2. Optimal Total Cost and Water Withdrawal Scenario for Different Scenarios
3.2.1. Meeting the Demand Without Use of Rain Water, Brackish Water, or Sea Water
3.2.2. Meeting the Demand with Rain Water but without Brackish or Sea Water
3.2.3. Meeting the Demand with Rain Water and Brackish Water, but without Sea Water
3.2.4. Meeting the Demand with Rain Water, Brackish Water, and Sea Water
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Verdaguer, M.; Molinos-Senante, M.; Clara, N.; Santana, M.; Gernjak, W.; Poch, M. Optimal fresh water blending: A methodological approach to improve the resilience of water supply systems. Sci. Total Environ. 2018, 624, 1308–1315. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xiong, W.; Zhang, W.; Wang, C.; Wang, P. Life cycle assessment of water supply alternatives in water-receiving areas of the South-to-North Water Diversion Project in China. Water Res. 2016, 89, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yang, J.; Wan, Z.; Yi, Y. Multi-water source joint scheduling model using a refined water supply network: Case study of Tianjin. Water 2018, 10, 1580. [Google Scholar] [CrossRef]
- Durán-Sánchez, A.; Álvarez-García, J.; del Río-Rama, M. Sustainable water resources management: A bibliometric overview. Water 2018, 10, 1191. [Google Scholar] [CrossRef]
- Choi, I.-C.; Shin, H.-J.; Nguyen, T.; Tenhunen, J. Water policy reforms in South Korea: A historical review and ongoing challenges for sustainable water governance and management. Water 2017, 9, 717. [Google Scholar] [CrossRef]
- Byeon, S.; Choi, G.; Maeng, S.; Gourbesville, P. Sustainable water distribution strategy with smart water grid. Sustainability 2015, 7, 4240–4259. [Google Scholar] [CrossRef]
- Labadie, J.W.; Fontane, D.G.; Lee, J.-H.; Ko, I.H. Decision support system for adaptive river basin management: Application to the Geum River basin, Korea. Water Int. 2007, 32, 397–415. [Google Scholar] [CrossRef]
- Mo, W.; Wang, R.; Zimmerman, J.B. Energy-water nexus analysis of enhanced water supply scenarios: A regional comparison of Tampa Bay, Florida, and San Diego, California. Environ. Sci. Technol. 2014, 48, 5883–5891. [Google Scholar] [CrossRef]
- Abdulbaki, D.; Al-Hindi, M.; Yassine, A.; Najm, M.A. An optimization model for the allocation of water resources. J. Clean. Prod. 2017, 164, 994–1006. [Google Scholar] [CrossRef]
- Han, Y.; Xu, S.-G.; Xu, X.-Z. Modeling multisource multiuser water resources allocation. Water Resour. Manag. 2008, 22, 911–923. [Google Scholar] [CrossRef]
- Huang, G.; Chang, N. The perspectives of environmental informatics and systems analysis. J. Environ. Inform. 2003, 1, 1–7. [Google Scholar] [CrossRef]
- Puleo, V.; Fontanazza, C.; Notaro, V.; Freni, G. Multi sources water supply system optimal control: A case study. Procedia Eng. 2014, 89, 247–254. [Google Scholar] [CrossRef]
- Wei, S.; Yang, H.; Abbaspour, K.; Mousavi, J.; Gnauck, A. Game theory based models to analyze water conflicts in the Middle Route of the South-to-North Water Transfer Project in China. Water Res. 2010, 44, 2499–2516. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Liu, W.; Fu, Q.; Zhang, Y.; Li, T.; Imran, K.M.; Abrar, F.M. Two-stage multi-water sources allocation model in regional water resources management under uncertainty. Water Resour. Manag. 2017, 31, 3607–3625. [Google Scholar] [CrossRef]
- Byeon, S.; Cho, W.; Lee, K.; Hwang, J.W. A Study on Development and Application of Island Type Water Balance Evaluation System. Int. J. Control Autom. 2015, 8, 49–58. [Google Scholar] [CrossRef]
- Park, H.; Woo, D.-S. Decision Support System for Blending of Multiple Water Resources and System Diagnosis in Water Treatment Plant. Int. J. Softw. Eng. Its Appl. 2014, 8, 43–54. [Google Scholar]
- Avni, N.; Eben-Chaime, M.; Oron, G. Optimizing desalinated sea water blending with other sources to meet magnesium requirements for potable and irrigation waters. Water Res. 2013, 47, 2164–2176. [Google Scholar] [CrossRef]
- Kim, J.; Kim, C.S.; Geem, Z.W. A memetic approach for improving minimum cost of economic load dispatch problems. Math. Probl. Eng. 2014, 2014, 906028. [Google Scholar] [CrossRef]
- Geem, Z.W. Economic dispatch using parameter-setting-free harmony search. J. Appl. Math. 2013, 2013, 427936. [Google Scholar] [CrossRef]
- Incheon Water Supply Basic Plan; Waterworks Headquarters Incheon Metropolitan City: Incheon, Korea, 2014.
- Byeon, S.J. Water Balance Assessment for Stable Water Management in Island Region. Ph.D. Thesis, University of Nice Sophia Antipolis, Nice, France, 28 November 2014. [Google Scholar]
- Wittholz, M.K.; O’Neill, B.K.; Colby, C.B.; Lewis, D. Estimating the cost of desalination plants using a cost database. Desalination 2008, 229, 10–20. [Google Scholar] [CrossRef]
- Hwang, M.-H.; Han, D.; Kim, I.S. Estimation of Water Production Cost from Seawater Reverse Osmosis (SWRO) Plant in Korea. J. Korean Soc. Environ. Eng. 2017, 39, 169–179. [Google Scholar] [CrossRef]
- Calculation Standards for Water Supply and Operation Costs; Ministry of Environment: Sejong, Korea, 2015.
- Tarnacki, K.; Meneses, M.; Melin, T.; Van Medevoort, J.; Jansen, A. Environmental assessment of desalination processes: Reverse osmosis and Memstill®. Desalination 2012, 296, 69–80. [Google Scholar] [CrossRef]
- Suk, S. An Estimate of Internal Carbon Pricing of Korean Companies under the Emission Trading Scheme. In Proceedings of the Korea Environmental Economics Association Joint Conference, Chuncheon, Korea, 1–2 February 2018; pp. 185–204. [Google Scholar]
- Wolfe, P. Methods of Non-Linear Programming; McGraw-Hill: New York, NY, USA, 1963. [Google Scholar]
- Duffuaa, S.O.; Shuaib, A.N.; Alam, M. Evaluation of optimization methods for machining economics models. Comput. Oper. Res. 1993, 20, 227–237. [Google Scholar] [CrossRef]
- Lee, H.-T.; Chen, S.-H.; Kang, H.-Y. A study of generalized reduced gradient method with different search directions. J. Quant. Manag. 2004, 1, 25–38. [Google Scholar]
- Lasdon, L.S.; Fox, R.L.; Ratner, M.W. Nonlinear optimization using the generalized reduced gradient method. Rev. Française DautomatiqueInform. Rech. Opérationnelle. Rech. Opérationnelle 1974, 8, 73–103. [Google Scholar] [CrossRef]
- Gabriele, G.; Ragsdell, K. The generalized reduced gradient method: A reliable tool for optimal design. J. Eng. Ind. 1977, 99, 394–400. [Google Scholar] [CrossRef]
- Sakhaei, Z.; Azin, R.; Osfouri, S. Assessment of empirical/theoretical relative permeability correlations for gas-oil/condensate systems. In Proceedings of the 1st Biennial Persian Gulf Oil, Gas and Petrochemical Energy and Environment Conference, Bushehr, Iran, 20 April 2016. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Han, M.; Kim, S. Local water independency ratio (LWIR) as an index to define the sustainability of major cities in Asia. Water Sci. Technol. Water Supply 2007, 7, 1–8. [Google Scholar] [CrossRef]
- Rygaard, M.; Binning, P.J.; Albrechtsen, H.-J. Increasing urban water self-sufficiency: New era, new challenges. J. Environ. Manag. 2011, 92, 185–194. [Google Scholar] [CrossRef]




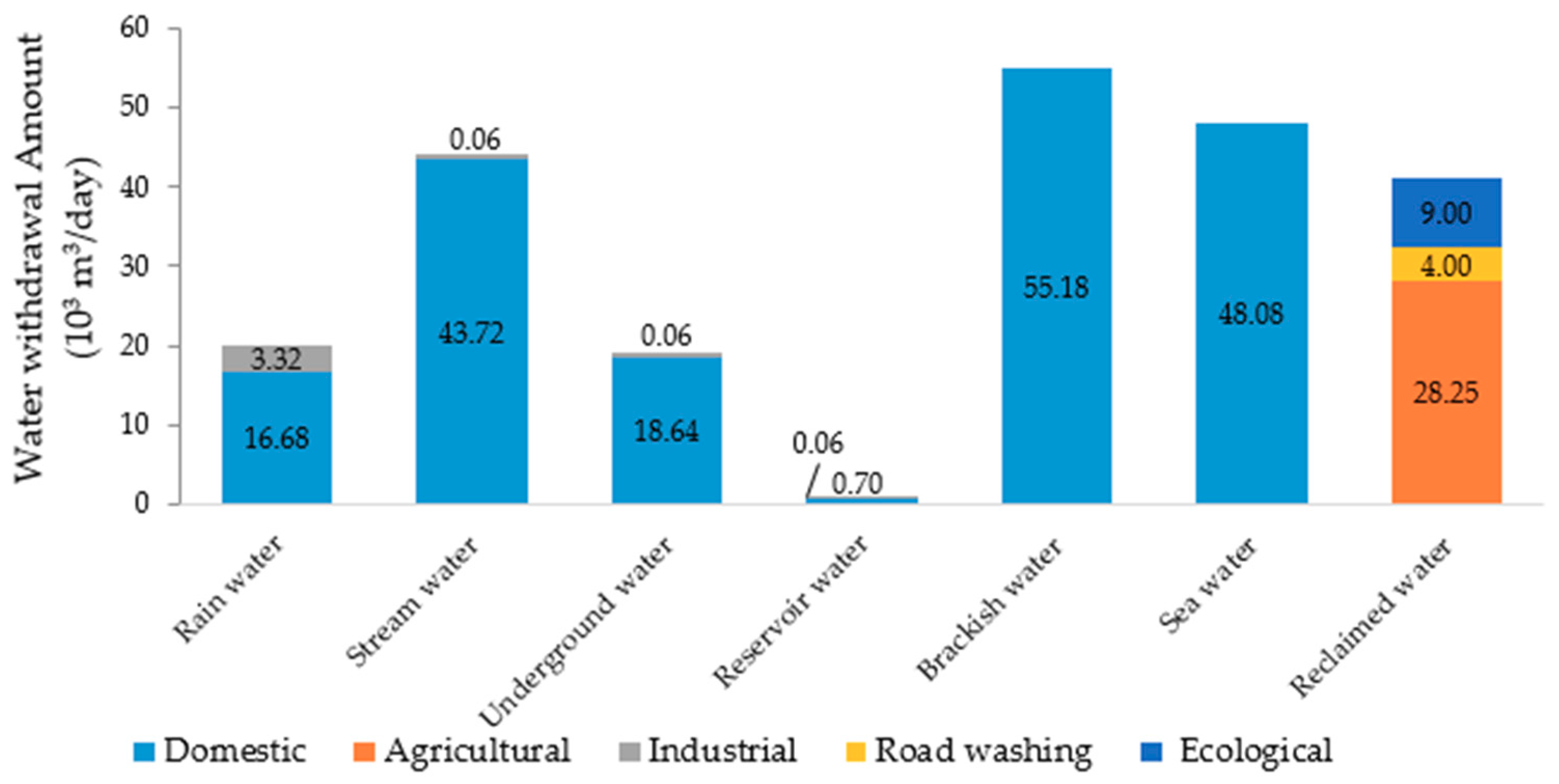
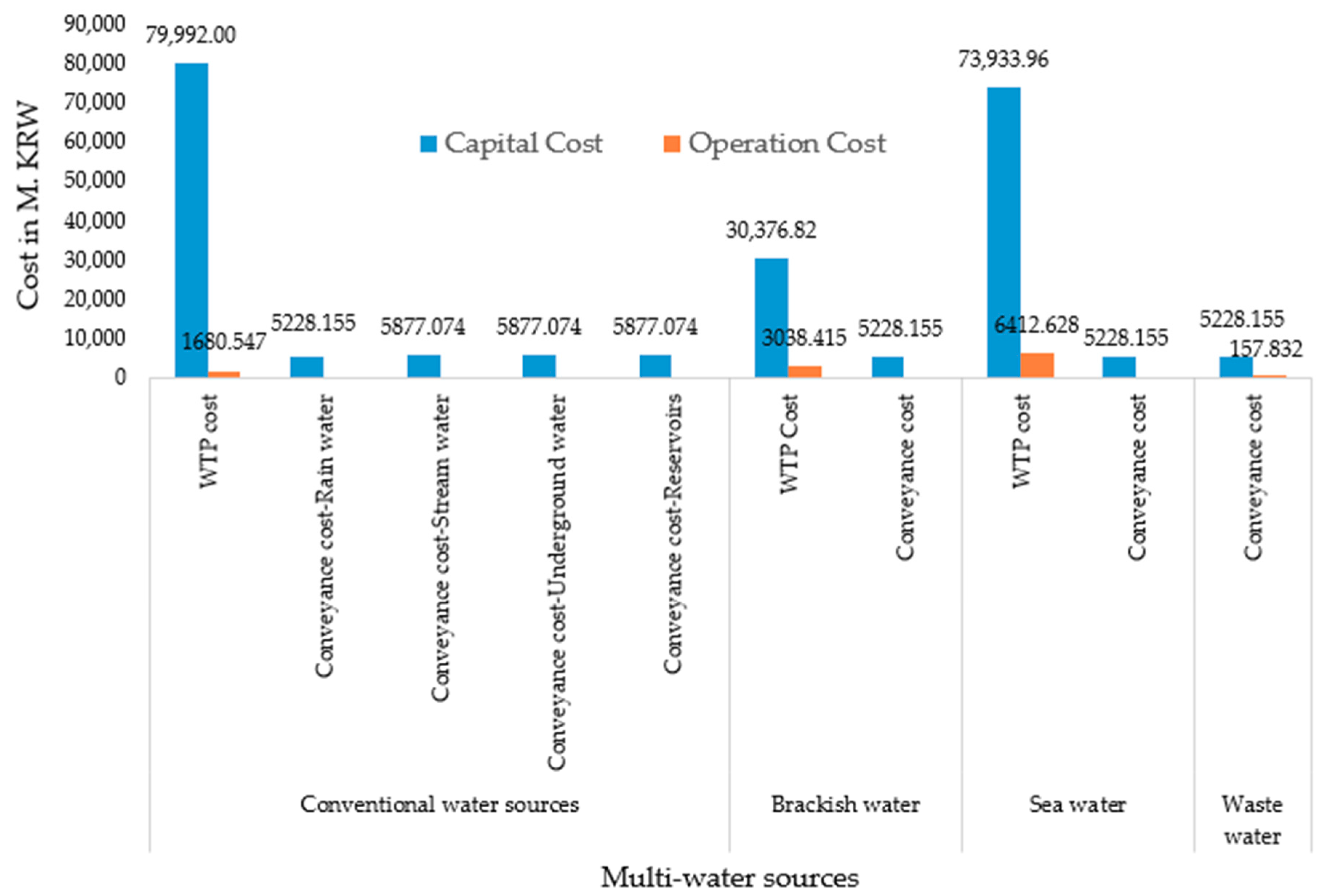
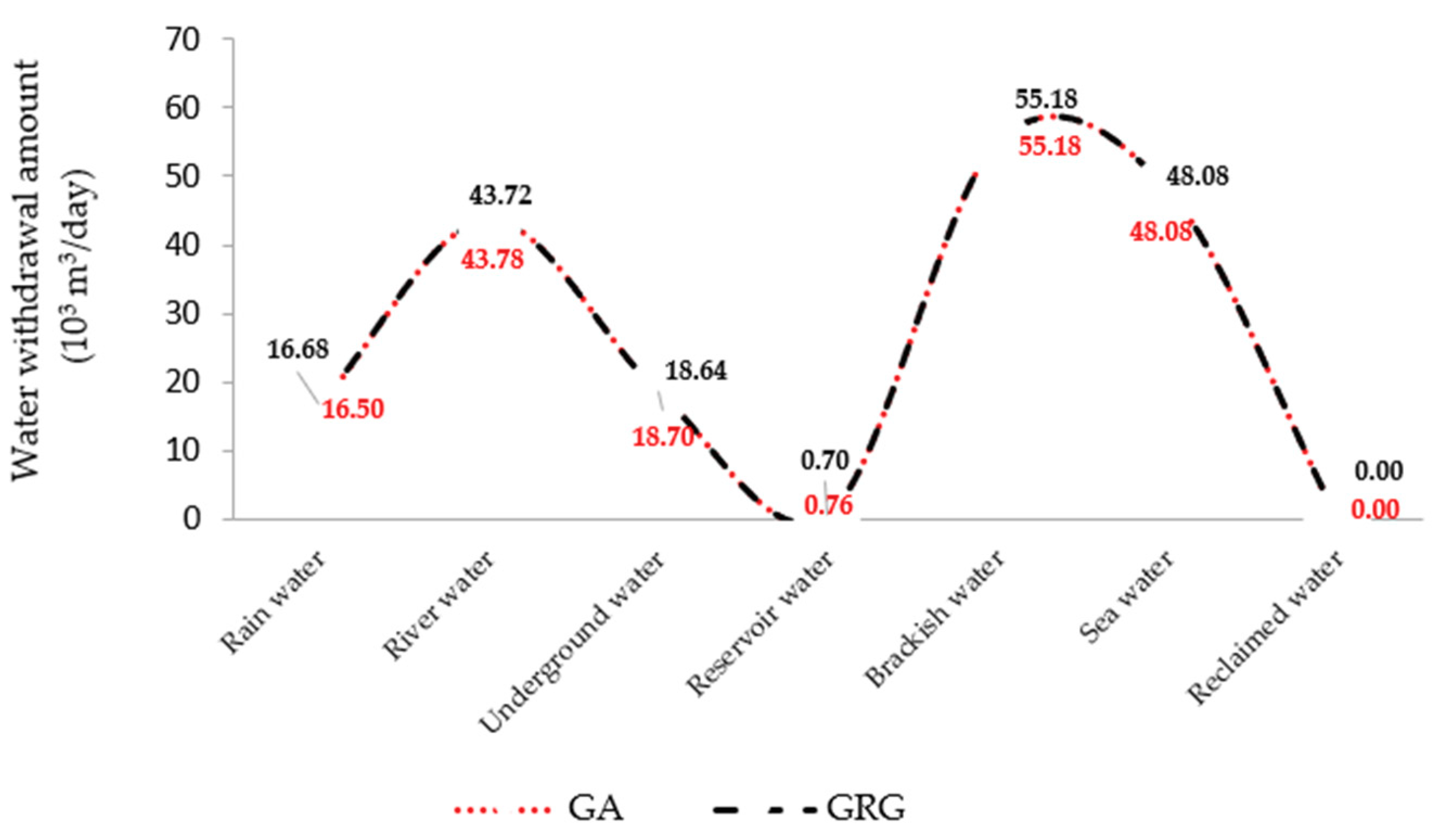
| Type of Water Source | Available Amount of Water (103 m3/day) |
|---|---|
| Rain water | 20 (proposed) |
| Stream water | 43.78 |
| Underground water | 18.7 |
| Reservoir water | 0.76 |
| Brackish water | 55.18 |
| Sea water | 50 (proposed) |
| Recycled water | 121 |
| Type of Water Demand | Predicted Amount of Water Demand for Year 2025 (103 m3/day) |
|---|---|
| Residential (Domestic) | 183 |
| Industrial | 3.5 |
| Agricultural | 28.25 |
| Gardening/Road Cleaning | 4.0 |
| Ecological | 9.0 |
| Water Sources | Water Users | ||||
|---|---|---|---|---|---|
| Domestic | Agricultural | Industrial | Road Washing | Ecological | |
| Rain water | √ | √ | √ | √ | √ |
| Stream water | √ | √ | √ | √ | √ |
| Underground water | √ | √ | √ | √ | √ |
| Reservoir water | √ | √ | √ | √ | √ |
| Brackish water | √ | √ | |||
| Sea water | √ | ||||
| Recycled water | √ | √ | √ | ||
| Type | Multi-Water Sources | ||||||
|---|---|---|---|---|---|---|---|
| Rain Water | Stream Water | Ground Water | Reservoir Water | Brackish Water | Sea Water | Recycled Water | |
| Scenario 1 | √ | √ | √ | √ | |||
| Scenario 2 | √ | √ | √ | √ | √ | ||
| Scenario 3 | √ | √ | √ | √ | √ | √ | |
| Scenario 4 | √ | √ | √ | √ | √ | √ | √ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gnawali, K.; Han, K.H.; Geem, Z.W.; Jun, K.S.; Yum, K.T. Economic Dispatch Optimization of Multi-Water Resources: A Case Study of an Island in South Korea. Sustainability 2019, 11, 5964. https://doi.org/10.3390/su11215964
Gnawali K, Han KH, Geem ZW, Jun KS, Yum KT. Economic Dispatch Optimization of Multi-Water Resources: A Case Study of an Island in South Korea. Sustainability. 2019; 11(21):5964. https://doi.org/10.3390/su11215964
Chicago/Turabian StyleGnawali, Kapil, Kuk Heon Han, Zong Woo Geem, Kyung Soo Jun, and Kyung Taek Yum. 2019. "Economic Dispatch Optimization of Multi-Water Resources: A Case Study of an Island in South Korea" Sustainability 11, no. 21: 5964. https://doi.org/10.3390/su11215964
APA StyleGnawali, K., Han, K. H., Geem, Z. W., Jun, K. S., & Yum, K. T. (2019). Economic Dispatch Optimization of Multi-Water Resources: A Case Study of an Island in South Korea. Sustainability, 11(21), 5964. https://doi.org/10.3390/su11215964







